A SHORT-TERM FORECASTING MODEL WITH INHIBITING NORMAL DISTRIBUTION NOISE OF SALE SERIES

Abstract

In view of the dissatisfactory forecasting capability of standard support vector machine (SVM) for product sale series with normal distribution noises, a new SVM, called g-SVM, with Gaussian function used as its loss function, is proposed. It is theoretically proved that an adjustable parameter of g-SVM is equal to not only the upper bound of the proportion of erroneous samples to total samples but also the lower bound of the proportion of support vectors to total samples; in other words, the number of erroneous samples is fewer than or equal to that of support vectors. A new version of particle swarm optimization (PSO) with the integration of Logistic mapping and standard PSO is proposed for an optimal parameter combination of g-SVM. With the above, a short-term intelligent forecasting method based on g-SVM and the proposed PSO is then put forth. The results of its application to car-sales forecasting indicate that the forecasting method is feasible and effective.

INTRODUCTION

Forecasting is an integral part of a marketing manager's role. Sales forecasts are crucial in order to understand market share and competition, future production needs, and determinants of sales, including promotion, pricing, advertising, and distribution (Frees and Miller 2004).

Product sales forecasting is a complex dynamic process whose duration is affected by various factors, in most of which are of random, fuzzy, and uncertain features. A kind of nonlinear mapping relationship is known to exist between the factors and sales series, but it is difficult to describe it by definite mathematical models. Moreover, the degeneracy is observed among the real sales series, triggered by stochastic errors. Noises existing in the process of data gathering or transmission may or may not be related to sales series. The ideal noise is called white noise, which is the worst estimation of degeneracy. Gaussian noise is a special case of white noise.

Product sales often exhibit strong seasonal variations. Historically, the major research efforts of modeling and forecasting seasonal data have been by traditional means, and many theoretical and heuristic methods have been developed in the last several decades. The available traditional quantitative approaches include heuristic methods, which include nonlinear regression models, the bilinear model (Tuan and Lanh 1981), the threshold autoregressive model (Tong 1983), and the autoregressive heteroscedastic model (ARCH) (Engle 1984). Among these models, the seasonal ARIMA model (Box and Jenkins 1994) is the most advanced forecasting model that has been successfully tested in many practical applications. In addition, it has been verified that the popular Winter's additive and multiplicative exponential smoothing models (Segura 2001) can be substituted by the equivalent ARIMA models. Artificial neural networks (ANNs) have been applied to sales forecasting because of their promising performance in the areas of control and pattern recognition (Kuo 2001). For time series with different complexities, there are optimal neural network topologies and parameters that enable them to learn more efficiently.

Using fewer and shorter series, Tang de Almeida, and Fishwick (1990) agree that for time series with long memory, neural network models and Box-Jenkins models produce comparable results. However, for time series with short memory, Tang, de Almeida, and Fishwick (1990) argue that neural networks (NNs) outperform the Box–Jenkins models. Recently, support vector machine (SVM) as a novel NN technique has gotten much attention in the field of fewer and shorter series (Niu, Wang, and Li 2005). The main difference between NN and SVM is the principle of risk minimization. ANN implements empirical risk minimization (ERM) to minimize the error of the training data. SVM, which seeks to minimize an upper bound of the generalization error instead of the training error, implements the principle of structural risk minimization (SRM) by constructing an optimal separating hyperplane in the hidden feature space. This eventually results in its better generalization performance of SVM than those of other ANN methods. As the training of SVM is equivalent to solving a linearly constrained convex quadratic programming problem, the solution to SVM is always global optimal and absent from local minima. Actually, the solution is determined by only support vectors that are a subset of training data points, so it can be represented sparsely.

However, the standard SVM encounters certain difficulties in real application. Some improved SVMs have been put forward to solve the concrete problems (Sun et al. 2004). Although the standard SVM that adopts ϵ-insensitive loss function has good generalization capability in some applications, it is difficult to deal with the normal distribution noise parts of series. Therefore, this study focuses on just the modeling of a new SVM that can handle the Gaussian noise parts of series.

For combining the principal characteristics of product sale forecasting in manufacturing industries, a short-term sales forecasting model is proposed on the basis of using SVM technology and inhibiting normal distribution noise. First, Gaussian function is used as loss function of the SVM. Then, a new v-SVM with Gaussian loss function is proposed, whose solution is also illuminated in this article. Finally, particle swarm optimization (PSO) with chaotic mapping for optimal the parameters of SVM with Gaussian loss function is proposed.

LITERATURE REVIEW

Forecasting of the future demand is central to the planning and operation of demand business at both macro and micro levels. At the organizational level, sales forecasts are taken as the essential inputs to many decision activities in various functional areas such as marketing, production/purchasing, as well as finance and accounting (Mentzer and Bienstock 1998). Sales forecasts also provide basis for regional and national distribution and replenishment plans. Reliable prediction of sales can improve the quality of business strategy (Chang, Liu, and Lai 2008). The importance of accurate sales forecasts to efficient inventory management at both disaggregated and aggregate levels has long been recognized.

Some classic methods such as ARIMA, Holt-Winter, and ARCH have been applied to sales forecasting (Tang, de Almeida, and Fishwick 1990; Kuo 2001; Chu and Zhang 2003). One of the major limitations of these methods is that they are essentially linear methods. In order to use them, users must specify the model form without the necessary genuine knowledge about the complex relationship in the data. Of course, if the linear models can approximate the underlying data and generate good precision, they should be considered as the preferred models over more complicated models, for linear models have the important practical advantage of easy interpretation and implementation. However, if the linear models fail to perform well in sample forecasting, more-complex nonlinear models should be used. One nonlinear model that has received extensive attention recently in forecasting is the artificial neural network (ANN, or NN; Kuo 2001; Sallehuddin and Shamsuddin 2009; Hartmann 2012). Inspired by the architecture of the human brain as well as the way it processes information, NNs are designed to be capable of learning from the data and experience, identifying the pattern or trend, and making predictions. The popularity of the NN model can be attributed to its unique capability to simulate a wide variety of underlying nonlinear behaviors. Indeed, research has provided theoretical underpinning of NN's universal approximation ability. That is, with appropriate architectures, NNs can approximate any type of function with any desired accuracy (Hornik, Stinchcombe, and White 1989). In addition, few assumptions about the model form are needed in applying the NN technique. Rather, the model is adaptively formed with the real data. This flexible data-driven modeling property has made the NN an attractive tool for many forecasting tasks, as data are often abundant.

The NN can approximate any nonlinear function, but it demands a great deal of training data. In comparison, the SVM proposed by Vapnik (1995) as a novel NN technique can train small samples, thus becoming popular in multiple objective discrete optimization (Aytug and Sayin 2009), supply chain demand forecasting (Carbonneau, Laframboise, and Vahidov 2008), shot transition detection (Cao and Cai 2007), credit risk assessment (Crook, Edelman, and Thomas 2007), product design time estimation (Yan and Xu 2007), pipeline defect prediction (Isa and Rajkumar 2009), crime hot-spots prediction (Kianmehr and Alhajj 2008), and customer churn analysis (Zhao et al. 2007). Its apparent advantage over conventional artificial neural networks is that it can deal with fewer data and provide a global and unique optimum. However, few publications on SVM address the product demand issues concerned (Carbonneau, Laframboise, and Vahidov 2008).

As an implementation of the structural risk minimization (SRM) principle in which the generalization error is bounded by the sum of the training error and a confidence interval term depending on Vapnik–Chervonenkis (VC) dimension, SVM has attracted many researchers in fields from machine learning to pattern classification for its fascinating properties such as high generalization performance and globally optimal solution (Priore et al. 2010; Aytug and Sayin 2009; Carbonneau, Laframboise, and Vahidov 2008; Cao and Cai 2007; Crook, Edelman, and Thomas 2007; Hua and Zhang 2006; Yan and Xu 2007; Zhao et al. 2007; Zhou, Lai, and Yu 2009; Yang, Lu, and Zhang 2010; Wang et al. 2010). This is because the generalization property of an SVM does not depend on the complete training data but only on a subset thereof, which is the so-called support vectors. In SVM, original input space is mapped into a higher dimensional feature space in which an optimal separating hyperplane is constructed on the basis of SRM to maximize the margin between two classes, in other words, to maximize the generalization ability. Recently, SVM has become a popular tool in time-series forecasting (Carbonneau, Laframboise, and Vahidov 2008) because of its remarkable characteristics such as good generalization performance, local minima absence, and sparse solution representation. However, for some concrete problems, such as time series with normal distribution noises, the standard SVM fails to perform well as a result of its shortcoming of ϵ-insensitive loss function. Thus, a new version of SVM is presented as a feasible solution.

Because the Gaussian function can match the normal distribution noise well and inhibit its effect on the forecasting precision, a v-SVM with Gaussian loss function is formulated herein, which is called g-SVM. Based on the g-SVM, a short-term product sales forecasting method is proposed. The rest of this article is organized as follows. The g-SVM is described next, in the section bearing that title. “Embedded Chaotic Particle Swarm Optimization” provides a new PSO for seeking the optimal parameters of g-SVM. The product sales forecasting method based on g-SVM and the proposed PSO is derived in “The Forecasting Method Based on ECPSO and g-SVM.” In “Application” an application to a car sales forecast is given, and then g-SVMis compared with the standard v-SVM and ARMA. The final section draws the conclusions.

g-SVM

The Gaussian function in many applications of SVM focuses on the field of kernel function, because it is of good learning capability, and it has been used for loss function in some fields as well (Aanen, Berg, and Vries 1992).

Compared with g-SVM, the slack variables of the least square SVM also appear in quadratic term, while it modifies inequality constraints into equality constraints. Under the condition of immovable inequality, the relationships between loss function and normal distribution noise are established in g-SVM. The function inhibiting the effect of normal distribution noise of sale series is considered during its establishment.

Based on the above analysis, we combine g-SVM with Gaussian function, and put forth a new SVM, called g-SVM.

Brief Review of Standard ϵ-SVM

SVM is a data-mining tool for building a model of a given system. The foundations of the SVM have been developed by Vapnik (1995), and the methodology is becoming renowned because of many useful features and promising empirical performance. SVM is a type of optimization technique in which prediction error and model complexity are simultaneously minimized. Let the training samples of a multi-input and single-output model be denoted as follows: , where input data sample represents the total number of training data samples with d input variables, and y _i is the output value of the i-th data vector in the dataset. In SVM for regression models (SVR), the aim is to find a pair w: weight vector with d dimension, b: bias), so that the output of the training vector x can be predicted by the real-valued function:

The goal is to find a function that has at most ϵ deviation from the actually obtained targets, which is called the ϵ-insensitive loss function and introduced by Vapnik (1995) and it can be expressed as:

During the optimization, the loss function does not penalize errors above and below some ϵ, where ϵ is chosen prior to the calculations. Thus, the goal of learning is to find a function with low risk on the test samples. This would mean good generalization. This type of SVR is called ϵ-insensitive SVM, or ϵ-SVM. It utilizes the structural risk minimization (SRM), which is defined as follows:

where R _exp denotes expected risk, R _emp denotes empirical risk, and R _complexity denotes the complexity risk. Similar to the supervised learning of a global model, in which the aim is to minimize the empirical risk, the aim of SRM is not only to minimize the empirical risk but also to find a simple function to minimize the complexity of the model. The flatter the functions, the less complex they are, and the closer they are to the linear functions. The lower the complexity of the SRM, the smaller the weight vector, which represents the complexity term. To ensure the minimum of the weight vector, Euclidian norm is used, in other words, . In mathematical terms, the objective function of ϵ-SVM with regression is as follows (Scholkopf et al. 2000):

where C is a constant variable that determines the trade-off between the complexity of the function and the errors, ϵ is a user defined parameter, which does not penalize the points whose model output deviates less than ϵ value from its actual output, and w and b are unknown values that represent the column vector with d dimensions and bias term, respectively. The slack variables, ξ _i ξ _i  ≥ 0, are introduced into the model to soften the optimization problem and prevent infeasible solutions. The parameters with the (*) index are supplied for the constraints that have negative (positive) error greater than ϵ. The assumption in Equation (1) is that it is possible to find such a function that approximates all training data pairs ( x _i , y _i ) with ϵ precision. The optimization problem is a convex quadratic program, which can be solved by using the well-known Lagrange multiplier method.

g-SVM Model

In the ϵ-SVM approach adopting ϵ-insensitive loss function, parameters ϵ(ϵ ≥ 0) and C(C > 0) are used to solve the optimal problem. Parameter ϵ controls the sparseness of the solution in an indirect way. However, it is difficult to come up with a reasonable value of ϵ without the prior information about the accuracy of output values. Schölkopf et al. (2000) modify the original ϵ-SVM into v-SVM described by Equation (5), where a new parameter v controls the number of support vectors and the points that lie outside of the ϵ-insensitive tube. Then, the value of ϵ in the v-SVM is traded off between model complexity and slack variables via the constant v.

For standard v-SVM, it is difficult to deal with the normal distribution noise of time series. To overcome the shortage of ϵ-insensitive loss of standard v-SVM, Gaussian function is selected as the loss function of v-SVM. The optimal problem inhibiting the normal distribution noise of time series is described as follows:

where C < 0 is a penalty factor, are slack variables, is an adjustable parameter, and ϵ an adjustable tube magnitude parameter. Parameter ϵ appears as the variable of the optimal problem, and its value is given by the final solution.

Problem (6) is a quadratic programming (QP) problem. The steps of its solution are given below.

	Step 1: Suppose the training sample set , where x i ∈ R d and y i ∈ R.
	Step 2: Select the kernel function K, adjustable parameter v, and penalty factor C. Construct the QP problem (6) of the g-SVM.
	Step 3: Define a dual problem by introducing Lagrangian multipliers:
	The Lagrangian multipliers can be determined by solving the problem (7).
	Step 4: For a new input x , construct the following regression function:
	Parameter b can be computed by Equation (9). By selecting the two scalars and , we have
	Parameter ϵ can be obtained by Equation (10) or Equation (11).

Definition 1

If SVM can classify the training sample set , the individual set outside ϵ tube is known as an erroneous sample.

Theorem 1

Let us consider a set of data points , which are independently and randomly generated from an unknown function. Specifically, x _i is a column vector of attributes, y _i is a scalar that represents the dependent variable, and l denotes the number of data points in the training set. The v-support vector machine with Gaussian loss function is used for regression analysis. If parameter ϵ^*, representing the size of the insensitive tube, is not equal to 0, then

1.	Suppose q represents the size of erroneous samples; then v ≥ q/l, namely, v is upper bound of the proportion of erroneous samples to total samples.
2.	Suppose q represents the size of support vectors; then v ≤ q/l, namely, v is lower bound of the proportion of support vectors to total samples.

	Proof. 1. Suppose q represents the size of erroneous samples. Equations (12) and (13) are deduced by the constraint conditions of problem (7) The support vectors of sample points outside ϵ tube meet the following formulation: Then, the following inequality can be established. Therefore, v is upper bound of the proportion of erroneous samples to total samples.
	2. By introducing Lagrangian multipliers, a Lagrangian function can be defined as follows: where are Lagrangian multipliers. Differentiating the Lagrangian function (16) with respect to ϵ, we have

According to the Karush–Kuhn–Tucker (KKT) conditions, when , we have and Equation (17) becomes . Suppose p represents the size of support vectors. Substituting or into , we have

Equation (18) indicates that the proportion (p/l) of support vectors (p) to total samples (l) is not less than v, namely, the parameter v is lower bound of the proportion to the total.

Therefore, when the size of sample points is close to infinitude, viz., is close to the proportion of support vectors to total samples as well as to the proportion of erroneous samples to the total.

It is seen that parameter v can be used to control the magnitude of support vectors and erroneous samples, which makes the theoretical basis for the selection of v. The generalization capability of g-SVM is evaluated by the magnitude of parameter v. It turns out that the generalization capability of v-SVM with Gaussian loss function excels that of ϵ-SVM with Gaussian loss function.

This completes the proof of Theorem 1.

Discussion on Parameters Optimization

Encoded Model and Variables Interval

The searching process of controlling support vector parameter, kernel function constant parameter, and penalty coefficient is a complicated continuous parameter optimization problem. The real code is used to represent the vector . The determination of variables interval is described as follows:

Relevant literature indicates that for a much bigger C, SVM adopting Gaussian kernel function tend to result in “excessive learning” when the constant coefficient of Gaussian kernel function is close to 0. SVM can accurately detach the training sample, but has no generalization capability for test sample. If is close to infinitude, the “lack learning” phenomenon appears in final results, when SVM partitions all training samples into the sort with a relatively large sample. It is obvious that the magnitude of is relative to the distance by means of the analysis of the Gaussian kernel formulation . Varying in the range for much less than the minimal distance among all sample points, is equivalent to , while varying in the range that is much greater than the maximal distance among all sample points is . Therefore, the searching space of can be determined as follows:

During constructing regression equation, penalty coefficient C can restrict the varying range of Lagrangian multiplier [see Equation (7)]. When exceeding a rather large value, C will lose the restriction effect and the corresponding complexity of SVM will reach an allowable supreme level in data space. The experience risk and generalization capability of SVM will change no longer. The mean distance among all sample points is taken as the varying range of parameter C. Thus the searching space of parameter C can be given by Equation (20):

The parameter v controlling support vector magnitude varies in [0, 1] in terms of Theorem 1.

The Design of Fitness Function

Owing to the unknown future data, the accurate forecasting error cannot be computed in a practical forecasting task. In addition, even if the error can be given, for evaluation methods, one forecast only cannot be taken as the final result because of the existing stochastic noise interference. Therefore, the forecasting error should be considered by mean method. For the same forecasting aim, the merits and demerits of the forecasting method can be judged by mean square error (MSE). The forecasting method with bigger MSE is of lower forecasting capacity.

The fitness function is key to seeking an optimal parameter combination in the forecasting task. The MSE is usually used as the fitness function in the following experiment, as described by Equation (21).

where y _i is the real datum from the sample set, is the forecasting datum of y _i , and l is the length of the test sample. Then, the fitness function is

EMBEDDED CHAOTIC PARTICLE SWARM OPTIMIZATION

Several parameters that affect the performance of the SVM seriously need to be designated; some researchers apply the intelligent optimization algorithms to find them (Liu, Zhuang, and Liu 2011). Effective ways to confirm the optimal parameters of the SVM model are still in dire need, for crossover errors commonly exist in the crossover validation method for determination of the penalty coefficient, controlling vector and kernel parameters. To solve the problem, a new PSO with chaotic mapping is proposed that is called the embedded chaotic particle swarm optimization (ECPSO). ECPSO, when utilized to optimize the parameters of g-SVM, can increase the diversity of individuals and searching efficiency.

Standard Particle Swarm Optimization

Similar to evolutionary computation techniques, PSO uses a set of particles representing potential solutions to the problem under consideration. The swarm consists of n particles, each of which has a position and a velocity for , and moves through an m-dimensional search space. According to the global variant of the PSO, each particle moves toward its best previous position and toward the best particle pg in the swarm. Let us denote the best previously visited position of the i-th particle that gives the best fitness value as , and the best previously visited position of the swarm that gives best fitness as .

The change of position of each particle from one iteration to another can be computed according to the distance between its current position and its previous best position and the distance between the current position and the best positions of swarm. Then the updating of velocity and particle position can be obtained by using the following equations:

where is the j-th component of the velocity vector of the i-th particle on the k-th generation, is the j-th component of the position vector of the i-th particle on the k-th generation, and w, the inertia weight, is employed to control the impact of the previous history of velocities on the current one. Accordingly, w regulates the trade-off between the global and local exploration abilities of the swarm. A large inertia weight can facilitate global exploration, whereas a small one tends to favor local exploration. A suitable value of w usually provides balance between global and local exploration abilities and consequently results in a reduction of the number of iterations required to locate the optimum solution. The iteration number is denoted by k, c ₁ is the cognition learning factor, c ₂ is the social learning factor, and r ₁ and r ₂ are random numbers uniformly distributed in the range [0, 1].

Thus, the particle flies through potential solutions toward and in a navigated way while still exploring new areas by the stochastic mechanism to escape from local optima. Because there is no actual mechanism for controlling the velocity of a particle, it was necessary to impose a maximum value on it. If the velocity exceeds the threshold, it is set equal to , which controls the maximum travel distance at each iteration to prevent this particle from flying past good solutions. The PSO is terminated with a maximal number of generations or when the best particle position of the entire swarm cannot be improved further after a sufficiently large number of generations. The PSO has shown its robustness and efficacy in solving function value optimization problems in real-number spaces.

The Improvement of PSO

Similar to genetic algorithm (GA), PSO is a population-based optimization tool. PSO is based on the metaphor of social interaction and communication such as bird flying (Kennedy and Eberhart 1995). Original PSO is distinctly different from other evolutionary-type methods in that it does not use the filtering operation (such as crossover and mutation) and the members of the entire population are maintained through the search procedure so that information is socially shared among individuals to direct the search toward the best position in the search space. It has fast converging characteristics and more global searching ability at the beginning of the run and a local searching near the end of the run. However, it sometimes has a slow fine-tuning ability of the solution quality. On solving problems with more local optima, PSO is more likely to explore local optima at the end of the run (Fan and Zahara 2007; Tasgetiren et al. 2007). To avoid this problem, the improvement on PSO is made as follows: utilizing a chaotic operator (Sun and Deng 2004) to generate a child chaotic population of each initial particle and leading to expand the adjacent searching space of each initial particle.

A most simple chaotic mapping, which was brought to the attention of scientists by May (1976) is Logistic mapping, whose equation is:

where X _n is the n-th chaotic number (n denotes the iteration number), µ = 4.

In the light of the aforementioned chaotic system theory, we propose herein the ECPSO, which consists of two PSOs dwelled in father and child processes, respectively. The local optimal particle is obtained from the child process, and the global one is obtained from the father process. Child chaotic colony of each particle from the child process consists of sequences generated from chaotic mapping. The local optimal particle obtained from the child process substitutes the original particle from the father process whereby it is necessary to make a random choice. This way is intended to improve the global convergence and prevent sticking to a local solution.

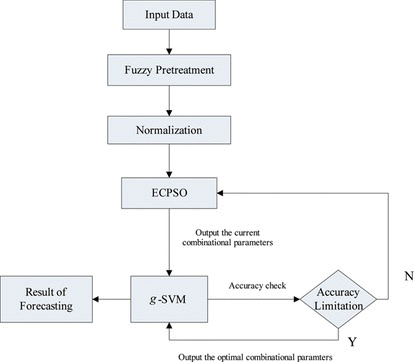
Combining the production forecasting with g-SVM, an intelligent forecasting system can be described as follows: ECPSO optimizes the parameters of g-SVM by training samples. It inputs the optimal parameters into g-SVM, trains the samples, and obtains the support vectors, and then forecasts the sale series, as shown in Figure 1.

FIGURE 1 Forecasting method based on ECPSO and g-SVM. (Color figure available online.)

THE FORECASTING METHOD BASED ON ECPSO AND g-SVM

The Product Sale Influencing Factors

Product sales forecasting is one of the regression forecasting problems in nature. In developing a sales forecast, the first important step is feature selection (new features are selected from the original inputs) or feature extraction (new features are transformed from the original inputs). All available factors can be used as the inputs, but irrelevant or correlated features could adversely impact the generalization performance because of the curse of the dimensionality problem. Thus, it is critical to perform feature selection or feature extraction in sales forecasting.

In our experiments, car demand series are selected from past demand records in a typical company. The detailed characteristic data and demand series of these cars compose the corresponding training and testing sample sets. During the process of the car demand series forecasting, six influencing factors, viz., brand famous degree (BF), performance parameter (PP), form beauty (FB), sales experience (SE), oil price (OP), and dweller deposit (DD) are taken into account.

Data normalization is essential to the performance of SVM. The min-max normalization method is employed to transform the data into the desired range [0, 1] as follows:

where is the result of the normalization, is the input data to be normalized, max (•) is the upper bound of all the j-th components in all input vectors, and min (•) is the lower bound of all the j-th components in all input vectors.

The Product Sales Forecasting Method and Learning Algorithm

The steps of computing the fitness function of ECPSO are listed below:

	Step 1: Initialize the original data by fuzzification and normalization, and then form training patterns.
	Step 2: Select the kernel function K( x,x ′), adjustable parameter v, and the penalty factor C. Construct the QP problem (6) of the g-SVM.
	Step 3: Solve the optimization problem and obtain the parameters . Compute the regression coefficient b by Equation (9).
	Step 4: For a new forecasting task, extract product sales characteristics and form a set of input variables x . Then compute the estimation result by Equation (8).
	Step 5: Compute the fitness function by Equations (21) and (22).

There are two PSOs dwelling, respectively, in father and child processes in the proposed ECPSO. The child process is carried out for n (the number of steps of particles) steps by means of Algorithm 2, and then n optimal chaotic particles are obtained and sent into the father process and substitute the original random particle of the father process. The global optimal particle is given for the father process by means of Algorithm 1.

The ECPSO is described in steps as follows:

Algorithm 1. Embedded Chaotic Particle Swarm Optimization (Father Process)

	Step 1: Data preparation: training, validation, and test sets are represented as Tr, Va, and Te, respectively. Particle initialization and ECPSO parameters setting: number of particles (n), particle dimension (2d), particle position , particle velocity , particle , consisting of particle position and velocity , where , number of maximal iterations (k max), error limitation of the fitness function (obj_lit), velocity limitation ( V max), inertia weight for particle velocity (w), and the constraint scope ([lb j, ub j]).
	Step 2: Set iterative variable: k = 0, and perform the training process from Step 3 to 8.
	Step 3: Call Algorithm 2 for n times, and then produce n particles with the chaotic characteristic and substitute the n initial particles. The new particle swarm consists of the n particles with the chaotic characteristic.
	Step 4: Set iterative variable: k = k + 1.
	Step 5: Compute the fitness function value of each particle of the new particle swarm from Step 3. Take the current particle as an individual extremum point of every particle and do the particle with minimal fitness value as the global extremum point.
	Step 6: Stop condition checking: if stopping criteria (maximum iterations predefined or the error accuracy of the fitness function) are met, go to Step 8. Otherwise, go to the next step.
	Step 7: Update the particle velocity and position by Equations ( 23) and (24) to form new particle swarms, and then go to Step 4.
	Step 8: End the training procedure, and output the optimal particle.

Algorithm 2. Embedded Chaotic Particle Swarm Optimization (Child Process)

	Step 1: Parameters setting: set the particle parameters of child chaotic colony of the i-th particle including the number of particles (m), particle dimension (2d), particle position, particle velocity , particle consisting of particle position and velocity , , number of maximal iterations (sub_k max), error limitation of the fitness function (sub_obj_lit), velocity limitation (sub_V max), and inertia weight for particle velocity (sub_w). Constraint range of is for .
	Step 2: Set iterative variable: sub_k = 0.
	Step 3: Child chaotic particle initialization: normalize initial value of velocity and position of the original particles from the father process into the range [0, 1]. Use the normalized velocity and position of the original particles as X 0 of the chaotic mapping Equation (25), and then generate sequences by Logistic mapping Equation (25) and form a child chaotic colony of the current particle. In other words, obtain the i-th particle from the father process and generate a chaotic particle swarm by chaotic mapping. The substeps are detailed as follows. 1. Transform the i-th particle into the range [0, 1], 2. Generate the current chaotic population of the i-th particle, taking as the starting value of Logistic mapping (25), and then obtain 2d chaotic series with m data points. Population consists of the 2d chaotic series 3. Generate the child chaotic population of the i-th particle, and transform the population into by Equation (28):
	Step 4: Compute the fitness function value of each particle from the child chaotic colony. Take the current particle as the individual extremum point of every particle and do the particle with minimal fitness value as the global extremum point. Stop condition checking: if stopping criteria (maximum iterations predefined or the error accuracy of the fitness function) is met, go to Step 5; otherwise, go to Step 7.
	Step 5: Set iterative variable: sub_k = sub_k + 1.
	Step 6: Update the particle position by Equations (23) and (24) to form new particle swarms, and then go to Step 4.
	Step 7: End the training procedure, and restore the optimal particle into the original constraint range. Output the restored optimal particle.

The steps of a short-term forecasting method based on ECPSO and g-SVM are described as follows:

	Step 1: Initialize the original data by normalization, and then form training patterns.
	Step 2: Select the appropriate kernel function K(x,x′), regularization parameter v and the penalty factor C. Construct the QP problem (6) of the g-SVM.
	Step 3: Solve the optimization problem and obtain the parameters . Compute the regression coefficient b by Equation (9).
	Step 4: For a new forecasting task, extract product sales characteristics and form a set of input variables x. Then compute the estimation result by Equation (8).

Many actual applications suggest that radial basis functions tend to perform well under general smoothness assumptions, so they should be considered, especially if no additional knowledge of the data is available. In this article, Gaussian radial basis function is used as the kernel function of g-SVM.

APPLICATION

In developing an SVM forecaster, the first important step is feature selection (new features are selected from the original inputs) or feature extraction (new features are transformed from the original inputs). In the development of the SVM, all available indicators can be used as the inputs, but irrelevant or correlated features could adversely impact the generalization performance due to the curse of the dimensionality problem. Thus, it is critical to perform feature selection or feature extraction in SVM. In our experiments, car sales series are selected from past sales records in a typical company. The detailed characteristic data and sale series of these cars compose the corresponding training and testing sample sets. During the process of the car sales series forecasting, six influencing factors, viz., brand famous degree (BF), performance parameter (PP), form beauty (FB), sales experience (SE), oil price (OP), and dweller deposit (DD) are taken into account. All linguistic information of influencing factors shown in Table 1 is dealt with by fuzzy comprehensive evaluation (Xu and Ren 2007) and transformed into numerical information.

TABLE 1 Influencing Factors of Product Sale Forecasting

Product characteristics	Unit	Expression
Brand famous degree (BF)	Dimensionless	Linguistic information
Performance parameter (PP)	Dimensionless	Linguistic information
Form beauty (FB)	Dimensionless	Linguistic information
Sales experience (SE)	Dimensionless	Linguistic information
Oil price (OP)	Dimensionless	Linguistic information
Dweller deposit (DD)	Dimensionless	Linguistic information

The proposed g-SVM has been implemented in MATLAB 7.1 programming language. The experiments are run on a 1.80 GHz Core(TM)2 CPU personal computer (PC) with 1.0 G memory under Microsoft Windows XP Professional. The initial father process parameters of ECPSO are given as follows: number of particles: n = 50; particle dimension: 2d = 6; inertia weight: w = 0.9; positive acceleration constants: c ₁, c ₂ = 2; the maximal iterative number: k _max = 100; the fitness accuracy of the normalized samples is equal to 0.0002; The initial child process parameters of ECPSO are given as follows: inertia weight: w = 0.9; positive acceleration constants: c ₁, c ₂ = 2; the maximal iterative number: k _max = 100; the fitness accuracy of the normalized samples is equal to 0.0002. The performance comparison between standard PSO and ECPSO is shown in Table 2.

TABLE 2 Performance of PSO and ECPSO

Algorithm	Iterative number	MSE
		Maximum	Minimum
PSO	8	0.000811549	0.000345837
ECPSO	7(Child process)	0.00071749	0.000378025

It is apparent that chaotic mapping can expand the adjacent searching space of each initial particle. Compared with PSO, ECPSO has better global searching capability and worse searching efficiency. It is obvious that the chaotic mapping operator can improve the global searching performance of ECPSO, compared with the standard PSO. ECPSO gives a better solution than the standard PSO in the same period. Moreover, ECPSO can focus on the neighborhood of an optimal solution more rapidly than the standard PSO. Nevertheless, ECPSO wastes excessive time in searching local optimum in the neighboring field of each particle. The standard PSO has good predominance over the efficiency of obtaining the final solution, which may be the local optimal solution but not the global one, while the ECPSO can obtain the global solution under the condition of excessive time consumption. However, the forecasting task focuses on how the models approximate the original series. Good model parameters promise better forecasting results. The forecasts focus on the approximate capability of the established models under permissive conditions. Thus, ECPSO is considered as an excellent technique to solve the parameter optimization problems of SVM.

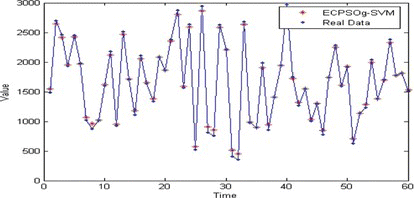
The optimal combinatorial parameters are obtained by Algorithm ECPSO, viz., C = 753, v = 0.86 and σ = 0.028. Figure 2. illuminates the sale series forecasting result given by ECPSO g-SVM.

FIGURE 2 Forecasting results from ECPSOg-SVM model. (Color figure available online.)

To verify the capacity of ECPSOg-SVM based on ECPSO and v-SVM with Gaussian loss function, autoregressive moving average (ARMA), PSOv-SVM based on PSO and standard v-SVM, and ECPSOv-SVM based on ECPSO and standard v-SVM are selected to deal with the above car sales series. Their results are shown in Table 3.

TABLE 3 Forecasting Results from Four Models

No.	Original data	Forecasting value
		ARMA	PSO v-SVM	ECPSO v-SVM	ECPSO g-SVM
1	1508	1656	1527	1520	1506
2	1808	1654	1819	1815	1805
3	1775	1624	1776	1782	1780
4	2382	1642	2329	2356	2378
5	1703	1656	1699	1713	1706
6	1383	1631	1385	1387	1388
7	2042	1656	1991	2010	2025
8	1235	1672	1287	1256	1245
9	1139	1731	1139	1148	1143
10	627	1665	704	685	644
11	1921	1679	1938	1931	1926
12	1589	1641	1605	1598	1591

The indexes MAE, MAPE and MSE are employed to evaluate the forecasting capacity of four models, as shown in Table 4.

TABLE 4 Error Analysis on Four Different Models

Model	MAE	MAPE	MSE
ARMA	352.92	0.3052	209070
PSO v-SVM	106.75	0.0663	82758
ECPSO v-SVM	17.08	0.0150	510
ECPSO g-SVM	6.42	0.0053	67.58

To represent the error trend well, the latest 12 months forecasting results are used to analyze the forecasting performance of the above models. It is clear that the forecasting accuracy given by SVM is better than that by autoregressive moving average (ARMA). The parameters optimized by ECPSO are a better choice to construct SVM model for the car sales series than those by PSO.

The indexes MAPE and MSE provided by ECPSOg-SVM with Gaussian loss function are also better than those of ECPSOv-SVM with ϵ-insensitive loss function, whereas MAE of ECPSOg-SVM is worse than that of ECPSO v-SVM. As a result of the nonlinear influence from multidimensional data, SVM with Gaussian loss function is found capable of handling the data with normal additive noise. As the ECPSO consists of two PSOs dwelled in the father process and the child process, respectively, it consumes more time than PSO does. Because g-SVM also obtains support vector by solving a quadratic programming problem, the runtime of ECPSOv-SVM is close to that of ECPSOg-SVM, that of PSOv-SVM being the shortest.

As is shown in Tables 3 and 4, the selection of loss function is the key to product sales forecasting. The optimal loss function in regression estimation is actually related to the noise in the data. For the normal additive noise, Gaussian loss function is the best choice. Considering the enterprise sale environment, some errors exist inevitably in the process of data collection and estimation. Thus, the above forecasting results are satisfying, and their application in car sales forecasting indicates that the forecasting method based on g-SVM is feasible and effective.

CONCLUSIONS

Product sales forecasting is the foundation of manufactory production planning and inventory controlling. With the increase of product complexity and diversity, enterprises need sales volume to arrange production planning and execute optimal controlling of production costs in the product life cycle. Compared with traditional methods, SVM is more appropriate for the forecasting case with multidimensional, nonlinear small sample featuring product sales series. As confirmed by our study, the SVM with Gaussian loss function proposed in this article can inhibit (penalize) the normal noise effectively and have good generalization property. The performance of the g-SVM is evaluated using the data of car sales, and the simulation results demonstrate that g-SVM is also effective in dealing with uncertain data and finite samples. Moreover, the embedded chaotic PSO algorithm formulated here can also be used by the g-SVM to seek optimized parameters.

Compared with ARMA, PSO v-SVM, ECPSOv-SVM, and ECPSOg-SVM have better MAE, MAPE, and MSE. Bothv-SVM and g-SVM overcome the “curse of dimensionality” and have some other desirable properties, such as strong learning capability for small samples, good generalization performance, insensitivity to noise or outliers, and automatic select of optimal parameters. Furthermore, Gaussian loss function can penalize the normal distribution noises from sample data. Therefore, in the process of establishing the forecasting models, many random errors (noises) of sales data are not ignored but penalized, upgrading the forecasting accuracy by a great deal.

However, as one of the limitations of the study, the complexity of the proposed ECPSO with chaotic mapping has not been fully explored and is sure to fall within the scope of our future research.

Acknowledgments

This research is supported by the National Natural Science Foundation of China under grants 50875046, 60934008, and 60904043. We thank Professor Li Lu for his valuable comments and suggestions.