Abstract
We consider the problem of utilizing a pack of m batteries serving n current demands in electric vehicles. When serving a demand, the current allocation might be split among the batteries in the pack. A battery’s life depends on the discharge current used for supplying the requests. Any deviation from the optimal discharge-current is associated with a penalty. Thus, the problem is to serve an online sequence of current requests in a way that minimizes the total penalty associated with the service.
We show that the offline problem, for which the sequence of current demands is known in advance, is strongly NP-hard and hard to approximate within an additive gap of Ω(m) from the optimum. For the online problem, we present a competitive algorithm associated with the redundant penalty at most m. Finally, we provide a lower bound of 1.5 for the multiplicative competitive ratio of any online algorithm.
Introduction
In the last few years, the idea of electrically powered cars has turned into reality. This old idea, from the early years of the automobile industry in the late 1890s, is now a real alternative to the gasoline powered vehicles (Kirsch Citation2000; Anderson and Anderson Citation2010). Electric vehicles (EVs) are currently considered the next generation of cars in the world of automobiles.
One of the most critical components of EV is the rechargeable battery (Affanni et al. Citation2005). The use of a battery as an energy source raises several issues such as limited driving ranges and high costs. Batteries are very expensive (Delucchi and Lipman Citation2001), thus, it is critically important to extend their lifetimes as much as possible. The battery’s life is affected by the way the current is discharged (allocated), which is the focus of this study. It is important to distinguish between the battery’s capacity and the battery’s life. The battery’s capacity is the amount of energy that can be stored in the battery (and later discharged), that is, the amount of energy of one charge–discharge cycle. The battery’s life is the total amount of energy that can be extracted from all charge–discharge cycles of the battery (MIT Electric Vehicle Team Citation2008). In other words, the battery’s life is the total accumulated energy extracted from a battery during its life.
The EV battery is actually a pack of cells that are connected in serial and in parallel in order to provide the voltage and current required for propulsion. Cells are serially connected in order to provide the required voltage, and the series are connected in parallel to provide the required current. Our work considers the current allocation provided by the individual cell-series in the batteries. For simplicity, we denote each cell-series as a battery. Hence, in the EV pack there are several batteries connected in parallel.
The most dominant factor of an EV battery’s life is the discharge current used. Each battery’s chemistry is designed to be discharged in a specific current, whereas higher or lower currents have negative effects on it (Benini et al. Citation2001b; Pedram and Wu Citation1999; Doyle and Newman Citation1997). Moreover, as demonstrated in (Laman and Brandt, Citation1988), an optimal discharge current exists for each battery and depends on the specific chemistry. Based on these insights, we propose a penalty function that maps each discharge current to a numeric value reflecting its detrimental effect on the battery’s life.
The common discharge method in EV is very simple and naïve: each current demand is supplied using all the batteries in the pack, and the load is equally divided. The rationale behind this method is simplicity of implementation; keep all batteries in the same condition (balanced) assuming that the lower the discharge current, the better. However, as described above, the behavior and performance of a real battery is more complex.
Our Results
Motivated by the possibility of extending the EV batteries’ lives by a smart operation, we propose an advanced online current allocation algorithm. We also analyze the problem theoretically and provide results regarding its complexity status under common theoretical measures.
The performance of a current allocation algorithm is evaluated according to its gap from an optimal allocation, that is, the gap from an allocation that serves all current demands with the minimal possible penalty. We provide hardness results for both the offline problem, for which the current demands are known in advance, and for the online problem, for which the sequence of current demands is unknown in advance. In practice, demands should be served without a priori knowledge of forthcoming demands. Therefore, the main algorithm we suggest is for the online problem. Clearly, all hardness results we provide for the offline problem also capture the online one. For the online problem, we also provide a lower bound on the competitive ratio of any deterministic algorithm.
A formal mathematical description of the problem is given in “Problem Definition.” In “Offline Problem,” we show that the problem of serving the requests with the minimal possible penalty is strongly NP-hard. Moreover, the problem is difficult to approximate within an additive gap of Ω(m) from the minimal possible penalty, where m is the number of batteries in the pack.
We then consider the online problem. In “An Almost Optimal Online Problem,” we suggest a competitive algorithm in which the total penalty might be larger than the minimal possible one by at most an additive gap of m, independent of the number of requests in the sequence and of the initial capacity of the batteries. Our result is optimal, that is, it is associated with the minimal possible penalty for a significant prefix of the sequence—as long as the remaining capacity of the batteries is not below some threshold. Thus, our algorithm is optimal in the sense that it guarantees minimal damage to the batteries’ lives when drivers charge their EV frequently enough and do not wait until the batteries are empty. Finally, in “A Lower Bound for the Multiplicative Competitive Ratio” we provide a lower bound of 1.5 for the competitive ratio of any online algorithm. Recall, an online algorithm has a competitive-ratio c if, for every possible instance, its objective value is within a factor of c from the optimum.
To the best of our knowledge, this work is the first to analyze the problem theoretically.
Our results can be applied to other resource allocation problems in which there are m servers (machines, batteries) that should serve n clients (jobs, current demands). Each client is associated with a request for some amount of resource. A request can be satisfied by several servers, in other words, the service of a request might split. There is a penalty associated with each allocation and the objective is to minimize the total penalty. This general problem appears in many domains. For example, in Human Resources (HR), it is reasonable to allocate tasks to workers such that each worker is assigned a specific workload, and any deviation from this workload causes some penalty, specifically, high workloads conflict with working time regulations, and low workloads might be unprofitable.
Related Work
Battery management and current allocation has been widely studied. Most of the previous work has been aimed at maximizing the battery’s lifetime, that is, the time until the battery is empty and needs to be recharged.
Algorithms for extending batteries’ lifetimes by various discharge allocation schemes were discussed in Benini and coauthors (2001a) and Rao, Vrudhula, and Rakhmatov (Citation2003). Several discharge schemes were proposed, including: (1) serial—discharging of a single battery each time until it is emptied and then discharging the next battery, (2) static switching—discharging of a single battery for a certain amount of time, (3) dynamic switching—discharging of each battery for a different amount of time depending on its physical state (e.g., remaining capacity), (4) parallel—discharging of all batteries together where the workload splits equally. In simulations and lab experiments the static and dynamic algorithms increased the lifetimes of the batteries significantly. In addition, the lifetime of batteries operated by both static and dynamic switching algorithms increased with the switching frequency.
The current demands of EVs are not known in advance and may be estimated using prediction methods based on driving profiles, driving stories, and demands’ histories. In Benini and colleagues (2003), discharge methods among multiple batteries were discussed in which the current requests and their distributions over time are known. We do not deal with this type of problem because we propose an online algorithm.
Problem Definition
The system consists of m identical batteries, , all having the same initial capacity C. There are n current demands, that is, requests for current, given as an online sequence
, where di is the current required to satisfy the ith request. The sequence, and in particular its length n, is unknown in advance, but it is guaranteed that the total capacity of the batteries can satisfy all requests, that is,
.
The ith request can be satisfied in various ways. Any allocation of di from the batteries is acceptable, and there are no constraints regarding the distribution of di among the batteries. However, there are “good” and “bad” allocations because an optimal discharge current exists.
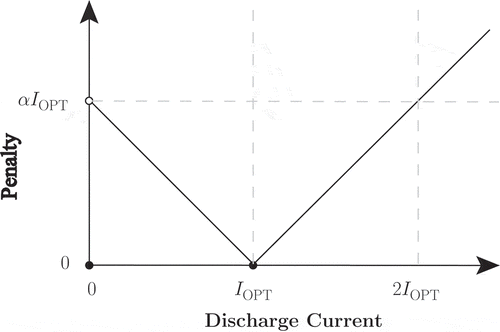
Based on our understanding of the electrochemical properties of the individual cell-series (Benini et al. Citation2001b; Pedram and Wu Citation1999; Doyle and Newman Citation1997), we define a penalty function that reflects the damage to the battery’s life from the discharge current. The actual penalty function depends on the specific chemistry of the battery. However, it is reasonable to assume the following basic structure. Let IOPT be the optimal discharge current whose supply results in maximization of the battery life. The penalty function should fulfill the following conditions.
The penalty for no discharge is 0.
The penalty for supplying IOPT is 0.
All other discharge currents have positive penalty values, according to their distance from IOPT.
We assume the following linear penalty function, described in . Let x be the discharge current, then for some parameter α > 0,
FIGURE 1 The penalty function.
By simple scaling of all demands and capacities, we assume throughout this article, without loss of generality, that IOPT = 1 and α = 1. We denote by the remaining capacity of battery Bj before current demand i. The goal is to determine the values
, where
is the discharge current (allocation) of battery Bj to supply the current demand i.
The Offline Problem
In this section, we consider the case in which all requests are known in advance. Although this is not the case in practice, from the theoretical aspect it is interesting because any hardness result for this model also captures the online problem. The problem can be described as follows.
Hardness of the Offline Problem
We first prove that the offline problem of serving all requests with the minimal possible penalty is strongly NP-hard. Next, we show that it is NP-hard to approximate the minimal possible penalty within an additive Ω(m) factor.
Theorem 3.1
The problem of serving all requests with the minimal possible penalty is strongly NP-hard, even if all current demands are known in advance.
Proof
We show a reduction from the 3-partition problem. The input to 3-partition is a set of n = 3m numbers, in other words, , such that
for all
, and
. The goal is to divide S into m subsets,
, such that
for all
. Each such subset must consists of exactly three numbers. The 3-partition problem is known to be strongly NP-hard (Garey and Johnson Citation1979).
Given S, we construct the following instance of our problem: m batteries, each with an initial capacity of C = 1, and n = 3m current demands, where the ith request is for di.
Claim 3.2
The set S has a 3-partition if and only if the minimum penalty for serving the requests is 2m.
Proof
Given a 3-partition of S, let be the required partition, in other words,
for all
. We serve the requests as follows: for every subset Sj, assume that
, then the corresponding three requests are served from battery j. All requests are less than 1, that is, di ≤ 1, thus the penalty from each is 1 – di. Accordingly, the total penalty for serving requests from battery j is
, and the total penalty for serving all 3m requests, as induced by the m sets is
.
For the other direction, assume that the requests are served such that the total penalty is 2m. Because all requests for current demand are less than 1, the penalty for serving request i is exactly , where
is the number of batteries for which
(that allocate some current to request i). Therefore, the total penalty is
. In order for this sum to be 2m, it must hold that
. Because n = 3m and mi values are nonnegative integer numbers, mi = 1 must be true for all i. In other words, each request is supplied by only a single battery. Also, the range of di, that is,
, implies that exactly three demands are served by each battery. Because the total current demand is exactly the total available energy, that is,
, it must be that for every
, the requests that are served by the jth battery constitute a total demand of exactly C = 1, and the mapping of requests to the batteries that serve them induces a 3-partition.
Our next hardness proof shows that the gap between the total penalty of any efficient algorithm and the penalty of an optimal algorithm is Ω(m). We use an idea suggested in a hardness proof for the problem of packing with item fragmentation (Shachnai, Tamir and Yehezkely Citation2008).
Theorem 3.3
For any m > 1, a set of requests exists such that for some P ≥ 0, the optimal serve of all the requests by m batteries constitute a total penalty P, whereas service of all the requests by m batteries with a total penalty less than is NP-hard.
Proof
Recall that denotes the number of batteries participating in the service of request i, in other words,
.
The proof is based on defining a set of requests: an instance σ, with the following attributes:
(A1) All the requests are small, that is,
for all i.
(A2) In the optimal solution, every request for current demand di is provided by a single battery, or, mi = 1 for all i.
(A3) If
The penalty for any allocation of is
. Thus, the total penalty for serving request i is
. Given that σ fulfills attributes (A1) and (A2), we conclude that the minimal penalty achieved by an optimal allocation is
. Also, by attribute (A3), the total penalty of any efficient algorithm is at least
. Therefore,
.
We now describe the construction of an instance σ that fulfills (A1) through (A3). For this, we assume that the batteries have different initial capacities and that m is even. Later we explain how these assumptions can be removed.
In order to achieve attribute (A3), we use a reduction from the Partition problem. The input for Partition is a set of positive integers with a total size of 2S. The goal is to determine whether a subset
of a total size S exists.
For a given number of batteries m and a given instance of Partition, , construct an instance for the current allocation problem with m batteries and
current demands. The current demands consists of
sets,
each comprising h requests. Let
be an integer. The set R0 comprises requests for current demands
; R1 comprises requests for current demands
, and in general,
Rℓ comprises requests for current demands
. The battery capacities are
and there are two batteries of each capacity. Note that the total required energy is exactly the total capacity of the batteries. Finally, let
. For simplicity of the description, the attributes are described assuming
; this is without loss of generality, because it is possible to scale all demands and capacities by a factor of
.
If a partition of the items in U into two sets of size S exists, then a current allocation fulfilling (A2) exists. Such an optimal allocation serves all the requests of Rℓ by the two batteries with a capacity of SMℓ. Because the total demand of the requests in Rℓ is exactly 2SMℓ and a partition exists, Rℓ can be partitioned into two sets of requests, each set with a total demand of SMℓ, and it is possible to serve all the requests such that every request is served by a single battery.
For the other direction, consider any service of the demands. Because the total required energy is exactly the total capacity of the batteries, for every battery j with SMℓ capacity, holds.
Claim 3.4
If some battery, Bj, serves only full requests, that is, for all i either is 0 or di, then a partition of U exists.
Proof
Assume that for some , a battery Bj with capacity SM j serves only full requests. First, note that no request from a set Rℓ where ℓ > j is serviced by battery Bj. This is true because each such request is larger than SMj (because
). Also, no request from a set Rℓ where ℓ < j is serviced by battery Bj. This is true because the total demand of requests from lower sets, (i.e.,
), is
, which is less than Mj for all
. Therefore, any service of requests from previous sets would prevent battery Bj from supplying all its capacity. This implies that no combination of demands from sets Rℓ where ℓ < j, can be supplied in any allocation in which the total capacity of battery Bj is used. It follows that battery Bj services only those requests from a single set, and by scaling by Mj, this service induces a partition of the original instance.
We conclude that if , then in any allocation provided by an efficient algorithm, every battery will serve at least one partial request. Thus, there are at least m/2 fractions of requests and attribute (A3) holds.
In order to extend the proof to instances with identical batteries, we set the capacities of all 2k batteries to SMk and add two filler requests of size to each set of demands Rℓ. Nonetheless, the total required energy is still exactly the total capacity of the batteries. The two smallest filler requests constitute a total size of
, which is larger than SMk for any M > 2. Therefore, in any allocation of full requests, each battery serves, at most, one filler request. Furthermore, the total demand of a nonfiller request is too small to fully utilize any battery, therefore, any fully utilized battery must serve exactly one filler request. Assume that some battery serves only full requests and let
be the demand of the filler request served by the battery. The rest of the energy is allocated to requests of a total demand SMz and the proof for the different capacity batteries can be applied.
If m is odd, we can add a single request for a current demand of SMk, and setting , we attain an instance to which the above reduction can be applied.
An Almost Optimal Online Algorithm
In this section, we describe an online current allocation scheme that is guaranteed to serve all requests in an instance σ with a penalty of at most . By Theorem 3.3, a lower bound of
also applies to the offline case. Therefore, our algorithm is optimal in the sense that only the constant factor in the additive term might be reduced. Another property of our algorithm is that for a significant prefix of the requests, an optimal allocation is guaranteed. This property implies that our algorithm guarantees minimal damage to the lifetimes of batteries of drivers who charge their EVs frequently enough and do not wait until the batteries are empty. The last demands (i.e., the demands when the batteries are almost empty) turn out to be the most challenging, because the amount of energy left in each battery may be negligable, and an optimal discharge current might not be possible.
The proposed solution distinguishes between two possible statuses of the batteries. As long as the status is AboveTheLine (to be defined later), the service of all requests is associated with the minimal possible penalty. Once the status is not AboveTheLine, our allocation might involve a redundant penalty. However, it is possible to bound this redundant penalty by m.
Algorithm 1 describes the current allocation scheme for a single request. Before serving request i, we sort the batteries in nonincreasing order of remaining capacity: . Ties are broken arbitrarily. For simplicity, because our analysis refers to a single request, di, at a time, we drop the index i whenever it is clear from the context. Specifically, d is the request, Cj is the remaining capacity of the battery Bj with the jth highest remaining capacity before the request, and xj is the current allocated to the request by battery Bj.
The algorithm considers separately different types of requests: (1) small requests—of size d ≤ 1, (2) large requests—of size d ≥ m, and (3) midsized requests—of size . We state that a midsized request for current d has a low fraction if
. Otherwise, the request has a high fraction. Note that a request has a low fraction if and only if
. For example, d = 2.3 has a low fraction, whereas d = 2.8 has a high fraction. For each type of request, the algorithm first tries to fulfill the request with the minimal possible penalty. If such an allocation is impossible, an allocation associated with some redundant penalty is determined.
In some cases, the algorithm calls the procedure GreedyAllocation, given in Algorithm 2. In this procedure, the allocation is done greedily from the battery with the lowest remaining capacity, moving to the next lowest battery when the first battery is emptied. Note that the order of the batteries is determined when Algorithm 1 is called and is not modified as a result of allocations done before GreedyAllocation is called.
In some cases, the algorithm allocates current in a balancing way among a selected set of batteries. That is, the current is allocated from the batteries in the set that have the highest remaining capacity, such that , while trying to balance the remaining capacities in the set after the allocation. This can be done by first allocating from battery B1, until C1 = C2, then allocating evenly from both batteries B1, B2, and so on, until the whole demand is allocated.
The batteries’ status before request i is defined as follows. Recall that the batteries are sorted in nonincreasing order of remaining capacity (i.e., ).
Table
Table
Definition 4.1
If and
for every j > 1, then the batteries’ status before request i is AboveTheLine.
The analysis of the algorithm is based on several observations. First, we show that as long as the batteries’ status is AboveTheLine, then the service of all requests is associated with the minimal possible penalty. Next, we bound the total possible penalty once the batteries’ status is not AboveTheLine.
Lemma 4.1
As long as the batteries’ status is AboveTheLine, the service of all requests is associated with the minimal possible penalty.
Proof
Consider a current demand, d, and use to denote the minimal possible penalty for supplying it.
If d ≤ 1, then , achieved by allocating all current from a single battery—as in our algorithm (line 4). If d ≥ m, then
, achieved by allocating at least 1 from each of the m batteries. Such an allocation is done in our algorithm (lines 10–11). Because the status is AboveTheLine (i.e.,
for every j ≥ 1), the two above allocations are possible.
If , then the minimal possible penalty is the distance of d from the nearest integer, given by
. In both cases, this value is at most 0.5. If the request has a low fraction, then penalty
can be achieved by allocating at least 1 from
batteries. If the request has a high fraction, then penalty
can be achieved by allocating at least 0.5 and at most 1 from
batteries. Such allocations are done in our algorithm (lines 18–19 and 31–32 respectively). Note that because the status is AboveTheLine (i.e.,
and
for every j > 1), the above allocations are possible. Therefore, if the batteries’ status before the allocation is AboveTheLine, then it is always possible to follow the suggested allocation, which is associated with the minimal possible penalty.
We conclude that the algorithm might cause a redundant penalty only when the batteries’ status is not AboveTheLine. In order to bound the total redundant penalty, we first bound the gap between the remaining capacities of any pair of batteries.
Claim 4.2
For any request i and two batteries, j, j’, .
Proof
The proof is by induction on the number of requests serviced, that is, on the value of i. Initially, before the first request (i = 1), all capacities equal C and the claim is clearly valid. Assume that the claim holds before the allocation of the ith request, we show it is valid also afterward. Let S denote the set of batteries allocating current to the ith request, that is, if and only if
.
Consider first the case that the batteries’ status is AboveTheLine, where the only relevant allocations are in lines 4, 10–11, 18–19 and 31–32. If both , then clearly the remaining capacities do not change and the gap between the remaining capacities remains the same. If both
, because the only relevant allocations are done in a balancing way, the gap between the remaining capacities can only decrease. If
and
, then it must hold that
and
. In this situation the maximal allocation of each battery is less than 1.5, as can be easily verified. In addition, because the allocations are done from batteries with high capacities, the (absolute) gap between the remaining capacities can only decrease.
When the batteries’ status is not AboveTheLine, either the maximal capacity of a battery is less than 1.5, which clearly implies that the maximal gap is less than 1.5, or the minimal capacity of a battery is less than 1. It is easy to verify that, in this case, either the maximal allocation of any single battery is 1.5 and the allocation is done from batteries with high capacities, or the algorithm allocates at least 1 from any battery with capacity at least 1 before allocating (greedily) current from the batteries with the low capacity.
We are now ready to bound the total redundant penalty after the batteries’ status is not AboveTheLine.
Theorem 4.3
The total penalty of the algorithm might be larger than the minimal possible penalty by at most m.
Proof
Let denote the minimal possible penalty and the penalty caused by the algorithm for servicing the ith request, respectively. Let
denote the redundant penalty, which occurred in the service of request i, and ei denote the number of batteries emptied as a result of servicing request i. Finally, let m′ denote the number of batteries with a positive remaining capacity after all requests are served, in other words,
. We show that
by showing that
. By Lemma 4.1, as long as the batteries’ status is AboveTheLine,
holds. Therefore, we need to bound the redundant penalty after the batteries’ status is not AboveTheLine. The batteries’ status is not AboveTheLine if one of the two following conditions is valid (1)
, (2)
and
.
Our analysis is based on combining the following three claims, whose proof follows.
Whenever condition (1) is valid,
Condition (2) might be valid only for a single request for which
Either m′ > 0, or for the last request, ei > 0 and
Claim 4.4
If and
, then
.
Proof
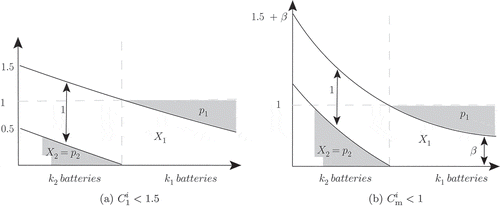
Except for one case (detailed as follows), redundant penalty is caused only when GreedyAllocation is called. Assume that GreedyAllocation allocates current from k1 batteries for which , and k2 batteries for which
(see ). Denote by K1, K2 the corresponding sets of batteries; by X1, X2 the total current allocated by GreedyAllocation from K1, K2, respectively; and by p1, p2 the total penalty for K1, K2, respectively.
FIGURE 2 Cases when the batteries’ status is not AboveTheLine.
Our analysis distinguishes between different possible values of di. If , then
. Note that k2 > 0 is impossible in this case, because a small request will be serviced optimally if some battery has remaining capacity of at least 1. Thus, the algorithm allocates di greedily from K1, of which at least k1 – 1 batteries are emptied. Thus, X1 = di and
. We find that
, or,
.
If and di has a low fraction, let
. It holds that
. The algorithm might have a redundant penalty in two cases:
If
If
If and di has a high fraction, let
. It holds that
. If k2 = 0, then the algorithm allocates
greedily from K1, of which at least k1 – 1 are emptied. Note that
. Thus,
. We find that
, that is,
. If
, then, as explained in the low-fraction case,
, thus,
, in other words,
.
If , then, by definition of the penalty function, we have
. It must hold that
because some battery must allocate more than 1 in order to fulfill a large request. By the algorithm, an initial allocation of 1 is determined for each of the k2 batteries before GreedyAllocation is called (in line 13). Because
, each such battery allocates in the greedy phase at most 0.5. The total penalty is, therefore,
. All batteries participating in GreedyAllocation, except perhaps the last one, are emptied, thus,
. If
, then
, and we are done.
If , then it must be that no battery was emptied before request i is serviced, in other words,
, as otherwise the remaining m – 1 (or fewer) batteries have total remaining capacity at most
and cannot fulfill a large request. This implies that
and
batteries allocates 1 to di before GreedyAllocation is called (in line 13). Thus,
. Also,
. Finally, because the single battery in K2 allocates at most 0.5 in the greedy allocation,
. Together with the fact that
, we get
, implying
. Combining the above,
, and
. Note that
as otherwise
and the allocation is optimal.
Next, we consider the case in which the batteries’ status is not AboveTheLine when and
. We bound the redundant penalty in this case and also show that the algorithm might accumulate a redundant penalty at most once before the condition
holds.
Claim 4.5
If and
, then
and
.
Proof
First note that when , the condition in line 21 is not valid and redundant penalty might be caused only by GreedyAllocation. By Claim 4.2, if
, then
. Assume that GreedyAllocation is called. According to the algorithm, this happens only after we set to 1 the allocation of each of the
batteries with
(lines 13, 25, 34). Thus, as a result of such an allocation, the remaining capacity of all batteries is less than 1.5, and in particular
.
Claim 4.2 also implies that because , no battery was emptied before request i is serviced, that is
. Let
. By Claim 4.2,
(see ). We have
, thus,
. Each K2 battery has capacity at most
and allocates an initial allocation of 1 before GreedyAllocation is called. Thus, the maximal penalty for each battery in K2 is
and
. Summing up,
. The number of emptied batteries is at least
. If
or
, then
.
If and
, we analyze separately different values of di. Because GreedyAllocation is called after allocating 1 from each of the
batteries with
, we have
. Moreover, because no battery is empty and
we have that
. Therefore,
If , let
.
. By Equation (2), we have
. Thus,
. Also,
. We conclude that
. Because
, it holds that
, thus,
, implying
.
If , then by Equation (2),
, implying
. We have
. Because
, it holds that
, thus,
implying
.
Finally, note that if , then because
, the algorithm is optimal.
Combining Claims 4.4 and 4.5, we find that for all requests for which , except perhaps for one, it holds that
. In addition, we have that for a single request, the one for which GreedyAllocation is called when
, it might be that
. To complete our analysis, we show that this gap of 1 is closed by the last request. In the proof below we assume that when the last request is supplied
, because otherwise, the scenario handled in Claim 4.5 never happens and there is no gap to bridge, that is, before the last request
.
Claim 4.6
Either , or for the last request,
and
.
Proof
If all batteries are emptied, then the last request empties the last battery. Assume that greedy empties k1 batteries for which , and k2 batteries for which
. The proof is identical to the proof of Claim 4.4—recall that
. The analysis in the proof of Claim 4.4 refers to
. Formally, it is shown that when
, it holds that
. When batteries are emptied,
, therefore, for the last request,
.
We conclude that either the last battery is not emptied, or, if it is emptied, for at least one request (the last one), at least one battery is emptied with no redundant penalty. This compensates for the additional penalty the algorithm might have accumulated when (discussed in Claim 4.5). Summing up, the total redundant penalty of the algorithm is, at most, m.
A Lower Bound for the Multiplicative Competitive Ratio
A more common performance measure of the online algorithm’s quality is its competitive ratio, defined as the maximal possible ratio between the algorithm’s objective value and an optimal one. In this section, we show that, according to this measure, no algorithm can be better than 1.5 competitive. Formally,
Theorem 5.1
For every online algorithm, ALG, a sequence of requests σ such that exists.
Proof
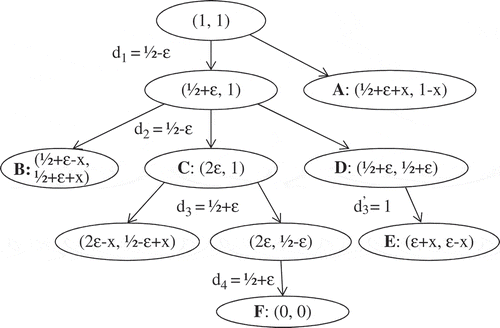
Consider an instance with m = 2 batteries with an initial capacity C = 1. The sequence σ is constructed by the adversary as a response to the behavior of the algorithm. The possible sequences, provided by the adversary, and the possible allocations of the algorithm are described in . Every node corresponds to a possible configuration of the batteries and is described as a vector of the remaining capacities.
FIGURE 3 Possible behavior of an online algorithm and the adversary.
The first request presented by the adversary is for . If the algorithm splits the service between the two batteries (configuration A in the figure), then
, whereas
. In this case, the adversary halts; the whole sequence is a single request, and the competitive ratio is arbitrarily close to 3 (by fixing ε → 0).
If the algorithm supplies the whole first request from a single battery, without loss of generality, from B1, then the adversary proceeds with . The algorithm can choose one of three options: split the service (configuration B), provide the whole request from battery B1 (configuration C), or provide the whole request from battery B2 (configuration D).
If the algorithm chooses to move to configuration B, the adversary halts. The penalty for the second request is . In addition to the penalty for the first request, the total penalty is
, whereas an optimal service has penalty
. The competitive ratio is arbitrarily close to 2.
If the algorithm chooses to move to configuration D, then the adversary proceeds with . The algorithm must serve the request
from both batteries (configuration E) with total penalty for the whole sequence
. An optimal service for this sequence (reaching configuration C and providing the whole request
from battery B2) would incur a penalty of
. The resulting competitive ratio is arbitrarily close to 2.
We are left with the case in which the algorithm chooses to move to configuration C. The adversary proceeds with . If the algorithm splits the service (left node of C), the penalty for the last request is 1.5 – ε and the total penalty for the whole sequence is
, whereas an optimal service for this sequence (providing the whole request d3 from battery B2) would incur a penalty of
. The resulting competitive ratio is arbitrarily close to 2.5, and larger than 1.5 for any ε ≤ 0.5. Otherwise (right node of C), the adversary proceeds with a final request
. The algorithm must move to configuration F. For the whole sequence the penalty is
, whereas an optimal service of this sequence (through configuration D) would incur a penalty of
. Thus, the competitive ratio for this scenario is 1.5.
We conclude that for any behavior of the algorithm, the adversary can proceed in a way that guarantees .
Discussion and Open Problems
This article presented studied the problem of utilizing the pack of batteries serving current demands in Electric Vehicles. We formulated the problem as a combinatorial optimization problem, provided hardness results that are valid even for the offline scenario, and suggested an efficient, almost optimal online algorithm. Several important problems remain open:
Consider additional penalty functions. In particular, nonlinear penalty functions as well as penalty functions that are not symmetric around the optimal discharge current.
Our algorithm (“An Almost Optimal Online Algorithm”) is guaranteed to have a redundant penalty of, at most, m. On the other hand, it is NP-hard to guarantee a redundant penalty lower than 0.5m, even in the offline case (Theorem 3.3). Can this gap be closed?
Consider the combination of several different battery packs in a single EV, each having its own optimal discharge current.
Additional problems arise when the model is extended to consider additional parameters such as battery temperature and other environmental effects. A totally different direction is to study adaptive switching algorithms that are based on learning the driver’s driving pattern.
REFERENCES
- Affanni, A., A. Bellini, G. Franceschini, P. Guglielmi, and C. Tassoni. 2005. Battery choice and management for new-generation electric vehicles. IEEE Transactions on Industrial Electronics 52(5):1343–1349.
- Anderson, C., and J. Anderson. 2010. Electric and hybrid cars: A history. Jefferson, NC, USA: McFarland.
- Benini, L., D. Bruni, A. Macii, E. Macii, and M. Poncino. 2003. Discharge current steering for battery lifetime optimization. IEEE Transactions on Computers 52(2):985–995.
- Benini, L., G. Castelli, A. Macii, E. Macii, M. Poncino, and R. Scarsi. 2001a. Extending lifetime of portable systems by battery scheduling. In Proceedings of the conference on design, automation and test in Europe, 197–203. Piscataway, NJ, USA: IEEE Press.
- Benini, L., G. Castelli, A. Macii, and R. Scarsi. 2001b. Battery-driven dynamic power management. IEEE Design & Test of Computers 18(2):53–60.
- Delucchi, M., and T. Lipman. 2001. An analysis of the retail and lifecycle cost of battery-powered electric vehicles. Transportation Research Part D: Transport and Environment 6(6):371–404.
- Doyle, M., and J. Newman 1997. Analysis of capacity–rate data for lithium batteries using simplified models of the discharge process. Journal of Applied Electrochemistry 27(7):846–856.
- Garey, M. R., and D. S. Johnson. 1979. Computers and intractability. A guide to the theory of np-completeness. New York, NY, USA: W.H. Freeman.
- Kirsch, D. 2000. The electric vehicle and the burden of history. New Brunswick, NJ, USA: Rutgers University Press.
- Laman, F., and K. Brandt. 1988. Effect of discharge current on cycle life of a rechargeable lithium battery. Journal of Power Sources 24(3):195–206.
- MIT Electric Vehicle Team 2008. A guide to understanding battery specifications. http://mit.edu/evt.
- Pedram, M., and Q. Wu. 1999. Design considerations for battery-powered electronics. In Proceedings of the 36th annual conference on design automation (DAC’99), 861–866. Washington, DC, USA: IEEE Computer Society.
- Rao, R., S. Vrudhula, and D. Rakhmatov. 2003. Analysis of discharge techniques for multiple battery systems. In Proceedings of the 2003 international symposium on low power electronics and design, 44–47. New York, NY, USA: ACM.
- Shachnai, H., T. Tamir, and O. Yehezkely. 2008. Approximation schemes for packing with item fragmentation. Theory of Computing Systems 43(1):81–98.