A New PSO-based Algorithm for Two-Dimensional Non-Guillotine Non-Oriented Cutting Stock Problem

ABSTRACT

In this paper, a new algorithm is proposed for the two-dimensional non-guillotine non-oriented cutting stock problem. The considered problem consists of cutting small rectangular pieces of predetermined sizes from large but finite rectangular plates. The objective is to generate cutting patterns that minimize the unused area and fulfill customer orders. The proposed algorithm is a combination of a new particle swarm optimization approach with a heuristic criterion inspired from the literature. The algorithm is tested on twenty-two instances divided into two sets. Corresponding results show the algorithm efficiency in optimizing the trim loss that is comprised between 2.6% and 7.8% for all considered instances.

Introduction

The cutting stock problem (CSP) is encountered in many production processes in different industrial sectors. Different variants of CSP can be defined according to the considered constraints and objectives e.g. the assortment problem which consists of identifying optimal dimensions of large objects from which small items (pieces) are to be cut, trim loss problem which consists of finding patterns optimizing materiel wastage for predefined pieces and large objects dimensions, etc. Four characteristics should be defined for each considered CSP (Dyckhoff 1990):

• Dimensionality: The literature deals with three categories of dimensions: 1D, 2D, and 3D CSPs.

• Kind of assignment: all stock material will be used but not all the orders must be fulfilled, or every order must be fulfilled but only a portion of stock will be used.

• Assortment of large objects: One large object to be cut, many identical large objects with similar dimensions, or different large objects with different dimensions.

• Assortment of small items to be cut: Few items of different dimensions, many items of many different dimensions, many items of relatively few different dimensions, or many identical items.

In case of two-dimensional cutting procedure, two variants are considered in the literature: The guillotine or edge to edge cutting when cutter must pass throughout the cutting plate without changing its direction, and the non-guillotine when the cutting tool may change direction before crossing the edge of the plate. The latter is provided in steel industry by modern cutting technologies such as laser resonator and rapid erosion.

Additional specifications are identified to characterize a two-dimensional cutting stock problem (2D-CSP), such as the raw material dimension: a CSP can be considered as a bin-packing problem when the raw material is presented as sheets with limited dimensions, or strip packing problem when pieces are to be cut from rolls with infinite height, and the possibility of pieces rotation when designing a pattern: called oriented if the orientation is not allowed, and or non-oriented if it is allowed.

In this paper, we focus on the trim loss problem and look for the cutting patterns that minimize the unused area. The considered problem is the 2D non-guillotine, non-oriented CSP with fixed identical plates’ dimensions, denoted in the literature as 2BP|R|F, while 2 for 2D, BP for Bin Packing, R for non-oriented, and F for Free that means non-guillotine. Many ordered items of relatively few dimensions must be totally fulfilled, and only a portion of stock sheets will be used with the assumption of an infinite number of available sheets.

It is worth to notice that CSP should be distinguished from cutting problem (CP). In fact, CP consists of finding the best cutting pattern that maximizes the sum of the profit of small items obtained from a large rectangle, whereas the CSP is the problem of cutting all required number of small rectangular pieces of different sizes from a set of rectangular sheets at a minimum sheet cost (Young-Gun and Kang 2002). Different heuristics and meta-heuristics have been developed in the literature to solve CSPs and related CPs since these problems belong to the category of NP-hard problems (Chu and Antonio 1999): Ayadi et al. (2009) and Ayadi, Cheikhrouhou, and Masmoudi (2012) proposed a hybrid heuristic based on the combination of bottom left and shelf algorithms for the guillotine CSP. Morabito and Arenales (1996) provided several rule-based heuristics to improve the cutting approach within a branch and bound procedure for non-guillotine CP. Other heuristics have been proposed in (Bengtsson 1982) and (El-Bouri et al. 1994) for a non-oriented bin-packing problem. El Hayek, Moukrim, and Nègre (2008) developed a heuristic based on the combination of the items maximal area concept and a heuristic metric for non-guillotine CP. Several meta-heuristics have been adopted, in particular the simulated annealing (Lai and Chan 1997), genetic algorithm (Beasley 2004), Tabu search (Alvarez-Valdes, Parreño, and Tamarit 2007), particle swarm optimization (PSO) (Barkallah, Ayadi, and Masmoudi 2014) (Ayadi and Barkallah 2016) (Ben Lagha, Dahmani, and Krichen 2014), etc. Gilmore and Gomory (1965) proposed a branch-and-price-and-cut algorithm, Beasley (1985) provided a branch and bound and a lower bound with a Lagrangian relaxation to an Mixed integer linear programming (MILP). Boschetti, Hadjinconstantinou, and Mingozzi (2002) provided a new linear mathematical model with new bounds obtained by relaxation. The reader is referred to (Dyckhoff, Scheithauer, and Terno 1997) for general surveys on CPs and to (Valério de Carvalho 2002) for a survey of the most popular Linear Programming (LP) methods for Bin-packing and CSPs. A review of models and solution methods included by (Belov 2003) and (Hassler and Sweeney 1991) are dedicated to 2-D CSPs, and a survey on two-dimensional packing problems is presented in (Lodi et al. 2010).

In this paper, a new algorithm is proposed for the considered CSP associated with the resolution of the corresponding CP. The developed approach is based on the definition of specific PSO operators and an adequate combination with a heuristic metric inspired from (El Hayek, Moukrim, and Nègre 2008). This approach is considered for patterns generation following an iterative procedure that is designed to solve the whole CSP. The algorithm efficiency is evaluated through its application to two sets of instances. The next section describes the proposed algorithm and the section following that reports the numerical results and corresponding discussions. The final section draws the conclusions and perspectives.

Developed algorithm for CSP

The proposed algorithm is based on dividing the problem into several sub-problems formulated as CPs. A corresponding approach is developed in order to solve each sub-problem and is iterated until reaching the optimized solution of considered SCP. The proposed approach for the CP is first presented; then, the global algorithm is addressed.

Proposed approach for CP

The proposed approach represents an adequate procedure to find a pattern with a minimized waste rate. It consists of defining optimal couples of pieces to be cut and corresponding placements in vacant rectangles in the pattern. A new PSO approach is developed in order to define the optimal order of pieces allocation; and a heuristic criterion inspired from (El Hayek, Moukrim, and Nègre 2008) is adopted in order to select the suitable vacant rectangle for each piece to be allocated.

PSO-based approach

PSO is a stochastic population-based meta-heuristic inspired from swarm intelligence. Its first application to optimization problems was proposed by (Kennedy and Eberhart 1995). In the basic formulation, a swarm consists of N particles flying around in a D-dimensional search space. The basis of the optimization process consists of evolving from a swarm to another by taking advantage from the cooperation between the particles. The success of some particles will influence the behavior of their peers.

Each particle is a candidate solution to the problem. In the adapted approach, a particle represents a specific order of the pieces references. This order is to be followed when designing a pattern by the allocation of ordered pieces to vacant rectangles until the saturation of the pattern. The proposed particle size is equal to 2.m.N_max components, where , H is the sheet height, w_j is the width of the j^th piece and m is the number of pieces references. Each reference appears in the reading vector of a particle N_max times for the first orientation and N_max times for the second orientation, since the considered problem is non-oriented.

The initial swarm is composed from particles obtained by a random dispersion of an initialized particle. The initialized particle orders the pieces’ references following the decreasing order of their heights.

Each particle is associated to a reading vector x_d representing its position in the decision space and a velocity vector v_d is used to update the particle position during the optimization. The position update is expressed in formulas (1) and (2):

(1)

(2)

where c₁, c₂ and c₃ are real parameters comprised between 0 and 1, p_d is the best known position of particle d, and g_d is the best known position of the entire swarm.

The comparison between particles follows their corresponding waste rates. Several specific operators have been considered to improve the particles. To illustrate the operator definitions, we consider an illustrative example of two particle positions x₁ and x₂ (Equations (3) and (4)) characterized by three pieces references for a CP with N_max = 1:

(3)

(4)

• Adapted subtraction operator

The subtraction of two particle positions is obtained through the subtraction of their components following formula (5):

(5)

The application of this operator to the illustrative example yields to particle x₃ expressed by Equation (6).

(6)

• Adapted velocities addition operator

The addition of two velocities v_1d and v_2d multiplied by corresponding c_j parameters is encountered in the definition of the particle velocity. The principle of this addition is given by formula (7):

(7)

• Adapted addition of a position and a velocity operator

The principle of adding a position to a velocity, as in formula (2), is given by formula (8):

(8)

Let us consider velocity v_d = x₃. The application of this operator to the illustrative example yields to the position x₄ expressed by Equation (9):

(9)

Pieces allocation procedure (PAP)

When designing the pattern corresponding to a particle, each piece is to be allocated to one of the pattern’s vacant rectangles. Thus, a list of vacant rectangles is considered, and contains all available spaces that can receive at least one of the ordered pieces. Vacant rectangles are identified with their bottom left corner coordinates (x_j,y_j) as well as their widths w_j and heights h_j. This list is initialized by the rectangle representing the whole sheet, and after each update, it is ordered following a heuristic criterion inspired from (El Hayek, Moukrim, and Nègre 2008). This criterion is a weighted sum of ratios that compare the dimensions of rectangles with the dimensions of the piece to be allocated as described in Equation (10). For each piece i, the candidate available rectangles are selected in the decreasing order of their criterion value o(i,j):

(10)

where

i:	=	piece reference;
j:	=	vacant rectangle reference;

q_k: Weights; 0 ≤ q_k≤ 1; k = 1,…,4 and .

When a piece is allocated to a vacant rectangle, the list of rectangles is updated following these PAP steps:

Step 1. Remove the vacant rectangle to which the piece is allocated.

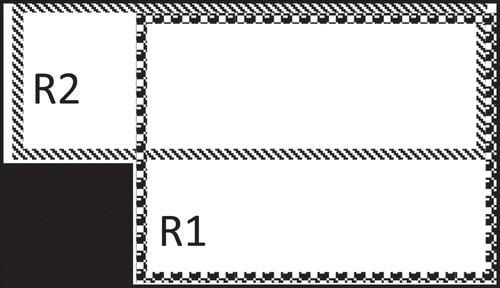
Step 2. Create two new rectangles limited by the attributed piece and the removed rectangle, as shown in Figure 1: one rectangle on the right of the piece (R1), and one above it (R2).

Figure 1. Step 2 of piece allocation.

Step 3. Check the inclusion of the created rectangles in the existing ones and remove included rectangle(s) if necessary.

Step 4. Update the list of vacant rectangles in order to avoid the overlaps between allocated piece and the rectangles. Table 1 represents an exhaustive enumeration of the fifteen possible overlapping configurations. The table shows an illustrative figure for each configuration, as well as a corresponding example and the new rectangles to be created for the update list. Added rectangles are referred as R_aj(x_j,y_j,w_j,h_j), where (x_j,y_j) are the coordinates of the rectangle’s bottom left corner and (w_j,h_j) are the rectangle’s width and height, respectively.

Table 1. Rectangles’ list updating.

N°	Configuration example	Creation of new rectangles
1		Rectangle above the piece Case 1: yr4 > yc4 → Ra1 (x, yp + hp, l, y + h—yp—hp) Case 2: yr4 ≤ yc4 → no creation of new rectangle Rectangle on the right Case 1: xr2 > xc2 → Ra2 (xp + lp, y, x + l—xp—lp, h) Case 2: xr2 ≤ xc2 → no creation of new rectangle Rectangle below the piece Case 1: yc1 > yr1 → Ra3 (x, y, l, yp—y) Case 2: yc1 ≤ yr1 → no creation of new rectangle
2		Rectangle above the piece Case 1: yr4 > yc4 → Ra1 (x, yp + hp, l, y + h—yp—hp) Case 2: yr4 ≤ yc4 → no creation of new rectangle Rectangle on the right Case 1: xr2 > xc2 → Ra2 (xp + lp, y, x + l—xp—lp, h) Case 2: xr2 ≤ xc2 → no creation of new rectangle Rectangle on the left Case 1: xc1 > xr1 → Ra3 (x, y, xp—x, h) Case 2: xc1 ≤ xr1 → no creation of new rectangle
3		Rectangle on the right Case 1: xr2 > xc2 → Ra1 (xp + lp, y, x + l—xp—lp, h) Case 2: xr2 ≤ xc2 → no creation of new rectangle Rectangle on the left Case 1: xc1 > xr1 → Ra2 (x, y, xp—x, h) Case 2: xc1 ≤ xr1 → no creation of new rectangle
4		Rectangle on the right Case 1: xr2 > xc2 → Ra1 (xp + lp, y, x + l—xp—lp, h) Case 2: xr2 ≤ xc2 → no creation of new rectangle Rectangle on the left Case 1: xc1 > xr1 → Ra2 (x, y, xp—x, h) Case 2: xc1 ≤ xr1 → no creation of new rectangle Rectangle below the piece Case 1: yc1 > yr1 → Ra3 (x, y, l, yp—y) Case 2: yc1 ≤ yr1 → no creation of new rectangle
5		Rectangle above the piece Case 1: yr4 > yc4 → Ra1 (x, yp + hp, l, y + h—yp—hp) Case 2: yr4 ≤ yc4 → no creation of new rectangle Rectangle on the left Case 1: xc1 > xr1 → Ra3 (x, y, xp—x, h) Case 2: xc1 ≤ xr1 → no creation of new rectangle Rectangle below the piece Case 1: yc1 > yr1 → Ra3 (x, y, l, yp—y) Case 2: yc1 ≤ yr1 → no creation of new rectangle
6		Rectangle on the right Case 1: xr2 > xc2 → Ra1 (xp + lp, y, x + l—xp—lp, h) Case 2: xr2 ≤ xc2 → no creation of new rectangle Rectangle below the piece Case 1: yc1 > yr1 → Ra3 (x, y, l, yp—y) Case 2: yc1 ≤ yr1 → no creation of new rectangle
7		Rectangle on the left Case 1: xc1 > xr1 → Ra3 (x, y, xp—x, h) Case 2: xc1 ≤ xr1 → no creation of new rectangle Rectangle below the piece Case 1: yc1 > yr1 → Ra3 (x, y, l, yp—y) Case 2: yc1 ≤ yr1 → no creation of new rectangle
8		Rectangle above the piece Case 1: yr4 > yc4 → Ra1 (x, yp + hp, l, y + h—yp—hp) Case 2: yr4 ≤ yc4 → no creation of new rectangle Rectangle on the right Case 1: xr2 > xc2 → Ra2 (xp + lp, y, x + l—xp—lp, h) Case 2: xr2 ≤ xc2 → no creation of new rectangle
9		Rectangle above the piece Case 1: yr4 > yc4 → Ra1 (x, yp + hp, l, y + h—yp—hp) Case 2: yr4 ≤ yc4 → no creation of new rectangle Rectangle on the left Case 1: xc1 > xr1 → Ra3 (x, y, xp—x, h) Case 2: xc1 ≤ xr1 → no creation of new rectangle
10		Rectangle above the piece Case 1: yr4 > yc4 → Ra1 (x, yp + hp, l, y + h—yp—hp) Case 2: yr4 ≤ yc4 → no creation of new rectangle Rectangle below the piece Case 1: yc1 > yr1 → Ra3 (x, y, l, yp—y) Case 2: yc1 ≤ yr1 → no creation of new rectangle
11		Rectangle on the right Case 1: xr2 > xc2 → Ra2 (xp + lp, y, x + l—xp—lp, h) Case 2: xr2 ≤ xc2 → no creation of new rectangle
12		Rectangle on the left Case 1: xc1 > xr1 → Ra3 (x, y, xp—x, h) Case 2: xc1 ≤ xr1 → no creation of new rectangle
13		Rectangle below the piece Case 1: yc1 > yr1 → Ra3 (x, y, l, yp—y) Case 2: yc1 ≤ yr1 → no creation of new rectangle
14		Rectangle above the piece Case 1: yr4 > yc4 → Ra1 (x, yp + hp, l, y + h—yp—hp) Case 2: yr4 ≤ yc4 → no creation of new rectangle
15		Rectangle above the piece Case 1: yr4 > yc4 → Ra1 (x, yp + hp, l, y + h—yp—hp) Case 2: yr4 ≤ yc4 → no creation of new rectangle Rectangle on the right Case 1: xr2 > xc2 → Ra1 (xp + lp, y, x + l—xp—lp, h) Case 2: xr2 ≤ xc2 → no creation of new rectangle Rectangle on the left Case 1: xc1 > xr1 → Ra2 (x, y, xp—x, h) Case 2: xc1 ≤ xr1 → no creation of new rectangle Rectangle below the piece Case 1: yc1 > yr1 → Ra3 (x, y, l, yp—y) Case 2: yc1 ≤ yr1 → no creation of new rectangle

Step 5. Check inclusions between created rectangles and existing ones and remove included ones.

Global algorithm for CSP

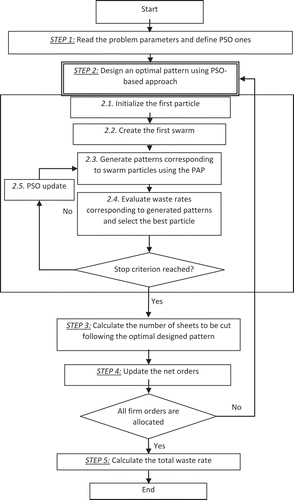
The provided algorithm iterates the approach described in the last section with updating the ordered pieces to be cut. The details of this algorithm are shown in Figure 2. The first step consists of reading the problem parameters (pieces dimensions and ordered quantities as well as sheet dimensions) and fixing the PSO parameters (c₁, c₂, c₃, swarm size, and maximum number of iterations). The second step concerns the design of optimal patterns by combining the PSO-based approach and the PAP. After initializing the first particle (Step 2.1), the first swarm is created through a random dispersion of this particle (Step 2.2). Patterns corresponding to the swarm’s particles are then generated using the described PAP (Step 2.3) and corresponding waste rates are identified in order to select the best pattern to be considered (Step 2.4). The particle swarm is updated using formulas (1) and (2) (Step 2.5), until reaching one of the two stopping criteria: the maximum number of iterations and no improvement of the waste rate for all particles. Step 3 corresponds to the calculation of sheets number to be cut following the optimal designed pattern without violating demand limitation constraints. After that, net orders are updated in Step 4, and the procedure is iterated until satisfying ordered quantities.

Figure 2. Proposed algorithm for solving CSP.

Numerical results

The proposed approach is applied to two sets of instances: the first one contains four designed instances for which the optimal solutions are known. This set serves for validation tests by comparing the performance of algorithm results with optimal ones. The second set consists of 18 instances for which optimal solutions are unknown. These instances are randomly generated with respect to real life bounds in order to evaluate the algorithm based on cases encoding real-world problems.

First set of instances

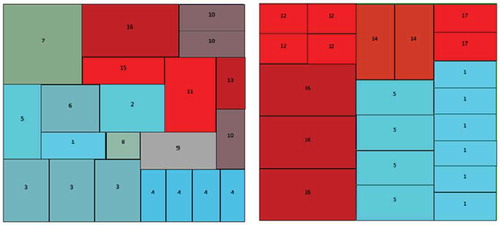
The patterns corresponding to each of the four instances are manually designed with specific pieces’ and sheets’ dimensions so that the corresponding optimal solutions are characterized with a null trim loss value. Corresponding patterns are reported in Appendix 1, and the number of used sheets following these optimal solutions are reported in Table 2 and labeled as NUS_min. Table 2 shows also pieces’ and sheets’ characteristics. For each piece type P_i to be cut, related data are represented as following: (height, width, demand). The number of piece types is equal to 8, 17, 16, and 12 for instances #1, #2, #3, and #4, respectively.

Table 2. First-set instance data and corresponding results.

Instance #	1	2	3	4
Sheetdimensions	1843 × 1400	1611 × 1550	1918 × 1660	1924 × 1568
Pieces related data
P1	(586, 350, 13956)	(431, 190, 7877)	(548, 442, 11857)	(481, 280, 18768)
P2	(415, 245, 10467)	(441, 342, 659)	(334, 274, 19009)	(524, 448, 6438)
P3	(340, 174, 10467)	(445, 301, 1977)	(490, 256, 2634)	(224, 219, 13384)
P4	(274, 220, 6978)	(366, 177, 2636)	(411, 221, 2496)	(262, 224, 7960)
P5	(645, 174, 10467)	(532, 251, 5471)	(216, 190, 17796)	(392, 352, 10870)
P6	(197, 187, 17445)	(389, 342, 659)	(398, 190, 5222)	(393, 336, 17844)
P7	(415, 214, 17445)	(573, 526, 659)	(586, 548, 4275)	(569, 504, 2712)
P8	(548, 350, 3489)	(221, 190, 659)	(668, 374, 3937)	(352, 140, 2172)
P9		(521, 269, 659)	(293, 282, 19904)	(588, 305, 5440)
P10		(437, 187, 659)	(373, 282, 11068)	(196, 244, 12200)
P11		(541, 343, 659)	(407, 373, 2232)	(448, 420, 1266)
P12		(324, 214, 4812)	(221, 274, 1506)	(392, 305, 1440)
P13		(373, 187, 659)	(374, 392, 1749)
P14		(546, 266, 2406)	(274, 255, 11736)
P15		(555, 199, 659)	(548, 222, 1604)
P16		(648, 374, 4268)	(432, 361, 5640)
P17		(431, 205, 2406)
NUSmin	3489	1862	4430	3939
NUSPSO	3634	1908	4665	4191
Trim loss (%)	3.99	4.67	5.47	6.09

The proposed approach is applied to each of the considered instances. Corresponding results (number of used sheets “NUS_PSO” and obtained trim loss) are reported in the last two rows of Table 2. Results show that the trim loss varies from 4% to 6% with respect to the considered instance, with a total trim loss for this first set equal to 4.8%. These results show the performance of the proposed algorithm in solving non-guillotine CSPs.

It is worth to notice that the proposed approach is the first heuristic adapting PSO technique with the proposed specific operators to the non-guillotine CSPs. This initiative shows that the issue of developing PSO-based algorithms considering the proposed operators for non-guillotine CSPs seems to be promising.

Second set of instances

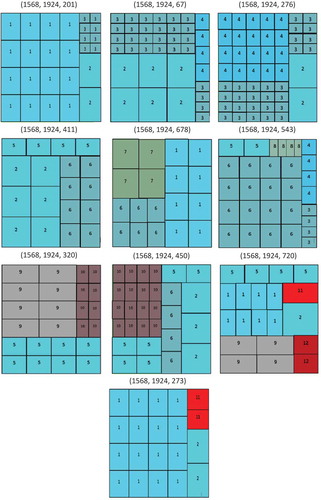
The second set concerns 18 instances that are randomly generated with a number of piece types between 2 and 18 as shown in Table 3. Piece heights and widths are randomly generated between 150 and 600 mm and demand between 1000 and 20000. Sheet dimensions are fixed to 2500 mm × 1850 mm.

Table 3. Results of second-set instances.

Instance #	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
Number of piece types	2	16	12	4	14	13	7	16	16	4	16	9	11	7	6	18	14	7
Number of patterns	3	32	21	9	26	23	14	34	30	9	33	16	19	12	10	40	26	14
NUSPSO	540	5029	7489	1192	5855	8055	2534	7214	4768	1630	7661	5265	6685	5828	2636	5938	7154	4002
Trim loss (%)	2.64	4.54	6.98	4.71	7.63	7.72	4.46	6.31	5.11	3.42	5.88	5.92	6.6	6.99	7.83	5.48	7.5	5.83

The instances are tested with the proposed approach and results are reported in Table 3. For each instance, the number of designed patterns, NUS_PSO, and corresponding trim loss are given. Results show that the trim loss is less than 7.8% for all instances with an average value equal to 6%. For five of the tested instances (#1, #2, #4, #7, and #9), the trim loss remains less than 5% with a specific low value for instance #1 equal to 2.6%. These results show a significant efficiency of the proposed approach in optimizing trim loss and consequently the use of raw materials for randomly generated instances inspired from real-world cases.

It is worth to note that instance #1—that is characterized by the lowest obtained trim loss—has the minimal problem dimension (with NUS_PSO = 540 sheets and only two pieces types) in comparison to all tested instances. However, we cannot say that the solution optimality depends on the problem dimension, based on the results of the other instances. Let’s consider instances #2 and #15 for example: results show that trim loss corresponding to instance #2 is equal to 4.54% counter a trim loss of 7.83% for instance #15 although the dimension of instance #2 is higher than the dimension of instance #15. In fact, the number of pieces types is equal to 16 and NUS_PSO = 5029 sheets for instance #2, while the number of pieces types is equal to 6 and NUS_PSO = 2636 sheets for instance #15 Thus, solution optimality depends on the adequacy between pieces and sheets dimensions.

Although results show the efficiency of the algorithm in reaching low trim loss, the number of generated patterns yielding to the optimized results can reach important values (c.f. 40 patterns for instance #16). From industrial practical perspective, this can generate additional set up costs related to necessary number of pattern changes in the cutting process.

Conclusions and perspectives

In this paper, a PSO-based approach with specific operators is provided to solve non-guillotine non-oriented CSP. The CSP is divided into several CPs that are solved iteratively. Computations are provided on two sets of instances showing and validating the efficiency of the algorithm. Results show a trim loss comprised between 2.6% and 7.8% for all considered instances, which confirms that algorithms adopting the PSO techniques are promising issues that should be well investigated for CSPs.

As future work, we propose to adapt the proposed approach to the case of multi-period non-guillotine CSP in a rolling planning horizon context. In addition, considering the problem as a bi-objective one in order to find a compromise between optimized trim loss and number of generated patterns can represent an interesting issue that meets real world industrial perspectives.

Appendix 1

For each instance from the first set, optimal patterns are represented and corresponding sheets’ width (W) and height (H) as well as number of sheets (NS) to be cut following each pattern are reported above the represented pattern as following: (W,H,NS).

1. Optimal patterns of instance #1:

   (1843, 1400, 3489)

   

2. Optimal patterns of instance #2:

   (1611, 1550, 659)(1611, 1550, 1203)

   

3. Optimal patterns of instance #3:

   

4. Optimal patterns of instance #4: