An improved PSO algorithm with genetic and neighborhood-based diversity operators for the job shop scheduling problem

ABSTRACT

The job shop scheduling problem (JSSP) is an important NP-hard practical scheduling problem that has various applications in the fields of optimization and production engineering. In this paper an effective scheduling method based on particle swarm optimization (PSO) for the minimum makespan problem of the JSSP is proposed. New variants of the standard PSO operators are introduced to adapt the velocity and position update rules to the discrete solution space of the JSSP. The proposed algorithm is improved by incorporating two neighborhood-based operators to improve population diversity and to avoid early convergence to local optima. First, the diversity enhancement operator tends to improve the population diversity by relocating neighboring particles to avoid premature clustering and to achieve broader exploration of the solution space. This is achieved by enforcing a circular neighboring area around each particle if the population diversity falls beneath the adaptable diversity threshold. The adaptive threshold is utilized to regulate the population diversity throughout the different stages of the search process. Second, the local search operator based on critical path analysis is used to perform local exploitation in the neighboring area of the best particles. Variants of the genetic well-known operators “selection” and “crossover” are incorporated to evolve stagnated particles in the swarm. The proposed method is evaluated using a collection of 123 well-studied benchmarks. Experimental results validate the effectiveness of the proposed method in producing excellent solutions that are robust and competitive to recent state-of-the-art heuristic-based algorithms reported in literature for nearly all of the tested instances.

Introduction

Job shop scheduling problem (JSSP) is a well-known practical optimization problem that is crucial in the planning and organization of industrial systems. JSSP is one of the most challenging scheduling problems due to the various constraints that are inevitable in practical applications. The objective of JSSP is to determine a schedule (the order of processing jobs over machines) in the shop so that a specified design criterion is optimized. The minimization of the total completion time of all operations known as the makespan (C_max) of the production sequence is mostly investigated in the literature. The minimization of the makespan reduces the production time and cost, increases resource utilization, and thus leads to high efficiency production systems. Another important criterion is the minimization of the average job tardiness which designates the ability to meet specific production due dates that exist in real manufacturing systems. JSSP has been a vigorous research area since it was first presented by Fisher and Thomson in 1963 and it was shown to be NP-complete (Garey, Johnson, and Sethi 1976). For a typical JSSP the number of possible solutions (both feasible and infeasible) is . Therefore, exhaustive search of the solution space is computationally expensive even for small-sized problems. Many approaches employing mathematical formulations and approximation methods have been presented. Exact methods, such as branch and bound (Heilmann 2003) and dynamic programming (Lorigeon, Billaut, and Bouquard 2002) have been efficient in solving small-sized instances of the problem. Though, these methods are computationally expensive for solving medium or large instances. Therefore, many approximate and heuristic strategies have been proposed to overcome the shortcomings of exact enumeration techniques and to find high-quality solutions in an acceptable computational time. Lagrangian relaxation (Chen and Luh 2003; Kaskavelis and Caramanis 1998), and Tabu search (TS) (Geyik and Cedimoglu 2004; Watson et al. 2003) have made significant achievements in improving the solution quality in JSSP.

In recent years, nature-inspired heuristics have emerged and have been applied successfully to solve difficult JSSP that are hard to solve by traditional techniques. Intelligent optimization algorithms such as ant colony optimization (Neto and Godinho Filho 2013; Zhang et al. 2006), artificial bee colony (ABC) (Banharnsakun, Sirinaovakul, and Achalakul 2012; Chong et al. 2006), genetic algorithms (GA) (Amirthagadeswaran and Arunachalam 2006; Liu, Tsai, and Chou 2006), particle swarm optimization (PSO) (Lian, Jiao, and Gu 2006; Xia and Wu 2006), simulated annealing (SA) (Suresh and Mohanasundaram 2006), neural networks (Yu and Liang 2001), and memetic algorithm (MA) (Gao et al. 2011) were reported to find optimal/near optimal solutions within reasonable computational time. Nevertheless, each metaheuristic has its own strength and weakness. Some of these methods can achieve excellent effectiveness and efficiency but require extensive implementation efforts and their performance is significantly dependent on the initial parameter selection and structure. PSO is a computational paradigm that efficiently utilizes the distributed and parallel computing capabilities of living swarms in nature (Eberhart and Kennedy 1995). The foremost advantage of PSO is its fast convergence, ease of implementation, and robustness which compares favorably with other optimization methods. Due to the attractive features of PSO, it has been applied to a wide-range of optimization problems including JSSP. Liao, Tseng, and Luarn (2007) extended the discrete version of PSO to solve the flowshop scheduling problems. Yongxian, Xiaotian, and Jinfu (2008) established a job shop scheduling model based on the PSO and investigated the problem of optimized execution of operations under limited resources. Tseng and Liao (2008) have exploited the PSO algorithm to solve the problem of the scheduling jobs on parallel machines with a total tardiness objective. Liu et al. (2011) proposed a multi-objective optimization model based on PSO to minimize the bottleneck machines’ makespan and the total products’ tardiness for machine tool job shop scheduling.

However, PSO lacks the ability to achieve good exploration-exploitation balance as it cannot effectively explore the whole solution space and possibly converge prematurely to local optima. Hybrid algorithms that combine two or more meta-heuristic techniques were developed to improve effectiveness and efficiency. Hybrid approaches aim to improve the performance by combining the advantages of different algorithms to improve both global and local search capabilities. Motivated by these perspectives, various hybrid PSO-based algorithms have been reported to improve the solution quality of the JSSP. Sha and Hsu (2006) proposed a PSO-TS hybrid algorithm. Tasgetiren et al. (2006) presented a hybrid method based on PSO and differential evolution and enhanced with an efficient local search based on variable neighborhood search (VNS). Ge, Du, and Qian (2007) utilized the efficient global search capability of PSO with the great ability of escaping local minima of SA by introducing an algorithm called hybrid evolutionary algorithm. In another research effort, Ge et al. (2008) introduced a hybrid algorithm incorporating PSO and artificial immune system (AIS) to solve the minimum makespan JSSP. Another hybrid swarm intelligence algorithm (MPSO) consisting of PSO, SA, and a multi-type individual enhancement scheme was developed by Lin et al. (2010). Tang et al. (2010) introduced a hybrid algorithm combining PSO and newly proposed evolutionary genetic operators to solve the JSSP. The algorithm was found to outperform regular standalone PSO and GA. Another PSO-GA hybrid algorithm was proposed by Liu et al. (2015). In their work, the PSO algorithm is redefined and modified by introducing genetic operators such as crossover and mutation to update particles in the population. Although most of these algorithms attain different mechanisms to escape local optima and premature convergence, no single algorithm is proven to be successful for finding an optimal solution for all problem sizes and complexities. In additions, most of the genetic and PSO operators utilized in these algorithms do not make use of knowledge of the JSSP problem domain. This may lead to the construction of infeasible solutions and inefficient exploration of the solution space.

In this paper, an improved PSO-based algorithm for the JSSP is introduced. The proposed algorithm incorporates several features to address drawback of prior algorithms. The main contributions of this work are as follows:

• The conventional PSO velocity and position operators are modified making use of the knowledge of the JSSP domain.

• New neighborhood-based operators are proposed to improve the population diversity through the search process. Neighborhood-based operators improve the search process by relocating neighboring particles to achieve broader exploration of the solution space. The neighborhood-based operators are adaptive to regulate the population diversity thru the different stages of the search process.

• An efficient neighborhood-based local search operator is introduced to perform local exploitation nearby best particles.

• Specially designed genetic operators are utilized to evolve stagnated particles in the swarm.

The structure of this paper is organized as follows: in the next section, the mathematical formulation of the JSSP is presented. In the section “Particle swarm optimization”, the conventional PSO algorithm is provided. The improved PSO algorithm and the proposed genetic and neighborhood-based diversity operators are explained in sections “Proposed algorithm” and “Genetic and neighborhood-based operators”, respectively. Computational results for benchmark instances and comparisons to existing algorithms are reported in the section “Experimental results”. Finally, concluding remarks and future research are summarized in the section “Conclusions and future work”.

Job shop scheduling problem

A typical JSSP can be described as follows: There are different jobs J = (J₁, J₂, …. J_n). Each job contains operations that have to be processed through different machines M = (M₁, M₂, ….. M_m). Each operation has to be performed without preemption on each machine for a predefined processing time. The order of processing machines is different from one job to another. The aim of JSSP is to find the optimal schedule and the starting time on each machine so that one or more design criteria are optimized. In this study, we attempt to find a schedule that minimizes the makespan of the jobs. That is the completion time of the last job processed in the system. The difficulty with JSSP is due to the high number of conjunctive and disjunctive constraints associated with real-world industrial applications. Two methods will be employed through this paper to formally model and represent solutions to the JSSP problem: the disjunctive graph model to specify the relative order of operations of each job processed on different machines and the Gantt chart to specify the set of start and completion times for all operations.

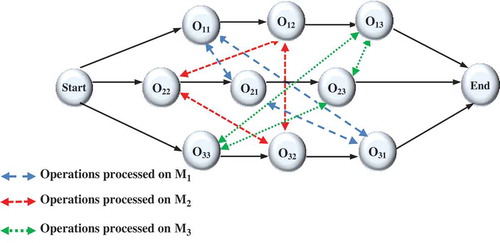
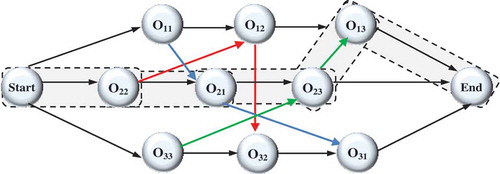
Consider the JSSP presented in Table 1. A typical JSSP may be characterized with a disjunctive graph G(N, A, E) as presented in Figure 1. N = {Start, End, O_ij for i = 1,2,…, ; j = 1,2,….} is the set of operations to be scheduled (represented by the nodes in the graph). O_ij characterizes the operation of the job i processed on machine j and is associated with a predefined processing time t_ij. Start and End are two dummy nodes with zero processing time used to characterize the beginning and the termination of the schedule, respectively. A is the set of conjunctive directed edges that correspond to precedence relations of operations of the same job (designated with directed solid lines). A = {(Start,O₁₁), (O₁₁,O₁₂), (O₁₂,O₁₃), (O₁₃, End), (Start,O₂₂), (O₂₂,O₂₁), (O₂₁,O₂₃), (O₂₃, End), (Start,O₃₃), (O₃₃,O₃₂), (O₃₂,O₃₁), (O₃₁, End)). E is the set of disjunctive non-directed edges which correspond to the precedence constraints of operations processed on the same machine the (denoted by dashed lines). E is the union of the subsets E₁ = {(O₁₁,O₂₁), (O₂₁,O₃₁), (O₃₁,O₁₁)}, E₂ = {(O₁₂,O₂₂), (O₂₂,O₃₂), (O₃₂,O₁₂)} and E₃ = {(O₁₃,O₂₃), (O₂₃,O₃₃), (O₃₃,O₁₃)}, where subset E_j designates edges which connect the operations processed on a particular machine j. The aim of the schedule is to determine the sequence of the operations processed on every machine, i.e. to find the directions of the non-directed edges that construct a path that traverse all nodes in each edge subset. A candidate schedule to the JSSP is presented in Figure 2. The critical path is defined as the longest path from the Start to the End node. Consequently, the length of critical path governs the longest completion time of the schedule.

Table 1. An example of JSSP.

Job	Machine sequence	Processing Time
J1	1-2-3	3-2-7
J2	2-1-3	4-6-2
J3	3-2-1	2-5-3

Figure 1. Disjunctive graph of a JSSP.

Figure 2. A feasible solution of the example in Figure 1.

Given any feasible schedule, we can determine the operation sequences and the completion time on each machine. The following symbols will be used throughout this paper.

O_ij: The operation of job i processed on machine j.

t_ij: The processing time of operation O_ij

S(O_ij): The start time of operation O_ij.

C(O_ij): The completion time of operation O_ij.

C_max: maximum makespan.

The JSPS problem based on minimizing the maximal makespan can be described as follows.

(1)

Subject to:

(2)

(3)

(4)

where D denotes a large positive number. and designate two index coefficient defined as follows:

(5)

(6)

Particle swarm optimization

PSO is a novel metaheuristic based on the phenomenon of cooperative intelligence proposed by Eberhart and Kennedy in 1995. PSO is derived from the social behavior of insect colonies and animal societies that live and interact in large groups. In particular, it mimics swarming actions observed in bird flocking or fish schooling. PSO is a population-based algorithm consisting of a group of processing elements (swarm) conceptualized as particles. Each particle, explores the solution space of the optimization problem to search for the optimum solution. Thus, each particle position characterizes a candidate solution for the problem. The position of the ith particle in D-dimensional search space is represented as X_i = (x_i1, x_i2,….., x_iD). The particle velocity characterizes the position variation between consecutive iterations and is represented by V_i = (v_i1, v_i2, …….., v_iD). Evolution is guided with a fitness function defined to evaluate the goodness of the acquired solution. The fitness value is calculated for each particle in the swarm and is compared to the fitness of the best previous value for that particular particle and to that of the best particle in the swarm. Similar to other nature-inspired algorithms, PSO is driven by two fundamental processes: the deviation process, which enables exploring different regions of the solution space, and the selection process, which assures the exploitation of previous information about the search space based on the defined fitness function. Each particle moves according to the velocity determined by the distance between the prior position of the particle and the, values. The main objective of the particle velocity are to keep the particle moving toward the global and local best solutions while maintaining inertia to avoid becoming trapped in local optima. The particles evolve by adjusting their velocity and position values according to the following equations:

(7)

(8)

where {i = 1, 2,…….,N}, and N is the swarm size. Constants c₁ and c₂ are cognitive and social parameters ∈[0, 1]. Appropriate fine-tuning of c₁ and c₂ results in faster convergence and alleviation of local minima. r₁ and r₂ are two random numbers, with uniform distribution U[0,1]. V_max is the maximum velocity value that confines the velocity vector, such that -V_max ≤ V_i(t + 1) ≤ V_max . In equation (7), the first term ω represents the inertia of previous velocity. Proper adjustment of ω provides a balance between global and local explorations and exploitations. Experimental results indicate that the PSO performance is improved if the inertia is initially set to a large value to promote global exploration at the early stages of the search process. This value should be gradually decreased to get more refined solutions as we approach the end of the search process. This can significantly reduce the number of iterations required to find a satisfactorily optimal solution. The inertia weight approach proposed by Eberhart and Shi (2001) is utilized in this work as follows:

(9)

where ω_min and ω_max are the minimum and maximum values of , t_max is the maximum number of iterations, and t is the current iteration. The second term in (7) is the “cognitive” component demonstrating the particular knowledge of the particle itself. The last term in (7) is the “social” component, representing the collaboration between all particles in the swarm. The iterative steps will continue until the termination condition is satisfied.

Proposed algorithm

Particle encoding

Defining the appropriate particle representation is essential to develop an appropriate problem mapping and to construct an efficient PSO-based schedule. Determining a schedule is equivalent to finding the order of the operations processed on each machine. Operation-based (permutation) encoding method is adopted in this paper to encode a schedule as a sequence of operations (Tsujimura, Mafune, and Gen 2001). For a JSSP, the length of a particle is containing a non-partitioned combination of integers from 1 to n. This encoding schema uses integer encoding to encode the schedule as a sequence of jobs and operations. Since each job consists of different operations that have to be processed on the m machines, each job number appears exactly m times in the particle. Each gene in particle denotes a specific operation of one of the n jobs. By examining the particle from left to right, the kth occurrence of a job number refers to the kth operation in the technological sequence of this job. 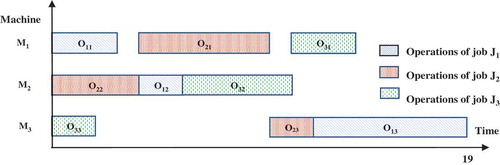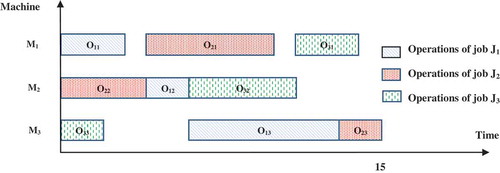For example, for the JSSP described in Table 1 and Figure 1, one possible solution is presented in Figure 2. The schedule can be represented by the particle [2 3 1 2 2 1 3 1 3], where 1, 2, and 3 denote the corresponding jobs J₁, J₂,and J₃, respectively. The particle in the above example can be interpreted as follows: the first 2 in the particle represents to the first operation of job J₂ to be processed first on machine M₂. Then, the first 3 characterizes the first operation of job J₃ to be processed on M₃. Similarly, the first 1 corresponds to the first operation of job J₁, which will be processed on M₁. The second 2 corresponds to the second operation of job J₂, which will be processed on machine M₁. The third 2 in the particle corresponds to the third operation of job J₂, which will be processed on machine M₃. Therefore, the particle [2 3 1 2 2 1 3 1 3] is decoded into the following operation sequence [O₂₂ O₃₃ O₁₁ O₂₁ O₂₃ O₁₂ O₃₂ O₁₃ O₃₁] as presented in Figure 3. The prominent advantage of this encoding is that it guarantees that any permutation in the particle can be indirectly decoded into a feasible solution. Operations are processed on the corresponding machines consecutively at the earliest permissible time. The corresponding feasible schedule is represented by the Gantt chart shown in Figure 4. Due to the precedence restrictions between different operations of the same job, idle time can occur in the Gantt chart between operations processed on the same machine.

Figure 3. Operation encoding of the feasible solution in Figure 2.

Figure 4. Gantt chart of the feasible solution constructed by operation decoding.

Initial population

Conforming to the operation-based representation method, the particle is set as a string of integers in the range [1, n]. It must be assured that each job index occurs exactly m times in each particle. This process is repeated to construct the N particles in the swarm. The initial population can be acquired by many methods such as diverse insertion, shifting bottleneck, or random methods, etc. However, the initial population has a limited effect on the quality of the final solution; nevertheless, it may affect the convergence time.

Fitness function

PSO preserves a swarm of particles that are evaluated in every iteration. In the proposed framework, evolution is guided with a fitness function that assesses the goodness of the particles based on their ability to minimize the makespan calculated according to the description in the section “Job shop scheduling problem”. Particle fitness values are calculated in every generation. Lower fitness values correspond to superior particles that need to be conserved for the subsequent generations.

Updating feasible solutions by PSO operators

Conventional PSO velocity and position equations are modified to conform to the discrete solution space of the JSSP. The velocity index of particle i at iteration t is defined as a sequence of swap operations as follow:

(10)

where , represents job positions 1, ] and L represents the length of the swap list which is an integer 1, n]. After generating the velocity index, the new particle velocity is computed using (7). The basic operations implemented for updating the particle velocity and position are explained below:

Subtraction between two positions: Assume that X₁and X₂ are two position vectors representing two different particles in the swarm. The subtraction between X₂–X₁ is a velocity vector. In (7) subtracting positions () and () result in two velocity vectors characterized as a sequence of swap operations. For example, consider the following values for the position vectors at iteration t:

[2 3 1 2 2 1 3 1 3], [2 3 1 2 1 1 3 2 3] and [3 3 1 2 3 1 2 1 2]

() = means the required sequence of swap operations to reach the target particle given the initial starting particle ). This is achieved by swapping the genes in positions 5 and 8 {.

Similarly,

() = ( is the required sequence of swap operators to reach the particle given the initial particle. To achieve this, first genes in positions 1 and 7 are swapped {(1, 7)} to get . Then genes in positions 5 and 9 {(5, 9)} are swapped to get which is the target particle. It should be mentioned that the arrangement of the swap operators in V is important as the operators in the sequence act on the particle in order.

Addition between position and velocity: Assume a position vector X and a velocity vector V. A new position X’ = X + V is found by applying the sequence of swap operations of V to X.

For example if [2 3 1 2 2 1 3 1 3] and V = {(1, 3), (4, 6)} then X’ is obtained by exchanging the genes in positions 1 and 3 followed by exchanging the genes in positions 4 and 6. Consequently, the new position particle X’ = [1 3 2 1 2 2 3 1 3].

Addition between two velocities: let V₁ and V₂ be two velocity vectors. To compute V₁ + V₂, we perform the sequence of swap operations of V₁, followed by the swap operations of V₂. The arrangement of the swap operators in V is important as the operators in the sequence act on the particle in order. For example if V₁ = {(1, 3), (4, 6)} and V₂ = {(2, 5)} then the velocity vector V₁ + V₂ = {(1, 3), (4, 6), (2, 5)}

Multiplication: Let c be the learning coefficient and V be the velocity. Coefficient c indicates the probability of performing a particular swap operator from the velocity list on the position vector. In every iteration, constants c₁ and c₂ are generated randomly in the interval [0, 1] such that c₁+ c₂ ≤ 1. The particle will move towards the local best with probability c₁, and will move towards the global best with probability c₂. Therefore, if c₁> c₂ then the term in (7) will dominate and the velocity vector will be characterized by the movement towards. Otherwise, the velocity will move towards For example, consider the following values for a JSSP at iteration t:

[2 3 1 2 2 1 3 1 3], [2 3 1 2 1 1 3 2 3]and [3 3 1 2 3 1 2 1 2]

{(2, 5), (7, 1)}, c₁ = 0.7, c₂ = 0.3, and

Termination condition

The iterative section of the algorithm will be repeated until the maximum number of iteration t_max is attained or the change in the fitness function does not exceed a certain threshold value. The algorithm terminates whenever one of these two conditions occurs. When the stopping criterion is met, the best particle in the swarm characterized by will be the recommended solution for the JSSP.

Genetic and neighborhood-based operators

Similar to other stochastic algorithms, premature convergence presents a major limitation for PSO during the search process. This is due to the fact that conventional PSO utilizes a deterministic attraction phase, in which particles are drawn to their local and global best values. This causes particles in the swarm to move rapidly to the same area of the search space increasing the similarities among the particles and hence decreasing the diversity of the population. Furthermore, it is often useful to search the neighborhood area of local optimal solutions as it may contain the global optimum. Motivated by these perspectives, genetic and two neighborhood-based search mechanisms are proposed in this section to enhance the population diversity and to perform local search.

Diversity enhancement operator

Different variants of the PSO algorithm have been reported in the literature to maintain swarm diversity and to avoid premature convergence. This is achieved through modifying the movement schema or the learning strategy of the particles. Riget and Vesterstrøm (2002) proposed a diversity-guided PSO, called ARPSO, which describes a repulsion phase based on a modified velocity update model. Sun, Xu, and Fang (2006) proposed a mutation operator conducted on the P_gbest to enhance the swarm diversity when it falls under a predefined threshold value. Arani et al. (2013) introduced a territorial PSO algorithm with a new collision operator and a social interaction schema which guides the particles in the direction of the weighted average of their ‘‘elite’’ neighbors. In the proposed algorithm a variable neighborhood-based diversity enhancement mechanism is utilized to improve population diversity. This is achieved by enforcing a circular neighboring area with a pre-defined radius R around each particle if the diversity of the population is less than a variable threshold value δ(t). The diversity of the swarm is characterized in terms of the scatter index among the particles measured by the average mean square distance as follows:

(11)

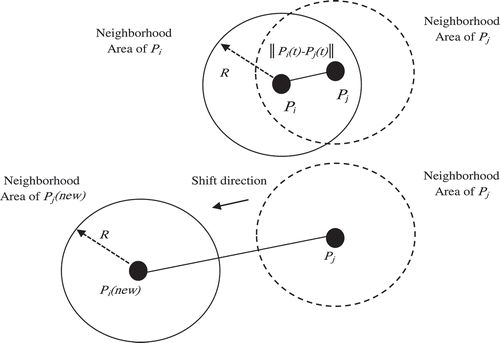
If Diversity (t) < δ(t), we check for neighborhood overlap between neighboring particles. If the neighborhood of one particle collides with another particle, a shifting operator operates on both of them according to Eq. (12) as presented in Figure 5. The weaker particle (the particle with higher makespan) will be shifted to the distance of 2R opposite to the stronger particle to generate new particles and as follows:

(12)

Figure 5. Diversity enhancement operator.

The shifted particle replaces the original particle only if it has a better fitness value. Otherwise the particle remains unchanged. For example particle P_i will be updated as follows:

(13)

where F_i and F_j are the fitness values of the two neighboring particles, and P_i(t) and P_j(t) are the positions of two particles at iteration t. This neighborhood operator guarantees that weak particles keep a definite distance from strong ones so that the precipitous clustering of particles can be prevented and weak particles are guided to search other regions of the solution space. The variable threshold δ(t) used in the algorithm gives the ability to control the diversity of the population throughout the different stages of the search process. Intuitively, it is crucial for the algorithm to have greater population diversity in the initial stages of the search process to avoid premature convergence. However, the propensity for convergence accelerates at the final stages of the search process. Therefore, the diversity threshold will start with a big value that is decreased gradually as the algorithm reaches. In this paper, the exponential decay function is employed for δ(t) as it provides an efficient particle distribution during the search process defined as follows:

(14)

where is the initial diversity threshold and K > 0 is the exponential decay constant.

Local search operator

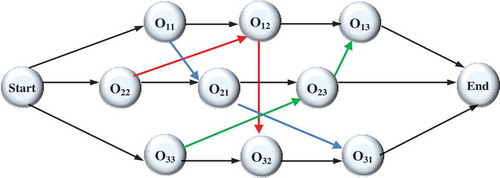
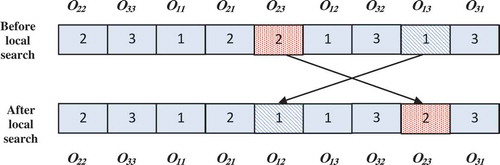
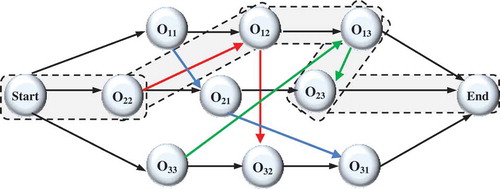
The local search process is imperative for efficient exploration of the solution space and avoiding getting trapped in local optima. The basic idea of the local search procedure is to transfer from one solution to another in the neighborhood of a candidate solution until an optimal solution is found. In this paper, neighbor particles are constructed based on critical path exploration. The makespan of a candidate solution is characterized by the length of its critical paths. Therefore, the makespan cannot be decreased without changing the present critical paths. The objective of the local search operator is to distinguish and break the existing critical paths to obtain a new schedule with a smaller makespan. A possible critical path can be characterized with a set of successive operations processed one by one without interruption and repetition from the start towards the end node. For example, if we consider the feasible schedule in Figure 2, the sequence of operations O₂₂→ O₂₁→ O₂₃→ O_13, represent the critical path of the schedule as shown in Figure 6. The Gantt chart presented earlier in Figure 4 designates the possible schedule of the JSSP. Idle time may exist in the Gantt chart between operations processed on the same machine due to the precedence constraints among operations of the same job. The makespan can be computed as the length of the critical path: C_max = t₂₂ + t₂₁ + t_{23 +} t₁₃ = 4 + 6 + 2 + 7 = 19.

Figure 6. Critical path of the feasible solution in Figure 2.

In this paper, the critical path is determined using the algorithm presented by Qing-Dao-Er-Ji and Wang (2012). Any operation on the critical path is called a critical operation. It is possible to partition the critical path into a number of blocks in which each block is the arrangement of adjacent critical operations that are processed on a particular machine. In Figure 6, the critical path is divided into three blocks, B₁ = {O₂₁} to be processed on M₁, B₂ = {O₂₂} to be processed on M₂ and B₃ = {O₂₃, O₁₃} to be processed on M₃. In the proposed algorithm, a local search operator based on the critical-path is employed to obtain new solutions by moving critical operations. The local search operator is performed on the global best particle and can be described as follows:

Step 1: Randomly select two operations α and β critical block B_j, where j [1, m]. If a critical block contains only one operation then the local search operator cannot be applied to that block.

Step 2: Generate a new particle by exchanging the positions of operations α and β.

Step 3: Evaluate, if F( then set and terminate. Else go back to Step 1.

If we apply the local search operator to the feasible solution shown in Figure 6, block B₃ = {O₂₃, O₁₃} is the only critical block containing more than one operation. The exchange of the two critical operations is illustrated in Figure 7. The distinctive graph and Gantt chart in Figures 8 and 9 present the feasible solution and the critical path after the local search operator. Critical path operations after the local search are O₂₂, O₁₂, O₁₃, O₂₃ and new C_max = t₂₂ + t₁₂ + t_{13 +} t₂₃ = 4 + 2 + 7 + 2 = 15.

Figure 7. An example of the local search operator.

Figure 8. Feasible solution and critical path after the local search operator.

Figure 9. Gantt chart of the feasible solution after the local search operator.

Genetic operators

Genetic operators impose a significant computational overhead if applied to all particles in the swarm. Therefore, genetic operators such as crossover and selection are applied to particles in which their local best does not change for a designated number of iterations. The selection of the particles is based on a non-linear ranking selection schema as explained in the following subsections.

Crossover operator

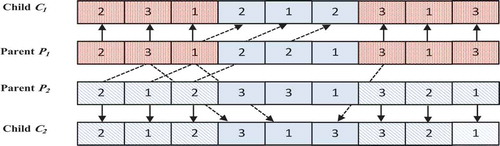
Two-point crossover is executed on the stagnated particle and another particle selected from the population poll. The conventional crossover operator is modified to guarantee that the offspring represents a feasible solution to the JSSP. The proposed crossover operator is described as follows:

Step 1: Given an JSSP, select two candidate solutions P₁ and P₂, respectively.

Step 2: Select two random indices r₁ and r₂ in the range [1,] such that r₁ < r₂.

Step 3: Copy the genes before r₁ and after r₂ in P₁ to the corresponding location in child C₁. Similarly, copy the genes before r₁ and after r₂ in P₂ to the corresponding location in child C₂.

Step 4: Empty genes in C₁ will be filled with genes of P₂ in the order presented by P₂. Genes in parent P₂ are read from left to right. If the gene has already occurred in C₁ m-times, then ignore it; otherwise, place the gene in the first empty location in C₁. The same procedure is utilized to construct child C_2.

Step 5: Evaluate C₁ and C₂, the child with a smaller makespan is to replace its parent in the current population.

An illustration of the crossover operator is presented in Figure 10.

Figure 10. An example of the crossover operator.

Non-linear ranking selection

Ranking methods employ the fitness function to map candidate solutions to a partially arranged set. All particles in the swarm are ranked from best to worst based on their fitness values. The selection probability of a particle (p) is calculated based on its rank (r) as follows:

(15)

Subject to:

(16)

where q ∈ [0, 1] is the probability of selecting the best individual and r is the rank of the individual defined as follows:

(17)

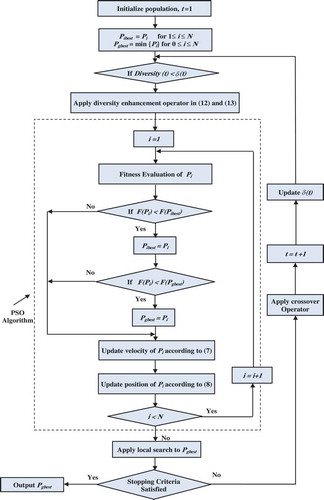
It can be seen that this selection probability doesn’t employ the absolute value of the fitness and hence it avoids fitness value scale transformations and prevents premature convergence. The proposed algorithm aims to balance the exploration and exploitation capabilities of the search process by containing both deterministic and stochastic components. The deterministic component in the algorithm is the iterative application of the conventional PSO. This component is helpful as it exploits the distributed capabilities of swarm intelligence to accelerate the convergence speed due to the attraction to preceding best particles and the global best particle. Whereas the stochastic component is present in the randomized selection, mutation, and crossover operators utilized in the neighborhood search phase. This component is beneficial in increasing the diversity of the swarm by adjusting the disparities between the particles. The main framework of the proposed PSO algorithm with neighborhood and genetic operators (PSO-NGO) is presented in the flowchart shown in Figure 11.

Figure 11. Flow chart of the PSO-NGO algorithm.

Experimental results

The performance of the PSO-NGO was assessed using benchmarks taken from the Operations Research (OR) Library. In addition, to verify the efficiency and validity of our algorithm on larger scale problems, we have chosen the test set designed by Taillard (1993) with sizes that correspond to real dimensions of practical industrial problems. In particular, a set of 123 instances from three classes of standard JSSP test problems were considered: 3 problems designed by Fisher and Thompson (1963): referred as Ft06, Ft10, and Ft20, 40 problems designed by Lawrence (1984): referred as La01–La40, and 80 problems designed by Taillard (1993): referred as Ta01–Ta80. The dimension of these problem instances range from 6 to 100 jobs and 5 to 20 machines. The objective of the PSO-NGO was the minimization of makespan described in (1). Constant D that confirms the satisfaction of operation precedence constraints and machine constraints in equations (2) and (3) was set to 10⁹. The proposed algorithm was implemented in C++ on an Intel Pentium IV 3GHz PC with 2GB of RAM. Due to the probabilistic nature of the algorithm and to ensure result consistency, 10 independent runs for each problem were performed to ensure meaningful results.

PSO and GA parameter setting

PSO parameters were chosen experimentally in order to get a satisfactory solution quality in an acceptable time span. Different parameter combinations from the PSO literature were examined (Eberhart and Shi 2001). During the preliminary experiment, four swarm sizes (N) of 10, 20, 50, and 100 particles were selected to test the algorithm. The outcome of N = 20 was superior and used for all further experiments. The maximal number of iterations was set to 200. The inertial weight ω was decreased linearly from ω_max to ω_min during iterations using equation (9). ω_max and ω_min were selected from the set {0.5, 0.7, 0.9} and {0.1, 0.3, 0.5}, respectively. The parameter combination that yielded the best results and that was used throughout the experiments is presented in Table 2.

Table 2. Parameter settings for PSO and GA.

Algorithm/Operator	Parameter name	Parameter value
PSO	Swarm size (N)	20
	Inertia weight (ω)	0.9 down to 0.3
	Learning parameters (c1) and (c2)	∈ [0, 1] such that c1+ c2 ≤ 1
	The maximum velocity (Vmax)	(
GA	Crossover probability (Pc)	0.8
	Probability of selecting best individual (q)	0.7

Genetic parameters such as the crossover probability (P_c) and the probability of selecting the best individual (q) also affect the performance of PSO-NGO. To select better values for these two control parameters, we investigated the performance of PSO-NGO under variant P_c and q values. P_c and q were selected from the set {0, 0.2, 0.4, 0.6, 0.8, 1} and {0.1, 0.3, 0.5, 0.7, 0.9, 1.0}, respectively. Therefore, there are possible choices for the combination. Preliminary experiments demonstrated that P_c = 0.8 and q = 0.7 are the relatively best choices and were used throughout the experiments.

Diversity enhancement operator parameter setting

The neighborhood-based diversity enhancement mechanism enforces a circular neighboring area with a predefined radius R around each particle. Experimental tests were conducted to find the best value for R. Radius R was chosen to change from 0 to 10 with 0.1 steps. In the preliminary experiments all test instances were considered for finding the best value of R. Experiments were conducted 10 times for each test instance and the average percentage error (APE) was calculated as follows:

(18)

where is the average makespan of the 10 runs of the test instance and is the value of the best known solution for the problem. The best results for all test instances were obtained when R was between 5.2 and 5.9. Furthermore, for high values of R, the performance of the algorithm would be degraded due to the fact that the particles would be stuck in the early stages of search process. Similarly, the performance of the algorithm is not satisfactory for low values of R since the particles would be trapped in local minima. Thus, it would be reasonable to use the value 5.6 for R.

Similarly, the initial diversity threshold and exponential decay constant (K) are used to adjust the diversity of the population throughout the different stages of the search process. It is essential to provide the particles with a greater diversity in the early stages of the search process to prevent them from prematurely clustering around local optima. Experimental tests have been conducted to obtain the best possible setting values for and K. Test instances La21, La27, La29, La37, La39, and La40 were employed for this purpose. was chosen to change from 0 to 5 with 0.1 steps and K was chosen to change from 0.1 to 2 with 0.1 steps. Each experiment was conducted 10 times for each test instance and the APE values were recorded. Experimental results demonstrated that that the minimum APE values for all test instances were obtained when was between 2.5 and 3 and K was between 1.2 and 1.4. Therefore, the values = 2.75 and K = 1.3 were used throughout the experiments.

Effect of different strategies

The proposed approach employs two strategies: neighborhood-based operators and genetic operators. To investigate the effect of these strategies, we studied the performance of the standard PSO, PSO with neighborhood-based operators (NPSO), PSO with genetic operators (GPSO), and the proposed PSO-NGO which includes both mechanisms. This will help to verify the effectiveness of these strategies separately. For the parameters, we have used the same settings as described in the sections “PSO and GA parameter setting” and “Diversity enhancement operator parameter setting”.

Table 3 presents the name of the benchmark problem, the problem size, the best known solution to the problem (BKS), and the value of the best solution found by each strategy in the 10 replications. In addition, Table 3 presents the APE calculated as presented earlier in (18) and the average percentage improvement (API) of the PSO-NGO against the other approaches (averaged over the 10 replications). The API is calculated as follows:

(19)

Table 3. Comparison of the different strategies: PSO, NPSO, GPSO, and PSO-NGO.

Problem	Size	BKS	PSO-NGO Best APE		PSO Best APE API			NPSO Best APE API			GPSO Best APE API
Ft06	6 x 6	55	55	0.000	55	0.000	0.000	55	0.000	0.000	55	0.000	0.000
Ft10	10 x 10	930	930	0.000	930	0.000	0.000	930	0.000	0.000	930	0.000	0.000
Ft20	20 x 5	1165	1165	0.000	1165	0.000	0.000	1165	0.000	0.000	1165	0.000	0.000
La01	10 x 5	666	666	0.000	666	0.000	0.000	666	0.000	0.000	666	0.000	0.000
La02	10 x 5	655	655	0.000	655	0.000	0.000	655	0.000	0.000	655	0.000	0.000
La03	10 x 5	597	597	0.000	597	0.000	0.000	597	0.000	0.000	597	0.000	0.000
La04	10 x 5	590	590	0.000	590	0.000	0.000	590	0.000	0.000	590	0.000	0.000
La05	10 x 5	593	593	0.000	593	0.000	0.000	593	0.000	0.000	593	0.000	0.000
La06	15 x 5	926	926	0.000	926	0.000	0.000	926	0.000	0.000	926	0.000	0.000
La07	15 x 5	890	890	0.000	890	0.000	0.000	890	0.000	0.000	890	0.000	0.000
La08	15 x 5	863	863	0.000	863	0.000	0.000	863	0.000	0.000	863	0.000	0.000
La09	15 x 5	951	951	0.000	951	0.000	0.000	951	0.000	0.000	951	0.000	0.000
La10	15 x 5	958	958	0.000	958	0.000	0.000	958	0.000	0.000	958	0.000	0.000
La11	20 x 5	1222	1222	0.000	1222	0.000	0.000	1222	0.000	0.000	1222	0.000	0.000
La12	20 x 5	1039	1039	0.000	1039	0.000	0.000	1039	0.000	0.000	1039	0.000	0.000
La13	20 x 5	1150	1150	0.000	1150	0.000	0.000	1150	0.000	0.000	1150	0.000	0.000
La14	20 x 5	1292	1292	0.000	1292	0.000	0.000	1292	0.000	0.000	1292	0.000	0.000
La15	20 x 5	1207	1207	0.000	1207	0.000	0.000	1207	0.000	0.000	1207	0.000	0.000
La16	10 x 10	945	945	0.000	946	0.106	0.106	945	0.000	0.000	945	0.000	0.000
La17	10 x 10	784	784	0.000	786	0.255	0.255	784	0.000	0.000	784	0.000	0.000
La18	10 x 10	848	848	0.000	850	0.236	0.236	848	0.000	0.000	848	0.000	0.000
La19	10 x 10	842	842	0.000	846	0.475	0.475	842	0.000	0.000	842	0.000	0.000
La20	10 x 10	902	902	0.000	907	0.554	0.554	902	0.000	0.000	902	0.000	0.000
La21	15 x 10	1046	1046	0.000	1062	1.530	1.530	1046	0.000	0.000	1055	0.860	0.860
La22	15 x 10	927	927	0.000	935	0.863	0.863	932	0.539	0.539	927	0.000	0.000
La23	15 x 10	1032	1032	0.000	1034	0.194	0.194	1032	0.000	0.000	1032	0.000	0.000
La24	15 x 10	935	935	0.000	955	2.139	2.139	940	0.535	0.535	950	1.604	1.604
La25	15 x 10	977	977	0.000	986	0.921	0.921	979	0.205	0.205	984	0.716	0.716
La26	20 x 10	1218	1218	0.000	1220	0.164	0.164	1218	0.000	0.000	1218	0.000	0.000
La27	20 x 10	1235	1235	0.000	1266	2.510	2.510	1235	0.000	0.000	1250	1.215	1.215
La28	20 x 10	1216	1216	0.000	1231	1.234	1.234	1216	0.000	0.000	1222	0.493	0.493
La29	20 x 10	1152	1163	0.955	1177	2.170	1.117	1177	2.170	1.117	1180	2.431	1.375
La30	20 x 10	1355	1355	0.000	1357	0.148	0.148	1355	0.000	0.000	1355	0.000	0.000
La31	30 x 10	1784	1784	0.000	1789	0.280	0.280	1784	0.000	0.000	1784	0.000	0.000
La32	30 x 10	1850	1850	0.000	1855	0.270	0.270	1852	0.108	0.108	1852	0.108	0.108
La33	30 x 10	1719	1719	0.000	1723	0.233	0.233	1719	0.000	0.000	1720	0.058	0.058
La34	30 x 10	1721	1721	0.000	1725	0.232	0.232	1721	0.000	0.000	1722	0.058	0.058
La35	30 x 10	1888	1888	0.000	1890	0.106	0.106	1888	0.000	0.000	1888	0.000	0.000
La36	15 x 15	1268	1268	0.000	1281	1.025	1.025	1268	0.000	0.000	1278	0.789	0.789
La37	15 x 15	1397	1397	0.000	1435	2.720	2.720	1415	1.288	1.288	1431	2.434	2.434
La38	15 x 15	1196	1196	0.000	1219	1.923	1.923	1213	1.421	1.421	1216	1.672	1.672
La39	15 x 15	1233	1233	0.000	1248	1.217	1.217	1241	0.649	0.649	1246	1.054	1.054
La40	15 x 15	1222	1224	0.164	1251	2.373	2.206	1237	1.227	1.062	1241	1.555	1.389
Average				0.026		0.555	0.529		0.189	0.163		0.350	0.324

Boldface indicates achievement of the best known solution

Where is the solution obtained by the proposed algorithm and H is the solution obtained by the approach compared against.

The PSO-NGO obtained the BKS for 41 test instances compared to 18, 34, and 29 for PSO, NPSO, and GPSO, respectively. The APE for the proposed PSO-NGO was 0.026 compared to 0.555, 0.189, and 0.350 for PSO, NPSO, and GPSO, respectively. The PSO-NGO achieved an API of 0.529, 0.163, and 0.324 over PSO, NPSO and GPSO.

From the comparison of NPSO with PSO, we can see that incorporating the neighborhood-based operators was effective for most test instances. NPSO achieved better results than stand-alone PSO in all test cases except for instances Ft06, Ft10, Ft20, La1- La15, and La29 where it achieved similar results. For La29, both NPSO and GPSO hardly improved the quality of solution. PSO performs better than GPSO on La29, while GPSO outperforms or achieves similar results to PSO for all the other test instances. By combining these two strategies, PSO-NGO obtains excellent performance. It outperforms other three PSO algorithms in most of the test instances. Specifically, for some of the high-dimensional problems using a single strategy can hardly achieve promising solutions such as in instances La37- La40 where both NPSO and GPSO fall into local minima, while PSO-NGO achieves satisfactory results. This is due to the fact that the neighborhood-based operators are improved variants of the conventional PSO algorithm that are based on the attraction to or. They help to accelerate the convergence rate of PSO, but run the risk of losing swarm diversity. On the other hand, the genetic operators help to increase the swarm diversity. Yet, they can slow down the convergence rate especially for high-dimensional problems. The hybridization of these two strategies in PSO-NGO achieves the desired balance between the exploration and exploitation search abilities.

Comparison with other metaheuristics

Results obtained by the PSO-NGO were compared to results reported in the literature such as: results obtained by TS with shifting bottleneck (TSSB) (Pezzella and Merelli 2000), hybrid PSO (HPSO) (Sha and Hsu 2006), hybrid PSO with VNS(PSO-VNS) (Tasgetiren et al. 2006), a multiple-type individual enhancement PSO (MPSO) (Lin et al. 2010), best-so-far artificial ABC (Banharnsakun, Sirinaovakul, and Achalakul 2012), the PSO and AIS Hybrid (PSO-AIS) (Ge et al. (2008), hybrid genetic algorithm (HGA) (Qing-Dao-Er-Ji and Wang 2012) and the MA (Gao et al. 2011). The parameters setting used for the proposed algorithm was reported earlier in the section “PSO and GA parameter setting”.

Table 4 presents the computational results of the experiments performed on 43 benchmark instances: Ft06, Ft10, Ft20, and La01–La40, taken from the OR Library. The table includes the name of the benchmark problem, the size, BKS, the value of the best solution found by the proposed algorithm in the 10 replications, the best values reported for the other algorithms, the APE for each algorithm and the API of the proposed PSO-NGO against the other approaches. For small benchmark instances Ft06, Ft10, Ft20, and La01– La19, all algorithms attained the optimal solution. For relatively larger instances La16–La40, the performance of the proposed algorithm was better than or similar to other algorithms. According to Table 4, the PSO-NGO algorithm found the best known solution for 41 out of the 43 test instances. This is similar to the results obtained by HPSO and Best-so-far ABC and better than MPSO, PSO-AIS, HGA, and MA which found 35, 32, 33, and 33 best known solutions, respectively. In particular, the two instances where the PSO-NGO algorithm did not yield the optimal solution were La29 and La40. For instance La29 the result obtained by the PSO-NGO algorithm (1163) was similar to HPSO and was worse than the results obtained by the HGA (1160). For instance La40, the solution found by the PSO-NGO algorithm (1224) was similar to the result obtained by HPSO, PSO-VNS, and Best-so-far ABC. The APE for the proposed PSO-NGO was 0.026 compared to 0.026, 0.087, 0.087, 0.148, 0.028, 0.325, 0.176 and 0.330 for HPSO, PSO-VNS, MPSO, Best-so-far ABC, PSO-AIS, HGA, and MA, respectively. The PSO-NGO achieved an API of 0.006, 0.122, 0.001, 0.299, 0.161, and 0.304 over PSO-VNS, MPSO, Best-so-far ABC, PSO-AIS, HGA, and MA, respectively.

Table 4. Computational results of PSO-NGO, HPSO, PSO-VNS, MPSO, Best-so-far ABC, PSO-AIS, HGA, and MA for Ft and La test problems.

Problem	Size	BKS	PSO-NGO Best APE		HPSO Best APE API			PSO- VNS Best APE API			MPSO Best APE API
Ft06	6 x 6	55	55	0.000	55	0.000	0.000	N/A	N/A	N/A	55	0.000	0.000
Ft10	10 x10	930	930	0.000	930	0.000	0.000	930	N/A	N/A	930	0.000	0.000
Ft20	20 x5	1165	1165	0.000	1165	0.000	0.000	1165	0.000	0.000	1165	0.000	0.000
La01	10 x5	666	666	0.000	666	0.000	0.000	N/A	N/A	N/A	666	0.000	0.000
La02	10 x 5	655	655	0.000	655	0.000	0.000	N/A	N/A	N/A	655	0.000	0.000
La03	10 x 5	597	597	0.000	597	0.000	0.000	N/A	N/A	N/A	597	0.000	0.000
La04	10 x 5	590	590	0.000	590	0.000	0.000	N/A	N/A	N/A	590	0.000	0.000
La05	10 x 5	593	593	0.000	593	0.000	0.000	N/A	N/A	N/A	593	0.000	0.000
La06	15 x 5	926	926	0.000	926	0.000	0.000	N/A	N/A	N/A	926	0.000	0.000
La07	15 x 5	890	890	0.000	890	0.000	0.000	N/A	N/A	N/A	890	0.000	0.000
La08	15 x 5	863	863	0.000	863	0.000	0.000	N/A	N/A	N/A	863	0.000	0.000
La09	15 x 5	951	951	0.000	951	0.000	0.000	N/A	N/A	N/A	951	0.000	0.000
La10	15 x 5	958	958	0.000	958	0.000	0.000	N/A	N/A	N/A	958	0.000	0.000
La11	20 x 5	1222	1222	0.000	1222	0.000	0.000	N/A	N/A	N/A	1222	0.000	0.000
La12	20 x 5	1039	1039	0.000	1039	0.000	0.000	N/A	N/A	N/A	1039	0.000	0.000
La13	20 x 5	1150	1150	0.000	1150	0.000	0.000	N/A	N/A	N/A	1150	0.000	0.000
La14	20 x 5	1292	1292	0.000	1292	0.000	0.000	N/A	N/A	N/A	1292	0.000	0.000
La15	20 x 5	1207	1207	0.000	1207	0.000	0.000	N/A	N/A	N/A	1207	0.000	0.000
La16	10 x10	945	945	0.000	945	0.000	0.000	945	0.000	0.000	945	0.000	0.000
La17	10 x10	784	784	0.000	784	0.000	0.000	N/A	N/A	N/A	784	0.000	0.000
La18	10 x10	848	848	0.000	848	0.000	0.000	N/A	N/A	N/A	848	0.000	0.000
La19	10 x10	842	842	0.000	842	0.000	0.000	842	0.000	0.000	842	0.000	0.000
La20	10 x10	902	902	0.000	902	0.000	0.000	N/A	N/A	N/A	902	0.000	0.000
La21	15 x10	1046	1046	0.000	1046	0.000	0.000	1047	0.096	0.096	1046	0.000	0.000
La22	15 x10	927	927	0.000	927	0.000	0.000	927	0.000	0.000	932	0.539	0.539
La23	15 x10	1032	1032	0.000	1032	0.000	0.000	N/A	N/A	N/A	1032	0.000	0.000
La24	15 x10	935	935	0.000	935	0.000	0.000	935	0.000	0.000	941	0.642	0.642
La25	15 x10	977	977	0.000	977	0.000	0.000	977	0.000	0.000	977	0.000	0.000
La26	20 x10	1218	1218	0.000	1218	0.000	0.000	N/A	N/A	N/A	1218	0.000	0.000
La27	20 x10	1235	1235	0.000	1235	0.000	0.000	1235	0.000	0.000	1239	0.324	0.324
La28	20 x10	1216	1216	0.000	1216	0.000	0.000	1216	0.000	0.000	1216	0.000	0.000
La29	20 x10	1152	1163	0.955	1163	0.955	0.000	1164	1.042	0.086	1173	1.823	0.860
La30	20 x10	1355	1355	0.000	1355	0.000	0.000	N/A	N/A	N/A	1355	0.000	0.000
La31	30 x10	1784	1784	0.000	1784	0.000	0.000	N/A	N/A	N/A	1784	0.000	0.000
La32	30 x10	1850	1850	0.000	1850	0.000	0.000	N/A	N/A	N/A	1850	0.000	0.000
La33	30 x10	1719	1719	0.000	1719	0.000	0.000	N/A	N/A	N/A	1719	0.000	0.000
La34	30 x10	1721	1721	0.000	1721	0.000	0.000	N/A	N/A	N/A	1721	0.000	0.000
La35	30 x10	1888	1888	0.000	1888	0.000	0.000	N/A	N/A	N/A	1888	0.000	0.000
La36	15 x15	1268	1268	0.000	1268	0.000	0.000	1268	0.000	0.000	1278	0.789	0.789
La37	15 x15	1397	1397	0.000	1397	0.000	0.000	1397	0.000	0.000	1411	1.002	1.002
La38	15 x15	1196	1196	0.000	1196	0.000	0.000	1196	0.000	0.000	1208	1.003	1.003
La39	15 x15	1233	1233	0.000	1233	0.000	0.000	1233	0.000	0.000	1233	0.000	0.000
La40	15 x15	1222	1224	0.164	1224	0.164	0.000	1224	0.164	0.000	1225	0.245	0.082
Average				0.026		0.026	0.000		0.087	0.006		0.148	0.122
Problem	Size	(Best-so-far) ABC Best APE API			PSO-AIS Best APE API			HGA Best APE API			MA Best APE API
Ft06	6 x 6	55	0.000	0.000	55	0.000	0.000	55	0.000	0.000	55	0.000	0.000
Ft10	10 x 10	930	0.000	0.000	930	0.000	0.000	930	0.000	0.000	930	0.000	0.000
Ft20	20 x 5	1165	0.000	0.000	1165	0.000	0.000	1165	0.000	0.000	1165	0.000	0.000
La01	10 x 5	666	0.000	0.000	666	0.000	0.000	666	0.000	0.000	666	0.000	0.000
La02	10 x 5	655	0.000	0.000	655	0.000	0.000	655	0.000	0.000	655	0.000	0.000
La03	10 x 5	597	0.000	0.000	597	0.000	0.000	597	0.000	0.000	597	0.000	0.000
La04	10 x 5	590	0.000	0.000	590	0.000	0.000	590	0.000	0.000	590	0.000	0.000
La05	10 x 5	593	0.000	0.000	593	0.000	0.000	593	0.000	0.000	593	0.000	0.000
La06	15 x 5	926	0.000	0.000	926	0.000	0.000	926	0.000	0.000	926	0.000	0.000
La07	15 x 5	890	0.000	0.000	890	0.000	0.000	890	0.000	0.000	890	0.000	0.000
La08	15 x 5	863	0.000	0.000	863	0.000	0.000	863	0.000	0.000	863	0.000	0.000
La09	15 x 5	951	0.000	0.000	951	0.000	0.000	951	0.000	0.000	951	0.000	0.000
La10	15 x 5	958	0.000	0.000	958	0.000	0.000	958	0.000	0.000	958	0.000	0.000
La11	20 x 5	1222	0.000	0.000	1222	0.000	0.000	1222	0.000	0.000	1222	0.000	0.000
La12	20 x 5	1039	0.000	0.000	1039	0.000	0.000	1039	0.000	0.000	1039	0.000	0.000
La13	20 x 5	1150	0.000	0.000	1150	0.000	0.000	1150	0.000	0.000	1150	0.000	0.000
La14	20 x 5	1292	0.000	0.000	1292	0.000	0.000	1292	0.000	0.000	1292	0.000	0.000
La15	20 x 5	1207	0.000	0.000	1207	0.000	0.000	1207	0.000	0.000	1207	0.000	0.000
La16	10 x 10	945	0.000	0.000	945	0.000	0.000	945	0.000	0.000	945	0.000	0.000
La17	10 x 10	784	0.000	0.000	784	0.000	0.000	784	0.000	0.000	784	0.000	0.000
La18	10 x 10	848	0.000	0.000	848	0.000	0.000	848	0.000	0.000	848	0.000	0.000
La19	10 x 10	842	0.000	0.000	842	0.000	0.000	844	0.238	0.238	842	0.000	0.000
La20	10 x 10	902	0.000	0.000	902	0.000	0.000	907	0.554	0.554	902	0.000	0.000
La21	15 x 10	1046	0.000	0.000	1046	0.000	0.000	1046	0.000	0.000	1055	0.860	0.860
La22	15 x 10	927	0.000	0.000	932	0.539	0.539	935	0.863	0.863	927	0.000	0.000
La23	15 x 10	1032	0.000	0.000	1032	0.000	0.000	1032	0.000	0.000	1032	0.000	0.000
La24	15 x 10	935	0.000	0.000	950	1.604	1.604	953	1.925	1.925	940	0.535	0.535
La25	15 x 10	977	0.000	0.000	979	0.205	0.205	981	0.409	0.409	984	0.716	0.716
La26	20 x 10	1218	0.000	0.000	1218	0.000	0.000	1218	0.000	0.000	1218	0.000	0.000
La27	20 x 10	1235	0.000	0.000	1256	1.700	1.700	1236	0.081	0.081	1261	2.105	2.105
La28	20 x 10	1216	0.000	0.000	1227	0.905	0.905	1216	0.000	0.000	1216	0.000	0.000
La29	20 x 10	1164	1.042	0.086	1184	2.778	1.806	1160	0.694	−0.258	1190	3.299	2.322
La30	20 x 10	1355	0.000	0.000	1355	0.000	0.000	1355	0.000	0.000	1355	0.000	0.000
La31	30 x 10	1784	0.000	0.000	1784	0.000	0.000	1784	0.000	0.000	1784	0.000	0.000
La32	30 x 10	1850	0.000	0.000	1850	0.000	0.000	1850	0.000	0.000	1850	0.000	0.000
La33	30 x 10	1719	0.000	0.000	1719	0.000	0.000	1719	0.000	0.000	1719	0.000	0.000
La34	30 x 10	1721	0.000	0.000	1721	0.000	0.000	1721	0.000	0.000	1721	0.000	0.000
La35	30 x 10	1888	0.000	0.000	1888	0.000	0.000	1888	0.000	0.000	1888	0.000	0.000
La36	15 x 15	1268	0.000	0.000	1281	1.025	1.025	1287	1.498	1.498	1281	1.025	1.025
La37	15 x 15	1397	0.000	0.000	1415	1.288	1.288	1407	0.716	0.716	1431	2.434	2.434
La38	15 x 15	1196	0.000	0.000	1213	1.421	1.421	1196	0.000	0.000	1216	1.672	1.672
La39	15 x 15	1233	0.000	0.000	1246	1.054	1.054	1233	0.000	0.000	1241	0.649	0.649
La40	15 x 15	1224	0.164	0.000	1240	1.473	1.307	1229	0.573	0.408	1233	0.900	0.735
Average			0.028	0.001		0.325	0.299		0.176	0.161		0.330	0.304

Boldface indicates achievement of the best known solution. N/A stands for “not available”.

We further tested PSO-NGO on Ta test problems: Ta01-Ta80 (Taillard 1993). The computational results are shown in Table 5. We particularly compared PSO-NGO with HPSO (Sha and Hsu 2006) and TSSB (Pezzella and Merelli 2000). The PSO-NGO obtained the BKS for 42 test instances compared to 27 and 31 for HPSO and TSSB, respectively. The APE for the proposed PSO-NGO was 0.433 compared to 0.566 and 0.812 for HPSO and TSSB, respectively. The PSO-NGO achieved an API of 0.155 and 0.378 over HPSO and TSSB. PSO-NGO performed better than HPSO on 37 test instance, obtained similar results for 39 test instances and worse results on only 4 test instances. In particular, in large scale problems () problem instances PSO-NGO outperformed HPSO in 9 out of 10 instances and obtained similar results in 1 test instance. Whereas, PSO-NGO performed better than TSSB on 44 test instance and obtained similar results for 36 test instances.

Table 5. Computational results of PSO-NGO, HPSO, and TSSB for Ta test problems.

Problem	Size	BKS	PSO-NGO Best APE		HPSO Best APE API			TSSB Best APE API
Ta01	15 x15	1231	1231	0.000	1231	0.000	0.000	1241	0.812	0.812
Ta02	15 x15	1244	1244	0.000	1244	0.000	0.000	1244	0.000	0.000
Ta03	15 x15	1218	1218	0.000	1218	0.000	0.000	1222	0.328	0.328
Ta04	15 x15	1175	1175	0.000	1175	0.000	0.000	1175	0.000	0.000
Ta05	15 x15	1224	1224	0.000	1224	0.000	0.000	1229	0.408	0.408
Ta06	15 x15	1238	1238	0.000	1238	0.000	0.000	1245	0.565	0.565
Ta07	15 x15	1227	1228	0.081	1228	0.081	0.000	1228	0.081	0.000
Ta08	15 x15	1217	1217	0.000	1217	0.000	0.000	1220	0.247	0.247
Ta09	15 x15	1274	1274	0.000	1274	0.000	0.000	1291	1.334	1.334
Ta10	15 x15	1241	1248	0.564	1249	0.645	0.080	1250	0.725	0.160
Ta11	20 x15	1359	1364	0.368	1366	0.515	0.147	1371	0.883	0.513
Ta12	20 x15	1367	1370	0.219	1370	0.219	0.000	1379	0.878	0.657
Ta13	20 x15	1342	1350	0.596	1350	0.596	0.000	1362	1.490	0.889
Ta14	20 x15	1345	1345	0.000	1345	0.000	0.000	1345	0.000	0.000
Ta15	20 x15	1339	1352	0.971	1350	0.822	−0.148	1360	1.568	0.592
Ta16	20 x15	1360	1364	0.294	1368	0.588	0.293	1370	0.735	0.440
Ta17	20 x15	1462	1470	0.547	1473	0.752	0.204	1481	1.300	0.748
Ta18	20 x15	1396	1404	0.573	1407	0.788	0.214	1426	2.149	1.567
Ta19	20 x15	1335	1335	0.000	1335	0.000	0.000	1351	1.199	1.199
Ta20	20 x15	1348	1358	0.742	1358	0.742	0.000	1366	1.335	0.589
Ta21	20 x20	1644	1655	0.669	1658	0.852	0.181	1659	0.912	0.242
Ta22	20 x20	1600	1618	1.125	1614	0.875	−0.247	1623	1.438	0.309
Ta23	20 x20	1557	1557	0.000	1559	0.128	0.128	1573	1.028	1.028
Ta24	20 x20	1646	1652	0.365	1654	0.486	0.121	1659	0.790	0.424
Ta25	20 x20	1595	1605	0.627	1616	1.317	0.685	1606	0.690	0.062
Ta26	20 x20	1645	1662	1.033	1662	1.033	0.000	1666	1.277	0.241
Ta27	20 x20	1680	1688	0.476	1690	0.595	0.118	1697	1.012	0.533
Ta28	20 x20	1603	1615	0.749	1617	0.873	0.124	1622	1.185	0.433
Ta29	20 x20	1625	1634	0.554	1634	0.554	0.000	1635	0.615	0.061
Ta30	20 x20	1584	1586	0.126	1589	0.316	0.189	1614	1.894	1.765
Ta31	30 x15	1764	1764	0.000	1766	0.113	0.113	1771	0.397	0.397
Ta32	30 x15	1795	1820	1.393	1823	1.560	0.165	1840	2.507	1.099
Ta33	30 x15	1791	1795	0.223	1818	1.508	1.281	1833	2.345	2.117
Ta34	30 x15	1829	1844	0.820	1844	0.820	0.000	1846	0.929	0.108
Ta35	30 x15	2007	2007	0.000	2007	0.000	0.000	2007	0.000	0.000
Ta36	30 x15	1819	1825	0.330	1825	0.330	0.000	1825	0.330	0.000
Ta37	30 x15	1771	1788	0.960	1795	1.355	0.391	1813	2.372	1.398
Ta38	30 x15	1673	1681	0.478	1681	0.478	0.000	1697	1.435	0.952
Ta39	30 x15	1795	1795	0.000	1796	0.056	0.056	1815	1.114	1.114
Ta40	30 x15	1674	1694	1.195	1698	1.434	0.236	1725	3.047	1.830
Ta41	30 x20	2018	2045	1.338	2047	1.437	0.098	2045	1.338	0.000
Ta42	30 x20	1949	1966	0.872	1970	1.077	0.203	1979	1.539	0.661
Ta43	30 x20	1858	1895	1.991	1899	2.207	0.211	1898	2.153	0.158
Ta44	30 x20	1983	2019	1.815	2019	1.815	0.000	2036	2.673	0.842
Ta45	30 x20	2000	2016	0.800	2010	0.500	−0.298	2021	1.050	0.248
Ta46	30 x20	2015	2040	1.241	2041	1.290	0.049	2047	1.588	0.343
Ta47	30 x20	1903	1930	1.419	1935	1.682	0.259	1938	1.839	0.415
Ta48	30 x20	1949	1993	2.258	1994	2.309	0.050	1996	2.411	0.151
Ta49	30 x20	1967	1990	1.169	1992	1.271	0.101	2013	2.339	1.156
Ta50	30 x20	1926	1975	2.544	1975	2.544	0.000	1975	2.544	0.000
Ta51	50 x15	2760	2760	0.000	2760	0.000	0.000	2760	0.000	0.000
Ta52	50 x15	2756	2756	0.000	2756	0.000	0.000	2756	0.000	0.000
Ta53	50 x15	2717	2717	0.000	2717	0.000	0.000	2717	0.000	0.000
Ta54	50 x15	2839	2839	0.000	2839	0.000	0.000	2839	0.000	0.000
Ta55	50 x15	2679	2679	0.000	2679	0.000	0.000	2684	0.187	0.187
Ta56	50 x15	2781	2781	0.000	2781	0.000	0.000	2781	0.000	0.000
Ta57	50 x15	2943	2943	0.000	2943	0.000	0.000	2943	0.000	0.000
Ta58	50 x15	2885	2885	0.000	2885	0.000	0.000	2885	0.000	0.000
Ta59	50 x15	2655	2655	0.000	2655	0.000	0.000	2655	0.000	0.000
Ta60	50 x15	2723	2723	0.000	2723	0.000	0.000	2723	0.000	0.000
Ta61	50 x20	2868	2868	0.000	2868	0.000	0.000	2868	0.000	0.000
Ta62	50 x20	2869	2942	2.544	2930	2.126	−0.408	2942	2.544	0.000
Ta63	50 x20	2755	2755	0.000	2755	0.000	0.000	2755	0.000	0.000
Ta64	50 x20	2702	2702	0.000	2702	0.000	0.000	2702	0.000	0.000
Ta65	50 x20	2725	2725	0.000	2735	0.367	0.367	2725	0.000	0.000
Ta66	50 x20	2845	2845	0.000	2848	0.105	0.105	2845	0.000	0.000
Ta67	50 x20	2825	2840	0.531	2840	0.531	0.000	2865	1.416	0.880
Ta68	50 x20	2784	2784	0.000	2784	0.000	0.000	2784	0.000	0.000
Ta69	50 x20	3071	3071	0.000	3071	0.000	0.000	3071	0.000	0.000
Ta70	50 x20	2995	2995	0.000	3005	0.334	0.334	2995	0.000	0.000
Ta71	100 x20	5464	5464	0.000	5519	1.007	1.007	5464	0.000	0.000
Ta72	100 x20	5181	5181	0.000	5211	0.579	0.579	5181	0.000	0.000
Ta73	100 x20	5568	5568	0.000	5581	0.233	0.233	5568	0.000	0.000
Ta74	100 x20	5339	5339	0.000	5355	0.300	0.300	5339	0.000	0.000
Ta75	100 x20	5392	5392	0.000	5466	1.372	1.372	5392	0.000	0.000
Ta76	100 x20	5342	5342	0.000	5396	1.011	1.011	5342	0.000	0.000
Ta77	100 x20	5436	5436	0.000	5444	0.147	0.147	5436	0.000	0.000
Ta78	100 x20	5394	5394	0.000	5394	0.000	0.000	5394	0.000	0.000
Ta79	100 x20	5358	5358	0.000	5363	0.093	0.093	5358	0.000	0.000
Ta80	100 x20	5183	5183	0.000	5209	0.502	0.502	5183	0.000	0.000
Average				0.433		0.566	0.155		0.812	0.378

Boldface indicates achievement of the best known solution

Experimental results presented in Tables 3, 4 and 5 validate the effectiveness of the proposed PSO-NGO algorithm in solving the minimal makespan JSSP in terms of robustness and solution quality.

Conclusions and future work

In this paper, an effective PSO-based scheduling algorithm for minimizing the makespan in the JSSP is presented. In the PSO system, a new model for updating the velocity and the position of the particles is proposed to conform to the JSSP. The conventional PSO algorithm is improved by defining two neighborhood-based operators to enhance population diversity and to avoid premature convergence to local optima. First, the diversity enhancement operator tends to improve the population diversity by relocating neighboring particles to avoid premature clustering and to achieve broader exploration of the solution space. This is achieved by enforcing a circular neighboring area around each particle if the diversity of the population falls less than the diversity threshold value. The diversity threshold is adaptively modified to regulate the population diversity throughout the different stages of the search process. Second, the local search operator is used to create new solutions in the neighborhood of candidate solutions based on critical path analysis. Moreover, the algorithm is reinforced with genetic well-known operators “selection” and “crossover” to evolve stagnated particles in the swarm. The proposed algorithm has been evaluated using 123 well-studied benchmarks. Computational results validate the effectiveness of the proposed algorithm in producing high quality solutions. Results are compared with those obtained using other existing algorithms and the proposed algorithm was found to yield reasonable improvement in solution robustness and quality in particular for large-sized problem instances.

There are several potential improvements to the proposed algorithm that can be investigated in future research. In this paper a single-criterion objective function based on makespan was studied. The proposed framework can be utilized for a wider range of objective functions or extended to multi-criteria objective functions. This is extremely important in practical real-life production problems where the appropriateness of a schedule is measured according to various objectives simultaneously. Further research can possibly be taken to compare the performance of various crossover and mutation operators in the proposed algorithm. Another possible research direction is considering a parallel implementation of the algorithm to reduce the computational time associated with the diversity enhancement operators. Moreover, the proposed algorithm can be extended to handle practical manufacturing situations such as dynamic arrivals, machine breakdown, or other factors that affect job status over time.