An Effective Way to Large-Scale Robot-Path-Planning Using a Hybrid Approach of Pre-Clustering and Greedy Heuristic

ABSTRACT

Robot-path-planning seeks the shortest path to optimize the motion cost for robots. In robot-path-planning, the computational time will significantly increase if the moving targets rise largely, also known as the large-scale TSP. Hence, the current algorithms for the shortest path planning may be ineffective in the large-scale TSP. Aimed at the real-time applications that a robot must achieve as many goals as possible within limited time and the computational time of a robot has to be short enough to provide the next moving signal in time. Otherwise, the robot will be trapped into the idle status. This work proposes a hybrid approach, called the pre-clustering greedy heuristic, to tackle the reduction of computational time cost and achieve the near-optimal solutions. The proposed algorithm demonstrates how to lower the computational time cost drastically via smaller data of a sub-group, divided by k-means clustering, and the intra-cluster path planning. An algorithm is also developed to construct the nearest connections between any two unconnected clusters, ensuring the inter-cluster tour is the shortest. As a result, by utilizing the proposed heuristic, the computational time is significantly reduced and the path length is more efficient than the benchmark algorithms, while the input data grow up to a large scale. In applications, the proposed work can be applied practically to the path planning with large-scale moving targets, for example, the employment for the ball-collecting robot in a court.

Introduction

Robot-path-planning has been prevailing in the field of robotics (Jahanshahi and Sari 2018). It aims to search the shortest path for a mobile robot, from a starting point to an ending one given in a finite workspace. In this research, the ending point is the same as the starting one, and every target past by the robot can be exactly visited once, which is the well-known traveling salesman problem (TSP). In the field of combinatorial optimization, it is a NP-hard problem (Holmqvist, Migdalas, and Pardalos 1997; Johnson and McGeoch 2007) for finding the shortest Hamiltonian cycle in a graph, where no algorithm with reasonable time is known for the solutions currently. Due to the NP-hard nature, it will be difficult to solve the large-scale TSP (Allwright and Carpenter 1989; Applegate and Cook 1993) when the moving targets become more and more, which requires enormous computational effort.

Aimed at the real-time applications, it is generally anticipated that a robot can achieve as many tasks or goals as possible within limited time. However, when the computational time is getting too long, it is unable to provide a robot with the next moving signal in time; instead, the robot will be mostly trapped into the idle status. Thus, it is necessary to alleviate a large part of idle status in a large-scale robot-path-planning, and some efficient heuristic algorithms have to be investigated, though only the near-optimal solutions are achieved.

This work proposes three models for the hybrid approach, combining the pre-clustering and construction method, and different variants of greedy searches, contributing on significant decrease of the computational complexity and searching of near-optimal solution paths. The proposed algorithm can be widely applied to the fields of logistics, traffic routing, and robotics, for example, to a robot for automatically collecting balls in a court.

The rest of this work is outlined below. Section 2 briefly addresses the related work. Section 3 specifies how to select the proper number of clusters to divide the large-scale input data based on the k-means clustering, as well as the construction method for nearest connection between two adjacent clusters. Section 4 proposes several variants of greedy searches within a cluster for a near-optimal path-planning. Section 5 shows the simulation results. Finally, Section 6 concludes the paper and gives the future prospection on this research.

Related Work

The TSP recommends that a successful salesman should travel in an efficient tour through as many cities as possible while each city can only be visited exactly once (Schrijver 2003). There are many variants of TSPs in the real world, and robot-path-planning in this work concerns the solution for the symmetric TSP. As a classical NP-hard combinatorial optimization problem, the symmetric TSP has attracted a plenty of developments on exact and heuristic algorithms. Menger established the groundwork in solving TSP in 1930, generally thought as the possible beginning year for mathematic study of the TSP (Giesen 2000). A series of exact and heuristic algorithms for the TSP have been proposed to search optimal and near-optimal solutions, respectively. An exact algorithm, typically derived from the linear programming formulation and combinatorial optimization of the TSP, is computationally expensive to solve the optimal tour under the large-scale path planning. To avoid tremendous time cost, numerous heuristic algorithms have been developed to search a near-optimal solution for the TSP. Through the heuristic algorithms, the approximate solutions can be obtained within competitively short computational time, but close enough to the globally optimal solution (Abdulkarim and Alshammari 2015).

Despite being designed in the early 1960s, the dynamic programming (DP) was broadly applied to solve TSP. The algorithm, holding the time complexity O(n²2ⁿ) and faster than the naive solution O(n!) for solving an n-city instance, has been developed by Bellman (1958, 1962), and Held and Karp (1962) over the past fifty years. It was hence called the Bellman-Held-Karp or Held-Karp algorithm, providing the best asymptotic bound that has been achieved to date. However, it still costs the exponential time and space complexity, which results in infeasibility even for slightly higher number of cities.

The branch-and-bound (B&B) algorithm (Laporte 1992; Lawler 1985) is essentially considered as a tree search, which performs an exhaustive search for the best solution in the search space, and explores the branch nodes in the search tree one by one to see if any new candidate solution can be yielded under examining the potential partial solutions. Meanwhile, a bound value is given to assess how a partial solution approaches the optima and to decide whether a better branch of the active node should be expanded. The B&B algorithm is an exact technique (i.e., gives definite exact optima); thus, it cannot solve the TSP in polynomial time.

The simulated annealing (SA) was a method introduced in 1983 to conquer the drawback of hill climbing (HC), which is highly possible to be trapped into only the local optimum when solving global optimization, like the TSP (Kirkpatrick, Gelatt, and Vecchi 1983). With the SA, a stochastic tour (solution) at each iteration is selected and reordered by slightly modifying the sequence of a few cities to obtain a new tour, till the approximate optimal solution can be finalized, as the value of probability acceptance function decreases progressively toward zero. Nevertheless, the repeated annealing of the SA often takes expensive time to compute the cost function. Moreover, the SA is still a kind of heuristic method so that it cannot tell whether it has found an optimal solution in the end.

The genetic algorithm (GA), invented by Holland (1975), is a widely used heuristic technique to search an optimally ordered sequence by imitating the progress of natural evolution. For solving the TSP, the GA (Potvin 1996) iterates the candidate solutions, represented by chromosomes in the population, until the best-fitted solution is found. The trial-and-error tuning is deeply necessary for all the parameters in the GA, such as the formulation of chromosomes, crossover operators, mutation rates, fitness functions, selection criterion of offspring. Therefore, the GA may be exposed to the risks of lasting for long convergence epochs and getting stuck in a local optimum. Consequently, the GA cannot absolutely find the global optimum for the TSP.

Though being efficient approaches to solve the TSP, heuristic algorithms would also suffer growing computational time cost when the scale of TSP becomes larger. Many researches proposed the partitioning methods to reduce the heavy computational time cost in the large-scale TSP. For solving an n-city instance by the Strip Algorithm (Strip) (Beardwood, Halton, and Hammersley 1959; Johnson, McGeoch, and Rothberg 1996; Karp and Steele 1985; Selamoglu, Salhi, and Sulaiman 2017), the minimal enclosing rectangle is divided into $\sqrt{n/3}$ equal-width vertical strips. For each strip the cities are ordered by top-bottom way; then, the entire tour is iteratively leveraged by running the strips from the leftmost to the rightmost, as well as the last edge from the final city in the rightmost strip to the first one in the leftmost strip.

Bentley (1992) proposed the Fast Recursive Partitioning (FRP), starting with the minimal enclosing rectangle, which is followed by the step that partitions each rectangle, which includes more than 15 cities, into two rectangles with nearly a half of cities. If the rectangle owns the length larger than the width, the median x-coordinate of cities, where a vertical partition occurs, can be found in the rectangle. As well, a horizontal partition can be found in a similar way. The derived rectangles with 15 or less cities are named buckets, nearest neighbors of which will be connected to form an overall tour.

The heuristic of Spacefilling Curve (SFC) (Platzman and Bartholdi 1989; L’Ecuyer et al. 2018) requires the time complexity of O(n log n) to solve an n-city problem, because it is essentially a sorting technique. It visits the cities along the spacefilling curve, containing 2 ^m identical triangles in the m-th partition of the entire dataset. Each successful partition can be retrieved by bisecting each triangle in the previous partitioning step, and then a list-sorting technique is employed to obtain the subtours for all partitions, which can be thus merged to a complete heuristic tour.

Karp’s (1977) Partitioning approach (Karp) firstly constructs the k-d tree (Bentley 1975) by recursively dividing all cities into smaller parts using cuts from both horizontal and vertical directions, until no set of the partition has more than an amount of cities, which is a setting parameter. Then the DP (Bellman 1958, 1962) is applied to solve the optimal paths for all partitioned subsets, and the shared medians are utilized to iterate the final entire tour.

This research proposes the hybrid approach, merging the advantages of k-means clustering and greedy search, called as the pre-clustering greedy heuristic, to obtain the near-optimal path for a mobile robot by combining pre-clustering and various greedy searches.

Pre-Clustering and Construction Method

When the input scale of the TSP grows larger and larger, it is crucial to shorten the computational time for a mobile robot to work continuously from the current step to the next one or without idling due to no moving signal sent in time. To divide a dataset would be one of the efficient methods to reduce the running time cost of algorithm. The proposed partitioning method, stimulated by the concept of the divide-and-conquer algorithm, separates the entire dataset into several segments using k-means clustering (Jain, Duin, and Mao 2000; Kaufman and Rousseeuw 1990). Then, the optimal path for each segment will be obtained using the algorithm proposed next section. Finally, the construction method connects all segments and obtains the entire solution path. In our proposed pre-clustering and construction methods, the computation loading on the embedded system will be dramatically lessened to continuously drive a mobile robot from one step to the next one, without suffering excessive idle time.

Pre-Clustering Method

The k-means clustering is an unsupervised machine learning algorithm, which has been used in a wide range of applications, such as data mining and optimization, because of its simplicity (Wagstaff et al. 2001). Given a set of n data points in m-dimensional space R^m and an integer k, it determines a set of k centers in R^m, in order to minimize the within-cluster sum of squares (WCSS) with respect to each cluster’s nearest center. This work employed the Lloyd’s algorithm, which has been successful in the clustering either the centers have been stabilized or the defined number of iterations, denoted by t, have been achieved. The latter was chosen to avoid infinite divergence in practical applications. Hence, when k, m, and t are constants, the Lloyd’s algorithm can behave in a manner of linear time complexity, which is O(nkmt).

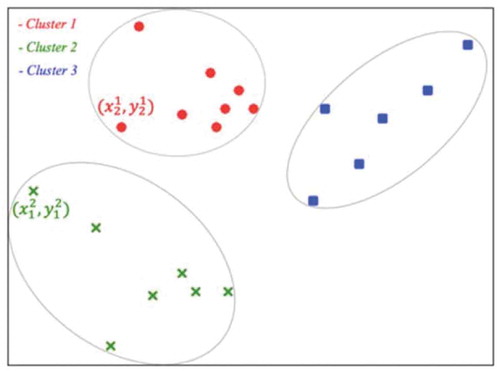
Figure 1 shows many balls laying in a court where each point represents a ball. The task of a mobile robot is to collect all balls at desired efficiency in order to reach maximum goals within limited power supply; that is, the robot should be running with as less idles as possible. To reduce the learning cost, the balls in Figure 2 are divided into three subgroups.

Figure 1. Demonstration of balls laying on the court

Figure 2. Grouping (by gray contours) of balls on the court

Construction Method

The proposed construction algorithm discovers the nearest points between any two adjacent clusters, and then yields the shortest distance between these two adjacent clusters. The optimal path inside each cluster also requires to be obtained.

(1) $\underset{\left(x_{\beta }^{\alpha },y_{\beta }^{\alpha }\right),\left(x_{{\beta }^{\ast }}^{{\alpha }^{\prime }},y_{{\beta }^{\ast }}^{{\alpha }^{\prime }}\right)}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}Dist\left(\left(x_{\beta }^{\alpha },y_{\beta }^{\alpha }\right),\left(x_{{\beta }^{\ast }}^{{\alpha }^{\prime }},y_{{\beta }^{\ast }}^{{\alpha }^{\prime }}\right)\right)$(1)

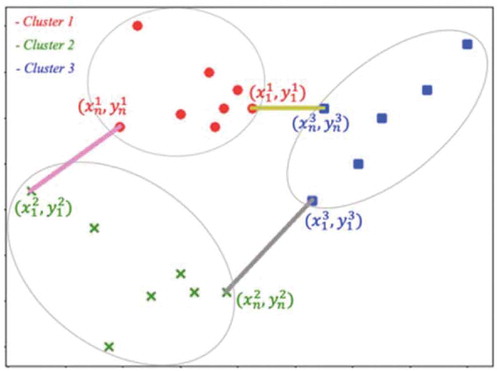
where the function of Dist is used to obtain the metric of Euclidean distance, and ($\alpha ,{\alpha }^{\prime }$) denotes each pair of any two adjacent clusters, which can be either of (1, 2), (2, 3), and (3, 1) from numbering three clusters annotated in Figure 2. The points within a cluster are parametrized as the variables $\beta$ and ${\beta }^{\ast }$, being any one integer chosen between 1 and n, respectively.

For example, if the second point in Cluster 1 and the first point in Cluster 2 are the nearest, the optimal solution for Equation (1)(1) $\underset{\left(x_{\beta }^{\alpha },y_{\beta }^{\alpha }\right),\left(x_{{\beta }^{\ast }}^{{\alpha }^{\prime }},y_{{\beta }^{\ast }}^{{\alpha }^{\prime }}\right)}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}Dist\left(\left(x_{\beta }^{\alpha },y_{\beta }^{\alpha }\right),\left(x_{{\beta }^{\ast }}^{{\alpha }^{\prime }},y_{{\beta }^{\ast }}^{{\alpha }^{\prime }}\right)\right)$(1) is the pair of $\left(x_2^1,y_2^1\right)$ and $\left(x_1^2,y_1^2\right)$, as illustrated in Figure 2.

With the same clusters and points as in Figure 2, Figure 3 displays the proposed algorithm for the nearest connection between any two clusters by utilizing the Euclidean metric to obtain the distance between any two points. The algorithm in Equation (1)(1) $\underset{\left(x_{\beta }^{\alpha },y_{\beta }^{\alpha }\right),\left(x_{{\beta }^{\ast }}^{{\alpha }^{\prime }},y_{{\beta }^{\ast }}^{{\alpha }^{\prime }}\right)}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}Dist\left(\left(x_{\beta }^{\alpha },y_{\beta }^{\alpha }\right),\left(x_{{\beta }^{\ast }}^{{\alpha }^{\prime }},y_{{\beta }^{\ast }}^{{\alpha }^{\prime }}\right)\right)$(1) spends the time complexity, O(n²). There exist three unconnected segments among all three clusters. As a result, it needs three cycles for calculating each nearest distance. And each cycle should recursively compute the distance of any two points, coming from two adjacent clusters.

Figure 3. Nearest connections among all clusters

Providing n points for each cluster, overall 3n² computational steps will be required to obtain three pairs of nearest points among three clusters. Figure 3 shows the final results for all nearest points; points in pair one are $\left(x_1^1,y_1^1\right)$ and $\left(x_n^3,y_n^3\right)$, points in pair two are $\left(x_1^2,y_1^2\right)$ and $\left(x_n^1,y_n^1\right)$, and points in the last pair are $\left(x_1^3,y_1^3\right)$ and $\left(x_n^2,y_n^2\right)$. The subscripts 1 and n represent the starting and ending points, respectively, for the TSP.

Variants of Greedy Heuristics

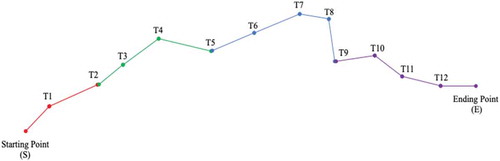
Prior to this section, all segments were derived by the pre-clustering method. This section addresses several variants of greedy heuristics to obtain the optimal tour inside each segment. As long as all the optimal paths inside all clusters are acquired, the optimal tour starting from and ending at $\left(x_1^1,y_1^1\right)$ can be also finalized. Generally speaking, the heuristic algorithms for the TSP usually obtain near-optimal solutions, where several crossing routes might occur to contribute to the excess tour length. In order to obtain the minimum excess tour, this work organizes candidates of greedy searches to determine the appropriate paradigm for lowering as many crosses as possible within each cluster. The proposed three variants of greedy searches are the entire, binary, and recursive models, where the binary and recursive models are designed for the utilization of multi-processing threads to save the overall computational time. From Figure 4 to 6, the starting and ending points represent the initial and final positions of a mobile robot, respectively, in the same cluster, as illustrated in Figure 3.

Figure 4. The route of entire greedy search

Entire Greedy Search (EG)

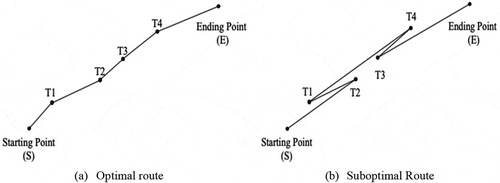
Once walking from the starting point (S), a mobile robot will determine the nearest point to itself as the next node in the tour using the greedy search. The correct optimal route in a cluster, S-T1-T2-T3-T4-E, is depicted as Figure 4(a), where at each node it moves toward the nearest node in next step. Figure 4(b) shows a suboptimal route sequenced as S-T2-T1-T4-T3-E. Node T2 is farther from node S than node T1, but after node S, the mobile robot firstly moves to T2 instead of T1. Likewise, posterior to node T1, farther node T4 is selected as the next node, instead of T3.

Binary Greedy Search (BG)

Inspired by the binary search, this model firstly finds the middle point (M) in the sequence of nodes, and two routes are planned simultaneously from the starting point (S) and the ending point (E) respectively, to node M. Then the two routes are combined into the final optimal route in a cluster. A cluster with nine nodes is shown for explanation, as described in Figure 5. In the first part, a sub-route from node S to node M is obtained as the sequence, S-T1-T2-T3-M, while in the second part, a sub-route from node E to node M has also resulted in the sequence, E-T7-T6-T5-M. To successfully combine the two sub-routes, the sub-route of the second part is reversed as the sequence, M-T5-T6-T7-E, and is appended to the sub-route of the first part. The final whole route will be sequenced as S-T1-T2-T3-M-T5-T6-T7-E.

Figure 5. The route of binary greedy search

Recursive Greedy Search (RG)

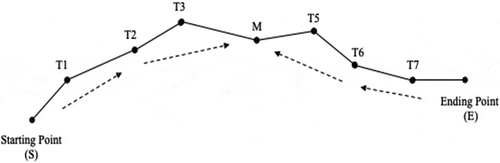
After the pre-clustering some clusters would contain more than 10 nodes; thus, a few crossing routes might occur in the planned route if the abovementioned models are utilized. Besides, the more nodes in one cluster, the more search time cost. Therefore, a solution is proposed to divide the first-hand cluster into several partitions, and to recursively solve the resulted partition by the aforementioned entire greedy search. As shown in Figure 6, the overall nodes are divided into four partitions, each sub-route of which will be optimized using the entire greedy search as S-T1-T2, T2-T3-T4-T5, T5-T6-T7-T8-T9, and T9-T10-T11-T12-E, respectively. At the final step, according to the bounding nodes, T2, T5, and T9, it can achieve the overall path, sequenced as S-T1-T2-T3-T4-T5-T6-T7-T8-T9-T10-T11-T12-E, after connecting all four sub-routes from the starting to the ending points in one first-hand cluster.

Figure 6. The route of recursive greedy search

Experimental Results

In this section, the experimental testbed and setup, and evaluation of our proposed algorithm, and comparison with other methods are presented.

Environment Setup

The experiments are carried out in the hardware platform, a portable computer equipped with the CPU of Intel Core i5 1.6 GHz and the RAM of 8 GB. Several testing instances are selected from the TSPLIB (Reineit) with a few hundreds to around 10 thousands of cities. Over the simulations, the results of running time are recorded for all selected testbeds.

Estimation

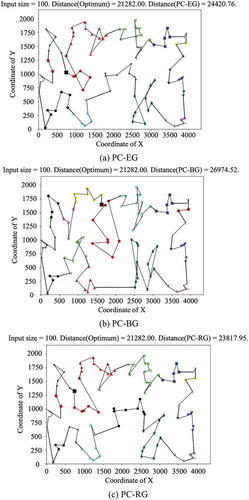
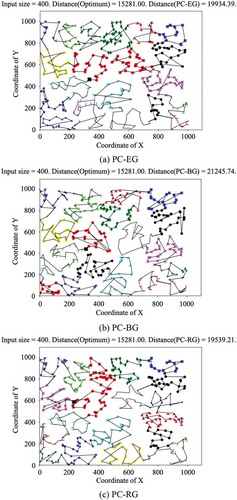
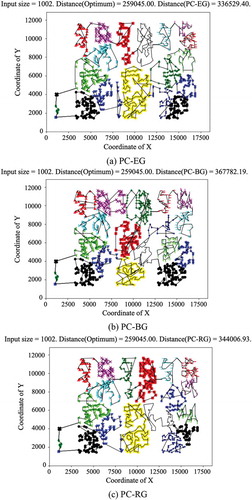
In this work the hybrid approach, divided into three models as PC-EG, PC-BG, and PC-RG, (PC-xG), represented as entire, binary, and recursive greedy searches, respectively, for all pre-clustered segments. The performances of the proposed approach, for three TSPLIB cases, such as kroA100, rd400, and pr1002, are demonstrated as shown from Figure 7–9. Observing the results, it can realize that when less crossing routes occur in the plot, the shorter tour length will be derived.

Figure 7. The resulted tour by the proposed approach for kroA100

Figure 8. The resulted tour by the proposed approach for rd400

Figure 9. The resulted tour by the proposed approach for pr1002

Firstly, for the case of kroA100 exhibited in Figure 7 (a), (b), and (c), the shortest path, solved by the model of PC-RG, possesses the least crossing routes among three models. For the second case of rd400 shown in Figure 8 (a), (b), and (c), the paths solved by the models of PC-EG and PC-RG present similar distribution of crossing routes. Among three subplots for the case pr1002 shown in Figure 9 (a), (b), and (c), the model of PC-EG that owns the shortest path also contains the minimal crossing routes.

As listed in Table 1, this work evaluates the performances of the different proposed heuristics for the TSPLIB cases with under 1,000 data points, each of which owns its optimum for the benching reference. The more percentage in Table 1 is, the less performance the algorithm offers, and vice versa. It can be found that the PC-RG performs better than the others under the cases with input sizes under 200. However, the PC-EG will be the better one to solve the path planning when the input size of the case climbs up to more than 200, which can be referred as the threshold input size for the large-scale path planning for mobile robots. Conversely, the PC-BG gives the worse performance than the other two models of PC-EG and PC-RG, and is getting worse with the increase of the input size. It can be observed from the results with input sizes larger than 200 in Table 1, the average percentage of excess of the PC-BG over the optimal bound is near or over 1.5 times as poor as the one of the PC-EG. For example, the result of the PC-EG is up to over 50% greater than the one of the PC-BG for the TSPLIB cases of pr299, d657, and rat783. Furthermore, it is worth to notice that the PC-EG can guarantee that the solution quality will not vary in much amount as the input size grows up, since its average percentages of excess fluctuate slightly around 30% over the optimal bound, for the cases with input sizes larger than 200. Therefore, in this work, the PC-EG can be firmly employed to solve the TSPLIB cases with more than 1,000 data points, deemed to be closer to the real-world applications.

Table 1. Running results in average percentage (%) of excess over the optimal bound provided by the TSPLIB, for algorithms of PC-EG, PC-BG, and PC-RG

	Algorithm
Case	PC-EG	PC-BG	PC-RG
eil51	13.4	13.7	12.1
kroA100	19.4	25.1	16.7
kroB200	26.1	31.6	25.1
pr299	25.2	42.0	28.7
rd400	30.3	44.6	34.6
rat575	30.8	45.9	36.5
d657	30.0	46.7	32.9
u724	33.8	45.3	37.3
rat783	30.1	47.7	36.3
pr1002	30.2	43.6	36.8

Table 2 presents the running results of more than 1,000 data points among the proposed model of PC-EG and other benchmark algorithms on the aspect of average percentage of excess – less for better performance – over the optimal bound provided by the TSPLIB. It can be apparently observed that the maximum tour by the proposed approach exceeds no more than 35% of the optimal bound, which is however surpassed by the other benchmarks for a majority of tested TSPLIB cases. For example, compared to other algorithms, the Strip (Vertical) and FRP obtain the worst running results with the excess of close to 100% over the optimal bound, which is three times as many as the PC-EG. As well, the results yielded by the algorithms of SFC and Karp exceed the optimal bound maximally in about twice amount as many as the PC-EG. Besides, the proposed algorithm PC-EG deviates from the optimal bound by smaller than 30%, which is much superior to other benchmark algorithms in Table 2, when the input size increases up to more than 10,000. It can be conclusively entailed that the proposed algorithm thoroughly outperforms other benchmarks in the TSPLIB cases with the larger input scales.

Table 2. Running results in average percentage (%) of excess over the optimal bound provided by the TSPLIB, for algorithms of PC-EG, Strip, FRP, SFC, and Karp

	Algorithm
Case	PC-EG	Strip (Vertical)	FRP	SFC	Karp
pr1002	30.2	52.2	64.1	40.7	42.2
pcb1173	33.1	29.7	61.1	40.9	43.3
rl1889	32.7	103.2	86.1	63.5	78.3
u2319	22.9	13.4	35.8	12.8	9.7
pcb3038	32.6	27.2	55.7	40.5	23.1
fnl4461	29.2	30.8	49.2	32.3	42.7
rl5915	31.6	115.8	95.9	60.3	55.0
rl5934	29.8	112.6	84.7	59.9	55.5
brd14051	27.6	44.5	52.3	31.6	37.8
d15112	27.7	43.1	49.6	32.3	59.5
d18512	26.3	34.5	53.0	30.5	45.8

Finally, in Table 3, the proposed algorithm holds the advantage on computational time cost by comparing it to the algorithms of FRP and Karp. For the cases with input sizes larger than 10,000 in Table 3, the Strip and SFC can obtain the running time below one minute, which is shorter than the time consumed by the remaining algorithms as the FRP, Karp, and the proposed one. Nevertheless, as shown in Table 2, the proposed algorithm PC-EG, computing much shorter paths than the Strip and SFC, can run a task with over 10,000 data points by spending between one and two minutes, which can be reasonably considered for the robots operating in several hours. On the other side, the two weakest algorithms of FRP and Karp spend longer time, from a half to four times larger than the proposed one PC-EG. In practice, the proposed algorithm guarantees that a robot will not act on overlong idle status during its working period, as well as walk on shorter paths than other partition-based benchmarks.

Table 3. Running time (seconds) for algorithms of PC-EG, Strip, FRP, SFC, and Karp

	Algorithm
Case	PC-EG	Strip (Vertical)	FRP	SFC	Karp
pr1002	2.6	0.8	1.2	0.4	3.8
pcb1173	3.0	1.0	1.6	0.6	4.0
rl1889	5.4	2.1	2.7	1.0	7.6
u2319	6.8	2.7	3.6	1.4	13.2
pcb3038	9.8	4.7	4.5	2.7	39.8
fnl4461	11.9	5.0	7.2	3.5	40.3
rl5915	18.4	10.3	23.2	9.2	71.3
rl5934	19.2	11.2	25.7	9.8	72.1
brd14051	56.9	30.1	79.5	26.3	376.5
d15112	72.3	39.6	96.3	42.9	406.7
d18512	93.2	41.4	127.6	46.8	450.8

Conclusion and Future Work

Aimed at the real-time applications that a robot must achieve as many goals as possible within limited time and the computational time of a robot has to be short enough to provide the next moving signal in time to avoid being trapped into the idle status. This work proposes a hybrid approach, combining the pre-clustering and construction methods with different types of greedy searches for a mobile robot in the large-scale TSP. While achieving only near-optimal solutions, it is verified that the proposed effective hybrid approach competes against other benchmark algorithm on significantly reducing the computational time. The pre-clustering based on the k-means algorithm is employed to partition the entire dataset into several clusters; then an algorithm, the construction method, is developed to shorten the connected paths between the adjacent clusters such that the overall path cost can be further reduced. Finally, by fusing three types of greedy searches, the proposed hybrid heuristics, PC-EG, PC-BG, and PC-RG are developed to solve the optimal paths in all clusters. For the large input scale over 10,000, the PC-EG, one of the three proposed heuristics, earns the best performance on the paths that are almost one time shorter than most of the benchmark algorithms in Table 2, and on the time cost that is between one and two minutes, which is sound for a several-hour operating robot not to act on overlong idle status during its working session. Cogently, the PC-EG is recommended to solve the large-scale path planning for a mobile robot with from a few hundreds to many thousands of moving targets in this work.

One of the possible applications of this work is to implement the ball-collecting robot in a court or many other real-world applications, such as the fields of logistics, traffic routing, components routing on the VLSI, the problem of plant locations in the plane, and various planar multi-vehicle delivery problems.

Acknowledgments

This research was partially sponsored by the Ministry of Science and Technology, Taiwan, under contract numbers MOST 108-2221-E-007-097 and MOST 105-2221-E-007-026-MY3.