Solution of combined economic and emission dispatch problems of power systems without penalty

ABSTRACT

In the present paper, the Optimization Without Penalty-based Optimization by Morphological Filter algorithm (OWP-based OMF) has been proposed to find the optimal solution for the Combined Economic and Emission Dispatch (CEED) problem. The objective function of the CEED problem is to minimize fuel cost and emission simultaneously while satisfying the load demand, equality and inequality constraints. The evaluation of OWP-based OMF performances is carried out on three test systems with 6, 10 and 40 generating units, with different constraints and various costs. The present paper shows that OWP-based OMF gives an accurate and effective solution of the CEED problem and outperforms the other tested algorithms.

Introduction

The electrical power system is planned and operated such that it could be reliable, economical, secure and to meet the environmental constraints. Economic Dispatch (ED) is the process of allocating the required load between the available generation units with minimal operational cost (Abido 2003). Economic Dispatch (ED) problem has become a crucial task in the operation and planning of power system (Chakrabarti and Halder 2010). It is very complex to solve because of a nonlinear objective function and a large number of constraints. Fossil-fuel-based power stations generate two-thirds of the electric power (Rex and Marsaline Beno 2017). The electricity produced from fossil fuel generator releases numerous noxious wastes. These comprise of carbon dioxide ($C{O}_2$), sulfur dioxide ($S{O}_2$), nitrogen oxide ($N{O}_x$) and some particles, which in turn pollutes the atmosphere. These harmful environmental pollutants emitted from fossil-fuel power plants can be reduced by appropriately distributing the load among the available generators. But this will result to an increase in operating costs of power plants. Therefore, a solution that balances emissions and fuel costs needs to be determined. This can be solved through Combined Economic and Emission Dispatch (CEED) problem. The main target of combined economic and emission dispatch is to minimize both fuel cost and emission simultaneously while satisfying the load demand, equality and inequality constraints.

Mostly, the CEED has been defined as a conflicting bi-objective optimization problem. Thus, the resolution of this kind of problem leads to a set of optimal solutions, called non-dominated solutions or Pareto solutions, instead of a single solution (Guesmi et al. 2020). From a mathematical viewpoint, approaches applied for solving CEED can be classifled into three categories. In the flrst category, fuel cost and emissions have been combined in a single-objective function by the linear weighted sum or normalizing fuel cost and emissions by using price penalty factors (Bhattacharjee, Bhattacharya, and Halder nee Dey 2014; Jiang, Ji, and Wang 2015a; Pazheri et al. 2015). The second category also converts the CEED into a single-objective problem but by incorporating the emissions in the system constraints (Jevtic et al. 2017; Palit and Chakraborty 2019). The third category involves both functions simultaneously where the Pareto set is generated in one run of the opted optimization algorithm (Morsali et al. 2014).

Researchers have been done studies to solve the CEED problem using classical and metaheuristic methods. The conventional mathematical optimization methods such as gradient method (Dodu et al. 1972), lambda iteration method(Aravindhababu and Nayar 2002), linear programming (Parikh and Chattopadhyay 1996), Lagrangian multiplier method (El-Keib, Ma, and Hart 1994), and classical technique based on coordination equations (Nanda 1994) have been implemented to solve CEED problem. However, most of them have difficulties in solving ED problems due to nonlinearity and nonconvexity fuel cost and emission characteristics. The conventional optimization methods prematurely converge to the local optimal solution and are sensitive to the initial starting value. Moreover, these methods are not able to find a solution with a significant computational time for CEED problem (Benasla, Belmadani, and Rahli 2014).

Metaheuristic optimization algorithms play a decisive role in alleviating the problems of traditional methods. Genetic algorithm (GA)(Hamid et al. 2005), simulated annealing (SA) (Wong and Fung 1993), particle swarm optimization (PSO) (Hamid et al. 2005), artificial bee colony (ABC) (Bhongade and Agarwal 2016), biogeography-based optimization (BBO) (Bhattacharya and Chattopadhyay 2010), flower pollination algorithm (FPA) (Abdelaziz, Ali, and Abd Elazim 2016), backtracking search algorithm (BSA) (Bhattacharjee, Bhattacharya, and Halder nee Dey 2015), lightning flash algorithm (LFA) (Kheshti et al. 2018) and real coded chemical reaction algorithm (RCCRO) (Bhattacharjee, Bhattacharya, and Halder nee Dey 2014) are the most popular metaheuristics. Certainly, different meta-heuristic algorithms have been employed to solve the CEED problem. Among the hybrid algorithms utilized in solving the CEED problem, we mention, (i) hybrids which combine two single-objective algorithms such as the artificial bee colony (ABC) algorithm is combined with simulated annealing (SA) in (Sundaram, Saranya, and Sangeetha 2013), two different metaheuristic algorithms PSO and firefiy algorithm is combined in (Arunachalam, AgnesBhomila, and Ramesh Babu 2014), hybrid firefiy and bat algorithm in (Gherbi, Bouzeboudja, and Gherbi 2016) and hybrid PSO-GSA in (Radosavljević 2016). (ii) Hybrids which combine two multi-objective algorithms such as multi-objective GA-PSO in (Agarwal and Nanavati 2016), hybrid NSGAII-MOPSO in (Sundaram and Erdogmus 2017) and hybrid MOPSO-Differential Evolution (DE) in (Gong, Zhang, and Qi 2010). Although these heuristic algorithms generate the best solution to the combined economic and emission dispatch problem, none of them guarantees the best optimal solution.

This paper presents the Optimization Without Penalty-based Optimization by Morphological Filter algorithm (OWP-based OMF)(Zaoui and Belmadani 2021) for solving Combined economic and emission dispatch problem. OWP-based OMF is a recent stochastic optimization algorithm inspired by morphological transformations. The algorithm is used in order to successfully solve different engineering optimization problems. It is clear from the literature survey that the application of OWP-based OMF to solve ELD, ECD and CEED problems has not been discussed yet. This encourages us to adopt OWP-based OMF to deal with these problems. The performance of proposed algorithm is evaluated on different test systems, which are 6 generating units, 10 generating units and 40 generating units. The results are compared with the other algorithms in the literature. The experimental result shows that the proposed algorithm dominates other heuristic algorithms. The remainder of this paper is organized as follows: Section 2 provides a brief description and mathematical formulation of ELD, ECD and CEED problems. In section 3, the concept of OWP-based OMF is presented. Section 4 shows the result on six, ten and forty unit test systems. The last section specifies the conclusion part.

Formulation of CEED problem

The CEED problem is to minimize the fuel cost and emissions as two competing objective functions at the same time with various equality and inequality constraints satisfaction. The problem can be formulated as follows.

Economic load dispatch (ELD)

The objective function of the ELD problem is minimizing the fuel cost for a specifled load demand while satisfying various system and unit constraints. Fuel costs are usually expressed as a quadratic function of output power (Wood, Wollenberg, and Sheblé 1996), as shown in equation 1(1) $FC=\sum _{i=1}^d({\gamma }_i{P}_i^2+{\beta }_i{P}_i+{\alpha }_i)$(1) .

(1) $FC=\sum _{i=1}^d({\gamma }_i{P}_i^2+{\beta }_i{P}_i+{\alpha }_i)$(1)

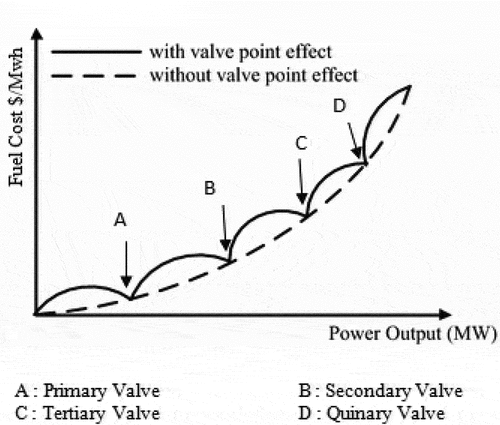
where FC is the total fuel cost of generations $(\mathrm{\$}/h)$, ${\gamma }_i$, ${\beta }_i$ and ${\alpha }_i$ are the fuel cost coefflcients of the $i^{th}$ unit, $P_i$ is the output power of the $i^{th}$ unit, and $d$ is the number of generation units. In practice valve point effect is considered as the fuel cost function of the generator. The sharp increase in losses due to the wire drawing effects which occur as each steam admission valve starts to open leads to the nonlinear rippled input output curve (Walters and Sheble 1993) as shown in Figure 1. The obtained cost function based on the rippled curve is more accurate modeling. Thus, the fuel cost function of each fossil fuel generator is given as the sum of a quadratic and a sinusoidal function (Senthil and Manikandan 2010).

(2) $FC=\sum _{i=1}^d({\gamma }_i{P}_i^2+{\beta }_i{P}_i+{\alpha }_i+\left|e_i\ast sin(f_i\ast (P_i^{min}-P_i))\right|)$(2)

Figure 1. Valve point loading effect.

where FC is the total fuel cost $(\mathrm{\$}/h)$ considering valve-point loadings, $e_i$ and $f_i$ are the fuel cost coefflcients of the $i^{th}$ unit that refect the valve-point effect.

Emission dispatch (EMD)

Fossil fuel-fired power plants emit sulfur oxides, nitrogen oxides, and carbon oxides. The total emission of these pollutants can be also expressed as the sum of a quadratic function and an exponential function. This function is illustrated as follows:

(3) $E=\sum _{i=1}^d(a_i{P}_i^2+b_i{P}_i+c_i+{\eta }_i\ast exp({\delta }_i\ast P_i))$(3)

where E is the total amount of emissions $(Kg/h)$, $a_i$, $b_i$, $c_i$, $\eta$ and $\delta$ are the emission coefflcients of the $i^{th}$ unit.

Constraints

During the minimization process, some equality and inequality constraints must be satisfied. In this process, an equality constraint is called a power balance and an inequality constraint is called a generation capacity constraint.

System power balance constraint

The minimization is performed subject to the equality constraint that the total electrical power generation should meet load demand and total transmission loss:

(4) $\sum _{i=1}^d{P}_i=P_D+P_L$(4)

where $P_D$ is the total load demand, and $P_L$ is the total power transmission losses which can be expressed as a function of the units output power and B-loss coefflcients. The simplest form of loss equation is Kron’s formula as presented in equation 5(5) $P_L=\sum _{i=1}^d\sum _{j=1}^d(P_i{B}_{ij}{P}_j)+\sum _{i=1}^d{B}_{0i}{P}_i+B_{00}$(5) .

(5) $P_L=\sum _{i=1}^d\sum _{j=1}^d(P_i{B}_{ij}{P}_j)+\sum _{i=1}^d{B}_{0i}{P}_i+B_{00}$(5)

where $B_{ij}$ is the $i{j}^{th}$ element of the loss coefflcients square matrix, $B_{0i}$ is the $i^{th}$ element of the loss coefflcients vector and $B_{00}$ is the loss coefflcient constant.

Power output constraints

According to this constraint, each generator should produce power within a minimum and maximum limit.

(6) $P_i^{min}\le P_i\le P_i^{max}i=1,2,3,\dots ,d$(6)

Combined economic emission dispatch (CEED)

The CEED problem can be formulated by combining two independent objectives, which are emission and fuel cost using a price penalty factor. In this way, the bi-objective CEED problem is expressed in a single-objective form. To solve the CEED problem, this form is intended to minimize while satisfying the constraints expressed above. The single-objective CEED problem is formulated as follows:

(7) $TC=w\times FC+(1-w)\times p_f\times E$(7)

where $TC$ is the total operating cost in $\mathrm{\$}/h$, $w$ is the weighting factor that can be varied between 0 and 1 and $p_f$ is the price penalty factor in $(\mathrm{\$}/kg$ or $\mathrm{\$}/ton)$. The various types of penalty factors are formulated in Table 1 (Dey, Basak, and Bhattacharyya 2021; Dey, Bhattacharyya, and Fausto Pedro García 2021; Dey et al. 2020; Dey, Roy, and Bhattacharyya 2018). By the following steps $p_f$ for a specified load demand can be calculated:

Table 1. Penalty factor calculation

Penalty factor types	Penalty factor formula
$p_{f_{j,max-max}}$	=$\frac{FC(P_j^{max})}{E(P_j^{max})}$
$p_{f_{j,min-min}}$	=$\frac{FC(P_j^{min})}{E(P_j^{min})}$
$p_{f_{j,max-min}}$	=$\frac{FC(P_j^{max})}{E(P_j^{min})}$
$p_{f_{j,min-max}}$	=$\frac{FC(P_j^{min})}{E(P_j^{max})}$
$p_{f_{j,average}}$	=$\frac{p_{f_{j,max-max}}+p_{f_{j,min-min}}+p_{f_{j,max-min}}+p_{f_{j,min-max}}}{4}$
$p_{f_{j,com}}$	=$\frac{p_{f_{j,average}}}{numberofgenerators}$

Step 1: Calculate $h_i$ for each unit according to 8:

(8) $h_i=\frac{F(P_i^{max})}{E(P_i^{max})}i=1,\dots ,d\mathrm{\$}/Kg$(8)

Step 2: Sort $h_i$ values in an ascending order.

Step 3: Add maximum output power of each unit one at a time starting from the unit with smallest $h_i$ until $\sum p_i^{max}\ge P_D$.

Step 4: $h_i$ associated with the last unit is $p_f$ for the given load demand (Benasla, Belmadani, and Rahli 2014).

The proposed algorithm

The Optimization Without Penalty-based Optimization by Morphological Filter algorithm (OWP-based OMF) is a new heuristic optimization algorithm described by (Zaoui and Belmadani 2021). This algorithm, which is based on the erosion process, it consists to flnd the minimum combination of pixel values in the neighborhood of morphological filter. OWP-based OMF has been adopted in this paper to solve ELD, EMD and CEED problems. The Optimization by Morphological Filters (OMF) algorithm is a stochastic optimization approach inspired by transformations of mathematical morphology where several morphological filters are launched in parallel and each of them returns a minimum found in its neighborhood. The general principle of the OMF algorithm is to compare the solution represented by the center of the filter with those represented by its neighbors. If one of the neighbors gives a better solution, then the center of this filter is moved to that neighbor. Otherwise, the size of the filter previously fixed decreases to visit a closer neighbor. The criterion for stopping this algorithm is visiting the search space until the size of the filter is negligible, close to zero. The algorithm starts with random generation, all variables generated must be ranged in the interval [0,R]. This is assured by normalization process (Postaire and Vasseur 1981) defined as follows:

$x{ }^{\mathrm{\prime }}=\frac{x-x_{min}}{x_{max}-x_{min}}\times R.$

The number of filters and the number of neighbors are fixed at the initialization step. During the search process, if a better neighbor is found, the center of the filter is moved on it. Otherwise, the size of the filter is reduced in order to check a closer neighborhood. The algorithm stops when the sizes of all the filters become too small $\le \in$. The reduction is ensured by the following formula:

(9) $filter\mathrm{\_}size=\frac{R}{C\times k},$(9)

where $R$ is the range of search space, $k$ denotes the number of reductions of the size of the actual filter and $C$ is a constant which is fixed in our case at $1.001$. In morphology, erosion decreases the outline of objects. This function is adapted by formula 9 to decrease the filter size.

The $i^{th}$ coordinate of each neighbor is calculated by taking one of the following options: do not change, shift left, shift right or take a random position. The first three possibilities are realized with the following equation:

(10) $x_{iNeighbor}=x_{iFilter}+a\times filter\mathrm{\_}size,$(10)

where $filter\mathrm{\_}size$ denotes the size of the filter in progress and $a$ is a parameter randomly chosen from the set $\{1,-1,0\}$. To explore unvisited regions of the search space and to diversify the search, the $i^{th}$ coordinate can be calculated using to the following formula:

(11) $x_{iNeighbor}=random\times R.$(11)

A constraint handling approach without penalty, called OWP (Optimization Without Penalty), is introduced for solving constrained optimization problems in order to force the respect of the constraints. Firstly, the approach consists in addition of a loop; call it intensification loop; which allows having more choice of neighbors and more chance of having feasible solutions. It intensifies the local search of the neighbors of each filter. Secondly, we ensure that the next criteria will be always enforced to compare two solutions at a time: a) Any feasible solution is preferred over an infeasible solution, b) Between two feasible solutions, the solution having the best value of the objective function is preferred, c) Between two infeasible solutions, the solution with a lower violation value is preferred. This violation can be evaluated in different ways:

1) The summation:

$DV(\overleftarrow{x})=\sum f_j^2.$

2) The average:

$DV(\overleftarrow{x})=\frac{\sum f_j^2}{NV}.$

3) The number of constraints not respected:

$DV(\overleftarrow{x})=NV.$

such as: $DV(x)$ is the degree of violation, $NV$ is the number of constraints not respected, the function $f_j$ measures the violation of the $j^{th}$ constraint.

The degree of violation qualifies the solution: If $(DV(x)>0)$ then the solution is considered as infeasible; if $(DV(x)\le 0)$ the solution is considered feasible. Under no circumstances, the violation degree is added to the objective function of the infeasible solution. So, the infeasible solution is not penalized and it is not rejected. Interested readers may refer (Zaoui and Belmadani 2021), which contains the detail of the OWP-based OMF Algorithm.

Case studies and results

To assess the efficiency of the OWP-based OMF, it has been applied to solve ELD, EMD and CEED problems by considering (03) three various test systems. These test systems are widely used as benchmarks in the power system field by many other researchers around the world for similar purposes. The results obtained from the OWP-based OMF are compared with other optimization algorithms, which have already been tested and reported by earlier authors. The parameters of the OWP-based OMF algorithm are presented in Table 2.

Table 2. The parameter for the OWP-based OMF algorithm

	NFilter	NNeighbor	NIntensification
Test System 1& 2	9	3	2
Test System 3	12	3	2

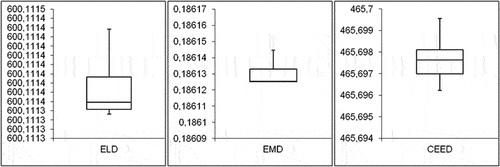
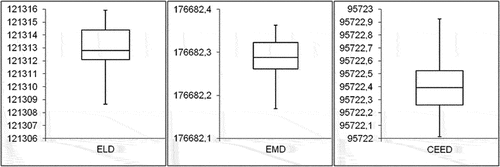
Both the Quade’s test and Friedman’s test were used to test the statistical significance (Derrac et al. 2011). Note that they were implemented by the KEEL software (Alcala-Fdez et al. 2009). Also, to further investigate the performance of the proposed algorithm in detail, we use the box plot that is commonly known as a statistical method for graphically depicting differences among groups of data. The boxplot is a summary of 30 sets of results obtained by OWP-based OMF while evaluating ELD, EMD and CEED problems for different test systems. The median is the line dividing the box, the upper and lower quartiles of the data, Q1-Q3 respectively, define the ends of the box. The minimum and maximum data points are drawn as points at the ends of the lines extending from the box.

Test System I:

The standard IEEE 30-bus consists of six generating units having quadratic cost and emission functions. This power system is interconnected by 41 transmission lines and the total system demand for the 21 load buses is 2.834 MW. The input data for the 6-generator system are taken from (Chatterjee, Ghoshal, and Mukherjee 2012). To compare our results with the results reported in previous works, the system is considered lossless. For this test system, the fuel cost given by equation 1(1) $FC=\sum _{i=1}^d({\gamma }_i{P}_i^2+{\beta }_i{P}_i+{\alpha }_i)$(1) , the emission given by equation 3(3) $E=\sum _{i=1}^d(a_i{P}_i^2+b_i{P}_i+c_i+{\eta }_i\ast exp({\delta }_i\ast P_i))$(3) and total cost given by equation 7(7) $TC=w\times FC+(1-w)\times p_f\times E$(7) are individually optimized.

Bold entries signify the best results

NR means not reported in the referred literature.

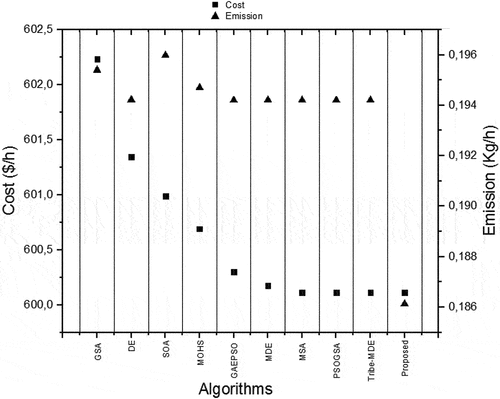
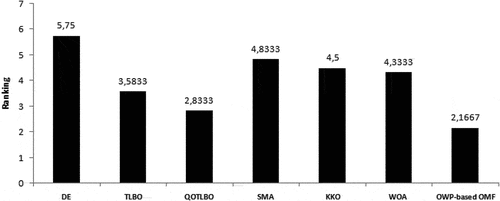
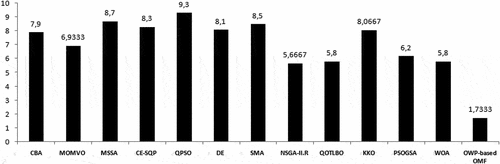
Table 3 presents the best solutions found by OWP-based OMF, including generation output of each unit for ELD, EMD and CEED problem. In Table 4, the optimization results are compared to other optimization algorithms in the recent literature. Except in the case of the fuel cost in CEED minimization, the minimum values of fuel cost, emission and total cost obtained from the proposed OWP-based OMF are lesser in comparison to reported best results in the literature. The result in the case of the CEED minimization obtained by OWP-based OMF can be approximately considered as a result with high cost and low pollution. From Figure 2, it appears that the proposed algorithm has the best performance when comparing other optimization algorithms. Furthermore, the rankings of multiple algorithms obtained by the Friedman’s test and Quade’s test is presented in Figure 3,4 respectively. These figures show that OWP-based OMF gets the first ranking between the compared algorithms.

Table 3. Best achieved solutions for test system I: 6 generators ($P_d=2.834MW$)

Units	ELD	EMD	CEED
PG1 (MW)	0.109719	0.390482	0.23286
PG2 (MW)	0.299766	0.493212	0.535011
PG3 (MW)	0.524298	0.502448	0.42019
PG4 (MW)	1.016198	0.453322	0.880278
PG5 (MW)	0.524298	0.502448	0.35909
PG6 (MW)	0.359719	0.492085	0.406568
Total generation (pu)	2.834	2.834	2.834
Fuel cost ($/h)	600.111385	633.284828	611.121863
Emission (ton/h)	0.205005	0.186125	0.195626
Total Cost ($/h)	–	–	465.697239

Table 4. Comparison of the minimum FC in ELD, minimum E in EMD, and minimum TC in CEED obtained by difirent algorithms for test system I: 6 generators

Algorithms	Fuel cost minimization	Emission minimization	Best compromise solution
	FC ($/h)	E (ton/h)	TC ($/h)	FC ($/h)	E (ton/h)
GSA (Jiang et al. 2015b)	602.2311	0.1954	1792.9181	618.4426	0.1981
DE (Niknam, Mojarrad, and Firouzi 2013)	601.3428	0.194217	NR	NR	NR
SOA (Benasla, Belmadani, and Rahli 2014)	600.986	0.18729*	1821.914	624.604	0.18708
MOHS (Sivasubramani and Swarup 2011)	600.6909	0.1947	NR	608.7367	0.2023
GAEPSO (Jiang et al. 2015b)	600.2978	0.1942	1788.4129	615.3802	0.1978
MDE (Niknam, Mojarrad, and Firouzi 2013)	600.173	0.194208	NR	NR	NR
MSA (Jevtic et al. 2017)	600.11141	0.19420	NR	606.80105	0.20329
PSOGSA (Radosavljević 2016)	600.11141	0.194203	NR	606.79829	0.203289
Tribe-MDE (Niknam, Mojarrad, and Firouzi 2013)	600.1114	0.194202	NR	NR	NR
OWP-based OMF	600.1113	0.186125	465.697239	611.121863	0.195626

*Emission calculated based on reported power generation and emission coefficients in (Benasla, Belmadani, and Rahli 2014) is equal to 0.195978.

Figure 2. Comparison of the results for $P_d=2.834MW$.

Figure 3. Ranking of OWP-based OMF and the compared algorithms by the Friedman’s test on test system I.

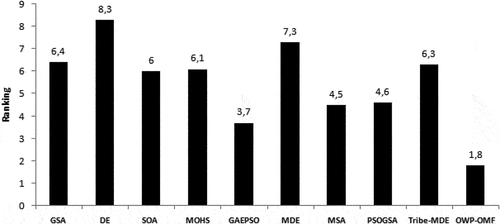
Figure 4. Ranking of OWP-based OMF and the compared algorithms by the Quade’s test on test system I.

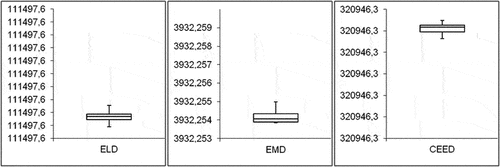
Based on the values mentioned in Table 5, the box plot figure was formed and is presented in Figure 5. From these plots, it is seen that the chances of getting minimum ELD, EMD or CEED is very high as each one of them has lower quartile near to its median from OWP-based OMF.

Table 5. Statistical results obtained over 30 runs with OWP-based OMF for test system 1

	Min	Max	Mean	Standard	Q1	Median	Q3	Time (s)
ELD	600.1114	600.1125	600.111503	0.000283	600.1114	600.1114	600.1114	0.094
EMD	0.186125	0.187046	0.186183	0.000200	0.1861	0.1861	0.186133	0.093
CEED	465.696222	465.699553	465.69757	0.000780	465.697	465.697	465.6981	0.031

Figure 5. Box plot-distributed results for ELD, EMD and CEED problems for test system I.

Test System II:

This case study consists of ten generation units considering the valve-point effect. The fuel cost coefficients, generators constraint, emission coefficients and transmission loss coefficients matrix are taken from (Basu 2011). The generation outputs of the most appropriate solutions for ELD, EMD and CEED problems for 2000 MW load demand are listed in Table 6. Table 7 shows the summarized results that are obtained by OWP-based OMF compared with various optimization algorithms for minimum FC in ELD, minimum E in EMD and minimum TC in CEED.

Table 6. Best achieved solutions for test system II: 10 generators ($P_d=2000MW$)

Units	ELD	EMD	CEED
PG1 (MW)	55	55	55
PG2 (MW)	80	80	80
PG3 (MW)	106.8771	80.9248	81.1085
PG4 (MW)	100.7023	81.1019	80.7725
PG5 (MW)	81.5370	160	160
PG6 (MW)	82.9221	240	240
PG7 (MW)	300	294.5495	291.5934
PG8 (MW)	340	297.6624	296.0321
PG9 (MW)	470	396.3406	398.8523
PG10 (MW)	470	396.0266	398.3150
Total generation (pu)	2087.0387	2081.6060	2081.6740
Power Loss	87.0386	81.6057	81.6790
Fuel cost ($/h)	111497.6407	116411.9936	116391.8270
Emission (ton/h)	4572.4396	3932.2538	3932.4035
Total Cost ($/h)	–	–	320946.3799

Table 7. Comparison of the minimum FC in ELD, minimum E in EMD, and minimum TC in CEED obtained by difirent algorithms for test system II: 10 generators

Algorithms	Fuel cost minimization	Emission minimization	Best compromise solution
	FC ($/h)	E (ton/h)	TC ($/h)	FC ($/h)	E (ton/h)	PL
DE (Basu 2011)	111500	3923.4*	NR	NR	NR	NR
TLBO (Roy and Bhui 2013)	111500	3932.2	NR	113471	4113.5	83.8459
QOTLBO (Roy and Bhui 2013)	111498	3932.2	NR	113460	4110.2	83.8433
SMA (Ahmed et al. 2021)	NR	NR	NR	113490	4108.6	83.89
KKO (Srivastava and Das 2020)	NR	NR	NR	113481	3982.85	84.17
WOA (Rex, Edwin, and Annrose 2019)	NR	NR	321220	113610	3989.5	82.9669
OWP-based OMF	111497.6407	3932.2538	320946.3799	116391.8270	3932.4035	81.6790

*Emission calculated based on reported power generation and emission coefficients in (Basu 2011) is equal to 3932.417288.

Bold entries signify the best results

NR means not reported in the referred literature.

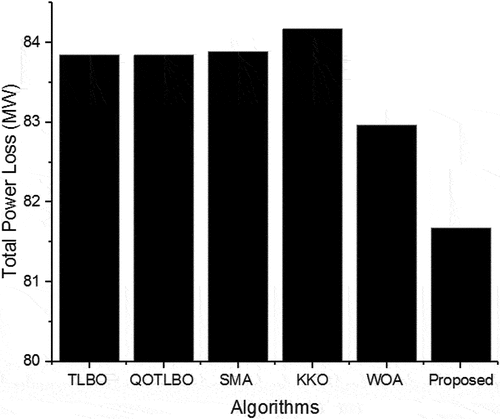
From this table, it can be seen that the proposed algorithm outperforms many algorithms used to solve ELD, EMD and CEED problems because these results are either better or comparable to those obtained using other algorithms. This highlights its ability to find better solutions. From Figure 6, it is observed that the proposed algorithm gives the better total power loss.

Figure 6. Comparison of the results for $P_{loss}$.

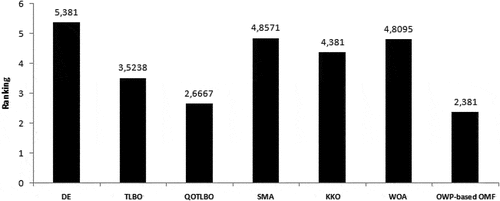
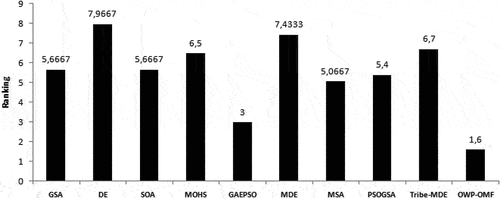
According to the results of the Friedman’s test and Quade’s test shown in Figure 7 and 8 respectively, OWP-OMF is ranked the first.

Figure 7. Ranking of OWP-OMF and the compared algorithms by the Friedman’s test on test system II.

Figure 8. Ranking of OWP-OMF and the compared algorithms by the Quade’s test on test system II.

A box plot figure was formed based on the values in Table 8 and is shown in Figure 9. From these plots, it’s evident that the OWP-based OMF can produce solutions which always remain closer to the best-obtained value in each trial; the median is smallest for the proposed algorithm.

Table 8. Statistical results obtained over 30 runs with OWP-based OMF for test system 2

	Min	Max	Mean	Standard	Q1	Median	Q3	Time (s)
ELD	111497.640	111497.642	111497.64	0.00039	111497.6414	111497.6416	111497.6418	0.031
EMD	3932.253	3932.255	3932.2542	0.00032	3932.2539	3932.2540	3932.2543	0.016
CEED	320946.384	320946.385	320946.39	0.00021	320946.384	320946.385	320946.3852	0.032

Figure 9. Box plot-distributed results for ELD, EMD and CEED problems for test system II.

Test System III:

This test system consists of forty (40) generating units with non-smooth fuel cost and emission level functions. The input data for the 40-generators test system are taken from (Basu 2011), which has a total load of 10,500 MW and no transmission losses are considered. Since this is a larger system with more nonlinear elements, it has more local minima, so it will be more difficult to achieve the global solution. Table 9 presents the optimum results obtained by OWP-based OMF for ELD, EMD and CEED problems.

Table 9. Best achieved solutions for test system III: 40 generators ($P_d=10500MW$)

Units	ELD	EMD	CEED	Units	ELD	EMD	CEED
PG1 (MW)	111.6961	114	114	PG21 (MW)	523.1440	439.4349	437.4749
PG2 (MW)	111.3125	114	114	PG22 (MW)	523.2872	439.4954	437.3899
PG3 (MW)	97.3397	120	120	PG23 (MW)	523.2862	439.6127	437.9355
PG4 (MW)	179.7161	169.3896	178.1443	PG24 (MW)	523.2782	439.7326	437.5263
PG5 (MW)	87.7900	97	97	PG25 (MW)	523.2517	440.1845	437.5633
PG6 (MW)	140	124.1845	129.9247	PG26 (MW)	523.2835	440.1239	437.6229
PG7 (MW)	259.5241	299.7437	300	PG27 (MW)	10	28.97960	19.5926
PG8 (MW)	284.5739	297.9777	299.8678	PG28 (MW)	10	28.9527	19.5290
PG9 (MW)	284.4869	297.2446	298.9768	PG29 (MW)	10	28.9676	19.5488
PG10 (MW)	130	130	130	PG30 (MW)	87.7587	97	97
PG11 (MW)	94	298.4228	307.6796	PG31 (MW)	190	172.3832	175.7052
PG12 (MW)	94	298.0930	307.0133	PG32 (MW)	190	172.3506	175.8870
PG13 (MW)	214.7560	433.5619	433.9764	PG33 (MW)	190	172.3367	175.1343
PG14 (MW)	394.2935	421.6761	408.9414	PG34 (MW)	164.7192	200	200
PG15 (MW)	394.1647	422.7523	411.9811	PG35 (MW)	194.3587	200	200
PG16 (MW)	394.2238	422.7974	411.9954	PG36 (MW)	199.6042	200	200
PG17 (MW)	489.2651	439.3725	452.0437	PG37 (MW)	109.9278	100.7880	104.1737
PG18 (MW)	489.2467	439.4338	452.1124	PG38 (MW)	110	100.8778	104.1864
PG19 (MW)	511.2367	439.3958	437.1739	PG39 (MW)	109.9198	100.8685	104.0048
PG20 (MW)	511.2989	439.4240	437.4983	PG40 (MW)	511.2548	439.4403	437.3952
	ELD		EMD		CEED
Total generation (pu)	10500		10500		10500
Fuel cost ($/h)	121308.4046		129855.4288		128595.9724
Emission (ton/h)	359798.2078		176682.3690		178557.2230
Total Cost ($/h)	–		–		95722.2719

Bold entries signify the best results

NR means not reported in the referred literature.

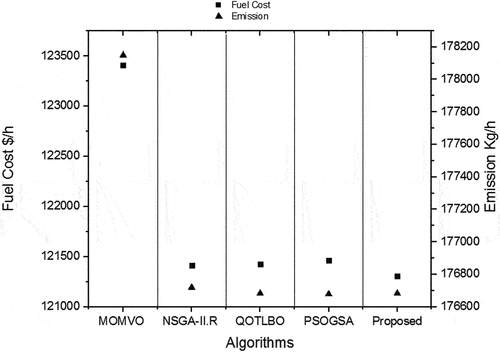
The results obtained using the OWP-based OMF are compared to some other algorithms reported in the literature as shown in Table 10. From this table, it can be seen that the proposed algorithm provides better results and outperforms many algorithms used to solve ELD, EMD and CEED problems. Except in the case of the fuel cost in CEED minimization, the minimum values of fuel cost, emission and total cost obtained from the proposed OWP-based OMF are lesser in comparison to reported best results in the literature. The result in the case of the CEED minimization obtained by OWP-based OMF can be approximately considered as a result with high cost and low pollution. From Figure 10, it appears that the proposed algorithm has the competitive performance when comparing other recent optimization algorithms.

Table 10. Comparison of the minimum FC in ELD, minimum E in EMD, and minimum TC in CEED obtained by difirent algorithms for test system III: 40 generators

Algorithms	Fuel cost minimization	Emission minimization	Best compromise solution
	FC ($/h)	E (ton/h)	TC ($/h)	FC ($/h)	E (ton/h)
CBA (Adarsh et al. 2016)	121412.5468	NR	NR	NR	NR
MOMVO (Sundaram 2020)	123410	178150	NR	125470	209910
MSSA (Elsayed et al. 2016)	121413.4686	NR	NR	NR	NR
CE-SQP (Subathra et al. 2015)	121412.88	NR	NR	NR	NR
QPSO (Meng et al. 2010)	121448.21	NR	NR	NR	NR
DE (Elsayed and El-Saadany 2015)	121412.68	NR	NR	NR	NR
SMA (Ahmed et al. 2021)	121413.0	NR	NR	NR	NR
NSGA-II.R (Kuk et al. 2021)	121414.50	176718.90	NR	125668.93	195668.93
QOTLBO (Roy and Bhui 2013)	121428.00	176682.50	NR	125161.00	206490.40
KKO (Srivastava and Das 2020)	NR	NR	NR	125852	210837
PSOGSA (Radosavljević 2016)	121461,429	176678,019	NR	128710,905	178591,659
WOA (Rex, Edwin, and Annrose 2019)	NR	NR	1510240	123644	213240
OWP-based OMF	121308.4046	176682.3690	95722.2719	128595.9724	178557.2230

Figure 10. Comparison of the results for $P_d=10500MW$.

Also, according to the results of the Friedman’s test and Quade’s test shown in Figure 11,12 OWP-OMF is ranked the flrst.

Figure 11. Ranking of OWP-OMF and the compared algorithms by the Friedman’s test on test system III.

Figure 12. Ranking of OWP-OMF and the compared algorithms by the Quade’s test on test system III.

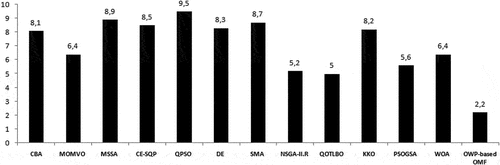
According to the values mentioned in Table 11, a box plot is formed, as shown in Figure 13. It can be concluded from these figures that the objective function value of each run is nearly close to the best result for each problem; ELD, EMD and CEED problems.

Table 11. Statistical results obtained over 30 runs with OWP-based OMF for test system 3

	Min	Max	Mean	Standard	Q1	Median	Q3	Time (s)
ELD	121307.08	121315.9	121312.97	1.741	121312.07	121312.80	121314.43	0.203
EMD	176682.20	176682.41	176682.34	0.043	176682.31	176682.33	176682.37	0.438
CEED	95722.01	95722.97	95722.39	0.200	95722.25	95722.39	95722.52	0.078

Figure 13. Box plot evaluation for ELD, EMD and CEED problems for test system III.

Conclusion

OWP-based OMF is one of the recent heuristic algorithms presented by ZAOUI and BELMADANI (Zaoui and Belmadani 2021) for solving engineering optimization problems. In this paper, OWP-based OMF is successfully applied to solve a combined economic and emission dispatch problem. The proposed algorithm is tested on three different test systems. Here, inequality constraints like valve-point loading, emission, transmission line loss are addressed. The results demonstrate the effectiveness and robustness of the proposed algorithm in solving the CEED problem. In addition, the results of the proposed OWP-based OMF algorithm have been compared to other heuristic algorithms published in the recent literature. The proposed algorithm can provide better solutions than other algorithms. It can be seen from the comparison that the proposed algorithm determines an effective and high-quality solution to the CEED problem.

Disclosure Statement

No potential conflict of interest was reported by the author(s).

Correction Statement

This article has been republished with minor changes. These changes do not impact the academic content of the article.