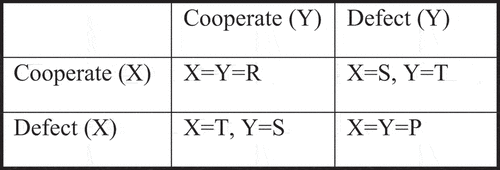The Effect of Defection in Maximizing Group Benefit

ABSTRACT

A variety of social dilemma scenarios are studied within the context of the prisoner’s dilemma, one of the most well-known concepts in modern game theory, and its variants. In the prisoner’s dilemma, studies typically emphasize the priority of maximizing the gain of each individual. In this paper, however, we focus on maximizing the benefit of the larger group, not each individual. It is worth noting that regardless of individual strategies in the prisoner’s dilemma, there is always a certain level of defection. These individual defections can be analyzed in a collective group setting from the perspective of game theory. We look into how much defection is required, if necessary, in order to optimize a group’s advantages, and analytically identify the specific effects of defection for the purpose of maximizing group benefit.

Introduction

The prisoner’s dilemma is a game theory framework illustrating two rational individuals making decisions in their own self-interest. Many social dilemma situations can be researched in the context of variations of this concept. Each player, regardless of the decision made by the other player, has an incentive to defect in one-shot interactions, or when the game is repeated for a finite number of times (Leyton-Brown and Shoham 2008). Therefore, although the decision of cooperation by both players provides the most optimal payoff, the decision of defection is a rational decision, and it provides Nash equilibrium, despite the worst payoff (Anatol Rapoport 2016; Nash 1951).

If two players repeat the same prisoner’s dilemma game in succession, however, and if it is given that both players remember the previous actions of all players, the game is called an iterated prisoner’s dilemma. In this version, the game is played repeatedly between the same players, who continuously have the opportunity to penalize the other for previous decisions. If information regarding the number of times the game is played is available to the players, then by backward induction the two rational players will betray each other repeatedly due to the same reasons as the single-shot variant. In an infinite or unknown length game, there is no fixed optimum strategy.

Numerous studies have been conducted on optimizing an individual’s benefit in the setting of the iterated prisoner’s dilemma. Each study attempts to identify the best strategies to maximize the benefit of an individual by alternating between cooperation and defection. Prisoner’s dilemma tournaments have been held to compete and test algorithms for such cases (Kaznatcheev and Artem 2015).

Each player has a tendency to be egotistical and defect to maximize his or her own benefit, not the profit of the group. However, without cooperation within the group, it is easy to come to the conclusion that the collective society is doomed from the start. In human civilization, people cooperate with one another, even when it logically makes more sense to do otherwise at the time. It is well established that mutual cooperation can indeed be optimal in the iterated prisoner’s dilemma (Axelrod 1984; Robert Trivers 1971). Many theoretical mechanisms for the emergence and maintenance of cooperation in social dilemma games have been reported thus far (Axelrod 1984; Martin 2006; Sigmund 2010).

In this paper, we look at the iterated prisoner’s dilemma issue from a different angle. We concentrate on the performance of the group as a whole, rather than on the performance of an individual. The goal is to maximize the group’s overall benefit, regardless of how each player performs.

Some members of a group cooperate, while others defect. Of course, some group members, as they cooperate and defect based on their individual strategies, will fare better than others. Given the present level of defection in a group, our focus is to analyze the effects of individual defection in terms of group benefit.

We look into whether pure angels that only choose to cooperate perform the best as a group, or if additional wickedness is required to maximize performance. How much defection, if necessary, is required to optimize a group’s advantages? In this study, we explore these problems, and seek to identify the effect of defection to maximize group benefit.

Related Work

Much research in the past has focused on predicting the optimal strategy in the iterated prisoner’s dilemma scenario. The infamous Axelrod’s Tournament, in which competitors submitted their strategies for the prisoner’s dilemma that competed via computer simulations to observe which one outputted the most overall gain marked the beginning of such study (Axelrod 1984). This experiment established the simple Tit-For-Tat strategy (Nowak and Sigmund 1992) as an extraordinarily successful way to foster cooperation and accumulate a large payoff: a player should cooperate if the opponent cooperated in the last round, and otherwise defect.

Nonetheless, no strategy is universally superior in such a tournament (Fudenberg and Maskin 1990; Martin 2006), because a player’s performance is dependent on the strategies of the opponent. Recent contributions to this literature introduced a new, previously undiscovered successful strategy Press and Dyson (2012).

Due to the frequent occurrence and the significance of the prisoner’s dilemma, many scientific disciplines besides traditional computer science and mathematics have also analyzed the concepts of cooperation and defection, e.g., evolutionary biology/genetics (Nowak and Sigmund 2004), sociology (Kollock 1998), psychology (Rand and Nowak 2013), and experimental economics (Bo Pedro and Frechette 2018).

Evolutionary game theory (Hofbauer and Sigmund 2003; Maynard Smith 1982), which models interactions from an individual’s point of view, centers attention on the strategies of the interacting agents, but without having direct regard to ecological dynamics. The payoffs obtained by individuals are expressed as fitness, which are usually fixed values determined by the strategies of the interacting individuals. Strategies with high payoffs will spread within the population, which can be achieved either by learning, copying, inheriting strategies, or even by defecting.

Studies surrounding prisoner’s dilemma also often discover new mechanisms for the evolution of cooperation: direct and indirect reciprocity (Axelrod and William 1981; Nowak and Sigmund 1998). This finding is supported by experimental evidence: people cooperate more in repeated prisoner’s dilemma games than in one-shot prisoner’s dilemma games, and cooperation levels increase in continuation probability (Bo Pedro and Frechette 2018; Rand and Nowak 2013).

The prisoner setting may seem straightforward, but there are in fact many examples in human interactions, as well as interactions in nature, that have similar payoff matrices. Therefore, the prisoner’s dilemma is of interest in many academic domains, including economics, politics, sociology, and evolutionary biology. Many natural processes have been abstracted into models in which living beings are engaged in endless games of the prisoner’s dilemma. This wide applicability of the prisoner’s dilemma gives the game its substantial importance.

There are numerous instances of the prisoner’s dilemma with the identical payoff matrix in both human and natural interactions. Numerous natural processes have been abstracted into models that feature infinite games of the prisoner’s dilemma among living beings.

Many animal behaviors have been specifically modeled as instances of the iterated prisoner’s dilemma. For example, when guppies inspect predators cooperatively in groups, they are thought to punish noncooperative inspectors (Brosnan, Earley, and Dugatkin 2003). Vampire bats are social animals that engage in reciprocal food exchange, in which the behavior can be explained by applying the payoffs from the prisoner’s dilemma.

In more recent works, the Prisoners’ dilemma game has been augmented by using a hesitant interval-valued intuitionistic fuzzy-linguistic term set (Bhaumik, Kumar Roy, and Wilhelm Weber 2020). In this work, linguistic terms in the interval are first expressed using linguistic semantics, before the corresponding indices are utilized for applying the method to real-world human trafficking problems.

They also proposed a new method for fuzzy matrix games where the game situation is represented by artificial neural networks through logic-gate switching circuits in a hesitant fuzzy environment (Bhaumikand Sankar Kumar Roy and Roy 2022).

Problem Formulation

The Prisoner’s Dilemma is a social dilemma game in which two players simultaneously take a choice between two options: to cooperate, or to defect. We assume that Figure 1 gives the payoff table of each transaction:

Figure 1. Payoff table of prisoner’s dilemma.

The entries of Figure 1 represent the payoffs that each player gains. If both players (player X and player Y) cooperate, they both receive payoff R as a reward. If both players defect, they receive P for punishment. If only one player defects and the other player cooperates, the defector receives T for temptation, and the cooperator gets S for sucker.

An intuitive real-life example of the Prisoner’s Dilemma is a scenario where farmers barter for supplies with their crops. The players of this game are farmers and traders. To the farmers, cooperation means rightfully exchanging their crops for supplies, while defection means taking supplies without giving any crops in exchange. Traders can choose to cooperate with farmers by giving supplies to farmers in exchange of crops or defect by taking the crops without payment.

To make the payoff table more realistic, we assume that $T>R>P>S$. Regardless of what the other player does, the payoff of playing defect is greater than the payoff of playing cooperate, while the payoff of mutual cooperation is higher than the payoff of mutual defection. Thus, rational players will end up in the less desirable outcome of mutual defection. Because $T>R$ and $P>S$, mutual defection is the only Nash equilibrium of the single-shot game.

We assume symmetry in the payoff matrix, meaning that when they use the same strategy, both parties get the same reward. Each row (column) corresponds to the action of the row (column) player, i.e., cooperate (C) or defect (D).

In this paper, we want to answer the following questions: 1) can defection actually increase the benefit to a group? 2) If so, how much defection is necessary to maximize the benefit of a group?

In our experiments, we have a (sufficiently large) group of $n$ players, and each player is supposed to engage in transactions with every other member of the group. (The case of random transactions between players is discussed later.) We consider a prisoner’s dilemma that is repeated for an uncertain, but predictably large, number of rounds.

There are many possible strategies for a player to choose from in the prisoner’s dilemma games. In this work, regardless of the strategies in a group, we will assume that there is $d$ ($0\le d\le 1$) fraction of defection in the population. In other words, the probability that a player defects in any given transaction is given as $d$.

The Effect of Defection in a Group

In this section, we analyze the effects of defection to maximize the benefit of the group using three different scenarios. First, we assume that transactions are made in a round-robin fashion. Second, we assume that transactions are made in a random fashion. Third, we assume that each transaction is associated with a cost. In each of these scenarios, the effect of defection in a group is discussed in the sections that follow.

Round-Robin Transactions

In our first experimental model, we assume that each player engages in a transaction with every other member of the group. We have the following cases, and the number of transactions for each case is given, respectively, as follows.

Suppose $B_{ti}$ means the benefit of agent $i$ at iteration $t$. At a certain iteration, the total benefit of the group is given as ${\sum }_i^n{B}_{ti}$. Therefore, our problem can be represented as a constraint optimization problem. Our goal is to find $d$ value that satisfies the following:

${\sum }_t^{\mathrm{\infty }}{\sum }_i^n{B}_{ti}$ subject to $T>R>P>S$

In a single round of round-robin transactions, given a certain value of $d$, we can observe the following:

1. Number of transactions when both parties’ defect: $2dn\left(dn-1\right)$

2. Number of transactions when both parties cooperate: 2$\left(1-d\right)n\left[\left(1-d\right)n-1\right]$

3. Number of transactions when one cooperates, and the other defects: 2$dn\left(1-d\right)n$

Since we focus on the benefit of the group, we let $TOT=\sum _i^n{B}_{it}$. After the completion of a single transaction for every player, the total benefit of the group is given as:

$TOT=2dn\left(dn-1\right)P+2\left(1-d\right)n\left[\left(1-d\right)n-1\right]R+2dn\left(1-d\right)n\left(T+S\right)$

$=2n^2\left[d\left(d-1/n\right)P+\left(1-d\right)\right[\left(1-d\right)-1/n\left]R+d\left(1-d\right)\left(T+S\right)\right]$

When $n$ is large enough, $1/n\to 0$. Therefore,

$TOT\approx 2n^2\left[d^{2}P+{\left(1-d\right)}^{2}R+d\left(1-d\right)\left(T+S\right)\right]$

Since $n$ is a constant, we simplify the above formula, as follows:

$AVG=TOT/2n^2=d^{2}P+{\left(1-d\right)}^{2}R+d\left(1-d\right)\left(T+S\right)$

Therefore, we can see that:

(1) $AVG=d^2\left(P+R-T-S\right)+d\left(T+S-2R\right)+R$(1)

Each individual may change his or her strategy at different iterations. However, since our goal is to estimate the effect of defection in a group, we assume $d$ value remains constant, regardless of the individual’s strategies. Since we assume the value of $d$ is fixed for each iteration, maximizing $AVG$ (the average benefit of a group in a single round) is equivalent to maximizing the benefit of the group in the repeated prisoner’s dilemma. Therefore, maximizing Equation (1)(1) $AVG=d^2\left(P+R-T-S\right)+d\left(T+S-2R\right)+R$(1) in a single iteration is the same as maximizing the group benefit in multiple iterations. Evidently, the higher the value of Equation (1)(1) $AVG=d^2\left(P+R-T-S\right)+d\left(T+S-2R\right)+R$(1) , the higher the total profit of the group. Thus, Equation (1)(1) $AVG=d^2\left(P+R-T-S\right)+d\left(T+S-2R\right)+R$(1) becomes the objective function of the problem.

Proposition 1:

When there is no defection (everybody cooperates), the average balance ($AVG$) is $R$. The proof is trivial because from the definition of AVG, $AVG=R$ when $d=0$.

Proposition 2:

When there is no cooperation (everybody defects), the average balance is $P$. The proof is trivial because from the definition of AVG, $AVG=P$ when $d=1$.

Since $R\ge P$ holds, we can see that the profit of cases with full cooperation is always better than those of all defects, meaning a society of selflessness is better off than that of greed.

Now let us consider more general cases where $0<d<1$. Our goal is to find the proper value of $d$ that maximizes Equation (1)(1) $AVG=d^2\left(P+R-T-S\right)+d\left(T+S-2R\right)+R$(1) . To solve this problem, the derivative of $AVG$ is given as follows:

$\frac{\mathrm{\partial }AVG}{\mathrm{\partial }d}=2\left(P+R-T-S\right)d+\left(T+S-2R\right)$

Suppose $F$ is the value of $d$ when $\frac{\mathrm{\partial }AVG}{\mathrm{\partial }d}=0$. The value of $F$ is given as:

(2) $F=\frac{T+S-2R}{2\left(T+S-P-R\right)}$(2)

Our goal is to maximize the average profit of a group in Equation (1)(1) $AVG=d^2\left(P+R-T-S\right)+d\left(T+S-2R\right)+R$(1) .

The shape of the objective function Equation (1)(1) $AVG=d^2\left(P+R-T-S\right)+d\left(T+S-2R\right)+R$(1) varies depending on the values of payoff values, and the maximum value of $AVG$ varies accordingly. We already assumed that $T>R>P>S$, and depending on these payoff values, we analyze the effect of $d$ to maximize $AVG$.

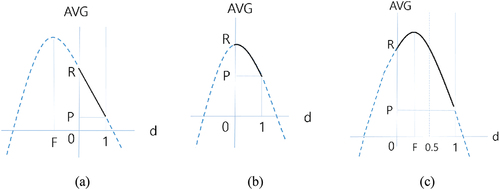
Case 1: $T+S<P+R$

In this case, the advantage of defection is relatively small, and defectors cannot receive a large benefit from defection. Since $P+R-T-S>0$, the parabola of the objective function opens upwards. Also, since $T+S<P+R$ and $T+S<P+R<2R$, both the numerator and denominator of $F$ Equation (2)(2) $F=\frac{T+S-2R}{2\left(T+S-P-R\right)}$(2) are negative, and $F>0.$

Since $2\left(T+S-P-R\right)-\left(T+S-2R\right)=T+S-2P<T+S-2R<0$ and $R>P$, $F<1$ from Equation (2)(2) $F=\frac{T+S-2R}{2\left(T+S-P-R\right)}$(2) . Therefore, Figure 2(a) gives the graph of Case 1:

Figure 2. The values of AVG when (a) $T+S<P+R$ and (b) $T+S=P+R$.

As a result, as the value of $d$ increases, the balance decreases monotonically. When $d=0$, the total balance of the group becomes maximum, while when $d=1$, it is minimum.

Proposition 3:

When $T+S<P+R$, the average profit monotonically decreases as d increases. Therefore, when $d=0$, the profit is maximized.

Case 2: $T+S=P+R$

When $T+S=P+R$, the value of $AVG$ is given as follows:

$AVG=d\left(T+S-2R\right)+R$

The object function now becomes linear, and the slope of the linear function is negative since:

$T+S-2R=P+R-2R=P-R<0$

Figure 2(b) describes the result of this case. We can see that as d increases, the value of AVG decreases in a linear order. Therefore, when d = 0, AVG=R, and when d = 1, AVG=P.

Case 3: $P+R<T+S<2R$

Since $P+R-T-S<0$, the parabola opens downwards, and the value of $F$ becomes negative, which is impossible to happen because $0\le d\le 1$.

$F=\frac{T+S-2R}{2\left(T+S-P-R\right)}$

Figure 3(a) gives the shape of the graph. Therefore, as the value of d increases, the balance decreases monotonically.

Figure 3. $AVG=P$ the values of AVG when (a) P+R<T+S<2R, (b) T+S=2R, and (c) T+S>2R.

Case 4: $P+R<T+S=2R$

In this case, the parabola still opens downwards, and $F=0$. Figure 3(b) shows the balance of the group. Therefore, as the value of $d$ increases, the profit decreases monotonically.

Case 5: $T+S>2R$

This is the case where the prize of cheating is big enough. Since $T+S>P+R$, $\left(T+S-2R\right)<\left(T+S-P-R\right)$, and $0<F<\frac{1}{2}$. Figure 3(c) gives us the shape of the graph.

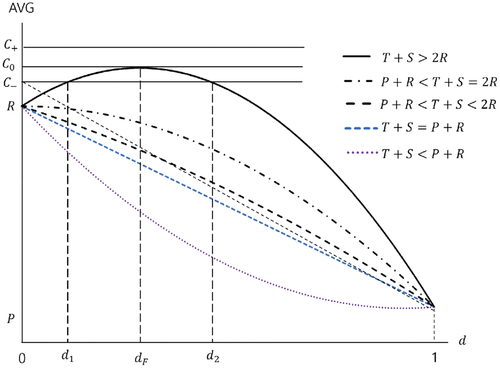
While all the cases described so far show similar characteristics (as the value of $d$ increases, the balance decreases monotonically), this case shows somewhat different behavioral characteristics.

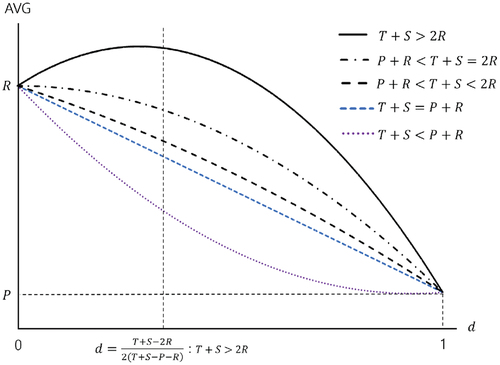
Since the balance of the group becomes maximal when $d=F$ ($0<F<1/2$), we can conclude that there should be some defections in the group to maximize the total balance of the group. In other words, a certain amount of necessary greed is required. However, the number of defectors should not exceed half of the group.

In fact, the group demonstrates the best performance when:

$d=\frac{T+S-2R}{2\left(T+S-P-R\right)}$

For example, suppose the payoff table is as follows

Table

	Cooperate (Y)	Defect (Y)
Cooperate (X)	X=Y=4	X=0, Y=10
Defect (X)	X=10, Y=0	X=Y=2

The group’s benefit becomes optimal when $F=\frac{T+S-2R}{2\left(T+S-P-R\right)}=\frac{10+0-2\ast 4}{2\left(10+0-2-4\right)}=0.25$. In this case, the average benefit each player can get per transaction is given as:

$\frac{{\left(T+S\right)}^2-4PR}{4\left(T+S-P-R\right)}=\frac{17}{4}=4.25$

Proposition 4:

When the value of $P$ approaches $R$, meaning the reward for cooperating is not sufficiently greater than the punishment of mutual defection, the value of $F$ becomes close to $1/2$. In this case, the value of AVG approaches $\frac{T+S+2R}{4}$.

Based on the results, we can conclude that as the number of defectors increases, the total balance of a group decreases monotonically, except for the case when $T+S>2R$.

1. In most cases, as the rate of defection increases, the benefit of the group decreases.

2. However, in the case of $T+S>2R$, the group benefit increases until $d$ reaches $\frac{T+S-2R}{2\left(T+S-P-R\right)}$, and after that, it decreases.

3. As the value of $T+S$ increases, the benefit of the group increases. When the defector takes large benefit from cooperation ($T+S$ is large), it increases the benefit of the group. In this particular case, because the reward of defection is large enough, the group needs a small percentage of defectors to maximize its combined performance. However, it is worth reiterating that even then, the percentage of defectors should not exceed half of the total population.

The optimal value of $d$ that maximizes the group benefit is as follows:

$d=\{\frac{T+S-2R}{2\left(T+S-P-R\right)},ifT+S>2R0,otherwise$

Figure 4 shows the relationship between $d$ and $AVG$ in different cases.

Figure 4. The effect of d values in various conditions.

Random Transactions

So far, we have assumed that each player engages in transactions with every other player in the group. In this section, we randomly select two players from the group, and let them interact with each other, and these random transactions are repeated in large numbers.

We observe whether this change provides the same analytical results as the round-robin transactions.

1. The probability that both parties’ defect is given as $dd$, and the benefit added to the group is $2P$.

2. The probability that both parties cooperate is $\left(1-d\right)\left(1-d\right)$, and the benefit added to the group is $2R$.

3. The probability that one cooperates while the other defects is given as $2d\left(1-d\right)$, and the benefit added to the group is $\left(T+S\right)$.

Therefore, given a value of $d$, the benefit that a certain transaction produces is calculated as:

$dd2P+\left(1-d\right)\left(1-d\right)2R+2d\left(1-d\right)\left(T+S\right)$

$=2d^{2}P+2{\left(1-d\right)}^{2}R+2d\left(1-d\right)\left(T+S\right)$

Because the above equation is beneficial for the two players (in the one transaction), the benefit of the single player can be obtained by dividing by 2:

$d^{2}P+{\left(1-d\right)}^{2}R+d\left(1-d\right)\left(T+S\right)$

$=d^2\left(P+R-T-S\right)+d\left(T+S-2R\right)+R$

We can see that the above equation is identical to Equation (1)(1) $AVG=d^2\left(P+R-T-S\right)+d\left(T+S-2R\right)+R$(1) .

Transactions with Cost

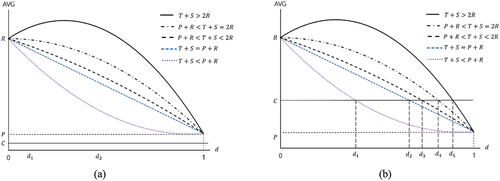
In the real world, transactions are usually associated with cost (e.g., paying tax). In this section, we take the cost of each transaction into consideration. Whenever a player makes a transaction, a certain amount of cost is deducted from the profit. For simplicity, we assume that the cost of each transaction C is the same. Figure 5 shows a payoff table of the prisoner’s dilemma, including cost C.

Figure 5. Payoff table with cost.

In this analysis, taking cost into consideration, we can analyze whether a group will collapse or continue to grow in the long run. If the balance of the individual is less than the cost to enact a transaction, individuals cannot make any transactions. Therefore, if the average balance of profit is less than the cost of a transaction, the group is doomed to collapse. Based on the payoff table in Figure 5, the average profit balance of each individual is given in Equation (3)(3) $=d^2\left(P+R-T-S\right)+d\left(T+S-2R\right)+R-C$(3) :

$AV{G}_C=d^2\left(P+R-T-S+2C-2C\right)+d\left(T+S-2R+2C-2C\right)+R-C$

(3) $=d^2\left(P+R-T-S\right)+d\left(T+S-2R\right)+R-C$(3)

We can easily see that:

$AV{G}_C=AVG-C$

This means that the group collapses if $AVG\le C$. In this case, no player can afford to make any transactions, because the balance is less than the minimum transaction cost.

We analyze the performance of the group (whether the group will grow or perish), depending on the value of cost $C$.

Case 1: $C\le P$

When the value of $C$ (cost) is less than or equal to $P$, the average benefit to the individual is greater than the cost. In this case, no individual has restrictions on transactions, and the group never collapses, regardless of $d$. Figure 6(a) shows the case of $C\le P$.

Figure 6. The effect of d when (a) C≤P and (b) P<C≤R.

Case 2: $P<C\le R$

In this case, the group may or may not collapse, depending on the value of $d$. Figure 6(b) shows the relationship between $AVG$ and $C$ value. The graph of $AVG$ intersects with $C$ in the following $d$ values:

$d=\frac{2R-T-S\pm \alpha }{2\left(P+R-T-S\right)}$ where $\alpha =\sqrt{{\left(T+S-2R\right)}^2-4\left(P+R-T-S\right)\left(R-C\right)}$.

1) when $T+S<P+R$

The group collapses when $d\ge d_1$, where $d_1=\frac{2R-T-S-\alpha }{2\left(P+R-T-S\right)}$. Figure 6(b) shows the value of $d_1$.

2) when $T+S=P+R$

The graph of $AVG$ is linear, and the group collapses when $d\ge d_2$, where $d_2=\frac{R-C}{2R-T-S}$. Figure 6(b) shows the value of $d_2$.

3) when $T+S>P+R$

The group collapses when $d\ge d_3$, where $d_3=\frac{2R-T-S+\alpha }{2\left(P+R-T-S\right)}$. Figure 6(b) shows the value of $d_3$.

The cases of 1) and 3) can be combined into the following formula. Therefore, we can say that the group collapses when:

$d\ge \frac{2R-T-S+\phi \left(T+S-P-R\right)\ast \alpha }{2\left(P+R-T-S\right)}$, where $\phi \left(x\right)=\{1,ifx>0-1,otherwise$

The values of $d_4$ and $d_5$ can be computed in a similar way, and they are shown in Figure 6(b) as well.

Case 3: $C>R$

This is the case where the cost of a transaction is greater than the reward from cooperation. Figure 7 shows the relationship between C and AVG when $C>R$.

Figure 7. The effect of d when C>R.

When $C>R$, we have the following cases, and the group may grow or perish depending on the values of $T+S$:

1) when $T+S\le 2R$

As shown in Figure 7, $C$ is always greater than the value of $AVG$(since $C>R$). Therefore, the group always collapses, regardless of the value of $d$.

2) when $T+S>2R$

In this case, the value of $AVG$ is maximum when $d_F=\frac{T+S-2R}{2\left(T+S-P-R\right)}$, shown in Figure 7. Also, the value of $AVG$ when $d_F=\frac{T+S-2R}{2\left(T+S-P-R\right)}$ is given as follows:

(4) $AV{G}_F=\frac{{\left(T+S\right)}^2-4PR}{4\left(T+S-P-R\right)}$(4)

Therefore, we can observe the following, depending on the value of $C$.

2–1) when $C<AV{G}_F$, denoted as $C_{-}$ and $C_0$ in Figure 7, the group collapses when $d\le d_1$ or $d\ge d_2$, where:

$d_1=\frac{2R-T-S-\alpha }{2\left(P+R-T-S\right)}$ and $d_2=\frac{2R-T-S+\alpha }{2\left(P+R-T-S\right)}$

2–2) when $C>AV{G}_F$ ($T+S>2R$), the $AV{G}_C$ value is always less than the value of $C$ (denoted as $C_{+}$ in Figure 7). Therefore, the group always collapses, regardless of the value of $d$.

Conclusions

Traditionally, research into the prisoner’s dilemma has primarily focused on maximizing the benefit of individuals. In this paper, we analyzed the effects of defection from the perspective of maximizing group benefit.

In both round-robin transactions and random transactions, we observed that as the number of defectors increases, the average balance of the group decreases monotonically, except for the case when $T+S>2R$. When $T+S>2R$, group benefit increases until $d$ reaches $\frac{T+S-2R}{2\left(T+S-P-R\right)}$, and decreases after that. In this particular case, because the reward of defection is large enough, the group needs a small percentage of defectors to maximize its performance. However, even in this case, the percentage of the defectors should not exceed half of the total population.

We also take the cost of transactions into consideration. By implementing cost, we predict whether the group will collapse or prosper in the long run. We have seen that when $C\le P$, the cost is too small, and the group never collapses. When $P<C\le R$, the group collapses when $d$ is greater than $\frac{2R-T-S+\phi \left(T+S-P-R\right)\ast \alpha }{2\left(P+R-T-S\right)}$. When $R<C\le AV{G}_F$, the group collapses when $d\le \frac{2R-T-S-\alpha }{2\left(P+R-T-S\right)}$ or $d\ge \frac{2R-T-S+\alpha }{2\left(P+R-T-S\right)}$. Finally, if $C>AV{G}_F$, the cost is too high, and the group always collapses, regardless of the value of $d$.

Acknowledgments

This study was, in part, supported by Dongguk University.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

The work was supported by the Dongguk University