ABSTRACT
Purpose: Confounding is an important problem in observational research. Improper modeling of the confounder will lead to residual confounding that may distort results and impact inferences. An example of this will be presented from research on age-related macular degeneration and depression.
Methods: A 3-year prospective cohort study was performed using data from the Canadian Longitudinal Study on Aging consisting of 30,097 individuals aged 45–85 years. Incident depression was assessed using the Center for Epidemiologic Studies Depression scale. Participants were asked if they had ever had a physician diagnosis of age-related macular degeneration (AMD). Multivariable Poisson regression was used. Age was modeled in four ways including as a linear term, as a 4-category variable, as a spline, and as a polynomial. Models were compared using the Akaike’s Information Criteria (AIC) with lower scores indicating better performance.
Results: The point estimates and inferences differed depending on how age was modeled. Age had a J-shape relationship with the incidence of depression. The model with the lowest AIC was when age was entered as a categorical variable. When age was modeled in this way, AMD was not significantly associated with the incidence of depression (relative risk (RR) = 1.21, 95% Confidence Interval (CI) 0.97, 1.53). By contrast, when age was modeled as a linear term, AMD was significantly associated with the incidence of depression (RR = 1.28, 95% CI 1.02, 1.61).
Conclusions: Researchers should clearly report their adjustment strategies and should be cautious when modeling the relationship between age and depression in order to minimize residual confounding.
Introduction
In trying to understand whether an exposure, like age-related macular degeneration (AMD), causes an outcome, like incident depression, researchers must be aware of confounding variables. A confounder is a variable that is related to both an exposure and an outcome and is not an intermediate variable in the causal pathway.Citation1 Regression is often used in an attempt to remove the confounding effect. However, improper modeling of the confounder will lead to residual confounding that may distort results and impact inferences.Citation2
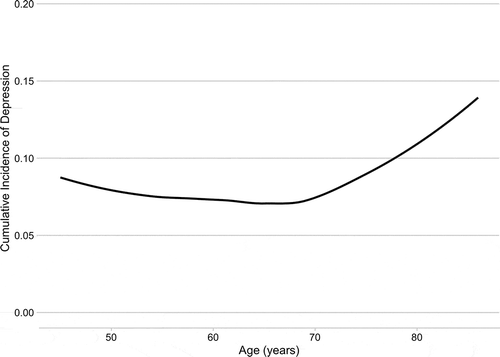
Age is often included as a confounder as many conditions vary in frequency throughout the lifespan. However, if researchers do not carefully investigate the relationship between age and an outcome, they may not correctly capture the confounding effect. For example, age may have a linear or non-linear relationship with an outcome. Kessler et al. and others have shown that age often has a non-linear relationship with the incidence of depression.Citation3,Citation4
The purpose of this paper is to demonstrate how to best adjust for age in examining the relationship between AMD and incident depressive symptoms using data from The Canadian Longitudinal Study on Aging.Citation5 The full methods and results on the association of visual impairment, eye disease, and the incidence of depressive symptoms are published in another paper.Citation6
Methods
Study population and design
A 3-year prospective cohort study of community-dwelling older adults was performed using data from rounds 1 and 2 of the Canadian Longitudinal Study on Aging (CLSA) Comprehensive cohort consisting of 30,097 individuals.Citation5 To be able to participate, participants had to be aged between 45 and 85 years, community-dwelling, cognitively unimpaired at baseline, speak English or French, and provide written informed consent. Briefly, the baseline assessment included a home visit and a data collection site visit done between December 2011 and July 2015. Follow-up data were obtained between July 2015 and December 2018 in a home visit and a data collection site visit. The follow-up rate was very high at 92%. Research Ethics Board approval was received from University of Ottawa (H-05-19-4466).
Data collection
Depression
The Center for Epidemiologic Studies Depression scale (CES-D10) was used to measure depressive symptomatology.Citation7 The CES-D10 consists of 10 items covering depressive symptomatology experienced during the past week and includes 4 response categories ranging from “rarely” to “all of the time”. Scores range from 0–30 with a score of 10 or greater indicating that a participant has screened positive for depression. Incident depression was present in those who had a score of 10 or higher at follow-up in those who scored less than 10 at baseline.
Demographic, health, and lifestyle data
Demographic data including age, sex, education, income, and marital status were collected during the in-home visit. Participants were asked if a doctor has ever told them that they have macular degeneration. Participants were asked if they had ever received a physician diagnosis of 9 chronic conditions which included diabetes, heart disease, stroke, osteoarthritis of the knee or hip, peripheral vascular disease, asthma, back problems, and Parkinson’s disease. As is often done in aging research, a comorbidity score was created based on the total number of the 9 chronic conditions listed above.Citation8 Smoking status was classified as either current, never, or former based on self-report.
Statistical analysis
Lowess smoothing was used to graph the outcome versus age. Multiple Poisson regression was used adjusting for potential confounding variables. An offset was not used since the follow-up time was identical for all participants. Based on the Lowess plot, age was modeled in four ways: 1) as a linear term, 2) as a categorical variable (45–54, 55–64, 65–74, 75–85 years), 3) as a spline term with knots at 55 and 75 years, 4) as a polynomial (age and age squared). Age was centered before the squared term was created. Models were compared using Akaike’s Information Criteria (AIC). Lower AIC scores are preferred as they indicate better model fit while discouraging overfitted models. Analyses were done using STATA SE Version 16 (College Station, Texas).
Results
Our analysis consisted of 22,558 people after excluding those with depression at baseline and those who were missing data on depressive symptoms at follow-up. Those with AMD were more likely to report depressive symptoms (11.1% versus 7.6%, crude RR = 1.46, 1.18, 1.82). Age showed a non-linear relationship with incident depression (). As shown in , the regression results differed according to how age was modeled. When age was entered as a linear term, AMD was associated with a higher risk of incident depression (RR = 1.28, 95% CI 1.02, 1.61, P = .032). However, when age was modeled as a categorical variable, as a spline term, or as a polynomial term, AMD was not statistically significantly associated with incident depression (P > .05). The AIC statistics indicated that Models 2 (categorical age) and 4 (polynomial age) fit the data the best while Model 1 (linear term for age) fit the data the worst.
Table 1. AMD and its relationship to the 3-year incidence of depression using different age-adjustment strategies
Discussion
In this sample of adults ages 45–85 years old, age had a nonlinear relationship with the incidence of depression. Modeling age as a linear term resulted in AMD having a statistically significant association with incident depression with an overestimated point estimate (RR = 1.28) while modeling age more appropriately as either a categorical or polynomial variable resulted in AMD not being statistically significantly related to incident depression and having a lower point estimate (RR = 1.21). The AIC statistics for the models with age as a categorical variable or a polynomial variable were similar. Categorical variables are often preferable to polynomial variables as they are easier to interpret. However, in the case of a nonlinear age association, it is necessary to use a sufficient number of categories to capture the non-linearity.
Other researchers have also presented examples of improper modeling of confounders in the cardiovascular and vaccine research fields.Citation9 Groenwold et al. note that it is often unclear how researchers are modeling age as no details are reported.Citation9 We encourage vision researchers to pay careful attention to the age and depression relationship to ensure residual confounding is minimized and to clearly report their adjustment strategies.
Acknowledgments
The authors wish to thank Dr. Marie-Hélène Roy-Gagnon for her help with the figure. No potential conflict of interest was reported by the authors.
Data availability
Data are available from the Canadian Longitudinal Study on Aging (www.clsa-elcv.ca) for researchers who meet the criteria for access to de-identified CLSA data.
Additional information
Funding
References
- Celantano DD, Szklo M. Gordis Epidemiology. 6th ed. Philadelphia: Elsevier; 2019.
- Brenner H, Blettner M. Controlling for continuous confounders in epidemiologic research. Epidemiology. 1997;8(4):429–434. doi:10.1097/00001648-199707000-00014.
- Kessler RC, Foster C, Webster PS, House JS. The relationship between age and depressive symptoms in two national surveys. Psychol Aging. 1992;7(1):119–126. doi:10.1037/0882-7974.7.1.119.
- Sutin AR, Terracciano A, Milaneschi Y, An Y, Ferrucci L, Zonderman AB. The trajectory of depressive symptoms across the adult life span. JAMA Psychiatry. 2013;70(8):803–811. doi:10.1001/jamapsychiatry.2013.193.
- Raina P, Wolfson C, Kirkland S, et al. Cohort profile: the Canadian Longitudinal Study on Aging (CLSA). Int J Epidemiol. 2019;48(6):1752–1753j. doi:10.1093/ije/dyz173.
- Grant A, Aubin M, Buhrmann R, Freeman EE. Visual impairment, eye disease, and the 3-year incidence of depression: the Canadian longitudinal study on aging. Ophthalmic Epidemiol. 2020;In Press. doi:10.1080/09286586.2020.1823425.
- Andresen EM, Malmgren JA, Carter WB, Patrick DL. Screening for depression in well older adults: evaluation of a short form of the CES-D (Center for Epidemiologic Studies Depression Scale). Am J Prev Med. 1994;10(2):77–84. doi:10.1016/S0749-3797(18)30622-6.
- Guralnik JM. Assessing the impact of comorbidity in the older population. Ann Epidemiol. 1996;6(5):376–380. doi:10.1016/S1047-2797(96)00060-9.
- Groenwold RH, Klungel OH, Altman DG, et al. Adjustment for continuous confounders: an example of how to prevent residual confounding. CMAJ. 2013;185(5):401–406. doi:10.1503/cmaj.120592.