Why Do Parameter Values in the Zipf-Mandelbrot Distribution Sometimes Explode?

ABSTRACT

The Zipf-Mandelbrot distribution serves as a mathematical model for ranked frequencies in many areas of scientific research, including linguistics. Many linguistic units, like e.g., words or word n-grams, follow this distribution. However, in some cases, such as for graphemes in linguistics or species abundance and diversity data in biology, the parameters of the Zipf-Mandelbrot distribution are virtually uninterpretable, as their values strongly depend on the precision of numerical methods used to estimate them (values from several tens to several hundreds are not uncommon). It is shown in the paper that these values can be explained by the convergence to the geometric distribution, which forces both parameters of the Zipf-Mandelbrot distribution to increase to infinity while their ratio converges to a constant. Some examples which illustrate this limit behaviour are presented.

1. Introduction and Motivation

The Zipf-Mandelbrot distribution (see e.g. Wimmer & Altmann, 1999, p. 666, the ZM distribution henceforward) was suggested by Mandelbrot (1953). It is defined as

$P_x=c{\left(x+b\right)}^{-a}x=1,2,\dots ,n,$

with c being a normalization constant, i.e.

$c={\left(\sum _{i=1}^n{\left(i+b\right)}^{-a}\right)}^{-1}$

Its non-truncated version,

$P_x=c{\left(x+b\right)}^{-a}x=1,2,\dots$

is known also as the Hurwitz distribution (in that case, $c^{-1}$ is the Hurwitz zeta function, see Johnson et al., 2005, p. 530). The ZM distribution is a generalization of the famous Zipf distribution. Its mathematical properties and statistical inference on its parameters are discussed e.g. in F. Izsák (2006a), J. Izsák (2006b), Young (2013), and Adil Khan et al. (2019). Families of related discrete probability distributions are presented in Zörnig and Altmann (1995) and in Kemp (2010).

The ZM distribution is used very often as a model for ranked frequencies in many areas of scientific research. As examples, we mention scientometrics (Ausloos, 2014; Silagadze, 1997), economics (Wu, 2007), medicine (Berclaz et al., 2012), and computer science (Wu et al., 2008). In biology, it is one of standard models for species abundance and diversity (Bach et al., 1988; Do et al., 2014; Huang & Zhan, 2014; J. Izsák & Pavoine, 2012; Juhos & Vörös, 1998; Wilson, 1991).

In linguistics, the ZM distribution serves most often as a model for word frequencies (see e.g. Bentz et al., 2014; Koplenig, 2018; Popescu et al., 2009), but it can be applied also to many other linguistic units. Thus, Egghe (1999) used it to model frequencies of multi-word phrases, and Ha et al. (2009) frequencies of word n-grams. Frequencies of word length motifs conform to the ZM distribution as well (Köhler & Naumann, 2008; Mačutek, 2009). On the opposite side, i.e. considering lower level linguistic units, syllable frequencies (Radojičić et al., 2019) and character frequencies (Riyal et al., 2016) were also shown to follow the model. Even word-like units in programming languages display the same behaviour (Zhang, 2008).

Attempts to use the ZM distribution also as a model for ranked grapheme frequencies in some Slavic languages can be found in Grzybek et al. (2004, 2006) and in Grzybek and Kelih (2005a). It seems that graphemes in alphabets¹ are one of a few exceptions among basic language units where the ZM distribution does not turn out to be a model with a satisfactory fit in general² (although it fits the data well for some languages, as will be shown in Section 3).

In principle, the ZM distribution has two free parameters, a and b, while the normalization constant c is uniquely determined by their values. However, several papers report a strong correlation between the parameter values when the distribution is fitted to data. According to J. Izsák (2006b, p. 114), [t]he parameters of the ZM distribution frequently correlate, and Koplenig (2018, p. 21) writes that both ZM parameters are strongly correlated. Wilson (1991, p. 43) writes that his fitting procedure does not converge with some datasets within a reasonable time, as the value of one parameter is becoming very large, with balancing changes in the other.³ As a result, the fit improves only slightly and the parameters attain unrealistic values.⁴

2. Convergence to the Geometric Distribution

Problems reported by Wilson (1991), i.e. very large and ever increasing values of the parameters, their correlation, and a very slow improvement of the fit, make the ZM distribution ‘suspicious’ in the sense that, in such cases, the distribution could converge to another one. Indeed, for the ZM distribution we have

$\frac{P_{x+1}}{P_x}=\frac{c{\left(x+b+1\right)}^{-a}}{c{\left(x+b\right)}^{-a}}={\left(\frac{x+b}{x+b+1}\right)}^a={\left(1-\frac{1}{x+b}\right)}^a$

and provided that

$a\to \mathrm{\infty },$

$b\to \mathrm{\infty },$

and

$\frac{a}{b}\to r,$

i.e. if both parameters of the ZM distribution increase to infinity, but their ratio converges to a constant, for every fixed $x$ we obtain the limit

In other words, the ratio of two neighbouring probabilities $P_{x+1}$ and $P_x$ does not depend on $x$, i.e. it is a constant. We thus proved that, under the conditions mentioned above, the ZM distribution converges to the geometric distribution with

$P_x=p{\left(1-p\right)}^{x-1}$$x=1,2,\dots$,

which is the only discrete probability distribution with this property. In this case, it holds

$p=1-e^{-r}.$

This proof is mathematically very simple, but, to our best knowledge, it has not appeared in the explicit form in the literature. We note that neither Wimmer and Altmann (1999), nor Johnson et al. (2005), i.e. none of the two probably most comprehensive books on discrete distributions, mentions this convergence, although they present many relations among discrete probability distributions, including limit distributions for special values of parameters. Some hints towards this limit behaviour can be found e.g. in Malacarne and Mendes (2000) and in Montemurro (2001). These two papers use a continuous approach, and thus speak about a convergence to the exponential function – it is a well-known fact that the exponential distribution is a continuous analogue of the geometric distribution.

Curiously enough, already Sigurd (1968, pp. 1–2) wrote that the ZM distribution, which he calls the Mandelbrot’s formula, has the disadvantage of having more parameters, which makes it more complicated to characterize the phoneme frequencies of a language (we remind that he compared it with the Zipf’s formula, but the comparison is true, with respect to the number of parameters, also for the geometric distribution). Some pages later (p. 13), he suggested that [a]s an alternative to Mandelbrot’s formula, geometric series may be used. No frequencies, only percentages rounded to one or two decimal places are presented in that paper, hence we cannot present exact results of fitting. However, given the convergence proved above, and the supposed similarity between grapheme and phoneme rank-frequency distributions, it could be said that the geometric distribution is not an alternative to the ZM distribution, but that from the limit point of view the two distributions coincide.

The convergence provides also a mathematical explanation why the parameters of the ZM distribution explode in some cases (like e.g. when the distribution is fitted to ranked frequencies of graphemes). Suppose that the ZM distribution is used as a model for such data. Given that the geometric distribution is its limit distribution, the parameters a and b are in theory ‘forced’ to tend to infinity. Their actual estimated values depend on the choice of software, programming language, optimization algorithm etc., but they are usually very high. The values increase with the increasing desired precision of optimization algorithms used to obtain them, while their ratio fluctuates around a constant.

3. Examples

Ranked grapheme frequencies in Bulgarian and Slovene (see Table 1; data were taken from Koščová et al., 2016) are used here to exemplify the limit behaviour of the ZM distribution which is described in Section 2. The goodness of fit of the models is evaluated in terms of the discrepancy coefficient $C=\frac{{\chi }^2}{N}$, with $C<0.02$ indicating an acceptable fit (see Mačutek & Wimmer, 2013, for details). The parameters were estimated by the minimum ${\chi }^2$ method, i.e. their values minimize the ${\chi }^2$ statistic. They were computed in the R statistical software environment. A short R script, which uses the function optim with the default choice of the function arguments, was created by the author of this paper.

Table 1. Grapheme rank-frequency distributions in Bulgarian and Slovene (data – observed frequencies, ZM – expected frequencies from the right truncated ZM distribution, geom – expected frequencies from the right truncated geometric distribution).

	Bulgarian			Slovene
rank	data	ZM	geom	data	ZM	geom
1	36,841	31,068.29	30,967.82	30,849	31,854.82	31,789.57
2	24,724	27,660.13	27,605.25	29,708	28,555.61	28,524.02
3	23,098	24,629.06	24,607.80	26,129	25,601.07	25,593.92
4	21,644	21,932.99	21,935.82	25,886	22,954.86	22,964.82
5	19,535	19,534.59	19,553.97	17,175	20,584.55	20,605.78
6	17,133	17,400.72	17,430.75	15,921	18,461.12	18,489.08
7	13,867	15,501.95	15,538.07	15,045	16,558.63	16,589.81
8	13,394	13,812.15	13,850.91	14,144	14,853.90	14,885.64
9	12,224	12,308.14	12,346.94	14,139	13,326.20	13,356.53
10	11,329	10,969.30	11,006.28	12,402	11,956.98	11,984.49
11	9197	9777.36	9811.19	11,569	10,729.66	10,753.40
12	8542	8716.05	8745.86	11,412	9629.42	9648.77
13	7950	7770.93	7796.21	10,029	8642.97	8657.61
14	7339	6929.18	6949.68	9167	7758.46	7768.27
15	6197	6179.39	6195.07	8753	6965.25	6970.28
16	5633	5511.44	5522.39	6441	6253.84	6254.26
17	5309	4916.31	4922.75	5515	5615.72	5611.80
18	4770	4385.99	4388.23	5336	5043.28	5035.34
19	4554	3913.37	3911.74	4755	4529.70	4518.09
20	4344	3492.12	3487.00	4429	4068.87	4053.97
21	4035	3116.61	3108.37	3054	3655.33	3637.53
22	3220	2781.82	2770.85	2923	3284.19	3263.87
23	2681	2483.30	2469.99	1967	2951.05	2928.59
24	2197	2217.10	2201.79	1893	2652.01	2627.76
25	1956	1979.68	1962.71	230	2383.53	2357.82
26	1936	1767.90	1749.60
27	1464	1578.97	1559.62
28	362	1410.41	1390.27
29	336	1259.99	1239.31
30	320	1125.76	1104.75
		a = 103.32	p = 0.1086		a = 103.24	p = 0.1027
		b = 887.7			b = 942.74
		C = 0.0165	C = 0.0164		C = 0.0195	C = 0.0193

We emphasize that Bulgarian and Slovene were chosen as examples because both the ZM distribution and the geometric distribution fit the data from these two languages sufficiently well, and our aim was to demonstrate the limit behaviour of the ZM distribution on real linguistic data. We do not claim that either of the two distributions is a general mathematical model for ranked grapheme frequencies.⁵

It is obvious that fitting the ZM and the geometric distribution results in very similar numbers. In addition, the value of the parameter p of the geometric distribution is very close to $1-e^{-\frac{a}{b}}$ (where a, b are the parameters of the ZM distribution) for both languages (Bulgarian: p = 0.1086, $1-e^{-\frac{a}{b}}=$ 0.1099; Slovene: p = 0.1027, $1-e^{-\frac{a}{b}}=$ 0.1037), which is a consequence of the convergence from Section 2.

The convergence of the ZM distribution to the geometric distribution under the conditions stated on Section 2 is demonstrated in Table 2, where the ZM distribution is fitted to the Bulgarian and Slovene data again, but now the maximum number of iterations in the R function optim is controlled (the default maximum is set to the value of 500). With the increasing numbers of iterations, the values of parameters a and b increase rapidly. The value of $1-e^{-\frac{a}{b}}$ gets closer to the optimized value of parameter p of the geometric distribution from Table 1, and the fit improves, but only to a very slight extent. We thus ‘copied’ the behaviour of the ZM distribution parameters reported by Wilson (1991, p. 43). The only noticeable difference – namely, all our fitting procedures were performed in a very short time – can be attributed to enormous advances in computer technology in the last 30 years.

Table 2. Convergence of the ZM distribution to the geometric distribution (max – the maximum number of iterations in the function optim; a, b – optimized parameters of the ZM distribution).

Bulgarian					Slovene
max	a	b	$1-e^{-\frac{a}{b}}$	C	max	a	b	$1-e^{-\frac{a}{b}}$	C
70	16.08	125.87	0.1199	0.0170	20	11.69	97.36	0.1131	0.0215
75	32.88	271.22	0.1142	0.0166	30	14.26	122.23	0.1101	0.0211
80	51.03	433.13	0.1111	0.0165	40	57.17	512.03	0.1056	0.0198
90	89.47	766.78	0.1101	0.0165	50	101.58	928.80	0.1036	0.0196

The similarity between the two models is highlighted also in Figure 1 for Slovene (the Bulgarian data give basically the same picture).

Figure 1. Rank-frequency distribution of graphemes in Slovene (white – observed frequencies, grey – expected frequencies from the right truncated ZM distribution, black – expected frequencies from the right truncated geometric distribution).

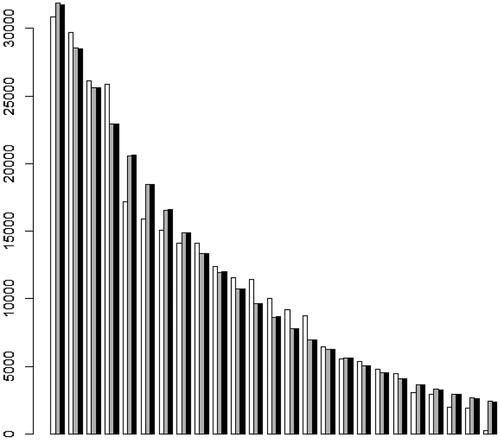
Grapheme frequencies in several other languages⁶ behave similarly, i.e. if one fits the data with the ZM distribution, the parameters a and b attain large values and the value of $1-e^{-\frac{a}{b}}$ is close to the optimized parameter p of the geometric distribution. The same is true for some data from individual texts in Russian, Slovak, and Ukrainian (see Grzybek et al., 2004, 2006; Grzybek & Kelih, 2005a, respectively). We note that in most of these cases the ZM distribution (as well as the geometric distribution) does not achieve a sufficiently good fit (i.e. $C>0.02$), and Bulgarian and Slovene data from Table 1 are, in this respect, more an exception than a rule.

4. Conclusion and Discussion

Understanding and explanations of linguistic phenomena belong to the aims of theoretical research in quantitative linguistics (see e.g. Altmann, 1993). It is obvious that a mathematical model with a good fit alone, without a linguistic interpretation of its parameters, does not contribute to the achievement of these aims. If one fits data with the ZM distribution and the estimated parameter values get unrealistically large, and, in addition, if the values strongly depend on the precision of numerical methods used, the parameters are virtually uninterpretable. If the conditions for the convergence from Section 2 are satisfied (i.e. if the ratio of the two parameters of the ZM distribution is stable in spite of the increase of the two particular values), the geometric distribution is a better model. Its goodness of fit is approximately the same under these conditions, and, moreover, it has only one parameter p with an obvious interpretation – it is the relative frequency of the most frequent item from the inventory of the linguistic units under study.

It remains an open question why graphemes and phonemes are exceptional among basic language units in the sense that their ranked frequencies do not follow the ZM distribution, and, instead, the negative hypergeometric distribution is a strong candidate for a general model. A relatively small grapheme inventory size (if compared with syllables, words, word n-grams, etc.) can be one of the reasons, as in such a case the tail of the rank-frequency distribution can be too short to be able to display ‘typical Mandelbrot’ properties, and the optimized parameter values suggest that the data be modelled with the geometric distribution rather than with the ZM distribution. We remind that according to the study by Riyal et al. (2016) mentioned in Section 1, ranked frequencies of characters⁷ in the Garhwali language can be modelled by the ZM distribution. However, this language uses the Devanagari script, which is an abugida (see Daniels, 1996). As such, it has a substantially larger character inventory than an alphabet. A character inventory of an abugida is similar – although not necessarily equal – to an inventory of syllables.

Specifically for grapheme frequency data, the two free parameters of the ZM distribution seem to depend on each other in such a way that only their ratio has an influence on the model. In other words, there remains only one free parameter, which makes the model less flexible. On the other hand, the negative hypergeometric distribution also has two free parameters, K and M. It seems they are strongly mutually correlated as well, however, there is a crucial difference between the mutual parameter relations in the ZM and the hypergeometric distributions. According to Grzybek (2007), there is a linear relation between K and M, i.e. $M={\alpha }_{1}K+{\beta }_1$, with ${\beta }_1$ depending, again linearly, on the inventory size $n$ (i.e. ${\beta }_1={\alpha }_{2}n+{\beta }_2$). These mathematically formulated links between the parameters of the model contribute to the explanation of the model, as they specify the character of the mutual relations between the parameters. But here, as opposed to fitting the grapheme and phoneme rank-frequency data with the ZM distribution, the number of free parameters does not decrease. Grzybek (2007) suggests that M depends on K, and indirectly also on the inventory size, but new parameters, those of the linear functions, appear. Thus, the negative hypergeometric distribution remains flexible enough to achieve a satisfactory goodness of fit.

If a too short tail of the rank-frequency distribution is indeed the cause why the ZM distribution with the optimized parameter values converges to the geometric distribution with only one free parameter, and consequently fails to achieve a good fit in general, the same could be expected to be observed also in other areas of linguistics if the inventory size of the phenomena under study is relatively small (such as several units or tens, but not hundreds of items). These numbers are typical for inventory sizes of some grammatical categories, e.g. for cases. Frequencies of grammatical cases in Czech from Mačutek and Čech (2013, p. 65) confirm this conjecture, the optimized parameters of the ZM distribution behave analogously to the ones in models from Section 3. However, more studies from this field are required, and for the time being we have only a single observation which does not have to represent a general tendency.

Disclosure Statement

No potential conflict of interest was reporter by the author.

Correction Statement

This article has been republished with minor changes. These changes do not impact the academic content of the article.

Additional information

Funding

This work was supported by the VEGA grant [2/0096/21].

Notes

1. Probably also in abjads. See Daniels (1996) for definitions of writing systems.

2. The same is most probably true also for phonemes. Grzybek and Kelih (2005b) and Grzybek and Rusko (2009) demonstrate similarities among rank-frequency distributions of letters, graphemes, and phonemes.

3. This formulation hints, in fact, at their correlation, although without using this term.

4. Unfortunately, according to personal communication with J.B. Wilson, those datasets are not available anymore.

5. Given the current state of research (see e.g. Wilson & Mačutek, 2020, and the references therein), the negative hypergeometric distribution (Wimmer & Altmann, 1999, pp. 465–468) seems to be the general model.

6. See e.g. data from the Slavic languages in Koščová et al. (2016), and from the Celtic languages in Wilson and Mačutek (2020). In both papers data from corpora, as opposed to individual texts, are presented.

7. Riyal et al. (2016) do not provide a definition of a character in their paper. See Köhler (2008) for a discussion on slightly differing definitions of a grapheme.