Teachers’ beliefs systems about improving transfer of algebraic skills from mathematics into physics in senior pre-university education

ABSTRACT

Senior pre-university education (SPE) students experience difficulties applying mathematics to physics. This paper reports the outcome of an online explorative quantitative study of teachers' belief systems about improving transfer of algebraic skills from mathematics into physics, conducted among 503 mathematics and physics teachers working in SPE. We used a questionnaire with 16 beliefs about improving transfer, and asked teachers to select a top 5 and distribute 50 points among them. We used agglomerative hierarchical clustering to cluster qualified SPE teachers with more than 10 years of teaching experience. We found 3 large clusters, each containing naïve and desirable beliefs about transfer. These clusters turned out to be rather coherent sets of beliefs. Hence, these clusters can be interpreted as belief systems, to a certain extent justifying Ernest's [(1991). The philosophy of mathematics education. London: Falmer.] idea to cluster teachers based on their belief systems. We found relations between our groups and those of Ernest. Since naïve beliefs turn out to be weak in each cluster, science teacher educators can help science teachers to change their harmful naïve beliefs, into desirable transfer enhancing beliefs. Furthermore, we discuss some implications of our results for science teacher educators, curricula, teachers and textbooks.

KEYWORDS:

• Coherent mathematics education
• quantitative research
• senior pre-university education
• teachers’ belief systems
• transfer of learning

Introduction

Complex transfer phenomenon

The application of mathematics in science is of major importance for students (Dierdorp, Bakker, van Maanen, & Eijkelhof, 2014; Quinn, 2013). However, research has shown that students encounter difficulties in science problems where mathematics is needed (Bagno, Berger, & Eylon, 2008; Cui, 2006; Karakok, 2009; NCTM, 2000; Rebello, Cui, Bennett, Zollman, & Ozimek, 2007; Roorda, 2012). For instance, Roorda (2012) mentions that his pre-university students who were taught differentiation in mathematics class, did not recognise in physics that the speed formula is the derivative of the displacement formula .

Even if students are successful in mathematics, transfer is not guaranteed (Karam, 2014). The study of Rebello et al. (2007) with students enrolled in an algebra-based physics course after they had taken a trigonometry course shows that even though their mathematics knowledge was sufficient, they encountered difficulties with mathematics in physics which was related to their inappropriate application of mathematics to physics problems. This makes transfer a complex phenomenon which needs to be further researched.

Why Do Students Lack Transfer?

The main reason for the lack of transfer is related to compartmentalised thinking (Gellish et al., 2007) in which students view mathematics and science as two separate subjects. This phenomenon is reinforced since mathematics and science in secondary education and at college level are taught as separate school disciplines. Overcoming this mental wall may be possible by means of coherent mathematics education (CME) (Berlin & White, 2012, 2014). CME aims at education that fosters connections between mathematics and science subjects.

The absence of transfer may also be related to the mismatch between teachers’ beliefs and classroom practice. Indeed, beliefs strongly affect teacher behaviour (Borg, 2015). For instance, mathematics and physics teachers who may naïvely think that transfer occurs automatically when students are extensively trained in mathematics class in the application of basic algebraic skills. In practice, however, they spend time on re-teaching mathematics in physics class, precious time they would rather spend on teaching physics, which may be frustrating them (Roorda, 2012; Turşucu, Spandaw, Flipse, & de Vries, 2017). Thus, naïve beliefs are harmful for transfer. In addition, in many countries’ science curricula are overloaded, compelling teachers to fit their curriculum into a seriously reduced instruction time (e.g. Lyons, 2006). This lack of time makes inefficient transfer of algebra even more harmful.

Article aim and central research question

There is a large body of research on transfer focusing on the effect of initial learning on new learning (e.g. Karam, 2014; Potgieter, Harding, & Engelbrecht, 2008; Rebello et al., 2007; Roorda, Goedhart, & Vos, 2015). This study extends the latter, but is different in the sense that it examines belief systems containing an organised set of mutually supportive beliefs (Borg, 2015; Mansour, 2009) about improving transfer of algebraic skills from mathematics into physics. Thus, we do not investigate individual beliefs. We especially examine belief systems consisting of desirable (Leatham, 2006) and naïve beliefs (Schoenfeld, 2014) about CME and transfer. Our extended definition of desirable (originally, beliefs that science teacher educators want teachers to hold) refers to beliefs required for productive, i.e. transfer enhancing teaching practice. This can be collaboration between the mathematics and physics department on using the same pedagogy in teaching mathematics (e.g. Alink, van Asselt, & den Braber, 2012; Quinn, 2013; Roorda, 2012), e.g. the application of the algebraic methods.

The relationship between belief systems containing naïve beliefs and transfer is highly under researched. In fact, our extensive literature research yielded only our previous studies on both individual beliefs and core beliefs about transfer of algebraic skills from mathematics in physics (Turşucu et al., 2017; Turşucu, Spandaw, Flipse, & de Vries, 2018).

Better understanding of this relationship is relevant from both an educational and a scientific point of view. As to science education, it may provide relevant information for the mathematics and physics curricula, teachers, textbooks and science teacher educators aiming at improvement of CME and transfer. Regarding the first, there is the possibility to connect the physics curriculum through content standards to the mathematics curriculum, e.g. by means of compatible notations. Consequently, these standards can be used as design principles for physics textbooks. For instance, mathematics textbooks providing physics context, or introduction paragraphs in physics textbooks in which equations and corresponding physics formulas are treated together (activation of prior mathematical knowledge). With regard to teachers, we refer to what both mathematics and physics teachers can do in their classrooms individually, and also to collaboration between both departments. Science teacher educators can use professional teaching programmes (Guskey, 2002) to make science teachers aware of their belief systems, reflect on them and change naïve beliefs such as automatic transfer above into desirable beliefs about transfer. Otherwise, because of the powerful socialisation effect in school, teachers are often observed to stick to ineffective teaching (Brown & McNamara, 2011).

Concerning scientific relevance, this study could contribute to the evaluation of a microscopic (Misfeldt, Jankvist, & Aguilar, 2016) and a macroscopic (Ernest, 1991) belief system model. The former model has its roots in cognitive psychology and deals with individual beliefs, and how they are related to each other in the structure of a belief system. The latter is concerned with how the social context of teaching (e.g. students, teachers and textbooks) influences a teachers’ belief system. In the next section we will explain these models and their relation in detail. This explains why we examined belief systems, rather than individual beliefs.

This paper reports the findings of a quantitative exploratory study on teachers’ belief systems containing naïve beliefs about improving transfer of algebraic skills to physics. The central research question is ‘What are the belief systems of mathematics and physics teachers about improving students’ transfer of algebraic skills from mathematics into physics for solving algebraic problems that occur in senior pre-university education?’.

Background

Transfer as the backbone of CME

Whereas mathematics can be viewed as the formal language of physics (Kjeldsen & Lützen, 2015), physics provides context and meaning for mathematics (Dierdorp et al., 2014). Connection of both disciplines is possible through alignment, e.g. similar concept descriptions, pedagogy of algebraic techniques and organisation of the learning process. The latter concerns organisation of the learning process to achieve a logical learning line across both subjects. In practice, however, certain mathematical concepts are taught in physics class before these were explained in math (Alink et al., 2012). Fostering alignment between both subjects may foster both students’ CME and transfer of mathematics into physics.

Transfer forms the backbone of the CME-approach and refers traditionally to the application of initial learning in a new learning situation (Lobato, Rhodehamel, & Hohensee, 2012), and is regarded as one of the main goals of education (Mestre, 2005). The expert (teacher) determines whether transfer happens or not by checking the learners’ (student) test answers to the expert’s correction scheme, implying a binary outcome: transfer exists or not. A key example concerns assessment of students’ solving for a variable in a formula, e.g. solving for the mass in the formula for kinetic energy . Each solution that does not match with of the correction scheme is regarded incorrect, and therefore associated with the absence of transfer.

Microscopic belief system model

Beliefs are instrumental in the definition of tasks and selection of cognitive tools, which are used to interpret, plan and make decisions concerning tasks (Borg, 2015). They play an essential role in organising knowledge and information, i.e. they help individuals to define the world and themselves. Therefore, beliefs have a major impact on teacher behaviour.

And what about changes in teacher behaviour? They are attributed to the structure of a belief system, rather than to individual beliefs (Leatham, 2006; Misfeldt et al., 2016). Such structures contain certain collections of mutually supportive beliefs with both varying centrality and psychological strength. Beliefs in the centre of the system are psychologically strong, and strongly connected to many other central beliefs, making them hard to change. Other beliefs, i.e. the more peripheral weak beliefs are founded and derived upon these central beliefs. The terms ‘central’ and ‘peripheral’ can be visualised as a group of concentric circles with varying radii (Singletary, 2012). While the inner-most circles represent the strong central beliefs, the outer circles concern the weak peripheral beliefs.

Both ‘central’ and ‘peripheral’ beliefs can be desirable or naïve. While the former improves transfer in physics lessons, the latter is harmful. It can occur that the central area of a teachers’ belief system contains (1) a set of only desirable beliefs, (2) a set of only naïve beliefs or a (3) ‘mixed state’ with a combination of desirable and naïve beliefs about transfer. Another picture is that of a ‘mixed state’ (4) distributed over the central-peripheral area. The first scenario is ideal, since all beliefs form a strong, coherent set of mutually supporting beliefs. Teachers with such beliefs are likely to improve students’ transfer in the classroom. The second scenario contains only harmful beliefs. Changing such strong beliefs would be very difficult. This makes it a least ideal scenario. We expect that our extracted belief systems belong to scenario (4).

This picture with strong and weak beliefs resembles that of an atom having a structure with a nucleus holding together various particles into a stable system. Particles in the nucleus can be regarded as the connected central and psychologically strong beliefs. The other particles which are further from the nucleus and less tightly bound to the system correspond to the peripheral weak beliefs. Hence, the belief system model above with varying centrality and psychological strength of beliefs can be regarded as a microscopic system.

Macroscopic belief system model

The upper rectangle in Figure 1 represents a teachers’ belief system (view) about the nature of mathematics (Ernest, 1991). This offers a foundation for the teachers’ espoused (mental) models of teaching and learning mathematics.

Figure 1. How a teachers’ belief system is affected by the social context of teaching (adopted from Ernest, 1991).

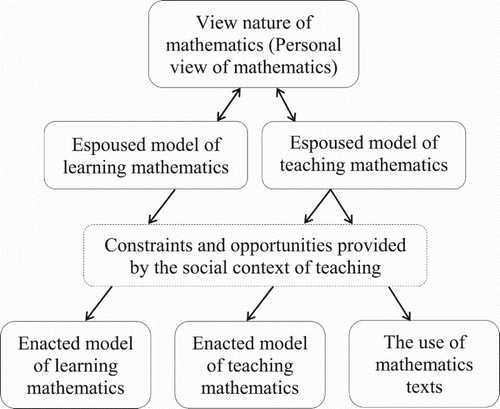
Influenced through constraints and affordances of the social context of teaching, these mental models are transformed (see downward arrows) into teaching practice (enacted models). The distinction between espoused and enacted is essential, since case studies have shown that there can be a great disparity between teacher’s espoused and enacted models (e.g. Brown & McNamara, 2011; Lloyd, Veal, & Howell, 2016).

In this study, we investigate belief systems including desirable and naïve beliefs. Hence, the upper rectangle in Figure 1 with underlying espoused models represents a teachers’ belief system with desirable and naïve beliefs about improving transfer. Contrary to the microscopic model above, Figure 1 can be regarded as macroscopic. We think that a macroscopic view is needed to understand and explain how, e.g. teachers and textbooks in the social context of teaching interact and influence transfer via espoused and enacted models. A microscopic view puts a lens on these espoused models, providing detailed understanding of how various central and peripheral beliefs of a belief system are related with each other.

What do both cognitive microscopic and macroscopic models concretely mean for classroom practice, for instance considering scenario 4? In case of the physics teacher strongly convinced about automatic transfer, he also might have a weak belief since, e.g. he is not that sure whether mathematics teachers providing physics context in mathematics class improves transfer (espoused models). In practice, however, he observes the opposite: students facing difficulties with mathematics in physics class, and the physics context contributing to enhancement of transfer (enacted models). Although there is a discrepancy between both models, this does not necessarily imply that the physics teacher will reflect on his espoused and enacted models and reconcile them to improve transfer. For that to happen, he needs to change his strong and weak beliefs rooted in respectively the central and peripheral area of his belief system. In contrast to his weak belief, his strong belief will resist heavily to change since it is connected to other neighbouring strong beliefs about transfer.

Curricula, teachers and textbooks in SPE

At the age of 12 (Grade-7), Dutch students start with pre-university education consisting of two phases. The first phase involves three years of junior pre-university education (JPE), and the second phase three years of senior pre-university education (SPE). JPE offers a variety of subjects accessible for all students. Based on their interests and talents, SPE-students should choose between one of the four profiles ‘culture and society’, ‘economics and society’, ‘science and health’ or ‘science and technology’ preparing them for university education. Physics students of the last cluster should choose mathematics B, and those of ‘science and health’ mathematics A or mathematics B. Mathematics B puts more emphasis on algebra than mathematics A (Netherlands Institute for Curriculum Development, 2018). The content of these subjects is determined by curricula (the intended curriculum) through core goals.

Textbooks (potential curriculum) mediate between these curricula and the actual teaching in classrooms (Valverde, Bianchi, Wolfe, Schmidt, & Houang, 2002). The limited description of the core goals leaves publishers room for different interpretations in textbooks. Teachers strictly follow these textbooks and teach these to their students (Stein & Smith, 2010; van Zanten & van den Heuvel-Panhuizen, 2014). Many teachers are unaware of curricula (e.g. Turşucu et al., 2017): for them textbooks are the curriculum.

This study examines belief systems with naïve beliefs about transfer by focusing on the key players in SPE, i.e. curricula, teachers and textbooks (Alink et al., 2012). We note that science teacher educators do not belong to this list. Their role is pivotal during the science teacher education programmes leading to a teaching qualification. This may also be the case for the short professional educational programmes. But when these teachers are ‘in service’, their teaching is directly influenced by curricula, teachers and textbooks.

Ernest’s educational model

In his theoretical-educational model Ernest (1991) combines the philosophy of mathematics, theories of intellectual and ethical development, and the sociological-historical theory into five different belief systems, each representing a social group: ‘Industrial Trainers’ (‘IT’ in short), ‘Old Humanists’ (‘OH’), ‘Progressive Educators’ (‘PrE’), ‘Public Educators’ (‘PuE’) and ‘Technological Pragmatists’ (‘TP’). These groups have different views (beliefs) about 12 different themes such as ‘View of mathematics’, ‘Theory of the child’, ‘Theory of society’, ‘Mathematical aims’ and ‘Theory of Teaching Mathematics’. In a sense, Ernest’s model can be regarded as a matrix consisting of 5 columns (each representing a social group) and 12 rows (each representing a theme) about the set of moral values, theory of society and philosophy of mathematics. The intersection of a column and a row corresponds to a social groups’ belief. Below we will briefly describe these social groups.

The ‘IT’ perspective is authoritarian and basic skills-centered, and concerns those teaching the workforce of industry. As to CME and transfer, this perspective does not take into account insightful learning, since for a well-balanced approach aiming at transfer both basic skills (Rittle-Johnson, Schneider, & Star, 2015) and conceptual understanding should be taught in an integrated manner (Drijvers, 2011 ; Kilpatrick, Swafford, & Findell, 2001). They view knowledge as dualistic (either knowledge may be right or wrong) and mathematics as absolute (unquestionable set of facts). The teacher demands rigid discipline of hard working, competitive students who attempt to acquire basic mathematical skills and numeracy, and social training in obedience. The calculator is restricted and there is no room for discussion and collaboration. Social issues and the interests of social groups have no place in mathematics (are neutral).

The pure mathematics centered ‘OH’ group refers to the elitist and cultured class. Knowledge is relativistic (its truth depends on the context), but math absolute. Because of their strong reliance on pure mathematics (especially logic), they are math-centered (not authority as ‘IT’). For them mathematics is the ‘Queen of the Sciences’ (Colyvan, 2012). They refuse to discuss applications, let alone issues on transfer of mathematics in science subjects.

Furthermore, these teachers grant anyone to have his or her own opinion, and they encourage their students to climb up the hierarchy of knowledge as far as possible: they should understand and be appreciate advanced mathematics.

The perspective of ‘PrE’ is learner-centered. Their decisions are humanistic and based upon universal principles such as empathy and caring. Knowledge is considered relativistic and mathematics absolute. Teachers offer non-intrusive guidance in a secure learning environment involving exploration, discovery, play, discussion and collaboration. Students should gain confidence, creativity and self-expression through mathematics. Their openness to collaboration may enable them to develop common teaching strategies between both departments, since this may be a powerful manner to tackle transfer problems (Roorda, 2012).

The group ‘PuE’ aims at education based on democratic socialist principles and values. Their perspective is social justice-centered. Knowledge is regarded relativistic. Mathematics is viewed as the fallible product of human invention (uncertain and corrigible). Collaboration and discussion are important pedagogical components. Like ‘PrE’, their focus on collaboration may enable both departments working together on transfer problems. Through math, students should be empowered and liberated as critical and literate citizens in society.

As to ‘TP’, knowledge is multiplistic (it may be sometimes right, sometimes wrong) whereas mathematics is absolute. Learning involves acquisition of basic skills (Rittle-Johnson et al., 2015) and solving practical problems using mathematics and information technology. Even though they are more progressive than ‘IT’ (e.g. not anti-calculator and not computer), there is again emphasis on procedural fluency, but no attention for insightful learning. Basic and problem-solving skills prepare them for the demands of industry. Indeed, they represent the interest of the industry.

Following Ernest (1991), we categorised teachers into groups based on their belief systems. Unlike our clusters, however, Ernest's (1991) groups are theoretical and not based on empirical data. Finally, his social groups are ‘package deals’: the members of his groups are supposed to either embrace or reject complete sets of beliefs. He does not admit belief systems mixing aspects of different groups. Neither does he allow for different degrees of belief. In practice, certain social groups may have ideas that overlap with other groups. We expect that this also holds for our study.

Previous two studies

In the previous two studies, we first investigated teachers’ individual beliefs (Turşucu et al., 2017) and then teachers’ core beliefs (Turşucu et al., 2018) about transfer of algebraic skills from mathematics in physics in SPE. In this regard, we interviewed 10 mathematics and 10 physics teachers. These interviews were based on the semi-structured questionnaire including one specific case about the students’ transfer problem from mathematics to physics for which solution algebraic skills were needed.

First study

We used open and axial coding to analyse interview data (Bryman, 2015). This resulted in the hierarchical common code tree for both mathematics and physics teachers containing 9 core themes (Coherence, Curriculum, Education, Pedagogy of algebra, Relation between scientific subjects, School subjects, Teacher, The use of textbooks and Transfer), and 28 sub themes including the continuum of approximately thirteen hundred teachers’ beliefs (Turşucu et al., 2017). The latter consisted of aspects influencing both students’ demonstration of CME and transfer. When implemented properly, these results may help to reduce physics teachers’ frustrations, since they may focus on physics concepts instead of spending extra time on re-teaching mathematics in physics class.

We saw that almost all teachers acknowledged the case presented to them and found it important that students are competent at applying algebraic skills in physics. Most of the teachers think that such transfer problems occur especially in Grade-10 of SPE.

In line with earlier research (e.g. Claxton, 1991; Osborne, 2013) most of the teachers think that the lack of transfer is related to compartmentalized thinking.

Contrary to physics teacher, most of the mathematics teachers mentioned that they did not feel the need to collaborate with physics teachers. This result makes the development of common teaching strategies to tackle transfer problems analogous to the case more difficult.

We found two opposite, extreme beliefs about how to transfer algebraic skills to physics. The first refers to automatic transfer in which extensive practice in math class will lead to transfer in physics. The second refers to reinventing the same mathematical wheel in different physics contexts. Most of the beliefs were in between these opposite beliefs.

Second study

The common code tree including teachers’ individual beliefs can be organised into belief systems. Nevertheless, this data set involved large amount of data that hampered us to extract belief systems in one single data reduction step. Therefore, we used the second cycle coding technique pattern coding (Saldaña, 2015) to further reduce and grasp the essence of the common code tree. This resulted in one set of 16 core beliefs (Turşucu et al., 2018) about constraints and affordances influencing both students’ demonstration of CME and students’ transfer of algebraic skills into physics. These core beliefs could be organised into what we named main categories: Collaboration, Curricula, Students, Teachers and Textbooks. This means that the nine core themes were condensed into these five categories. In the teachers’ eyes these are the main issues to focus on to improve transfer. We also found which main category corresponded to these nine core themes.

Based on earlier literature on transfer (e.g. Alink et al., 2012; Quinn, 2013; Roorda, 2012), some of the core beliefs were identified as harmful naïve beliefs, and others as productive desirable beliefs (espoused models) (Schoenfeld, 2014). Naïve beliefs may stand in the way of transfer because these may be transformed into teaching practice (enacted models). Through professional development programmes (Guskey, 2002) aiming at transfer both models should be reconciled.

The dataset of 16 core beliefs is sufficiently reduced to extract belief systems with desirable and naïve beliefs in a last data reduction step. We will explain this in detail below.

Methodology

Firstly, we explain the transformation of sixteen core beliefs into 16 claims. Secondly, the development of an online survey and how we ran it is explained. This survey included 16 claims that were used in the short questionnaire. Thirdly, we will describe the data collection method. Fourthly, the extraction of belief systems is described.

Step 1: forming of claims

The 16 core beliefs were converted into sixteen claims, which were clearly phrased using the six functions of language of Jacobson (Hébert, 2011). Also the relation between the central research question and the claims was emphasised. We combined both requirements. The claims were (1) phrased positively, (2) understandable without any explanation, (3) verbalised as factual as possible and (4) used well-known language for both mathematics and physics teachers. This should lead to 16 claims about improving students’ demonstration of CME and transfer of algebraic skills from math in physics.

To warrant intersubjectivity, the whole procedure above was discussed by the first and third author and two independent researchers until 100% consensus was reached on the formulation of claims among all researchers. Next, these claims were transformed into a short questionnaire.

Step 2: development of online survey and running it

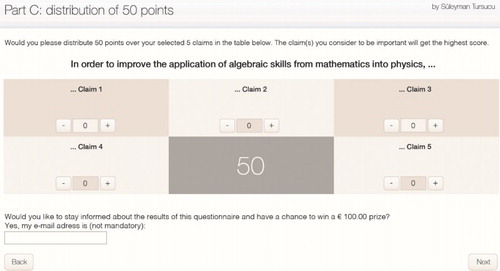
The online survey we developed for mathematics and physics teachers consisted of four parts, each corresponding to a separate webpage (Sue & Ritter, 2012). On the first webpage teachers were introduced to background information about the first author, together with the aims and purpose of the survey. On the second webpage respondents were asked to answer questions about their gender, profession and number of years of teaching experience. The 16 claims were incorporated in the short questionnaire and used on the third webpage. Here, mathematics and physics teachers were asked to select their top 5. Because of two reasons the questionnaire was introduced through the transfer problem in the case (Turşucu et al., 2017): to give the respondents an idea about what is meant with algebraic skills and since the claims were based on these skills. Webpage four deals with the multi-criteria assessment tool (Belton & Stewart, 2002) that we have developed, because there was no such digital tool available. This is illustrated in Figure 1. To gain more insight into the relative weights between these five claims (top 5), teachers were asked to distribute 50 points over these claims.

The number ‘50’ in the centre of this tool has a dynamic display that changes with each distribution operation and returns the remaining points. In the pilot-study social science experts and teachers mentioned that this display helped them to concentrate on the distribution of their points over the claims, and gain more insight in the remaining points after each operation. This helped them achieving a well-balanced point distribution (Figure 2).

Figure 2. Multi-criteria assessment tool in which teachers distribute 50 points over their selected 5 claims.

Step 3: data collection method

We used self-selection sampling (Bryman, 2015) to gather data. About 300 schools in urban areas including most capitals of provinces and the bigger cities in the Netherlands were invited to participate in this study. We also invited about 100 sub-urban and 30 rural schools. The respondents consisted of mathematics and physics teachers from all levels of secondary education. To achieve a high response rate among these respondents we offered a € 100,00 reward.

Step 4: extraction of teachers’ belief systems

The notion of ‘belief system’ was modelled as follows. For each of the 16 claims we have an empirical distribution of scores. We clustered the teachers such that all teachers in a certain cluster have similar scores on the 16 claims. A belief system is then the system of 16 empirical distributions for the corresponding cluster of teachers. So, to find belief systems, we had to cluster the teachers. To this extent we used the clustering technique agglomerative hierarchical clustering (AHC) (Everitt & Dunn, 2001). After the belief systems were extracted, the first and second author triangulated on which of these were considered as useful for this study and which were not. They reached 100% consensus on the final set of belief systems.

Results

Firstly, we will present the 16 claims translated from Dutch to English. Secondly, the teachers who participated in this study are shown. Thirdly, the total scores of experienced teachers are presented. Fourthly and fifthly, the belief systems of respectively the very and most experienced teachers are shown.

16 claims

The set of 16 claims is depicted below in Table 1. Each core belief in the previous study (Turşucu et al., 2018) was converted into the corresponding claim using the criteria above. The naïve claim numbers are 2, 3, 7, 9 and 16.

Table 1. Set of 16 claims about CME and improving transfer.

Claim number	Rationale
To improve the application of algebraic skills from mathematics into physics …
1.	… the collaboration between mathematics and physics teachers should have more priority.
2.	… mathematics A should contain more algebraic skills than is the case now.
3.	… mathematics should contain more algebra.
4.	… mathematics teachers need more time to cooperate with physics teachers.
5.	… the content of mathematics and physics textbooks should be adjusted.
6.	… mathematics and physics teachers should be able to explain relevant basic knowledge about mathematics.
7.	… mathematics and physics teachers should follow the content of their textbooks.
8.	… students should recognize physics contexts.
9.	… students should practice more algebraic skills during physics lessons.
10.	… mathematics and physics teachers should use the same notations in formulas.
11.	… prior mathematical knowledge should be activated during physics lessons.
12.	… students should see relations between contexts of both mathematics and physics.
13.	… mathematics and physics teachers should work together to improve the application of these algebraic skills.
14.	… mathematics should incorporate more physics contexts.
15.	… to a lesser extent students should see mathematics and physics as separate subjects.
16.	… the physics curriculum should contain more manipulation of formulas than is the case now.

Participating teachers in this study

Our sample included 503 teachers from all levels of secondary education. After some preliminary analyses, we decided to focus on qualified senior pre-university teachers, since the transfer problems under consideration take mainly place in their Grade-10 classes (Roorda, 2012; Turşucu et al., 2017). We restricted our attention to teachers with more than five years of teaching experience. This left us with 274 senior pre-university teachers, including 188 male and 86 female teachers. The results are listed below in Table 2.

Table 2. Distribution of years of teaching experience over number of participating mathematics and physics teachers.

Teaching experience (years)	6–10	11–20	20–	Total
Mathematics	31	59	77	167
Physics	28	38	41	107
Total	59	97	118	274

During the analysis in the next section we will refer to these 274 teachers as ‘experienced teachers’. The 97 teachers (61 male and 36 female) with more than 10 years of teaching experience will be called ‘very experienced teachers’, and the 118 teachers (89 male and 29 female) with more than 20 years of teaching experience ‘most experienced teachers’.

Total scores of experienced teachers

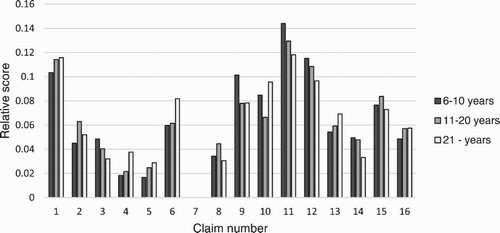
A first impression of the opinions of these 274 experienced teachers can be obtained from the relative scores on the 16 claims. These are given in Figure 3 (normalised to a total of 1) for the three subgroups of 59 experienced teachers (white bar), the 97 very experienced (grey bar), and the 118 most experienced teachers (black bar). Remarkably, not a single teacher had chosen claim number 7 in his or her top 5! Claim number 11 has the highest total score.

Figure 3. Relative total scores of the 274 experienced teachers over the 16 claims.

To gain more some insight into the differences of the three experience levels with respect to the distribution of the scores, we plotted a boxplot for each of the 16 claims (Figure 4), again for the whole group of 274 qualified teachers with more than 5 years of teaching experience.

Figure 4. Boxplot of the total scores of 274 teachers showing medians, outliers and quartile scores.

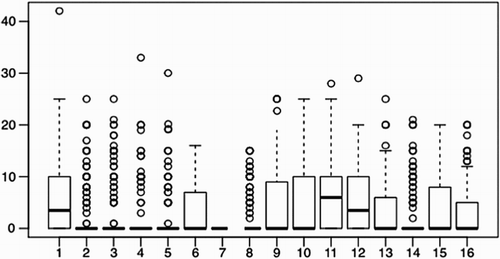
We see that most claims have zero median and most scores have quite a few outliers, i.e. scores larger than the third quartile plus 1.5 times the interquartile range (Cohen, Cohen, West, & Aiken, 2013). Correlations between the 16 claims were low. Even when we restrict to the subsample of 97 very experienced teachers or 118 most experienced teachers, all correlations were small. Their squares (explained variance) were smaller than 0.10. Small correlations make principal component analysis (PCA) and factor analysis ‘pointless’ (Everitt & Hothorn, 2011, p. 157). This finding was confirmed by the PCA scree-plots. These lacked a clear ‘elbow’, which implies that there is no natural choice for choosing the number of dimensions.

AHC produces a tree, also called dendrogram. The method starts with the leaves of the tree, i.e. the teachers in the case at hand. It joins the individuals whose scores are closest with respect to a specified measure. Next, the distances between the clusters thus obtained are compared and the closest clusters are joined to agglomerated clusters. In the next step, one gets next level agglomerated clusters. And so on, until all teachers are teachers are joined in one supercluster at the root (see e.g. Figure 5). The distance between clusters which are merged in clusters of the next level is called the ‘height’ (Figure 5). Two choices should be made to produce a tree: a distance function on the set of 16-dimensional scores and a ‘linkage method’ used to define the distance between clusters. We took complete linkage as recommended by Everitt and Hothorn (2011). This means that the distance between two clusters X and Y is defined as the maximal distance between points x in X and y in Y.

Figure 5. Dendogram for the 97 very experienced teachers using dichotomised scores.

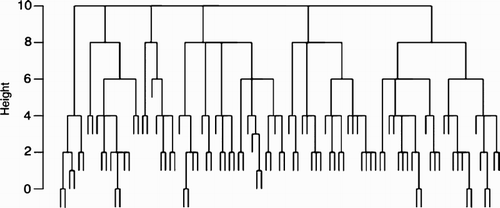
We used the statistical programming language R to produce the trees using the command ‘hclust’. Dichotomized scores (taking 1 for positive scores and 0 for zero scores) in combination with Manhattan distance and complete linkage produced the trees with the clearest clustering. For example, in Figure 5, we see that the 97 very experienced teachers with 11–20 years of teaching experience form 6 clusters. Note that the first splitting near the root occurs at the same height (h = 8) in the tree. If we use non-dichotomised scores, we get trees whose splitting heights are not so nicely and evenly distributed as in Figure 5. Different choices of the height, which are quite arbitrary, would lead to different number of clusters.

Belief systems of very experienced teachers

The tree for the 97 qualified SPE mathematics and physics teachers with more than 10 years of teaching experience is shown in Figure 6. At the most fundamental level, this tree clusters these teachers into 6 clusters, which we will call BS1(VE) to BS6(VE) (‘BS’ for ‘belief system’ and ‘VE’ for ‘very experienced’). The ‘height’ is the Manhattan distance between the clusters. The 6 clusters BS1(VE) to BS6(VE) merge at height 10, which means that the distance between these clusters equals 10. Their sizes are 6, 12, 8, 24, 20 and 27. They contain 3, 9, 5, 18, 9 and 15 mathematics teachers and 3, 3, 3, 6, 11 and 12 physics teachers, respectively. We focused on the three largest clusters BS4(VE), BS5(VE) and BS6(VE), covering 74% of the 97 teachers, since the other three clusters are rather small.

Figure 6. Mean scores and errors for the three largest clusters BS4(VE), BS5(VE) and BS6(VE) of very experienced teachers.

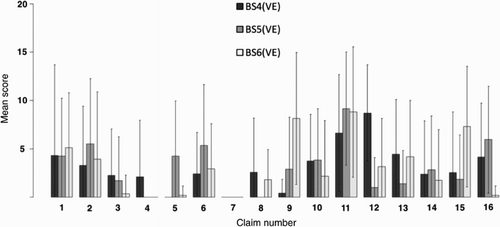
A first impression of these belief systems can be obtained from Figure 6, which shows the mean (non-dichotomised) scores of these three clusters on the 16 claims. The total of the 16 means equals 50 for each cluster. The error bars correspond to one standard deviation.

Belief systems of most experienced teachers

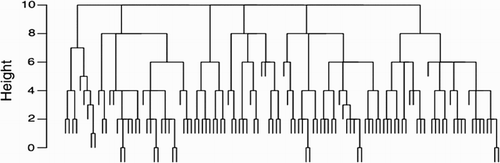
We performed the same analysis for the group of 118 most experienced-qualified pre-senior university teachers, i.e. teachers with more than 20 years of teaching experience. They are different individuals than those in the clusters in the analysis of the 97 very experienced teachers.

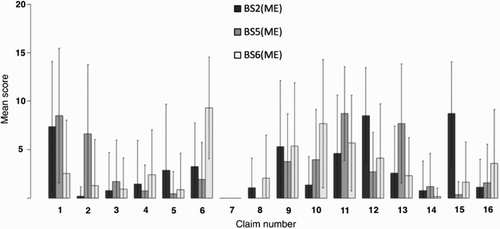
The tree is given in Figure 7. We again found six belief systems, which we denoted as BS1(ME) (‘ME’ for ‘most experienced’) up to BS6(ME). The belief systems contain 9, 26, 9, 15, 27 and 32 teachers, respectively. We ignored the small belief systems BS1(ME), BS3(ME) and BS4(ME). Belief system 2 contains 20 math teachers and 6 physics teachers. For BS5(ME) these numbers are 17 and 10, and for BS6(ME) these numbers are 23 and 9, respectively. The three belief systems BS2(ME), BS5(ME) and BS6(ME) cover 72% of the 118 most experienced teachers.

Figure 7. Dendogram for the 118 most experienced teachers using dichotomized scores.

Figure 8 shows the mean scores on the 16 claims for the three largest belief systems BS2(ME), BS5(ME) and BS6(ME). Again, the total of the 16 means equals 50 for each belief system. As in Figure 7, the error bars again correspond to 1 standard deviation. We immediately see some remarkable features, e.g. BS2(ME) gives a high score to claim 15, BS5(ME) puts much weight on claims 2 (naïve belief) and 13, whereas BS6(ME) is distinguished by its high score on claim 6.

Figure 8. Mean scores and errors for the three largest clusters BS2(ME), BS5(ME) and BS6(ME) of most experienced teachers.

Results interpretation

In this and later sections, the words claim and belief are used interchangeably to denote one of the 16 claims in Table 1. We focused on belief systems including beliefs with the highest scores, and neglected those with the lowest scores.

Very experienced teachers: BS4(VE), BS5(VE) and BS6(VE)

The highest scores in BS4(VE) belong to claims 12, 11, 13, 1 and 16 (naïve belief). The focus is on collaboration between mathematics and physics teachers and making links between math and physics class. Prior mathematical knowledge should be activated in physics class and students should see (or rather: be helped to see) the relations between contexts used in math and physics class. Mathematics and physics should work together to improve transfer of algebraic skills to physics. More generally, collaboration between these teachers should have more priority. The lowest scores in BS4(VE) belong to claims 7, 5 and 9, which centre around the textbooks. Teachers with this belief system do not believe that following or adjusting textbooks is important to improve transfer, nor do they believe that algebraic skills should be practiced more in physics class.

The highest scores in BS5(VE) belong to claims 11, 16 (naïve belief), 2 (naïve belief) and 6. The focus is on the teacher and on the curriculum. The physics teachers should activate prior mathematical knowledge in their classes and they should be able to explain basic mathematics. The physics curriculum should pay more attention to manipulation of formulas and the curriculum for mathematics A should give more weight to algebraic skills than now is the case. The lowest scores in BS5(VE) correspond to claims 7, 4, 8 and 12 which centre around students. Teachers do not believe that students seeing relations between contexts used in both math and physics class is important to improve transfer. Nor do they believe that more collaboration of mathematics and physics teachers is the key to improvement of transfer.

Finally, the highest scores in BS6(VE) were given to claims 11, 9 (naïve belief) and 15. These centre around the student and the teacher. Their mathematical pre-knowledge should be activated, they should practice algebraic skills in physics class more than they do now, and they should learn to see the connections between mathematics and physics. The lowest scores in BS6(VE) belong to claims 7, 4, 16, 5 and 3. There is a focus on the textbook and the curriculum. These teachers do not believe that the content of textbooks should be followed, nor do they believe that its content should be changed.

Comparing BS4(VE), BS5(VE) and BS6(VE)

The most remarkable differences among the strong claims between BS4(VE) and BS5(VE) are the scores on claims 12, 13 and 6. BS4(VE) rates claim 12 nine times more important and claim 13 three times more important than does BS5(VE). We conclude that collaboration between mathematics and physics teachers and connecting contexts used in physics and math class are far more important to BS4(VE) than to BS5(VE). Conversely, claim 6 is rated twice as high by BS5(VE) compared to BS4(VE). Hence, physics teachers explaining basic mathematics is deemed more important in BS5(VE) than in BS4(VE).

The strong claim of BS4(VE) with the highest ratio BS4(VE): BS6(VE) is number 16 (naïve belief) (BS4(VE) = 22 × BS6(VE)). The strong claim of BS6(VE) with the highest ratio BS6(VE): BS4(VE) is number 9 (naïve belief) (BS6(VE) = 20 × BS4(VE)). We conclude that BS4(VE) teachers believe much stronger than their BS5(VE) colleagues that more algebra in the physics curriculum is beneficial for the transfer of algebra to physics. BS6(VE) teachers, on the other hand, believe stronger in algebraic practice in physics class.

Finally, we compare BS5(VE) to BS6(VE). The most distinguishing strong claims are number 16 (naïve belief) (BS5(VE) = 32 × BS6(VE)), number 15 (BS6(VE) = 4 × BS5(VE)), and 9 (naïve belief) (BS6(VE) = 3 × BS5(VE)). Teachers belonging to BS5(VE) believe more strongly than BS5(VE) teachers that adjustments of the physics curriculum are important to improve transfer. Conversely, BS6(VE) teachers have a stronger focus on student related claims: these students should learn to see the connections between mathematics and physics and they should practice algebra in physics class.

Table 3 summarises this analysis. The items ‘11, 9 (naïve belief), 15’ in the last column of the first row are the numbers of the strongest beliefs in BS6(VE). Similarly, ‘7, 5, 9 (naïve belief)’ in the third row of the first column are the numbers of the weakest beliefs in BS4(VE). Finally, ‘6 (2)’ in the BS4(VE)-row of the BS5(VE)-column means that among the strong beliefs of BS5(VE), claim 6 had the highest ratio BS5(VE): BS4(VE), namely BS5(VE) = 2 × BS4(VE). The entries ‘12 (9), 13 (3)’ in the BS5(VE)-row of BS4(VE)-column means that among the strong claims of BS4(VE), number 12 and 13 had the highest ratio BS4(VE): BS5(VE), namely 9 and 3, respectively.

Table 3. Comparison of strong beliefs in BS4(VE), BS5(VE) and BS6(VE).

Weak	Strong	12, 11, 13, 1, 16	11, 16, 2, 6	11, 9, 15
	Row < Column	BS4(VE)	BS5(VE)	BS6(VE)
7 5 9	BS4(VE)		6 (2)	9 (naïve belief) (20)
7 4 8 12	BS5(VE)	12 (9) 13 (3)		5 (4) 9 (naïve belief) (3)
7 4 16 5 3	BS6(VE)	16 (naïve belief) (22)	16 (naïve belief) (32)

Most experienced teachers: BS2(ME), BS5(ME) and BS6(ME)

The claims with the highest scores in BS2(ME) are claim number 15, 12 and 1. The focus is on students and on collaboration. Teachers believe that to improve transfer, students should learn to see the relations between physics and mathematics, and teachers should work together. The claims with the lowest scores in BS2(ME) are claim number 7, 2, 14 and 3. These centre around curricula. Teachers in this belief system do not believe that changing curricula are the most important steps to improve transfer.

The claims with the highest scores in BS5(ME) are claim number 11, 1, 13 and 2 (naïve belief). The focus is on collaboration. Teachers in this believe system think that mathematics and physics teachers should collaborate to improve the algebraic skills of their students, physics teachers should activate mathematical pre-knowledge in their classes, whereas mathematics A classes should pay more attention to algebra. The claims with the lowest scores in BS5(ME) are claim number 7, 8, 15 and 5. These centre around students and on the textbooks. Teachers in this belief system do not attach much importance to their students seeing connections between mathematics and physics. Neither do they think that teachers should follow the content of textbooks or make adjustments in textbooks.

The claims with the highest scores in BS6(ME) are claim number 6, 10, 11 and 9 (naïve belief). The focus is on teachers. To improve transfer, they should both be able to explain basic mathematics and use the same notations. Physics teachers should activate mathematical pre-knowledge and students practice more algebraic skills in physics class. The claims with the lowest scores in BS6(ME) are claim number 7, 14 and 5. Teachers in this belief system do not believe that following and changing textbooks will help greatly to improve transfer.

Comparing BS2(ME), BS5(ME) and BS6(ME)

The strong claims distinguishing most between BS2(ME) and BS5(ME), i.e. the strong claims for BS2(ME) with the highest ratio BS2(ME): BS5(ME) and the strong claims for BS5(ME) with the highest ration BS5(ME): BS2(ME), are number 15 (BS2(ME) = 24 × BS5(ME)) and number 2 (naïve belief) (BS5(ME) = 34 × BS2(ME)). Connecting mathematics and physics is far more important for BS2(ME) than for BS5(ME), whereas more algebra in the mathematics A curriculum is far more important to BS5(ME).

The strong claims distinguishing best between BS2(ME) and BS6(ME) are number 15 (BS2(ME) = 5 × BS6(ME)), number 1 (BS2(ME) = 3 × BS6(ME)) and number 10 (BS6(ME) = 6 × BS2(ME)). BS2(ME) focuses more on students, who should learn to see the connections between mathematics and physics. BS6(ME) focuses on the teachers, who should use compatible notations.

Finally, we compare BS5(ME) to BS6(ME). The most distinguishing strong claims are number 2 (naïve belief) (BS5(ME) = 5 × BS6(ME)), number 1 (BS5(ME) = 3 × BS6(ME)), number 13 (BS5(ME) = 3 × BS6(ME)), number 6 (BS6(ME) = 5 × BS5(ME)) and numbers 16 (naïve belief) (BS6(ME) = 2 × BS5(ME)). Teachers in BS5(ME) think that collaboration between mathematics and physics teachers and adapting the mathematics A curriculum are more important for improving transfer than their colleagues in BS6(ME) think. Teachers adhering to BS6(ME), on the other hand, attach more weight than BS5(ME) teachers do to adapting the physics curriculum and to physics teachers explaining basic mathematics. In short, BS5(ME) teachers focus on math class and math teachers, whereas BS6(ME) teachers focus on physics class and physics teachers. Table 4 summarises this analysis.

Table 4. Comparison of strong beliefs in BS2(ME), BS5(ME) and BS6(ME).

Weak	Strong	15, 12, 1	11, 1, 13, 2	6, 10, 11, 9
	Row < Column	BS2(ME)	BS5(ME)	BS6(ME)
7 2 14 3	BS2(ME)		2 (naïve belief) (34)	10 (6)
7 8 15 5	BS5(ME)	15 (24)		6 (5) 16 (2)
7 14 5	BS6(ME)	15 (5) 1 (3)	2 (5) 1 (3) 13 (3)

Belief systems including naïve beliefs: very and most experienced teachers

Based on the analysis above, we present five belief systems, each consisting of desirable and naïve beliefs which are depicted and explicated in Table 5. BS2(ME) is not included, since it has no naïve beliefs. The strength of beliefs in increasing order is also illustrated. This information is obtained from Figures 6 and 8, and will be used in the last section. It can be seen that the number of naïve beliefs in a belief system may differ. Except for BS5(VE), the other clusters contain one naïve belief. Remarkably, claim numbers 6 and 16 are absent for the most experienced teachers. On the other hand, the very and most experienced teachers share claim numbers 2 and 9.

Table 5. The five belief systems we have found include desirable and naïve (in bold) beliefs. The last column concerns the increasing strength of beliefs in a belief system.

Belief system	Naive beliefs	Desirable beliefs	Increasing strength of beliefs
BS4(VE)	16	1, 11, 12, 13	16, 1, 13, 11, 12
BS5(VE)	2, 6	6, 11	6, 2, 16, 11
BS6(VE)	9	11, 15	15, 9, 11
BS5(ME)	2	1, 11, 13	2, 13, 1, 13
BS6(ME)	9	6, 10, 11	9, 11, 10, 6

Also remarkable is that claim number ‘16’ of BS4(VE), number ‘2’ of BS5(ME) and number ‘9’ of BS6(ME) are both naïve and the weakest beliefs. The naïve beliefs number ‘2’ and ‘16’ of BS5(VE), and number ‘9’ of BS6(VE) are also weak. Overall, we can say that the naïve beliefs in the last column are the weakest beliefs, i.e. has least strength.

Comparing belief systems: very versus most experienced teachers

BS4(VE) seems to correspond to BS5(ME), both attaching much weight to claims 1, 11 and 13. To improve transfer, they focus on collaboration. Hence, we refer to both clusters as the ‘Collaboration-oriented group’ (‘COG’). BS5(VE) matches with BS6(ME), both believing strongly in claims 6 and 11. Since they focus on teachers, we called them the ‘Teacher-oriented group’ (‘TOG’). BS6(VE) and BS2(ME) we called the ‘Student-oriented group’ (‘SOG’) because they share a strong belief in claim 15 with a clear focus on students.

Discussion and conclusion

With regard to the central research question ‘What are the belief systems of mathematics and physics teachers about improving students” transfer of algebraic skills from mathematics into physics for solving algebraic problems that occur in senior pre-university education?’ we conducted an online survey among 503 mathematics and physics secondary school teachers. The survey included the 16 claims in Table 1 about improving transfer. Teachers were asked to select their top 5. Data were analysed by means of AHC. We focused on teachers with more than 10 years of teaching experience in SPE. This led to the large clusters BS2(ME), BS5(ME) and BS6(ME) for the 118 most experienced teachers (ME), and the large clusters BS4(VE), BS5(VE) and BS6(VE) for the 97 very experienced teachers (VE). Except for BS2(ME), the other clusters consist of both desirable and naïve beliefs. Despite these naïve beliefs, overall each of these clusters contain an organised set of mutually supporting beliefs about transfer. Since such clusters with coherent beliefs are interpreted as belief systems (Misfeldt et al., 2016; Singletary, 2012), we have empirical evidence for the existence of belief systems. To a certain extent, this also justifies Ernest’s (1991) theoretical idea to cluster teachers based on their belief systems.

BS2(ME), claim numbers 7 and 11

Following the line of Leatham (2006) and Singletary (2012), the peripheral area of BS2(ME) enabling weak beliefs may be empty, i.e. may not contain naïve beliefs about transfer. In addition, the central part includes productive desirable beliefs. Consequently, teachers transforming such belief systems (espoused models) into teaching practice (enacted models) (Ernest, 1991) are more likely to foster transfer than teachers having belief systems with naïve beliefs. Indeed, with regard to improvement of transfer, there is a match between the espoused and enacted models. Remarkably, this is also the only belief system lacking the desirable claim (number 11) with the highest total score among all other clusters. On the other hand, claim number 7 is absent in BS2(ME). Like all other clusters they seem to be aware of this naïve belief, but naively seem to be unaware of the importance of claim number 11. We recommend to further examine this apparent contradiction, e.g. by investigating why teachers in this cluster neglected this claim by means of a qualitative in depth-interview. Furthermore, the top scores of claim number 11 in the remaining clusters is not that surprising. Indeed, the importance of activation of prior knowledge is a well-known issue in the context of learning and instruction in relation to better students’ achievements (e.g. Hailikari, Katajavuori, & Lindblom-Ylanne, 2008).

Claim number 11 has implications for science education. Regarding curriculum materials, policy makers should take this matter into account as a key design principle in which both subjects are connected to each other. These curricula are transformed into textbooks which are closely followed by Dutch teachers who teach them to their students (van Zanten & van den Heuvel-Panhuizen, 2014). This strongly suggests that physics textbooks need introduction paragraphs containing prior mathematical knowledge about the physics subject that will be treated. For instance, when the task is to solve for in the aforementioned kinetic energy formula , the textbook may first refer to the mathematics equation that students have already seen in mathematics class, also explicating that both expressions are analogous with respect to their algebraic structure. After solving for the mathematics equation , the textbook solves for the physics formula . Beyond textbooks, also physics teachers play a role in connecting mathematics to physics. Even mentioning that formulas in physics are rooted in mathematics class or writing mathematics and physics expressions next to each other may contribute to transfer (Alink et al., 2012; Turşucu et al., 2017). Furthermore, the mathematics teacher can reinforce this transfer process by referring to the physics class.

In case of science teacher educators, the implication is twofold. Through both ‘professional teaching programmes’ (Guskey, 2002) and ‘science teacher education programmes leading to a teaching qualification’, they should make ‘in service’ and ‘pre-service’ science teachers aware of their belief systems, reflect on them and change naïve beliefs into desirable beliefs about transfer. Otherwise, their naïve beliefs will probably lead to teaching practice which is harmful for CME and transfer.

Although activation of prior knowledge is considered important, it requires sufficient organisation of the learning process. Mathematical concepts should be taught before they are explained in physics class. In case of physics teachers above, they may examine students’ mathematics textbooks or have conversation with mathematics teachers to align both subjects. Regarding textbooks, these should be connected through content developed by the same publisher. Otherwise, i.e. when two different publishers are involved, alignment is made very difficult since each of them pursue different aims (Alink et al., 2012).

The connections above are pivotal in overcoming compartmentalised thinking (Gellish et al., 2007) and could strengthen coherence between mathematics and science education (Berlin & White, 2012, 2014).

The finding that not a single teacher had chosen claim number 7 above shows that they feel that following the content of textbooks does not contribute sufficiently to improving transfer. Further research, e.g. textbook analysis could provide insight in the extent to which math and physics textbooks take this matter into account. We also recommend conducting qualitative interviews with teachers, since both studies complement each other.

Other relevant desirable beliefs

Beyond claim number 11, other desirable beliefs with high scores are 1, 6, 10 and 13 (see Table 5). Remarkably, claim numbers 1, 10 and 13 all concern collaboration between mathematics and physics teachers. Contrary to the previous qualitative studies in which the major part of mathematics teachers did not feel the need to work together with physics teachers (Turşucu et al., 2017, 2018), this quantitative study reveals that many mathematics teachers think that collaboration between both departments should be given more priority (number 1). This is good news, since sufficient collaboration is essential to enhance both CME and transfer (Berlin & White, 2012, 2014; Quinn, 2013).

On the individual level, we even think that explaining relevant basic mathematical knowledge (number 6) should be a pre-requisite in science teacher education programmes leading to a teaching qualification. Furthermore, both on the collaboration and the individual level the mathematics and physics subjects should be connected through alignment of equations, formulas, notations (number 10), better application of algebraic skills (number 13) and the same pedagogy of teaching algebraic skills such as the application of algebraic techniques to manipulate expressions in both subjects. Such alignment aspects also apply to curricula and textbooks used in SPE (Alink et al., 2012). In addition, science teacher educators should use these aspects in teaching materials for science teacher education programmes. Here, we did not mention mathematics teacher educators, because basic mathematical knowledge is already incorporated in the SPE mathematics curriculum (‘Netherlands Institute for Curriculum Development’, 2018), and thus part of the SPE teacher education programme. Furthermore, without a solid basis in school mathematics, especially school algebra, working on students’ transfer of algebraic skills to physics is hardly possible. Probably, this makes individual mathematics and physics teachers pivotal in the classroom. Still, there should be collaboration above between both teacher groups. In line with earlier, we conclude that both individual and collaborative efforts are like two sides of the same coin.

Belief systems with naïve beliefs

Based on earlier studies (Leatham, 2006; Misfeldt et al., 2016; Singletary, 2012), the weakest beliefs in a belief system are located in the peripheral area. Since we had theoretically grounded naïve beliefs (e.g. Alink et al., 2012; Quinn, 2013; Roorda, 2012; Turşucu et al., 2018) (second column of Table 5), one would expect that the empirically determined weakest beliefs (last column of Table 5) are these already identified naïve beliefs. Indeed, there is a match between them, implying that we verified a theoretical construct with empirical data. We conclude that the naïve beliefs in Table 5 correspond to the weak beliefs rooted in the peripheral area of the belief systems we have found. On the other hand, the desirable beliefs in the last column have the strongest psychological strength and are strongly connected to other central beliefs.

To change the empirically naïve beliefs into desirable beliefs, clusters in the peripheral area in which they are stored, should be disturbed. This is possible, since naïve beliefs are the weakest beliefs. The good news is that most of the teachers’ strong beliefs in these clusters are already desirable; they are productive and transfer enhancing. Otherwise, i.e. when the naïve beliefs would have been very strong (aforementioned second scenario), it would be very difficult to change them.

To make such changes one needs to use the microscopic belief system model above and the macroscopic model of Ernest (1991) together. Through professional development programmes (Guskey, 2002), science teacher educators who are well informed about these models could make teachers having naïve beliefs explicitly aware of their belief systems. They can use Figure 1 with espoused and enacted models to explain how, e.g. teachers, students and textbooks influence a teachers’ belief system. Thereafter, teachers may reflect on them to improve transfer. Thus, teachers belonging to BS5(VE) need extra attention, since they have not one, but two naïve beliefs in their belief system.

The remarkable difference in the number of belief systems with naïve beliefs, and the number of naïve beliefs between the most experienced and very experienced teachers in Table 5 may be explained by the extent of their awareness of the harmful and unproductive nature of naïve beliefs (espoused models) for teaching practice (enacted models). This implies that the more experienced teachers are, the less their number of clusters containing naïve beliefs, and the less their number of naïve beliefs become.

Furthermore, we have seen that the distinction between the macroscopic and microscopic model of belief systems turned out to be useful. The first model containing espoused and enacted models (Ernest, 1991) was used to explain and understand how the social context of teaching influences a teachers’ belief system, and the second one which is a detailed cognitive description of the espoused models to understand how the weak naïve beliefs and the strong desirable beliefs in a belief system are related to each other. We recommend future studies on this matter to use both models together.

Ernest’s social groups and our groups

As expected, the construction of an educational matrix model analogous to that of Ernest (1991) was not possible, because our obtained belief systems are not pairwise disjoint, i.e. some beliefs occur in several belief systems. For example, claim number 11 appears in several belief systems, whereas Ernest’s five social groups (belief systems) are pairwise disjoint. Our model of the notion of ‘belief system’, being a system of 16 score distributions, is more detailed than Ernest’s black-or-white approach in which a belief system either contains or excludes a given claim. Furthermore, Ernest’s model is theoretical, whereas our model is based on empirical data. Indeed, we can ask to what extent Ernest’s ‘technological pragmatist’ really exists.

Ernest’s model and this study concern different issues, but have mathematics education in common. As to ‘Industrial Trainers’ (‘IT’) and the ‘Teacher-oriented group’ (‘TOG’), both of them share the emphasis on teachers to respectively teach mathematics (authoritarian) and improve transfer. Whereas for ‘IT’ math teachers should drill their students basic mathematics according to ‘back to the basics’ (Ernest, 1991, p. 129), for ‘TOG’ they should be able to explain basic mathematics and students should activate prior mathematical knowledge (espoused models). Contrary to ‘IT’, the ‘TOG’ perspective is more likely to enhance CME and transfer (enacted models), since there is a match between their espoused and enacted models. To improve transfer, ‘IT’ should reconcile both models by considering insightful learning (Kilpatrick et al., 2001) with their naïve belief on basic skills. The latter also holds for the industry-centred ‘Technological Pragmatists’ (‘TP’).

The ’Old Humanists’ (‘OH’) have no direct commonalities with the clusters that we have obtained. Nevertheless, there is one issue that needs to be mentioned. In the previous qualitative study (Turşucu et al., 2017) we have seen that like ‘OH’ some math teachers (small number N) view math as the ‘Queen of the Sciences’ (Colyvan, 2012) and refuse to discuss applications in mathematics class. This quantitative study should also contain teachers belonging to ‘OH’, since our sample is much larger than that of the previous study. They might have participated in this study because of external motivations, e.g. winning the € 100,00 reward. Such teachers cannot have coherent clusters, since they are not interested in applications. Accordingly, their data might have been ‘lost’ as noise.

The social group ‘Progressive Educators’ (‘PrE’) and ‘Student-oriented group’ (‘SOG’) are both student-centred. The latter group thinks that this will improve transfer, whereas ‘PrE’ that this will enhance students’ confidence, creativity and self-expression. Like ‘PrE’, the decisions of ‘SOG’ might be based upon universal principles such as empathy and caring for children. In addition, ‘SOG’ might also be as progressive as ‘PrE’ towards collaboration. Unfortunately, our data do not show these claims.

Furthermore, like ‘OH’ the group, Public Educators (‘puE’) do not have direct commonalities with ‘COG’, ‘SOG’ or ‘TOG’.

Finally, it is worthwhile to mention that neither the belief systems identified in this study, nor those described by Ernest (1991) focus on teaching practice in which both basic algebraic skills and conceptual understanding are taught in an integrated manner (Drijvers, 2011; Rittle-Johnson et al., 2015). For CME and transfer to occur, both concepts should be treated together.

Limitations of this study

Our findings are based on 118 qualified VE teachers, and 97 ME teachers in SPE. This group of 215 teachers consists of 136 mathematics and 79 physics teachers. The Netherlands has 2903 qualified mathematics and 1330 qualified physics teachers in SPE (‘Ministry of Education, Culture and Science’, 2018), also giving a ratio of roughly 2:1. Furthermore, the 118 VE teachers had a gender-ratio (male–female) of 1:1 for mathematics, and 5:1 for physics teachers. For the 97 ME teachers this was 2:1 for mathematics and 13:1 for physics teachers. Unfortunately, there are no data available on the gender-ratio of qualified ME and VE mathematics and physics teachers in Dutch SPE, so we cannot judge how well our sample represents the national situation. The vast majority in our sample is familiar with both SPE and senior general secondary education (SGSE). Furthermore, the algebraic skills needed in physics class in both types of education are quite similar. Therefore, in case of representability of our sample above, we expect our results to be generalisable for both SPE and SGSE in the Netherlands. However, this does not hold for prepatory vocational secondary education (PVSE), since the algebraic skills needed in SPE and SGSE are fundamentally different from those in PVSE (‘Netherlands Institute for Curriculum Development’, 2018). This would lead to different belief systems (claims) about CME and transfer. At this point, we recommend conducting a separate study to investigate the national gender-ratios of both mathematics and physics teachers in SPE in relation with the number of years of teaching experience. This should lead to statements about national representability and generalizability of this study.

The content of subjects in SPE in the Netherlands is determined through centralised national curricula, which shape to a very large extent the content of textbooks and also teachers who faithfully follow and teach these to their students (Stein & Smith, 2010; van Zanten & van den Heuvel-Panhuizen, 2014). Consequently, they affect teachers’ beliefs (claims) about CME and transfer. Such centralised curricula do not exist in many other countries (Valverde et al., 2002). Thus, we do not expect that our results are generalisable to other countries outside the Netherlands – even if this study was generalisable for Dutch SPE.

Among three classes of clustering techniques, i.e. AHC, optimisation methods and mixture models, we used the first option and discarded the third option, because it pre-supposes knowledge of latent variables. A standard optimisation method is the k-means method. It has several disadvantages. First, it imposes a spherical structure on the data, i.e. it assumes that the data points are grouped in more or less spherical clusters in 16-dimensional space. We have no a priori reason to expect this to be true. Second, one has to choose the number k of clusters in advance. Third, the algorithm starts with random cluster centres, which resulted in rather different clusters in each run of the k-means algorithm. Therefore, we used AHC, since it does not have these disadvantages. Furthermore, this method also turned out to be objective, leading to nicely distributed clustering of belief systems including very clear splitting heights.

During the analysis of the belief systems, we focused on the three largest clusters for both teacher groups, and neglected 28% of the most experienced teachers and 26% of the very experienced teachers. Thus, we based our results on respectively the 72% and 74% of the extracted clusters. But what if these small clusters contain important information about, e.g. naïve beliefs (claims)? Such unproductive beliefs may impede students’ experience of CME and their transfer. Therefore, we recommend to further investigate this matter.

Reliability of the statistical analysis

Figures 6 and 8 show the mean scores and standard deviations of the large clusters for the very experienced and most experienced teachers, respectively. Some error bars are quite large compared to the means. This large dispersion within a belief system is usually due to a few outliers in the cluster. Our description of the main characteristics of the two triples of belief systems and the differences between these belief systems remains valid even taking this dispersion into account.

Disclosure statement

No potential conflict of interest was reported by the authors.

ORCID

Süleyman Turşucu http://orcid.org/0000-0002-5308-8793

Steven Flipse http://orcid.org/0000-0002-7400-1490

Additional information

Funding

This work was supported by Nederlandse Organisatie voor Wetenschappelijk Onderzoek [grant number 023.003.074].