A generalised FK model for the 558 line defect in graphene

ABSTRACT

Defects in two-dimensional nanomaterials do not always affect their properties negatively, but often have useful functionality. The 558 line defect in graphene distinctively acts as a quasi-one-dimensional metallic wire and a valley filter, which is already experimentally realised. To have a thorough understanding of the 558 line defect in graphene, we have extended the conventional FK model and have applied the model to theoretically investigate the structure of the 558 line defect, which agrees well with the first-principle simulation result. In the generalised FK model, it is vital to take into account bond energy correction to the interatomic force of atoms on the defect line. The generalised FK model can be used to predict structures of one-dimensional topological defects in other two-dimensional materials.

KEYWORDS:

• Frenkel–Kontorova model
• graphene
• 558 line defect

1. Introduction

Since graphene was first isolated in 2004 [1], a great quantity of studies of two-dimensional (2D) materials have been intensively developed [2–6]. Their extraordinary physical and chemical properties have made 2D materials extremely popular in materials science and engineering. A variety of lattice defects will inevitably emerge during 2D materials synthesis or processing, and consequently degrade mechanical and thermal properties of pristine materials. On the other hand, the introduction of defects can act as an approach to tuning their electronic structure at the nanoscale for applications [7, 8].

In recent years, line defects in two-dimensional materials have attracted special attention in valleytronics [9–12]. Because 2D materials with a line defect have a translational symmetry along the defect line and a mirror symmetry with respect to the defect line, they usually exhibit two degenerate valleys at the Fermi level and become good candidates for valley filter. The 558 line defect in graphene [13], which consists of a repeat sequence of two pentagonal and an octagonal $s{p}^2$-hybridised carbon rings, is one of the simplest form of line defects. There is still lack of theoretical investigation on the defect structure, which may be an important approach to predicting new line defects in two-dimensional materials.

In this paper, we have extended the standard Frenkel–Kontorova (FK) model [14–18] to study the structure of 558 line defect in graphene. In our model, the 558 line defect in graphene is considered as a carbon atomic chain surrounded by two graphene half-lattices. And the two graphene half-lattices generate a natural periodic substrate potential. The atomic motion is restricted along the defect line direction due to the symmetry of the two graphene half-lattices.

2. Computational methods

In this work, first-principles density functional theory (DFT) calculations are performed using the Vienna Ab-initio Simulation Package (VASP) code [19, 20], to investigate the atomic structure of the 558 line defect in graphene and the interaction between carbon atoms on the defect line and the surrounding two graphene half-lattices, i.e. the periodic substrate potential. The generalised gradient approximation (GGA) is used to approximate the exchange-correlation functional with the Perdew–Burke–Ernzerhof (PBE) approach [21]. The projector-augmented wave (PAW) method [22] is applied with an energy cutoff of 400 eV. Periodic boundary conditions are employed in all directions for graphene supercells and a vacuum region of 15 Å between adjacent layers is added. For the evaluation of substrate potential, a large $a\times \frac{19}{\sqrt{3}}a$ rectangular simulation supercell with 25 atoms is built where a is the lattice constant of pristine graphene, and the Brillouin zone is sampled with a $11\times 3\times 1$ Monkhorst–Pack [23] k-point mesh. For the investigation of atomic structure, a $2a\times \frac{19}{\sqrt{3}}a$ rectangular supercell with 50 atoms is adopted and a $5\times 3\times 1$ k-point mesh is used. In this case, all atomic coordinates are fully relaxed by using the conjugate gradient (CG) algorithm until total energy and atomic forces are converged to ${10}^{-5}$ eV and 0.01 eV/Å respectively. The first-principles simulation we undertook shows no buckling of the defect structure perpendicular to the graphene sheet.

3. Model and results

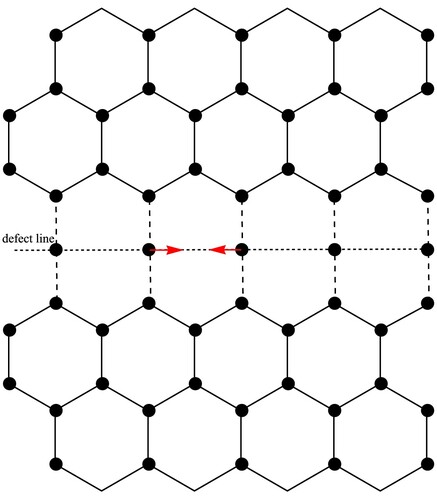
First, we construct the unstable equilibrium configuration of 558 line defect in graphene, as shown in Figure 1. The unstable equilibrium structure has the same period with pristine graphene along the defect line. We take the unstable equilibrium structure as the initial configuration. If there is any disturbance, the domain boundary of the two graphene half-lattices will be reconstructed and form a periodic structure consisting of octagonal and pentagonal carbon rings, i.e. 558 line defect. The period of 558 line defect along the defect line direction is twice the pristine graphene.

Figure 1. The unstable equilibrium configuration of 558 line defect in graphene, which can be regarded as a carbon atomic chain with period a subjected in the middle of two graphene half-lattices.

The free energy of the 558 line defect consists of two parts: (1) $E=E_{sub}+E_{int},$(1) where the first term is the interaction of the carbon atomic chain with the substrate potential generated by the two graphene half-lattices, while the second term is the interaction of the nearest neighbours in the chain.

According to the periodicity of 558 line defect, the displacement of carbon atoms in the chain satisfies (2) $u_n=-u_{n+1}=-u_{n-1}.$(2) Therefore the defect has an even energy distribution at lattice points on the defect line.

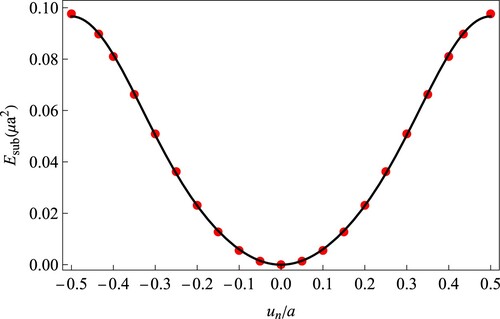
The substrate potential energy is evaluated from first-principles calculations as mentioned above. In the calculation, the two graphene half-lattices are fixed, while the carbon atomic chain is moved along the defect line direction. As shown in Figure 2, the substrate potential energy can be well described as follows: (3) $E_{sub}=\sum _n\frac{\mu a^2}{16}{\sin }^2\frac{\pi u_n}{a}(1+\mathrm{\Delta }{\sin }^4\frac{\pi u_n}{a}),$(3) where $\mu =156.6$ N/m [24, 25] is the shear modulus, a = 2.46 Å is the lattice constant and $\mathrm{\Delta }=0.55$.

Figure 2. The substrate potential generated by the two graphene half-lattices, which is a function of displacement. The red dots are calculated results by first-principles simulation and the solid line is the fitting curve by Equation (3(3) $E_{sub}=\sum _n\frac{\mu a^2}{16}{\sin }^2\frac{\pi u_n}{a}(1+\mathrm{\Delta }{\sin }^4\frac{\pi u_n}{a}),$(3) ).

Because two neighbour carbon atoms form covalent bond when their distance is close to the bond length during the reconstructing process, the bond energy correction is taken into account as well as the harmonic interaction of nearest carbon atoms into the interatomic interaction energy, (4) $E_{int}=\sum _{n}2\text{β}{u}_n^2+{\varphi }_b\left(u_n\right).$(4) The elastic constant β is related to the wave velocity of the decoupled atomic chain [26] (5) $\text{β}=\frac{\mu (1+\nu )(7+11\nu )a^2}{8\sqrt{3}(1-\nu )(1+3\nu )},$(5) where $\nu =0.16$ [24, 25] is the Poisson's ratio. The bond energy correction can be well described by a Morse potential [27] (6) ${\varphi }_b\left(u_n\right)=-{\varphi }_0{e}^{-\frac{(2u_n-(a-\tau ){)}^2}{{\eta }^2}},$(6) where ${\varphi }_0=-6.1$ eV is the bond energy of graphene, $\tau =1.43$ Å is the bond length, and $\eta =0.16a$ represents the force range limiting the bond formation.

From the free energy equations (1(1) $E=E_{sub}+E_{int},$(1) ), (3(3) $E_{sub}=\sum _n\frac{\mu a^2}{16}{\sin }^2\frac{\pi u_n}{a}(1+\mathrm{\Delta }{\sin }^4\frac{\pi u_n}{a}),$(3) ) and (4(4) $E_{int}=\sum _{n}2\text{β}{u}_n^2+{\varphi }_b\left(u_n\right).$(4) ), it follows the force balance equation: (7) $-\frac{\mathrm{\partial }{E}_{int}}{\mathrm{\partial }{u}_n}=-\frac{\mathrm{\partial }{E}_{sub}}{\mathrm{\partial }{u}_n},$(7) and we obtain (8) $-4\text{β}{u}_n+f_b=-\frac{\mathrm{\partial }{E}_{sub}}{\mathrm{\partial }{u}_n},$(8) where $f_b$ comes from bond energy correction, (9) $f_b=-\frac{\mathrm{\partial }{\varphi }_b}{\mathrm{\partial }{u}_n}.$(9) The displacement of carbon atoms in the chain is easily solved to be (10) $u_n=\pm 0.205a.$(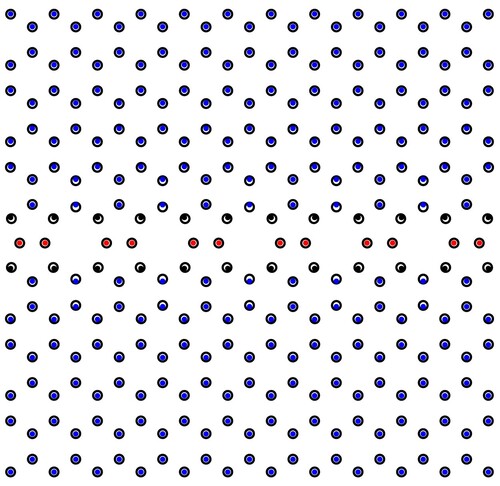10) Obviously the two solutions are equivalent. As shown in Figure 3, even though the distortion of the two graphene half-lattices is neglected, the theoretical result is quite in agreement with the first-principles simulation result.

Figure 3. Atomic arrangements of a 558 line defect in graphene result from the generalised FK model (dots) and the first-principles simulation (circles).

In this generalised FK model, the second harmonic term is kept as shown in Equation (3(3) $E_{sub}=\sum _n\frac{\mu a^2}{16}{\sin }^2\frac{\pi u_n}{a}(1+\mathrm{\Delta }{\sin }^4\frac{\pi u_n}{a}),$(3) ), to precisely describe the substrate potential generated by the two graphene half-lattices, while a simple sinusoidal form is insufficient. More importantly, the interatomic interaction takes into account the bond energy correction of carbon atoms. 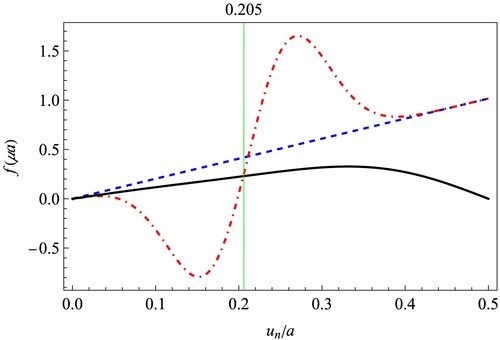As shown in Figure 4, the solution to the force balance Equation (8(8) $-4\text{β}{u}_n+f_b=-\frac{\mathrm{\partial }{E}_{sub}}{\mathrm{\partial }{u}_n},$(8) ) cannot be found if only the harmonic interaction between nearest neighbours is considered. It seems of prevailing significance to consider the bond energy correction when discussing defect structure in covalent bonded materials.

Figure 4. Comparison between the two sides of the force balance equation (8(8) $-4\text{β}{u}_n+f_b=-\frac{\mathrm{\partial }{E}_{sub}}{\mathrm{\partial }{u}_n},$(8) ). The black solid curve represents the substrate force generated by the two graphene half-lattices, i.e. the right-hand side of Equation (8(8) $-4\text{β}{u}_n+f_b=-\frac{\mathrm{\partial }{E}_{sub}}{\mathrm{\partial }{u}_n},$(8) ). The other two curves represent the interatomic interaction force in the chain. The red dashed and dotted curve takes both the force terms on the left-hand side of Equation (8(8) $-4\text{β}{u}_n+f_b=-\frac{\mathrm{\partial }{E}_{sub}}{\mathrm{\partial }{u}_n},$(8) ) into account, while the blue dashed curve only takes in the first harmonic term as the conventional FK model. It is clear that the blue and black curves only intersect at zero, but the red and black curves intersect at both zero and 0.205a.

4. Conclusion

In summary, a generalised FK model has been developed to investigate the 558 line defect in graphene. The model describes a chain of carbon atoms which are on the defect line, subjected to a periodic substrate potential generated by the two surrounding graphene half-lattices. Although the assumption that carbon atoms on the defect line interact only with nearest-neighbours is taken, we have shown that bond energy correction to the interatomic force is vital. The generalised FK model can be used to predict structures of one-dimensional topological defects in other two-dimensional materials, and these defects influence physic properties of corresponding two-dimensional materials at the nanoscale.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data Availability Statement

The data that support the findings of this study are available within the article.

Additional information

Funding

This work is supported by National Natural Science Foundation of China (Grant No. 61904019), Natural Science Foundation of JiangSu Province (Grant No. BK20211061) and Changzhou Sci&Tech Program (Grant No. CM20223013).