 ?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.ABSTRACT
Carbon footprints and other environmentally extended input–output indicators are obtained as aggregations of emissions embodied in supply chains (EESCs), which express the emissions occurring in a specific production activity to satisfy a given volume of final demand. Here we derive theoretical approximations of the expectations of and covariances between EESCs, as a function of the expectations of and covariances between source data (technical coefficients, emission coefficients and final demand volumes) through a Taylor expansion. We report an empirical test of those approximations, using a sample of 5 global multi-regional input–output models in the year 2007, of which we extract 22 single-region input–output systems with 17 sectors. We find that approximations of multipliers perform better than those of EESC, and approximations of expectations perform better than those of covariances.
1. Introduction
Applications of input–output (IO) analysis (Miller and Blair, Citation2009) often deal with the calculation of socioeconomic or environmental impacts of consumption decisions. For concreteness, in the present study we focus on carbon footprints (Hertwich and Peters, Citation2009), keeping in mind that the work developed here applies equally to other environmentally extended input–output (EEIO) indicators, such as consumption-based carbon accounts (CBCAs) (Afionis et al., Citation2017) or emissions embodied in trade (Davis and Caldeira, Citation2010). All such quantities are constructed by aggregating emissions embodied in supply chains (EESCs), which express how much the volume of consumption of a product generates in terms of emissions of a particular sector. The economic and environmental data required for the calculation of EESCs are subject to a wide variety of measurement errors (Sato, Citation2014). A particular component in the calculation of an EESC is an input–output multiplier, which express how much the final demand of the products of a sector generates in the total demand of the outputs of (possibly) another sector.
When researchers are interested in calculating the uncertainty of carbon footprints these are often performed numerically using Monte Carlo simulations (Lenzen et al., Citation2010; Rodrigues et al., Citation2018). In order to circumvent the need to perform numerical calculations, and also to generate theoretical insights, it would be convenient if there were analytical formulas linking the expectations of and covariances between the source data and the expectations of and covariances between EESCs.
Although we are not aware of the existence of such formulas for EESCs there is a long tradition in the exploration of the theoretical link between the expectations of and covariances between source data and the expectations of and covariances between multipliers, reviewed by Kop Jansen (Citation1994) and more recently by Temursho (Citation2017). Pioneer work was developed by Evans (Citation1954) and Quandt (Citation1958). The culmination of this literature was the work of ten Raa and Kop Jansen (Citation1998), who proposed analytical formulas for the expectations of and covariances between multipliers when technical coefficients are subject to measurement errors, which generalized and unified the earlier developments of West (Citation1986), Lahiri and Satchell (Citation1986) and ten Raa and Steel (Citation1994), among others. In parallel to the study of uncertainty in IO analysis there is a large literature on the uncertainty of life-cycle assessment (Heijungs et al., Citation2006; Heijungs and Lenzen, Citation2014; Igos et al., Citation2018). In particular, Heijungs and Lenzen (Citation2014) addressed the calculation of the variance of a footprint, as a function of variances of technical coefficients. As far as we are aware no extension of the expressions of ten Raa and Kop Jansen (Citation1998) has ever been proposed in the literature, to estimate the expectations of and covariances between derived quantities, such as EESCs.
The goal of this paper is twofold. First, we derive analytical formulas for the calculation of the expectations of and covariances between EESCs when the expectations of and covariances between source data are known. This is carried out in Section 2. Second, we report an empirical application of the performance of the derived formulas, in Section 3. Section 4 closes the paper. An Appendix available online describes the derivation and error metrics employed in the empirical analysis.
2. Theory
In this section, we present the functional forms of the proposed approximations of the expectations of and covariances between EESCs. In order to make sense of this result, we also report the assumptions and calculation method underlying the derivation.
2.1. Notation and problem formulation
In this paper, we adhere as much as possible to the conventional notation of probability theory and linear algebra. We use uppercase letters to denote a random variable and lowercase to denote a realization; with italic denoting scalar and bold denoting a vector or matrix object. If T, and
are arbitrary random variables with a continuous density function then their expectation and covariance are, respectively:
(1)
(1)
(2)
(2)
where
is the density function and E[g(T)] = ∫ f(t)g(t)dt. In this paper we are interested in obtaining these two properties (expected value and covariance) of a return variable vector,
, which is a function of a control variable,
, as S = g(T), when the function
and variables
and
are as specified below.
In the analysis of the results, we will split a covariance into standard deviations and a correlation. The standard deviation is the square root of the variance and correlation is the covariance divided by the product of the corresponding standard deviations. Thus, for arbitrary random variables T, and
we define these quantities respectively as
(3)
(3)
(4)
(4)
In the analysis of the results we will also report percentiles. The z percentile of a random variable X is the value x such that P(X ≤ x) = z%.
Mathematically, we define EESC, denoted , as the upstream emissions occurring in production sector i resulting from the consumption of item j in consumption vector k. The set of all ESSCs can be arranged in the nS × nS matrix
calculated as
(5)
(5) where the Leontief inverse,
, is in turn obtained from the matrix of technical coefficients as
(6)
(6) In the preceding expressions
is the identity matrix, a circumflex or
represents diagonal;
is a vector of production emission coefficients, specifying the volume of carbon emissions per unit of economic output; and
is a vector of final demand category k, specifying the volume of expenditure in each product category. The length of
and
is
and the size of
and
is
, where
is the number of sectors. The system is assumed to be in symmetric format, product-by-product or industry-by-industry (UN, Citation2018), and we use ‘sector’ as a neutral term to refer to either products or industries. The iterator k runs over k = 1,…,nF where
is the number of final demand categories. The coefficients of
and
are further obtained from flow data, but how their expectations and covariances are related is not covered here. We refer to an element of
as a multiplier.
The theoretical problem addressed in this paper is to obtain explicit formulas for the expectation and covariances
as a function of the expectation and covariances of
,
and
(where the latter has size
), where i, j, l and m are sectors and k, n are final demand categories. The expectation of and covariances between carbon footprints can be afterwards obtained by summing over the appropriate EESCs.
Mathematically, if is a carbon footprint (or another EEIO indicator), then:
(7)
(7)
(8)
(8)
(9)
(9)
where
is the expectation,
is the covariance, and Φ, Ψ, Ω,
,
and
are appropriate sets. For concreteness consider a multiregional context in which each k iterates over final demand categories and regions. A carbon footprint of household consumption is obtained by selecting a product j and household final consumption of a region k, and then summing over all sectors where emissions occur, i. For example, if we are interested in the carbon footprint of beverages in Australian households, then k corresponds to Australian households and j to beverages. A CBCA is obtained by summing over every final demand category k of the region of interest and summing over every i and j. Emissions embodied in trade and other EEIO indicators are obtained by selecting and aggregating over other iterator ranges.
We address this theoretical problem (calculating and
) by using the formulas for the expectations of and covariances between functions of random variables, S = g(T), proposed by ten Raa and Kop Jansen (Citation1998), in which the covariance formula was in turn taken from Klein (Citation1956) and Kmenta (Citation1971). These expressions are derived as, respectively, second- and first-order Taylor approximations around the expectation of the source data:
(10)
(10)
(11)
(11)
Equation Equation10
(10)
(10) is equivalent to Equation 5 of ten Raa and Kop Jansen (Citation1998) and Equation Equation11
(11)
(11) is equivalent to Equation 4 of the same publication. In order to find analytical expressions for
and
we need to systematically obtain all relevant first and second partial derivatives, where Equations Equation5
(5)
(5) –Equation6
(6)
(6) define the function, and replace them in Equations Equation10
(10)
(10) –Equation11
(11)
(11) . The derivation is reported in Appendix A.
2.2. Taylor approximations
The formulas proposed by ten Raa and Kop Jansen (Citation1998) for the expectation of and covariances between multipliers (Equations 26 and 27 in that publication) are:
(12)
(12)
(13)
(13)
Appendix B shows the equivalence between Equation Equation12
(12)
(12) and Equation 26 of ten Raa and Kop Jansen (Citation1998). In the preceding expressions the left-hand side is adjoined with the upperscript ‘Tay’ to denote that it is a Taylor approximation, and we used the short-hand L* = (I−A)−1. Inserting expressions A.9–A.12 in Equation Equation10
(10)
(10) yields the expectation of an EESC:
(14)
(14)
Term
is described in Equation Equation12
(12)
(12) . Following the same conventions, inserting expressions A.5–A.6 in Equation Equation11
(11)
(11) yields the covariances between EESCs:
(15)
(15)
In the preceding expression term
is described in Equation Equation13
(13)
(13) .
Equations Equation14(14)
(14) –Equation15
(15)
(15) are generalizations of the formulas proposed by ten Raa and Kop Jansen (Citation1998). Their formulas for the expectation of and covariance between multipliers
, Equations Equation12
(12)
(12) –Equation13
(13)
(13) can be recovered from our expressions by making the emission intensity and final demand volume unitary and deterministic, i.e. setting
and
.
3. Empirical application
In this section, we report an empirical application, of which the primary goal is the assessment of the numerical performance of the derived formulas of the expectations of and covariances between IO multipliers and EESCs. In order to do so, we need to characterize the expectations of and covariances between source data of an EEIO model. After reporting the source data and processing performed on them we describe the performance of the Taylor approximations in replicating the empirical expectations and covariances.
3.1. Data sources and processing
The main data source of this study is a set of five global product-by-product (Miller and Blair, Citation2009) multiregional IO (MRIO) databases that were harmonized and tailored to calculate country/region-level global carbon footprints in the year 2007. These five MRIOs are constructed from the Exiobase (Wood et al., Citation2015) (http://exiobase.eu), WIOD (Dietzenbacher et al., Citation2013) (http://www.wiod.org/), EORA (Lenzen et al., Citation2012) (http://worldmrio.com/, OECD (Wiebe and Yamano, Citation2016) (http://www.oecd.org/sti/ind/input-outputtablesedition2015accesstodata.htm) and GTAP (Peters et al., Citation2011) (https://www.gtap.agecon.purdue.edu/ databases. Each MRIO database was harmonized to nR = 22 regions, nS = 17 sectors per region and a single category of final demand per country, primary inputs and carbon emission types. The regional classification consists of 20 countries covering 78% of global CO emissions and 2 aggregate regions. The list of regions and sectors can be found in Appendix C, and the concordance with the original MRIOs can be found in Owen et al. (Citation2014) and Steen-Olsen et al. (Citation2014). We did not use the original values reported in each original MRIO but the values obtained after the procedure described in section “Data compression” of Rodrigues et al. (Citation2018).
From this global model a set of single-region models was extracted. That is, only the blocks along the main diagonal of the full
matrix were used to obtain the
matrices of each region r. From the multi-regional
matrix (
) each single-region
of size
with
was obtained as follows:
and
. In words, the consumption matrix of each region has two columns: the first is the vector of consumption of domestically produced goods and the second is the vector of exports. Emission intensities were obtained by splitting the multiregional vector
into its appropriate regional components
.
Now considering a single region we can skip superscript r. For both the IO system (,
and
) and the multipliers,
, and EESCs,
, we calculate the expectations and covariances using suitable discrete versions of Equations Equation1
(1)
(1) –Equation2
(2)
(2) :
(16)
(16)
(17)
(17)
In the preceding expressions
,
and
represent the k-th realization of random variable T,
and
, respectively.
is the number of distinct MRIOs used in the analysis. The resulting quantities,
,
,
and
are the true values against which the performance of the Taylor approximation will be examined.
An alternative approach to obtain the expectations of and covariances between either or
would be to perform Monte Carlo integration, as in Heijungs and Lenzen (Citation2014). Using that method probability distributions are assumed and parameterized for the source data, and a large number of realizations is taken, from which samples of
and
are obtained. In the present study, we do not follow this approach to avoid having to make further assumptions by specifying probability distributions for the source data.
The question of how representative this data set is was previously discussed in Rodrigues et al. (Citation2018). It turns out that when compared with the literature survey of Hertwich and Peters (Citation2009), most source data variances are higher than reported in the literature. However, this is the only dataset that we know in which covariances in the source data can be estimated, and therefore use it for the empirical application.
3.2. Results
In this subsection, we examine the performance of the formulas derived in Section 2.2. We do so by examining the deviation between the true value of a given variable, calculated as described in Section 3.1, and the Taylor approximation, through the formulas reported in Appendix D. We calculate the deviation (or error) of a particular approximation for each multiplier or EESC and then study the distribution of errors across all multipliers or EESCs. We sequentially examine the performance of the mean of and covariances between either multipliers or EESCs. For ease of interpretation the analysis of covariances is split into variances and correlations.
Figure shows the histograms of the errors of the Taylor approximation, for the expectation of, standard deviation of and correlations between either multipliers or EESCs. Additionally, we report in Table selected percentiles.
Figure 1. Histograms of the errors of the Taylor approximation (in %). (a) Expectation of multiplier. (b) Expectation of EESC. (c) Standard deviation of multiplier. (d) Standard deviation of EESC. (e) Correlation between multipliers. (f) Correlation between EESCs.
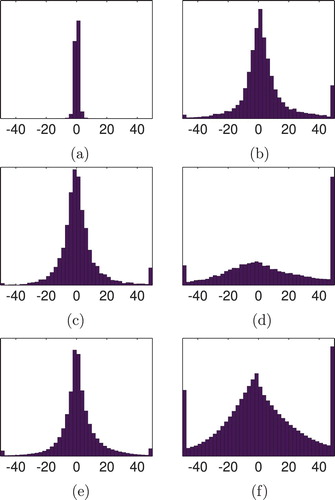
Table 1. Percentiles of the errors of the approximations.
Examination of Figure and Table shows that for less than 10% of data points is the error of the Taylor approximation of the expectation of a multiplier larger than 3%. Hence, we can say that the performance of the approximation is reasonable. Furthermore, the distribution of errors is reasonably symmetric, meaning that the number of over- and under-estimated data points is roughly the same.
The performance of the approximation for the expectation of an EESC, and the variance and correlation a multiplier is clearly worse, with around 20% of data points having an error which is either below −10% or higher than 15%. Besides the decrease in performance in these cases the distribution of errors is also right-skewed, suggesting some degree of over-estimation.
Finally, the performance of the approximation for the variance of an EESC and the correlation between EESCs is even worse, with more than 50% of estimates being off by less than −10% or by more than 15%. The variance of an EESC performs particularly bad and exhibits a strong degree of over-estimation.
4. Discussion and conclusions
Carbon footprints and other environmentally extended input–output indicators are constructed as aggregations of emissions embodied in supply chains (EESCs), which indicate the emissions occurring in a given production activity to satisfy a certain volume of final demand. In this study we have developed approximations for the expectations of and covariances between EESCs as, respectively, second- and first-order Taylor approximations, extending the work of ten Raa and Kop Jansen (Citation1998) for multipliers. We have then presented a case study in which we examine the performance of the proposed approximations. The empirical analysis shows that the Taylor approximation does not perform always well: the formulas for multiplier expectations performs very well, the formulas for the covariance between EESCs performs poorly and the other formulas lead to an intermediate result.
Of course, empirical results depend on the particularities of the empirical data. In the case examined here it was found by Rodrigues et al. (Citation2018) that there is more variation in the environmental extension and final demand volumes than in technical coefficients. Hence, the approximations that involve only data with low variances (multipliers) perform better than approximations that involve data with higher variance (EESCs). We conclude that the Taylor approximations of expectations of and covariances between either multipliers or EESCs should be used only when the variances in the source data are small.
In principle it is possible to obtain better approximations by performing a higher-order Taylor expansion, but the expressions would become more cumbersome. If a source data sample is available or a multivariate probability distribution can be assumed, from the point of view of practical calculations there is little benefit of having a theoretically accurate but very cumbersome expression, as in that case a numerical Monte Carlo integration can be performed instead.
The analytical formulas developed in this study are relevant for practitioners who wish to explore from a theoretical point of view the statistical properties of carbon footprints. This, in turn, has policy implications as it will allow for a better understanding of the uncertainty in empirical applications. The empirical results of this study are a contribution to the still narrow field of empirical studies of the uncertainty of carbon footprints, which we believe requires further attention.
Supplemental Material
Download Zip (184.5 KB)Disclosure statement
No potential conflict of interest was reported by the authors.
ORCID
João F. D. Rodrigues http://orcid.org/0000-0002-1437-0059
Rong Yuan http://orcid.org/0000-0002-9328-2064
Hai Xiang Lin http://orcid.org/0000-0002-1653-4854
References
- Afionis S., Sakai M., Scott K., Barrett J. and Gouldson A. (2017) Consumption-Based Carbon Accounting: Does It Have a Future? Wiley International Review: Climate Change, 8, e438. doi:10.1002/wcc.438
- Davis S.J. and Caldeira K. (2010) Consumption-Based Accounting of CO2 Emissions. Proceedings of the National Academy of Sciences, 107, 5687–5692. doi:10.1073/pnas.0906974107
- Dietzenbacher E., Los B., Stehrer R., Timmer M. and de Vries G. (2013) The Construction of the World Input-Output Tables in the WIOD Project. Economic Systems Research, 25, 71–98. doi: 10.1080/09535314.2012.761180
- Evans W.D. (1954) The Effect of Structural Matrix Errors on Interindustry Relations Estimates. Econometrica, 22, 461–480. doi: 10.2307/1907437
- Heijungs R. and Lenzen M. (2014) Error Propagation Methods for LCA – A Comparison. The International Journal of Life Cycle Assessment, 19, 1445–1461. doi:10.1007/s11367-014-0751-0
- Heijungs R., de Koning A., Suh S. and Huppes G. (2006) Toward An Information Tool for Integrated Product Policy: Requirements for Data and Computation. Journal of Industrial Ecology, 10, 147–158. doi:10.1162/jiec.2006.10.3.147
- Hertwich E.G. and Peters G.P. (2009) Carbon Footprint of Nations: A Global, Trade-linked Analysis. Environmental Science & Technology, 43, 6414–6420. doi:10.1021/es803496a
- Igos E., Benetto E., Meyer R., Baustert P. and Othoniel B. (2018) How to Treat Uncertainties in Life Cycle Assessment Studies?. International Journal of Life Cycle Assessment. doi:10.1007/s11367-018-1477-1
- Klein L. (1956) A Textbook of Econometrics. Evanston, IL, Peterson and Co..
- Kmenta J. (1971) Elements of Econometrics. New York, Macmillan.
- Kop Jansen P.S.M. (1994) Analysis of Multipliers in Stochastic Input-Output Models. Regional Science and Urban Economics, 24, 55–74. doi:10.1016/0166-0462(94)90019-1
- Lahiri S. and Satchell S. (1986) Properties of the Expected Value of the Leontief Inverse: Some Further Results. Mathematical Social Sciences, 11, 69–82. doi: 10.1016/0165-4896(86)90005-3
- Lenzen M., Wood R. and Wiedmann T. (2010) Uncertainty Analysis for Multi-region Input-Output Models – A Case Study of the UK's Carbon Footprint. Economic Systems Research, 22, 43–63. doi: 10.1080/09535311003661226
- Lenzen M., Kanemoto K., Moran D. and Geschke A. (2012) Mapping the Structure of the World Economy. Environmental Science & Technology, 46, 8374–8381. doi: 10.1021/es300171x
- Miller R.E. and Blair P.D. (2009) Input-Output Analysis: Foundations and Extensions (2nd ed.). Cambridge, UK, Cambridge University Press.
- Owen A., Steen-Olsen K., Barrett J., Wiedmann T. and Lenzen M. (2014) A Structural Decomposition Approach to Comparing MRIO Databases. Economic Systems Research, 26, 262–283. doi:10.1080/09535314.2014.935299
- Peters G.P., Andrew R. and Lennox J. (2011) Constructing an Environmentally Extended Multi-regional Input-Output Table Using the GTAP Database. Economic Systems Research, 2, 131–152. doi: 10.1080/09535314.2011.563234
- Quandt R. (1958) Probabilistic Errors in the Leontief System. Naval Research Logistics Quarterly, 5, 155–170. doi: 10.1002/nav.3800050207
- Rodrigues J.F.D., Moran D., Wood R. and Behrens P. (2018) Uncertainty of Consumption-Based Carbon Accounts. Environmental Science & Technology, 52, 7577–7586. doi:10.1021/acs.est.8b00632
- Sato M. (2014) Embodied Carbon in Trade: A Survey of the Empirical Literature. Journal of Economic Surveys, 28, 831–861. doi: 10.1111/joes.12027
- Steen-Olsen K., Owen A., Hertwich E. G. and Lenzen M. (2014) Effects of Sector Aggregation on CO2 Multipliers in Multiregional Input-Output Analyses. Economic Systems Research, 26, 284–302. doi:10.1080/09535314.2014.934325
- Temursho U. (2017) Uncertainty Treatment in Input-Output Analysis. In T. ten Raa (ed.) Handbook of Input-Output Analysis. Cheltenham, UK, Edward Elgar Publishing Ltd, 407–463.
- ten Raa T. and Kop Jansen P. (1998) Bias and Sensitivity of Multipliers. Economic Systems Research, 10, 275–284. doi:10.1080/762947112
- ten Raa T. and Steel M.F.J. (1994) Revised Stochastic Analysis of an Input-Output Model. Regional Science and Urban Economics, 24, 361–371. doi: 10.1016/0166-0462(93)02039-6
- UN (2018) Handbook on Supply, Use and Input-Output Tables with Extensions and Applications. Studies in Methods (Series F) No. 74, Rev. 1, United Nations, New York, USA. https://unstats.un.org/unsd/nationalaccount/gcItemIO.asp.
- West G.R. (1986) A Stochastic Analysis of an Input-output Model. Econometrica, 54, 363–374. doi: 10.2307/1913156
- Wiebe K. and Yamano N. (2016) Estimating CO2 Emissions Embodied in Final Demand and Trade Using The OECD ICIO 2015 – Methodology and Results. Technology and Industry Working Papers, Paris, France, OECD Science.
- Wood R., Stadler K., Bulavskaya T., Lutter S., Giljum S., Koning A.D., Kuenen J., Schutz H., Acosta-Fernandez J., Usubiaga A., Simas M., Ivanova O., Weinzettel J., Schmidt J.H., Merciai S. and Tukker A. (2015) Global Sustainability Accounting-Developing Exiobase for Multi-regional Footprint Analysis. Sustainability, 7, 138–163. doi: 10.3390/su7010138
