Solving scheduling tournament problems using a new version of CLONALG

Abstract

The travelling tournament problem (TTP) is an important and well-known problem within the collective sports research community. The problem is NP-hard which makes difficult finding quality solution in short amount of time. Recently a new kind of TTP has been proposed ‘The Relaxed Travelling Tournament Problem’. This version of the problem allows teams to have some days off during the tournament. In this paper, we propose an immune algorithm that is able to solve both problem versions. The algorithm uses moves which are based on the team home/away patterns. One of these moves has been specially designed for the relaxed travel tournament instances. We have tested the algorithm using well-known problem benchmarks and the results obtained are very encouraging.

Keywords:

• CLONALG
• artificial immune algorithm
• relaxed travelling tournament problem

1. Introduction

The travelling tournament problem (TTP) is a NP-hard problem and many methods have already been proposed in the literature to solve it. For bigger instances the most successful methods are those based on metaheuristics such as simulated annealing and tabu search with a post-processing local search procedure, Anagnostopoulos, Michel, Van Hentenryck, and Vergados (2006), Di Gaspero and Schaerf (2007), Chen, Kendall, and Berghe (2007) and Van Hentenryck and Vergados (2007). Trick and Bao have proposed a new form of TTP: The relaxed travelling tournament Problem (RTTP) (Trick, 2010). In this version, the teams can have days off between matches. RTTP is still a very hard problem and only instances with at most 10 teams have known upper bounds. On the other hand, artificial immune systems (AISs) have been applied successfully for solving very complex problems such as virus detection, some travelling salesman problem instances and 3-colouring problems (Riff, Zuniga, & Montero, 2010). In this paper, we introduce new components to the Clonal Selection Algorithm (CLONALG) (De Castro & Timmis, 2002) for solving instances of the TTP. Our goal is to show the versatility of the immune inspired algorithms which can solve TTP as well as RTTP.

The contributions of this paper are:

• New components for CLONALG that help it to tackle TTP and RTTP,

• A new move focused on maximising the time away of the teams whose trip costs from home are more expensive, and

• New bounds for RTTP

It is important to note that our initial goal is not to obtain the best algorithm to solve these instances but to show that an improved version of CLONALG is able to solve these kinds of problems in an adaptive and competitive way compared to other metaheuristics. This paper is organised as follows: In the following sections we briefly present the TTP and the CLONALG framework. The new components for the algorithm are introduced in Section 4. The results obtained using our approach for solving various instances of TTP and RTTP are reported in Section 5. Finally, the conclusion and future work are presented in Section 6.

2. TTP and RTTP

The TTP (Easton, Nemhauser, & Trick, 2001) is a sports timetabling problem which involves two issues in creating timetables: assignment feasibility (tournament structure) and optimisation (reducing distance travelled by the teams). The objective is, given a number of teams N and a distance matrix D_{i, j}, to find a double round robin tournament which minimises the distance travelled. The trip length constraint establishes the minimum and the maximum number of consecutive home/away matches allowed during the tournament. Usually, the lower and upper boundaries are 1 and 3, respectively. A solution must also satisfy one of the following constraints:

• No repeaters: Matches that involve the same pair of teams (i, j) must not take place in consecutive rounds.

• Mirrored: The first half of the tournament should be a single round robin tournament and the second is obtained by mirroring the first one.

The double round robin structure requires 2(N−1) rounds, N/2 matches must take place every round, each pair of teams must play twice during the tournament exchanging homes, and all teams must play only one match every round. This problem is a real challenge to both, complete and incomplete combinatorial optimisation techniques.

Best complete techniques like DFS* (Uthus, Riddle, & Guesgen, 2009a) are able to find the optimum for small instances of up to eight teams and recently the same authors have reported optimum values for 10 team instances using IDA* (Uthus, Riddle, & Guesgen, 2012) an A*-based algorithm. Finding the optimum requires long execution time. For bigger instances the most successful methods are those based on metaheuristics. A simulated annealing for TTP (TTSA) is proposed in Anagnostopoulos et al. (2006) and Van Hentenryck and Vergados (2007). This approach has found several of the best solutions so far. Ant colony optimisation (ACO) with constraint processing techniques is proposed in Uthus, Riddle, and Guesgen (2009b), the results were promising and their algorithm outperforms other ACO approaches. A hybrid method is presented in Lim, Rodrigues, and Zhang (2006) using simulated annealing and hill climbing. Tabu search has also being successfully applied to TTP in Di Gaspero and Schaerf (2007). In the field of hyper-heuristics, an ant based hyper-heuristic is introduced in Chen et al. (2007) and a learning hyper-heuristic is given in Misir, Wauters, Verbeeck, and Vanden Berghe (2009). Both obtaining good results. In Section 5.2 we compare our results with the state-of-the-art algorithms for TTP.

2.1. Definition of TTP

The formal definition of TTP is replicated as following (Easton et al., 2001):

Definition 2.1

TTP

• Input: n, the number of teams; D a n×n integer distance matrix; L and U integer parameters

• Output: A double round robin tournament on the n teams such that:

• The number of consecutive home games and consecutive away games are between L and U inclusive, and

• The total distance travelled by the teams is minimised

There are two optional constraints: the games between same opponents cannot happen in consecutive time slots, which is called no repeaters constraint; the second half of the tournament is mirrored to the first half, which is called mirroring constraint. Note that these two requirements cannot be relevant at the same time, because the mirrored schedule guarantees no repeaters.

The RTTP considers that each team schedule has exactly k days off (byes). Free days are ignored for determining the length of a homestand or roadtrip, and in determining whether a repeater has occurred. Some bounds are already known for the benchmarks NL4, NL6 and NL8 using k=1, k=2 and k=3.

2.2. Definition of RTTP

The formal definition of RTTP is replicated as follows (Trick, 2010):

Definition 2.2

RTTP

• Input: n, the number of teams; D a n×n integer distance matrix; L, U, B, O integer parameters

• Output: A double round robin tournament on the n teams such that:

• The number of consecutive home games and consecutive away games are between L and U inclusive,

• The total number of byes per team is K,

• The total distance travelled by the teams is minimised

The no repeaters and mirroring constraints are optional as defined in TTP. The tournament structure becomes relaxed when days off between games are allowed, however byes must be ignored when computing the number of consecutive home/away games and also when determining whether a repeater has occurred or not.

3. A description of CLONALG

AISs have been defined as adaptive systems inspired by the natural immune system and applied to problem solving. In this paper, we are interested in CLONALG, an artificial immune algorithm based on clonal selection principle (De Castro & Timmis, 2002). It follows the basic theory of the adaptive immune response to pathogens. Roughly speaking, the components of the algorithm are cells, antibodies, and a potentially dangerous invader, named antigen. The immune system reproduces those cells that are able to recognise an antigen. Cells which match well are cloned (create copies of themselves), and the better is the match, the more clones are generated. During this process, hyper-mutation is applied to clones, which may improve their antigen recognition. The better the parent cell match, the less mutations the clone suffers. Moreover, the clonal selection process also retains the best cells as memory cells, resulting in a much more efficient system in further encounters with the recognised antigen. The Algorithm 3.1 shows the CLONALG algorithm.

The algorithm randomly generates a population of Cells and computes their fitness. The iterative process begins by constructing a sub-population B_a of size n, composed by the n best antibodies belonging to the population of Cells. A new population of clones P_c is constructed by generating C clones of each element on B_a. This population of clones follows a mutation process in order to improve the evaluation of the clones. The set of cells is updated including the n best antibodies from and incorporates n₂ new randomly generated antibodies to construct the population of size n₁.

The CLONALG framework is a general guide to design artificial immune systems. When using this framework to design an immune algorithm for a specific problem, the main research task consists in defining all of its components, the same way that this is done for other techniques like genetic algorithms. To help the search of the immune algorithm, this design process must take into account the knowledge of the problem.

4. Artificial immune algorithm for TTP

We call our algorithm (Artificial Immune System for Relaxed TTP). The algorithm must be able to manage soft and hard constraints. The search space for our algorithm is defined by the hard constraints, that is any move application must satisfy all hard constraints. In the following sections we describe in detail the components of the algorithm.

4.1. Representation

Definition 4.1

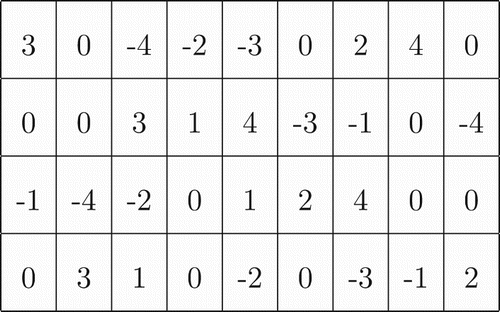
Given the set of N teams, and the set of M rounds, and k byes, for a round robin scheduling we define the representation TM as the tournament matrix, where the value of each element tm_ij indicates the opponent of team T_i in the round R_j. More precisely,

• with

• tm_ij>0 when the match is at home,

• tm_ij<0 when the match is away,

• 0 when it is a bye.

Figure 1 shows an example of the tournament matrix considering four teams, six rounds and three byes. In this example, that is the optimal solution for NL4 instance, team 3 will play away in the three first rounds and it has a bye in rounds four, eight and nine.

Figure 1. Representation matrix (N=4).

Remark 1 There are no zero values in the representation when the problem to be solved is not a relaxed one.

4.2. Managing constraints

TTP is a very hard problem and it has many constraints to be satisfied. In our approach we consider those related to the double round robin structure as hard constraints, and the moves take their satisfaction into account. The non-structural constraints of no repeaters and trip length are managed by a penalisation on the fitness function.

4.3. Fitness function

In order to guide the algorithm to find good quality solutions which also satisfy the constraints, the algorithm uses Equation (1) which computes the penalty function W_l for the constraint l (l=1 No repeaters constraint, l=2 trip length constraint). In this equation is the average distance among teams and δ_l is the penalty factor associated to the violation of the constraint l.

Finally, Equation (2) defines the fitness function F_Rttp, considering all rounds, φ_i is the total travelled distance of team i and v_l is the number of violated non-structural constraints in a scheduling candidate

The distance value when a team has a bye is considered equal to zero. Thus, if team 5 has the sequence [−1 0 −3], the distance to be computed for this tuple is the distance between the locations of teams 1 and 3, instead of a sequence [−1 0 3], the distance will be the distance between the locations of teams 1 and 5. Thus the zero value is ignored for computing the fitness function.

Remark 2 Note that a sequence [−1 −2 0 −3 −4] is considered infeasible, because a maximum of three away games is permitted, analogously the sequence [−1 −2 0 −3 4] is a feasible one. The bye is considered as a joker day.

Using this function the algorithm quickly focuses its search on feasible solutions by trying to find candidate solutions that reduce the penalisations.

4.4. Moves

The algorithm uses seven moves. The following five moves have been proposed for a simulated annealing algorithm in Anagnostopoulos et al. (2006):

• Swap Homes (T_i,T_j): Exchanges teams T_i and T_j matches home (matrix elements sign).

• Swap Rounds (R_i,R_j): Exchanges rounds R_i and R_j schedules.

• Swap Teams (T_i,T_j): Exchanges two teams T_i and T_j matches.

• Partial Swap Rounds (T_i,R_j,R_k): For a team T_i, exchanges round R_j match for R_k round match.

• Partial Swap Teams (T_i,T_j,R_k): For a round R_k, exchanges teams T_i and T_j matches.

These moves produce many changes to the candidate solution, however none of them take explicitly into account the travelling cost involved. Thus, in order to guide the algorithm to search better solutions in terms of reducing the travelling cost, we use a move called Away Tuple Group.

4.4.1. Move away tuple group

As the cost of a team schedule corresponds to the cost of its away matches (trips), the idea is to try to group its trips to reduce the travelling cost. Before explaining the move we require the following definitions:

Definition 4.2 (Pattern Matrix)

Given a Tournament Matrix TM, we define the associated Pattern Matrix of size N×M, such that

Definition 4.3 (Away tuple)

Whenever we refer to an ‘away tuple’ we define any continuous sequence of character A.

Definition 4.4 (Extendible away tuple)

An extendible away tuple is an away tuple that can be modified in order to increase the continuous A character sequence size.

Because the upper limit for the trip length is 3, only feasible away tuples that could be extended are A and AA.

Definition 4.5 (Set of grouping candidates)

Given PM(i, j), for each team T_i, the set of its grouping candidates is composed by all the extendible away tuples identified in PM(i, j).

Algorithm 4.1 describes the move.

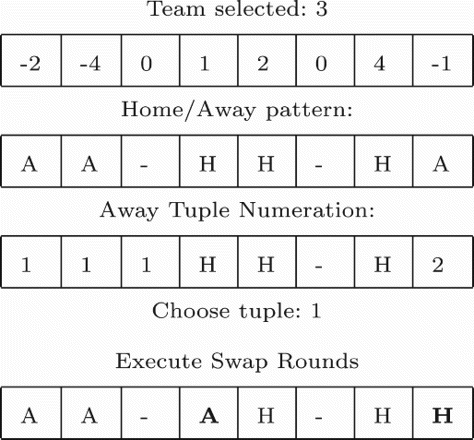
The process selects a team and identifies the away tuples for this team. An away tuple can be grouped if it is possible to change from home to away one of its adjacent rounds. Then, a tuple is selected and the Swap Homes move is executed in order to append one away more to the tuple. When the Swap Homes can be applied either to the left or to the right, the direction is randomly chosen. Figure 2 shows an example of the procedure which uses the home/away patterns of a candidate solution considering 10 rounds. The candidate solutions generated by applying all the moves always satisfy the hardest constraints related to the double round robin structure.

Figure 2. Away-tuple-group move: at the top, a selected team and its home/away pattern. In the bottom the pattern obtained after applying swap homes moves to the second randomly selected tuple.

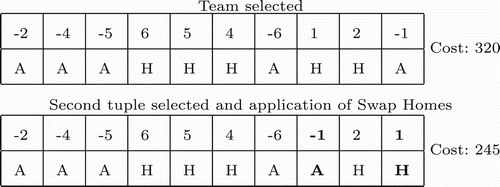
A simple exhaustive swap move could be included instead of this move, but when the problem becomes more difficult to be solved, it is important to better discriminate among the swapping options regarding to the goal.

4.4.2. Moves focused on free-days

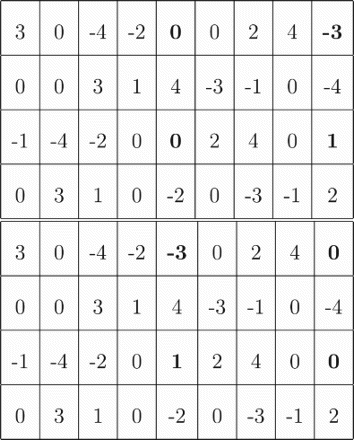
None of the moves presented above takes into account when some byes are allowed in the planning. Thus, we have designed two moves which are focused on the free-days: Swap Byes Matches and Grouping Away using Byes. The Swap Byes Matches move tries to interchange data from two rounds: a round where teams T₁ and T₂ have a free-day. The second round is when these two teams are playing together. Figure 3 shows the application of this move between teams 1 and team 3. In this case, the match between teams 1 and 3 is changed from round 5 to 9, and now both teams have a free-day in round 5 instead of round 9. It is a very quick move and very useful, because the optimisation process requires a good management of the byes. The byes allow to extend the away period of a team. Thus, the byes positioning is very important for obtaining a good solution for the problem.

Figure 3. Swap byes matches – teams (1,3).

In order to guide the algorithm to search better solutions in terms of reduction of the travelling cost, we have designed Grouping Away using Byes. As the cost of a team schedule corresponds to the cost of its away matches (trips), the idea is to try to group the trips of the teams with the more expensive travelling costs using the byes. The procedure begins with the teams with more expensive away costs. Before explaining the move we require the following definitions:

Definition 4.6 (Pattern byes matrix)

Given a Tournament Matrix TM, we define the associated Pattern Byes Matrix of size such that and

Definition 4.7 (Away pattern)

Whenever we refer to an ‘away pattern’ we define any continuous sequence without character H.

Definition 4.8 (Extendible away group)

An extendible away group is an away pattern that can be modified in order to increase the continuous sequence size of non-character H.

Because the upper limit for the trip length is 3, the only feasible away tuples when we consider k=1 byes are A, AA, A-, AA-, -A, -AA, A-A.

Definition 4.9 (Set of grouping candidates)

Given PM(i, j), for each team T_i, the set of its grouping candidates is composed by all the extendible away group identified in PM(i, j).

The Algorithm 4.2 describes the proposed move. An away pattern can be grouped if it is possible to change from home to away in one of the neighbours round. Then, a tuple is selected and the Swap Rounds move is executed in order to append one away more to the tuple. When the Swap Rounds can be made either to the left or to the right, the direction is randomly chosen.

Figure 4 shows an example of the procedure which uses the home/away patterns of the candidate solution. The candidate solutions generated by applying all the moves always satisfy the hardest constraints related to the double round robin structure.

Figure 4. Grouping-away-byes.

4.5. Algorithm

Our algorithm for the TTPs is described in Algorithm 4.3. The initial solutions are obtained from the following three simple steps:

• The algorithm uses the ‘polygon method’ (Ribeiro & Urrutia, 2007) to create a single round robin structure (graph 1-factorization), then

• this structure is mirrored and

• homes are randomly assigned to complete the double round robin tournament.

In line (3) in Algorithm 4.3, r_c is the clonation rate which represents the percentage of the repertoire to be selected. After that the algorithm obtains the set of clones generated using the affinity proportional in Equation (3), proposed by De Castro and Von Zuben (2002), where f_c is the clonal factor, n₁ the repertoire size and l the antibody ranking.

4.5.1. Hyper-mutation

The hyper-mutation procedure, according to CLONALG, should be inversely proportional to the antibody affinity. In our approach, we use the antibody ranking as an hyper-mutation level indicator. It determines the number of moves to apply to each clone. Algorithm 4.4 shows the procedure where (sol_i) is the best new antibody obtained after applying the five moves (op_k): Swap Homes, Swap Rounds, Swap teams, Partial Swap Rounds, Partial Swap Teams. In case byes are allowed the Swap Bye Matches move is also applied. This new antibody can be modified by the Grouping-Away-Byes move if there are byes allowed and it improves the value of the sol_i fitness function. If there are not byes the Away-tuple-group move is applied following the same idea of improving the current solution. The key idea of both the Grouping-Away-Byes and the Away-tuple-group is to reduce the travelling cost of the candidate solution obtained by applying the previous moves. It corresponds to a refinement process.

4.5.2. Diversity selection

The population of clones is composed of the union between cells and the hyper-mutated population P_c. The selection to construct the new set of cells is different from the original CLONALG. In our approach, the selection does not only search the best antibodies but it also considers that an antibody to be included in the selected_cells set must also be as different as possible to those already belonging to this set. That means, it is not sufficient to be a good antibody in terms of the fitness function. Moreover, the new antibody must also have different TM values.

The diversity for each antibody in P_c is measured by the average of the hamming distance between its home/away pattern and the home/away pattern of the antibodies that are already members of the selected_cells set. The goal of this procedure is to select the most different antibodies, in terms of their home/away patterns, from the set of the best ones. A diversity threshold is reduced when none of the antibodies has the required diversity level. This procedure, described in Algorithm 4.5, avoids a premature convergence of the immune algorithm.

5. Experiments and results

Three sets of experiments¹ have been done:

• To compare the original CLONALG with our approach.

• To give a comparison among our approach and the best known ones in this research domain.

• To show our results in the RTTP instances.

5.1. Comparing different versions of CLONALG

The tests are carried out with three algorithms:

• the first one is the original version of CLONALG,

• the second one corresponds to another version of CLONALG which only includes our diversity procedure (DCLONALG), and

• our approach () which includes both the diversity procedure and the Away-tuple-group move.

The first goal of these tests is to evaluate the improvement obtained using our approach respect to the original algorithm. The second goal is to evaluate the impact of the new move on the algorithm. For these experiments we have compared the algorithms using tests instances from the National League of The Major League Baseball in United States (NL) and from the Rugby League composed of teams from New Zealand, Australia and South Africa (SUPER).

Remark 3 It is important to note that these algorithms have been tuned for each instance to be solved. Because TTP is a very hard problem doing a fine tuning helps the three algorithms to obtain a better behaviour. We would like to compare among their better behaviours solving each instance.

5.1.1. Tests set-up

The algorithms use a population of size 10. We consider both non-structural constraints to be of equal importance to satisfy, and they have therefore the same weight factor of 0.5. The three algorithms have been run 50 times, each of them using 1000 iterations. For DCLONALG and the d t value is 0.9 and is 0.1. These algorithms use three other parameters: r_c (clonation rate), f_c (clonal factor) and r_r (replacement rate, related to the number of new antibodies included at each iteration). These parameters are tuned by considering all of the values of their range, and selecting the best one for each algorithm and for each instance.

The best results obtained by each type of algorithm when solving NL instances are in Table 1. For SUPER instances the best results are in Table 2.

Table 1.  Best travel distance for NL instances.

BEST	NL8	NL10	NL12	NL14	NL16
CLONALG	40,414	66,714	124,997	230,010	333,347
DCLONALG	40,156	62,669	121,904	220,657	319,490
	39,947	62,103	120,572	213,854	312,907

Table 2.  Best travel distance for SUPER instances.

BEST	S8	S10	S12	S14
CLONALG	190,510	348,814	512,652	715,078
DCLONAG	182,457	323,475	498,088	684,693
RAISTTP	182,409	322,845	497,668	675,219

We can conclude that both the diversity strategy and the Away-tuple-group move have been useful for the algorithm to find better solutions than the original CLONALG. Tables 3 and 4 show the average of the solutions obtained for the three algorithms using the different parameter values for (clonal rate) r_c, (clonal factor) f_c and (replacement rate) r_r reported in Table 5.

Table 3.  Average travel distance for NL instances.

Avg.	NL8	NL10	NL12	NL14	NL16
CLONALG	43,632	70,272	134,677	249,319	350,140
DCLONALG	42,149	68,807	132,629	242,220	348,946
	40,347	67,672	123,447	220,113	319,965

Table 4.  Average travel distance for SUPER instances.

Avg.	S8	S10	S12	S14
CLONALG	231,043	383,632	562,817	790,466
DCLONAG	208,883	365,855	544,520	775,981
	184,241	330,198	503,210	699,172

Table 5.  Best parameters for the algorithms.

				CLONALG			DCLONALG
	rc	fc	rr	rc	fc	rr	rc	fc	rr
NL8	0.7	0.6	0.3	0.8	0.1	0.2	1	0.8	0.2
NL10	0.7	1	0.3	0.8	0.4	0.3	0.9	0.7	0.4
NL12	0.8	0.8	0.3	0.5	1	0	0.6/0.7	0.6	0.4
NL14	0.8	0.8	0.2	0.7	0.7	0.1	0.5	1	0.3
NL16	0.7	0.8	0.3	1	0.7	0.6	0.5	0.7	0.2
S8	1	0.7	0.2	0.7	0.7	0.2	0.8/0.9	0.5	0.3
S10	0.9	0.7	0.5	1	0.9	0	0.8	0.9	0.3
S12	0.9	1	0.2	1	1	0	0.5	1	0.2
S14	0.6	1	0.2	0.8	1	0.1	0.8	0.8	0.3

From these tables, we can observe that the new move allows the reduction of the average travelled distance of best solutions.

5.1.2. Statistical analysis

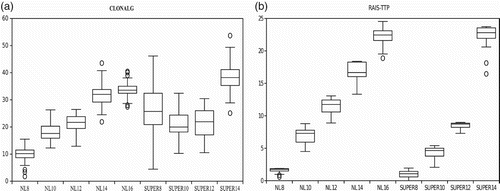
In order to appreciate the statistical significance of the results we present the box-plots generated for each instance tested with respect to the distance from the best known solution. We note that the standard deviation of the best solutions found by the algorithm is strongly reduced as it can be observed from the box-plots in Figure 5(a) and 5(b). Note that the scale of y-axis in the boxplots are not the same, because their boundary values are quite different. For each instance the y-axis represents the difference, in percentage, between the best solution we obtain and the best known solution.

Figure 5. Boxplots of CLONALG and RAIS_TTP. (a) CLONALG box-plot and (b) RAIS_TTP box-plot.

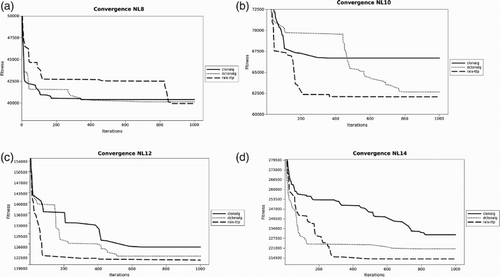
5.1.3. Convergence graphs

In this section we show the convergence graphs in Figure 6 for all NL instances and for the Super14 instance. From the graphs, we note that CLONALG is more frequently trapped in a local optima. Both DCLONALG and RAIS_TTP continue changing the best value found during more iterations than CLONALG. The diversity selection procedure proposed, allows both algorithms to visit other areas of the search space. The best final results are obtained by .

Figure 6. Convergence graphs. (a) Convergence NL8, (b) convergence NL10, (c) convergence NL12, (d) convergence NL14, (e) convergence NL16 and (f) convergence SUPER14.

5.2. Comparison with other algorithms for TTP

In order to have a fair comparison with other well-known algorithms, we have tuned our algorithm including all instances, using an automatic tuning algorithm. For these tests all runs use the same parameter values as it is done for the other algorithms reported in the literature.

Tables 6 and 7 report the best values obtained using our approach with 30000 iterations for the smaller problems and 200000 iterations for the biggest one. The solutions found by well-known existing techniques are also included in the tables. Our results are very encouraging.

Table 6.  Comparison with the state-of-the-art algorithms, best solution found for NL instances.

	NL8	NL10	NL12	NL14	NL16
PBSA (Van Hentenryck and Vergados, 2007)	–	–	110,729	188,728	261,687
TTSA (Anagnostopoulos et al., 2006)	39,721	59,583	111,248	189,766	267,194
TS (Di Gaspero and Schaerf, 2007)	–	59,583	111,483	190,174	270,794
L. HYP (Misir et al., 2009)	39,721	59,583	112,873	196,058	279,330
SA + HC (Lim et al., 2006)	39,721	59,821	115,089	196,363	274,673
ACO (Uthus et al., 2009b)	39,721	59,583	112,521	195,627	278,456
VNS-CS (Nogueira Lacerda, 2007)	41,928	65,193	120,906	208,824	287,130
ANT HYP. (Chen et al., 2007)	40,361	65,168	123,752	225,169	321,037
This paper	39,721	59,910	119,174	204,082	292,203
Best known	39,721	59,436	110,729	188,728	261,687
GAP percent;	0	0.8	7.6	8.1	11.7

Table 7.  Comparison with the other algorithms, best solution found for SUPER.

	S8	S10	S12	S14
L. Hyp. (Misir et al., 2009)	182,409	318,421	467,267	599,296
This paper	182,409	321,896	490,868	657,577
Best known	182409	316329	463876	571632
GAP %	0	1.8	5.8	15.0

5.2.1. Comparison with other algorithms: RTTP

In Table 8 we report the best results obtained using our approach for solving NL instances and the best known solutions. The results have been obtained using 100 runs. The parameter values obtained by tuning are clonation rate and clonation factor equal to 1 and the replace rate equals 0.3. We have also found feasible solutions for the bigger NL instances with the results in Table 9.

Table 8.  Comparison with best-known solutions for RTTP.

NL4, k=1	NL4, k=2	NL4, k=3
Best known	8160	8160	8044
This paper	8160	8160	8044
	NL6, k=1	NL6, k=2	NL6, k=3
Best known	23,124	22,557	22,557
This paper	23,124	22,557	22,557
	NL8, k=1	NL8, k=2	NL8, k=3
Best known	39,128	38,761	38,670
This paper	39,128	38,761	38,680

Table 9.  New feasible solutions for relaxed NL instances.

NL10	k=1	k=2	k=3
This paper	59,425	59,373	59,582
NL12	k=1	k=2	k=3
This paper	117,680	119,067	116,082
NL14	k=1	k=2	k=3
This paper	209,616	209,137	205,690
NL16	k=1	k=2	k=3
This paper	307,125	300,188	297,426

As far as we know these are the first reported results for these instances. We cannot prove that they are the optimal values, but they are feasible solutions. We have also implemented an algorithm for checking the feasibility of the solutions found by our approach, using various k values.

6. Conclusion

We have introduced an immune-inspired algorithm based on the CLONALG framework to solve instances of the TTP and RTTP. One difficulty found when applying the original CLONALG framework is that the algorithm gets stuck in local optima very quickly, showing that its capacity of exploration is strongly reduced to a few number of iterations. To solve this issue, we have defined a new way for selecting memory cells. Our approach does not focus only on having a good set of cells in memory in terms of their fitness function, but also on their structural diversity, allowing the algorithm to cover more search space during the search. The obtained results show that the clonal selection algorithm is able solve TTP and RTTP, moreover with few adaptation is able to do it competitively.

Solving TTP and RTTP is very challenging and finding quality solutions requires great computational effort and effective search techniques. We propose a new move to guide the search effectively and whose application is not limited to an immune approach. This move can be used by other techniques to search in its neighbourhood for reduced travel costs.

The algorithm parameters have great impact on its performance, in this work some parameter values were set by the rule of thumb while the most relevant were tuned per instance. The algorithm performs better using different parameter values for each instance of TTP and RTTP, this indicates that a dynamic parameter control strategy could be useful. We consider defining such mechanism as future work, thus a study of the algorithm parameters and their interactions will be performed in order to thoroughly understand its behaviour. To continue testing our algorithm we consider tackling bigger instances as the following challenge.

Acknowledgements

This work is supported by the Fondecyt Project 1120781.

Funding

The authors would like to thank Dr Xavier Bonnaire for his helpful remarks.

Notes

1. The hardware platform for the experiments was a PC Intel Corei7-920 with 4GB RAM under the Linux Mandriva 2010 operating system. The algorithm has been implemented in C++.