A centerline symmetry and double-line transformation based algorithm for large-scale multi-objective optimization

Abstract

The search space of large-scale multi-objective optimization problems (LSMOPs) is huge because of the hundreds or even thousands of decision variables involved. It is very challenging to design efficient algorithms for LSMOPs to search the whole space effectively and balance the convergence and diversity at the same time. In this paper, to tackle this challenge, we develop a new algorithm based on a weighted optimization framework with two effective strategies. The weighted optimization framework transforms an LSMOP into multiple small-scale multi-objective optimization problems based on a problem transformation mechanism to reduce the dimensionality of the search space effectively. To further improve its effectiveness, we firstly propose a centerline symmetry strategy to select reference solutions to transform the LSMOPs. It takes not only some non-dominated solutions but also their centerline symmetric points as the reference solutions, which can enhance the population diversity to avoid the algorithm falling into local minima. Then, a new double-line transformation function is designed to expand the search range of the transformed problem to further improve the convergence and diversity. With the two strategies, more widely distributed potential search areas are provided and the optimal solutions can be found easier. To demonstrate the effectiveness of our proposed algorithm, numerical experiments on widely used benchmarks are executed and the statistical results show that our proposed algorithm is more competitive and performs better than the other state-of-the-art algorithms for solving LSMOPs.

Keywords:

• Centerline symmetry
• reference solution
• transformation function
• weighted optimization
• large-scale multi-objective optimization

1. Introduction

Many real-world applications can be formulated as multi-objective optimisation problems (MOPs), such as route resource allocation (Gong et al., 2012; Y. Zhang et al., 2017), scheduling (Yuan & Xu, 2015), image processing (Gong & Zhou, 2018), cyber-physical social systems (Wang et al., 2020), and so on. Evolutionary algorithms, such as genetic algorithm (GA) (Zhao et al., 2020), particle swarm optimisation (PSO) (Nagra et al., 2020; Too et al., 2022), and differential evolution (DE) (Li et al., 2022; Zhao et al., 2021), have the characteristics of self-organisation and self-learning. Therefore, they are widely used in the field of optimisation. In the past few decades, many multi-objective optimisation evolutionary algorithms (MOEAs) have been developed for solving MOPs. They can be classified into three categories: Pareto dominance-based MOEAs (Deb et al., 2002; J. Liu, Wang, Wang, et al., 2019; Maltese et al., 2018; Sun et al., 2020; Xue & Wang, 2017), decomposition-based MOEAs (Dai & Wang, 2015a, 2015b; Dai et al., 2015; J. Liu, Wang, Fan, et al., 2019; E. Song & Li, 2022), and indicator-based MOEAs (Bader & Zitzler, 2011; Beume et al., 2007; Bringmann & Friedrich, 2010; Russo & Francisco, 2014; While et al., 2012). These MOEAs are very effective for small and medium scale MOPs.

However, with the development of technology, more and more decision variables are involved in the multi-objective optimisation models established for real-world engineering problems. For example, flight safety systems optimisation (Everson & Fieldsend, 2006) has more than 1500 decision variables, EEG time series data optimisation (Goh et al., 2015, may 25–28) involves more than 4800 decision variables, and the number of decision variables increases exponentially with the increase of layers in the deep neural network architecture optimisation problem (Tian et al., 2021). These MOPs with more than 100 decision variables are called LSMOPs. As the number of decision variables increases, the search space of MOPs will increase exponentially. The existing MOEAs perform not well for LSMOPs because of the huge search space. Therefore, many scholars have been attracted to study LSMOPs in recent years and numerous related algorithms have been developed, which can be classified into three categories.

The algorithms in the first category apply the divide-and-conquer technique to solve LSMOPs (Antonio & Coello, 2013, 2016; Cao et al., 2020, 2017; H. Chen et al., 2020; Ma et al., 2016; A. Song et al., 2016; X. Zhang et al., 2018). For example, Antonio et al. divide the decision variables into several equal-length subcomponents using the existing random grouping method. Each subproblem evolves collaboratively with other subproblems based on a differential evolution algorithm to optimise the LSMOPs (Antonio & Coello, 2013). Song et al. propose a dynamic random grouping method, which determines the number of groups dynamically according to the quality of the obtained solutions in each cycle (A. Song et al., 2016). After grouping, a decomposition-based MOEA, i.e. MOEA/D (Q. Zhang & Li, 2007), is used to optimise each subgroup. Because of the conflicts among the objectives, the existing grouping methods proposed for large-scale single-objective optimisation problems cannot be well applied in LSMOPs. Some decision variable analysis techniques and grouping strategies are proposed to group the decision variables for LSMOPs. Ma et al. propose an MOEA based on decision variables analysis (MOEA/DVA). In MOEA/DVA, the decision variables are classified into three types, i.e. convergence-related, diversity-related and mixed variables, according to their contributions to the convergence and diversity of the algorithm. Then the existing large-scale global optimisation grouping method is used to further divide the convergence-related variables into subgroups and the small-scale sub-MOPs are optimised collaboratively (Ma et al., 2016). To improve the grouping accuracy, Cao et al. apply the recursive differential grouping method to MOEA/DVA to adjust the misclassified variables in the three types of groups (Cao et al., 2017). Based on the main idea of MOEA/DVA, Zhang et al. group the decision variables into convergence-related and diversity-related variables instead of the three types by using the k-means clustering strategy to reduce the dimensionality of the LSMOPs (X. Zhang et al., 2018). However, these decision interaction analysis methods will consume a large number of computation resources, leading to low computational efficiency.

The algorithms in the second category propose some effective strategies to accelerate the search for LSMOPs (Gu & Wang, 2020; He et al., 2022; Hong et al., 2019; Tian et al., 2020; Yi et al., 2018, 2020; Y. Zhang et al., 2020). The evolutionary algorithm based on a direction-guided adaptive offspring generation (DGEA) (He et al., 2022) proposes an adaptive reproduction mechanism to guide the population evolution, thereby producing promising offspring based on the selected parents with strong convergence and diversity. Hong et al. present a diversity enhancement strategy to guide the population towards different regions of the Pareto frontier, to avoid the algorithm falling into local minima (Hong et al., 2019). The large-scale multi-objective competitive swarm optimiser algorithm (LMOCSO) (Tian et al., 2020) designs a new two-stage particle updating mechanism to update the position of each particle to solve LSMOPs with complicated landscapes. The updated particles are determined by the competitive mechanism of the competitive swarm optimiser (Tian et al., 2020). However, since these algorithms do not apply any dimensionality reduction strategy, the scale of the problem is still large and it requires a large number of function evaluations for the algorithms to search the whole decision variable space.

The algorithms belonging to the third category are based on non-grouping dimensionality reduction strategy, e.g. problem transformation technology and fuzzy technology (He et al., 2019; R. Liu et al., 2020; Qin et al., 2021; Tang et al., 2020; Zille et al., 2018). For example, A large-scale multi-objective optimisation framework via problem reformulation called LSMOF is proposed to reduce the dimension of the decision variables. It first presents a bi-direction weight variable association mechanism that associates two weight vectors to one selected solution to specify the search directions to accelerate the population evolution. Then by using a performance indicator, it reformulates an LSMOP into a small-scale SOP (He et al., 2019). By doing this, the search space is narrowed down from the whole space to several straight lines, which accelerates the convergence of the algorithm for solving LSMOPs. However, its performance is easily affected by the selection of reference points. Qin et al. design a directed sampling strategy based on LSMOF, which samples solutions based on the uniformly distributed search directions to reformulate the original problem to improve the population diversity (Qin et al., 2021). However, the sharp reduction of the search space still affects the population diversity of this kind of algorithm to a certain extent. Zille et al. propose a weighted optimisation framework (WOF) to transform the LSMOP into several small-scale MOPs. It first divides the n-dimensional decision variables into g (g<n) subgroups by adopting the existing grouping methods, e.g. random grouping (Omidvar et al., 2010), ordered grouping (W. Chen et al., 2010), and differential grouping (Omidvar et al., 2014). The variables in one subgroup are appointed with the same weight variable. By using a transformation function, an original n-dimensional LSMOP can be converted into a g-dimensional MOP with g weight vectors as decision variables, thereby reducing the dimensionality of the original LSMOP. Yang et al. present a fuzzy decision variables framework for LSMOPs to reduce the decision variable search space. It consists of two stages: fuzzy evolution and precise evolution (Yang et al., 2021). In the fuzzy evolution, it blurs the decision variables to reduce the search space to accelerate the convergence of the algorithm. Then the existing MOEAs are used to optimise the original problem to maintain the population diversity in the precise evolution stage. The algorithms in this category are more effective than those of the other two categories. Among the algorithms in this category, WOF is a very effective algorithm. However, its effectiveness is also affected by the selection of reference points. And the form of the transformation function also has a great impact on the search range of the transformed problem, thus affecting the performance of WOF. It is necessary for us to study effective strategies to enhance the performance of WOF to improve the ability to solve LSMOPs.

Based on the analysis of the related works, we can know that the research on large-scale multi-objective optimisation algorithms (LSMOAs) is still in the early stage. In this paper, to alleviate the limitations of WOF and improve the accuracy of solving LSMOPs, we present a new algorithm with two effective strategies based on WOF. The main innovations are summarised as follows:

1. A new centreline symmetry strategy for selecting reference solutions is presented to improve the diversity of WOF.

2. A new transformation function is designed to expand the search range for the selected reference solutions.

3. A new algorithm with the above two strategies is proposed and numerical experiments are carried out on widely used LSMOP benchmarks to verify its performance.

The remaining structure of this paper is shown below. Section 2 introduces the basic idea of WOF and the motivation of this paper. Our proposed algorithm is elaborated in Section 3. Section 4 shows the numerical experiments and analysis of the results. Finally, in Section 5, the conclusion is given.

2. Preliminary and motivation

The purpose of LSMOAs based on problem transformation is to achieve dimensionality reduction. Among them, WOF is a very effective algorithm. Because our algorithm is designed based on WOF, in this section, we elaborate on the main idea of WOF and then analyse its limitations. Subsequently, the motivation of this paper is presented.

2.1. The main idea of WOF

There are two stages in WOF. In the first stage, the original large-scale problem $\mathit{F}$ is transformed into several low-dimensional MOPs to reduce the search space of the decision variable space. In the second stage, one of the existing MOEAs is used to optimise the original problem $\mathit{F}$. Specifically, in the first stage, suppose ${\mathit{x}}^{\ast }$ is an optimal solution of the n-dimensional problem $\mathit{F}$. For any solution $\mathit{x}$ and a linear transformation function $\psi (\mathit{w},\mathit{x})=\{w_1{x}_1,w_2{x}_2,\dots ,w_n{x}_n\}$, we can find a real number optimal vector ${\mathit{w}}^{\ast }$ such that $\psi (\mathit{w},\mathit{x})={\mathit{w}}^{\ast }\mathit{x}={\mathit{x}}^{\ast }$. Then, for an arbitrary but fixed solution ${\mathit{x}}^{\prime }$, we can optimise $\mathit{w}$ instead of optimising ${\mathit{x}}^{\prime }$. To reduce the dimensionality of the original problem, WOF decomposes n decision variables into g groups, where $g<n$. Then assign the same weight $w_i$ to the variables in the same group $G_i$, where $i=1,2,\dots ,g$, i.e. (1) $\psi (\mathit{w},\mathit{x})=(\underset{w_1}{\underbrace{w_1{x}_1,\dots ,w_1{x}_l}},\dots ,\underset{w_g}{\underbrace{w_g{x}_{n-l+1},\dots ,w_g{x}_n}})$(1) where l denotes the size of each group. Then, by taking a fixed ${\mathit{x}}^{\prime }$, the problem $\mathit{F}$ of optimising n-dimensional $\mathit{x}$ is transformed into the problem ${\mathit{F}}^{\prime }$ of optimising g-dimensional $\mathit{w}$, thereby reducing the dimensionality of the LSMOPs. In WOF, to keep the population diversity, m solutions in the first non-dominated front are selected as the reference solutions according to the crowding distance to execute the transformation, and then m transformed low-dimensional MOPs are optimised. Finally, m optimal weight vectors ${\mathit{W}}^{\ast }=\{{\mathit{W}}_1,{\mathit{W}}_2,\dots ,{\mathit{W}}_m\}$ are used to update the individuals of the original problem according to the transformation function.

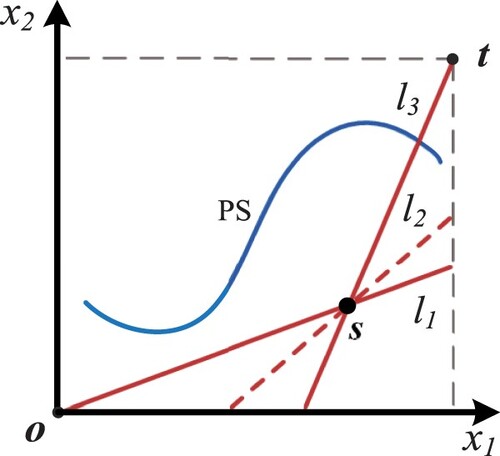
Geometrically speaking, the result of the above problem transformation is to narrow the whole search space to m straight lines. In Figure 1(a), the blue curve PS denotes the Pareto optimal set (PS) and $\mathit{s}$ is a selected reference solution. $\mathit{o}$ and $\mathit{t}$ denote the origin and the upper boundary point, respectively. After using transformation functions, e.g. the linear transformation function, the search range is reduced from the whole 2D space to one straight line. Searching along the straight line can obtain the optimal solution or the sub-optimal solution more quickly than searching on the entire two-dimensional space.

Figure 1. Illustration examples of WOF. (a) The search space transformation and (b) The effect of reference solution selection on the search range.

Based on the principle of the problem transformation method, we can know that the search for the transformed problem ${\mathit{F}}^{\prime }$ focuses on some potential areas which may result in faster convergence. However, due to the drastic reduction of the search space, the population diversity will deteriorate. Therefore, in the second stage of WOF, to make up for the diversity loss caused by optimising the transformed problem, the original problem $\mathit{F}$ is optimised by the existing MOEAs. Since optimising the original problem $\mathit{F}$ in the whole search space may obtain all possible solutions in the whole space, which may improve the population diversity. For details of the algorithm, please refer to WOF (Zille et al., 2018).

2.2. Motivation

According to the principle of WOF, we can know that factors affecting the search range are the selection of the grouping method, reference solutions, and the transformation function. Since the correlation between decision variables of LSMOPs is complex, there is still no effective large-scale multi-objective grouping method to group the decision variables of LSMOPs reasonably. At present, the commonly used grouping methods of WOF are the ones proposed for large-scale global optimisation problems, e.g. random grouping, linear grouping, ordered grouping, and differential grouping. The influence of the four grouping methods on WOF has been investigated in the original paper and the results show that WOF using the ordered grouping method is more competitive. Therefore, in our proposed algorithm, the ordered grouping method is still used to group the decision variables. In this paper, we focus on the influence of the latter two factors, i.e. the selection of reference solutions and the transformation function.

As shown in Figure 1(b), if the selected reference solutions are located in a small area of the search space, the transformed search range may be concentrated in a certain area as shown by the six straight lines. The search range is far away from PS, which may cause the algorithm to fail to find the optimal solutions. Thus, how to select appropriate reference solutions to expand the search coverage of the algorithm and improve the population diversity is an urgent problem to enhance the performance of WOF.

Additionally, the transformation function can determine the search directions for the selected reference solutions. As shown in Figure 1, the linear transformation function transforms the search space into one straight line based on one reference solution. If the LSMOP is complicated and the optimal solutions or the sub-optimal solutions do not locate near the line, the efficiency of WOF will be affected. Thus, it is an effective way to improve the performance of the WOF in solving LSMOPs by designing a new transformation function to add potential search directions.

3. The proposed algorithm

In this section, we propose a new weighted optimisation algorithm with a centerline symmetry strategy for selecting reference solutions and a double-line transformation function, referred to as CSDT, for solving LSMOPs. The main framework is shown in Algorithm 1. CSDT begins with the population initialisation and is followed by two stages. In the first stage, according to our proposed selection mechanism in Section 3.1, m solutions with relatively wide distribution are selected as reference solutions for the problem transformation. Subsequently, one of the existing grouping methods is used to group the decision variables into g subgroups. For each reference solution, the original problem $\mathit{F}$ is transformed into a g-dimensional problem ${\mathit{F}}^{\prime }$ based on the transformation function designed in Section 3.2. Then, the transformed problem ${\mathit{F}}^{\prime }$ is optimised by the existing MOEAs to obtain promising weight vectors. These weight vectors are utilised to reproduce new promising offspring based on the original population by applying the transformation function. Optimizing the transformed problem can reduce the search space of the algorithm and can concentrate the search in the potential search areas, thereby significantly accelerating the population convergence. Subsequently, the existing MOEAs are utilised to optimise the problem $\mathit{F}$ to obtain solutions with good diversity in the second stage.

In the following, we will introduce the details of the proposed selection strategy and transformation function.

3.1. A new reference solutions selection strategy

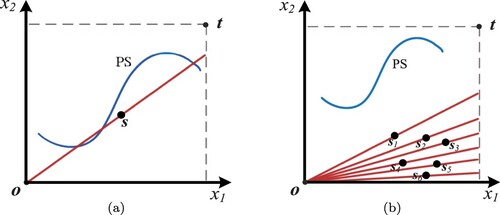
In this section, we design a strategy to select widely distributed solutions to transform the original problem to get some widely distributed search lines. For the convenience of description, we define the diagonal line connecting the upper and lower boundary points of the decision variable space as the centreline. The details are as follows.

Firstly, select m/2 best solutions by using the existing environmental selection method, e.g. NSGA-II, where m is the number of the reference solutions to be selected. Generate m/2 centreline symmetry points based on the m/2 best solutions selected before. The method of generating centreline symmetry points is described in the following.

As shown in Figure 2(a), suppose that $\mathit{s}$ is one of the selected best solutions, $\mathit{p}$ is its projection point on the centreline. For the convenience, suppose $\mathit{t}$ and the origin $\mathit{o}$ are the upper and lower boundary points of the decision variable space in this paper, respectively. Since points $\mathit{p}$, $\mathit{t}$ and $\mathit{o}$ are on the same straight line, we can get $k\ast (\mathit{p}-\mathit{o})=\mathit{t}-\mathit{o}$, where $k=|\mathit{p}-\mathit{o}|/|\mathit{t}-\mathit{o}|$ is a real number between [0,1]. Once we get the value of k, the coordinates of $\mathit{p}$ can be obtained. Since $|\mathit{p}-\mathit{o}|=|\mathit{s}-\mathit{o}|\cos \theta =(\mathit{s}-\mathit{o})\ast (\mathit{t}-\mathit{o})/|\mathit{t}-\mathit{o}|$, where θ is the angle between the vector $\mathit{s}-\mathit{o}$ and $\mathit{t}-\mathit{o}$, and also the angle between $\mathit{p}-\mathit{o}$ and $\mathit{t}-\mathit{o}$, we can get $k=|\mathit{p}-\mathit{o}|/|\mathit{t}-\mathit{o}|=(\mathit{s}-\mathit{o})\ast (\mathit{t}-\mathit{o})/(|\mathit{t}-\mathit{o}{|}^2)$. Then, the coordinates of $\mathit{p}$ can be gotten by $\mathit{p}=\mathit{o}+k\ast (\mathit{t}-\mathit{o})$. Based on the obtained $\mathit{p}$, the symmetry point of $\mathit{s}$ can be generated by $\mathit{r}=2\ast \mathit{p}-\mathit{s}$.

Figure 2. Illustrations of the reference solution generation mechanism. (a) Centerline symmetry point generation for one solution and (b) Centerline symmetry point generation for multiple solutions.

According to the above method, m/2 centreline symmetry points can be generated. These points and the m/2 best solutions selected previously are taken as reference solutions. After transformation, the search space of the transformed problem can be expanded to widely distributed straight lines.

Take a 2D space in Figure 2(b) as an example. Suppose that m is 6. ${\mathit{s}}_1\sim {\mathit{s}}_3$ are the reference solutions selected by NSGA-II. Three straight lines passing through ${\mathit{s}}_1\sim {\mathit{s}}_3$ are the search range of the transformed problem using the linear transformation function, which is far away from the PS. According to the reference solutions generation method, we can obtain the centreline symmetry points of ${\mathit{s}}_1\sim {\mathit{s}}_3$, i.e. ${\mathit{r}}_1\sim {\mathit{r}}_3$. Then, ${\mathit{s}}_1\sim {\mathit{s}}_3$ and ${\mathit{r}}_1\sim {\mathit{r}}_3$ are taken as reference solutions to transform the original problem. From Figure 2(b), we can see that after the transformation, the search range of the transformed problem is increased by three straight lines passing through ${\mathit{r}}_1\sim {\mathit{r}}_3$. The six lines are relatively widely distributed in the decision variable space. Searching along these lines, the algorithm can find the solutions of PS easier.

3.2. A new transformation function

In WOF, three transformation functions are proposed to transform the original problem. Specifically, the forms of the product transformation ${\psi }_1$ and the interval-intersection transformation ${\psi }_3$ are basically the same. They narrow the whole search subspace to a straight line connecting the origin $\mathit{o}$ and the corresponding selected reference solution, which is denoted by $l_1$ in Figure 3. The p-value transformation ${\psi }_2$ narrows the search space to the straight line passing through the corresponding selected reference solution and parallel to the centreline as displayed by $l_2$ in Figure 3.

Figure 3. The search ranges for different transformation functions.

Here, we design a double-line transformation function to increase the search range and search directions for the selected reference solutions. The new transformation function is as follows. (2) $\{\begin{array}{ll}{x}_{i,new}=x_i+(w_j-1.5)\ast (t_i-x_i),& w_j>1\\ x_{i,new}=x_i+(w_j-0.5)\ast (x_i-o_i),& w_j\le 1\end{array}{w}_j\in [0,2]$(2) where $x_i$ is the value of ith dimension of $\mathit{x}$, and $w_j$ is the weight vector assigned to the jth group of decision variables that $x_i$ belongs to.

Based on the designed transformation function, the search range of the original problem can be narrowed down to two straight lines, i.e. $l_1$ and $l_3$ as shown in Figure 3. If $w_j\le 1$, the algorithm searches along the line $l_1$, otherwise it searches along the line $l_3$. From Figure 3, we can see that the search range is expanded to more promising areas, which may make it easier to find promising solutions quickly. This can further improve the efficiency of the existing MOEAs to solve LSMOPs.

4. Experiments and results

In this section, we conduct the numerical experiments on widely used multi-objective benchmarks UF1-UF10 (Q. Zhang et al., 2008), WFG1-WFG9 (Huband et al., 2006), and LSMOP1-LSMOP9 (Cheng et al., 2017) to empirically demonstrate the effectiveness of our CSDT. And the comparison with MOEA/DVA (Ma et al., 2016), LSMOF (He et al., 2019), DGEA (He et al., 2022), and WOF (Zille et al., 2018) is made. All the numerical experiments are carried out on PlatEMO (Tian et al., 2017) of Matlab 2015b on a computer with Intel(R) Xeon(R) CPU E5-2630 v4 @2.20GHz and 128G RAM. IGD (Zitzler et al., 2003) is used to comprehensively access the convergence and diversity of the obtained non-dominated solutions set. The smaller the IGD value is, the better the algorithm performs.

4.1. Parameter settings

For each test problem, the number of the objectives is set to 2 and 3, respectively. The dimension of the decision variables is set to 200, 500, and 1000, respectively. Since our proposed algorithm is an improved version of WOF and the main framework of WOF is not changed, the values of the same parameters in CSDT and WOF are consistent with those set in WOF (Zille et al., 2018). For example, the number of reference solutions m is set to 10. The ratio of function evaluations spent in the first stage δ is 0.5, which means that we allocate 50 percent of the total function evaluations to each stage. The ordered grouping method is used in these two algorithms and the number of groups g is 4. In WOF, the p-value transformation function is applied to transform the original problems since it is the best one among the three proposed functions. The optimisation algorithm used in each stage is particle swarm optimisation in CSDT and the original WOF. As for the other three compared algorithms, i.e. MOEA/DVA, DGEA, and LSMOF, the parameters are set to their default values. To ensure the fairness of the comparison experiments, the population size is set to 100 for all the compared algorithms. To ensure the convergence of the compared algorithms, we set the maximum number of function evaluations (FEs) to 500,000 for all algorithms.

On all instances, every algorithm runs independently 20 times. The Wilcoxon rank-sum test with a significance level of 0.05 (Carrasco et al., 2020) is applied to display the statistical results of compared algorithms. In the statistical results, “+”, “=”, and “−” mean that the compared algorithm is statistically better than, comparable to, and worse than the proposed algorithm.

4.2. Investigation of effectiveness of the two strategies

To investigate the effectiveness of our proposed strategies, we conducted numerical experiments on UF and WFG benchmarks. In the experiments, WOF-CS is the algorithm WOF with the reference solution selection strategy embedded, and WOF-DT is the algorithm WOF with the new transformation function embedded. We compare the performance of WOF-CS, WOF-DT, and the proposed algorithm CSDT with that of the original algorithm WOF on UF and WFG benchmarks. The IGD results are shown in Tables 1 and 2.

Table 1. IGD values of WOF with different strategies on UF benchmarks, where the best results on each test instance is highlighted.

Problem	M	D	WOF-CS	WOF-DT	CSDT	WOF
UF1	2	200	7.6391e−2 (8.42e−3) +	7.8510e−2 (1.09e−2) =	7.4842e−2 (5.03e−3) +	8.4876e−2 (1.23e−2)
		500	7.8605e−2 (3.76e−3) =	7.8199e−2 (2.18e−3) =	7.6796e−2 (3.21e−3) =	8.3559e−2 (1.71e−2)
		1000	7.7721e−2 (3.57e−3) +	7.7433e−2 (3.65e−3) +	7.7473e−2 (1.62e−3) +	8.2531e−2 (5.37e−3)
UF2	2	200	6.9400e−2 (9.34e−4) +	7.3345e−2 (1.17e−3) +	7.0063e−2 (9.66e−4) +	8.4675e−2 (3.97e−3)
		500	7.1113e−2 (5.34e−4) +	7.3501e−2 (1.81e−3) +	7.0944e−2 (6.75e−4) +	8.8861e−2 (4.36e−3)
		1000	7.1125e−2 (8.99e−4) +	7.4213e−2 (1.31e−3) +	7.0708e−2 (3.90e−4) +	9.2473e−2 (5.79e−3)
UF3	2	200	5.8410e−2 (2.13e−3) =	5.7738e−2 (2.07e−3) =	5.6395e−2 (1.68e−3) +	5.8435e−2 (1.67e−3)
		500	3.4058e−2 (1.94e−3) =	3.2910e−2 (1.56e−3) =	3.1558e−2 (7.15e−4) +	3.3819e−2 (1.23e−3)
		1000	2.5222e−2 (1.32e−3) =	2.3564e−2 (1.42e−3) +	2.2863e−2 (1.02e−3) +	2.6529e−2 (1.95e−3)
UF4	2	200	5.2990e−2 (5.09e−3) =	5.0841e−2 (3.46e−3) +	4.9435e−2 (3.36e−3) +	5.6930e−2 (4.56e−3)
		500	5.7327e−2 (1.09e−2) =	5.0172e−2 (2.48e−3) +	4.9321e−2 (3.39e−3) +	5.7961e−2 (4.27e−3)
		1000	5.6464e−2 (8.48e−3) =	5.0687e−2 (6.10e−3) +	4.9576e−2 (3.48e−3) +	5.7667e−2 (3.24e−3)
UF5	2	200	8.2976e−1 (3.10e−1) =	1.0698e+0 (4.04e−1) =	1.0589e+0 (2.72e−1) =	9.3659e−1 (3.80e−1)
		500	1.1998e+0 (5.33e−1) =	1.8640e+0 (1.18e−1) =	1.7622e+0 (3.01e−1) =	1.6024e+0 (5.26e−1)
		1000	2.0084e+0 (9.03e−2) =	2.0032e+0 (4.50e−2) =	1.9815e+0 (7.69e−2) =	1.9566e+0 (2.90e−1)
UF6	2	200	2.4363e−1 (8.80e−2) =	2.5947e−1 (6.32e−2) =	2.4402e−1 (6.24e−2) =	3.2407e−1 (1.22e−1)
		500	3.2773e−1 (8.64e−2) =	3.2087e−1 (1.49e−2) =	2.8993e−1 (3.25e−2) +	3.4794e−1 (6.42e−2)
		1000	3.4923e−1 (4.80e−2) =	3.2751e−1 (8.00e−3) +	2.9232e−1 (5.82e−2) +	3.6727e−1 (3.72e−2)
UF7	2	200	6.1506e−2 (3.11e−3) =	5.9764e−2 (3.96e−3) =	6.2972e−2 (2.04e−3) =	5.8610e−2 (5.12e−3)
		500	7.6966e−2 (7.78e−3) =	7.1856e−2 (2.19e−3) +	1.0118e−1 (9.36e−2) −	7.8868e−2 (1.18e−2)
		1000	7.6588e−2 (1.61e−3) +	7.5787e−2 (1.75e−3) +	7.4906e−2 (1.93e−3) +	8.0447e−2 (3.62e−3)
UF8	3	200	2.0360e−1 (1.52e−2) +	1.9788e−1 (9.94e−3) +	2.1050e−1 (1.55e−2) =	2.2485e−1 (2.20e−2)
		500	2.0631e−1 (7.53e−3) +	2.0025e−1 (5.92e−3) +	1.9821e−1 (6.06e−3) +	2.1848e−1 (1.17e−2)
		1000	2.0555e−1 (7.27e−3) =	2.0405e−1 (1.68e−2) =	1.9857e−1 (7.65e−3) +	2.1171e−1 (6.61e−3)
UF9	3	200	4.7554e−1 (1.68e−3) +	4.7205e−1 (3.33e−2) +	4.7694e−1 (2.22e−3) +	5.0181e−1 (2.60e−2)
		500	4.8972e−1 (1.68e−3) +	5.0673e−1 (3.74e−3) +	4.8966e−1 (1.86e−3) +	5.3932e−1 (1.46e−2)
		1000	4.9589e−1 (8.59e−4) +	5.1798e−1 (6.26e−3) +	4.9616e−1 (6.94e−4) +	5.5864e−1 (2.31e−2)
UF10	3	200	3.4552e+0 (5.82e−1) =	2.7283e+0 (3.85e−1) +	2.7055e+0 (3.95e−1) +	3.5003e+0 (4.03e−1)
		500	4.3700e+0 (2.10e−1) =	3.1740e+0 (3.52e−1) +	3.4126e+0 (3.18e−1) +	4.3766e+0 (4.62e−1)
		1000	4.6921e+0 (2.33e−1) =	2.8992e+0 (6.31e−1) +	3.1526e+0 (4.80e−1) +	4.6280e+0 (2.08e−1)
$+/-/=$			11/0/19	19/0/11	22/1/7

Table 2. IGD values of WOF with different strategies on WFG benchmarks, where the best results on each test instance is highlighted.

Problem	M	D	WOF-CS	WOF-DT	CSDT	WOF
WFG1	2	200	1.1139e+0 (5.71e−2) =	1.1108e+0 (1.88e−1) =	1.0959e+0 (7.60e−2) =	1.0728e+0 (1.53e−1)
		500	1.1244e+0 (9.72e−2) =	1.1732e+0 (1.32e−1) =	1.1631e+0 (2.60e−2) =	1.1619e+0 (1.03e−1)
		1000	1.1088e+0 (1.11e−1) =	1.1863e+0 (1.10e−1) =	1.1603e+0 (1.45e−2) =	1.1475e+0 (1.58e−1)
	3	200	1.5267e+0 (3.04e−2) =	1.2500e+0 (2.18e−1) +	1.2414e+0 (2.58e−1) +	1.4771e+0 (1.25e−1)
		500	1.4830e+0 (9.93e−2) =	1.4769e+0 (6.27e−2) +	1.4130e+0 (1.58e−1) +	1.5261e+0 (1.16e−2)
		1000	1.5191e+0 (2.82e−2) =	1.3402e+0 (1.73e−1) +	1.5185e+0 (5.51e−2) =	1.5451e+0 (3.50e−2)
WFG2	2	200	1.4396e−2 (9.52e−4) +	2.3910e−2 (4.41e−3) +	1.4531e−2 (7.31e−4) +	1.0409e−1 (5.88e−2)
		500	3.3876e−2 (1.72e−3) +	6.4822e−2 (6.48e−3) +	3.4904e−2 (1.30e−3) +	2.0759e−1 (2.70e−2)
		1000	7.6968e−2 (8.64e−4) +	1.0647e−1 (8.05e−3) +	7.7117e−2 (1.20e−3) +	2.5979e−1 (1.98e−2)
	3	200	2.1085e−1 (8.72e−3) +	2.2095e−1 (1.16e−2) +	2.1721e−1 (1.01e−2) +	2.5554e−1 (8.22e−3)
		500	6.4437e−1 (8.30e−2) +	6.3702e−1 (8.23e−2) +	5.9806e−1 (1.06e−1) +	7.2613e−1 (7.99e−2)
		1000	5.7730e−1 (7.99e−2) +	6.6763e−1 (5.80e−2) =	6.2116e−1 (3.69e−2) +	6.9056e−1 (5.71e−2)
WFG3	2	200	1.6512e−2 (6.04e−4) +	3.0757e−2 (3.54e−3) +	1.6374e−2 (7.21e−4) +	7.3310e−2 (8.31e−3)
		500	4.0059e−2 (1.12e−3) +	7.1744e−2 (8.09e−3) +	3.8905e−2 (3.10e−3) +	1.5022e−1 (1.21e−2)
		1000	8.2036e−2 (5.40e−4) +	1.1313e−1 (1.04e−2) +	8.2011e−2 (5.11e−4) +	2.0435e−1 (9.48e−3)
	3	200	7.5386e−2 (1.46e−2) +	9.3949e−2 (1.38e−2) +	7.2270e−2 (9.51e−3) +	1.4177e−1 (2.86e−2)
		500	8.0382e−2 (5.84e−3) +	1.0146e−1 (9.79e−3) +	7.6111e−2 (3.59e−3) +	1.2697e−1 (8.53e−3)
		1000	1.2638e−1 (4.34e−3) +	1.4706e−1 (5.93e−3) +	1.2406e−1 (2.57e−3) +	1.8107e−1 (1.47e−2)
WFG4	2	200	1.9615e−2 (1.06e−3) +	3.3637e−2 (5.28e−3) +	2.0659e−2 (3.18e−3) +	4.7118e−2 (7.86e−3)
		500	5.0650e−2 (3.30e−3) +	9.9475e−2 (6.95e−3) +	5.1119e−2 (2.48e−3) +	1.2238e−1 (9.37e−3)
		1000	1.1102e−1 (1.96e−2) +	1.6247e−1 (8.84e−3) +	1.1246e−1 (1.23e−2) +	1.7245e−1 (7.99e−3)
	3	200	3.1970e−1 (1.68e−2) =	3.0353e−1 (9.20e−3) +	2.9866e−1 (6.47e−3) +	3.2314e−1 (9.41e−3)
		500	6.9000e−1 (8.87e−2) =	7.0465e−1 (9.70e−2) =	6.7172e−1 (1.13e−1) =	7.5532e−1 (9.30e−2)
		1000	7.7980e−1 (1.02e−1) =	7.3677e−1 (9.65e−2) =	7.4058e−1 (7.34e−2) =	8.2199e−1 (1.35e−1)
WFG5	2	200	6.9640e−2 (8.11e−3) =	7.2002e−2 (1.74e−3) =	6.8751e−2 (6.54e−3) +	7.4890e−2 (4.42e−3)
		500	9.2693e−2 (4.00e−3) =	8.8582e−2 (3.23e−3) +	8.6547e−2 (3.51e−3) +	9.5777e−2 (8.27e−3)
		1000	1.4012e−1 (1.27e−2) =	1.1988e−1 (1.06e−2) +	1.2436e−1 (5.00e−3) +	1.3883e−1 (8.71e−3)
	3	200	2.7574e−1 (9.40e−3) =	2.7543e−1 (6.12e−3) =	2.7680e−1 (1.18e−2) =	2.7237e−1 (8.00e−3)
		500	7.3498e−1 (7.57e−2) −	7.2040e−1 (6.83e−2) −	7.0279e−1 (7.87e−2) −	6.3746e−1 (5.50e−2)
		1000	6.7745e−1 (6.93e−2) =	7.5634e−1 (9.94e−2) =	7.6281e−1 (5.78e−2) =	7.3766e−1 (1.12e−1)
WFG6	2	200	1.8177e−2 (1.11e−3) +	1.6976e−2 (4.80e−4) +	1.7027e−2 (7.53e−4) +	1.9993e−2 (2.18e−3)
		500	2.0713e−2 (2.13e−3) =	2.0241e−2 (1.42e−3) =	1.9832e−2 (1.03e−3) =	2.1311e−2 (2.57e−3)
		1000	2.0967e−2 (2.22e−3) +	2.2440e−2 (1.89e−3) =	2.3875e−2 (2.35e−3) =	2.4419e−2 (2.32e−3)
	3	200	2.6771e−1 (1.08e−2) =	2.6502e−1 (1.29e−2) =	2.5989e−1 (7.72e−3) =	2.6979e−1 (9.92e−3)
		500	3.4647e−1 (2.40e−2) +	4.3196e−1 (6.59e−2) =	3.8359e−1 (6.35e−2) =	4.3344e−1 (8.11e−2)
		1000	5.4531e−1 (1.64e−1) =	4.3855e−1 (2.98e−2) =	4.3966e−1 (5.68e−2) =	4.7273e−1 (6.22e−2)
WFG7	2	200	1.8494e−2 (1.48e−3) +	2.2067e−2 (2.09e−3) +	1.7454e−2 (1.16e−3) +	1.2053e−1 (4.97e−2)
		500	4.4436e−2 (2.02e−3) +	7.7618e−2 (7.16e−3) +	4.2665e−2 (2.67e−3) +	1.2001e−1 (5.87e−3)
		1000	1.0708e−1 (7.08e−3) +	1.4403e−1 (6.95e−3) +	1.0762e−1 (6.12e−3) +	1.8217e−1 (2.15e−2)
	3	200	2.8211e−1 (1.46e−2) +	2.8197e−1 (2.07e−2) +	2.8698e−1 (1.83e−2) +	3.2585e−1 (1.39e−2)
		500	6.5016e−1 (1.26e−1) +	5.9304e−1 (1.09e−1) +	6.2679e−1 (1.06e−1) +	7.8960e−1 (1.23e−1)
		1000	6.6890e−1 (1.35e−1) =	6.6826e−1 (8.38e−2) =	6.5700e−1 (1.14e−1) =	7.6476e−1 (1.12e−1)
WFG8	2	200	1.8191e−1 (1.13e−1) =	1.0992e−1 (1.16e−1) +	8.3834e−2 (9.10e−2) +	1.9439e−1 (1.12e−1)
		500	2.5055e−1 (6.64e−3) =	2.2495e−1 (6.80e−3) +	2.2625e−1 (3.97e−3) +	2.5172e−1 (5.29e−3)
		1000	2.5715e−1 (8.77e−3) +	2.4124e−1 (4.58e−3) +	2.4105e−1 (7.20e−3) +	2.7400e−1 (6.67e−3)
	3	200	6.4449e−1 (1.99e−2) =	6.2974e−1 (1.13e−1) =	5.6794e−1 (1.31e−1) =	6.2640e−1 (1.95e−2)
		500	7.5454e−1 (4.76e−2) =	7.7508e−1 (8.73e−2) =	7.2636e−1 (8.05e−2) =	7.5043e−1 (6.43e−2)
		1000	8.2025e−1 (5.06e−2) =	7.9795e−1 (7.72e−2) =	8.0742e−1 (4.95e−2) =	8.5673e−1 (5.78e−2)
WFG9	2	200	3.7961e−2 (9.11e−3) +	3.2081e−2 (9.73e−4) +	3.2151e−2 (1.11e−3) +	5.3242e−2 (1.03e−2)
		500	7.1848e−2 (2.81e−2) =	4.3994e−2 (3.04e−3) +	4.5652e−2 (4.16e−3) +	8.4410e−2 (2.19e−2)
		1000	5.4483e−2 (6.24e−3) =	5.1933e−2 (2.56e−3) =	5.1195e−2 (6.41e−3) =	6.5643e−2 (2.08e−2)
	3	200	3.5586e−1 (2.09e−2) =	3.4864e−1 (2.93e−2) =	3.4775e−1 (1.37e−2) =	3.6687e−1 (2.50e−2)
		500	4.1323e−1 (2.66e−2) =	3.9042e−1 (2.30e−2) +	4.0078e−1 (3.72e−2) =	4.2906e−1 (2.73e−2)
		1000	4.5726e−1 (5.23e−2) =	4.0164e−1 (3.39e−2) =	4.3676e−1 (2.14e−2) =	4.1960e−1 (4.24e−2)
$+/-/=$			25/1/28	32/1/21	32/1/21

Firstly, comparing the results of WOF-CS and WOF in Tables 1 and 2, we can see that the results obtained by WOF-CS are statistically better than those obtained by WOF on the two benchmark suites. Specifically, for UF benchmarks, WOF-CS wins on 11 out of 30 instances and ties on the remaining instances. It performs significantly better than WOF mainly on UF1, UF2, UF5, UF8, and UF9 instances. For WFG benchmarks, WOF-CS wins on 25/54 instances and loses only on 1/54 instances on WFG benchmarks. The better results obtained by WOF-CS mainly focus on all instances of WFG2, WFG3, WFG4, and WFG7, and bi-objective instances of WFG1, WFG6, WFG8, and WFG9. This indicates that the proposed reference solution strategy is effective. Select widely distributed solutions to transform the original problem can provide widely distributed search lines for the algorithm to search. Along these lines, the algorithm can obtain solutions with better diversity, which may help WOF jump out the local minima and find better optimal solutions while ensuring the acceleration for population convergence.

Secondly, comparing the results of WOF-DT and WOF, we can see that the performance of WOF-DT is significantly better than that of WOF on UF and WFG benchmarks. To be specific, for UF benchmarks, WOF-DT performs statistically better than WOF on 19 instances. It obtains better results than WOF on all UF benchmarks except UF5 and 200-D UF7. For WFG benchmarks, WOF-CS performs statistically better than WOF on 32 out of 54 instances and worse than WOF only on 1 instance. The better results obtained by WOF-DT mainly focus on all instances of WFG1, WFG2, WFG3, WFG4, WFG6, WFG7, and WFG9, and bi-objective instances of WFG5 and WFG8, and tri-objective WFG1. This demonstrates that our designed transformation function is more competitive. As described in Section 3.2, our proposed transformation function can narrow down the search space into two straight lines based on one reference solution and provide more potential search areas and search directions than the existing ones. It can help the algorithms find more promising solutions quickly, thereby improving the efficiency of solving LSMOPs.

Furthermore, the performance of CSDT that combines the two proposed strategies on WOF is also investigated. From Tables 1 and 2, CSDT outperforms WOF with 22 wins, 1 lose, and 7 ties on UF benchmarks, and performs statistically better than WOF with 32 wins, 1 lose, and 21 ties on WFG benchmarks. This demonstrates that our proposed algorithm is more efficient than the original WOF for solving LSMOPs. Moreover, the best results obtained by CSDT are more than those obtained by the algorithms embedded with one single strategy. Specifically, WOF-CS obtains 5 best results, WOF-DT obtains 6 best results, and CSDT finds 17 best results on 30 UF benchmarks. And on 54 WFG instances, WOF-CS gets 14 best results, WOF-DT gets 13 best results, and CSDT obtains 24 best results. This proves that CSDT gives full play to the advantages of the two strategies and greatly improves the ability of WOF to solve LSMOPs.

In summary, the above comparative analysis demonstrates that the two strategies we proposed are effective and can significantly improve the performance of WOF in solving LSMOPs.

4.3. Comparisons with state-of-the-arts

To demonstrate the performance of CSDT, we compare CSDT with three state-of-the-art LSMOAs, i.e. MOEA/DVA, LSMOF, and DGEA, on UF benchmarks, WFG benchmarks, and LSMOP benchmarks, respectively. The statistical IGD results achieved by the four compared algorithms are shown in Tables 3 to 5.

Table 3. IGD values of the four compared algorithms on UF benchmarks, where the best results on each test instance is highlighted.

Problem	M	D	MOEADVA	LSMOF	DGEA	CSDT
UF1	2	200	9.9828e−3 (2.90e−4) +	1.2683e−1 (2.83e−2) −	1.8754e−1 (4.30e−2) −	7.4842e−2 (5.03e−3)
		500	3.3985e−1 (1.28e−2) −	1.3284e−1 (2.79e−2) −	3.3438e−1 (5.72e−2) −	7.7010e−2 (3.33e−3)
		1000	8.9887e−1 (1.99e−2) −	1.3415e−1 (2.02e−2) −	2.9859e−1 (3.71e−2) −	7.7802e−2 (1.32e−3)
UF2	2	200	6.3946e−3 (1.34e−4) +	7.6070e−2 (2.34e−3) −	1.2792e−1 (2.08e−2) −	7.0063e−2 (9.66e−4)
		500	1.8019e−1 (3.28e−3) −	8.3138e−2 (1.60e−3) −	2.2520e−1 (1.26e−2) −	7.1027e−2 (6.60e−4)
		1000	4.2745e−1 (4.44e−3) −	9.0002e−2 (1.18e−3) −	2.5100e−1 (9.66e−3) −	7.0708e−2 (3.90e−4)
UF3	2	200	4.7698e−2 (1.28e−3) +	1.0472e−1 (8.77e−3) −	9.0786e−2 (3.56e−3) −	5.6395e−2 (1.68e−3)
		500	2.5532e−1 (5.16e−3) −	1.0546e−1 (9.67e−3) −	1.1492e−1 (1.36e−3) −	3.1655e−2 (7.74e−4)
		1000	5.2951e−1 (2.91e−3) −	1.1977e−1 (5.35e−3) −	1.1962e−1 (1.95e−3) −	2.2863e−2 (1.02e−3)
UF4	2	200	3.7175e−2 (1.17e−4) +	5.6342e−2 (1.35e−3) −	9.0786e−2 (4.32e−3) −	4.9435e−2 (3.36e−3)
		500	9.6900e−2 (2.23e−4) −	6.0542e−2 (6.58e−4) −	9.4807e−2 (3.37e−4) −	4.9618e−2 (3.75e−3)
		1000	1.4482e−1 (6.32e−4) −	7.2746e−2 (2.13e−3) −	1.3487e−1 (9.41e−4) −	4.9576e−2 (3.48e−3)
UF5	2	200	4.8141e−1 (1.59e−2) +	4.4337e−1 (2.33e−2) +	2.5820e+0 (8.44e−2) −	1.0589e+0 (2.72e−1)
		500	2.4084e+0 (3.55e−2) −	6.9006e−1 (6.72e−2) +	2.6899e+0 (3.60e−2) −	1.7667e+0 (3.37e−1)
		1000	4.1068e+0 (5.84e−2) −	1.0427e+0 (2.38e−1) +	2.2941e+0 (6.72e−2) −	1.9815e+0 (7.69e−2)
UF6	2	200	8.4327e−2 (1.39e−3) +	4.1885e−1 (1.38e−1) −	5.2626e−1(3.04e−1) −	2.4402e−1 (6.24e−2)
		500	1.3974e+0 (3.83e−2) −	4.4945e−1 (1.23e−1) −	5.2552e−1 (1.42e−1) −	2.8254e−1 (3.24e−2)
		1000	3.6389e+0 (7.33e−2) −	5.2582e−1 (1.14e−1) −	8.4044e−1 (1.33e−1) −	2.9232e−1 (5.82e−2)
UF7	2	200	6.3345e−2 (8.20e−4) =	3.6492e−1 (3.02e−3) −	1.1063e−1 (6.68e−2) −	6.2972e−2 (2.04e−3)
		500	3.9498e−1 (1.80e−2) −	3.7062e−1 (6.54e−3) −	5.8073e−1 (5.81e−2) −	1.0876e−1 (1.05e−1)
		1000	9.5711e−1 (1.60e−2) −	3.1239e−1 (1.28e−1) −	5.8568e−1 (1.98e−2) −	7.4906e−2 (1.93e−3)
UF8	3	200	2.4732e−1 (1.31e−1) =	3.0261e−1 (1.92e−2) −	4.3226e−1 (1.43e−2) −	2.1050e−1 (1.55e−2)
		500	8.0745e−1 (9.20e−3) −	4.4849e−1 (1.74e−2) −	6.9041e−1 (1.25e−2) −	1.9821e−1 (6.06e−3)
		1000	1.8183e+0 (5.56e−2) −	5.0657e−1 (1.45e−2) −	8.1552e−1 (3.93e−2) −	1.9875e−1 (8.09e−3)
UF9	3	200	1.7071e−1 (1.91e−1) +	4.9639e−1 (2.38e−3) −	6.3310e−1 (1.27e−2) −	4.7694e−1 (2.22e−3)
		500	8.8701e−1 (3.95e−2) −	5.1812e−1 (3.32e−3) −	7.9425e−1 (1.09e−2) −	4.8966e−1 (1.86e−3)
		1000	2.0072e+0 (4.67e−2) −	5.4671e−1 (4.36e−3) −	1.4159e+0 (5.73e−2) −	4.9617e−1 (7.36e−4)
UF10	3	200	8.7711e−1 (2.60e−2) +	4.8454e−1 (2.78e−3) +	3.5172e+0 (4.09e−1) −	2.7055e+0 (3.95e−1)
		500	5.5328e+0 (1.75e−1) −	6.3285e−1 (1.11e−1) +	6.0811e+0 (3.29e−1) −	3.4126e+0 (3.18e−1)
		1000	1.0469e+1 (1.80e−1) −	8.8025e−1 (2.20e−1) +	5.9670e+0 (2.37e−1) −	3.0837e+0 (4.54e−1)
$+/-/=$			8/20/2	6/24/0	0/30/0

Table 4. IGD values of the four compared algorithms on WFG benchmarks, where the best results on each test instance is highlighted.

Problem	M	D	MOEA/DVA	LSMOF	DGEA	CSDT
WFG1	2	200	2.2501e+0 (3.79e−3) −	8.8728e−1 (4.26e−2) +	1.2957e+0 (3.48e−3) −	1.0959e+0 (7.60e−2)
		500	2.2779e+0 (4.03e−3) −	1.2615e+0 (2.17e−2) −	1.3175e+0 (3.38e−3) −	1.1631e+0 (2.60e−2)
		1000	2.2769e+0 (4.66e−3) −	1.2823e+0 (4.17e−3) −	1.3133e+0 (4.57e−3) −	1.1603e+0 (1.45e−2)
	3	200	2.6357e+0 (1.08e−2) −	1.5266e+0 (7.90e−3) −	1.5294e+0 (5.62e−3) −	1.2414e+0 (2.58e−1)
		500	2.6777e+0 (9.57e−3) −	1.5378e+0 (5.33e−3) −	1.5414e+0 (4.23e−3) −	1.4130e+0 (1.58e−1)
		1000	2.6814e+0 (7.14e−3) −	1.5457e+0 (2.41e−2) =	1.5345e+0 (4.82e−3) =	1.5213e+0 (5.82e−2)
WFG2	2	200	8.2589e−1 (1.04e−2) −	4.0004e−1 (2.50e−2) −	3.6063e−1 (2.08e−2) −	1.4531e−2 (7.31e−4)
		500	1.3125e+0 (1.60e−1) −	4.3075e−1 (1.75e−3) −	4.4757e−1 (2.27e−2) −	3.4904e−2 (1.30e−3)
		1000	1.2611e+0 (1.66e−1) −	4.3725e−1 (1.46e−3) −	4.8432e−1 (2.15e−2) −	7.7117e−2 (1.20e−3)
	3	200	1.5898e+0 (1.05e−2) −	5.9697e−1 (1.78e−1) −	8.0009e−1 (2.57e−1) −	2.1629e−1 (9.98e−3)
		500	1.8796e+0 (1.14e−1) −	7.0804e−1 (7.66e−2) −	1.0183e+0 (2.28e−1) −	5.9806e−1 (1.06e−1)
		1000	1.8942e+0 (6.91e−2) −	6.9805e−1 (1.03e−1) =	1.0019e+0 (2.54e−1) −	6.1863e−1 (3.86e−2)
WFG3	2	200	8.2383e−1 (3.08e−2) −	2.4716e−1 (2.79e−2) −	2.1749e−1 (2.44e−2) −	1.6374e−2 (7.21e−4)
		500	9.9047e−1 (3.13e−2) −	2.5473e−1 (4.02e−2) −	3.3174e−1 (1.58e−2) −	3.8905e−2 (3.10e−3)
		1000	1.0538e+0 (2.93e−2) −	2.6597e−1 (3.58e−2) −	3.3859e−1 (2.82e−2) −	8.2011e−2 (5.11e−4)
	3	200	1.0463e+0 (7.24e−2) −	2.3014e−1 (1.50e−2) −	6.7253e−1 (7.31e−2) −	7.2270e−2 (9.51e−3)
		500	1.2360e+0 (5.79e−2) −	2.4850e−1 (2.08e−2) −	7.2975e−1 (2.71e−2) −	7.6111e−2 (3.59e−3)
		1000	1.3331e+0 (2.69e−2) −	2.5900e−1 (2.14e−2) −	8.1800e−1 (5.76e−2) −	1.2435e−1 (2.59e−3)
WFG4	2	200	1.1764e+0 (2.43e−2) −	4.2930e−2 (4.05e−3) −	3.5013e−1 (2.67e−2) −	2.0659e−2 (3.18e−3)
		500	1.2586e+0 (4.40e−2) −	4.6815e−2 (8.04e−3) =	4.5532e−1 (1.27e−2) −	5.1119e−2 (2.48e−3)
		1000	1.3250e+0 (2.56e−2) −	4.3178e−2 (6.43e−3) +	4.6767e−1 (2.99e−2) −	1.1246e−1 (1.23e−2)
	3	200	2.3653e+0 (7.52e−2) −	4.8207e−1 (3.29e−2) −	1.2016e+0 (3.30e−2) −	2.9866e−1 (6.47e−3)
		500	2.5104e+0 (3.53e−2) −	6.1514e−1 (3.20e−2) =	1.2256e+0 (3.53e−2) −	6.7172e−1 (1.13e−1)
		1000	2.5340e+0 (4.72e−2) −	6.6200e−1 (3.71e−2) +	1.1122e+0 (6.12e−2) −	7.4869e−1 (7.40e−2)
WFG5	2	200	1.0515e+0 (4.55e−2) −	3.4414e−2 (2.41e−2) +	4.0990e−1 (2.53e−2) −	6.8751e−2 (6.54e−3)
		500	1.1882e+0 (3.74e−2) −	7.1574e−2 (3.20e−2) =	5.3976e−1 (2.48e−2) −	8.6547e−2 (3.51e−3)
		1000	1.2803e+0 (2.58e−2) −	1.1795e−1 (4.71e−2) =	5.5739e−1 (2.34e−2) −	1.2436e−1 (5.00e−3)
	3	200	1.9188e+0 (3.96e−2) −	6.3378e−1 (1.18e−1) −	1.3446e+0 (4.50e−2) −	2.7680e−1 (1.18e−2)
		500	2.0786e+0 (2.64e−2) −	7.8067e−1 (5.07e−2) −	1.3584e+0 (3.89e−2) −	7.0279e−1 (7.87e−2)
		1000	2.1376e+0 (6.82e−2) −	7.6626e−1 (7.80e−2) =	1.3498e+0 (4.94e−2) −	7.6100e−1 (6.15e−2)
WFG6	2	200	1.0987e+0 (4.58e−2) −	8.4879e−2 (3.68e−2) −	2.4663e−2 (3.60e−3) −	1.7027e−2 (7.53e−4)
		500	1.2154e+0 (2.50e−2) −	9.5527e−2 (6.74e−2) −	2.6106e−2 (3.65e−3) −	1.9832e−2 (1.03e−3)
		1000	1.3227e+0 (2.23e−2) −	8.5541e−2 (6.42e−2) −	2.6313e−2 (2.34e−3) −	2.3875e−2 (2.35e−3)
	3	200	1.6614e+0 (7.96e−2) −	3.0145e−1 (1.85e−2) −	3.3108e−1 (4.91e−3) −	2.5989e−1 (7.72e−3)
		500	1.7842e+0 (5.12e−2) −	3.2480e−1 (2.47e−2) +	2.8383e−1 (1.62e−2) −	3.8359e−1 (6.35e−2)
		1000	1.9008e+0 (2.53e−2) −	3.1286e−1 (1.27e−2) +	5.3253e−1 (6.00e−3) −	4.4647e−1 (5.67e−2)
WFG7	2	200	1.0654e+0 (3.28e−2) −	1.5083e−1 (1.00e−2) −	5.3780e−1(2.23e−2) −	1.7454e−2 (1.16e−3)
		500	1.2868e+0 (2.30e−2) −	2.0738e−1 (1.14e−2) −	6.1372e−1 (2.45e−2) −	4.2665e−2 (2.67e−3)
		1000	1.3108e+0 (2.11e−2) −	2.0810e−1 (7.62e−3) −	6.4470e−1 (2.44e−2) −	1.0762e−1 (6.12e−3)
	3	200	2.1538e+0 (4.36e−2) −	6.7725e−1 (2.61e−2) −	1.0422e+0 (4.86e−2) −	2.8698e−1 (1.83e−2)
		500	2.3162e+0 (6.20e−2) −	9.3412e−1 (2.88e−2) −	1.1549e+0 (3.91e−2) −	6.2679e−1 (1.06e−1)
		1000	2.3132e+0 (6.97e−2) −	9.7350e−1 (2.79e−2) −	1.1047e+0 (2.31e−2) −	6.5700e−1 (1.14e−1)
WFG8	2	200	1.1632e+0 (2.86e−2) −	4.1219e−1 (3.54e−3) −	3.7513e−1 (1.93e−2) −	8.3834e−2 (9.10e−2)
		500	1.1898e+0 (2.49e−2) −	4.3161e−1 (4.46e−3) −	3.9365e−1 (1.96e−3) −	2.2625e−1 (3.97e−3)
		1000	1.2775e+0 (2.82e−2) −	4.3636e−1 (4.79e−3) −	4.3873e−1 (2.22e−3) −	2.4105e−1 (7.20e−3)
	3	200	2.0221e+0 (4.17e−2) −	1.0253e+0 (7.55e−2) −	9.4654e−1 (3.76e−2) −	5.6794e−1 (1.31e−1)
		500	2.0806e+0 (6.70e−2) −	1.0749e+0 (5.79e−2) −	1.0969e+0 (5.46e−2) −	7.2636e−1 (8.05e−2)
		1000	2.1714e+0 (4.60e−2) −	1.0689e+0 (6.22e−2) −	1.2010e+0 (5.19e−2) −	8.0742e−1 (4.95e−2)
WFG9	2	200	1.2065e+0 (5.13e−2) −	8.7535e−2 (4.02e−2) −	1.7681e−1 (6.81e−2) −	3.2151e−2 (1.11e−3)
		500	1.5245e+0 (3.32e−2) −	2.7761e−2 (1.10e−2) +	1.1581e−1 (3.27e−2) −	4.5652e−2 (4.16e−3)
		1000	1.5176e+0 (5.20e−2) −	3.2543e−2 (1.90e−2) +	1.2942e−1(2.09e−2) −	5.1195e−2 (6.41e−3)
	3	200	2.2188e+0 (5.16e−2) −	5.3562e−1 (5.65e−2) −	4.7132e−1 (2.11e−2) −	3.4775e−1 (1.37e−2)
		500	2.2080e+0 (3.74e−2) −	3.3183e−1 (7.32e−2) +	5.3799e−1 (1.43e−2) −	4.0078e−1 (3.72e−2)
		1000	2.2216e+0 (2.74e−2) −	5.3243e−1 (1.24e−1) =	6.9980e−1 (2.78e−2) −	4.3676e−1 (2.14e−2)
$+/-/=$			0/54/0	9/37/8	0/53/1

Table 5. IGD values of the four compared algorithms on LSMOP benchmarks, where the best results on each test instance is highlighted.

Problem	M	D	MOEADVA	LSMOF	DGEA	CSDT
LSMOP1	2	200	5.3801e−2 (2.59e−3) −	5.0688e−1 (3.56e−2) −	1.6053e−1 (6.08e−2) −	2.2902e−2 (2.33e−3)
		500	1.4839e+0 (1.14e−1) −	6.0736e−1 (3.84e−2) −	2.9286e−1 (3.48e−2) −	5.6057e−2 (2.85e−3)
		1000	4.4844e+0 (2.78e−1) −	6.2783e−1 (2.68e−2) −	3.0144e−1 (2.11e−2) −	7.3401e−2 (3.21e−3)
	3	200	8.4163e−2 (4.04e−3) +	2.2067e−1 (1.47e−3) −	5.2965e−1 (6.88e−2) −	1.6380e−1 (1.18e−2)
		500	1.2802e+0 (1.05e−1) −	2.4629e−1 (4.01e−3) −	7.8063e−1 (3.95e−2) −	1.7863e−1 (1.75e−2)
		1000	4.2683e+0 (1.78e−1) −	4.7945e−1 (7.08e−3) −	4.7697e−1 (4.41e−2) −	1.8539e−1 (1.72e−2)
LSMOP2	2	200	1.3681e−1 (7.95e−4) −	3.6890e−2 (3.68e−3) −	2.1152e−2 (5.53e−4) −	1.0698e−2 (3.65e−4)
		500	6.8352e−2 (3.25e−4) −	2.4541e−2 (1.58e−3) −	1.3231e−2 (2.14e−4) −	8.7229e−3 (3.10e−4)
		1000	3.9643e−2 (2.66e−4) −	1.9070e−2 (3.24e−4) −	9.1426e−3 (3.39e−4) −	7.3567e−3 (2.80e−4)
	3	200	1.0845e−1 (2.18e−3) −	1.4564e−1 (4.16e−3) −	7.1169e−2 (3.27e−3) −	8.8311e−2 (5.55e−3)
		500	7.9438e−2 (5.68e−3) −	9.1579e−2 (8.69e−3) −	4.7343e−2 (3.27e−3) −	6.3588e−2 (1.49e−3)
		1000	6.6026e−2 (2.29e−3) −	7.2640e−2 (5.29e−3) −	4.3112e−2 (3.35e−3) −	5.6226e−2 (1.82e−3)
LSMOP3	2	200	2.6061e+0 (8.13e−1) −	7.0537e−1 (2.04e−2) +	1.3259e+0 (8.23e−2) −	1.0377e+0 (2.66e−1)
		500	1.9483e+2 (2.11e+2) −	1.5605e+0 (6.78e−4) −	1.5671e+0 (7.04e−2) −	1.1774e+0 (2.78e−1)
		1000	5.1022e+2 (6.21e+2) −	1.5725e+0 (6.97e−4) −	9.4512e−1 (1.12e−2) +	1.1852e+0 (2.09e−1)
	3	200	1.6138e+0 (2.99e−1) −	4.2256e−1 (4.97e−2) +	8.1206e−1 (3.31e−2) +	8.6050e−1 (6.98e−4)
		500	6.3833e+1 (4.07e+1) −	6.5824e−1 (2.64e−2) +	8.5267e−1 (2.63e−2) =	8.6072e−1 (0.00e+0)
		1000	1.7427e+2 (1.28e+2) −	8.0530e−1 (2.17e−2) +	8.4572e−1 (6.17e−2) =	8.6072e−1 (0.00e+0)
LSMOP4	2	200	7.1392e−2 (4.86e−3) −	9.7128e−2 (7.78e−3) −	4.0406e−2 (2.07e−3) −	2.3212e−2 (6.24e−3)
		500	6.8616e−2 (5.99e−4) −	5.8837e−2 (5.62e−3) −	5.5264e−2 (7.59e−4) −	3.4079e−2 (8.73e−4)
		1000	5.8330e−2 (4.15e−4) −	4.0332e−2 (2.47e−3) −	3.8278e−2 (2.13e−4) −	1.9888e−2 (5.67e−4)
	3	200	1.3182e−1 (4.57e−3) +	2.7696e−1 (8.99e−3) −	2.1121e−1 (1.13e−2) =	2.1289e−1 (1.36e−2)
		500	1.3264e−1 (3.98e−3) =	2.2720e−1 (5.16e−3) −	1.0513e−1 (4.80e−3) +	1.3250e−1 (1.27e−2)
		1000	1.1292e−1 (5.46e−3) −	1.4543e−1 (3.57e−3) −	6.7158e−2 (9.66e−4) +	8.5539e−2 (3.66e−3)
LSMOP5	2	200	1.1954e−1 (6.23e−3) −	7.4209e−1 (1.17e−16) −	7.5342e−2 (1.05e−3) −	2.7665e−2 (2.51e−3)
		500	4.4253e+0 (1.82e−1) −	7.4209e−1 (1.17e−16) −	7.4209e−1 (4.52e−2) −	1.0381e−1 (8.32e−3)
		1000	1.0411e+1 (2.70e−1) −	7.4209e−1 (1.17e−16) −	2.3607e+1 (6.72e−1) −	1.4909e−1 (1.08e−2)
	3	200	1.7116e−1 (8.06e−3) +	4.8166e−1 (4.06e−2) −	3.2572e−1 (3.44e−2) −	2.5159e−1 (6.64e−2)
		500	3.1025e+0 (1.68e−1) −	5.2491e−1 (1.97e−2) −	5.1637e−1 (3.26e−2) −	3.4096e−1 (1.07e−1)
		1000	7.8202e+0 (3.58e−1) −	5.3932e−1 (3.00e−3) −	5.2150e−1 (4.79e−2) −	2.8122e−1 (6.43e−2)
LSMOP6	2	200	8.6475e−1 (1.30e−1) −	3.5736e−1 (3.78e−3) −	3.2919e−1 (1.47e−2) −	6.7471e−2 (1.81e−2)
		500	2.2045e+2 (3.17e+2) −	3.1988e−1 (6.14e−4) −	1.9955e−1 (2.26e−2) −	1.0902e−1 (1.42e−2)
		1000	1.0130e+3 (1.08e+3) −	3.1228e−1 (4.25e−4) −	2.3386e−1 (1.67e−2) −	1.2645e−1 (8.82e−3)
	3	200	1.3213e+1 (3.54e+0) −	8.8794e−1 (2.62e−1) =	1.3086e+0 (2.37e−2) −	8.1500e−1 (7.46e−2)
		500	2.0768e+3 (3.07e+2) −	6.8256e−1 (2.72e−2) +	5.4954e−1 (3.65e−2) +	8.7344e−1 (9.43e−2)
		1000	1.1563e+4 (2.25e+3) −	7.2286e−1 (2.48e−2) =	7.3309e−1 (6.02e−2) =	7.9534e−1 (8.19e−2)
LSMOP7	2	200	1.4658e+1 (4.21e+0) −	1.3123e+0 (1.40e−1) =	8.5414e+0 (6.83e−1) −	1.3772e+0 (2.90e−2)
		500	5.9572e+3 (7.31e+2) −	1.4976e+0 (2.13e−3) −	1.5089e+0 (3.08e−2) −	1.3677e+0 (1.23e−1)
		1000	2.6284e+4 (1.13e+3) −	1.5078e+0 (7.65e−4) =	1.5120e+0 (2.88e−2) −	1.3354e+0 (1.53e−1)
	3	200	2.0135e+0 (1.19e+0) −	9.4448e−1 (3.49e−2) =	9.4744e−1 (2.04e−2) =	9.1610e−1 (1.13e−2)
		500	3.1789e+2 (2.11e+2) −	8.8777e−1 (9.56e−3) −	9.5900e−1 (2.35e−2) −	8.6732e−1 (1.54e−3)
		1000	6.7820e+2 (5.25e+2) −	8.6292e−1 (2.44e−3) −	8.0658e−1 (2.37e−2) −	7.1780e−1 (1.38e−1)
LSMOP8	2	200	8.9179e−2 (4.49e−3) −	7.4209e−1 (1.17e−16) −	7.9941e−2 (1.06e−3) −	5.0500e−2 (1.47e−2)
		500	4.0392e+0 (1.63e−1) −	7.4209e−1 (1.17e−16) −	3.5025e−1 (3.44e−2) −	8.3393e−2 (3.32e−3)
		1000	8.7524e+0 (4.02e−1) −	7.4209e−1 (1.18e−16) −	7.4209e−1 (2.75e−2) −	1.2911e−1 (6.53e−3)
	3	200	1.1233e−1 (5.20e−3) =	3.5386e−1 (2.16e−2) −	2.3044e−1 (2.52e−2) −	1.1418e−1 (1.23e−2)
		500	6.0174e−1 (2.58e−2) −	3.4818e−1 (2.05e−2) −	1.4534e−1 (1.40e−2) −	9.3786e−2 (3.13e−3)
		1000	6.5376e−1 (6.68e−2) −	3.2810e−1 (3.85e−2) −	1.2787e−1 (1.41e−2) −	8.7762e−2 (2.81e−3)
LSMOP9	2	200	1.8349e−1 (1.42e−2) +	8.1004e−1 (1.17e−16) =	4.9898e−1 (2.61e−2) −	8.1004e−1 (1.17e−16)
		500	5.3545e+0 (6.04e−1) −	8.0886e−1 (1.89e−4) =	4.6338e−1 (1.70e−3) +	8.0880e−1 (2.32e−3)
		1000	2.2439e+1 (1.23e+0) −	8.0675e−1 (2.94e−4) −	1.3776e+0 (2.16e−1) −	7.2462e−1 (1.24e−1)
	3	200	3.9642e−1 (3.01e−2) +	1.5379e+0 (2.34e−16) −	9.9704e−1 (8.54e−2) +	1.3636e+0 (3.17e−1)
		500	1.1972e+1 (1.20e+0) −	1.4594e+0 (1.66e−1) =	1.7182e+0 (2.37e−1) −	1.2691e+0 (2.94e−2)
		1000	5.0059e+1 (2.62e+0) −	1.1450e+0 (6.54e−5) −	9.0215e+0 (5.21e−1) −	7.3466e−1 (2.43e−1)
$+/-/=$			5/47/2	5/41/8	7/42/5

From Table 3, we can find that our proposed CSDT obtains 18 best results, MOEA/DVA obtains 6 best results, and LSMOF obtains 6 best results on 30 UF instances. Specifically, CSDT outperforms MOEA/DVA with 20 wins, 8 loses, and 2 ties. It performs significantly better than LSMOF on all instances except UF5 and UF10. And on all instances, the performance of CSDT is statistically better than that of DGEA.

On 54 WFG instances, it can be seen from Table 4 that our proposed CSDT obtains 45 best results and LSMOF obtains 13 best results. To be specific, CSDT outperforms MOEA/DVA and DGEA on all WFG test instances. CSDT performs statistically better than LSMOF on 37 instances and performs worse on 9 instances. It performs very well on almost all test instances of WFG2, WFG3, WFG7, and WFG8. On bi-objective WFG6, tri-objective WFG5, and most instances of WFG1, CSDT also has a good performance.

From Table 5, we can see that among the four compared algorithms, CSDT obtains 37 best results, MOEA/DVA obtains 6 best results, LSMOF obtains 6 best results, and DGEA obtains 5 best results on 54 LSMOP instances. Specifically, CSDT outperforms MOEA/DVA with 47 wins, 5 loses, and 2 ties. It performs significantly better than LSMOF on 41 instances and performs worse on 5 instances. Compared to LSMOF, it finds better solutions for all the instances of LSMOP1, LSMOP2, LSMOP4, LSMOP5, LSMOP8, and bi-objective LSMOP6. As for DGEA, CSDT outperforms it with 42 wins, 7 loses, and 5 ties.

Overall, CSDT is the best one among the four compared algorithms for solving LSMOPs. The poor performance of MOEA/DVA may be due to the numerous FEs consumption on decision variable correlation analysis which is not required in CSDT. The sub-problems obtained by grouping variables cannot be fully optimised, thus failing to find better solutions. DGEA needs to search the entire decision variable space of LSMOPs in the optimisation process, which makes it not easy to find optimal solutions quickly. Whereas in CSDT, we only need to search along several potential straight lines in the first stage, which significantly accelerates the population convergence. Therefore, the optimisation efficiency of CSDT is much higher than that of DGEA. As for LSMOF, it narrows the entire search space into several straight lines, which accelerates the convergence of the algorithm significantly. However, the search space is too small compared to the whole decision search space, which may lose the population diversity and make the algorithm fall into local minima. CSDT pays attention to ensuring the diversity of the population when reducing the search space. It searches in more areas with convergence and diversity potential, which can enhance the diversity of the obtained offspring while ensuring their convergence, thereby finding better optimal solutions than LSMOF.

To more intuitively illustrate the effectiveness of CSDT, we give the variations of IGD curves got by MOEA/DVA, LSMOF, DGEA, and CSDT on 500-dimensional bi-objective UF2, WFG2, LSMOP2, and 1000-dimensional tri-objective UF8, WFG8, LSMOP8 in Figure 4. In Figure 4, the horizontal axis represents the number of FEs and the vertical axis denotes the IGD values obtained by the algorithms. These curves can reflect the search performance of the compared algorithms with the evolution. As can be observed, the convergence curve of CSDT can quickly reach smaller IGD values than the other three compared algorithms on these six instances. In the first stage of CSDT, i.e. before 250,000 FEs, the curves converging quickly to a small value without stagnation indicates that our proposed strategies can provide more potential search range to avoid the algorithm falling into the local optimal solutions and accelerate the convergence of the algorithm.

Figure 4. The variations of IGD values obtained by the four compared algorithms on UF2, UF8, WFG2, WFG8, LSMOP2, and LSMOP8. (a) UF2. (b) WFG2. (c) LSMOP2. (d) UF8. (e) WFG8 and (f) LSMOP8.

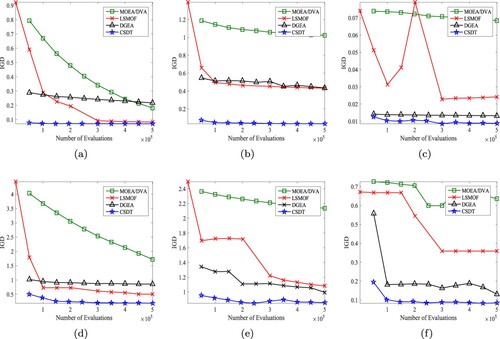
Based on the above results and analysis, it can be seen that our proposed CSDT is effective, and its comprehensive performance is more competitive than the state-of-the-art algorithms for solving LSMOPs.

4.4. Parameter sensitivity analysis

To analyse the effect of the number of reference vectors m, in this section, we conduct a parameter sensitivity analysis experiment on UF and WFG benchmarks. The values of m are set to 4, 10, 20, and 50, respectively. The experimental results are displayed in Tables 6 and 7.

Table 6. IGD values of CSDT with different values of m on UF benchmarks, where the best results on each test instance is highlighted.

Problem	M	D	m = 4	m = 20	m = 50	m = 10
UF1	2	200	8.7557e−2 (9.27e−3) −	7.8246e−2 (7.59e−3) =	9.0288e−2 (7.28e−3) −	7.4842e−2 (5.03e−3)
		500	8.9311e−2 (1.24e−2) −	7.9024e−2 (2.95e−3) =	8.6199e−2 (3.95e−3) −	7.6796e−2 (3.21e−3)
		1000	8.8677e−2 (7.79e−3) −	7.7212e−2 (1.82e−3) =	8.2566e−2 (3.23e−3) −	7.7464e−2 (1.90e−3)
UF2	2	200	8.2020e−2 (3.23e−3) −	6.9648e−2 (1.08e−3) =	7.3537e−2 (1.81e−3) −	7.0063e−2 (9.66e−4)
		500	8.6486e−2 (3.92e−3) −	7.1369e−2 (8.39e−4) =	7.4852e−2 (1.21e−3) −	7.0944e−2 (6.75e−4)
		1000	8.4264e−2 (4.87e−3) −	7.1424e−2 (6.24e−4) =	7.4663e−2 (1.41e−3) −	7.1013e−2 (4.17e−4)
UF3	2	200	5.9470e−2 (1.62e−3) −	5.6645e−2 (2.10e−3) =	5.8356e−2 (2.42e−3) =	5.6395e−2 (1.68e−3)
		500	3.7296e−2 (2.42e−3) −	3.1255e−2 (6.05e−4) =	3.1807e−2 (7.78e−4) =	3.1558e−2 (7.15e−4)
		1000	2.8868e−2 (2.18e−3) −	2.2376e−2 (6.26e−4) =	2.2352e−2 (1.20e−3) =	2.2590e−2 (9.47e−4)
UF4	2	200	7.9404e−2 (1.11e−2) −	5.2671e−2 (5.23e−3) =	5.9832e−2 (1.78e−3) −	4.9435e−2 (3.36e−3)
		500	7.6056e−2 (1.10e−2) −	5.3901e−2 (5.45e−3) =	6.2374e−2 (5.51e−3) −	4.9321e−2 (3.39e−3)
		1000	7.6191e−2 (1.39e−2) −	5.1841e−2 (5.15e−3) =	6.0703e−2 (2.53e−3) −	4.9657e−2 (3.20e−3)
UF5	2	200	8.2115e−1 (1.86e−1) +	1.3199e+0 (2.52e−1) =	1.3357e+0 (3.97e−1) =	1.0589e+0 (2.72e−1)
		500	9.5889e−1 (4.13e−1) +	1.7630e+0 (3.55e−1) =	1.8813e+0 (1.00e−1) =	1.7622e+0 (3.01e−1)
		1000	1.5073e+0 (4.74e−1) +	1.9460e+0 (9.23e−2) =	2.0372e+0 (1.11e−1) =	1.9942e+0 (8.28e−2)
UF6	2	200	3.0758e−1 (1.48e−1) =	2.5758e−1 (8.06e−2) =	2.7778e−1 (6.02e−2) =	2.4402e−1 (6.24e−2)
		500	4.0797e−1 (1.12e−1) −	2.7227e−1 (5.80e−2) =	2.9754e−1 (2.71e−2) =	2.8993e−1 (3.25e−2)
		1000	3.9124e−1 (7.62e−2) −	2.9229e−1 (2.89e−2) =	3.3407e−1 (1.44e−2) −	2.9538e−1 (5.57e−2)
UF7	2	200	5.1009e−2 (4.91e−3) +	8.7403e−2 (8.63e−2) =	8.8693e−2 (8.40e−2) =	6.2972e−2 (2.04e−3)
		500	7.8643e−2 (3.95e−3) +	7.3238e−2 (9.93e−4) =	7.8154e−2 (4.00e−3) +	1.0118e−1 (9.36e−2)
		1000	1.1131e−1 (8.92e−2) −	7.5481e−2 (1.60e−3) =	8.4685e−2 (7.49e−3) −	7.4834e−2 (1.84e−3)
UF8	3	200	3.3101e−1 (6.79e−2) −	2.1974e−1 (2.06e−2) =	3.1528e−1 (4.15e−2) −	2.1050e−1 (1.55e−2)
		500	3.4925e−1 (8.49e−2) −	2.4097e−1 (3.62e−2) −	3.6342e−1 (2.13e−2) −	1.9821e−1 (6.06e−3)
		1000	3.7321e−1 (8.69e−2) −	2.3192e−1 (3.13e−2) −	3.8665e−1 (4.56e−2) −	1.9857e−1 (7.65e−3)
UF9	3	200	4.8620e−1 (3.18e−2) =	4.6922e−1 (3.00e−2) =	5.0123e−1 (1.88e−2) −	4.7694e−1 (2.22e−3)
		500	5.3291e−1 (1.37e−2) −	4.9131e−1 (1.28e−3) −	5.3261e−1 (2.91e−2) −	4.8966e−1 (1.86e−3)
		1000	5.3360e−1 (1.61e−2) −	4.9696e−1 (1.21e−3) =	5.6514e−1 (6.16e−2) −	4.9616e−1 (6.94e−4)
UF10	3	200	3.1065e+0 (2.73e−1) −	2.7529e+0 (3.36e−1) =	3.1076e+0 (4.72e−1) =	2.7055e+0 (3.95e−1)
		500	3.5853e+0 (3.70e−1) =	3.4013e+0 (4.85e−1) =	3.9684e+0 (4.80e−1) −	3.4126e+0 (3.18e−1)
		1000	3.8565e+0 (1.99e−1) −	3.7233e+0 (4.30e−1) −	4.4752e+0 (2.90e−1) −	3.1526e+0 (4.80e−1)
$+/-/=$			5/22/3	0/4/26	1/19/10

Table 7. IGD values of CSDT with different values of m on WFG benchmarks, where the best results on each test instance is highlighted.

Problem	M	D	m = 4	m = 20	m = 50	m = 10
WFG1	2	200	1.2217e+0 (1.95e−2) −	1.1504e+0 (1.23e−1) −	1.2161e+0 (1.40e−2) −	1.0959e+0 (7.60e−2)
		500	1.2473e+0 (3.12e−3) −	1.1936e+0 (1.66e−2) −	1.2420e+0 (1.12e−2) −	1.1631e+0 (2.60e−2)
		1000	1.2535e+0 (3.94e−3) −	1.1923e+0 (4.15e−2) −	1.2466e+0 (1.33e−2) −	1.1594e+0 (1.51e−2)
	3	200	1.5435e+0 (1.99e−2) −	1.3391e+0 (2.20e−1) =	1.5367e+0 (2.05e−2) −	1.2414e+0 (2.58e−1)
		500	1.5216e+0 (1.09e−2) −	1.5035e+0 (8.27e−2) −	1.5274e+0 (1.08e−2) −	1.4068e+0 (1.66e−1)
		1000	1.5260e+0 (1.14e−2) =	1.5184e+0 (1.47e−2) =	1.5235e+0 (1.86e−2) =	1.5183e+0 (5.20e−2)
WFG2	2	200	1.5987e−1 (9.92e−2) −	1.4802e−2 (8.34e−4) =	8.4230e−2 (1.01e−1) −	1.4531e−2 (7.31e−4)
		500	1.3841e−1 (7.21e−2) −	3.5502e−2 (2.34e−3) =	8.8239e−2 (5.64e−2) −	3.4646e−2 (1.08e−3)
		1000	1.7356e−1 (5.46e−2) −	7.8678e−2 (2.43e−3) =	1.3504e−1 (6.54e−2) −	7.7021e−2 (1.23e−3)
	3	200	2.5747e−1 (1.01e−1) =	2.1694e−1 (8.04e−3) =	2.7658e−1 (1.26e−1) =	2.1629e−1 (9.98e−3)
		500	6.7725e−1 (9.92e−2) −	5.7966e−1 (7.63e−2) =	6.2020e−1 (8.12e−2) =	5.7849e−1 (9.14e−2)
		1000	6.8840e−1 (9.64e−2) −	6.7498e−1 (1.09e−1) =	6.2400e−1 (9.58e−2) =	6.2069e−1 (3.48e−2)
WFG3	2	200	4.7152e−2 (9.16e−3) −	1.6862e−2 (8.36e−4) =	2.4797e−2 (1.24e−2) −	1.6374e−2 (7.21e−4)
		500	1.1883e−1 (9.19e−3) −	4.1726e−2 (4.24e−3) −	6.9425e−2 (3.38e−2) −	3.8577e−2 (3.10e−3)
		1000	1.6231e−1 (8.13e−3) −	8.2609e−2 (8.47e−4) =	1.2018e−1 (4.06e−2) −	8.1958e−2 (5.12e−4)
	3	200	1.1704e−1 (2.01e−2) −	7.0053e−2 (1.92e−2) =	1.1462e−1 (2.14e−2) −	7.5048e−2 (1.26e−2)
		500	1.0158e−1 (1.12e−2) −	8.1257e−2 (5.40e−3) −	1.1123e−1 (1.70e−2) −	7.5481e−2 (3.17e−3)
		1000	1.5682e−1 (1.13e−2) −	1.2710e−1 (3.75e−3) −	1.5859e−1 (1.51e−2) −	1.2378e−1 (2.59e−3)
WFG4	2	200	5.9793e−2 (1.18e−2) −	2.4047e−2 (4.57e−3) −	4.1877e−2 (9.36e−3) −	2.0659e−2 (3.18e−3)
		500	1.1290e−1 (9.49e−3) −	6.4189e−2 (6.72e−3) −	1.0286e−1 (1.32e−2) −	5.1097e−2 (2.62e−3)
		1000	1.7391e−1 (7.33e−3) −	1.1499e−1 (1.65e−2) =	1.5922e−1 (7.29e−3) −	1.1328e−1 (1.27e−2)
	3	200	3.4209e−1 (1.61e−2) −	3.0469e−1 (1.27e−2) =	3.2150e−1 (7.73e−3) −	3.0051e−1 (8.45e−3)
		500	6.6557e−1 (1.16e−1) =	7.2461e−1 (9.58e−2) =	7.0631e−1 (8.68e−2) =	6.8156e−1 (1.15e−1)
		1000	7.2355e−1 (7.10e−2) =	7.0142e−1 (3.45e−2) =	7.1425e−1 (8.83e−2) =	7.4054e−1 (6.92e−2)
WFG5	2	200	8.0274e−2 (4.21e−3) −	7.2198e−2 (1.01e−3) −	8.4680e−2 (3.63e−3) −	6.8751e−2 (6.54e−3)
		500	1.0756e−1 (1.05e−2) −	8.8137e−2 (3.14e−3) =	1.1209e−1 (4.88e−3) −	8.6880e−2 (3.55e−3)
		1000	1.5723e−1 (1.34e−2) −	1.2605e−1 (5.05e−3) =	1.5277e−1 (1.09e−2) −	1.2471e−1 (5.18e−3)
	3	200	3.5023e−1 (4.72e−2) −	2.7092e−1 (1.04e−2) =	2.8272e−1 (9.91e−3) =	2.7590e−1 (1.15e−2)
		500	6.9786e−1 (5.91e−2) =	6.9058e−1 (3.36e−2) =	6.9980e−1 (4.29e−2) =	7.1161e−1 (7.80e−2)
		1000	7.5399e−1 (6.49e−2) =	7.4169e−1 (7.40e−2) =	7.8676e−1 (5.98e−2) =	7.4670e−1 (7.46e−2)
WFG6	2	200	1.9262e−2 (1.64e−3) −	1.7392e−2 (1.41e−3) =	3.0100e−2 (5.92e−3) −	1.7027e−2 (7.53e−4)
		500	2.2396e−2 (3.05e−3) =	2.0518e−2 (1.96e−3) =	2.0723e−2 (1.01e−3) =	1.9947e−2 (1.02e−3)
		1000	2.6018e−2 (4.09e−3) =	2.6281e−2 (6.61e−3) =	2.2355e−2 (4.19e−3) =	2.3463e−2 (2.08e−3)
	3	200	2.8449e−1 (2.76e−2) −	2.6617e−1 (1.94e−2) =	2.9882e−1 (1.55e−2) −	2.6113e−1 (8.28e−3)
		500	4.1514e−1 (9.44e−2) =	4.1422e−1 (6.64e−2) =	4.2373e−1 (7.83e−2) =	3.7151e−1 (5.38e−2)
		1000	4.8899e−1 (1.07e−1) =	4.3947e−1 (3.92e−2) =	4.5057e−1 (3.30e−2) =	4.3404e−1 (5.64e−2)
WFG7	2	200	1.0873e−1 (5.72e−2) −	1.7687e−2 (9.37e−4) =	2.0646e−2 (1.74e−3) −	1.7454e−2 (1.16e−3)
		500	1.1619e−1 (1.22e−2) −	4.6243e−2 (2.18e−3) −	5.5297e−2 (4.32e−3) −	4.2431e−2 (2.72e−3)
		1000	1.6539e−1 (6.10e−3) −	1.1075e−1 (7.04e−3) =	1.1782e−1 (6.01e−3) −	1.0778e−1 (6.47e−3)
	3	200	3.2676e−1 (1.67e−2) −	2.8545e−1 (1.60e−2) =	3.0058e−1 (1.85e−2) =	2.8635e−1 (1.74e−2)
		500	6.9197e−1 (1.57e−1) =	6.8778e−1 (1.40e−1) =	6.5362e−1 (9.56e−2) =	6.4184e−1 (9.99e−2)
		1000	6.8507e−1 (4.32e−2) =	7.0235e−1 (8.69e−2) =	7.4857e−1 (1.04e−1) =	6.5420e−1 (1.01e−1)
WFG8	2	200	2.5764e−1 (1.33e−1) −	1.8662e−1 (1.38e−1) =	2.4256e−1 (7.82e−2) −	8.3834e−2 (9.10e−2)
		500	2.6929e−1 (7.32e−3) −	2.4091e−1 (6.18e−3) −	2.6104e−1 (6.57e−3) −	2.2637e−1 (4.20e−3)
		1000	2.7989e−1 (9.78e−3) −	2.4226e−1 (6.85e−3) =	2.6747e−1 (7.17e−3) −	2.4133e−1 (7.58e−3)
	3	200	6.6088e−1 (3.25e−2) =	6.3172e−1 (1.84e−2) =	6.2452e−1 (1.81e−2) =	5.7951e−1 (1.29e−1)
		500	7.7821e−1 (9.03e−2) =	7.3589e−1 (4.49e−2) =	7.6648e−1 (7.11e−2) =	7.2217e−1 (8.42e−2)
		1000	8.6302e−1 (5.36e−2) =	8.0420e−1 (7.85e−2) =	8.7891e−1 (5.16e−2) −	8.1531e−1 (5.35e−2)
WFG9	2	200	4.4371e−2 (7.25e−3) −	3.2046e−2 (7.01e−4) =	4.0119e−2 (6.15e−3) −	3.2151e−2 (1.11e−3)
		500	5.2839e−2 (1.10e−2) =	5.1392e−2 (8.33e−3) =	9.1436e−2 (2.71e−2) −	4.5533e−2 (4.40e−3)
		1000	6.3430e−2 (1.05e−2) −	5.8789e−2 (9.46e−3) =	1.0134e−1 (2.36e−2) −	5.2405e−2 (5.45e−3)
	3	200	3.8642e−1 (3.87e−2) −	3.5143e−1 (2.27e−2) =	3.8441e−1 (3.07e−2) −	3.4472e−1 (1.61e−2)
		500	4.3016e−1 (3.31e−2) =	3.8774e−1 (1.97e−2) =	4.4794e−1 (3.97e−2) −	3.9575e−1 (3.56e−2)
		1000	4.4343e−1 (5.08e−2) =	4.2605e−1 (1.83e−2) =	5.1328e−1 (6.42e−2) −	4.3216e−1 (2.13e−2)
$+/-/=$			0/36/18	0/12/42	0/36/18

From Table 6, we can find that on 30 UF instances, the number of the best results obtained by CSDT with m = 4, 20, 50, and 10 is 4, 8, 1, and 17, respectively. When m = 10, the performance of CSDT is the best. CSDT with m = 20 performs better than that with m = 4 and 50, and performs slightly worse than that with m = 10. For convenience, we use CSDT-num to represent CSDT with m = num. When compared with CSDT-10, CSDT-4 performs significantly worse on 22 instances, CSDT-50 performs significantly worse on 19 instances, and CSDT-20 performs significantly worse on only 4 instances. The performance of CSDT-10 is comparable to that of CSDT-20 on 26/34 instances.

From Table 7, we can see that on 54 WFG instances, the number of the best results obtained by CSDT with m = 4, 20, 50, and 10 is 1, 10, 1, and 42, respectively. Similar to UF benchmarks, when m = 10, the performance of CSDT is also the best on WFG benchmarks. When compared with CSDT-10, both CSDT-4 and CSDT-50 perform statistically worse on 36 instances, and CSDT-20 performs significantly worse on 12 instances. Moreover, the performance of CSDT-10 is comparable to that of CSDT-20 on 42/54 instances.

Overall, we can conclude that when m takes a moderate value, such as $m=10$ or 20, the performance of CSDT is good. When m takes a relatively large value, such as m = 50, or a relatively small value, such as $m=4$, the performance of CSDT is not as good as that when m takes 10 or 20. When m is relatively large, the algorithm needs to optimise relatively more transformed problems in the first stage. Since the computing resources allocated to each stage are fixed, it will reduce the computing resources that can be allocated to each transformed problem, resulting in insufficient optimisation of each transformed problem. Therefore, the solutions found by the algorithm are relatively poor. However, when m is relatively small, the number of the transformed problems is relatively less. Although each transformed problem can be optimised sufficiently, the search range is relatively small than that when $m=10$ or 20.

5. Conclusion

In this paper, we present a new algorithm based on WOF for LSMOPs, named CSDT. To alleviate the limitations of WOF, in the first stage, we take the centreline symmetry points to replace half of the reference solutions chosen in WOF to transform the problem. It can avoid the search range of the transformed problem being concentrated in a small area of search space, thereby improving the search efficiency of the algorithm. Then, to enhance the diversity of the algorithm while ensuring its convergence, a double-line transformation function is designed to add more potential search areas. Subsequently, in the second stage, PSO is applied to search the whole space of the original problem to improve the diversity of CSDT. To investigate the effectiveness of the two strategies and the general performance of CSDT, we conducted numerical experiments on three widely used benchmark suites. The performance of CSDT is compared with that of the original WOF, MOEA/DVA, LSMOF, and DGEA. The statistical results indicate that CSDT significantly improves the performance of the WOF and outperforms the other four compared algorithms.

However, since our proposed algorithm pays more attention to diversity than WOF, its performance may be slightly inferior to WOF for problems that are difficult to obtain convergence solutions. Moreover, since our proposed algorithm is proposed based on WOF, its performance will be affected by the results of decision variable grouping. In the future, an important task for us is to study advanced multi-objective grouping techniques to reasonably group the decision variables of LSMOPs. Furthermore, finding potential areas and directions to guide the algorithm search is also an effective method that we need to study for solving LSMOPs.

We have to point out that there are many other kinds of computational intelligence algorithms applicable to the problems, e.g. the algorithms to mimic the behaviours of different animals (like monarch butterfly optimisation (MBO), earthworm optimisation algorithm (EWA), elephant herding optimisation (EHO)). Due to the page limits, we do not list these references.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work is supported by the National Natural Science Foundation of China (NO. 61872281).