Helix dynamics in a membrane transport protein: comparative simulations of the glycerol-3-phosphate transporter and its constituent helices

Abstract

The glycerol-3-phosphate transporter (GlpT) is a member of the major facilitator superfamily (MFS). GlpT is an organic phosphate/inorganic phosphate antiporter. It shares a similar fold with other MFS transporters (e.g. LacY and EmrD) consisting of 12 transmembrane (TM) helices which form two domains (each of six TM helices) surrounding a central ligand-binding cavity. The TM helices (especially the cavity-lining helices) contain a large number of proline and glycine residues, which may aid in the conformational changes believed to underline the transport mechanism. Molecular dynamics simulations in a phospholipid bilayer have been used to compare the conformational properties of the isolated TM helices with those in the intact GlpT protein. Analysis of these simulations focuses on the role of proline-induced flexibility in the TM helices. Our results are consistent with the proposed rocker switch mechanism for transport by GlpT. In particular, the simulations highlight the cavity-lining helices (H4, H5, H10 and H11) as being significantly flexible, suggesting that the transport mechanism may involve intra-helix motions in addition to pseudo-rigid body motions of the N- and C-terminal domains relative to one another.

• Transporter
• GlpT
• proline
• transmembrane helix
• molecular dynamics

Introduction

Membrane proteins are encoded by ca. 25% of all genes [1], [2] and have diverse key functional roles in cells, including transport of metabolites across cell membranes. It is estimated that membrane proteins account for up to 50% of future drug targets [3], [4]. However, only ca. 130 unique high-resolution structures are known for membrane proteins (http://blanco.biomol.uci.edu).

The major class of membrane proteins corresponds to those formed bundles of transmembrane (TM) α-helices. Within this class, transport proteins constitute a major division (http://www-biology.ucsd.edu/∼msaier/transport/). Thus, in the Escherichia coli genome alone there are more than 350 transport proteins, which can be grouped into 60 families or superfamilies [5]. Among them are transporters driven by ATP hydrolysis (i.e. primary active transporters), and those for which transport is driven by an electrochemical gradient, sometimes known as secondary active transporters. The largest family of secondary active transporters are the major facilitator superfamily (MFS), with 70 members identified in the E. coli genome [6].

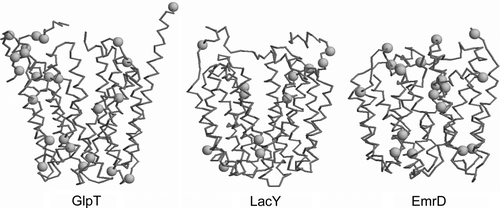
The X-ray structures determined of three MFS members have been determined: lactose permease (LacY; PDB id 1PV6; 3.5 Å resolution) [7], glycerol-3-phosphate transporter (GlpT; PDB id 1PW4; 3.3 Å resolution) [8], and the multi-drug transporter EmrD (PDB id 2GFP; 3.5 Å resolution) [9]. There is also a three dimensional structure of the oxalate transporter OxlT from cryo-electron microscopy [10] which has been modelled on the basis of GlpT and LacY [11]. These structures share a common architecture [12], consisting of 12 TM helices with both the N- and C-termini located on the cytoplasmic side of the membrane. The N-terminal domain of 6 TM segments is related by 2x-pseudosymmetry to the C-terminal domain of 6 TM segments. For example, in GlpT (an organic phosphate/inorganic phosphate (Pi) antiporter) [13–15] it is suggested that transport occurs via a rocker-switch type of movement between the N- and C-terminal domains [16–18]. The cavity of GlpT in the crystal structure is open to the cytoplasm and eight helices (H1, H2, H4, H5 and H7, H8, H10, H11) which line this cavity are distorted curved so as to form a funnel-like shape. Although these proteins share vary little sequence identity [19] it is quite evident that these cavity-lining TM helices contain multiple proline and glycine residues, which may facilitate the large conformational changes that these proteins are thought to undergo during their transport mechanisms (see Supplementary information, Figure S1, online version only).

In general, proline residues are believed to play key structural and functional roles in α-helical membrane proteins [20–25]. In particular, a proline at position i of an α-helix may distort the structure due to the loss of the stabilizing backbone hydrogen bond to residues i-3 and i-4 and the pyrrolidine ring places steric constraints on the conformation of the preceding residues. The two structural factors introduce potential flexibility into the helix and may result in substantial kink and swivel motions observed in the turn before the proline residue. Both structural bioinformatics [26] and simulations on simple models of TM α-helices containing proline [27], point towards this residue as having a capacity to form a molecular hinge. It appears that TM helix flexibility mediated by specific sequence motifs, such as those containing proline or glycine, could have important consequences for the mechanism of membrane proteins such as receptors [28], ion channels [29], and transporters [30].

Current models of membrane folding and stability emphasize the importance of isolated TM helices as independent structural domains [31–34]. For example, studies of LacY have shown that NMR and computer simulations may be combined to explore stability and flexibility patterns in the isolated helices [35]. These may be compared with helix dynamics in simulations of the intact LacY protein [36] in order to explore the role of the intrinsic flexibility of TM helices in functional important conformational changes.

Molecular dynamics (MD) simulations provide a computational tool for probing the structure and dynamics of membrane proteins in detergent micelles [37] and lipid bilayers [38], [39]. They may be used to explore the conformational properties of structures ranging from simplified TM helices [27] to complex transport proteins [36], [40]. Thus, to further analyse the role of proline in TM α-helices of MFS proteins we have undertaken a systematic comparison of conformational properties of the isolated TM helices with those of the intact protein in an MD simulation of GlpT. Interestingly, 5 out of 8 helices that line the pore of GlpT contain centrally located proline residues. Furthermore, as noted by, e.g. [12], “the GlpT structure has several helices that bend in the same, or near the same, places as in LacY, utilizing proline and glycine residues to facilitate these bends”. For example, the GxPP motif of H4 of GlpT is replaced by a GxPx motif in H4 of LacY, and the GxP motif of H8 in GlpT is replaced by a PxP motif in H8 of EmrD. Thus it is of some interest to characterize more fully the conformational properties of the proline-containing helices of GlpT. This comparison of GlpT and its TM helices should also provide some insights into the role of tertiary factors in the conformational properties of the helices.

Methods

Single helix simulations

The coordinates of the X-ray structure (1PW4) of GlpT were downloaded from http://www.rcsb.org/, and all 12 TM helices were extracted using their secondary structure as defined by DSSP [41]. The 12 TM helices were embedded in a pre-equilibrated DMPC bilayer, aligned approximately parallel to the membrane normal. A similar system set-up has been used in previous single helix simulations [27]. The solvent-accessible molecular surface of the helix was used as a template to remove lipids, and a short energy minimization was performed to remove any close contacts between the helix and the lipid environment. Water and counterions were then added. A 1 ns simulation during which the non-H atoms of the helix were restrained (to equilibrate the system) was followed by a 10 ns unrestrained MD run. Thus a total of 120 ns were recorded for the 12 isolated helices.

Simulations were performed using GROMACS v3.1.4 (www.gromacs.org) [42] with an extended united atom version of the GROMOS96 forcefield [43] (ffG43a1), along with the SPC water model [44]. All energy minimizations used < 500 steps of steepest descents to relax any steric contacts generated during setup. For the equilibration period, harmonic position restraints were applied to the heavy atoms of the peptide, with a force constant of 1000 kJ mol^-1 nm^-2. Periodic boundary conditions were employed, and long range electrostatic interactions were treated using particle mesh Ewald (PME) summation [45] with a 1 nm cut-off for the real space calculation. A 1 nm cut-off was used for the van der Waals interactions. All simulations were performed in the constant number of particles, pressure and temperature (NPT) ensemble. During the simulation the temperature was controlled using the Berendsen thermostat [46] at 310 K with a coupling constant τ_T=0.1 ps and the pressure was controlled using the Berendsen barostat with a coupling constant of τ_P=1 ps. The LINCS algorithm [47] was used to constrain bond lengths. The simulation timestep was 2 fs and coordinates saved for analysis every 2 ps.

GlpT simulation

The crystal structure of GlpT has 14 residues unresolved between Asp-226 to Thr-240, corresponding to the loop region that connects the N- and C-terminal domains. These residues were inserted using MODELLER [48], [49] version 6.0. 100 models were generated and the lowest energy conformer was used. An energy minimization was then run to relax any close contacts. GlpT was then inserted into a previously equilibrated DMPC bilayer/water system. A similar system set-up has been used previously in other MFS simulations [36], [50]. Briefly the solvent-accessible molecular surface of the protein was used as a template to remove lipids, and a short energy minimization was performed to remove any close contacts between the protein and the lipid environment. All the ionisable residues were in their default charge; Na⁺ and Cl^- ions were then added to give a salt concentration of 0.1 M. The system was then equilibrated for 2 ns with the protein restrained (force constant of 1000 kJ mol^-1 nm^-2). The restraints were then removed from the protein and the system was simulated for 15 ns. For both the equilibration and final production run the Berendsen barostat and thermostat were employed, with τ_p=1 ps and τ_T=0.1 ps. Periodic boundary conditions were employed and the long range electrostatic interactions were treated using particle mesh Ewald summation [45]. The LINCS algorithm was used to constrain the bond lengths [47]. The timestep of the simulation was 2 fs and the coordinates of the simulations were saved every 2 ps.

Results

Simulation systems

Two classes of simulation were performed. The first was a set of 12 simulations (H1–H12) of the isolated TM α-helices of GlpT (Table I), each simulated individually in a DMPC bilayer (Figure 1A). The second class was a simulation of the intact GlpT protein, again in a DMPC bilayer (Figure 1B). The motivation behind these two classes of simulation was to explore the conformational properties of the TM helices, especially those containing proline residues, both as isolated TM helices (thus mimicking the TM helix as an independent folding unit inserted via the translocon [51]) and within the intact GlpT protein.

Figure 1.  Simulation systems. (A) Transmembrane helix (H4; pink, with the residue P139 and P140 in blue) in a DMPC bilayer. (B) The GlpT molecule, with the proline-containing TM helices in pink and other TM helices in blue. In both diagrams the phosphorus atoms of the lipid headgroups are shown as brown spheres.

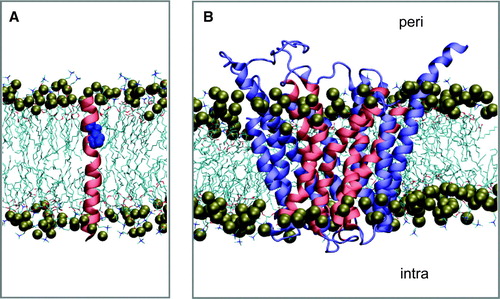
Table I.  Sequences of TM helices of GlpT.

Helix	Sequence
H1	D^20PTYRRLRWQIFLGIFFGYAAYYLVRKNFALAMPYLVE^57
H2	D^64LGFALSGISIAYGFSKFIMGSVSD^88
H3	V^94FLPAGLILAAAVMLFMGF^112
H4	A^121VMFVLLFLCGWFQGMGWPPCGRTMVH^147
H5	Q^153RGGIVSVWNCAHNVGGGIPPLLFLLGM^180
H6	L^190VMPAFCAILVALFAFAM^207
H7	K^253LLWYIAIANVFVYLLRYGILDWSPTYLKE^282
H8	L^288DKSSWAYFLYEYAGIPGTLLCGWMSDKV^316
H9	G^322ATGVFFMTLVTIATIVYWM^341
H10	P^347TVDMICMIVIGFLIYGPVMLIGLHALE^374
H11	A^380AGTAAGFTGLFGYLGGSVAASAIVGYTVD^409
H12	G^415GFMVMIGGSILAVILLIVVMIGEKRRHEQLLQEL^449

Key proline residues are in bold, and glycine residues of key GX_NP motifs are underlined.

Structural drift of the intact protein and of the helices

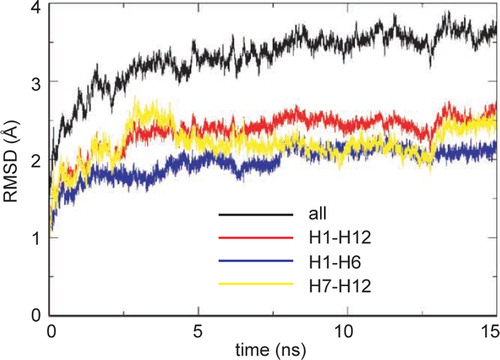
The root-mean-square deviation (RMSD) of Cα atoms from the initial structure can be used to measure the overall conformational drift of a membrane protein over the course of a simulation (Figure 2). Examining the RMSD vs. time for all residues in GlpT together, it can be seen that there is a steep initial rise (to ∼ 3 Å) followed by a steady slow increase to ∼ 3.5 Å by the end of the simulation. However, if one excludes the loops (which on their own have a final α RMSD of ∼ 4.5 Å) and examines the RMSD for just the helices of the TM domain (i.e. H1 through H12 inclusive) then a plateau value of ∼ 2.5 Å is reached after ∼ 3 ns and maintained for the remainder of the simulation. If the RMSD of the helices is further decomposed into the N-terminal (helices H1 through H6) and C-terminal (H7–H12) domains, both have a slightly lower (∼ 2 Å) RMSD, suggesting a degree of intra-domain motion, as is also seen in LacY simulations [36].

Figure 2.  Conformational drift in the GlpT simulation, measured as the root-mean-square deviation (RMSD) of the Cα atoms of GlpT for all atoms (black), the TM α-helices (H1–H12, red), the N-terminal domain (H1–H6, blue), and the C-terminal domain ( H7–H12, yellow), measured relative to the initial starting structure at t=0 ns.

Having established that the degree of conformational drift in the GlpT protein TM domain (i.e. excluding loops) is modest, and comparable to that in simulations of other membrane proteins [38]), it is informative to examine the extent of the conformational drift for the individual helices, both within the intact protein and as simulations of the isolated TM helices (Figure 3).

Figure 3.  Conformational drift of the individual TM helices. The Cα RMSDs are compared for each TM helix in the intact GlpT protein simulation (black lines) and in the simulations of the isolated TM helices (red lines).

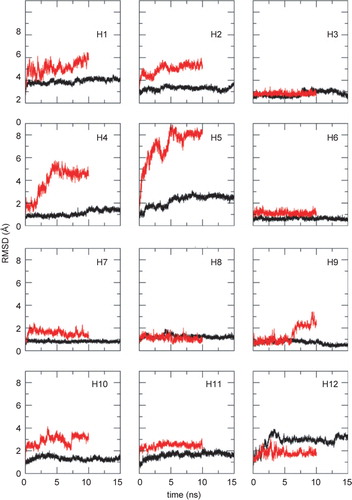
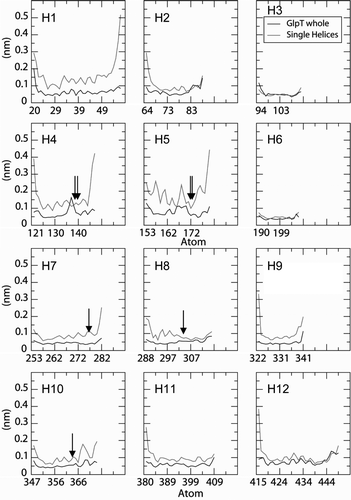
Eight out of the 12 isolated helices have larger structural drifts than the same helices within the protein. In particular, the RMSDs for the isolated helix simulations of two proline-containing TM helices, H4 and H5, are significantly higher than for the corresponding helices within GlpT. This is possibly due to the GxPP motif in both of the helices, (which is known to greatly increase the flexibility of a TM α-helix [27]). Only for H12 is the RMSD higher for the intact protein than for the isolated helix, due to a bend at residue E443.

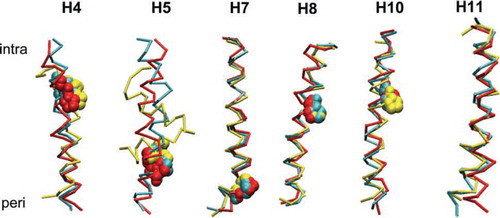
In Figure 4 we show superimposed structures of the proline-containing helices (H4, H5, H7, H8, and H10) and an example of a non-proline helix (H11), comparing their X-ray structures (in GlpT) with their end of simulation structures. It is clear that there are significant structural differences between the isolated and GlpT simulation structures for H4, H5 and H11, but not for H7, H8 and H10, reflecting the additional restraints on helix flexibility imposed by packing within the intact protein in addition to having to span a lipid bilayer. Interestingly, the isolated H5 simulation adopts a helix-turn-helix conformation due to a GGGxPP motif. The inherent flexibility of this helix may play a mechanistic role in the function of the protein.

Figure 4.  Superimposed snapshots of helices H4, H5, H7, H8, H10 and H11. The colour scheme is: cyan = helix from the X-ray structure of GlpT; red = helix from GlpT simulation at t = 15 ns; and yellow = helix is from the isolated helix simulation at t = 10 ns. Proline residues are shown in space-fill format. The intracellular and periplasmic ends of the helices are denoted by ‘intra’ and ‘peri,’ respectively.

Analysis of secondary structure

Analysis of the time dependent secondary structure (Figure 5) in the simulations can provide more information as to whether the proline-containing motifs in the TM helices can form molecular hinges [27]. In general the TM helices, both within GlpT and in their isolated form, retain most of their α-helicity throughout the simulations. This is especially true of those helices which do not contain a proline (e.g. H2 in Figure 3), which generally only show limited loss of α-helicity at their termini. H3 and H6 are the only helices that do not show any deviation from α-helicity when simulated in isolated form or within the full protein simulation (data not shown). These two helices are thought to act as scaffolding helices of the protein and define where the protein resides in the bilayer [8].

Figure 5.  Analysis of TM helix secondary structure (using DSSP) in the intact GlpT (left hand) and isolated TM helix (right hand) simulations. Results are shown for the key proline-containing helices (H4, H5, H7, H8, H10) and for H2 as a proline-free helix. The colour code is as follows: Blue: α-helix; yellow: turn; green: bend; purple: π-helix; grey: 3₁₀-helix; white: coil. The black arrows indicate the location of the proline residues.

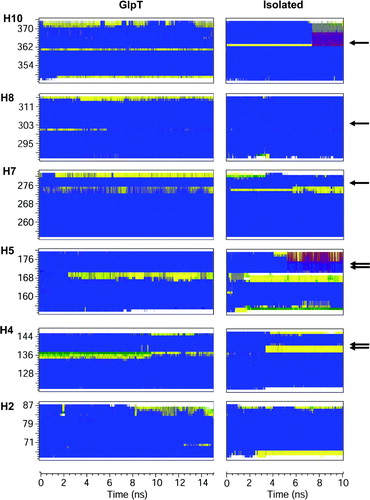
In the case of the proline-containing helices, some local loss of α-helicity is observed, consistent with molecular hinge behaviour. This is seen in H4, H5, H7 and H10, with local loss of α-helicity (in the turn of helix before the proline residue) in both the GlpT and isolated helix simulations. H5 shows a marked increase in loss of helicity in both simulations, but this loss is more noticeable in the isolated system. H8 behaves rather differently: there is initially a locally non-α-helical region before the proline in the GlpT simulation, but this largely reverts to α-helix both later in the GlpT simulation and early on in the isolated H8 simulation. This suggests that tertiary factors are important to stabilize the distortion of this helix.

Local helix mobility was also analysed by calculating the time-averaged root-mean-squared fluctuation (RMSF) of the Cα atoms for each residue (not shown – see Supplementary Information, online version only). As anticipated, the isolated helices show higher overall RMSF values than the corresponding helices in the intact protein. Of the isolated proline-containing helices, H5 exhibited a marked increase in the Cα RMSF in the turn before the proline residue, which was less pronounced in H5 of GlpT.

Inter- and intra-helical H-bonds

Proline is unable to make hydrogen bonds to the carbonyl group of the residue four preceding it. This i-4 carbonyl residue can be compensated by H-bonding to residues around the proline or by, in some instances, by H-bonding to water molecules (summarized in supplementary information, Table S1, online version only). In both the GlpT and isolated TM helix simulations, the carbonyl groups of residues i-4 to the proline are seen to H-bond to the residues i-1 or i–2 to the proline. Additionally, in the GlpT simulations some inter-helical H-bonds are seen e.g. the C = O of M136 H-bonds to the Y41 sidechain. Overall, the GlpT simulation suggests that the proline-containing helices within the protein are packed tightly to other helices due to the presence of inter-helical hydrogen bonding. All the carbonyl groups i-4 to proline, whether in GlpT or the isolated helices, are stabilized by backbone H-bonds and or intra-helical H-bonding.

Proline-induced hinges

The characterization of the proline-induced hinges in more detail (Table II), both in the isolated helices and within GlpT, is important to understanding possible roles of such hinges in intact transport proteins. Helices H4 and H7 have been examined in some depth (Figure 6), as both show considerable hinge bending (unlike H8), whilst neither shows substantial loss of α-helicity in the isolated helix (unlike H5). In general the kink angles of proline-helices from the GlpT simulation resemble the kink angles of the static crystal structure (Table II), suggesting that the surrounding helices do not allow the full conformational space to be sampled, unlike the case of the isolated helices.

Figure 6.  Snapshots from the simulations of two of the proline-containing helices (H4 and H7). In each case 20 equally spaced (in time) snapshots are shown over the course of the simulation. The colour of the snapshots are on the RGB scale, where red is at the start of the simulation, blue is at the end of the simulation and white is the crystal structure helix.

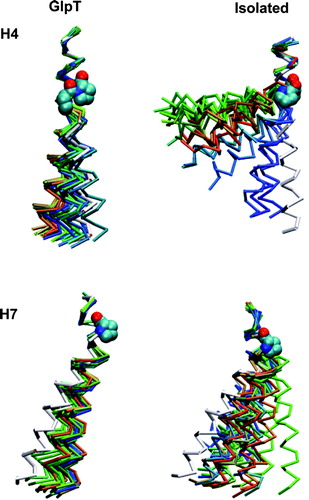
Table II.  Comparison of TM helix kink angles.

	Kink angle (°)
	Helix H4	Helix H5	Helix H7	Helix H8	Helix H10
X-ray structure	17	8	37	25	8
GlpT simulation	17±7	18±8	32±6	24±6	12±7
Isolated helix simulations	35±14	45±11	24±12	17±7	22±8

The hinge motion of proline-containing helices may be analysed in terms of helix kink and swivel angles [26], [27]. Direct analysis of the trajectories of isolated H4, H7 and of these helices in GlpT (Figure 7A, 7C) suggests marked anisotropic molecular hinge motion in H4 (more so in the isolated H4 than in the GlpT simulation), in contrast with more restricted motion in H7. Principal component analysis (PCA) may be used to simplify the kink/swivel angle analysis by, e.g. focusing on the motion represented by the first eigenvector [52], [53]. The first eigenvector accounted for about 20–40% of the overall motion of the helices and reveals a clear, well defined kink/swivel. The motions depicted by the other eigenvectors were less clear-cut and thus our analysis was focused on the first eigenvector. Application of this to H4 and H7 (Figure 7B, 7D) reveals a clear helix kink motion for both H4 and H7. The directionality and magnitude of kinking for H4 is more marked for the isolated helix simulation. For H7 the helix becomes less kinked in both simulations.

Figure 7.  Kink and swivel angle analysis [26] for helices H4 and H7 in the intact GlpT and isolated helix simulations. (A) and (C) show the kink/swivel angle plots derived directly from the trajectories. (B) and (D) show the corresponding plots for the trajectory projected onto the 1st eigenvector as revealed by PCA (see text for details).

Possible functional consequences

How might the molecular hinges within the proline-containing helices impact upon the mechanism of GlpT? GlpT is thought to operate via a rocker-switch type of movement with a single binding site alternating between the inward facing and outward facing conformations [8], [16]. The substrate translocation pathway can be visualized as a pore-like cavity between the N- and C-terminal domains (Figure 8). Eight helices line the cavity, H1, H4, H7, and H10 on the two sides; H5 and H8 at the back; and H2 and H11 at the front.

Figure 8.  Effects of GlpT motions on the ligand binding cavity. (A) View of the central cavity of GlpT (from the intracellular side) showing those cavity-lining helices which contain prolines in red. (B) The ligand binding cavity of GlpT (displayed using HOLE [68]) analysis at the start (t = 0 ns) and end (t = 15 ns) of the GlpT simulation. Protein is shown in trace representation and the helices coloured from blue (H1) to red (H12). The surface lining of the cavity is coloured according to radius, blue:>1.15 Å; red:>1.15 Å > diameter > 0.6 Å and green: 0.6 Å.

The cavity of the protein is open on the intracellular (i.e. cytoplasmic) side. The phosphate substrate (which enters from the cytoplasm) is negatively charged and therefore it is not surprising that the substrate-binding site is positively charged. Residues R45 and R269, on helices H1 and H7 respectively, are found at the closed end of the molecule and are proposed to form the substrate binding site. These two residues are conserved amongst the organophosphate: phosphate antiporter (OPA) family [17] and seem to be essential in the transport mechanism of GlpT [54]. In the crystal structure, the shortest distance between R45 and R269 is ∼ 10 Å. In the absence of the substrate this distance decreases during the simulation to ∼ 6 Å, as the N- and C-terminal domains close (Figure 8B). A similar degree of closure of the two domains is also seen in other simulations of MFS transporters, of LacY [36]).

In conclusion, we can suggest that helices H3 and H6 act as scaffolding helices that undergo relatively little conformational changes whether in the isolated form or as part of the protein. Helices H4, H5, H10 and H11 are relatively flexible when simulated in isolation, suggesting they may play a key role in conformational transitions of the intact protein. Significantly, these helices line the ligand-binding cavity of the protein and are related by a pseudo two-fold symmetry.

Discussion

It is useful to reflect on the relevance of this study to understanding the transport mechanism(s) of MFS proteins. Comparison of simulations of the isolated TM helices and of the same helices within the intact protein provides useful information on the intrinsic conformational flexibility of the helices and how this is manifested within GlpT. In the context of the alternating access model for solute transporters [55], the nature of TM helix flexibility and how it may contribute to the overall conformational properties of the GlpT protein is of some mechanistic relevance, even if it does not reveal the final mechanism of the transporter.

Whilst the role of prolines in static kinks of TM helices is well established [26], and the dynamics of such kinks have been explored in simplified models [27] and in e.g. the S6 helix of Kv channels [56], a more systematic and comparative computational analysis of all such helices from a given membrane transport protein has, to the best of our knowledge, yet to be published. Furthermore, a number of experimental studies have recently addressed the structural [57] and functional [58] consequences of proline-to-alanine mutations in bacteriorhodopsin, the latter study suggesting a functionally relevant dynamic role for helix kinks. Thus, in the current study we have presented one of the first comparisons of single TM helix simulations with simulations of an intact membrane transport protein. As anticipated the single helices in isolation were more flexible than the corresponding helices within the intact GlpT structure. Notable exceptions were helices H3 and H6, which behaved in a similar fashion when simulated in isolation or in the whole protein. The high relative flexibility of H4, H5, H10 and H11 in isolation suggests that these may play a dynamic key role in functionally relevant conformational transitions of the intact transport protein, especially as these helices line the central cavity of the protein. The more general relevance of this is discussed further below.

Of course, there are differences in the conformational properties changes when comparing the proline-containing TM helices simulated in intact GlpT with those simulated in isolation. For example, loss of helicity of H10 was around I361 in the GlpT simulation and whilst around G363 for the isolated helix. In general, the kink and swivel angles are smaller for proline-containing helices within intact GlpT simulations than when in isolation. Thus the overall fold of the protein may modulate kink angles of the TM helices [57], [59]. For example, carbonyl groups i-4 to a proline (which are exposed during kinking) may form inter-helical hydrogen bonds with the side chains of residues on other helices, as seen within the simulation of the intact GlpT protein. This would suggest that the helices might pack closely to the proline-helices to form hydrogen bonds to the carbonyl group i-4 to proline. This would be favourable interaction to compensate for the loss of the hydrogen bond by proline.

Supplementary Figure S1. Comparison of the locations of proline residues (green spheres at Cα atoms) for the Cα traces (blue) of GlpT, LacY and EmrD.

It may be argued that the motions observed in the simulations of the isolated helices may simply represent their relaxation away from their constrained whole-protein conformation [57] rather than flexibility inherent in the function of the protein. This may indeed be the case, and a direct test would require, e.g., mutation and structure determination of substations for proline in the TM helices of GlpT. However, the frequent occurrence of proline residues in TM helices coupled with the difficulties of accommodating substitutions with prolines at new positions [59] agues in favour of a functional role. In trying to understand the role of proline-mediated kinks in function of intact transport proteins, it is therefore important to better understand the nature of the changes in conformation which they permit in the key structural elements of such proteins, namely the TM helices.

At this point it is important to consider the technical limitations of this study. With regards to the single helix simulations, we employed a set-up in which the helix was positioned perpendicular to the plane of the bilayer. Whilst it is possible that this initial set-up of the single helix simulations may lead to a biasing of the kinking/swivel of the helices, the helices generally tilt to accommodate the hydrophobic segment of the helix within the core of the bilayer within a few nanoseconds. The initial protocol insertion also facilitated comparison with previous studies of more idealized proline-kinked TM helices [27]. It is also implicit in the current study that TM helices insert as independent domains (mimicking the proposed model of insertion via the translocon [34], although it is likely that some TM helices are inserted in a pairwise fashion. With particular reference to GlpT, it is not yet known if the latter applies, and if so for which TM helices. One way to assess the independent stability of isolated TM helices is to examine the degree of consensus in sequence based prediction [60]. Applying such analysis to GlpT yields a clear prediction for all of the TM helices other than H8. It might therefore be of interest in future studies to explore the conformational properties of isolated hairpins of H7-H8 and/or H8-H9 in order to gain a greater understanding of possible mechanism of TM helix insertion for the GlpT protein.

The other main limitation of the current study is the relatively short (ca. 10 ns) timescales sampled. The X-ray structure of GlpT is in an inward-facing conformation and although the N-and C-terminal domains do close to a limited extent over the course of the 15 ns simulation, the protein does not undergo a complete transition to the open facing conformation. This is not surprising as MFS transport rates are ∼ 100 s^-1. However, by comparing with similarly short simulations of the isolated TM helices, for which kinking and swivelling of helices may occur on an ns timescale [27] one may gain some insights into possible flexible elements within the intact protein. It would perhaps be of interest to use enhanced sampling methods (e.g. replica exchange [61]) to explore the energetics of proline-induced hinges in the isolated helices and in the intact GlpT protein.

The results of this study help to inform the proposed rocker switch mechanism [8], [16–18] for GlpT. In particular, those TM helices that are significantly flexible in their isolated state (H4, H5, H10 and H11) line the pore of the protein and are related by a pseudo two-fold symmetry, Figure 8A. Such flexibility could be expected to aid in the rocker-switch mechanism by facilitating conformational change of the two domains of the protein compared to a rigid body mechanism. Indeed, extended multiple MD simulations of LacY [36] also suggest that domain closure may occur by a combination of rigid-body movements of domains and of motions of helices, especially H4, H5, H10, and H11, and also that a degree of intra-helix flexibility appears to be important.

Our results may also be of relevance to MFS proteins other than GlpT. Several MFS members have been modelled on basis of GlpT [19], [62], [63] and homologous structures (e.g. [11], [50], [64]. Thus, insights from studies of the conformational properties of GlpT may be of more general relevance. For example, TM helix H5 of antiporter MFSs contains a proline- and glycine-rich motif which mutational studies have shown to be of functional importance in the tetracycline efflux protein Tet(L) [30]. This is of especial interest as GlpT H5 shows considerable flexibility both in intact protein and isolated H5 helix simulations. In other transporters, for example helix X (i.e. TM10) of the NhaA antiporter contains a GxP motif, the kinking of which simulations suggest may play a functionally important role in regulation of dynamics by pH [65]. The three crystal structures for MFS transporter proteins reveal several proline and glycine residues in their TM regions. MFS transporters are thought to operate via a rocker switch mechanism, with a substantial conformational change possibly aided by the presence of these prolines and glycines. Our results are therefore compatible with a version of the rocker switch mechanism which allows for a degree of TM helix flexibility (see also [36]).

Proline and glycine residues have also been suggested to aid in the function of vSGLT (a member of the solute sodium symporter family) [55] and of LeuT (a bacterial member of the neurotransmitter sodium symporter family) [66], which share a common 14 TM architecture. The vSGLT and LeuT structures appear to be in inward-facing and outward-facing conformations respectively. Faham et al. [55] explored the mechanism of vSGLT protein by superimposing the core domains of vSGLT and of LeuT. Interestingly they highlight conserved glycine and proline residues that facilitate the structural rearrangements proposed to transport the solute across the membrane.

Supplementary Figure S2. Cα root mean square fluctuation (RMSF) profiles as a function of residue number for the 12 Tm helices of GlpT, from the single helix simulations (red lines) and for the same helices within the intact GlpT simulation (black lines).The vertical arrows indicate the locations of proline residues.

More generally still, there is an ongoing debate with respect to the role of proline-kinked helices in bacteriorhodopsin and related proteins, and in particular whether proline residues play a dynamic functional role (as ‘transmission elements of conformational change’ [58]) or a more general structural role via stabilization of TM helix kinks [57], [59], [67]. Simulation studies of the isolated TM helices may also be able to inform this more general discussion.

Supplementary Table S1. Hydrogen bonds formed to the residues i-4 preceding the praline.

		H-bonds to residues		Number of H-bonds to water
Helix	C = O i-4 to praline	GlpT simulation	Isolated TH helix simulation	GlpT	Isolated TH helix simulation
4	Gly-135	Gly-137 Trp-138	Gly-137 Trp-138	24	7
4	Met-136	Trp-138 Tyr-41 (OH)	Trp-138	4	5
5	Gly-168	Gly-170 Ile-171 Tyr-300 (OH)	His-165 Gly-170	3	3
5	Gly-169	Ile-171	Ile-171	0	0
7	Leu-273	Trp-275 Ser-276 Ser-276 (OH)	Ser-276 Ser-276 (OH)	0	686
8	Tyr-300	Asn-166 (NH2) Gly-302 Ile-303	Gly-302 Ile-303 Gly-305	8	0
10	Leu-360	Tyr-362 Gly-363	Tyr-362 Gly-363 Val-365	0	0

Acknowledgements

This work was supported by grants from the BBSRC (via the MPSi consortium and a studentship to RD'R) and EPSRC (via the Bionanotechnology IRC), and from the Wellcome Trust. Our thanks to our colleagues, especially Alessandro Grottesi, Peter Bond, and John Holyoake, for their insightful comments on this work.

Declaration of interest: The authors report no conflicts of interest. The authors alone are responsible for the content and writing of the paper.