Prediction of body weight using body measurements in some sheep and goats in Qatar

ABSTRACT

The study aimed to identify the relationship between body measurements and the weight of sheep and goats. A total of 324 heads of sheep and 261 heads of goats were used. Measuring of body weight (BWt) and body measurements as heart girth (HG), height at wither (HW) and body length (BL) were taken on both types of animals for 3 successive months. Correlations between body weight and measurements were tested. Linear and non-linear regressions of body weight on the most correlated body measurements were calculated. HG, HW and BL were significantly related to BWt. HG had the largest correlation coefficient. Power regression had the highest coefficient of determination (R² = 0.91) and lowest error of estimate (SE = 7.42). The power regression model (BWt = 0.0006*HG^2.5608) was tested against the actual weight of another animal’s population of 119 heads of goats and 171 heads of sheep using paired t-test analysis. No significant variation was observed between the actual and estimated body weights. The model overestimated weight by 1.5%. It was concluded that body weight could be estimated with a high accuracy using the corrected model BWt (kg) = (0.0006*(HG^2.5608))–(1.5*(0.0006*(HG^2.5608)/100)).

KEYWORDS:

• Girth
• length
• model
• non-linear
• relationship

Introduction

Small ruminants are the major livestock raised in Qatar. According to Al-Ghanim et al. (2022), they resemble 88.5% (62.4% were sheep and 26.1% were goats) of the total livestock population which amounted to 1,476,363 heads. Camels and cattle were 8.1% and 3.4% of this population, respectively. Awassi, Erbi, Najdi sheep and Shami and Aaridi goats were well-recognized breeds in Qatar. They adapted more easily to the harsh environmental conditions of the country. Awassi breed resembled 57% of the sheep population followed by the Erbi breed, which accounted for 34% of the sheep population, whereas the other sheep breeds and crosses represented only 9% of the sheep population. Aaridi goat’ breed, accounted for 67% of the population of goats, whereas the Shami breed was 13% and the other breeds and their crosses accounted were 20%.

Body weight and body measurements are crucial selection criteria for improving livestock production. The weight and measurements of animals significantly affect farmer or breeder income (Ajafar et al. 2022; Al-Thuwaini and Al-Hadi 2022). The most used way to assess body mass is weighing animals with a suitable scale balance. However, such a device is too expensive for most traditional animal holders. Agamy et al. (2015) stated that the best method for determining of animal’s weight without a scale is to predict body weight from body measurements. Linear measurements are indicators of an animal’s body growth (Goe et al. 2001; Attah et al. 2004). Body growth is a complex biological process that is induced by differential development rates of growth of the different body tissues. External measurements usually reflect the development of the skeleton and/or soft tissues of the body. The various lengths, heights and girths of live animals were used to assess the relationship between these variables and live weight. The use of these measurements in estimating live weight has been reported by several authors (Atta and El Khidir 2004; Adeyinka and Mohammed 2006; Fajemilehin and Salako 2008; Olatunji-akioye and Adeyemo 2009; Agamy et al. 2015; Sam et al. 2016). For animals growing over a wide weight range, the relationship between live weight and heart girth has been curvilinear (Lawrence and Fowler 1997). For cattle, Brody (1945) added that body weight changed with a cubed heart girth. Atta and El Khidir (2004) examined the reliability of body measurements based on heart girth, wither height and scapula-ischial length to predict the live weight of Sudan Nilotic sheep using a nonlinear regression equation. The reviewed literature revealed that different models were developed to estimate body weight using body measurements for different breeds and conditions. The aim of this study was to establish a regression equation model that could be potentially used to predict body weight in sheep and goats under field conditions in Qatar.

Materials and methods

Site of the research

The current study was carried out in the Animal Research Station at Alsheehaniya Municipality at 25°21’ N and 51°14’ E, about 25 km west of the capital Doha.

In the research station, three breeds of sheep (Awassi, Najdi and Erbi) and two breeds of goats (Aaridi and Shami) are raised. All animals were reared under an intensive system i.e. stall feeding. All breeds are maintained under the same environmental conditions, each in its own barns. Each breed is accommodated, fed and managed in groups according to similarity of age and physiological status i.e. adult males, dry females, milking females, weaned females and weaned males. Newborns are separated from their dams during the night. The barns are half-shaded, sandy-floored and equipped with stainless steel drinkers and feeders. Dry females, mature bucks, rams and weaners were fed on dried Rhodes as roughages at the rate of 1 kg/head/day, while pregnant and suckling females were fed on dried alfalfa at the same rate. Pelleted concentrate feed of 16% crude protein content that mainly contained soybean meal, barley grains and wheat bran was fed to all animals at rates ranging between 200 and 450 g/head//day according to the physiological status of animals. Salt licks and clean drinking water were always available in front of animals. During the suckling period, lambs and kids were fed with their mother’ milk to be weaned at approximately 100 days of age. All animals in the station are weighed regularly on a monthly basis.

Experiments

The experimental part of the research consists of two experiments:

1. The main experiment for the collection of the basic data required to build the mathematical model. Body weight and measurements were collected for three successive months (November 2021 to January 2022).

2. Sensitivity testing experiment for the examination of the uncertainty in the output of the built mathematical model (Saltelli 2002). Body weight and measurements were taken to examine the sensitivity of best fitted equation obtained from the main experiment.

Animals

For the main experiment, all animals in the station were available. After the exclusion of visually pregnant ewes and does, five hundred and eighty-five sheep and goats were used in this experiment. Table 1 shows the distribution of type, sex and breed of the used animals.

Table 1. Distribution of experimental animals according to type, breed and sex.

Type	Breed	Male	Female	Totals
Goats	Shami	54	132	186
	Aaridi	27	48	75
	Total	81	180	261
Sheep	Erbi	12	37	49
	Awassi	81	149	230
	Najdi	15	30	45
	Total	108	217	324
All groups		189	397	585

Another population of animals of 290 heads was used for the sensitivity testing experiment. These animals were kept in another animal’s holding. Table 2 shows the distribution of type, sex and breeds of the animals used in the sensitivity testing experiment.

Table 2. Distribution of sensitivity testing animals according to type, breed and sex.

Type	Breed	Female	Male	Total
Goats	Shami	24	26	50
	Aaridi	49	20	69
	Total	73	46	119
Sheep	Najdi	30	16	46
	Erbi	28	14	42
	Awassi	43	40	83
	Total	101	70	171
All groups		174	116	290

Data collection

For the two experiments, animals were fasted for 12 h before weighing in early morning. Using a digital small ruminant, balance animals were weighted to the nearest 100 g. After weighing, linear body measurements were taken using a flexible measuring tape to the nearest 0.5 cm. Body measurements were taken according to that described by Atta and El Khidir (2004):

• - Body length (BL): (Scapulo-ischial length), the distance from the dorsal tip of the scapula to the tip of the ischium

• - Height at wither (HW): Vertical distance from the highest point of the shoulder (wither) to the ground surface at the level of the foreleg

• - Heart girth (HG): The body circumference at a point immediately posterior to the front leg and perpendicular to the body axis.

Statistical analyses

Using the data obtained from the main experiment, Pearson’s correlations of body weight and the different body measurements were computed for pooled data and types (sheep and goats) and sex (males and females) groups (StatSoft 2011). Regression analysis was employed to predict live weight from body measurements. For the pooled data, Stepwise multiple linear regression analysis was performed. Simple linear and non-linear regressions were also tested for the measurements of the highest correlation coefficient. Linear, exponential, logarithmic and power mathematical models were tested for best fitting by comparing the coefficient of determination (R²) and the error of estimate. The equations with the largest R² and smallest error were considered the best-fitting equations. For the regression model of the highest R², t-test described by Ali (2008) was used to examine the regression coefficients for the significance of the difference between types of animals (sheep vs. goats), sex (males vs. females) and breeds of sheep (Awassi vs. Erbi, Awassi vs. Najdi and Erbi vs. Awassi) and goats (Aaridi vs. Shami). A stepwise multiple regression analysis was performed to test the performance of body weight prediction models using combinations of the body measurements.

Using the data obtained from the sensitivity testing experiment, the body weight of animals was estimated according to the best-fitted equation resulting from the main experiment. A paired t-test was performed to test the significance of the difference between the estimated and actual body weight of this population of animals.

Results

Table 3 shows the correlation coefficients of body weight and the examined body measurements. The results revealed that all the correlations were significant (P < 0.05). HG always was the measure of the highest correlation coefficient. Table 4 illustrates the performance of regression models used to describe the relationship between body weight (y) and heart girth (x) for the pooled data. The power model had the highest determination coefficient (R²) and lowest error of the estimate. Power regressions for the different types, sexes and breeds of the experimental animals are shown in Table 5. All the regressions were significant. In the same table, the statistical analysis for the significance of the difference of regression coefficients of animal types (sheep vs. goats), sex (males vs. females) breeds of sheep (Awassi vs. Erbi, Awassi vs. Najdi and Erbi vs. Awassi) and goats (Aaridi vs. Shami). The statistical analyses revealed no variations among the examined groups.

Table 3. Correlation coefficients of weight with body measurements.

	Pooled	Sheep	Goats	Males	Females
HG	0.9292	0.9104	0.9424	0.9409	0.9301
HW	0.8787	0.8103	0.9011	0.8916	0.8705
BL	0.8208	0.7896	0.9138	0.8401	0.8082

HG is the heart girth.

HW is the height at wither.

BL is the body length.

Table 4. Parameters of the different mathematical models of regression of body weight (y) on heart girth (x) for the pooled data.

	Linear	Exponential	Logarithmic	Power
Formula	y = a + b*x	y = a*e^(b*x)	y = a + b*ln(x)	y = a*x^b
R^2	0.8633	0.8185	0.8875	0.9129
Error of estimate	7.5494	7.9603	8.6993	7.4208
A	−60.5737	2.8499	98.3380	0.0006
B	1.3321	0.0333	−383.0900	2.5608

R² is the coefficient of determination.

a is the regression intercept.

b is the regression coefficient.

Table 5. Parameters and statistical analysis of Power regressions of body weight (y) on heart girth (x) for the different animals’ groups (type, sex and breeds).

	N	A	b	R^2	SE b	SE D	Calculated t-value	df	Critical t-value at 5%	Critical t-value at 1%
Goats	777	0.0003	2.7694	0.9278	0.0365	0.2973	−0.4621	862	1.96	2.59
Sheep	973	0.0001	2.9068	0.9068	0.0519
Male	564	0.0003	2.7286	0.9329	0.0364	0.2597	0.9461	762	1.96	2.59
Female	1186	0.0008	2.4829	0.9150	0.0310
Sheep female	650	0.0001	2.9494	0.9320	0.0563	0.3345	−0.1387	430	1.96	2.59
Sheep male	323	0.0001	2.9958	0.9387	0.0556
Awassi	690	0.0001	2.9507	0.9289	0.0472	0.4046	1.3429	239	1.97	2.6
Erbi	146	0.0011	2.4074	0.7380	0.1165
Awassi	690	0.0001	2.9507	0.9289	0.0472	0.3690	0.4702	227	1.97	2.6
Najdi	137	0.0002	2.7772	0.9012	0.0890
Erbi	146	0.0011	2.4074	0.7380	0.1165	0.4534	−0.8157	139	1.98	2.62
Najdi	137	0.0002	2.7772	0.9012	0.0890
Goat female	536	0.0006	2.5702	0.9210	0.0466	0.3137	−1.3325	330	1.97	2.6
Goat male	241	0.0001	2.9882	0.9359	0.0518
Aaridi	224	0.0006	2.5777	0.9269	0.0700	0.3347	−0.8070	317	1.97	2.6
Shami	553	0.0002	2.8478	0.9344	0.0420

N is the number of observations.

R² is the coefficient of determination.

a is the regression intercept.

b is the regression coefficient.

SE b is the standard error of the regression coefficient.

SE d is the standard error of the difference of regression coefficient.

The calculated t-value is the calculated t-test value.

Critical t-value at 5% is tabulated critical t-test value at the probability of error 5%.

Critical t-value at 1% is tabulated critical t-test value at the probability of error 1%.

Table 6 shows the parameters of the stepwise regression. R² and error of estimate were considered as criteria for selecting the appropriate linear model. The equation of combination of the three linear measurements (step 4) had the largest R² and smallest standard error. In this equation, HG resembled 69% of regression coefficients, whereas BL and WH resembled 19% and 13%, respectively.

Table 6. Parameters of stepwise multiple regression of body weight on the linear body measurements.

	Step 1	Step 2	Step 3	Step 4
Adjusted R^2	0.8633	0.8852	0.8785	0.8874
Error of estimate	7.5494	6.9172	7.1147	6.8501
A	−60.5737	−69.2164	−70.4738	−71.9270
b of HG	1.3321	1.0633	0.9978	0.9666
b of BL		0.4196		0.3256
b of WH			0.5100	0.2394

R² is the coefficient of determination.

a is the regression intercept.

HG is the heart girth.

HW is the height at wither.

BL is the body length.

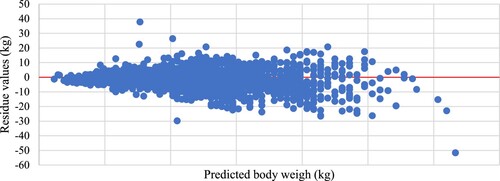
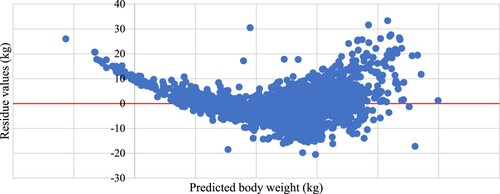
Regressing the residue values (actual weight – predicted weight) on the predicted weight illustrated the trend of the model prediction. (Figure 1) shows the regression of residue values on body weight predicted by the power model estimation, whereas (Figure 2) shows the regression of residue values on body weight predicted by the multiple regression estimation. The former figure illustrates a homogeneous trendless distribution of residues with the increase in body weight. Whereas the latter figure demonstrates that the residue values concentrated above zero at the low and heavy weights and below zero at the medium weights indicating that the model underestimated predication at low and heavy weights and overestimated the prediction at medium weights.

Figure 1. Plotting of body weight predicted by the power regression model on its residue values.

Figure 2. Plotting of body weight predicted by the multiple regression model on its residue values.

Model sensitivity testing

Table 7 demonstrates the results of testing of significance of the difference between values of measured and estimated body weight of animals used to test the sensitivity of the power model. There was no significant variation (P > 0.05) between the measured and predicted body weight values. The difference between measured and estimated weights (kg) (Estimated weight –Measured) and the percentage of this difference (100*Difference between measured and estimated weights/estimated weight) were calculated and the prediction formula was then corrected by subtracting the percentage of difference. $\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{g}\mathrm{e}\mathrm{o}\mathrm{f}\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}={\displaystyle \frac{\mathrm{E}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}\mathrm{w}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}-\mathrm{M}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{w}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}}{\mathrm{E}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}\mathrm{w}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}}\times 100}$

Table 7. Statistical examination of the difference between measured and estimated body weights of sensitivity testing population.

	Measured weight (Kg)	Estimated weight (kg)
No. of observations	290	290
Mean	51. 7	52.5
Standard deviation	19.42	18.28
Calculated t-value	0.527
P	0.598
Difference (kg)	0.8
Percentage of difference (%)	1.5%

The calculated t-value is the calculated t-test value.

P is the probability of error.

$\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{g}\mathrm{e}\mathrm{o}\mathrm{f}\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}={\displaystyle \frac{52.2-51.7}{52.2}\times 100=1.5\text{\%}}$So the corrected formula was

Estimated body weight = (0.0006*(HG^2.5608))–(1.5*(0.0006*(HG^2.5608)/100)).

Discussion

Phenotypic correlation (R) is one of the most common and useful statistics that describes the degree of relationship between two variables. The present significant positive correlations between body weight and the examined body measurements were reported by all the reviewed literature (Yakubu 2010; Patil et al. 2013; Shirzeyli et al. 2013; Agamy et al. 2015; Singh et al. 2020). The observed highest correlation coefficient was also noticed for sheep breeds by Atta and El Khidir (2004), Elsheikh et al. (2012), Sam et al. (2016) and Ali et al. (2017) and in goat by Nsoso et al. (2003) Thiruvenkadan (2005), Khan et al. (2006), Abdel-Mageed and Ghanem (2013) and Abd-Alla (2014). Lawrence and Fowler (1997) added that skeletal measurements (wither height and body length) were less variable for body weight compared to heart girth. It is documented that there is a close relationship between the distance around an animal’s heart girth and its body weight (Otoikhian et al. 2008). Choosing heart girth as the predictor of body weight in the present study, complies with the observations of Singh et al. (2020), Kamarudin et al. (2011) and Ravimurugan et al. (2013). They reported that since it has the highest correlation with body weight, it may be used as a selection criterion to improve body weight indirectly, and it is the most practical way to estimate the live weight of goats. These findings agree with those of Nigm et al. (1995) who found that heart girth was the best single predictor and accounted for 77% of the variation in body weight of Merino males. Agamy et al. (2015) noted that the best equation for predicting the live body weight of Rahmani lambs was attained when heart girth and body length were included in the equation with the coefficient of determination (R²) being 92%. In the same context, Abdel-Moneim (2009) found that body length and heart girth accounted for 47 and 86% of the body weight of Barki and Rahmani, respectively, whereas both paunch girth and body length represented 93% of the variation in Ossimi’s body weight.

Topal et al. (2003) reported that the coefficient of determination of regression (R²) and error of estimate (SE) might be confidently applied to investigate the fitting state of simple and multiple regression models for the estimation of body weight in livestock. Accordingly, the present power model was reported as the best-fitting regression since it has the highest determination coefficient (R²) and lowest error of estimate. These findings agreed with those reported by Brody (1945). In the same context, Atta and El Khidir (2004) studied the relationship between body weight and linear measurements of Nilotic sheep (from birth to onset of puberty). They found that the regressions of live weight on body measurements showed a non-linear relationship based on y = ax^b. where the prediction of the body weight of Nilotic sheep can be based on y = 0.0001668×^2.867 for males and y = 0.0010674×^2.407 for females, where y and x are body weight and heart girth, respectively. The present power regression equations did not show any significant variation due to animal types (sheep vs. goats), sex (males vs. females) breeds of sheep (Awassi vs. Erbi, Awassi vs. Najdi and Erbi vs. Awassi) and goats (Aaridi vs. Shami). This agreed with the observations of Sam et al. (2016). They reported that the coefficient of determination was highest in the equations with pooled data (irrespective of age) compared to equations formed at different age groups hence, the obtained equations may be used to predict the body weight of West African dwarf goats at different age groups.

The present stepwise multiple regression analysis showed that the equation of the three linear measurements (step 4) had the largest R² and smallest standard error. In this equation, HG resembled 69% of measurement regression coefficients, whereas BL and WH resembled 19% and 13%, respectively. Similar observations were reported by Shirzeyli et al. (2013), Sam et al. (2016) and Singh et al. (2020). They noticed the increase of R² values and decrease of SE values when the number of combined body measurements increased compared to HG alone as body weight predictors. Tadesse et al. (2012) stated that heart girth and length were the most appropriate parameters to predict body weight in the established regression equations. Lawrence and Fowler (1997); Atta and El Khidir (2004) and Chitra et al. (2012) noted that the coefficient of determination of multiple regression of heart girth and any other linear measurement of body weight was slightly higher than that of the simple regression of heart girth on body weight. However, they concluded that live weight estimations based on two or more body measurements were not more accurate than the estimations based on heart girth alone. This conclusion was in line with the present result of regressing values of residue on values of body weight prediction according to the multiple regression model. As illustrated in (Figure 2) this model underestimated prediction at low and heavy weights and overestimated the prediction at medium weights. Whereas the power model depending on HG alone (Figure 1) illustrated a homogeneous trendless distribution of residues with the increase in body weight.

To test the accuracy of the present proposed power model equation, it was examined against the actual body of another small ruminant population. The results indicated the prediction model overestimated actual body weight by about 1.5%. Such error was also mentioned by Johanson and Hildman (1954). They noted that estimating the live weight of cattle from heart girth measurement is slightly greater than the actual body weight. Accordingly, an allowance for variations was added to the equation that is equal to the percentage of the difference between the predicted and actual body weight. To conclude with the corrected model formula:

Body weight (kg) = (0.0006*(HG^2.56))–(1.5*(0.0006*(HG^2.56)/100)).

Conclusion

Body weight and linear body measurements were significantly correlated with each other. Heart girth is the most suitable linear measurement for body weight prediction. The best-fitting model was obtained when the heart girth was included in a power regression equation offering accurate prediction of body weight. So at the field bases body weight can be estimated with a high accuracy using the corrected model:

Body weight (kg) = (0.0006*(HG^2.56))–(1.5*(0.0006*(HG^2.56)/100)).

Therefore, with such a management decision system, performance improvement and genetic resource conservation may be more promising.

Acknowledgements

The authors acknowledge the sincere efforts of workers in the Animal Production Research Station of the Agricultural Research Department. The logistic support received from the department administration is also gratefully acknowledged.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data availability statement

Raw data were generated at the Animal Research Station, Department of Agricultural Researches, Ministry of Municipalities – Qatar. Derived data supporting the findings of this study are available from the corresponding author [M. Atta] on request.