Recent developments on the power graph of finite groups – a survey

Abstract

Algebraic graph theory is the study of the interplay between algebraic structures (both abstract as well as linear structures) and graph theory. Many concepts of abstract algebra have facilitated through the construction of graphs which are used as tools in computer science. Conversely, graph theory has also helped to characterize certain algebraic properties of abstract algebraic structures. In this survey, we highlight the rich interplay between the two topics viz groups and power graphs from groups. In the last decade, extensive contribution has been made towards the investigation of power graphs. Our main motive is to provide a complete survey on the connectedness of power graphs and proper power graphs, the Laplacian and adjacency spectrum of power graph, isomorphism, and automorphism of power graphs, characterization of power graphs in terms of groups. Apart from the survey of results, this paper also contains some new material such as the contents of Section 2 (which describes the interesting case of the power graph of the Mathieu group M11) and Section 6.1 (where conditions are discussed for the reduced power graph to be not connected). We conclude this paper by presenting a set of open problems and conjectures on power graphs.

Keywords:

• Group
• power graph
• connectivity
• spectrum
• automorphism
• isomorphism
• independence number

Mathematics Subject Classification(2000):

• 05C25
• 05C40
• 05C45
• 05C78

1. Introduction

The study of graphical representation of an algebraic structure, especially a semigroup or a group become an energizing research topic over the recent couple of decades, prompting many intriguing outcomes and questions. In this context, the most well-known class of graphs is the Cayley graph. Cayley graphs were firstly presented in 1878, very much considered, and has numerous applications and well-studied. In particular, Cayley graphs of finite groups are used as routing network in parallel computing due to the basic properties that Cayley graph are regular and vertex-transitive. The notion of the power graph of a group is a very recent development in the domain of graphs from groups. The concept of directed power graph $\overrightarrow{\mathit{P}}(G)$ of a group G, introduced by Kelarev and Quinn [51], is a digraph with vertex set G and for any $a,b\in G,$ there is a directed edge from a to b in $\overrightarrow{\mathit{P}}(G)$ if and only if $a^k=b,$ where $k\in \mathbb{N}.$ For a semi-group, it was first considered in [53] and further studied in [52]. All of these papers used the brief term ‘power graph’ to refer to the directed power graph, with the understanding that the undirected power graph is the underlying undirected graph of the directed power graph. Motivated by this, Chakrabarty et al. [20] introduced the concept of an undirected power graph $\mathit{P}(G)$ of a group G, which was defined as follows: Given a group G, the power graph $\mathit{P}(G)$ of G is the simple undirected graph with vertex set G and two vertices $a,b\in G$ are adjacent in $\mathit{P}(G)$ if and only if $b\ne a$ and $b^k=a$ or $a^k=b,k\in \mathbb{N}.$ After that the undirected power graph became the main focus of study by several authors in [2, 13, 15, 31, 60, 61].

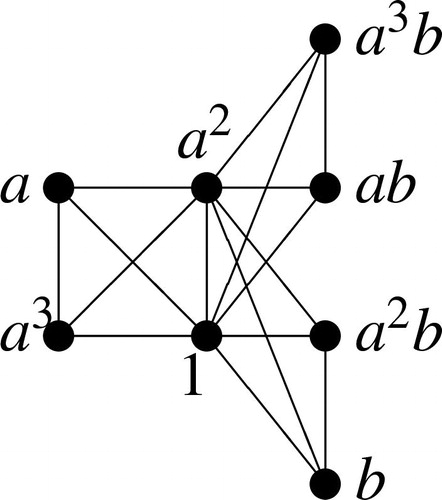
As a simple example, we show the power graph of the group shown in Figure 1. $$Q_8=〈a,b|a^4=1,b^2=a^2,b^{-1}ab=a^{-1}〉.$$

Figure 1. The power graph of Q₈.

Many researchers have contributed towards the understanding of power graphs of groups, especially after 2010. In 2013, Abawajy et al. [2], made a survey about the power graphs in which they provided results about Eulerian, Hamiltonian, and complete characterizations of power graphs. Also, they collected and provided information about the number of edges, chromatic number, clique number, planarity, and isomorphism of power graphs. However, the authors did not explore properties like the spectrum, connectivity, automorphisms of power graphs. Motivated by this, we review both the classical as well as recent results on the power graphs from finite groups. We cover almost every known result about power graphs published after 2013 and also those results which are not available in the previous survey paper [2].

2. A case study: M₁₁

We begin by considering an example in some detail, the Mathieu group M₁₁, a simple group of order $7920=2^4{.3}^2.5.11;$ this group is small enough to be manageable but large enough to illustrate some interesting phenomena. Information about M₁₁ can be found in the Atlas of Finite Groups [30] or discovered using the computer algebra system GAP [43]. We will obtain information about the power graph, and also a construction of an interesting bipartite graph of large girth.

For this section, we only need the definition of the power graph given in the preceding section: the vertex set is the group G; two vertices a and b are joined if one is a power of the other. Let $\Gamma =\mathit{P}(M_{11}).$

The identity is joined to all other vertices in Γ (this is true in any finite group). This also means that the identity is an isolated vertex in the complement of Γ. To analyse further, we remove the identity, giving the so-called reduced power graph ${\mathit{P}}_0(M_{11}).$

Of the remaining vertices, elements of order 11 and 5 are joined only to their powers; these form 144 complete graphs of size 10 and 396 complete graphs of size 4. (Now we observe that the non-identity elements form a single connected component in the complement of the power graph, since for any two such elements x and y, there is an element z of order 11 such that $x,y\notin 〈z〉)$.

We remove the vertices of orders 5 and 11, and consider the remaining 4895 vertices, corresponding to elements whose orders are divisible by the primes 2 or 3 only. In detail, there are 165 of order 2, 440 of order 3, 990 of order 4, 1320 of order 6 and 1980 of order 8. Next we notice that vertices which generate the same cyclic subgroup have the same closed neighbourhood in the graph. (We will define $x\sim y$ to mean that x and y generate the same cyclic group.) Computation shows that the converse is false; the relation ∼ has 2035 equivalence classes, while the relation “same closed neighbourhood” has 1540. If we collapse each equivalence class of the second relation to a single vertex, we obtain a graph with 1540 vertices. This graph contains pairs of vertices with the same open neighbourhoods; collapsing such pairs yields a graph with 1210 vertices, in which no further such reduction is possible. These two reductions preserve connectedness and some other graph-theoretic properties.

We find that the automorphism group of this 1210-vertex graph is the Mathieu group M₁₁, acting with four orbits, of sizes 165 (twice), 220 and 660. Numbering these orbits $O_1,\dots ,O_4,$ let m_ij be the number of edges from a fixed vertex of O_i to a vertex of O_j; the resulting matrix $M=(m_{ij})$ is given by $$M=\left(\begin{array}{cccc}0& 1& 0& 0\\ 1& 0& 0& 4\\ 0& 0& 0& 3\\ 0& 1& 1& 0\end{array}\right).$$

The matrix shows that the graph is bipartite, the bipartite blocks being $O_1\cup O_4$ and $O_2\cup O_3.$ Its diameter and girth are both 20. The edges between O₁ and O₂ form a matching. We obtain an interesting graph with vertex set $O_2\cup O_3$ in which two vertices adjacent if they lie in different orbits but have a common neighbour in O₄. The graph is bipartite; vertices in O₂ have valency 4 while those in O₃ have valency 3. The diameter and girth are both equal to 10, and the automorphism group is again M₁₁.

3. Outline of the survey

This article has been carefully divided into 14 sections. In Section 4, we present the required definitions and notations. Section 5 investigates connectedness of power graphs, including minimal separating sets, disconnecting sets, and results on the vertex connectivity, the edge connectivity along with the relationship between the vertex connectivity and edge connectivity of the power graph of various groups. Section 6 elaborates the results on the connectivity of proper power graphs in which the number of components and the diameter of proper power graphs are also considered. Sections 7 and 8 deal with independence number and perfectness of power graphs, respectively. Section 9 has been devoted to the spectrum of power graphs, which includes the Laplacian spectrum and the adjacency spectrum of power graphs of certain finite groups. The relationship between the vertex connectivity and algebraic connectivity of the power graphs of some finite groups are also presented in this section. Section 10 presents results related to the isomorphism of power graphs, which includes power graphs of infinite groups also. Section 11 contains results on the automorphism of power graphs of finite groups. Followed by this, in Section 12, we present those results which provide the direct connection between the power graphs and their corresponding groups. Section 13 contains other properties of power graphs that cannot be classified into various sections mentioned above. Apart from survey of results, this paper also contains some new material such as Sections 2 and 6.1. We conclude this paper by giving certain open problems and conjectures in Section 14.

4. Definitions and notations

In this section, we present some definitions and notations from group theory and number theory as well as graph theory in order to make this paper self-contained. We use standard definitions and results from [38, 42, 76] for group theory and [8–10, 34] for graph theory which we restate here along with our notations. $\mathbb{N}$ denotes the set of all natural numbers. For a positive integer n, Euler’s phi function $\varphi (n),$ denotes the number of non-negative integers less than n that are relatively prime to n. When we consider the prime factorization of a positive integer $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\cdots p_m^{{\alpha }_m},$ it is assumed that $m\ge 2,$ $p_1<p_2<\cdots <p_m$ are primes and ${\alpha }_i\in \mathbb{N}$ for all i with $1\le i\le m.$

4.1. Group theory

Throughout this paper, G denotes a group that may be of finite or infinite order, with identity e. Let Z(G) denote the center of the group G. For a group G, let ${\pi }_e(G)=\{o(a):a\in G\},$ where o(a) is the order of the element a. The exponent of a finite group G, denoted by $\text{exp}\hspace{0.17em}(G),$ is the least common multiple of orders of all its elements. Let $\pi (G)$ be the set of all prime numbers p dividing the order of G, equivalently primes p such that G has an element of order p. A group G is called torsion-free if $o(a)=\infty$ for all $a\in G\setminus \left\{e\right\}.$ A group G is said to be of bounded exponent, if there exists $n\in \mathbb{N}$ such that $a^n=e$ for all $a\in G.$ A group G is said to be an EPO-group if every non-identity element of G is of prime order. A finite Abelian group G with identity e is called CP group if the order of every non-identity element is a power of a prime number. A group G is locally finite if every finitely generated subgroup $H=〈a_1,a_2,\dots ,a_k〉$ of G, is of finite order. Further, G is called locally center-by-finite, if every finitely generated subgroup H of G has centre of finite index in H. We use $〈S〉$ for the subgroup of G generated by the subset S. Let $\sigma (G)$ be the number of cyclic subgroups and $\tau (G)$ denote the order of the smallest cyclic subgroup of G.

Define a relation ∼ on G by $a\sim b$ if $〈a〉=〈b〉,$ where $〈a〉$ is the cyclic subgroup of G generated by $a\in G.$ It can be seen that ∼ is an equivalence relation on G. We denote the equivalence class containing $a\in G$ under ∼ by $[a].$ We note here that if $a\sim b,$ then a and b are joined in the power graph of G, and they have the same neighbours (except for one another).

${\mathbb{Z}}_n=\{\overline{0},\overline{1},\dots ,\overline{n-1}\}$ denotes the finite cyclic group of order n. The notation ${\mathbb{Z}}_m^n$ means that the direct product of n copies of ${\mathbb{Z}}_m.$ $S({\mathbb{Z}}_n)$ denotes the set of all generators together with the identity element of the group ${\mathbb{Z}}_n.$ That is, $S({\mathbb{Z}}_n)=\{\overline{a}:1\le a<n,\gcd (a,n)=1\}\cup \left\{\overline{0}\right\}.$ We use the following:

• $D_{2n}=〈a,b|a^n=b^2=e, ab=b{a}^{-1}〉$ denotes the dihedral group of order 2n;

• $Q_{4n}=〈a,b|a^{2n}=e,a^n=b^2,ab=b{a}^{-1}〉$ denotes the dicyclic group of order 4n. If n is a power of 2, this group is the generalized quaternion group.

• S_n and A_n denote the symmetric group and the alternating group on the set of n symbols, respectively.

For $\sigma \in A_n,$ the support of σ is denoted by $\text{Supp}(\sigma )$ and is defined by $\text{Supp}(\sigma )=\{i:\sigma (i)\ne i\}.$

We recall here a theorem of Burnside (see [44, Theorem 12.5.2]):

Theorem 4.1.

[44, Theorem 12.5.2] Let G be a finite group whose order is a power of a prime p. Suppose that G has a unique subgroup of order p. Then either

1. G is cyclic; or

2. p = 2 and G is a generalized quaternion group.

4.2. Graph theory

Throughout this paper $\Gamma =(V,E)$ denotes a graph with vertex set V and edge set E. $\delta (\Gamma )$ denotes the minimum among degrees of vertices in Γ. For a subset $A\subseteq V$ of vertices in a graph $\Gamma =(V,E),$ the induced subgraph $〈A〉$ is the subgraph of Γ with vertices in A and edges with both ends in A. A set of vertices T of a graph Γ is said to be a separating set or cut-set, if its removal increases the number of connected components of Γ. T is called a minimal separating set or minimal cut-set if none of its non-empty proper subset is a separating set. If T is of least cardinality, then it is called a minimum separating set or minimum cut-set of Γ. The cardinality of a minimum separating set is called the vertex connectivity of Γ and it is denoted by $\kappa (\Gamma ).$

A subgraph of $\Gamma =(V,E)$ is one of the form $(V\prime ,E\prime ),$ where $V\prime \subseteq V$ and $E\prime \subseteq E$ such that the vertices on each edge of $E\prime$ lie in $V\prime .$ If all edges of V with both vertices in $V\prime$ belong to $E\prime ,$ it is an induced subgraph; if $V\prime =V,$ it is a spanning subgraph. A graph Δ is a forbidden subgraph for Γ if no induced subgraph of Γ is isomorphic to Δ. A disconnecting set of Γ is a set of edges whose removal increases the number of connected components of Γ. A disconnecting set is said to be minimal if none of its proper subsets disconnects Γ. A minimum disconnecting set of Γ is a disconnecting set of Γ with least cardinality. If $A,B\subseteq V(\Gamma ),$then the set of all edges having one end in A and the other in B is denoted by $E[A,B].$ If $A=\left\{v\right\},$ we write $E[v,B]$ instead of $E[A,B].$ The diameter, $\text{diam}(\Gamma ),$ of a graph Γ is the maximum distance between two vertices of Γ. If Γ is not connected, the diameter is defined to be $\infty .$ The girth of Γ, denoted by $g(\Gamma ),$ is the length of a shortest cycle in $\Gamma .$ A subset $X\subset V$ of $\Gamma =(V,E)$ is called an independent set, if there does not exist any edge in Γ whose both end vertices are in X. The cardinality of a largest independent set, denoted by $\beta (\Gamma )$ is called independence number of Γ. A complete subgraph of Γ is called a clique, and the supremum of size of cliques in Γ, denoted by $\omega (\Gamma )$ is called the clique number of Γ. A subset $S\subset V$ of Γ is called a dominating set, if for any $v\in V,$ either $v\in S$ or there exists a vertex $w\in S$ such that v is adjacent to w. The cardinality of a minimum dominating set is denoted by $\gamma (\Gamma )$ and is called the dominating number of Γ.

For $\Gamma =(V,E)$ and $a\in V,$ the neighbourhood of a is denoted by N(a) and its defined as $N(a)=\{b\in V|b\mathrm{ }\text{is}\mathrm{ }\text{adjacent}\mathrm{ }\text{to}\mathrm{ }a\}.$ We sometimes call this the open neighbourhood of a, as opposed to the closed neighbourhood $N(a)\cup \left\{a\right\}.$ The chromatic number of Γ is denoted by $\chi (\Gamma )$ is the smallest number of colors needed to color the vertices of Γ so that no two adjacent vertices receive the same color.

A graph Γ is called perfect if the chromatic number of any finite induced subgraph of Γ is equal to its clique number. We recall the Strong Perfect Graph Theorem of Chudnovsky et al. [29], which characterizes perfect graphs by forbidden subgraphs and is given in Theorem 8.1(ii) of this survey.

Other interesting classes of graphs such as cographs, chordal graphs, split graphs, and threshold graphs, and the concepts of open and closed twins and twin reduction, will be introduced later.

5. Connectivity of power graphs

This section is divided into six subsections, which are devoted to the results based on vertex connectivity of power graphs, edge connectivity of power graphs and equality of these two parameters. Recall that for a given group G, the power graph $\mathit{P}(G)$ of G is the simple undirected graph with vertex set G and two vertices $a,b\in G$ are adjacent in $\mathit{P}(G)$ if and only if $b\ne a$ and $b^k=a$ or $a^k=b,$ for some $k\in \mathbb{N}.$ The power graph of any finite group is connected with diameter at most 2, since there is an edge from any non-identity group element to the identity. In other words, {e} is a dominating set in $\mathit{P}(G).$

5.1. Vertex connectivity of power graphs of finite cyclic groups

The finite cyclic group ${\mathbb{Z}}_n,$ the dihedral group $D_{2n},$ and the dicyclic group $Q_{4n}$ play an important role in the deeper parts of finite group theory, and invariably they appear as subgroups of a given group. The connectivity of the power graph of certain finite cyclic groups of particular order and their generalization was dealt in [21, 22, 26]. In continuation of these results, Panda and Krishna [70] focused on the power graph of finite cyclic groups in general and obtained minimal separating sets of the power graph $\mathit{P}({\mathbb{Z}}_n),$ which in turn gives the vertex connectivity of the power graph $\mathit{P}({\mathbb{Z}}_n).$ For a given $X\subset {\mathbb{Z}}_n,X^c={\mathbb{Z}}_n\setminus X$ and $〈X^c〉$ is the induced subgraph of $\mathit{P}({\mathbb{Z}}_n)$ induced by X^c.

Recall that $S({\mathbb{Z}}_n)$ denotes the set of all generators together with the identity of the group ${\mathbb{Z}}_n.$ For an arbitrary element $a\in {\mathbb{Z}}_n,$ a is some power of each of the generators of ${\mathbb{Z}}_n$ and some power of a is the identity. Due to this, every element in $S({\mathbb{Z}}_n)$ is adjacent to every other element in $\mathit{P}({\mathbb{Z}}_n).$ Hence the induced subgraph $〈S{({\mathbb{Z}}_n)}^c〉$ plays some vital role in the connectivity of $\mathit{P}({\mathbb{Z}}_n).$ For a subset $A\subset {\mathbb{Z}}_n,$ $A^{*}=A\setminus \left\{e\right\}.$

Chattopadhyay and Panigrahi [21, 22], determined the tight lower bound for the vertex connectivity of power graphs corresponding to cyclic groups ${\mathbb{Z}}_n$ and gave exact value of $\kappa (\mathit{P}({\mathbb{Z}}_n))$ when n is a power of some prime number. After that, many researchers extended these results and gave an upper bound of $\kappa (\mathit{P}({\mathbb{Z}}_n))$ for different values of n. Also, the vertex connectivity of the dihedral group $D_{2n},$ dicyclic group $Q_{4n},$ non-cyclic finite nilpotent group and non-cyclic abelian group of finite order were computed. The results in this regard are given below:

Theorem 5.1.

[21, Theorem 3]. The vertex connectivity $\kappa (\mathit{P}({\mathbb{Z}}_n))$ of the power graph of the finite cyclic group ${\mathbb{Z}}_n,$ can be computed as follows:

1. $\kappa (\mathit{P}({\mathbb{Z}}_n))=n-1$ when $n=1 or p^{\alpha },$ where p is a prime number and α is an non negative integer;

2. $\kappa (\mathit{P}({\mathbb{Z}}_n)))\ge \varphi (n)+1,$ when $n\ne p^{\alpha }.$ Further equality holds when $n=p_1{p}_2$ for distinct primes p₁ and p₂.

In 2015, Chattopadhyay and Panigrahi [22], obtained another lower bound for the vertex connectivity of power graphs of certain finite cyclic groups and the same is given below.

Theorem 5.2.

[22, Theorem 2.7] Let $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}$, where ${\alpha }_1,{\alpha }_2\in \mathbb{N}$ and p₁, p₂ are distinct primes. Then the vertex connectivity $\kappa (\mathit{P}({\mathbb{Z}}_n))$ of $\mathit{P}({\mathbb{Z}}_n)$ satisfies the inequality $\kappa (\mathit{P}({\mathbb{Z}}_n))\le \varphi (n)+p_1^{{\alpha }_1-1}{p}_2^{{\alpha }_2-1}.$

Theorem 5.3.

[22, Theorem 2.9] For $n=p_1{p}_2{p}_3,$ where $p_1<p_2<p_3$ are primes, the vertex connectivity $\kappa (\mathit{P}({\mathbb{Z}}_n))$ of $\mathit{P}({\mathbb{Z}}_n)$ satisfies the inequality $\kappa (\mathit{P}({\mathbb{Z}}_n))\le \varphi (n)+p_1+p_2-1.$

A natural question that arises is whether the converse of Theorem 5.1 is true. Since no information was provided by the authors in [21], Panda and Krishna [70], gave the answer for the above question in affirmative.

Lemma 5.4.

[70, Lemma 2.4] Let n > 1 be an integer which is not a prime number. Then the following statements hold:

1. If n is not prime power then every separating set of $\mathit{P}({\mathbb{Z}}_n)$ contains $S({\mathbb{Z}}_n).$

2. $\kappa (\mathit{P}({\mathbb{Z}}_n))=1+\varphi (n)+\kappa 〈S{({\mathbb{Z}}_n)}^c〉.$

3. If $p_1<p_2<\cdots <p_m$ are factors of n, then ${\mathbb{Z}}_n^c={\cup }_{i=1}^n〈{\overline{p_i}}^{*}〉.$

Proposition 5.5.

[70, Proposition 2.5] For $n\in \mathbb{N}$, the following statements are equivalent:

1. $n=p_1{p}_2$, where $p_1\ne p_2$ are primes;

2. $S({\mathbb{Z}}_n)$ is a separating set of $\mathit{P}({\mathbb{Z}}_n);$

3. $\kappa (\mathit{P}({\mathbb{Z}}_n))=\varphi (n)+1.$

In [70], Panda and Krishna improved Theorems 5.2 and 5.3 by giving exact expression of $\kappa (\mathit{P}({\mathbb{Z}}_n))$ where n is the product of powers of two distinct primes and the same is given below.

Proposition 5.6.

[70, Theorem 2.38] Assume that $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}$, where p₁, p₂ are distinct primes and ${\alpha }_1,{\alpha }_2\in \mathbb{N}.$ Then $\kappa (\mathit{P}({\mathbb{Z}}_n))=\varphi (n)+p_1^{{\alpha }_1-1}{p}_2^{{\alpha }_2-1}$. In fact, for $n\ne p_1{p}_2,〈{\overline{p_1{p}_2}}^{*}〉$ is a minimum separating set of $〈S{({\mathbb{Z}}_n)}^c〉.$

Corollary 5.7.

[70, Theorem 2.39] If $n=2^{\alpha }{p}^{\beta },\alpha ,\beta \in \mathbb{N}$ and p is an odd prime, then $\kappa (\mathit{P}({\mathbb{Z}}_n))=\frac{n}{2}.$

In the following theorem, we see the exact expression for $\kappa (\mathit{P}({\mathbb{Z}}_n))$ where n is the product of three distinct primes.

Theorem 5.8.

[70, Theorem 2.40] If $n=p_1{p}_2{p}_3$, where $p_1<p_2<p_3$ are primes, then $[\overline{p_1{p}_3}]\cup [\overline{p_2{p}_3}]$ is a minimum separating set of $〈S{({\mathbb{Z}}_n)}^c〉$ and consequently, $\kappa (\mathit{P}({\mathbb{Z}}_n))=\varphi (n)+p_1+p_2-1.$

In article [70], the authors provided certain sharp upper bounds for $\kappa (\mathit{P}({\mathbb{Z}}_n))$ and proved that equality holds if $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}$ or $n=p_1{p}_2{p}_3.$

Theorem 5.9.

[70, Theorem 2.23] Suppose $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\cdots p_m^{{\alpha }_m}$. Then $$\kappa (\mathit{P}({\mathbb{Z}}_n))\le {\theta }_1(n):=\varphi (n)+\frac{n}{p_m}-p_m^{{\alpha }_m-1}\varphi \left(\frac{n}{p_m^{{\alpha }_m}}\right).$$

Theorem 5.10.

[70, Theorem 2.35] Suppose n is not of the form $p_1{p}_2$ and $n=p_1^{{\alpha }_1}\cdots p_m^{{\alpha }_m}.$ Then $$\kappa (\mathit{P}({\mathbb{Z}}_n))\le {\theta }_2(n):=\varphi (n)+\frac{n}{p_m^{{\alpha }_m}}+\varphi \left(\frac{n}{p_m^{{\alpha }_m}}\right)(p_m^{{\alpha }_m-1}-2).$$

In the following theorem, the authors compared these upper bounds ${\theta }_1(n)$ and ${\theta }_2(n)$ obtained in Theorems 5.9 and 5.10.

Theorem 5.11.

[70, Theorem 2.36] Suppose n is not a product of two primes and having factorization $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\cdots p_m^{{\alpha }_m}$. Then

1. ${\theta }_1(n)={\theta }_2(n)$ if and only if ${\alpha }_m=1$, or m = 2 and $p_1=2$;

2. ${\theta }_1(n)>{\theta }_2(n)$ if and only if ${\alpha }_m\ge 2$ and ${\prod }_{i=1}^{m-1}(1-\frac{1}{p_i})<\frac{1}{2}$;

3. ${\theta }_1(n)<{\theta }_2(n)$ if and only if ${\alpha }_m\ge 2$ and ${\prod }_{i=1}^{m-1}(1-\frac{1}{p_i})>\frac{1}{2}.$

Chattopadhyay et al. [26] independently obtained both the upper bounds ${\theta }_1(n)$ and ${\theta }_2(n)$ given in Theorems 5.9 and 5.10. Moreover, they proved that if $2\varphi (p_1\cdots p_{m-1})>p_1\cdots p_{m-1},$ then the bound ${\theta }_1(n)$ is sharp. i.e., $\kappa (\mathit{P}({\mathbb{Z}}_n))={\theta }_1(n)$ (see (i) and (iii) of Theorem 5.12). As a consequence, if $p_1\ge m,$ then $\kappa (\mathit{P}({\mathbb{Z}}_n))={\theta }_1(n)$ (see Corollary 5.13). It was shown in Theorem 5.14 that the bound ${\theta }_2(n)$ is sharp. i.e., $\kappa (\mathit{P}({\mathbb{Z}}_n))={\theta }_2(n)$ for integers $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}{p}_3^{{\alpha }_3},$ with $2\varphi (p_1{p}_2)<p_1{p}_2$ so necessarily $p_1=2.$ However, in view of Example 3.4 [26], equality may not hold in Theorem 5.10 in general if $2\varphi (p_1{p}_2\cdots p_{m-1})<p_1{p}_2\cdots p_{m-1}.$

Theorem 5.12.

[26, Theorem 1.3] Let $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\cdots p_m^{{\alpha }_m}$. Then the following hold:

1. If $2\varphi (p_1{p}_2\cdots p_{m-1})>p_1{p}_2\cdots p_{m-1}$, then $\kappa (\mathit{P}({\mathbb{Z}}_n))=$ $$\varphi (n)+p_1^{{\alpha }_1-1}{p}_2^{{\alpha }_2-1}\cdots p_m^{{\alpha }_m-1}[p_1{p}_2\cdots p_{m-1}-\varphi (p_1{p}_2\cdots p_{m-1})].$$

   Further, there exists only one subset X of ${\mathbb{Z}}_n$ with $\left|X\right|=\kappa (\mathit{P}({\mathbb{Z}}_n))$ such that the induced subgraph $〈X^c〉$ of $\mathit{P}({\mathbb{Z}}_n)$ is disconnected.

2. If $2\varphi (p_1{p}_2\cdots p_{m-1})<p_1{p}_2\cdots p_{m-1}$, then $\kappa (\mathit{P}({\mathbb{Z}}_n))\le \varphi (n)+p_1^{{\alpha }_1-1}{p}_2^{{\alpha }_2-1}\cdots p_{m-1}^{{\alpha }_{m-1}-1}[p_1{p}_2\cdots p_{m-1}+\varphi (p_1{p}_2\cdots p_{m-1})(p_m^{{\alpha }_m-1}-2)].$

3. If $2\varphi (p_1{p}_2\cdots p_{m-1})=p_1{p}_2\cdots p_{m-1}$, then $m=2,p_1=2(\text{so}\mathrm{ }\text{that} n=2^{{\alpha }_1}{p}_2^{{\alpha }_2}) \mathit{and} \kappa (\mathit{P}({\mathbb{Z}}_n))=\varphi (n)+2^{{\alpha }_1-1}{p}_2^{{\alpha }_2-1}.$

Moreover, there are exactly α₂ subsets X of ${\mathbb{Z}}_n$ with $\left|X\right|=\kappa (\mathit{P}({\mathbb{Z}}_n))$ such that induced subgraph $〈X^c〉$ of $\mathit{P}({\mathbb{Z}}_n)$ is disconnected.

The following result is a consequence of Theorem 5.12 (i) and (ii), when the total number of distinct prime divisors of n less than or equal to the smallest prime divisor of n.

Corollary 5.13.

[26, Corollary 1.4] If $p_1\ge m$, then $$\kappa (\mathit{P}({\mathbb{Z}}_n))=\varphi (n)+p_1^{{\alpha }_1-1}{p}_2^{{\alpha }_2-1}\cdots p_m^{{\alpha }_m-1}[p_1{p}_2\cdots p_{m-1}-\varphi (p_1{p}_2\cdots p_{m-1})].$$

By proving the following theorem, the authors exhibited that the bound is sharp for many values of n.

Theorem 5.14.

[26, Theorem 1.5] Let $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}{p}_3^{{\alpha }_3}$, where ${\alpha }_i\in \mathbb{N},$ for each $1\le i\le 3$ and $p_1<p_2<p_3$ are primes. If $2\varphi (p_1{p}_2)<p_1{p}_2$, then $$p_1=2 \mathit{and} \kappa (\mathit{P}({\mathbb{Z}}_n))=\varphi (n)+2^{{\alpha }_1-1}{p}_2^{{\alpha }_2-1}[(p_2-1)p_3^{{\alpha }_3-1}+2].$$

Further, there is only one subset X of ${\mathbb{Z}}_n$ with $\left|X\right|=\kappa (\mathit{P}({\mathbb{Z}}_n))$ such that the induced subgraph $〈X^c〉$ of $\mathit{P}({\mathbb{Z}}_n)$ is disconnected.

In view of the fact proved in Theorem 5.14, the vertex connectivity of $\mathit{P}({\mathbb{Z}}_n)$ is completely determined for $m\le 3.$ A natural question arises: can we find vertex connectivity of $\mathit{P}({\mathbb{Z}}_n)$ when n has more than three prime factors? that is m > 3. Chattopadhyay et al. [27] gave partial affirmative answer to this question. Let $$\begin{array}{c}{\theta }_3(n)=\varphi (n)+\frac{n}{p_1{p}_2\cdots p_m}[\varphi (p_1{p}_2\cdots p_{m-1})+\varphi (p_1{p}_2\cdots p_{m-2}{p}_m)+\\ p_1{p}_2\cdots p_{m-2}-\varphi (p_1{p}_2\cdots p_{m-2})].\end{array}$$

In the following theorem, it is observed that ${\theta }_3(n)$ is an upper bound for the vertex connectivity of the power graph in certain cases of n.

Theorem 5.15.

[27, Theorem 1.1] Let $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\cdots p_m^{{\alpha }_m},m\ge 3,p_1<p_2<\cdots <p_m$ are primes and ${\alpha }_i\in \mathbb{N}$ for $1\le i\le m$. Then $\kappa (\mathit{P}({\mathbb{Z}}_n))\le {\theta }_3(n).$

Theorem 5.16.

[27, Theorem 1.2] Let $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\cdots p_m^{{\alpha }_m},m\ge 3,p_1<p_2<\cdots <p_m$ are primes and ${\alpha }_i\in \mathbb{N}$ for $1\le i\le m$. If ${\alpha }_m\ge 2$, then $\kappa (\mathit{P}({\mathbb{Z}}_n))=\min \{{\theta }_1(n),{\theta }_j(n):1\le j\le m,{\alpha }_j\ge 2\}$, where $${\theta }_j(n)=\varphi (n)+\frac{n}{p_1{p}_2\cdots p_m}\times \frac{1}{p_j^{{\alpha }_j-1}}\left[\frac{p_1{p}_2\cdots p_m}{p_j}+\varphi \left(\frac{p_1{p}_2\cdots p_m}{p_j}\right)(p_j^{{\alpha }_j-1}-2)\right].$$

Theorem 5.17.

[27, Theorem 1.3] Let $n=p_1{p}_2\cdots p_m,m\ge 3$, where $p_1<p_2<\cdots <p_m$ are primes. Then $\kappa (\mathit{P}({\mathbb{Z}}_n))=\min \{{\theta }_3(n),{\theta }_1(n)\}.$

5.2. Vertex connectivity in power graphs of other groups

In this subsection, we are concerned with the vertex connectivity of power graphs of other groups such as the dihedral and dicyclic groups. Chattopadhyay et al. [21] obtained results on the vertex connectivity of these groups:

Theorem 5.18.

[21, Theorem 5] The identity element e of $D_{2n}$ is a cut vertex of the dihedral group $\mathit{P}(D_{2n})$ and so $\kappa (\mathit{P}(D_{2n}))=1$ for all $n\ge 2.$

Theorem 5.19.

[21, Theorem 7] For all $n\ge 2,$ the vertex connectivity of the dicyclic group $Q_{4n}$ is given by $\kappa (\mathit{P}(Q_{4n}))=2.$

Proposition 5.20.

[70, Corollary 3.4] If G is a non-cyclic abelian group of order $n=p^{\alpha }$, where p is a prime number and $\alpha \in \mathbb{N}$, then $\kappa (\mathit{P}(G))=1.$

In [28], the authors computed the vertex connectivity of power graphs of some special classes of groups which includes finite non-cyclic nilpotent groups, finite non-cyclic abelian groups and non-cyclic groups of finite orders.

In this and following results, we denote by $\mathcal{M}(G)$ the collection of all maximal cyclic subgroups of G. If H is a cyclic subgroup of G, then $\tilde{H}$ denotes the set of non-generators in H.

Theorem 5.21.

[28, Theorem 1.2] Let G be a finite non-cyclic nilpotent group of order $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\cdots p_m^{{\alpha }_m},m\ge 2$. Let P_i be the Sylow p_i-subgroup of G, for each $1\le i\le m$ and assume that each of them is cyclic except P_r for some $r\in \{1,2,\dots ,m\}$ and that P_r is not a generalized quaternion group if r = 1 and $p_1=2$. Set $Q=P_1\cdots P_{r-1}{P}_{r+1}\cdots P_m$. If $p_r\ge m+1$ or if $2\varphi (p_1\cdots p_{m-1})>p_1\cdots p_{m-1}$, then Q is the only minimal separating set of $\mathit{P}(G)$ and so $\kappa (\mathit{P}(G))=\frac{n}{p_r^{{\alpha }_r}}.$

Theorem 5.22.

[28, Theorem 1.3] Let G be a non-cyclic abelian group of order $p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}$ and P₁, P₂ denote its Sylow p_i-subgroups for i = 1, 2. Then following statements hold good.

1. Suppose that one of the Sylow subgroups is non-cyclic. If P_i is non-cyclic, then P_j is a minimum separating set of $\mathit{P}(G)$ and so $\kappa (\mathit{P}(G))=\left|P_j\right|=p_j^{{\alpha }_j}$, where $\{i,j\}=\{1,2\}$. In fact, if $p_1\ge 3$, or $p_1=2$ and P₂ is non-cyclic, then there exists only one minimum separating set of $\mathit{P}(G).$

2. Suppose both Sylow subgroups are non-cyclic. If $p_1\ge 3$ and G has a maximal cyclic subgroup M of order $p_1{p}_2$, then $\kappa (\mathit{P}(G))=\min \{\left|P_1\right|,\varphi (\left|M\right|)\}.$

3. Suppose both P₁ and P₂ are non-cyclic and P₁ is elementary abelian. Then $\kappa ((\mathit{P}(G)))=\min \{\left|P_1\right|,\varphi (\left|M\right|)\}$, where M is maximal cyclic subgroup of G of least possible order.

Remark 5.23.

If $p_1=2$ and exactly one of the Sylow subgroups G is non-cyclic in Theorem 5.22(i), then we can have more than one minimum separating set of $\mathit{P}(G)$ (see [28, Example 4.3]).

Theorem 5.24.

[28, Theorem 1.4] Let G be a non-cyclic abelian group of order $p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}{p}_3^{{\alpha }_3}$ and P_i be a Sylow p_i-subgroup of G for $i\in \{1,2,3\}$. Suppose that exactly two Sylow subgroups of G are cyclic. Then the following statements hold.

1. If $p_1=2$ and P₁ is non-cyclic, then $\kappa (\mathit{P}(G))=\min \{\left|P_1{P}_2\right|,\kappa (\mathit{P}(M))\}$, where M is a maximal cyclic subgroup of G of least possible order. More precisely, if $\left|M\right|=2^{\alpha }{p}_1^{{\alpha }_1}{p}_2^{{\alpha }_2}$ for some $\alpha \in \mathbb{N}$, then $$\kappa (\mathit{P}(G))=\{\begin{array}{cc}\left|P_2{P}_3\right|\hfill & \mathit{\text{if}} \alpha >1;\hfill \\ \kappa (\mathit{P}(M))\hfill & \mathit{\text{if}} \alpha =1.\hfill \end{array}$$

2. If $p_1=2$ and P_k is non-cyclic, then $P_1{P}_j$ is the only minimum separating set of $\mathit{P}(G)$ and so $\kappa (\mathit{P}(G))=\left|P_1{P}_j\right|=p_1^{{\alpha }_1}{p}_j^{{\alpha }_j}$, where $\{j,k\}=\{2,3\}.$

3. If $p_1\ge 3$ and P_k is non-cyclic, then $P_i{P}_j$ is the only minimum separating set of $\mathit{P}(G)$ and so $\kappa (\mathit{P}(G))=\left|P_i{P}_j\right|=p_i^{{\alpha }_i}{p}_j^{{\alpha }_j}$, where $\{i,j,k\}=\{1,2,3\}.$

Remark 5.25.

[28] One can see that $\kappa (\mathit{P}(G))$ in Theorem 5.24(i) can also be obtained using the expression in Theorem 5.14.

5.3. Separating sets of power graphs

Recall that ∼ on G is defined by $a\sim b$ if $〈a〉=〈b〉,$ where $〈a〉$ is the cyclic subgroup of G generated by $a\in G.$ It can be seen that ∼ is an equivalence relation on G. We denote the equivalence class of containing $a\in G$ under ∼ by $[a].$ The quotient graph of $\mathit{P}(G)$ is called the quotient power graph of G and is denoted by $\tilde{\mathit{P}}(G).$

Theorem 5.26.

[70, Theorem 2.16] Let G be a finite group. If T is a minimal separating set of $\mathit{P}(G)$, then T is a union of ∼ classes.

Theorem 5.27.

[70, Theorem 2.17] For $T\subset G$, T is a minimal separating set of $\mathit{P}(G)$ if and only if $[T]$ is a minimal separating set of $\tilde{\mathit{P}}(G)$ and T is a union of ∼ classes.

Theorem 5.28.

[70, Theorem 2.18] Let T be a separating set of $\mathit{P}(G)$. Then T is a minimal separating set of $\mathit{P}(G)$ if and only if $[T]$ is a minimal separating set of the quotient power graph $\tilde{\mathit{P}}(G).$

Lemma 5.29.

[70, Lemma 2.16] Let G be a finite group and $a\in G$. Then the following are equivalent:

1. N(a) is a separating set of $\mathit{P}(G).$

2. $N([a])$ is a separating set of $\tilde{\mathit{P}}(G).$

3. There exists some $b\in G$ such that a is not adjacent to b.

Lemma 5.30.

[70, Lemma 2.29] Let G be finite group and $a\in G$ with $o(a)\ge 3$. Then N(a) is not a minimal separating set of $\mathit{P}(G).$

Theorem 5.31.

[70, Theorem 2.21] If $n\in \mathbb{N}$ is not of the form $p_1{p}_2$ and $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\cdots p_m^{{\alpha }_m},$ then, for any $1\le j\le m,$ ${\cup }_{i=1,i\ne j}^m〈{\overline{p_i{p}_j}}^{*}〉$ is a minimal separating set of the induced subgraph $〈S{({\mathbb{Z}}_n)}^c〉.$

Now a natural question arises: what will happen with power graphs of non-cyclic finite groups? Motivated by this, Chattopadhyay et al. [28], proved some results on power graphs by considering some special classes of groups including non-cyclic finite nilpotent groups and non-cyclic Abelian groups of finite order which are corresponding to their maximal cyclic subgroups. First, let us see the case of a non-cyclic group.

Proposition 5.32.

[28, Proposition 2.2] Suppose G is a non-cyclic group and let $M\in \mathcal{M}(G)$. If $A=G\setminus M$ and $B=M\setminus \tilde{M}$, then (A, B) forms a separation of $\mathit{P}(G\setminus \tilde{M})$. In particular, $\tilde{M}$ is a separating set of $\mathit{P}(G).$

Proposition 5.33.

[28, Proposition 2.6] Suppose G is a non-cyclic group and T is a minimal separating set of $\mathit{P}(G)$. Then the following are equivalent:

1. If T has no element which will generate a member of $\mathcal{M}(G)$, then $\mathit{P}(M\setminus T)$ is connected for every $M\in \mathcal{M}(G).$

2. If T is a minimal cut-set of $\mathit{P}(G)$ and $\mathit{P}(M\setminus T)$ is connected for every $M\in \mathcal{M}(G)$, then T has no element which will generate a member of $\mathcal{M}(G).$

Proposition 5.34.

[28, Proposition 2.16] If G has at least two non-cyclic Sylow subgroups, then, for any $M\in \mathcal{M}(G),T=\overline{M}$ is a minimal separating set of $\mathit{P}(G).$

Proposition 5.35.

[28, Proposition 2.17] Let G be a nilpotent group of order $n=p_1^{{\alpha }_1}\cdots \mathrm{ }{p}_m^{{\alpha }_m},m\ge 2$ and P_r is neither cyclic nor a generalized quaternion group for some $r\in \{1,2,\dots ,m\}$. Then $Q=P_1{P}_2\cdots P_{r-1}{P}_{r+1}\cdots P_m$ is a minimal separating set of $\mathit{P}(G).$

5.4. Disconnecting Sets in power graphs

In [71], Panda and Krishna determined minimum disconnecting sets of power graphs of finite cyclic groups, dihedral groups, dicyclic groups and abelian p-groups of finite order.

Corollary 5.36.

[71, Corollary 4.8] Let $n\in \mathbb{N}$ and $p_1<p_2<p_3<p_4$ be prime numbers.

1. If $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2},{\alpha }_1,{\alpha }_2\in \mathbb{N},$ then for any $\overline{a}\in [p_2^{\overline{{\alpha }_2}}],E\left[\overline{a},〈p_2^{\overline{{\alpha }_2}}〉\cup {\cup }_{i=0}^{{\alpha }_2-1}\left[\overline{p_2^i}\right]-\overline{a}\right]$ is a minimum disconnecting set of $\mathit{P}({\mathbb{Z}}_n);$

2. If $n=p_1{p}_2{p}_3$, then for any $\overline{a}\in [\overline{p_3}],E\left[\overline{a},〈\overline{p_3}〉\cup [\overline{1}]-\overline{a}\right]$ is a minimum disconnecting set of $\mathit{P}({\mathbb{Z}}_n);$

3. Let $n=p_1{p}_2{p}_3{p}_4.$

   If n is odd or $p_4\ge p_3+\frac{2(p_3-1)}{p_2-1}$, then for any $\overline{a}\in [\overline{p_4}],E\left[\overline{a},〈\overline{p_4}〉\cup \left[\overline{1}\right]-\overline{a}\right]$ is a minimum disconnecting set of $\mathit{P}({\mathbb{Z}}_n).$

   Otherwise, for any $\overline{b}\in \left[\overline{p_3{p}_4}\right],E\left[\overline{b},〈\overline{p_3{p}_4}〉\cup [\overline{p_3}]\cup [\overline{p_4}]\cup [\overline{1}]-\overline{b}\right]$ is a minimum disconnecting set of $\mathit{P}({\mathbb{Z}}_n).$

Theorem 5.37.

[71, Theorem 5.2] Let G be a finite abelian p-group for some prime p and $\psi :G\to {\mathbb{Z}}_{p^{{\alpha }_1}}\times {\mathbb{Z}}_{p^{{\alpha }_2}}\times \cdots \times {\mathbb{Z}}_{p^{{\alpha }_m}}$ be an isomorphism with $\tau (G)=p^{{\alpha }_t}$. If $g\in G$ is such that all components of $\psi (g)$ are $\overline{0}$ except t^th, say $\overline{a}$, satisfying $\gcd (a,p)=1$, then $E\left[g,{\psi }^{-1}(<\psi (g)>)-g\right]$ is a minimum disconnecting set of $\mathit{P}(G).$

Theorem 5.38.

[71, Theorem 5.3] For $n\ge 3,\delta (\mathit{P}(D_{2n}))=1$. Moreover, for any $0\le i<n$, edge between e and $a^{i}b$ is a cut-edge of $\mathit{P}(D_{2n}).$

Theorem 5.39.

[71, Theorem 5.4] For $n\ge 2,\delta (\mathit{P}(Q_{4n}))=3$. Moreover, for any $0\le i\le n-1,E\left[a^{i}b,\{e,a^n,a^{n+i}b\}\right]$ and $E\left[a^{n+i}b,\{e,a^n,a^{i}b\}\right]$ are minimum disconnecting sets of $\mathit{P}(Q_{4n}).$

5.5. Equality of vertex and edge connectivity of power graphs

Now, we can ask the question: is there any relationship between graph invariants like vertex degree and diameter of power graph and its vertex connectivity and edge connectivity? The answer to this question is affirmative; this was proved in [71]. In fact, it was proved that ${\kappa }^{\prime }(\mathit{P}(G))=\delta (\mathit{P}(G)),$ since $\text{diam}(\mathit{P}(G))=2.$ But, this result is not true for $\kappa (\mathit{P}(G))$ in general. However, the authors of [71] examine the relationship between vertex connectivity and the minimum degree of power graphs of finite groups. They first explain some necessary conditions under which the vertex connectivity and the minimum degree of power graphs of finite groups coincide and computed the minimum degree when the equality holds for cyclic groups. Also, they gave a necessary and sufficient condition for $\kappa (\mathit{P}({\mathbb{Z}}_n))=\delta (\mathit{P}({\mathbb{Z}}_n)).$

Theorem 5.40.

[71, Theorem 6.2] Let G be a group of finite order at least 2 and $\kappa (\mathit{P}(G))=\delta (\mathit{P}(G))$. If $G\ne {\mathbb{Z}}_{p^{\alpha }}$, for some prime p is prime, $\alpha \in \mathbb{N}$ and $\delta (\mathit{P}(G))=\mathrm{deg}(a)$, then following hold:

1. N(a) is a minimum separating set of $\mathit{P}(G);$

2. a is an element of order 2 in G. Consequently, G is a group of even order.

Theorem 5.41.

[71, Theorem 6.4] If $n\ne p^m,m\in \mathbb{N}$ and $\kappa (\mathit{P}({\mathbb{Z}}_n))=\delta (\mathit{P}({\mathbb{Z}}_n))=k(\mathit{say})$, then $k=\mathrm{deg}\left(\overline{\frac{n}{2}}\right)=n-\frac{n}{2^{\alpha }}$, where α is the largest integer such that $2^{\alpha }$ divides n.

Corollary 5.42.

[71, Corollary 6.5] If $n\ne p^m,m\in \mathbb{N}$ and $\kappa (\mathit{P}({\mathbb{Z}}_n))=\delta (\mathit{P}({\mathbb{Z}}_n))$, then $\left\{\overline{0}\right\}\cup \underset{a|\frac{n}{2},a\ne \frac{n}{2}}{\cup }[\overline{a}]$, say A, is a minimum separating set and $E\left[\overline{\frac{n}{2}},A\right]$ is a minimum disconnecting set of $\mathit{P}({\mathbb{Z}}_n).$

Theorem 5.43.

[71, Theorem 6.7] For $n\in \mathbb{N},\kappa (\mathit{P}({\mathbb{Z}}_n))=\delta (\mathit{P}({\mathbb{Z}}_n))$ if and only if $n=p_1^{{\alpha }_1}$ for some prime p₁ and ${\alpha }_1\in \mathbb{N}$ or $n=2p_2^{{\alpha }_2}$ for some prime $p_2>2$ and ${\alpha }_2\in \mathbb{N}.$

Theorem 5.44.

[71, Theorem 6.8] If G is a finite abelian p-group, then $\kappa (\mathit{P}(G))=\delta (\mathit{P}(G))$ if and only if $\sigma (G)=1$ or $\tau (G)=2.$

Theorem 5.45.

[71, Theorem 6.9] For $n\in \mathbb{N}$, the following hold:

1. For $n\ge 3,\kappa (\mathit{P}(D_{2n}))=\delta (\mathit{P}(D_{2n}));$

2. For $n\ge 2,\kappa (\mathit{P}(Q_{4n}))\ne \delta (\mathit{P}(Q_{4n})).$

In 2018, Panda and Krishna [71], calculated the minimum degree of power graphs of finite cyclic groups ${\mathbb{Z}}_n,$ for some particular values of n. Also, they gave sharp upper bound for $\delta (\mathit{P}({\mathbb{Z}}_n))$ for any $n\in \mathbb{N}.$ Following this, Panda et al. [72], generalized these results for several other values of n.

Lemma 5.46.

[71, Lemma 4.3] For a finite group G, $\delta (\mathit{P}(G))=\left|G\right|-1$ if and only if $G=\left\{e\right\} or {\mathbb{Z}}_{p^{\alpha }}$ for some prime number p and $\alpha \in \mathbb{N}.$

Theorem 5.47.

[71, Theorem 4.4] Let n > 1 be an integer.

1. If n is not a power of a prime number, then $\delta (\mathit{P}({\mathbb{Z}}_n))=\varphi (n)+1+\delta (〈S{(Z_n)}^c〉)$. Consequently, $\delta (\mathit{P}({\mathbb{Z}}_n))\ge \varphi (n)+1.$

2. $\delta (\mathit{P}({\mathbb{Z}}_n))=\varphi (n)+1$ if and only if $n=2p$ for some prime $p\ge 3.$

Theorem 5.48.

[71, Theorem 4.6] Let $n\in \mathbb{N}$ and $p_1<p_2<p_3<p_4$ be prime numbers.

1. If $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2},{\alpha }_1,{\alpha }_2\in \mathbb{N}$, then $\delta (\mathit{P}({\mathbb{Z}}_n))=(p_2^{{\alpha }_2}-1)\varphi (p_1^{{\alpha }_1})+p_1^{{\alpha }_1}-1$ and it is attained by the element $\overline{p_2^{\alpha 2}}.$

2. If $n=p_1{p}_2{p}_3$, then $\delta (\mathit{P}({\mathbb{Z}}_n))=\varphi (n)+p_1{p}_2-1$ and it is attained by the element $\overline{p_3}.$

3. Let $n=p_1{p}_2{p}_3{p}_4$. If n is odd or $p_4\ge p_3+\frac{2(p_3-1)}{p_2-1}$, then $\delta (\mathit{P}({\mathbb{Z}}_n))=\varphi (n)+p_1{p}_2{p}_3-1$ and it is attained by the element $\overline{p_4}$. Otherwise, $\delta (\mathit{P}({\mathbb{Z}}_n))=(p_2-1)(p_3{p}_4+1)+1$ and it is attained by the element $\overline{p_3{p}_4}.$

Corollary 5.49.

[71, Corollary 4.7] Let $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\cdots p_m^{{\alpha }_m},$ $${\eta }_1(n)=\frac{n}{p_m^{{\alpha }_m}}+(p_m^{{\alpha }_m}-1)\varphi \left(\frac{n}{p_m^{{\alpha }_m}}\right)-1$$ and $${\eta }_2(n)=\frac{n}{p_{m-1}{p}_m}+\varphi (n)+\varphi \left(\frac{n}{p_m}\right)+\varphi \left(\frac{n}{p_{m-1}}\right)-1.$$

Then ${\eta }_1(n),{\eta }_2(n)$ are sharp upper bounds of $\delta (\mathit{P}({\mathbb{Z}}_n)).$

The following is a generalization of Theorem 5.48 to several other values of n.

Theorem 5.50.

[72, Theorem 1.2] Let $n=p_1{p}_2\cdots p_m,m\ge 3$ and $p_1,p_2,\dots ,p_m$ are prime numbers with $p_1<p_2<\cdots <p_m$. Then $\delta (\mathit{P}({\mathbb{Z}}_n))=\min \{\mathrm{deg}(\overline{p_{m-1}{p}_m}),\mathrm{deg}(\overline{p_m})\}$. Further, $$\delta (\mathit{P}({\mathbb{Z}}_n))=\mathrm{deg}(\overline{p_m}) \mathit{\text{if}}\mathrm{ }\mathit{\text{and}}\mathrm{ }\mathit{\text{only}}\mathrm{ }\text{if} \varphi (p_m)\ge \left(\frac{p_1{p}_2\cdots p_{m-2}}{\varphi (p_1{p}_2\cdots p_{m-2})}-1\right)\varphi (p_{m-1}).$$

In particular, if $\varphi (p_m)\ge (m-2)\varphi (p_{m-1})$, then $\delta (\mathit{P}({\mathbb{Z}}_n))=\mathrm{deg}(\overline{p_m}).$

For an arbitrary integer n, under certain conditions involving its prime divisors, the following theorem is proved on the minimum degree of $\mathit{P}({\mathbb{Z}}_n).$

Theorem 5.51.

[72, Theorem 1.3] Let $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\cdots p_m^{{\alpha }_m},m\ge 2,p_1<p_2<\cdots <p_m$ are primes and ${\alpha }_i\in \mathbb{N}$ for $1\le i\le m$. Suppose that any of the following two conditions holds:

1. $2\varphi (p_1{p}_2\cdots p_m)\ge p_1{p}_2\cdots p_m,$

2. $\varphi (p_{i+1})\ge m\varphi (p_i)$ for each $i\in \{1,2,3,\dots ,m-1\}.$

If $t\in \{2,3,\dots ,m\}$ is the largest integer such that ${\alpha }_t\ge {\alpha }_j$ for $2\le j\le m,$ then $\delta (\mathit{P}({\mathbb{Z}}_n))=\min \{\mathrm{deg}(\overline{p_s^{{\alpha }_s}}):t\le s\le m\}.$

Using the above Theorem 5.51, the authors proved the following Corollary by which minimum degree of the power graph of a finite cyclic group can be calculated.

Corollary 5.52.

[72, Corollary 1.4] Let $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\cdots p_m^{{\alpha }_m},m\ge 2,p_1<p_2<\cdots <p_m$ are primes and ${\alpha }_i\in \mathbb{N}$ for $1\le i\le m$. Suppose that any of the following two conditions holds:

1. $p_1\ge m+1$ and $p_m>m{p}_{m-1},$

2. $p_{i+1}>m{p}_i$ for each $i\in \{1,2,\dots ,m-1\}.$

Then $\delta (\mathit{P}({\mathbb{Z}}_n))=\mathrm{deg}(\overline{p_m^{{\alpha }_m}}).$

Remark 5.53.

Theorem 5.48 can be obtained from Theorems 5.50 and 5.51 and it was proved in [72].

If n has exactly three prime divisors, then following theorem shows that the minimum degree of the power graph of ${\mathbb{Z}}_n$ can be calculated without any condition as stipulated in Theorem 5.51.

Theorem 5.54.

[72, Theorem 1.5] Let $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}{p}_3^{{\alpha }_3}$ where $p_1<p_2<p_3$ are primes and ${\alpha }_i\in \mathbb{N}$ for $1\le i\le 3$. Then, $$\delta (\mathit{P}({\mathbb{Z}}_n))=\mathit{min}\{\mathrm{deg}(\overline{p_2^{{\alpha }_2}}),\mathrm{deg}(\overline{p_3^{{\alpha }_3}})\}.$$

It is already known that any abelian group of finite order is isomorphic to an unique product of cyclic groups of prime power order [15].

Theorem 5.55.

[71, Theorem 5.1] Let G be an abelian group of order $p^{\alpha }$, where p is prime and $\alpha \in \mathbb{N}$. Then $\delta (\mathit{P}(G))=\tau (G)-1.$

5.6. The complement of the power graph

The complement of the power graph of a finite group is always connected, apart from isolated vertices. (The isolated vertices are just the sets described in Theorem 6.1.)

Theorem 5.56.

[14, Theorem 9.9] Let G be a finite group. Then the complement of the power graph of G consists of a set of isolated vertices together with (if G is not cyclic of prime power order) a single connected component with diameter at most 2.

If the group G has an element x of order greater than 2, then x is joined to x² in ${\mathit{P}}_0(G),$ so the complement of the power graph is not complete. Thus, in the above theorem, the diameter is 2 except in the case when G is an elementary abelian 2-group.

Other connectivity questions relating to the complement of the power graph have not been studied yet.

6. Connectivity in proper power graphs

It is known that $\mathit{P}(G)$ is connected for any group G, since {e} is a dominating set. A natural question is: what will be the effect on connectivity properties of $\mathit{P}(G)$ if we remove the identity element from the vertex set of $\mathit{P}(G)$? This section is dedicated to all results based on the connectivity of proper power graph ${\mathit{P}}_0(G)$ (power graph without identity element) of a group G.

Before beginning, we should address the question whether there may be vertices other than identity which are joined to all other vertices in the group. In other words, which elements $a\in G$ have the property that, for all $b\in G,$ either a is a power of b or b is a power of a?

Theorem 6.1.

[13, Proposition 4]; [17, Theorem 4] Let G be a finite group. The set of vertices which are joined to all other vertices in $\mathit{P}(G)$ is

1. G, if G is cyclic of prime power order;

2. the set of generators of G together with the identity, if G is cyclic but not of prime power order;

3. Z(G), if G is a generalized quaternion group;

4. {e}, in any other case.

To investigate connectivity, it makes sense to delete all such vertices; but, in all cases except cyclic and generalized quaternion groups, this just requires us to delete the identity, giving ${\mathit{P}}_0(G).$ The remaining cases can be dealt with separately.

6.1. Conditions for non-connectedness

We begin with a general condition for the reduced power graph not to be connected.

Theorem 6.2.

Let G be a finite group which is not of prime power order. Let p be a prime dividing $\left|G\right|$. Suppose that, for all primes $q\ne p$, there is no element of order pq in G. Then ${\mathit{P}}_0(G)$ is not connected.

The hypothesis implies that there is no edge of the power graph between an element whose order is a power of p and one whose order is not a power of p. We saw an example of this in our discussion of the Mathieu group M₁₁, where the primes 5 and 11 have this property, and elements of orders 5 and 11 form complete graphs not connected to anything else in the reduced power graph. The property of the theorem is not uncommon: many (but not all) finite simple groups have such a prime. See Conjecture 6.7 below.

A finite group is called a CP-group or EPPO group if every non-trivial element of the group has prime power order. For example, a p-group is also a CP-group. Following a lot of earlier research, the CP-groups have been determined in [19, Theorem 1.7]. It follows from the preceding theorem that, in a CP-group G, the set of elements of p-power order is a union of connected components of ${\mathit{P}}_0(G).$

A more general condition uses the Gruenberg–Kegel graph. The Gruenberg–Kegel graph, or prime graph, of a finite group G is the graph whose vertex set is the set of prime divisors of $\left|G\right|,$ with an edge joining primes p and q whenever G contains an element of order pq. This graph has been the subject of a lot of research: see [19] for a summary.

Theorem 6.3.

Let G be a finite group whose Gruenberg–Kegel graph is disconnected. Then ${\mathit{P}}_0(G)$ is disconnected.

For suppose that π is a connected component of the Gruenberg–Kegel graph. Then there can be no edge in ${\mathit{P}}_0(G)$ joining an element whose order is a π-number to one whose order is not a π-number. For suppose that there were such an edge {a, b}. Then b is not a power of a, so a is a power of b. But then the order of b is divisible by both a prime $p\in \pi$ and a prime $q\notin \pi ;$ so some power of a has order pq, a contradiction.

We note that these graphs were introduced by Gruenberg and Kegel to study the integral group ring of G, in particular the decomposability of its augmentation ideal, in an unpublished manuscript in the 1970s. One of their main results was a structure theorem for groups with disconnected Gruenberg–Kegel graph; this was published by Williams (a student of Gruenberg) in 1981 [80]:

Theorem 6.4.

Let G be a finite group whose Gruenberg–Kegel graph is disconnected. Then one of the following holds:

1. G is a Frobenius or 2-Frobenius group;

2. G is an extension of a nilpotent π-group by a simple group by a π-group, where π is the set of primes in the connected component containing 2.

Here, a 2-Frobenius group is a group G with normal subgroups H and K with $H\le K$ such that

• K is a Frobenius group with Frobenius kernel H;

• G/H is a Frobenius group with Frobenius kernel K/H.

A typical example is the group G = S₄, with K = A₄, H = V₄ (the Klein group), and $G/K\cong S_3.$

The simple groups in Case (ii) have been determined in several papers by Williams, Kondrat’ev and Mazurov.

6.2. Components in proper power graph

In 2014, Moghaddamfar et al. [65], computed some properties of proper power graphs ${\mathit{P}}_0(G),$ which are summarized below. Here, for any group G, $\pi (G)$ denotes the set of all prime divisors of $\left|G\right|.$

Theorem 6.5.

[65, Lemma 4.1, Corollary 4.1, Lemma 4.3, Lemma 4.4] Let G be a finite group. Then the following hold:

1. If $o(G)=p^{\alpha },$ for some prime p and positive integer α, then ${\mathit{P}}_0(G)$ is connected if and only if G has a unique minimal subgroup. and only if G is either a cyclic group or a generalized quaternion group.

2. If $\pi (Z(G))\ge 2$, then ${\mathit{P}}_0(G)$ is connected.

3. If $\pi (G)\ge 2$ and center of G is a p-group for some $p\in \pi (G),$ then the proper power graph ${\mathit{P}}_0(G)$ is connected if and only if every non-central element a of order p there exists a non p-element b such that $a\sim b$ in ${\mathit{P}}_0(G).$

In connection with the first part, Theorem 4.1 shows that these groups are cyclic or generalized quaternion.

In 2015, Pourgholi et al. [74], proved that the number of edges in the power graphs of a simple group of order n is at most the number of edges in the power graph of the cyclic group of order n. They also proposed the following question on non-Abelian simple groups with 2-connected power graphs.

Question 6.6

[74, Question 2.1] Determine all non-Abelian simple groups with 2-connected power graphs.

Following this, Bubboloni et al. [11] and Doostabadi and Farrokhi [37], independently presented negative examples for this question. (If the reduced power graph is not connected, then the power graph cannot be 2-connected. We gave examples at the start of this section.) In [3], Narges Akbari et al. modified the above question and proposed the following conjecture.

Conjecture 6.7

[3, Conjecture] The power graph of a non-Abelian simple group G is 2-connected if and only if G is isomorphic to the alternating group A_n where n = 3 or $n\notin P\cup (P+1)\cup (P+2)\cup (2P)\cup (2P+1)$ and P is the set of all prime numbers.

Having proposed the above conjecture, Narges Akbari et al. [3] proved that this conjecture true for some classes of finite simple groups. The relevant result is given below.

Theorem 6.8.

[3, Main Theorem] Let p be a power of a prime number. The proper power graphs of the sporadic groups, Ree groups ${}^2{F}_4(p)$ and ${}^2{G}_2(p)$, the Chevalley group $A_1(p),A_2(p),B_2(p),C_3(p)$ and $F_4(p)$, the projective unitary group $U_3(p)$ and the projective symplectic group $S_4(p)$ are disconnected.

It seems that the following result is the best for connectivity of power graphs without identity of periodic groups.

Lemma 6.9.

[49, Lemma 2.1] Let G be a periodic group. Then ${\mathit{P}}_0(G)$ is connected if and only if for any two elements a, b of prime orders with $a\sim b$, there exist elements $a=a_0,\dots ,a_m=b$ such that $o(a_{2i})$ is prime, $o(a_{2i+1})=o(a_{2i})o(a_{2i+2})$ for $i\in \{0,1,2,\dots ,m/2\}$ and a_i is adjacent to $a_{i+1}$ for $i\in \{0,1,\dots ,m-1\}.$

In [37], the authors calculated the number of connected components of the power graph of a special class of finite groups including nilpotent groups, Hughes-Thompson group, Suzuki group $\text{Sz}(m),$ symmetric group S_n and alternating group A_n on n symbols. The results in this regard have been clubbed and presented below:

Corollary 6.10.

[37, Corollary 2.2] If G is a finite group with exactly one element of order 2, then ${\mathit{P}}_0(G)$ is connected.

Theorem 6.11.

[37, Theorem 2.5] Let G be a finite p-group. Then there exists a one-to-one correspondence between the connected components of ${\mathit{P}}_0(G)$ and the minimal cyclic subgroups of G.

Theorem 6.12.

[37, Theorem 2.6(i)] Let G be a finite p-group. Then the number of connected components of ${\mathit{P}}_0(G)$ is same as the number of subgroups of G of order p. In particular ${\mathit{P}}_0(G)$ is connected if and only if G is a cyclic p-group or a generalized quaternion 2-group.

For a group G and a prime number p, the Hughes subgroup $H_p(G)$ of G is defined as the subgroup generated by all elements of G whose orders are different from p. A finite group G is called a Hughes-Thompson group if G is not a p-group and $H_p(G)\subset G$ for some prime divisor p of $\left|G\right|.$ Recall that $c(\Gamma )$ denotes the number of connected components of a graph $\Gamma .$

Theorem 6.13.

[37, Theorem 3.2] Let G be a Hughes-Thompson group and p be a prime such that $H_p(G)\ne G$. Then the number of connected components of ${\mathit{P}}_0(G)$ is equal to $1+\frac{o(G)}{p}$ if $H_p(G)$ is not a p-group, and it is equal to $c({\mathit{P}}_0(H_p(G)))+\frac{o(G)}{p}$, otherwise.

Theorem 6.14.

[37, Theorem 3.4] Let G be a Frobenius group with kernel K and complement H. Then ${\mathit{P}}_0(H)$ is connected and the number of connected components of ${\mathit{P}}_0(G)$ is $o(K)+1$ if K is not a p-group and it is $o(K)+c({\mathit{P}}_0(K))$ if K is a p-group.

Theorem 6.15.

[37, Theorem 3.5] If $G=\text{PGL}(2,p^n)$ (p is odd), then the number of connected components of ${\mathit{P}}_0(G)$ is equal to $\frac{p^{2n+1}-1}{p-1}.$

Theorem 6.16.

[37, Theorem 3.6] If $G=\text{PSL}(2,p^n)$, then the number of connected components of ${\mathit{P}}_0(G)$ is equal to $\frac{p^{2n+1}-1}{p-1}.$

Theorem 6.17.

[37, Theorem 3.7] If $G=\text{Sz}(m)$ (Suzuki group), then the number of connected components of ${\mathit{P}}_0(G)$ is equal to $\frac{1}{2}{m}^3{(m+1)}^2-m^2+m-1$, where $m=2^{2n+1}.$

Theorem 6.18.

[37, Theorem 4.2] Let $G=S_n$ be the symmetric group $(n\ge 2).$

1. If $n=p\ge 11$, then number of connected components of ${\mathit{P}}_0(G)$ is equal to $(p-2)!+1.$

2. If $n=p+1\ge 12$, then number of connected components of ${\mathit{P}}_0(G)$ is equal to $(p+1)(p-2)!+1.$

3. If $n=2,3,4,5,6,7,8$, then number of connected components of ${\mathit{P}}_0(G)$ is equal to $1,4,13,31$, 83, 128 and 961, respectively.

Theorem 6.19.

[37, Theorem 4.7] Let $G=A_n$ be the alternating group $(n\ge 3).$

1. If $n=p\ge 11$, then the number of connected components of ${\mathit{P}}_0(G)$ is equal to $(p-2)!+\frac{p(p-1)(p-4)!}{2}+1$ if p – 2 is prime, it is equal to $\frac{4p(p-2)(p-4)!}{(p-1)}+1$, if $\frac{p-1}{2}$ is prime, and it is equal to $(p-2)!+1$ if neither $(p-2)$ nor $\frac{(p-1)}{2}$ is a prime.

2. If $n=p+1\ge 12$, then the number of connected component of ${\mathit{P}}_0(G)$ is equal to $(p+1)(p-2)!+\frac{4p(p-2)!}{p+1}+1$ if $\frac{p+1}{2}$ is prime, it is equal to $(p+1)(p-2)!+1$ $+\frac{4p(p+1)(p-2)(p-4!)}{(p-1)}$ if $\frac{p-1}{2}$ is prime, and it is equal to $(p+1)(p-2)!+1$ if neither $\frac{(p+1)}{2}$ nor $\frac{(p-1)}{2}$ is a prime.

3. If $n=p+2\ge 13$, then the number of connected components of ${\mathit{P}}_0(G)$ is equal to $p!+\frac{1}{2}[(p+2)(p+1)(p-2)!]+1$ if p + 2 and $\frac{(p+1)}{2}$ are primes, it is equal to $p!+\frac{1}{2}[(p+1)(p+2)(p-2)!]+1$ if p + 2 is prime but $\frac{(p+1)}{2}$ is not prime, it is equal to $\frac{1}{2}[(p+2)(p+1)(p-2)!]+\frac{4p(p+2)(p-2)!}{p(p+1)}+1$ if $\frac{p+1}{2}$ is prime but p + 2 is not prime, and it is equal to $p!+1$, if neither p + 2 nor $\frac{p+1}{2}$ is prime.

4. If $n=2p\ge 14$, then the number of connected components of ${\mathit{P}}_0(G)$ is equal to $2p(2p-3)!+\frac{(2p-1)!}{p(p-1)}+1$ if $2p-1$ is prime, and it is equal to $\frac{(2p-1)!}{p(p-1)}+1$ if $2p-1$ is not prime.

5. If $n=2p+1\ge 11$, then number of connected components of ${\mathit{P}}_0(G)$ is equal to $(2p-1)!+1+\frac{(2p+1)(2p-1)!}{p(p-1)}$ if $2p+1$ is prime, it is equal to $\frac{(2p+1)(2p-1)!}{p(p-1)}+p(2p+1)(2p-3)!+1$ if $2p-1$ is prime,and it is equal to $\frac{(2p+1)(2p-1)!}{p(p-1)}+1$ otherwise.

6. If $n=2p+2\ge 12$, then ${\mathit{P}}_0(G)$ is connected when $2p+1$ is not prime, and it is disconnected with $2(p+1)(2p-1)!+1$ connected components if $2p+1$ is prime.

7. If $n=3,4,5,6,7,8,9,10$, then the number of connected components of ${\mathit{P}}_0(G)$ is equal to 1, 7, 31, 121, 421, 962, 5442, and 29345 respectively.

Now, we present some results on the connectivity of the proper graph of a finite p-group proved by Panda et al. [70].

Proposition 6.20.

[70, Proposition 3.1] Let G be a finite p-group and $a\in G^{*}$ is of order p. Then a is adjacent to every other vertices of the component of the proper power graph ${\mathit{P}}_0(G)$ that contains a.

Proposition 6.21.

[70, Proposition 3.2] If G is a finite p- group, then each component of ${\mathit{P}}_0(G)$ has exactly p – 1 elements of order p.

Theorem 6.22.

[70, Theorem 3.3] Let G be an finite abelian p-group isomorphic to the direct product of m cyclic groups. Then the number of components of ${\mathit{P}}_0(G)$ is $p^{m-1}+p^{m-2}+\cdots +1.$

It follows from Theorem 3.3 [70] that the proper power graph of a non-cyclic abelian p-group has more than one component. This leads to the fact stated in Corollary 5.20. Cameron et. al [17], considered the question of connectivity of the proper power graph of infinite groups.

Lemma 6.23.

[17, Lemma 1] If ${\mathit{P}}_0(G)$ is connected, then G is a torsion-free or a periodic group.

Theorem 6.24.

[17, Theorem 7] Let G be a locally center-by-finite group which is torsion free. Then ${\mathit{P}}_0(G)$ is connected if and only if G is isomorphic to a subgroup of $\mathbb{Q}.$

If G is a finite p-group, then ${\mathit{P}}_0(G)$ is connected if and only if G is a cyclic group or a generalized quaternion group $Q_{2^n}.$ For infinite case, we have the following result.

Theorem 6.25.

[17, Theorem 9] Let G be infinite locally finite p-group. Then ${\mathit{P}}_0(G)$ is connected if and only if $G\cong C_{p^{\infty }}$ for some prime number p, or $G\cong Q_{2^{\infty }}.$

6.3. Distance in proper power graphs

Recall that the diameter of a graph Γ is the maximum distance between pairs of vertices in Γ. Thus the diameter of a complete graph is precisely 1. It can be seen that not every proper power graph is connected. For example, the proper power graph of any dihedral group is disconnected since the involutions are isolated vertices. In [32], Curtin et al. focused on the groups with low diameter proper power graphs and proved the following results.

Lemma 6.26.

[32, Lemma 12] For a finite group G, suppose that ${\mathit{P}}_0(G)$ has a diameter at most 3. Then any Sylow subgroup of G either a cyclic group or a generalized quaternion 2-group.

We remark that groups satisfying the conclusion of those lemma can be determined by using group-theoretic characterization theorems including Glauberman’s $Z^{*}$-Theorem and the Gorenstein –Walter Theorem.

Theorem 6.27.

[32, Theorem 14] For a finite group G, the proper power graph ${\mathit{P}}_0(G)$ has diameter at most 2 if and only if G is nilpotent and all of its Sylow subgroups are cyclic groups or generalized quaternion 2-groups. Moreover, if both these conditions hold, then the power graph $\mathit{P}(G)$ and proper power graph ${\mathit{P}}_0(G)$ have the same diameter.

Corollary 6.28.

[32, Corollary 15] Let G be a finite group. If ${\mathit{P}}_0(G)$ has diameter 3, then G is not nilpotent.

Lemma 6.29.

[32, Lemma 16] Let G be a finite group. If ${\mathit{P}}_0(G)$ has diameter at most 3, then elements of G with prime order commute.

Corollary 6.30.

[32, Corollary 19] If G is a non-Abelian simple group, then ${\mathit{P}}_0(G)$ has diameter at least 4.

In 2015, Alireza et al. [37], proved some results on the proper power graph of finite groups and among other results, they proved that the connected proper power graph ${\mathit{P}}_0(G)$ has diameter at most 4, 26, or 22 when G is a nilpotent group, symmetric group, or alternating group, respectively. These results lead to a conjecture which claims that connected proper power graphs of finite groups must have bounded diameter.

Theorem 6.31.

[37, Theorem 2.4] Let G be a finite group such that Z(G) is not a p-group. Then ${\mathit{P}}_0(G)$ is connected. Moreover, $\text{diam}({\mathit{P}}_0(G))\le 6$ and the bound is sharp.

Theorem 6.32.

[37, Theorem 2.6] Let G be finite nilpotent group.

1. If G is a p-group, then the number of connected components of ${\mathit{P}}_0(G)$ is the same as the number of subgroups of G of order p. In particular, ${\mathit{P}}_0(G)$ is connected if and only if G is a cyclic p-group or a generalized quaternion 2-group.

2. If G is not a p-group and each of the Sylow p-subgroup of G is a cyclic p-group or a generalized quaternion 2-group, then ${\mathit{P}}_0(G)$ is connected and $\text{diam}({\mathit{P}}_0(G))=2.$

3. If G is not a p-group and G has a Sylow p-subgroup, which neither a cyclic $p-$group nor a generalized quaternion 2-group, then ${\mathit{P}}_0(G)$ is connected and $\text{diam}({\mathit{P}}_0(G))=4.$

Utilizing the above theorem, one can classify all finite groups for which the proper power graph is of diameter at most three. The characterization in this regard is given below.

Theorem 6.33.

[37, Theorem 2.8] Let G be a finite group.

1. $\text{diam}({\mathit{P}}_0(G))=1$ if and only if G is a cyclic p-group.

2. $\text{diam}({\mathit{P}}_0(G))=2$ if and only if G is nilpotent which is not a cyclic p-cyclic and the Sylow p-subgroups of G are either a cyclic p-group or a generalized quaternion 2-group.

3. $\text{diam}({\mathit{P}}_0(G))=3$ if and only if G is not nilpotent and G has exactly one subgroup of order p for all $p\in \pi (G).$

Lemma 6.34.

[37, Lemma 3.3] Let G be a group of fixed-point-free automorphisms of some finite group. Then ${\mathit{P}}_0(G)$ is connected. If G is solvable, then $\text{diam}({\mathit{P}}_0(G))\le 6$. If G is not solvable, then $\text{diam}({\mathit{P}}_0(G)\le 12$ and the equality holds only if G has a maximal subgroup M of index 2 such that $M=L\times SL(2,p)$ for some solvable group L and prime p. In both cases, if $Z(G)\ne 1$, then $\text{diam}({\mathit{P}}_0(G))\le 4.$

Theorem 6.35.

[37, Theorem 4.2(i)] If $n\ge 9$ and neither n nor n – 1 is a prime, then ${\mathit{P}}_0(S_n)$ is connected and $\text{diam}({\mathit{P}}_0(S_n))\le 26.$

Theorem 6.36.

[37, Theorem 4.7(i)] Let $n\ge 3$. If $n,n-1,n-2,\frac{n}{2},\frac{(n-1)}{2},\frac{(n-2)}{2}$ are not primes, then ${\mathit{P}}_0(A_n)$ is connected and $\text{diam}({\mathit{P}}_0(A_n))\le 22.$

Recently, in [73], the authors have improved the upper bound of diameter of proper power graphs of alternating groups to 11, for n > 51.

7. Independence Number of power graphs

In [79], Tamizh Chelvam et al. proved some results on the power graph of a finite abelian group in which they provided a lower bound for the independence number of the power graph of a finite group, computed the independence number of an elementary abelian p-group and characterized all finite abelian groups whose power graph has independence number 2.

Theorem 7.1.

[79, Theorem 7] Let G be a finite group of order $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\cdots p_m^{{\alpha }_m}$, where p_i are distinct primes and ${\alpha }_i\ge 1$ are integers. Then independence number $\beta (\mathit{P}(G))\ge m.$

Theorem 7.2.

[79, Theorem 8] Let G be an elementary abelian group of order pⁿ for some prime number p and positive integer n and $\mathcal{\ell }=\frac{p^n-1}{p-1}.$ Then $\mathit{P}(G)\cong K_1+{\cup }_{i=1}^{\mathcal{\ell }}{K}_{p-1}$ and $\beta (\mathit{P}(G))=\mathcal{\ell }.$

Theorem 7.3.

[79, Theorem 10] Let G be a finite abelian group. Then $\beta (\mathit{P}(G))=2$ if and only if G is a cyclic group of order $p_1^{\alpha }{p}_2$, where p₁ and p₂ are distinct primes and α is a positive integer.

In 2018, Ma and Lu [59] provided sharp lower and upper bounds for the independence number of $\mathit{P}(G)$ and characterized the groups achieving the bounds. Also, they determined the independence number $\mathit{P}(G)$ of certain finite groups. Finally, they classified all finite groups G, whose power graphs have independence number 3 or $o(G)-2.$ For a group G, we have ${\Omega }_P=\{P\subseteq S:\mathrm{P}\mathrm{ }\text{is}\text{ a }\text{subgroup}\mathrm{ }\text{of}\text{ G }\text{of}\mathrm{ }\text{prime}\mathrm{ }\text{order}\}.$ A maximal cyclic subgroup of G is a cyclic subgroup, which is not a proper subgroup of some proper cyclic subgroup of G. Denote by ${\mathcal{M}}_G$ the set of all maximal cyclic subgroups of G.

Theorem 7.4.

[59, Theorem 2.1] For any finite group G, $$\left|{\Omega }_P\right|\le \beta (\mathit{P}(G))\le \sum _{M\in \mathcal{M}(G)}\beta (\mathit{P}(M)).$$

Next, we state a characterization of the groups satisfying the lower bound given in Theorem 7.4.

Theorem 7.5.

[59, Theorem 2.3] $\beta (\mathit{P}(G))=\left|{\Omega }_G\right|$ if and only if the following two conditions occur:

1. For each $M\in \mathcal{M}(G),\left|M\right|=p_1^{\alpha },p_1^{\alpha }{p}_2$ or $p_1{p}_2{p}_3$, where p₁, p₂, p₃ are distinct primes and $\alpha \in \mathbb{N}.$

2. If $\mathit{P}({\cup }_{j=1}^{\mathcal{\ell }}{M}_0^j)$ is connected, where $\mathcal{\ell }\ge 2$ is positive integer and $M_j\in \mathcal{M}(G)$ for each $1\le j\le \mathcal{\ell }$, then $\beta (\mathit{P}({\cup }_{j=1}^{\mathcal{\ell }}{M}_0^j))=\left|{\cup }_{j=1}^{\mathcal{\ell }}{\Omega }_{M_j}\right|.$

Corollary 7.6.

[59, Corollary 2.4] $\beta (\mathit{P}(D_{2n}))=\left|{\Omega }_{D_{2n}}\right|$ if and only if $n=p_1^{\alpha },p_1^{\alpha }{p}_2$ or $p_1{p}_2{p}_3$, where $p_1,p_2,p_3$ are distinct primes and α is a positive integer.

Recall that a finite group is called a CP-group or EPPO group if every non-trivial element of the group has prime power order.

Corollary 7.7.

[59, Corollary 2.5] Let G be a finite CP group. Then $\beta (\mathit{P}(G))=\left|{\Omega }_G\right|$ if and only if either $G={\mathbb{Z}}_{p^{\alpha }}$ or G is a non-cyclic group such that every two maximal cyclic subgroups have trivial intersection.

Proposition 7.8.

[59, Proposition 2.8] Let G be a finite group with $$\beta (\mathit{P}(G))=\sum _{m\in \mathcal{M}(G)}\beta (\mathit{P}(M)).$$

If G has two distinct maximal cyclic subgroups M₁ and M₂, then $$\beta (\mathit{P}(M_1\cup M_2))=\beta (\mathit{P}(M_1))+\beta (\mathit{P}(M_2)).$$

Theorem 7.9.

[59, Theorem 2.9] Let G be a group with $\mathcal{M}(G)=\{M_1,M_2,\dots ,M_t\}$. Then the following are equivalent:

1. $\beta (\mathit{P}(G))=\sum _{M\in \mathcal{M}(G)}\beta (\mathit{P}(M));$

2. For each $1\le i\le t$, there exists an independent set D_i of M_i such that $\left|D_i\right|=\beta (\mathit{P}(M_i))$ and for distinct indices i, j, $D_i\cap D_j=\varnothing$, and $D_i\cup D_j$ is an independent set of $\mathit{P}(G);$

3. Let $\mathit{P}({\cup }_{j=1}^{\mathcal{\ell }}{M}_0^j)$ be a connected component of ${\mathit{P}}_0(G)$ for some $\mathcal{\ell }\le t.$ Then $$\beta (\mathit{P}({\cup }_{j=1}^{\mathcal{\ell }}{M}_0^j))=\sum _{j=1}^t\beta (\mathit{P}(M_0^j)).$$

Corollary 7.10.

[59, Corollary 2.10] If every two distinct maximal cyclic subgroup of G have trivial intersection, then $\beta (\mathit{P}(G))=\sum _{M\in \mathcal{M}(G)}\beta (\mathit{P}(M)).$

Corollary 7.11.

[59, Corollary 2.11] If G is p-group, then $\beta (\mathit{P}(G))=\sum _{M\in M_G}\beta (\mathit{P}(M))=\left|\mathcal{M}(G)\right|.$

Corollary 7.12.

[59, Corollary 2.16] For a finite CP group G, following are equivalent

1. $\beta (\mathit{P}(G))=\left|{\Omega }_G\right|;$

2. $\left|\mathcal{M}(G)\right|=\left|{\Omega }_G\right|;$

3. Either $G\cong {\mathbb{Z}}_{p^{\beta }}$ or G is non-cyclic group such that every two maximal cyclic subgroup have trivial intersection.

Theorem 7.13.

[59, Theorem 4.1] Let G be a group. Then $\beta (\mathit{P}(G))=3$ if and only if G is one of the following groups:

1. $Q_8;$

2. ${\mathbb{Z}}_2\times {\mathbb{Z}}_2;$

3. ${\mathbb{Z}}_{p_1{p}_2{p}_3}$, where $p_1,p_2,p_3$ are distinct primes;

4. ${\mathbb{Z}}_{p_1^2{p}_2^{\beta }}$, where $\beta \ge 2$ is a positive integer.

Theorem 7.14.

[59, Theorem 4.2] Let G be a finite group of order n. Then $\beta (\mathit{P}(G))=n-2$ if and only if $G\cong {\mathbb{Z}}_3$ or D₃.

In the next few theorems, we present results on the independence number of the power graph of an infinite group G.

Theorem 7.15.

[1, Theorem 1]. Let G be a group and $\beta (\mathit{P}(G))<\infty$. Then $\left[G:Z(G)\right]<\infty$ and G is locally finite.

Theorem 7.16.

[1, Theorem 3] Let G be an abelian group such that $\beta (\mathit{P}(G))<\infty$. Then either G is finite or $G\cong C_{p^{\infty }}\times H$, where H is a finite group and $p\nmid o(H).$

Theorem 7.17.

[1, Theorem 4] Let p be a prime number and G be a p-group such that $\beta (\mathit{P}(G))<\infty$. Then either G is finite or $G\cong C_{p^{\infty }}.$

In the following theorem, the authors exploit Theorem 7.17 and extend in Theorem 7.16 to nilpotent groups.

Theorem 7.18.

[1, Theorem 6] Let G be an infinite nilpotent group. Then $\beta (\mathit{P}(G))<\infty$ if and only if $G\cong C_{p^{\infty }}\times H$, for some prime number p, where H is a finite group and $p\nmid o(H).$

In the same article, the authors posed the question, does above theorem hold without assuming nilpotence? Cameron et al. [17] gave an affirmative answer to this question.

Theorem 7.19.

[17, Theorem 3] Let G be a group satisfying $\beta (\mathit{P}(G))<\infty$. Then either G is finite, or $G\cong C_{p^{\infty }}\times H$, where H is a finite group and $p\nmid o(H).$

As a corollary of this result, Cameron et al. [17] proved the following corollary.

Corollary 7.20.

[17, Corollary 1] Let G be a group whose power graph $\mathit{P}(G)$ has finite independence number. Then the independence number and clique cover number of $\mathit{P}(G)$ are equal.

8. Perfectness of the power graph

Recall that a finite graph is perfect if every induced subgraph has clique number equal to chromatic number. In the next theorem, we recall several facts about perfect graphs. The comparability graph $\Psi (P)$ of a partially ordered set $(P,\le )$ is the simple graph with the vertex set P and two distinct vertices x and y adjacent if and only if either $x\le y$ or $y\le x.$

Theorem 8.1.

1. If a graph is perfect, then its complement is perfect (The Weak Perfect Graph Theorem, Lovász [56]).

2. A graph is perfect if and only if it contains no odd cycle or complement of an odd cycle of length at least 5 as an induced subgraph (The Strong Perfect Graph Theorem, Chudnovsky et al. [29]).

3. The comparability graph of a partial order, and its complement, are perfect (Dilworth’s Theorem, [35]).

Theorem 8.2.

[1,4,40] The power graph of a finite group is the comparability graph of a partial order, and hence is a perfect graph. In particular, its clique number and chromatic number are equal, and the clique number and chromatic number of the complement are also equal.

For consider the directed power graph $\overrightarrow{\mathit{P}}(G),$ with a loop at each vertex. This is a partial preorder, a reflexive and symmetric relation. Writing $x\equiv y$ if each of x and y precedes the other in the partial preorder (that is, if each is a power of the other); this is an equivalence relation, and the equivalence classes are partially ordered. Refining this relation by a total order on each equivalence class, we obtain a partial order whose comparability graph is $\mathit{P}(G).$

8.1. Induced subgraphs

Any induced subgraph of the comparability graph of a partial order is itself a comparability graph. Subject to this, power graphs are universal:

Theorem 8.3.

[14, Theorem 5.4] For any finite graph Γ which is the comparability graph of a partial order, there exists a finite group G such that Γ is an induced subgraph of $\mathit{P}(G).$

However, groups of prime power order are more restricted.

Theorem 8.4.

[18, Lemma 3.1] Let G be a finite group of prime power order. Then

1. if (x, y, z) is a 3-vertex induced path in the power graph of G, then $x\to y$ and $z\to y$ in the directed power graph;

2. $\mathit{P}(G)$ does not contain a path or cycle on 4 vertices as an induced subgraph.

Apart from perfect graphs, there are various other interesting classes of graphs which are defined by forbidden induced subgraphs. Let P_n, C_n and K_n denote the path, cycle and complete graph with n vertices, and $2K_2$ the graph consisting of two disjoint edges. Some other graph classes considered are

1. cographs, with no induced P₄;

2. chordal graphs, with no induced C_n for n > 3;

3. split graphs, with no induced P₄, C₅ or $2K_2$ [46];

4. threshold graphs, with no induced P₄, K₄ or $2K_2.$

We refer to [18] for further discussion of these graph classes.

Theorem 8.5.

[18, Theorems 3.2, 4.3 and 5.1]

1. Let G be a finite nilpotent group. Then $\mathit{P}(G)$ is a cograph if and only if either G has prime power order, or G is cyclic with order the product of two distinct primes.

2. Let G be a finite nilpotent group. Then $\mathit{P}(G)$ is a chordal graph if and only if either G has prime power order, or G has just two prime divisors p and q, the Sylow p-subgroup is cyclic, and the Sylow q-subgroup has exponent q.

3. Let G be an arbitrary finite group. Then the following are equivalent:

   1. $\mathit{P}(G)$ is a split graph;

   2. $\mathit{P}(G)$ is a threshold graph;

   3. G is cyclic of prime power order, or an elementary abelian or dihedral 2-group, or cyclic of order 2p, or dihedral of order $2p^n$ or 4p, where p is an odd prime.

A preliminary result towards the characterisation of finite groups whose power graph is split was given in [57].

One of the most important questions about power graphs of finite groups is:

Problem 8.6. For which finite groups G is $\mathit{P}(G)$ a cograph?

We will see another reason for examining this question in Section 11.

Theorem 8.5(i) gives useful information, since it shows that, if $\mathit{P}(G)$ is a cograph, then any nilpotent subgroup of G is either of prime power order or a cyclic group whose order is the product of two distinct primes. This greatly restricts the possible groups: here is a sample result.

Theorem 8.7.

[14, Proposition 8.7] Suppose that q is a prime power. If q is a power of 2, then let $l=q-1$ and $m=q+1$; if q is odd, let $l=(q-1)/2$ and $m=(q+1)/2$. Let $G=\text{PSL}(2,q)$. Then $\mathit{P}(G)$ is a cograph if and only if each of l and m is either a power of a prime number or the product of two distinct primes.

Finding all groups $\text{PSL}(2,q)$ whose power graph is a cograph is thus a number-theoretic problem. As noted in [14], the values of d up to 200 for which $q=2^d$ satisfies the conditions of the theorem are 1, 2, 3, 4, 5, 7, 11, 13, 17, 19, 23, 31, 61, 101, 127, 167, and 199.

Problem 8.8. Are there infinitely many prime powers q for which the number-theoretic conditions of Theorem 8.7 are satisfied?

We note that the smallest non-Abelian simple group whose power graph is not a cograph is the alternating group A₇ [14, Table 1].

8.2 Further results

In 2015, Alireza et al. [4] proved the following results on the clique number and the chromatic number of power graphs. The chromatic number was calculated earlier by Mirzagar et al. [64, Theorem 2]. We have reformulated their results somewhat. First we deal with cyclic groups.

Theorem 8.9.

[4, Theorem 7] Let f(n) be the clique number of the power graph of the cyclic group ${\mathbb{Z}}_n$ of order n.

1. The function f is given by the recurrence $$f(1)=1,\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}f(n)=\varphi (n)+f(n/p)\mathrm{ }\mathit{\text{for}}\mathrm{ }n>1,$$ where $\varphi$ is Euler’s totient function and p is the smallest prime divisor of n.

2. Let $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\cdots p_m^{{\alpha }_m}$ such that $p_1<p_2<\cdots <p_m$. Then $\omega (\mathit{P}({\mathbb{Z}}_n))=\varphi (n)+\varphi \left(\frac{n}{p_1}\right)+\cdots +\varphi \left(\frac{n}{p_m}\right)+\varphi \left(\frac{n}{p_1^{{\alpha }_1}}\right)+\varphi \left(\frac{n}{p_1^{{\alpha }_1}{p}_2}\right)+\cdots +\varphi \left(\frac{n}{p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}}\right)+\cdots +\varphi \left(\frac{n}{p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\cdots p_r}\right)+\cdots \mathrm{ }\backslash \backslash +\varphi \left(\frac{n}{p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\cdots p_{i-1}^{{\alpha }_{i-1}}}\right)+\varphi (1).$

3. The chromatic number of $\mathit{P}({\mathbb{Z}}_n)$ is equal to the clique number.

For the first part, we notice that the $\varphi (n)$ generators of ${\mathbb{Z}}_n$ are dominating vertices, and so lie in every maximal clique; it can be shown that the remainder of a clique must lie in a proper subgroup, and the best we can do is to take the largest such subgroup. The second part follows by expanding the recurrence, and the third holds because the power graph is perfect.

From this result it is possible to obtain an estimate for the clique number:

Theorem 8.10.

$$\varphi (n)\le \omega (\mathit{P}({\mathbb{Z}}_n))\le 3\varphi (n).$$

In fact, it can be shown that $$\lim \sup \omega (\mathit{P}({\mathbb{Z}}_n))/\varphi (n)=2.6481017597\dots$$

where the constant on the right has the analytic expression $$\sum _{k\ge 0}\prod _{i=1}^k\frac{1}{p_i-1}.$$

From these results we can give a formula, found by Mirzagar et al. and Alireza et al. [4, 57] for $\omega (\mathit{P}(G))$ for any group G. Recall that ${\pi }_e(G)$ denotes the set of all orders of elements of G.

Theorem 8.11.

Let G be a finite group. Then the clique number and chromatic number of $\mathit{P}(G)$ are both equal to $$\max \{f(m):m\in {\pi }_e(G)\},$$

where f is the function defined in Theorem 8.9.

This holds because any edge (and hence any clique) in the power graph of a group G is contained in a cyclic subgroup of G. Note that $k|m$ implies $f(k)\le f(m),$ so we can restrict the maximization to the set of elements of ${\pi }_e(G)$ which are maximal with respect to divisibility.

The function f is not monotonic, so the value given by Theorem 8.11 is not equal to f(m) where $m=\max {\pi }_e(G)$ in general. Consider, for example, the group $G=\text{PGL}(2,11).$ The maximal (under divisibility) elements of ${\pi }_e(G)$ are 10, 11 and 12; and we have $f(10)=f(12)=9$ but $f(11)=11.$ So the clique number and chromatic number of G are equal to 11.

However, in an abelian group G, the maximal element of ${\pi }_e(G)$ is the exponent of G, and all elements of ${\pi }_e(G)$ are divisors of the exponent; so the equation $\omega (\mathit{P}(G))=f(\max {\pi }_e(G))$ does hold.

Note also that, since a cyclic subgroup is a clique in the enhanced power graph, we have $\omega ({\mathit{P}}_e(G))=\max {\pi }_e(G).$

In the following theorem, the authors characterized all power graphs which are uniquely colorable.

Theorem 8.12.

[57, Theorem 2.8] Let G be a finite group. Then $\mathit{P}(G)$ is uniquely colorable if and only if G is an elementary abelian 2-group or a cyclic group of prime power order.

Aalipour et al. [1] proved that that the chromatic number of the power graph of G is finite if and only if the clique number of the power graph of G is finite and this statement is also equivalent to the finiteness of exponents of G. They also proved that the clique number of the power graph of G is at most countable. The fact that the chromatic number is also at most countable was subsequently proved in [78]. If there exists an integer n such that for all $g\in G,g^n=e,$ then G is said to be of bounded exponent.

Lemma 8.13.

[1, Lemma 7] Let G be a group. If $\omega (\mathit{P}(G))$ is finite, then G is of bounded exponent.

Theorem 8.14.

[1, Theorem 10] The clique number of the power graph of any group is at most countably infinite.

Utilizing Lemma 8.13 to colour the power graph with a finite set of colours, we require the group to be of a bounded exponent. It was proved that, for such groups, the resulting power graph is always perfect and can be finitely coloured. To prove this result, Aalipour et al. [1] use the concept of comparability graph. Let $\le$ be a binary relation on the elements of a set P. If $\le$ is reflexive and transitive, then $(P,\le )$ is called a pre-ordered set. All partially ordered sets are pre-ordered. The comparability graph $\Psi (P)$ of a pre-ordered set $(P,\le )$ is the simple graph with the vertex set P and two distinct vertices x and y are adjacent if and only if either $x\le y$ or $y\le x$ (or both).

This is relevant to the power graph since the directed power graph of a group is a pre-ordered set and the power graph is its comparability graph.

Aalipour et al. [1] proved the following with regard to chromatic and clique numbers of power graphs of groups.

Corollary 8.15.

[1, Corollary 13] For every group G, the following statements are equivalent:

1. $\chi (\mathit{P}(G))<\infty ;$

2. $\omega (\mathit{P}(G))<\infty ;$

3. G is of finite exponent.

Moreover, the clique number of $\mathit{P}(G)$ does not exceed the exponent of G. We give an improved version of Aalipour et al. [1, Corollary 14]. Again the function f is as in Theorem 8.9. If G has finite exponent, then ${\pi }_e(G)$ is a finite set (all its elements are divisors of the exponent of G).

Corollary 8.16.

Let G be a group of finite exponent n. Then $$\chi (\mathit{P}(G))=\omega (\mathit{P}(G))=\max \{f(n):n\in {\pi }_e(G)\}.$$

If G is abelian with exponent e, then $\chi (\mathit{P}(G))=\omega (\mathit{P}(G))=f(e).$

Remark 8.17. Theorem 7.19 can be deduced using the fact that the power graph of the group of finite exponent is perfect, together with the weak Perfect Graph Theorem of Lovász [56], asserting that the complement of a finite perfect graph is perfect. This argument also requires a compactness argument to show that the clique cover number of $\mathit{P}(G)$ is equal to the maximum clique cover number of its finite subgroups. However in [17], Cameron et al. gave more elementary argument which gives us a formula for the independence number of $\mathit{P}(C_{p^{\infty }}\times H),$ where $p\nmid o(H).$

Corollary 8.18.

[1, Corollary 15] Let H be a subgroup of G and $\left|G:H\right|<\infty$. Then $$\omega (\mathit{P}(H))<\infty \mathit{\text{if}}\mathrm{ }\mathit{\text{and}}\mathrm{ }\mathit{\text{only}}\mathrm{ }\mathit{\text{if}} \omega (\mathit{P}(G))<\infty .$$

The following example shows that a similar assertion does not hold for the independence number.

Example 8.19.

[1, Example 16] Let $G=C_2\times C_{2^{\infty }}$ and $H=\left\{0\right\}\times C_{2^{\infty }}.$ Thus $\left|G:H\right|=2.$ Since $\mathit{P}(H)$ is a complete graph, $\beta (H)=1.$ Clearly, the set $\left\{1\right\}\times C_{2^{\infty }}$ is an independent set and so $\beta (\mathit{P}(G))=\infty .$

9. Spectrum of power graphs

9.1. Adjacency spectrum of power graphs

For any simple graph Γ with vertex set $\{v_1,v_2\cdots ,v_n\},$ the adjacency matrix $A(\Gamma )=(x_{ij})$ is defined as the n × n matrix, where x_ij = 1 if v_i is adjacent to v_j, and 0 otherwise. The adjacency characteristic polynomial of a graph Γ is given by $\Phi (\Gamma ,a)=\det (aI-A(\Gamma )).$ The eigenvalues of $A(\Gamma )$ are called eigenvalues of the graph Γ and denoted by ${\mu }_i(\Gamma ),i=1,2,3\cdots ,n.$ Clearly, $A(\Gamma )$ is a real symmetric matrix and so all its eigenvalues are real. Thus, they can be arranged in a non-decreasing order as ${\mu }_1\ge {\mu }_2\cdots \ge {\mu }_n.$ The multiset of all eigenvalues of Γ is called the spectrum of Γ denoted by $\sigma (\Gamma )$ and the largest eigenvalue μ₁ is called the spectral radius of Γ.

Mehranian et al. [63] computed the spectrum of the power graph of cyclic groups, dihedral groups, elementary abelian groups of prime power order. In the following theorem, the authors calculated the characteristic polynomial of $\mathit{P}({\mathbb{Z}}_n)$ and ${\mathit{P}}_0({\mathbb{Z}}_n).$

Theorem 9.1.

[63, Theorem 2.4] Suppose $d_i,1\le i\le t$, are all non-trivial divisors of n. Define $$T=\left(\begin{array}{cccccccc}\varphi (n)& & \varphi (d_1)& & \varphi (d_2)& & \cdots & \varphi (d_t)\\ \varphi (n)+1& & \varphi (d_1)-1& & {\alpha }_{d_1{d}_2}& & \cdots & {\alpha }_{d_1{d}_t}\\ \varphi (n)+1& & {\alpha }_{d_2{d}_1}& & \varphi (d_2)-1& & \cdots & {\alpha }_{d_2{d}_t}\\ ⋮& & ⋮& & ⋮& & & ⋮\\ \varphi (n)+1& & {\alpha }_{d_t{d}_1}& & {\alpha }_{d_t{d}_2}& & \cdots & \varphi (d_t)-1\end{array}\right)$$ and ${\alpha }_{d_i{d}_j}=\{\begin{array}{cc}\varphi (d_j)\hfill & \mathit{\text{if}} d_i|d_j \text{or} d_j|d_i,\hfill \\ 0\hfill & \mathit{\text{otherwise}}.\hfill \end{array}.$

Then the characteristic polynomial of the power graph $\mathit{P}({\mathbb{Z}}_n)$ and the proper power graph ${\mathit{P}}_0({\mathbb{Z}}_n)$ can be computed as follows:

1. $\Phi (\mathit{P}({\mathbb{Z}}_n),x)=\Phi (T,x){(x+1)}^{n-t-1};$

2. $\Phi ({\mathit{P}}_0({\mathbb{Z}}_n),s)=\Phi (T^{\prime },x){(x+1)}^{n-t-2}$, where the entries of $T^{\prime }$ equal to those of T in all columns but the first and each entry of the first column of $T^{\prime }$ is one less the corresponding entry of T.

The following theorem gives us the characteristic polynomial of the power graph $\mathit{P}(D_{2n})$ and the proper power graph ${\mathit{P}}_0(D_{2n})$ of the dihedral group $D_{2n}.$

Theorem 9.2.

[63, Theorem 2.5] Suppose n is a prime power. Then the characteristic polynomial of the power graph $\mathit{P}(D_{2n})$ and proper power graph ${\mathit{P}}_0(D_{2n})$ of the dihedral group $D_{2n}$ can be computed as:

1. $\Phi (\mathit{P}(D_{2n}),x)=a^{n-1}{(x+1)}^{n-2}(x^3-(n-2)x^2-(2n-1)x+n^2-2n),$

2. $\Phi ({\mathit{P}}_0(D_{2n}),x)=x^n{(x+1)}^{n-2}(x-(n-2)).$

In the following theorem, the authors obtained the characteristic polynomial and also computed the eigenvalues of the power graph of an elementary abelian group $E(p^n),$ where p is a prime number.

Theorem 9.3.

[63, Theorem 2.7] For a prime number p, let $\mathcal{\ell }=\frac{p^n-1}{p-1}$. Then $$\Phi (\mathit{P}(E(p^n)),x)=(x-{(p-2)}^{\mathcal{\ell }-1}){(x+1)}^{(p-2)\mathcal{\ell }}(x^2-(p-2)x-(p^n-1)).$$

In particular, the eigenvalues of $\mathit{P}(E(P^n))$ are –1 with multiplicity $(p-2)\mathcal{\ell },p-2$ with multiplicity $\mathcal{\ell }-1$ and two simple eigenvalues $x_{1,2}=\frac{p-2\pm \sqrt{{(p-2)}^2+4(p^n-1)}}{2}.$

Hamzeh et al. [47] generalized some results proved in [63] through some more results on power graphs and they are presented below.

Theorem 9.4.

[47, Theorem 3.9] The characteristic polynomial of $\mathit{P}(D_{2n})$ can be computed as follows: $$\Phi (\mathit{P}(D_{2n}),x)=x^{n-1}{(x+1)}^{n-t-2}[x(x+1)\Phi (T,x)-n\Phi (T^{\prime },x)].$$ where $d_i,1\le i\le t$, are all non-trivial divisors of n, $$\begin{array}{c}T=\left(\begin{array}{cccccccc}\varphi (n)& & \varphi (d_1)& & \varphi (d_2)& & \cdots & \varphi (d_t)\\ \varphi (n)+1& & \varphi (d_1)-1& & {\alpha }_{d_1{d}_2}& & \cdots & {\alpha }_{d_1{d}_t}\\ \varphi (n)+1& & {\alpha }_{d_2{d}_1}& & \varphi (d_2)-1& & \cdots & {\alpha }_{d_2{d}_t}\\ ⋮& & ⋮& & ⋮& & & ⋮\\ \varphi (n)+1& & {\alpha }_{d_t{d}_1}& & {\alpha }_{d_t{d}_2}& & \cdots & \varphi (d_t)-1\end{array}\right)\\ \\ T^{\prime }=\left(\begin{array}{cccccccc}\varphi (n)-1& & \varphi (d_1)& & \varphi (d_2)& & \cdots & \varphi (d_t)\\ \varphi (n)& & \varphi (d_1)-1& & {\alpha }_{d_1{d}_2}& & \cdots & {\alpha }_{d_1{d}_t}\\ \varphi (n)& & {\alpha }_{d_2{d}_1}& & \varphi (d_2)-1& & \cdots & {\alpha }_{d_2{d}_t}\\ ⋮& & ⋮& & ⋮& & & ⋮\\ \varphi (n)& & {\alpha }_{d_t{d}_1}& & {\alpha }_{d_t{d}_2}& & & \varphi (d_t)-1\end{array}\right).\end{array}$$ and ${\alpha }_{d_i{d}_j}=\{\begin{array}{cc}\varphi (d_j)\hfill & \mathit{\text{if}} d_i|d_j \text{or} {\mathrm{d}}_{\mathrm{j}}{|\mathrm{d}}_{\mathrm{i}}\hfill \\ 0\hfill & \mathit{\text{otherwise}}.\hfill \end{array}.$

Theorem 9.5.

[47, Theorem 3.11] The characteristic polynomial of ${\mathit{P}}_0(Q_{4n})$ can be computed as follows: $$\Phi ({\mathit{P}}_0(Q_{4n}),x)={(x+1)}^{3n-t-2}[\Phi (T,x){(x-1)}^n+\Phi (T^{″},x)\Phi (T^{\prime },x)-x{(x-1)}^n\Phi (T^{″},x)],$$ where $d_i,1\le i\le t$, are all non-trivial divisors of 2n. $$\begin{array}{c}T=\left(\begin{array}{cccccccc}\varphi (2n)-1& & \varphi (d_1)& & \varphi (d_2)& & \cdots & \varphi (d_t)\\ \varphi (2n)& & \varphi (d_1)-1& & {\alpha }_{d_1{d}_2}& & \cdots & {\alpha }_{d_1{d}_t}\\ \varphi (2n)& & {\alpha }_{d_2{d}_1}& & \varphi (d_2)-1& & \cdots & {\alpha }_{d_2{d}_t}\\ ⋮& & ⋮& & ⋮& & & ⋮\\ \varphi (2n)& & {\alpha }_{d_t{d}_1}& & {\alpha }_{d_t{d}_2}& & & \varphi (d_t)-1\end{array}\right),\\ \\ T^{\prime }=\left(\begin{array}{ccccccccc}0& & 2& & 2& & \cdots & & 2\\ 1& & 1& & 0& & \cdots & & 0\\ 1& & 0& & 1& & \cdots & & 0\\ ⋮& & ⋮& & ⋮& & ⋮& & \\ 1& & 0& & 0& & \cdots & & 1\end{array}\right),\\ \\ T^{″}=\left(\begin{array}{cccccccc}\varphi (2n)-2& & \varphi (d_1)& & \varphi (d_2)& & \cdots & \varphi (d_t)\\ \varphi (2n)-1& & \varphi (d_1)-1& & {\alpha }_{d_1{d}_2}& & \cdots & {\alpha }_{d_1{d}_t}\\ \varphi (2n)-1& & {\alpha }_{d_2{d}_1}& & \varphi (d_2)-1& & \cdots & {\alpha }_{d_2{d}_t}\\ ⋮& & ⋮& & ⋮& & & ⋮\\ \varphi (2n)-1& & {\alpha }_{d_t{d}_1}& & {\alpha }_{d_t{d}_2}& & & \varphi (d_t)-1\end{array}\right).\end{array}$$ and ${\alpha }_{d_i{d}_j}=\{\begin{array}{cc}\varphi (d_j)\hfill & \mathit{\text{if}} d_i|d_j \text{or} d_j|d_i\hfill \\ 0\hfill & \mathit{\text{otherwise}}.\hfill \end{array}.$

Chattopadhyay et al. [25] obtained both upper and lower bounds for the spectral radius of the power graph of ${\mathbb{Z}}_n$ and characterized the graphs for which these bounds are extremal. Further, they computed spectra of power graphs of the dihedral group $D_{2n}$ and dicyclic group $Q_{4n}$ partially and gave bounds for the spectral radii of these graphs.

In Theorem 9.1, the characteristic polynomial of $\mathit{P}({\mathbb{Z}}_n)$ has been obtained in terms of the characteristic polynomial of the quotient matrix T whose entries are some functions of the divisors of n. Also, note that the spectral radius of $\mathit{P}({\mathbb{Z}}_n)$ is the same as that of the matrix T. Since the increase in the number of factors of n leads to a rapid increase of the degree of the polynomial of T, it is sometimes too complicated to find the exact value of the spectral radius of $\mathit{P}({\mathbb{Z}}_n).$ Therefore, one can use some graph invariants like vertex degrees and diameter to approximate the spectral radius. The following theorem gives both upper and lower bounds for the spectral radius of $\mathit{P}({\mathbb{Z}}_n)$ in terms of the maximum and minimum degrees of the non-identity non-generator elements of ${\mathbb{Z}}_n.$

Theorem 9.6.

[25, Theorem 2.1] If $n\ge 3$ is natural number, then the spectral radius ${\mu }_1(\mathit{P}({\mathbb{Z}}_n))$ of $\mathit{P}({\mathbb{Z}}_n)$ satisfies $${\mu }_1(\mathit{P}({\mathbb{Z}}_n))\ge \frac{1}{2}\left[(d_{\min }-1)+\sqrt{{(2\mathcal{\ell }-1-d_{\min })}^2+4\mathcal{\ell }(n-\mathcal{\ell })}\right]$$ and $${\mu }_1(\mathit{P}({\mathbb{Z}}_n))\le \frac{1}{2}\left[(d_{\max }-1)+\sqrt{{(2\mathcal{\ell }-1-d_{\max })}^2+4\mathcal{\ell }(n-\mathcal{\ell })}\right]$$ where $\mathcal{\ell }=\varphi (n)+1,d_{\max }$ and $d_{\min }$ are the maximum and minimum degrees of the non-identity non-generator elements of ${\mathbb{Z}}_n$ respectively. Furthermore, equality holds in both the bounds if and only if $n=p^{\alpha }$, for any prime number p and any positive integer α.

The next result provides the characteristic polynomial of $\mathit{P}(D_{2n})$ in terms of characteristic polynomials of $\mathit{P}({\mathbb{Z}}_n)$ and ${\mathit{P}}_0({\mathbb{Z}}_n).$

Theorem 9.7.

[25, Theorem 2.2] For any integer $n\ge 3$, the characteristic polynomial of $\mathit{P}(D_{2n})$ is given by $$\phi (\mathit{P}(D_{2n}),x)=x^{n-1}\left[x\Phi (\mathit{P}({\mathbb{Z}}_n),x)-n\Phi ({\mathit{P}}_0({\mathbb{Z}}_n),x)\right].$$

Remark 9.8.

In the above theorem, the characteristic polynomial of $\mathit{P}(D_{2n})$ has been obtained for any natural number $n\ge 3$ whereas in Theorem 9.2, the characteristic polynomial of $\mathit{P}(D_{2n})$ is given only when n is a prime power.

Theorems 9.9 and 9.10 provide upper and lower bounds on ${\mu }_1(\mathit{P}(D_{2n}))$ and ${\mu }_1(\mathit{P}(Q_{4n}))$ respectively in terms of ${\mu }_1(\mathit{P}({\mathbb{Z}}_n)).$

Theorem 9.9.

[25, Theorem 2.3]. For any integer $n\ge 3$, the spectral radius ${\mu }_1(\mathit{P}(D_{2n}))$ of $\mathit{P}(D_{2n})$ satisfies $${\mu }_1(\mathit{P}({\mathbb{Z}}_n))<{\mu }_1(\mathit{P}(D_{2n}))\le {\mu }_1(\mathit{P}({\mathbb{Z}}_n))+\sqrt{n}.$$

Theorem 9.10.

[25, Theorem 2.4] For any integer $n\ge 2$, the spectral radius ${\mu }_1(\mathit{P}(Q_{4n}))$ of $\mathit{P}(Q_{4n})$ satisfies $${\mu }_1(\mathit{P}({\mathbb{Z}}_{2n}))<{\mu }_1(\mathit{P}(Q_{4n}))\le {\mu }_1(\mathit{P}({\mathbb{Z}}_{2n}))+2\sqrt{n}.$$

In the following theorem, full spectrum of the power graph of the generalized quaternion group $Q_{4n}$ is computed.

Theorem 9.11.

[25, Theorem 2.5] For any integer n of the form $n=2^{\alpha },\alpha \in \mathbb{N}$, the characteristic polynomial of $\mathit{P}(Q_{4n})$ is given by $$\Phi (\mathit{P}(Q_{4n}),x)={(x-1)}^n{(x+1)}^{3n-2}\left[\frac{(x^2-4n-1)(x-2n+3)}{x-1}-2(a+1)\right].$$

9.2. Laplacian Spectrum of power graphs

For any finite simple undirected graph $\Gamma ,$ the Laplacian matrix $L(\Gamma )$ is given by $L(\Gamma )=D(\Gamma )-A(\Gamma ),$ where $A(\Gamma )$ is the adjacency matrix of Γ and $D(\Gamma )$ is the diagonal matrix of vertex degrees. Clearly $L(\Gamma )$ is a real symmetric matrix and so all its eigenvalues are real. For a graph Γ on n vertices, we denote the Laplacian eigenvalues of Γ by ${\lambda }_1(\Gamma )\ge {\lambda }_2(\Gamma )\ge \cdots \ge {\lambda }_n(\Gamma )$ always arranged in non-increasing order and repeated according to their multiplicity. Since $L(\Gamma )$ is symmetric, positive semi-definite and singular, and all its eigenvalues are non-negative and ${\lambda }_n(\Gamma )=0.$ To know, more interesting facts about Laplacian eigenvalues of a graph, we refer the survey paper [66]. Let ${\lambda }_1,\dots ,{\lambda }_m$ be the distinct Laplacian eigenvalues with corresponding multiplicities $t_1,\dots ,t_m.$ Then the Laplacian spectrum is denoted by $$\left(\begin{array}{ccccc}{\lambda }_1& & \dots & & {\lambda }_m\\ t_1& & \dots & & t_m\end{array}\right).$$

It is known that [33], the Laplacian eigenvalue with multiplicity 0 of a graph Γ is equal to the number of connected components of Γ. Thus, one gets that the second smallest Laplacian eigenvalue ${\lambda }_{n-1}(\Gamma )>0$ if and only if Γ is connected. Fiedler [41], called ${\lambda }_{n-1}(\Gamma )$ as the algebraic connectivity of Γ, viewing it as a measure of connectivity of Γ. The largest Laplacian eigenvalue ${\lambda }_1(\Gamma )$ is called the Laplacian spectral radius of Γ. A graph is called Laplacian integral if all its Laplacian eigenvalues are integers. In [41], Fiedler proved that the algebraic connectivity ${\lambda }_{n-1}(\Gamma )$ of a noncomplete graph Γ does not exceed its vertex connectivity $\kappa (\Gamma ).$

The Laplacian spectrum of a graph has a number of applications, including random walks, expansion properties, and statistical efficiency and optimality properties. See [8] for some of these.

We write the characteristic polynomial $\det (xI-L(\Gamma ))$ of $L(\Gamma )$ by $\Theta (\Gamma ,x)$ instead of $\Theta (L(\Gamma ),x)$ and called $\Theta (\Gamma ,a)$ the Laplacian characteristic polynomial of Γ.

Let Γ be a graph with vertex set $V(\Gamma )=\{v_1,v_2,\dots ,v_n\}.$ Then, for the vertices $v_1,v_2,\dots v_i$ in Γ, $L_{v_1,v_2,\dots ,v_i}(\Gamma )$ is defined as the principal submatrix of $L(\Gamma )$ formed by deleting rows and columns corresponding to the vertices $v_1,v_2,\dots ,v_i.$ In particular, if i = n, then for convention it is taken as $\Theta (L_{v_1,v_2,\dots ,v_n}(\Gamma ,x))=1.$

Chattopadhyay [22] obtained the Laplacian spectrum of $\mathit{P}({\mathbb{Z}}_n)$ and $\mathit{P}(D_{2n})$ for particular values of n. In fact, the relationship between the spectrum of these two power graphs are discussed. Also, they gave sharp lower and upper bounds for algebraic connectivity of $\mathit{P}({\mathbb{Z}}_n).$

Panda [68] considered various aspects of Laplacian spectra of power graphs of finite cyclic groups, dicyclic groups, and finite p-groups. More specifically, Panda [68] determined completely the Laplacian spectral radius of power graphs of all of these groups apart from the algebraic connectivity and its multiplicity. Then, the equality of the vertex connectivity and the algebraic connectivity is characterized for power graphs of all of the above classes of groups. Orders of dicyclic groups with Laplacian integral power graphs are determined. Moreover, it is proved that the notion of equality of the vertex connectivity and the algebraic connectivity and the notion of Laplacian integral are equivalent for power graphs of dicyclic groups. All possible values of Laplacian eigenvalues are obtained for power graphs of finite p-groups and hence it is proved that power graphs of finite p-groups are Laplacian integral.

In the following theorem, the authors gave an expression for Laplacian characteristic polynomial of $\mathit{P}({\mathbb{Z}}_n)$ in terms of the characteristic polynomial of $L_{\overline{0},\overline{g_1},\overline{g_2}\cdots ,{\overline{g}}_{\varphi (n)}}(\mathit{P}({\mathbb{Z}}_n)),$ where ${\overline{g}}_i(i=1,2,\dots ,\varphi (n))$ are the generators of ${\mathbb{Z}}_n.$

Theorem 9.12.

[22, Theorem 2.2] For each positive integer $n\ge 2$, let ${\overline{g}}_i(i=1,2,\dots ,\varphi (n))$ be the generators of ${\mathbb{Z}}_n$. Then $$\Theta (\mathit{P}({\mathbb{Z}}_n),x)=\frac{x{(x-n)}^{\varphi (n)+1}}{(x-\varphi (n)-1)}\Theta (L_{\overline{0},{\overline{g}}_1,{\overline{g}}_2,\dots ,{\overline{g}}_{\varphi (n)}}(\mathit{P}({\mathbb{Z}}_n),x).$$

Corollary 9.13.

[22, Corollary 2.3] If n is a prime, then the Laplacian spectrum of $\mathit{P}({\mathbb{Z}}_n)$ is given by $$\left(\begin{array}{cc}0& n\\ 1& n-1\end{array}\right).$$

Corollary 9.14.

[22, Corollary 2.4] For each non-prime positive integer n > 3, the multiplicity of n as a Laplacian eigenvalues of $\mathit{P}({\mathbb{Z}}_n)$ is at least $\varphi (n)+1.$

Theorem 9.15.

[22, Theorem 2.5] For $n=p_1{p}_2$, where p₁ and p₂ are distinct primes, the Laplacian spectrum of $\mathit{P}({\mathbb{Z}}_n)$ is $$\left(\begin{array}{ccccc}0& \varphi (n)+1& n-p_1+1& n-p_2+1& n\\ 1& 1& p_2-2& p_1-2& \varphi (n)+1\end{array}\right).$$

Corollary 9.16.

[22, Corollary 2.6] For any two distinct primes p₁ and p₂, the algebraic connectivity of $P(Z_{p_1{p}_2})$ is $\varphi (p_1{p}_2)+1.$

The following result is a consequence of Theorem 5.2 in which a sharp upper bound of the algebraic connectivity is given.

Corollary 9.17.

[22, Corollary 2.8] For $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}$, where p₁ and p₂ are distinct primes and ${\alpha }_1,{\alpha }_2\in \mathbb{N}$, the algebraic connectivity ${\lambda }_{n-1}(\mathit{P}({\mathbb{Z}}_n))\le \varphi (n)+p_1^{{\alpha }_1-1}{p}_2^{{\alpha }_2-1}$, equality holds if ${\alpha }_1=1={\alpha }_2.$

Corollary 9.18.

[22, Corollary 2.10] For $n=p_1{p}_2{p}_3$, where p₁, p₂ and p₃ are distinct primes with $p_1<p_2<p_3$, the algebraic connectivity ${\lambda }_{n-1}(\mathit{P}({\mathbb{Z}}_n))\le \varphi (n)+p_1+p_2-1.$

In the following theorem, the authors gave a lower bound for the algebraic connectivity of $\mathit{P}({\mathbb{Z}}_n),$ for arbitrary positive integer $n\ge 2.$

Theorem 9.19.

[22, Theorem 2.12] For each positive integer $n\ge 2$, the algebraic connectivity of $\mathit{P}({\mathbb{Z}}_n)$ ${\lambda }_{n-1}(\mathit{P}({\mathbb{Z}}_n))$ satisfies the inequality ${\lambda }_{n-1}(\mathit{P}({\mathbb{Z}}_n))\ge \varphi (n)+1$. Equality holds if n is either a prime or a product of two distinct primes.

In the following theorem Panda [68] obtained the multiplicity of n as a Laplacian eigenvalue of $\mathit{P}({\mathbb{Z}}_n)$ for all $n\in \mathbb{N}.$

Theorem 9.20.

[68, Theorem 10] For an integer n > 1, multiplicity of the Laplacian eigenvalue n of $\mathit{P}({\mathbb{Z}}_n)=\{\begin{array}{cc}\hfill & n-1 \text{if} n \text{is}\text{ a }\text{prime}\mathrm{ }\text{power};\hfill \\ \hfill & \varphi (n)+1 \text{otherwise}.\hfill \end{array}$

Recall that $S({\mathbb{Z}}_n)$ denotes the set of all generators together with the identity of the group ${\mathbb{Z}}_n$ and $〈S{({\mathbb{Z}}_n)}^c〉$ is the induced subgraph of the power graph of ${\mathbb{Z}}_n.$ Observe that $\Theta (〈S{({\mathbb{Z}}_n)}^c〉,x-\varphi (n)-1)$ equals with the characteristic polynomial of the submatrix of $L(\mathit{P}({\mathbb{Z}}_n))$ obtained by deleting rows and columns corresponding to the elements of $S{({\mathbb{Z}}_n)}^c.$ Thus, using Theorem 9.12, the authors proved the following lemma.

Lemma 9.21.

[68, Lemma 7] If the integer n > 1 is not a prime number, then $${\lambda }_i(\mathit{P}({\mathbb{Z}}_n))=\{\begin{array}{cc}n\hfill & \mathit{\text{if}} 1\le i\le \varphi (n)+1;\hfill \\ {\lambda }_{i-\varphi (n)-1}(〈S{({\mathbb{Z}}_n)}^c〉)+\varphi (n)+1\hfill & \mathit{\text{if}} \varphi (n)+2\le i\le n-1;\hfill \\ 0 \hfill & \mathit{for} i=n.\hfill \end{array}$$

Hamzeh et al. [47] denoted the set of all cyclic subgroups of finite group G by $\mathit{C}(G)=\{C_1,C_2,\dots C_k\}$ be and Δ_G(renamed for the sake of convenience) be the simple undirected graph with vertex set $\mathit{C}(G)$ in which two cyclic subgroups are adjacent if one is contained in other. Let $K_{a_i}$ be the complete graph of order $a_i=\varphi (\left|C_i\right|).$ If $K_G=\left\{K_{a_i}\right|a_i=\varphi (\left|C_i\right|),C_i\in \mathit{C}(G)\},$ then the power graph $\mathit{P}(G)$ is isomorphic to Δ_G-join of $K_{a_1},K_{a_2},\dots ,K_{a_k},$ see [39] for details.

Theorem 9.22.

[47, Theorem 3.17] The Laplacian spectrum of $\mathit{P}(G)={\Delta }_G[K_{a_1},\dots ,K_{a_k}]$ can be calculated as follows: $$\begin{array}{c}{\sigma }_L(\mathit{P}(G))=\left\{\underset{j=1}{\overset{k}{\cup }}{(N_j+a_i)}^{a_j-1}\right\}\cup \sigma (C),\\ \text{where}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}{N}_j=\{\begin{array}{cc}\sum _{C_i\in N_{{\Delta }_G(C_i)}}{a}_i\hfill & \mathit{\text{if}} N_{{\Delta }_G(C_i)}\ne \varnothing \hfill \\ 0\hfill & \mathit{\text{otherwise}}.\hfill \end{array}\\ {\rho }_{\mathcal{\ell },q}={\rho }_{q,\mathcal{\ell }}=\{\begin{array}{cc}\sqrt{a_{\mathcal{\ell }}{a}_q}\hfill & \mathit{\text{if}} c_{\mathcal{\ell }}\subseteq c_q \text{or} c_q\subseteq c_{\mathcal{\ell }}\hfill \\ 0\hfill & \mathit{\text{otherwise}}.\hfill \end{array}\\ \text{and}\text{\hspace{1em}\hspace{1em}C}=\left(\begin{array}{ccccccc}{N}_1& & -{\rho }_{\mathcal{\ell },2}& & \cdots & & -{\rho }_{\mathcal{\ell },k}\\ -{\rho }_{2,1}& & N_2& & \cdots & & -{\rho }_{2,k}\\ ⋮& & ⋮& & ⋮& & ⋮\\ -{\rho }_{\mathcal{\ell },k}& & -{\rho }_{2,k}& & \cdots & & N_k\end{array}\right).\end{array}$$

In Theorem 9.12, the Laplacian polynomial of $\mathit{P}({\mathbb{Z}}_n)$ was obtained. Hamzeh et al. [47] applied the Theorem 9.22 and provided a complete description of the Laplacian spectrum of $\mathit{P}({\mathbb{Z}}_n)$ in [47, Corollary 3.18]. Also in [47], the authors determined the Laplacian spectrum of $\mathit{P}({\mathbb{Z}}_n)$ when n is a prime power and a product of two distinct primes using Theorem 9.22.

In the following theorem, Laplacian characteristic polynomial of $\mathit{P}(D_{2n})$ is calculated in terms of Laplacian characteristic polynomial of $\mathit{P}({\mathbb{Z}}_n).$

Theorem 9.23.

[22, Theorem 3.1] For any integer $n\ge 3,$ $$\Theta (\mathit{P}(D_{2n}),x)=\frac{{(x-1)}^n(x-2n)}{x-n}\Theta (\mathit{P}({\mathbb{Z}}_n),x).$$

Theorem 9.24.

[22, Theorem 3.2] For each non-prime positive integer n > 3, Laplacian eigenvalues of $\mathit{P}(D_{2n})$ in terms of that of $\mathit{P}({\mathbb{Z}}_n)$, are given by $${\lambda }_i(\mathit{P}(D_{2n}))=\{\begin{array}{cc}2n\hfill & \mathit{\text{for}} i=1\hfill \\ {\lambda }_i(\mathit{P}({\mathbb{Z}}_n))=n\hfill & \mathit{\text{for}} 2\le i\le \varphi (n)+1\hfill \\ {\lambda }_i(\mathit{P}({\mathbb{Z}}_n))\hfill & \mathit{\text{for}} \varphi (n)+2\le i\le n-1\hfill \\ 1\hfill & \mathit{\text{for}} n\le i\le 2n-1\hfill \\ 0\hfill & \mathit{\text{for}} i=2n.\hfill \end{array}$$

In [22], Laplacian spectrum of $\mathit{P}(D_{2n})$ were also calculated and the authors proved that the Laplacian spectrum of $\mathit{P}(D_{2n})$ is the union of that of $\mathit{P}({\mathbb{Z}}_n)$ and $\{2n,1\}.$

Corollary 9.25.

[22, Corollary 3.3] If n is a prime power, then the Laplacian eigenvalues of $\mathit{P}({\mathbb{Z}}_n)$ are 0 and n with multiplicities 1 and n – 1, respectively, and the spectrum of $\mathit{P}(D_{2n})$ is given by $$\mathit{P}(D_{2n})=\left(\begin{array}{cccc}0& 1& n& 2n\\ 1& n& n-2& 1\end{array}\right).$$

Corollary 9.26.

[22, Corollary 3.4] For each positive integer $n\ge 3$, the algebraic connectivity of $\mathit{P}(D_{2n})$, namely, ${\lambda }_{2n-1}(\mathit{P}(D_{2n}))$ is equal to 1.

If n is a product of two distinct primes, then by applying Theorems 9.15 and 9.24, we have the following result.

Corollary 9.27.

[22, Corollary 3.5] If $n=p_1{p}_2$, where p₁ and p₂ are distinct primes, then the Laplacian spectrum of $\mathit{P}(D_{2n})$ is given by $$\mathit{P}(D_{2n})=\left(\begin{array}{ccccccc}0& 1& \varphi (n)+1& n-p_1+1& n-p_2+1& n& 2n\\ 1& n& 1& p_2-2& p_1-2& \varphi (n)& 1\end{array}\right).$$

In the following lemma, the authors gave bounds for the algebraic connectivity of power graph $\mathit{P}(Q_{4n})$ of the group $Q_{4n}.$

Lemma 9.28.

[68, Lemma 9] For any integer $n\ge 2$, the algebraic connectivity of $\mathit{P}(Q_{4n})$ satisfies $1<{\lambda }_{4n-1}((Q_{4n}))\le 2.$

The following theorem, provides the multiplicity of the Laplacian spectral radius of $\mathit{P}(Q_{4n}).$

Theorem 9.29.

[68, Theorem 12] For any integer $n\ge 2$, the Laplacian eigenvalue 4n of $\mathit{P}(Q_{4n})$ has multiplicity two if $Q_{4n}$ is a generalized quaternion and one otherwise.

The following result determines when exactly a dicyclic group is a generalized quaternion in terms of its power graph.

Proposition 9.30.

[68, Proposition 1] For any integer $n\ge 2$, aⁿ is adjacent to all other vertices of $\mathit{P}(Q_{4n})$ if and only if $Q_{4n}$ is generalized quaternion.

Lemma 9.31.

[68, Lemma 6] Let G be a finite group of order $n\ge 3$. Then the algebraic connectivity of $\mathit{P}(G)$ is 1 if and only if its vertex connectivity is 1.

Let G be a group. For $a\in G,$ $U(a)=\{h\in G:a\in 〈h〉\}$ and $\widehat{U}(a)=U(a)\setminus [a].$ Let $\Gamma (a)$ be the subgraph of $\mathit{P}(G)$ induced by U(a). We denote the component of ${\mathit{P}}_0(G)$ containing a by C(a). For the above subsets and subgraphs, the underlying group will always be clear from context.

Remark 9.32.

[68, Remark 1] For any group G and $a\in G,$ the multiplicity of the Laplacian eigenvalue 0 of $\Gamma (a)$ is one.

Lemma 9.33.

[68, Lemma 11] Let G be a finite p-group of order n and $a\in G$ be an element of order p. Then $C(a)=\Gamma (a).$

For $g,h\in G,$ we say that $[h]$ is a primitive class of g if $[g]=[h^p]$ and $h\ne e.$ We denote the number of primitive classes of any $g\in G$ by $\pi (g).$ It should be noted that if G is finite p-group, then for any $a\in G,$ we cannot have $\pi (a)=0$ and o(a) = 1 simultaneously.

Lemma 9.34.

[68, Lemma 12] If G is a finite p-group and $a\in G$ with $\pi (a)=0$, then $\Gamma (a)=P([a])\cong K_{\varphi (o(a))}$. Consequently, $\Theta (\Gamma (a),x)=x{(x-\varphi (o(a)))}^{\varphi (o(a))-1}.$

The following proposition iteratively describes the structure of the power graph of a finite p-group.

Proposition 9.35.

[68, Proposition 2] Let G be a finite p-group and $a\in G$. If $\pi (a)>0$ and the distinct primitive classes of a be $[h_1],[h_2],\dots ,[h_{\varphi (a)}]$, then $$\Gamma (a)\cong K_{\varphi (o(a))}\vee \left\{\Gamma (h_1)+\Gamma (h_2)+\cdots +\Gamma (h_{\pi (a)})\right\}.$$

In particular, for a = e, $\mathit{P}(G)\cong K_1\vee \left\{\Gamma (h_1)+\Gamma (h_2)+\cdots +\Gamma (h_{\pi (e)})\right\}.$

Proposition 9.36.

[68, Proposition 3] Let G be a finite p-group and $a\in G$. If $\pi (a)>0$ and the distinct primitive classes of a be $[h_1],[h_2],\dots ,[h_{\varphi (a)}]$, then $$\Theta (\Gamma (a),x)=\frac{x{(x-\left|U(a)\right|)}^{\varphi (o(a))}}{x-\varphi (o(a))}\prod _{i=1}^{\pi (a)}\Theta (\Gamma (h_i),x-\varphi (o(a)).$$

In particular, for a = e, $\Theta (\mathit{P}(G),x)=\frac{x(x-\left|G\right|)}{x-1}{\prod }_{i=1}^{\pi (e)}\Theta (\Gamma (h_i),x-1).$

Proposition 9.37.

[68, Proposition 6] If G is a group of order p², then the Laplacian spectrum of $\mathit{P}(G)$ is either $$\left(\begin{array}{cc}0& p^2\\ 1& p^2-1\end{array}\right)or\left(\begin{array}{cccc}0& 1& p& p^2\\ 1& p& (p+1)(p-2)& 1\end{array}\right).$$

Theorem 9.38.

[68, Theorem 14] Let G be a finite p group of order $n\ge 3$. Then the following statements are equivalent.

1. The algebraic connectivity of $\mathit{P}(G)$ is 1.

2. The multiplicity of the Laplacian eigenvalue n of $\mathit{P}(G)$ is one.

3. G is neither cyclic nor generalized quaternion.

9.3. Equality of algebraic and vertex connectivity of power graphs

The following lemma proved by Kirkland [54] is useful for the characterization of graphs with equal vertex connectivity and algebraic connectivity.

Theorem 9.39.

[54, Theorem 2.1] Let Γ be a non-complete and connected graph on n vertices. Then $\kappa (\Gamma )={\lambda }_{n-1}(\Gamma )$ if and only if it can be written as ${\Gamma }_1\vee {\Gamma }_2$, where ${\Gamma }_1$ is disconnected graph on $n-\kappa (\Gamma )$ vertices and ${\Gamma }_2$ is a graph on $\kappa (\Gamma )$ vertices with ${\lambda }_{n-1}({\Gamma }_2)\ge 2\kappa (\Gamma )-n.$

In the following theorem, the authors determined all n for which vertex and algebraic connectivity of $\mathit{P}({\mathbb{Z}}_n)$ are equal.

Theorem 9.40.

[68, Theorem 11] For any integer $n>1,\kappa (\mathit{P}({\mathbb{Z}}_n))={\lambda }_{n-1}(\mathit{P}({\mathbb{Z}}_n))$ if and only if n is a product of two distinct primes.

In the next theorem, the authors proved the equivalence of various properties of Laplacian spectra for power graphs of dicyclic groups.

Theorem 9.41.

[68, Theorem 13] For any integer $n\ge 2$, the following statements are equivalent:

1. The vertex connectivity and algebraic connectivity of $\mathit{P}(Q_{4n})$ are equal;

2. The algebraic connectivity of $\mathit{P}(Q_{4n})$ is 2;

3. The algebraic connectivity of $\mathit{P}(Q_{4n})$ is an integer;

4. $\mathit{P}(Q_{4n})$ is Laplacian integral;

5. $Q_{4n}$ is generalized quaternion.

Next theorem shows that the vertex connectivity and the algebraic connectivity of power graphs of finite p-groups are equal exactly when it is not cyclic.

Theorem 9.42.

[68, Theorem 15] Let G be a finite p-group of order n. Then $\kappa (\mathit{P}(G))={\lambda }_{n-1}(\mathit{P}(G))$ if and only if G is not cyclic.

Ankir Raj et al. [75] obtained results on the Laplacian spectrum of $\mathit{P}({\mathbb{Z}}_{p^m}^n).$

10. Isomorphism of power graphs

In 2010, Cameron [13], proved that if undirected power graphs of two finite groups are isomorphic, then their directed power graphs are also isomorphic. However, it is not true that any from one power graph to another preserves the orientation of edges, and the mentioned result fails for an infinite group. For a counter example one can see [15,16]. In 2019, Cameron et al. [16], considered power graphs of torsion-free groups and proved the following theorems.

Theorem 10.1.

[16, Theorem 1.2] Let H be a group with $\mathit{P}(H)$ isomorphic to $\mathit{P}(\mathbb{Z})$. Then H is isomorphic to $\mathbb{Z}$ and only isomorphism from $\mathit{P}(\mathbb{Z})$ to $\mathit{P}(H)$ induces an isomorphism from $\overrightarrow{\mathit{P}}(\mathbb{Z})$ to $\overrightarrow{\mathit{P}}(H).$

Theorem 10.2.

[16, Theorem 1.3] Let G and H be nilpotency class 2 torsion-free groups. Then $\mathit{P}(G)\cong \mathit{P}(H)$ implies $\overrightarrow{\mathit{P}}(G)\cong \overrightarrow{\mathit{P}}(H).$

In [16], some examples were provided to exhibit that even under the hypotheses of Theorems 10.1 and 10.2, $\mathit{P}(G)\cong \mathit{P}(H)$ need not imply $G\cong H.$ Further examples were also provided to show that some more hypothesis on G is needed for the above property.

Theorem 10.3.

[16, Theorem 5.4] Let G be a countable torsion-free group which is not cyclic, but in which each non-identity element lies in a unique maximal cyclic subgroup. Let H be a group with $\mathit{P}(H)\cong \mathit{P}(G)$. Then

1. Each non-identity element of H lies in a unique maximal cyclic subgroup;

2. $\overrightarrow{\mathit{P}}(H)\cong \overrightarrow{\mathit{P}}(G)$;

3. Any isomorphism from $\mathit{P}(G)$ to $\mathit{P}(H)$ induces an isomorphism from $\overrightarrow{\mathit{P}}(G)$ to $\overrightarrow{\mathit{P}}(H).$

Moreover, all groups G satisfying the hypothesis have isomorphic power graphs.

Theorem 10.4.

[16, Theorem 1.5] Let $\mathbb{Q}$ be the additive group of rational numbers, and $G={\mathbb{Q}}^n$. Then, for a group H, if $\mathit{P}(G)\cong \mathit{P}(H)$, then $\overrightarrow{\mathit{P}}(H)\cong \overrightarrow{\mathit{P}}(G)$. Moreover, if n = 1, then any isomorphism from $\mathit{P}(G)$ to $\mathit{P}(H)$ either preserves or reverses the orientation of edges.

In the same article [16], the authors posed the following open problem.

Problem 10.5. [16, Problem Section 8]] If G is a torsion free nilpotent group of class 2, and H a group with $\mathit{P}(G)\cong \mathit{P}(H),$ is it true that $\overrightarrow{\mathit{P}}(H)\cong \overrightarrow{\mathit{P}}(G)$?

Zahirović [81] gave an affirmative answer to this problem:

Theorem 10.6

(Theorem 21, [81]). Let G be a torsion-free group of nilpotency class 2. Let H be a group such that $\mathit{P}(G)\cong \mathit{P}(H)$. Then $\overrightarrow{\mathit{P}}(H)\cong \overrightarrow{\mathit{P}}(G).$

Subsequently, Zahirović proved a stronger result, applying to all groups, and showing clearly the special role played by the Prüfer groups $C_{p^{\infty }}:$

Theorem 10.7.

[82, Theorem 3.18] Let G be a group with the following property: G has no subgroup H isomorphic to $C_{p^{\infty }}$ which has trivial intersection with any subgroup K not contained in H. If G₁ is a group with $\mathit{P}(G)\cong \mathit{P}(G_1)$, then $\overrightarrow{\mathit{P}}(G)\cong \overrightarrow{\mathit{P}}(G_1).$

Corollary 10.8.

[82, Corollary 3.19] Any two torsion-free groups having isomorphic power graphs have isomorphic directed power graphs.

11. Automorphism groups of power graphs

The set of all automorphisms of a graph Γ forms a permutation group $\text{Aut}(\Gamma ),$ acting on the object set $V(\Gamma ),$ called the automorphism group of Γ. One can refer to [12] for the terminology and main results of permutation group theory.

Let A and B be permutation groups acting on object sets X and Y respectively. Define $$B\wr A=\{(a,f)|a\in A,f:X\to B\},(a,f)(x,y)=(ax,b_{x}y)$$ where $f(x)=b_x.$ $B\wr A$ is the wreath product of B and A, in its usual imprimitive action.

11.1. General remarks

The first thing one notices about automorphism groups of power graphs is that they are extremely large, so that naive analysis with computer algebra software runs into difficulties. For example, the automorphism group of $\mathit{P}(A_5)$ has order $$668594111536199848062615552000000.$$

We begin this section by exploring the reason for this phenomenon.

There is one general fact about automorphism groups of power graphs:

Theorem 11.1.

[14, Section 10] Let G be a non-trivial group. Then $\text{Aut}(\mathit{P}(G))$ has a non-trivial normal subgroup which is a direct product of symmetric groups.

We saw this in our exploration of the Mathieu group M₁₁ earlier. Let N(x) be the set of neighbours of x in a graph Γ. We say that two vertices x, y of Γ are open twins if $N(x)=N(y);$ closed twins if $\left\{x\right\}\cup N(x)=\left\{y\right\}\cup N(y);$ and twins if they are either open or closed twins. Then

• if x and y are twins, then the transposition (x, y), fixing all other vertices of Γ, is an automorphism;

• the relation of being twins is an equivalence relation.

Hence the direct product of symmetric groups on the twin classes is a normal subgroup of $\text{Aut}(\Gamma ).$

Now the theorem above follows from the observation that, in any non-trivial finite group G, the twin relation in the power graph is not the relation of equality. Indeed, recall the relation ∼ defined by $x\sim y$ if $〈x〉=〈y〉,$ see Section 5.3. If $x\sim y,$ then x and y are closed twins; so the set of generators of each cyclic subgroup is contained in a twin class, necessarily non-trivial if the order of the elements is greater than 2. This covers all cases except that when G is an elementary abelian 2-group. But in this case, the power graph is a star $K_{1,2^d-1},$ where $\left|G\right|=2^d,$ and clearly all non-identity elements are open twins.

In order to describe further the automorphism group of $\mathit{P}(G),$ we need to be able to describe the quotient group $\text{Aut}(\mathit{P}(G))/N,$ where N is the direct product of symmetric groups on the closed twin classes in G. This problem was addressed by Feng et al. [40]; we will state their result later in this section. They describe the quotient as a permutation group on the set of cyclic subgroups of G which preserves order, inclusion and non-inclusion.

Continuing our analysis of $\mathit{P}(A_5):$ the group A₅ has 15 cyclic subgroups of order 2, 10 of order 3 and 6 of order 5. So the subgroup N is $S_2^{10}\times S_4^6,$ and the quotient is $S_{15}\times S_{10}\times S_6;$ the product of the orders of these groups is the number quoted earlier.

As we saw in our discussion of the Mathieu group M₁₁, the closed twin relation does not necessarily coincide with the relation ∼, although it contains this relation. We can analyse further. If we collapse each twin class of Γ to a single vertex, we obtain a new graph Δ; and, if N is the direct product of symmetric groups on the twin classes, then $\text{Aut}(\Gamma )/N$ is a subgroup of $\text{Aut}(\Delta ).$

It may be that Δ also has twins, in which case the reduction can be repeated until no twins remain. It is easy to show that the final result is independent of the order in which the twin reduction is done. Of course, the final result may be a graph with a single vertex, but it is known when this happens:

Theorem 11.2.

[14, Propositions 7.2 and 10.1]

1. A finite graph is a cograph if and only if the process of iterated twin reduction terminates with the one-vertex graph.

2. The automorphism group of a cograph can be built from the trivial group by the operations “direct product” and “wreath product with a symmetric group”.

It is observed in [14] that the power graph of every finite simple group of order less than 2500 is a cograph. But we saw earlier that the power graph of M₁₁ is not a cograph.

The above results give added importance to Problem 8.6: for which finite groups G is $\mathit{P}(G)$ a cograph?

11.2. Specific results

The first result about automorphism groups of power graphs was obtained by Cameron and Ghosh [15], where they proved that the only finite group whose automorphism group is the same as that of its power graph is the Klein four-group. Alireza et al. [4], obtained the following fact about the automorphism group of the power graph of the cyclic group ${\mathbb{Z}}_n.$ This result can be interpreted in the light of Theorem 11.1, since elements of the same order in a cyclic group are twins (and the identity lies in the twin class of the generators).

Theorem 11.3.

[4, Theorem 8] $\text{Aut}(\mathit{P}({\mathbb{Z}}_n))$ has a subgroup isomorphic to $$S_{\varphi (n)+1}\times \prod _{d|n,d\ne 1,n}{S}_{\varphi (d)}.$$

Corollary 11.4.

[4, Corollary 4] Let n be a natural number such that for every $a\ne b\in {\mathbb{Z}}_n,\mathrm{deg}(a)\ne \mathrm{deg}(b)$ whenever $o(a)\ne o(b)$. Then $$\text{Aut}(\mathit{P}({\mathbb{Z}}_n))\cong S_{\varphi (n)+1}\times \prod _{d|n,d\ne 1,n}{S}_{\varphi (d)}.$$

In the same article, the authors stated the following conjecture.

Conjecture 11.5. [4, Conjecture 1] For every natural number n, $$\text{Aut}(\mathit{P}({\mathbb{Z}}_n))\cong S_{\varphi (n)+1}\times \prod _{d|n,d\ne 1,n}{S}_{\varphi (d)}.$$

Mehranian et al. [62] settled this conjecture in 2016 and proved the following result.

Theorem 11.6.

[62, Theorem 2.3] For any natural number n, $$\text{Aut}(\mathit{P}({\mathbb{Z}}_n))=\{\begin{array}{cc}{S}_n\hfill & \text{if}n\mathit{\text{is a prime power}};\hfill \\ S_{\varphi (n)+1}\times \prod _{d|n,d\ne 1,n}{S}_{\varphi (d)}\hfill & \mathit{\text{otherwise}}.\hfill \end{array}$$

Corollary 11.7.

[62, Corollary 2.4] The automorphism group of the power graph $\mathit{P}(D_{2n})$ is given below: $$\text{Aut}(\mathit{P}(D_{2n}))=\{\begin{array}{cc}{S}_{n-1}\times S_n\hfill & \mathit{\text{if}}n\mathit{\text{is a prime power}};\hfill \\ S_n\times \prod _{d|n}{S}_{\varphi (d)}\hfill & \mathit{\text{otherwise}}.\hfill \end{array}$$

In [40], same result is proved independently and they also asserted the following result on the automorphism group of the directed power graph $\overrightarrow{\mathit{P}}(D_{2n}).$ For $n\ge 3,$ $$\text{Aut}(\overrightarrow{\mathit{P}}(D_{2n}))\cong \prod _{d|n}{S}_{\varphi (d)}\times S_n.$$

Moreover, in [62], the automorphism group of $\mathit{P}({\mathbb{Z}}_{p_1{p}_2}),\mathit{P}({\mathbb{Z}}_{p_1{p}_2{p}_3})$ and $\mathit{P}({\mathbb{Z}}_{p_1^2{p}_2^2})$ are computed as follows.

1. $\text{Aut}(\mathit{P}({\mathbb{Z}}_{p_1{p}_2}))\cong S_{\varphi (p_1{p}_2)+1}\times S_{p_1-1}\times S_{p_2-1}.$

2. $\text{Aut}(\mathit{P}({\mathbb{Z}}_{p_1{p}_2{p}_3}))\cong S_{\varphi (p_1{p}_2{p}_3)}\times S_{p_1-1}\times S_{p_2-1}\times S_{p_3-1}\times S_{\varphi (p_1{p}_2)}\times S_{\varphi (p_1{p}_3)}\times S_{\varphi (p_2{p}_3)}.$

3. $\text{Aut}(\mathit{P}({\mathbb{Z}}_{p_1^2{p}_2^2}))\cong S_{\varphi (p_1^2{p}_2^2)+1}\times S_{p_1-1}\times S_{\varphi (p_1^2)}\times S_{p_2-1}\times S_{\varphi (p_2^2)}\times S_{\varphi (p_1{p}_2)}\times S_{\varphi (p_1{p}_2^2)}\times S_{\varphi (p_1^2{p}_2)}.$

Finally, Z. Mehranian [62] posed the following open problem.

Problem 11.8. [62, Question 3.1]What is the automorphism group of $\mathit{P}(G),$ where G is a sporadic group?

Subsequently A.R. Ashrafi et al. [6] computed the automorphism group of certain finite groups listed below along with their generating relations. $$\begin{array}{c}{Q}_{4n}=〈a,b|a^{2n}=e, a^n=b^2, ab=b{a}^{-1}〉;\\ S{D}_{8n}=〈a,b|a^{4n}=b^2=e, \mathit{bab}=a^{2n-1}〉;\\ V_{8n}=〈a,b|a^{2n}=b^4=e, \mathit{aba}=b^{-1}, a{b}^{-1}a=b〉.\end{array}$$

Note that the paper also describes a group $U_{6n}$ of order 6n which, like $V_{8n}$ of order 8n, taken from an exercise on page 178 of the book [50]. However, the relations for $U_{6n}$ are stated incorrectly in [6]. The correct presentation is $$U_{6n}=〈a,b|a^{2n}=b^3=e, a^{-1}ba=b^{-1}〉.$$

It seems likely that this is just a transcription error, and that the correct group is analysed in the paper; but since detailed proof is not included, we have not been able to check this.

The results concerning the automorphism group of above finite groups are listed below:

Theorem 11.9.

[6, Theorem 1.1]

1. For $n\ge 3,$ $$\text{Aut}(\mathit{P}(Q_{4n}))=\{\begin{array}{cc}{S}_{2n-2}\times S_2\times (S_2\wr S_n)\hfill & \mathit{\text{if}}\mathit{n}\mathit{\text{is}}\mathit{\text{ a }}\mathit{\text{power}}\mathrm{ }\mathit{\text{of}}\mathrm{ }2;\hfill \\ \prod _{d|2n}{S}_{\varphi (d)}\times (S_2\wr S_n)\hfill & \mathit{\text{otherwise}}.\hfill \end{array}$$

2. For $n\ge 2,$ $$\text{Aut}(\mathit{P}(S{D}_{8n}))=\{\begin{array}{cc}{S}_{4n-2}\times S_{2n}\times (S_2\wr S_n)\hfill & \text{if}\mathrm{ }n\mathit{\text{is}}\mathit{\text{ a }}\mathit{\text{power}}\mathrm{ }\mathit{\text{of}}\mathrm{ }2;\hfill \\ \prod _{d|4n}{S}_{\varphi (d)}\times S_{2n}\times (S_2\wr S_n)\hfill & \mathit{\text{otherwise}}.\hfill \end{array}$$

   is an integer such that $3\nmid t$. Then

3. For $n=2^{k}t,$ with a nonnegative integer k and some positive odd integer t, $$\text{Aut}(\mathit{P}(V_{8n}))=\{\begin{array}{cc}{S}_{2n}\times S_2\wr S_n\times \prod _{d|2n,d\nmid n}{S}_{\varphi (d)}\wr S_2\times \prod _{d|2n}{S}_{\varphi (d)}\hfill & k=0;\hfill \\ S_{2n+1}\times S_2\wr S_n\times \prod _{\mathcal{\ell }=0}^{k-1}{S}_{2^{\mathcal{\ell }}}^2\times S_{2^k}\wr S_2\hfill & t=1,k\ge 1;\hfill \\ S_{2n}\times S_2\wr S_n\times \prod _{d|t}{S}_{\varphi (d)}^4\times \prod _{s=2}^k\prod _{d|2^{s}t,d\nmid 2^{s-1}t}{S}_{\varphi (d)}^2\times \hfill & \hfill \\ \mathrm{ }\prod _{d|2^{k+1}t,d\nmid 2^{k}t}{S}_{\varphi (d)}\wr S_2,\hfill & t>1,k\ge 1.\hfill \end{array}$$

Ashrafi et al. [6] also compute the automorphism groups of the power graphs of the sporadic simple groups M₁₁ and J₁. However, we warn readers that their results are not correct. We have given a correct analysis for M₁₁ in Section 2 of the present paper. Theorem 11.9(i) was also proved by M. Feng et al. [40]. Also they asserted that the following result for the automorphism group of directed power graph $\overrightarrow{\mathit{P}}(Q_{4n}).$

For $n\ge 3,$ $$\text{Aut}(\overrightarrow{\mathit{P}}(Q_{4n}))\cong \prod _{d|2n}{S}_{\varphi (d)}\times S_2\wr S_n.$$

We now turn to the general analysis of the automorphism group of the power graph by Feng et al. [40].

As mentioned earlier, let $\mathit{C}(G)=\{C_1,\dots ,C_k\}$ be the set of all cyclic subgroups of a group G. For $C\in \mathit{C}(G),$ let S(C) be the set of all generators of C and $\mathit{S}(C_i)=\{\mathit{S}{(C_i)}_1,\mathit{S}{(C_i)}_2,\dots ,\mathit{S}{(C_i)}_k\}.$

Define I(G) as the set of permutations σ on $\mathit{C}(G)$ preserving order, inclusion and non-inclusion, $i.e.,\left|C_i^{\sigma }\right|=\left|C_i\right|$ for each $i\in \{1,\dots ,k\}$ and $C_i\subset C_j$ if and only if $C_i^{\sigma }\subset C_j^{\sigma }.$ Note that I(G) is a permutation group on $\mathit{C}(G).$ This group induces the faithful action on the set G: (1) $$G\times I(G)\to G,\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}(\mathit{S}{(C_i)}_j,\sigma )\to {(\mathit{S}{(C_i)}^{\sigma })}_j.$$(1)

We remark that it suffices to consider the action of I(G) on the set of maximal cyclic subgroups of G, since a cyclic group contains at most one cyclic subgroup of each possible order.

For $\Omega \subseteq G,$ let $S_{\Omega }$ denote the symmetric group on $\Omega .$ Since G is the disjoint union of $S(C_1),\dots ,S(C_k),$ we get the faithful group action on G: (2) $$G\times \prod _{i=1}^k{S}_{\mathit{S}(C_i)}\to G,\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}(\mathit{S}{(C_i)}_j,({\xi }_1,\dots ,{\xi }_k)\to {(\mathit{S}{(C_i)}_j)}^{{\xi }_i}.$$(2)

With the above notations, we have the following theorem proved by M. Feng et al. [40].

Theorem 11.10.

[40, Theorem 2.1] Let G be a finite group. Then $$\text{Aut}(\overrightarrow{\mathit{P}}(G))=\left(\prod _{i=1}^k{S}_{\mathit{S}(C_i)}\right)⋊I(G),$$

where I(G) and ${\prod }_{i=1}^k{S}_{\mathit{S}(C_i)}$ act on G as in (1)(1) $$G\times I(G)\to G,\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}(\mathit{S}{(C_i)}_j,\sigma )\to {(\mathit{S}{(C_i)}^{\sigma })}_j.$$(1) and (2)(1) $$G\times I(G)\to G,\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}(\mathit{S}{(C_i)}_j,\sigma )\to {(\mathit{S}{(C_i)}^{\sigma })}_j.$$(1) , respectively.

In the power graph $\mathit{P}(G),$ for $a,b\in G,$ define $a\equiv b$ if $N[a]=N[b].$ Observe that $\equiv$ is an equivalence relation. Let cl(a) denote the equivalence class containing a. Write ${\rm Y}(G)=\{cl(a)|a\in G\}=\{cl(u_1),\dots ,cl(u_{\mathcal{\ell }})\}.$ Since G is the disjoint union of $cl(u_1),\dots ,cl(u_{\mathcal{\ell }}),$ the following is a faithful group action on the set G: (3) $$G\times \prod _{i=1}^{\mathcal{\ell }}{S}_{cl(u_1)}\to G,(a,({\tau }_1,{\tau }_2,\dots ,{\tau }_{\mathcal{\ell }}))\to a^{{\tau }_i}, \mathit{where} a\in cl(u_i).$$(3)

Similar to the last theorem, we have the following for the automorphism group of undirected power graph.

Theorem 11.11.

[40, Theorem 2.2] Let G be a finite group. Then $$\text{Aut}(\mathit{P}(G))=\left(\prod _{i=1}^{\mathcal{\ell }}{S}_{{\overline{u}}_i}\right)⋊I(G),$$

where I(G) and ${\prod }_{i=1}^{\mathcal{\ell }}{S}_{cl(u_i)}$ act on G as in (1)(1) $$G\times I(G)\to G,\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}(\mathit{S}{(C_i)}_j,\sigma )\to {(\mathit{S}{(C_i)}^{\sigma })}_j.$$(1) and (3)(1) $$G\times I(G)\to G,\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}(\mathit{S}{(C_i)}_j,\sigma )\to {(\mathit{S}{(C_i)}^{\sigma })}_j.$$(1) respectively.

Our observation that it suffices to consider the action of I(G) on maximal cyclic subgroups now shows that Theorem 11.6 can be derived from this result. For, if G is cyclic, then it has onlly one maximal cyclic subgroup, and so I(G) is the trivial group; thus, $\text{Aut}(G)$ is just the direct product of cyclic groups on the closed twin equivalence classes.

12. Characterization of finite groups through power graphs

In this section, we present those results by which, one can characterize finite groups in terms of their power graphs and vice versa. Tamizh Chelvam et al. [79] proved the following characterizations for the power graph of an arbitrary finite group.

Theorem 12.1.

[79, Theorem 4] Let G be a finite group with n elements. Then the following are equivalent:

1. $\mathit{P}(G)=K_{1,n-1};$

2. $\mathit{P}(G)$ is a tree;

3. Every element of G is its own inverse.

Theorem 12.2.

[79, Theorem 5] Let G be a finite group of order $p_1{p}_2$, where p₁ < p₂ are primes. Then

1. G is cyclic if and only if $\mathit{P}(G)=(K_{p_1-1}\cup K_{p_2-1})+K_{\varphi (p_1{p}_2)+1};$

2. G is non-cyclic if and only if $\mathit{P}(G)=K_1+(p_2{K}_{p_1-1}\cup K_{p_2-1}).$

A. Doostabadi et al. [36] characterized all finite groups G whose power graphs are claw-free, $K_{1,4}$ free or C₄ free and they are given below.

Theorem 12.3.

[36, Theorem 2.2] If G is a finite group, then $\mathit{P}(G)$ is claw free if and only if G is a cyclic group of order $p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}$ where $\{{\alpha }_1,{\alpha }_2\}\cap \{0,1\}\ne \varnothing .$

Theorem 12.4.

[36, Theorem 2.6] If G is a finite group, then $\mathit{P}(G)$ is $K_{1,4}$-free if and only if G is isomorphic to one of the groups $Q_8,{\mathbb{Z}}_2\times {\mathbb{Z}}_2,{\mathbb{Z}}_{p^k},{\mathbb{Z}}_{p_1{p}_2{p}_3}$ or ${\mathbb{Z}}_{p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}}$, where $\{{\alpha }_1,{\alpha }_2\}\cap \{0,1,2\}\ne \varnothing$ and p₁, p₂, p₃ are distinct primes.

Lemma 12.5.

[36, Lemma 3.1] Let G be a finite group. Then $\mathit{P}(G)$ has a induced 4-cycle if and only if there exist non-trivial elements a, b in G such that $〈a〉\nleqq 〈b〉,〈b〉\nleqq 〈a〉$ and $〈a〉\cap 〈b〉$ is not a prime power group.

Corollary 12.6.

[36, Corollary 3.2] Let G be a finite group whose non-trivial elements have prime power orders. Then $\mathit{P}(G)$ is C₄-free.

Theorem 12.7.

[36, Theorem 3.5] Let G be a finite nilpotent group. Then $\mathit{P}(G)$ is C₄-free if and only if G is isomorphic either of the following:

1. ${\mathbb{Z}}_{p_1{p}_2{p}_3};$

2. P × Q, $H_{p_1}(P)$ is cyclic and $\text{exp}\hspace{0.17em}(Q)=p_2$, in which P is a p₁ group and Q is a p₂ group;

3. p₁ group,

where $p_1,p_2,p_3$ are distinct primes.

In the same paper, the authors proved further results for groups G where the center Z(G) is divisible by at least two primes.

Theorem 12.8.

[36, Theorem 3.6] Let G be a group with C₄-free power graph. If Z(G) is not a p-group, then

1. $G\cong {\mathbb{Z}}_{p_1{p}_2{p}_3};$

2. $G=P\times Q$ or $G=(P\times Q)⋊{\mathbb{Z}}_{p_2}$, where P is cyclic, $\text{exp}\hspace{0.17em}(Q)=p_2$ and $C_G(P)=P\times Q;$

3. $G=D_{2^n}⋊Q$, where $\text{exp}\hspace{0.17em}(Q)=p_2;$

4. $G={\mathbb{Z}}_{p_1^n}⋊Q$, where $\text{exp}\hspace{0.17em}(Q)=p_2;$

5. $G={\mathbb{Z}}_{p_1{p}_2}\times ({\mathbb{Z}}_{p_3}⋊{\mathbb{Z}}_{p_1})$, where $C_G(S_{p_3}(G))\cong {\mathbb{Z}}_{p_1{p}_2{p}_3};$

6. $G={\mathbb{Z}}_{p_1{p}_2}\times ({\mathbb{Z}}_{p_3}⋊{\mathbb{Z}}_{p_1{p}_2})$, where $C_G(S_{p_3}(G))\cong {\mathbb{Z}}_{p_1{p}_2{p}_3}.$

Theorem 12.9.

[36, Theorem 3.7] Let G be a finite group with C₄-free power graph, which is not prime power group. If Z(G) is a p-group which is not an elementary abelian p-group, then Z(G) is cyclic and $\text{exp}\hspace{0.17em}(S_{p_2(G)})=p_2$ for every $p_1\ne p_2$. Also, for every p₂-element a,

1. $\pi (C_G(a))=\{p_1,p_2\};$

2. $S_{p_1}(C_G(a))$ is a normal cyclic subgroup of $C_G(a);$

3. $C_G(a)=〈a〉\times S_{p_2}(C_G(a))$, or $C_G(a)=(〈b〉\times S_{p_2}(C_{C_G(a)}(b)))⋊{\mathbb{Z}}_{p_2}$ if p₁ is odd prime, where $〈b〉=S_{p_1}(C_G(a))$ and $\pi (G)$ is the set of all prime divisors of o(G).

Theorem 12.10.

[36, Theorem 3.8] Let G be a finite group with C₄-free power graph, which is not prime power group. If Z(G) is an elementary abelian p₁-group of order $>p_1$ then for every p₂-element $b(p_1\ne p_2)$, we have $\pi (C_G(x))=\{p_1,p_2\}$ and if $o(a)>p_2$, then

1. $\text{exp}\hspace{0.17em}(S_{p_1}(C_G(a)))=p_1$ and $S_{p_2}(C_G(a))$ is a normal cyclic subgroup of $C_G(a);$

2. $C_G(a)=S_{p_1}(C_G(a))\times S_{p_2}(C_G(a))$ or $(S_{p_1}(C_{C_G(a)}(b))\times S_{p_2}(C_G(a)))⋊{\mathbb{Z}}_{p_1},$

3. where $〈b〉=s_{p_2}(C_G(a)).$

In the following, we present some graph theoretical characterizations of the power graph.

Lemma 12.11.

[74, Lemmas 1.1–1.3]

1. $\mathit{P}(G)$ is Eulerian if and only if o(G) is odd;

2. $\mathit{P}(G)$ for a finite group G is tree if and only if G is an elementary abelian 2-group;

3. $g(\mathit{P}(G))=3$ if and only if G is not an elementary abelian 2-group. Moreover, if $\mathit{P}(G)$ is 2-connected then $g({\mathit{P}}_0(G))=3.$

Mirzargar et al. [64] conjectured that the power graph $\mathit{P}({\mathbb{Z}}_n)$ has the maximum number of edges among all power graphs of finite groups of order n. In the following, Pourgholi et al. [74] proved this conjecture for finite simple groups.

Theorem 12.12.

[74, Theorem 2.3] If G is a finite simple group of order n, then $\left|E(\mathit{P}(G))\right|\mathrm{ }\le \left|E(\mathit{P}({\mathbb{Z}}_n))\right|.$

Amiri et al. [5, Theorem 2] proved that among all finite groups of any given order, the cyclic group of that order has the maximum number of edges in its power graph.

Now, we present a characterization of finite groups whose power graph is a union of complete subgraphs which share the identity element of G.

Theorem 12.13.

[74, Theorem 2.4] Let G be a finite group with $o(G)=p^{\alpha }$. Then $\mathit{P}(G)$ is a union of complete subgraphs which share the identity element of G if and only if G is isomorphic to a cyclic group, p-group of exponent p or a dihedral group.

Theorem 12.14.

[69, Theorem 1.1] A finite group G is non-cyclic group of prime exponent if and only if $\mathit{P}(G)$ is non-complete and minimally edge-connected.

Theorem 12.15.

[69, Theorem 1.2] A finite group is an elementary abelian 2-group of rank at least 2 if and only if $\mathit{P}(G)$ is non-complete and minimally vertex connected.

13. Properties of power graphs

In this section, we collect all the miscellaneous properties of power graphs.

13.1. Relationship between power graph and Cayley graph

In 2015, Chattopadhyay [23], obtained some relationship between the power graph and the Cayley graph of a finite cyclic group motivated by an open problem given in survey [2]. For a group G and a subset S of G not containing the identity element e and satisfying $S^{-1}=\{a^{-1}:a\in S\}=S,$ the Cayley graph of G with edge set S, Cay(G, S) is an undirected graph with vertex set G and two vertices $a,b\in G$ are adjacent in Cay(G, S) if and only if $a{b}^{-1}\in S.$ Let $U_n=\{\overline{a}\in {\mathbb{Z}}_n:\gcd (a,n)=1\}.$ In this subsection, we denote the vertex deleted subgraph $\mathit{P}({\mathbb{Z}}_n)\setminus S({\mathbb{Z}}_n)$ of $\mathit{P}({\mathbb{Z}}_n)$ by ${\mathit{P}}_S({\mathbb{Z}}_n)$ and similarly Cay${}_S({\mathbb{Z}}_n,U_n)=\mathit{Cay}({\mathbb{Z}}_n,U_n)\setminus S({\mathbb{Z}}_n).$ Also, for any graph Γ, $\overline{\Gamma }$ is the complement of Γ.

Theorem 13.1.

[23, Theorem 2.1] If $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}$, where p₁, p₂ are distinct primes and ${\alpha }_1,{\alpha }_2$ are positive integer, then ${\mathit{P}}_S({\mathbb{Z}}_n)$ is a spanning graph of $\overline{Ca{y}_S({\mathbb{Z}}_n,U_n)}$. These two graphs are equal if and only if ${\alpha }_1=1={\alpha }_2.$

As mentioned in [48], ${\mathbb{Z}}_n\cong {\prod }_{i=1}^m{\mathbb{Z}}_{p_i^{{\alpha }_i}}$ as group (under addition) through the isomorphism $g:{\mathbb{Z}}_n\to {\prod }_{i=1}^m{\mathbb{Z}}_{p_i^{{\alpha }_i}}$ defined by $g({[a]}_n)=({[a]}_{p_1^{{\alpha }_1}},\dots ,{[a]}_{p_m^{{\alpha }_m}}).$ Note that the mapping $g=f^{-1}:{\prod }_{i=1}^m{\mathbb{Z}}_{p_i^{{\alpha }_i}}\to {\mathbb{Z}}_n$ is also a group isomorphism.

Theorem 13.2.

[23, Theorem 2.2] Let $n=p_1^{{\alpha }_1}\cdots p_m^{{\alpha }_m},$ $T_i={\mathbb{Z}}_{p_i^{{\alpha }_i}}\setminus \left\{\overline{0}\right\},i=1,2,\dots ,m$ and T be the image of ${\prod }_{i=1}^m{T}_i$ under the group isomorphism $f:{\prod }_{i=1}^m{Z}_{p_i^{{\alpha }_i}}\to {\mathbb{Z}}_n$. Then $\mathit{Cay}({\mathbb{Z}}_n,T)$ is isomorphic to $\mathit{P}({\mathbb{Z}}_{p_1^{{\alpha }_1}})\times \mathit{P}({\mathbb{Z}}_{p_2^{{\alpha }_2}})\times \cdots \times \mathit{P}({\mathbb{Z}}_{p_m^{{\alpha }_m}}).$

In the rest of the theorems of this section, the edge set appear in $\mathit{Cay}({\mathbb{Z}}_n,T)$ will be that the subset of ${\mathbb{Z}}_n$ as proved in Theorem 13.2.

Theorem 13.3.

[23, Theorem 3.1] For the power graph $\mathit{P}({\mathbb{Z}}_{p_1{p}_2})$, where p₁, p₂ are distinct primes, we have the following.

1. ${\mu }_2(\mathit{P}({\mathbb{Z}}_{p_1{p}_2}))\le \frac{p_1+p_2}{2}-2$ and ${\mu }_j(\mathit{P}({\mathbb{Z}}_{p_1{p}_2}))=-1,j=3,4,\dots ,p_1{p}_2-1;$

2. $-\frac{p_1+p_2}{2}-2\le {\mu }_{p_1{p}_2}(\mathit{P}({\mathbb{Z}}_{p_1{p}_2}))\le -1;$

3. $E_N(\mathit{P}({\mathbb{Z}}_{p_1{p}_2}))\le 2p_1{p}_2+p_1+p_2-6$ where $E_N(\mathit{P}(G))$ denotes the energy of the power graph $\mathit{P}(G).$

It is known [55] that, for any two graphs ${\Gamma }_1$ and ${\Gamma }_2,E_N({\Gamma }_1\times {\Gamma }_2)=E_N({\Gamma }_1)E_N({\Gamma }_2).$ From $E_N(\mathit{P}({\mathbb{Z}}_{p_i^{{\alpha }_i}}))=2(p_i^{{\alpha }_i}-1),1\le i\le m,$ one can apply Theorem 13.2, to find the energy of $\text{Cay}({\mathbb{Z}}_n,T).$

Theorem 13.4.

[23, Theorem 3.2] Let $n=p_1^{{\alpha }_1}\cdots p_m^{{\alpha }_m}$ be the prime factorization of natural number n > 1. Then $$E_N(\mathit{Cay}({\mathbb{Z}}_n,T))=E_N(\mathit{P}({\mathbb{Z}}_{p_1^{{\alpha }_1}}))E_N(\mathit{P}({\mathbb{Z}}_{p_2^{{\alpha }_2}}))\cdots E_N(\mathit{P}({\mathbb{Z}}_{p_m^{{\alpha }_m}}))=2^m\prod _{i=1}^m(p_i^{{\alpha }_i}-1).$$

In the following few results, the authors of same article compared the energy of the power graph and the Cayley graph.

Corollary 13.5.

[23, Corollaries 3.1 and 3.2]

1. For $n=p_1{p}_2$, where p₁, p₂ are distinct odd primes, $E_N(\mathit{P}({\mathbb{Z}}_n))\le E_N(\mathit{Cay}({\mathbb{Z}}_n,T));$

2. For $n=2p$, where p is an odd prime, $E_N(\mathit{P}({\mathbb{Z}}_n))>E_N(\mathit{Cay}({\mathbb{Z}}_n,T)).$

Theorem 13.6.

[23, Theorem 3.3] For any natural number n > 1, $$E_N(\mathit{Cay}({\mathbb{Z}}_n),T)\ge E_N(\mathit{Cay}({\mathbb{Z}}_n,U_n)).$$

Corollary 13.7.

[23, Corollary 3.3] For $n=2p$, where p is an odd prime, $$E_N(\mathit{P}({\mathbb{Z}}_n))>E_N(\mathit{Cay}({\mathbb{Z}}_n,U_n)).$$

13.2. Rainbow connection number of the power graph

A path P in a graph Γ is called rainbow, if any two edges in P are of different colors. If Γ has a rainbow path from a to b for each pair of vertices a and b, then Γ is called a rainbow connected under the coloring f, and f is called a rainbow k-coloring of Γ.

Ma et al. [58] studied the rainbow connection number of the power graph $\mathit{P}(G)$ of a finite group G. In fact, they determined the rainbow connection number of $\mathit{P}(G)$ if G has maximal involutions or G is nilpotent, and proved that the rainbow connection number of $\mathit{P}(G)$ is at most three if G has no maximal involutions. The rainbow connection numbers of power graphs of some non-nilpotent groups are also determined. The results in this connection are given below.

Theorem 13.8.

[58, Theorem 2.1] Let G be a finite group with $o(G)\ge 3$. Then $$rc(\mathit{P}(G))=\{\begin{array}{cc}3,\hfill & \mathit{\text{if}} 1\le \left|M_G\right|\le 2;\hfill \\ \left|M_G\right|,\hfill & \mathit{\text{if}} \left|M_G\right|\ge 3.\hfill \end{array}$$ where M_G is the set of all maximal involutions of G.

Theorem 13.9.

[58, Theorem 3.1] Let G be a finite group with no maximal involutions.

1. If G is cylic, then $rc(\mathit{P}(G))=\{\begin{array}{cc}1,\hfill & \mathrm{ }\mathit{\text{if}}\mathrm{ }\left|G\right|\mathrm{ }\mathit{\text{is}}\mathit{\text{ a }}\mathit{\text{prime}}\mathrm{ }\mathit{\text{power}};\hfill \\ 2,\hfill & \mathrm{ }\mathit{\text{otherwise}}.\hfill \end{array}$

2. If G is non-cyclic, then $rc(\mathit{P}(G))=2$ or 3.

Proposition 13.10.

[58, Proposition 3.2] If G is a finite group of order $p_1^{\alpha }{p}_2$, where p₁ < p₂ are primes such that the following conditions hold:

1. Each Sylow p₁-subgroup is cyclic and the Sylow p₂-subgroup is unique;

2. The intersection of all Sylow p₁-subgroups is of order $p_1^{\alpha -1};$

3. $p_1^{\alpha -1}\ge p_2.$

Then $rc(\mathit{P}(G))=2.$

Proposition 13.11.

[58, Proposition 3.3] Let G be a non-cyclic finite group with no maximal involutions. If G possess more than one subgroup of order p, where p is a prime divisor of o(G), then $rc(\mathit{P}(G))=3.$

Corollary 13.12.

[58, Corollary 3.4] If G is a non-cyclic nilpotent group with no maximal involutions. Then $$rc(\mathit{P}(G))=\{\begin{array}{cc}2,\hfill & \mathit{\text{if}} G\cong Q_8\times {\mathbb{Z}}_n \mathit{\text{for some odd}}n;\hfill \\ 3,\hfill & \mathit{\text{otherwise}}.\hfill \end{array}$$

13.3. Vertex degrees of power graphs

In 2015, Alireza et al. [4] computed the degree of all vertices in $\mathit{P}({\mathbb{Z}}_n)$ and the same is given below.

Theorem 13.13.

[4, Theorem 9] The degree of an arbitrary vertex a in $\mathit{P}({\mathbb{Z}}_n)$ is $$\mathrm{deg}(a)=d-1+\sum _{rd|n,r\ge 2}\varphi (rd),\mathit{\text{where}}d\mathit{\text{is}}\mathrm{ }\mathit{\text{the}}\mathrm{ }\mathit{\text{order}}\mathrm{ }\mathit{\text{of}}\mathrm{ }a\mathit{\text{in}} {\mathbb{Z}}_n.$$

Sehgal and Singh [77] gave a precise formula to count the degree of a vertex in the directed power graphs of finite abelian groups of prime power order. We shall write $d_G^{+}(a),d_G^{-}(a)$ and $d_G^{\pm }(a)$ respectively to denote out-degree of a, in-degree of a and the number of bidirectional edges on a in the digraph $\overrightarrow{\mathit{P}}(G).$

By the definition of directed power graph $\overrightarrow{\mathit{P}}(G),$ it is very easy to check that $d_G^{+}(g)=|〈g〉|-1=o(g)-1$ and $d_G^{\pm }(g)=\varphi (o(g))-1.$ We thus precisely obtain $d_G(g)=o(g)-\varphi (o(g))+d_G^{-}(g).$ To determine the degree $d_G(g)$ of a non-identity group element g, it is therefore sufficient to count the in-degree $d_G^{-}(g).$ However, it is easy see that $d_G^{-}(g)=\left|\right\{h\in G:g\ne h \text{and} \mathrm{g}\in 〈\mathrm{h}〉\left\}\right|.$ We start our investigation on the in-degree $d_G^{-}(g)$ of a non-identity group element g of G.

Theorem 13.14.

[77, Theorem 3.2] Let $G=〈a_1〉\times 〈a_2〉\cdots \times 〈a_n〉$ be an abelian p-group where $\left|a_r\right|=p^{m_r}$ and $1\le m_1\le m_2\cdots \le m_n$. If $a={\prod }_{\alpha =1}^n{a}_{\alpha }^{i_{\alpha }}$ is a nonidentity element of G and $o(a_{\alpha }^{i_{\alpha }})=p^{t_{\alpha }}$, then $$d_G^{-}(a)=-1+\varphi (o(a))\prod _{\beta =0}^{\min \{m_{k+1}-t_k+1,\dots ,m_n-t_n\}}{p}^{\left(\sum _{j=1}^n\min \{m_j,\beta \}\right)}.$$

In the following, the authors gave a new proof to show that the power graph of a cyclic group of prime-power order is complete, using degree formula.

Corollary 13.15.

[77, Corollary 3.3] If G is a cyclic p-group, then the power graph $\mathit{P}(G)$ is complete.

If G is the internal direct product of its normal subgroups with the condition that their orders are mutually relatively prime, then we have the following theorem.

Theorem 13.16.

[77, Theorem 3.5] Let G be a finite group and let $H_1,H_2,\dots ,H_n$ be normal subgroups of G such that $(o(H_i),o(H_j))=1$ for $i\ne j$. If G is internal direct product of subgroups $H_1,H_2,\dots ,H_n,$ then, for an element $a=a_1{a}_2\cdots a_n$ of the group G, with $a_i\in H_i$ we have the following:

1. $d_G^{+}(a)=({\prod }_{i=1}^n(d_{H_i}^{+}(a_i)+1))-1;$

2. $d_G^{-}(a)=({\prod }_{i=1}^n(d_{H_i}^{-}(a_i)+1))-1;$

3. $d_G^{\pm }(a)=({\prod }_{i=1}^n(d_{H_i}^{\pm }(a_i)+1))-1.$

Using Theorem 13.16, the authors determined the degree of a vertex in the power graph of a finite abelian group.

Theorem 13.17.

[77, Theorem 3.6] Let $G=G(p_1)\times \cdots \times G(p_m)$ be an abelian group of order $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\cdots p_m^{{\alpha }_m}$, where each $G(p_i)$ is a normal subgroup of G of order $p^{{\alpha }_i}$ Then, for a non-identity element $a=a_1{a}_2\cdots a_m$ of the abelian group G with $a_i\in G(p_i),$ we have the following:

1. $d_G^{+}(a)=({\prod }_{i=1}^m(d_{G(p_i)}^{+}(a_i)+1))-1;$

2. $d_G^{-}(a)=({\prod }_{i=1}^m(d_{G(p_i)}^{-}(a_i)+1))-1;$

3. $d_G^{\pm }(a)=({\prod }_{i=1}^m(d_{G(p_i)}^{\pm }(a_i)+1))-1.$

13.4. Cycles in power graphs

In 2009, Chakrabarty et al. [20], studied about the Hamiltonian nature of the power graph. In fact they proved that, for any positive integer $n\ge 3,\mathit{P}({\mathbb{Z}}_n)$ is Hamiltonian and raised the following conjecture.

Conjecture 13.18. [20, Conjecture, Section 4] The power graph $\mathit{P}(U_n)$ is Hamiltonian except for the values $n=2^{\alpha }{p}_1{p}_2\cdots p_m,n\ge 3,$ where $p_1,p_2,\dots ,p_m$ are Fermat primes and $\alpha ,m$ are non-negative integers, $\alpha \ge 2$ for m = 0, 1 and $m\ge 2$ for $\alpha =0,1$

Following Chakrabarty et al., Pourgholi et al. [74] provided counter examples and disproved the above conjecture.

Example 13.19.

[74, Counterexamples 2.1–2.3]

1. If $n=2^{\alpha }\times 3^2,\alpha \ge 3,$ then $\mathit{P}(U_n)$ does not have a Hamiltonian cycle;

2. If $n=2^{\alpha }\times 7,\alpha \ge 2,$ then $\mathit{P}(U_n)$ does not have a Hamiltonian cycle;

3. If $n=2^2\times 3^2\times p,$ where p is a Fermat prime, then $\mathit{P}(U_n)$ does not have a Hamiltonian cycle.

Corollary 13.20.

[74, Corollary 2.1] Suppose G is a finite p-group. Then $\mathit{P}(G)$ has a Hamiltonian cycle if and only if $o(G)\ne 2$ and G is cyclic.

Corollary 13.21.

[74, Corollary 2.2] If p is an odd prime, then the power graph of a p-group is 2-connected if and only if it is Hamiltonian.

Mukherjee [67], described a new structural description of power graphs through vertex weighted directed graphs. Actually Mukherjee [67] developed the theory of weighted Hamiltonian paths in a weighted graph and solved the Hamiltonian question completely for the power graphs of a class of finite abelian groups, namely ${\mathbb{Z}}_{p_1}^n\times {\mathbb{Z}}_{p_2}^m.$

Theorem 13.22.

[67, Theorem 4.12] The power graph $\mathit{P}({\mathbb{Z}}_{p_1}^n\times {\mathbb{Z}}_{p_2}^m)$, where p₁, p₂ are distinct primes, is Hamiltonian if and only if $m(p_2-1)\ge n-1$ and $n(p_1-1)\ge m-1$ and $m(p_2-1)+n(p_1-1)\ge mn-1.$

In [57], the authors classified finite groups whose power graphs are unicyclic.

Proposition 13.23.

[57, Proposition 4.1] Let G be a finite group. Then $\mathit{P}(G)$ has no cycles if and only if G is an elementary abelian 2-group.

Lemma 13.24.

[57, Lemma 4.3] There exist no EPO-groups G of order $2^{\alpha }3$ for some positive integer $\alpha \ge 3$ such that $\mathit{P}(G)$ is unicyclic.

Theorem 13.25.

[57, Theorem 4.4] If G is a finite group, then $\mathit{P}(G)$ is unicyclic if and only if $G\cong S_3$ or ${\mathbb{Z}}_3.$

13.5. Product of power graphs

In this subsection, we consider products of power graphs. Let ${\Gamma }_i=(V_i,E_i)$ for i = 1, 2 be two graphs. Then the product graph is defined as the graph ${\Gamma }_1⊠{\Gamma }_2=(V_1\times V_2,E),$ where $((a_1,b_1),(a_2,b_2))\in E$ if one of the following three conditions is true:

• $a_1=a_2$ and $(b_1,b_2)\in E_2;$

• $(a_1,a_2)\in E_1$ and $b_1=b_2;$

• $(a_1,a_2)\in E_1$ and $(b_1,b_2)\in E_2.$

This graph is referred to in the literature as the strong product. There are many types of products of graphs that are defined between any two graphs. In particular, we will refer the following two products in this paper. See [45, pp. 37, 74, and 49] for further details.

Let ${\Gamma }_1$ and ${\Gamma }_2$ be two graphs.

1. The direct product ${\Gamma }_1\times {\Gamma }_2$ (also called the categorical product) of ${\Gamma }_1$ and ${\Gamma }_2$ is the simple graph with vertex set $V({\Gamma }_1\times {\Gamma }_2)=V({\Gamma }_1)\times V({\Gamma }_2),$ in which $(a_1,b_1)$ is adjacent to $(a_2,b_2)$ if and only if a₁ is adjacent to a₂ in ${\Gamma }_1$ and b₁ is adjacent to b₂ in ${\Gamma }_2.$

2. The Cartesian product ${\Gamma }_1\square {\Gamma }_2$ of ${\Gamma }_1$ and ${\Gamma }_2$ is the simple graph whose vertex set is $V({\Gamma }_1\square {\Gamma }_2)=V({\Gamma }_1)\times V({\Gamma }_2),$ in which $(a_1,b_1)$ is adjacent to $(a_2,b_2)$ if and only if $a_1=a_2$ and b₁ is adjacent to b₂ or a₁ is adjacent to a₂ and $b_1=b_2.$

The notation for each of these three products is supposed to suggest the corresponding product of two copies of K₂; see Figure 2.

Figure 2. Products of graphs and groups.

Mukherjee [67] defined the abstract power graph and product of abstract power graphs and called them “strong product”. A graph $\Gamma =(V,E)$ along with a map $f:E\to \mathbb{P}(\mathbb{N}),$ where $\mathbb{P}(\mathbb{N})$ is the power set of $\mathbb{N},$ is called an abstract power graph if there exists a group H such that $\Gamma =\mathit{P}(H)$ and $f(g,h)=\{k\in \mathbb{N}:g^k=h\}.$ Let ${\Gamma }_1$ and ${\Gamma }_2$ be two abstract power graphs with corresponding edge functions f₁ and $f_2.$ Then the strong product ${\Gamma }_1\otimes {\Gamma }_2=({\Gamma }_1\times {\Gamma }_2,E_1\otimes E_2)$ where $((a_1,b_1),(a_2,b_2))$ is an edge in $E_1\otimes E_2$ if $f_1(a_1,b_1)\cap f_2(a_2,b_2)\ne \varnothing .$

We note the risk of terminological confusion here: Mukherjee’s strong product is defined in a different category, namely graphs with edges labelled by sets of natural numbers. We use the symbol ⊗ for this product.

Theorem 13.26.

[67, Theorem 2.13] For any finite groups G₁, G₂, $\mathit{P}(G_1\times G_2)=\mathit{P}(G_1)\otimes \mathit{P}(G_2).$

Theorem 13.27.

[67, Theorem 2.14] Let G₁, G₂ be two groups of co-prime orders. Then $\mathit{P}(G_1)\otimes \mathit{P}(G_2)=\mathit{P}(G_1)⊠\mathit{P}(G_2).$

Bhuniya et al. [7] proved that the power graph of the direct product of two groups is not in general isomorphic to the direct, Cartesian or strong product of the power graphs of the factors. Also, they introduced a new product of graphs which they called the generalized product; they proved that power graph of the direct product of groups is isomorphic to the generalized product of their power graphs.

Proposition 13.28.

[7, Proposition 2.2] Let G₁ and G₂ be two non-trivial finite groups. Then $\mathit{P}(G_1\times G_2)$ is not isomorphic to $\mathit{P}(G_1)\square \mathit{P}(G_2).$

In the following example, Bhuniya et al. [7], proved that $\mathit{P}(G_1\times G_2)$ is neither isomorphic to the direct product nor to the strong product of $\mathit{P}(G_1)$ and $\mathit{P}(G_2).$

Example 13.29.

Consider $G_1=G_2={\mathbb{Z}}_2.$ Then $\mathit{P}({\mathbb{Z}}_2\times {\mathbb{Z}}_2)$ has precisely three edges, each edge emanating from the identity of ${\mathbb{Z}}_2\times {\mathbb{Z}}_2,$ whereas $\mathit{P}({\mathbb{Z}}_2)⊠\mathit{P}({\mathbb{Z}}_2)$ is the complete graph K₄ and $\mathit{P}({\mathbb{Z}}_2)\times \mathit{P}({\mathbb{Z}}_2)$ is a graph with precisely two edges. In Figure 2, we show this: note that $\mathit{P}({\mathbb{Z}}_2)$ is the edge K₂, while ${\mathbb{Z}}_2\times {\mathbb{Z}}_2$ is the Klein group V₄.

13.6. Some more properties of power graphs

In this section, we collect some more important properties of power graphs.

Theorem 13.30.

[1, Theorem 17] If $\mathit{P}(G)$ is a triangle-free graph, then G is an elementary abelian 2-group, and $\mathit{P}(G)$ is a star.

Theorem 13.31.

[1, Theorem 18] Let G be a group. Then following are equivalent.

1. $\mathit{P}(G)$ is connected;

2. G is periodic;

3. $\gamma (\mathit{P}(G))=1;$

4. $\text{diam}(\mathit{P}(G))\le 2.$

Theorem 13.32.

[1, Theorem 19] If $\mathrm{deg}(a)<\infty$ for every $a\in G$, then G is a finite group.

The next theorem is the analogue for infinite groups of Theorem 6.1.

Theorem 13.33.

[17, Theorem 10] Let G be an infinite group. Suppose that $x\in G$ has the property that for all $y\in G$, either x is a power of y or vice versa. Assume that $x\ne e$. Then the following hold:

1. If G is not a torsion group, then G is infinite cyclic and x is a generator;

2. If G is locally finite, then either $G=C_{p^{\infty }}$ for some prime p, and x is arbitrary; or $G=Q_{2^{\infty }}$ and x has order 2.

Theorem 13.34.

[75, Theorem 3.9] Let $a=(a_1,\dots ,a_r,a_{r+1},\dots ,a_s)$ be a vertex in the graph $\mathit{P}({\mathbb{Z}}_2^r\times {\mathbb{Z}}_4^s)$ such that o(a) = 2.

1. If $a_i\ne 0$ for some $i(1\le i\le r)$, then $\mathrm{deg}(a)=1;$

2. If a_i = 0 for all $i(1\le i\le r)$, then $\mathrm{deg}(a)=2^{r+s}+1.$

Proposition 13.35.

[75, Proposition 3.10] The total number of elements of order two in the group ${\mathbb{Z}}_2^r\times {\mathbb{Z}}_4^s$ having degree 1 and degree $2^{r+s+1}$ in $P({\mathbb{Z}}_2^r\times {\mathbb{Z}}_4^s)$ are $2^s(2^r-1)$ and $(2^s-1)$, respectively.

As a direct consequence of Theorem 13.34 and Proposition 13.35, we have the following immediate theorem that describes the power graph $\mathit{P}({\mathbb{Z}}_2^r\times {\mathbb{Z}}_4^s).$

Theorem 13.36.

[75, Theorem 3.11] $\mathit{P}({\mathbb{Z}}_2^r\times {\mathbb{Z}}_4^s)\cong K_1+(2^s(2^r-1)K_1\cup (2^s-1)(K_1+2^{r+s-1}{K}_2)).$

Theorem 13.37.

[4, Theorem 4] Let G be a finite group. The proper power graph ${\mathit{P}}_0(G)$ is regular if and only if G is isomorphic to the cyclic p-group or $\text{exp}\hspace{0.17em}(G)=p$, where p is prime.

Theorem 13.38.

[65, Theorem 4.2] Let G be a non-trivial finite group. Then ${\mathit{P}}_0(G)$ is strongly regular if and only if G is a p-group of order $p^{\alpha }$ for which $\text{exp}\hspace{0.17em}(G)=p or p^{\alpha }$ for some prime p and natural number $\alpha .$

In 2013, Tamizh Chelvam et al. [79] proved some results on the power graphs and they are listed below.

Theorem 13.39.

[79, Propositions 1 and 2, Theorems 3, 6 & 11]

1. Let G be a group with at least one non-self-inverse element. Then $gr(\mathit{P}(G))=3;$

2. Let G be a finite group with n elements and Z(G) be its center. If $\mathrm{deg}(a)=n-1$ in $\mathit{P}(G)$, then $a\in Z(G);$

3. Let G be a finite group with n elements. Then $\mathit{P}(G)$ is a graph with $\frac{1}{2}\sum _{a\ne e}o(a)$ edges if and only if every element other than identity of G is of prime order;

4. Let G be a finite group. Then $\mathit{P}(G)$ is Eulerian if and only if G is a group of odd order;

5. Let G be a finite abelian group. Then $\mathit{P}(G)$ is a uni-cyclic graph if and only if $G\cong Z_3.$

Theorem 13.40.

[65, Theorems 4.3 and 4.4] Let G be a non-trivial finite group. Then

1. ${\mathit{P}}_0(G)$ is bipartite if and only if ${\pi }_e(G)\subseteq \{1,2,3\};$

2. ${\mathit{P}}_0(G)$ is planar if and only if ${\pi }_e(G)\subseteq \{1,2,\dots ,6\}.$

Theorem 13.41.

[32, Theorem 24] ${\mathit{P}}_0(G)$ is Eulerian if and only if G is a cyclic 2-group or a generalized quaternion 2-group.

Theorem 13.42.

[4, Theorem 1] Let G be an infinite group. Then $\mathit{P}(G)$ is complete if and only if $G\cong {\mathbb{Z}}_{p^{\infty }}$ for some prime p.

Theorem 13.43.

[4, Theorem 2] Let G be a group. Then $\mathit{P}(G)$ is planar if and only if G is a torsion group and ${\pi }_e(G)\subseteq \{1,2,3,4\}$, where ${\pi }_e(G)=\{o(a):a\in G\}.$

Corollary 13.44.

[4, Corollary 1] If G is a group with planar power graph, then $\chi (\mathit{P}(G))=\max \{o(a):a\in G\}.$

Pourgholi et al. [74] proved some results on 2-connected power graphs which are summarized below.

Theorem 13.45.

[74, Theorems 2.1 and 2.2, Lemmas 2.1 and 2.2]

1. Suppose G is a p-group. The power graph $\mathit{P}(G)$ is 2 -connected if and only if G is a cyclic or generalized quaternion group.

2. Let G be a finite nilpotent group. If G is not a p-group, then the power graph $\mathit{P}(G)$ is 2-connected.

3. Let G and H are groups of finite order such that $(o(G),o(H))=1$. If G is cyclic of prime order, then $\mathit{P}(G\times H)$ is 2-connected.

4. Let G be a finite group with $o(G)\ne p$, where p is a prime number. If $\max \{o(a):a\in G\}=p$, then $\mathit{P}(G)$ is not 2-connected.

14. Conclusion and avenues for future research

Algebraic graph theory was initially developed as an intersection of algebra (both abstract and linear) and graph theory. Many concepts of abstract algebra have facilitated the study of graphs from algebraic structures with applications in computer science. On the other hand, graph theory has also helped to characterize certain properties of algebraic structures. We reviewed both the classical as well as the recent results and presentation is centered around a single yet rich structure, namely the power graphs of groups. The literature on the topic of this paper is vast, and we gave almost all the significant results published on power graphs. We hope to have delivered a survey as seen from the perspective of algebraic graph theory, that brought the reader from the basics to the research frontier in power graphs of groups. We want to conclude by listing a few fundamental open problems.

Some unsolved problems in this area, have already been presented within the sections, and we also redirect the interested reader to the survey article [2] for open questions that are still unsolved. Further, we compile and list some of the interesting problems. The list is by no means complete and is colored by our own interests and experiences.

Problem 14.1. Determine the exact expression for $\kappa (\mathit{P}({\mathbb{Z}}_n))$ and $\delta (\mathit{P}({\mathbb{Z}}_n)),$ for $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\cdots p_m^{{\alpha }_m},$ where $m\ge 2,p_1<p_2<\cdots <p_m$ are primes ${\alpha }_i\in \mathbb{N}$ for all $1\le i\le m.$

Problem 14.2. [1] Characterize all groups G having the property that the power graph $\mathit{P}(G)$ is connected even when the set of vertices in a dominating set is removed from $\mathit{P}(G).$

Ashrafi et al. [6] made the following conjecture.

Conjecture 14.3. The automorphism group of the power graph of each group is a member of $\mathit{F},$ where $\mathit{F}$ denotes the set of all groups that can be constructed from symmetric groups by direct or wreath product.

However, this conjecture is not correct. The computations reported in Section 2 show that the automorphism group of $\mathit{P}(M_{11})$ has the group M₁₁ as a homomorphic image. However, there are many groups G for which $\mathit{P}(G)$ is a cograph; and we observed in Theorem 11.2 that the automorphism group of a cograph belongs to the class $\mathit{F}.$ So we regard Problem 8.6 as an important topic for research, and as a substitute for the conjecture of Ashrafi et al.

Conjecture 14.4. [37] There exists a real number k such that $\text{diam}({\mathit{P}}_0(G))\le k$ for all finite groups G with connected proper power graph.

Conjecture 14.5. [68] For $n\ge 2,$ the following are equivalent.

1. The algebraic connectivity of $\mathit{P}({\mathbb{Z}}_n)$ is an integer;

2. $\mathit{P}({\mathbb{Z}}_n)$ is Laplacian integral;

3. n is a prime power or product of two primes.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

The research work of Ajay Kumar is supported by Council of Scientific and Industrial Research, India – University Grants Commission JRF, New Delhi, India, through Ref No.: 19/06/2016(i)EU-V/Roll No: 417267. Lavanya Selvaganesh is financially supported by Science and Engineering Research Board, India, through Grant No.: MTR/2018/000254 under the scheme MATRICS. T. Tamizh Chelvam is supported by CSIR Emeritus Scientist Scheme of Council of Scientific and Industrial Research (No.21 (1123)/20/EMR-II), Government of India.