Generalization of MacNeish’s Kronecker product theorem of mutually orthogonal Latin squares

Abstract

The subject of mutually orthogonal Latin squares (MOLSs) has fascinated researchers for many years. Although there is a number of intriguing results in this area, many open problems remain to which the answers seem as elusive as ever. Mutually orthogonal graph squares (MOGSs) are considered a generalization to MOLS. MOLS are considered an area of combinatorial design theory which has many applications in optical communications, cryptography, storage system design, wireless communications, communication protocols, and algorithm design and analysis, to mention just a few areas. In this paper, we introduce a technique for constructing the mutually orthogonal disjoint union of graphs squares and the generalization of the Kronecker product of MOGS as a generalization to the MacNeish’s Kronecker product of MOLS. These are useful for constructing many new results concerned with the MOGS.

Keywords:

• Latin squares
• graph squares
• Kronecker product

2010 MATHEMATICS SUBJECT CLASSIFICATION:

• 05C70
• 05B30

1. Introduction

Hereafter, we denote by E(G) the edge set of the graph $G,$ $F\cup H$ the disjoint union of the graphs F and $H, lG$ the disjoint $l$ copies of the graph G, P_n the path with n vertices, $G\otimes H$ the Kronecker product of the graphs G and H, and $K_{m,n}$ the complete bipartite graph with independent sets of sizes m and n.

Latin squares are one of the most fascinating areas of discrete mathematics, connected to coding theory and statistics, with applications to cryptography and computer science. They are essential for anyone who is running experiments, whether in a manufacturing plant or in a chemistry lab. The definition of Latin squares is simple and natural. A Latin square of side n is an n × n matrix with entries from a set A with n different elements, where each element of A appears once in every row and every column. Although Latin squares have many useful properties, for some statistical applications these structures are too restrictive. The more general concepts of graph squares and orthogonal graph squares offer more flexibility. The graph squares can be defined as follows. Let $G$ be a subgraph of $K_{n,n}$ with n edges. A square matrix $L$ of order $n$ is a G-square if every element in ${\mathbb{Z}}_n=\{0,1,\dots ,n-1\}$ occurs exactly $n$ times and the graphs $G_j$ where $j\in {\mathbb{Z}}_n$ with $E(G_j)=\{(x,y):L(x,y)=j\}$ are isomorphic to G. It is clear that the G-square represents the edge decomposition of $K_{n,n}$ by G. The rows of an $n\times n$ square are labeled with the elements of ${\mathbb{Z}}_n\times \left\{0\right\},$ and the columns are labeled with the elements of ${\mathbb{Z}}_n\times \left\{1\right\}.$

Definition 1.1.

Suppose L and M are graph squares of order n based on symbol sets A_L and A_M respectively. M is orthogonal to L if, for every $a\in A_L,$ the set of n positions in L occupied by a contain every member of $A_M.$ Equivalently, suppose we construct from L and M an $n\times n$ array (L, M) of ordered pairs, where (a, b) occurs in position (i, j) if and only if a occurs in position (i, j) of L and b occurs in position (i, j) of M, then M is orthogonal to L if every possible ordered pair with first element in A_L and second element in A_M occurs in the new array.

A set of graph squares $M_0,\dots ,M_{l-1}$ is mutually orthogonal, or a set of MOGS, if for every $0\le a<b\le l-1, M_a$ and M_b are orthogonal. Let us write N(n, G) for the number of squares in the largest possible set of mutually orthogonal G-squares of order n.

Theorem 1.2.

([6, 15]) For every bipartite graph G with $n\ge 2$ edges we have $N(n,G)\le n.$

Example 1.3.

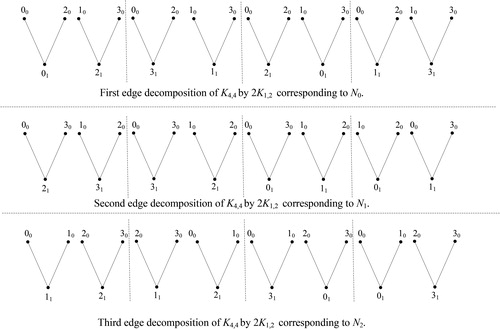
$(i)$ Three mutually orthogonal Latin squares, $L_0,L_1,$ and L₂ of order 4. $$L_0=\left[\begin{array}{cccc}1& 2& 3& 0\\ 0& 3& 2& 1\\ 2& 1& 0& 3\\ 3& 0& 1& 2\end{array}\right],L_1=\left[\begin{array}{cccc}1& 2& 3& 0\\ 3& 0& 1& 2\\ 0& 3& 2& 1\\ 2& 1& 0& 3\end{array}\right],L_2=\left[\begin{array}{cccc}1& 2& 3& 0\\ 2& 1& 0& 3\\ 3& 0& 1& 2\\ 0& 3& 2& 1\end{array}\right].$$ $(ii)$ Three mutually orthogonal $2K_{1,2}$-squares, $N_0,N_1,$ and N₂ of order 4, see [9]. For more illustration, see Figure 1. $$N_0=\left[\begin{array}{cccc}0& 3& 2& 1\\ 2& 1& 0& 3\\ 0& 3& 2& 1\\ 2& 1& 0& 3\end{array}\right], N_1=\left[\begin{array}{cccc}2& 3& 0& 1\\ 3& 2& 1& 0\\ 3& 2& 1& 0\\ 2& 3& 0& 1\end{array}\right], N_2=\left[\begin{array}{cccc}3& 0& 1& 2\\ 3& 0& 1& 2\\ 2& 1& 0& 3\\ 2& 1& 0& 3\end{array}\right].$$

Figure 1. Three edge decompositions corresponding to $N_0,N_1,$ and $N_2.$

Since the MOGS are considered the generalization of the MOLS, then the MOGS may be important in statistics, cryptography and computer science. For several applications on MOLS, see [13]. They primarily used in the design of experiments. This means that they are important in all areas of human investigation. MOLS are related to combinatorics, geometry, finite fields. We know many constructions for the MOGS, yet there are at least as many unsolved problems.

Since Euler first asked about MOLS for solving the thirty-six officers problem, substantial progress has been made for solving many problems concerned with the MOLS. The celebrated theorems of Bose, Shrikhande, and Parker [2, 3] are the biggest breakthroughs, and the research of Wilson [16]. Many efforts have been concentrated on refining and finding new applications for these approaches. For a brief survey of constructions of MOLS, see [4]. El-Shanawany [6] conjectured that if p is a prime number, then $N(p,P_{p+1})=p,$ where $P_{p+1}$ is the path on p + 1 vertices. Sampathkumar et al. [15] proved this conjecture. The authors of [7] computed $N(n,G)$ where $G\cong {\mathbb{P}}_{p+1}(F).$ In [8], the $N(n,G)=k\ge 3$ has been computed, where $G$ represents disjoint copies of certain subgraphs of $K_{n,n}.$ Higazy [11] determined N(n, G) for all possible subgraphs G with n-edges when n = 3, 4. El-Shanawany and El-Mesady [9] defined the Kronecker product of MOGS of the complete bipartite graphs and used this method to construct the new mutually orthogonal disjoint union of some complete bipartite graphs squares. The authors of [10] have constructed the MOGS for disjoint union of paths. Mutually orthogonal certain graph squares have been built in [9]. There are close connections between the MOGS and the orthogonal arrays [12]. New types of topological structures can be constructed based on the new graphs constructed in this paper, see [1, 5].

2. Mutually orthogonal disjoint union of graphs squares

In Proposition 2.1, if we have $k_1$ mutually orthogonal Latin squares of order m and k₂ mutually orthogonal G_l-squares of order $n,l\in {\mathbb{Z}}_m.$ Then, we construct $k=\min \{k_1,k_2\}$ mutually orthogonal $(G_0\cup G_1\cup G_2\cup \dots \cup G_{m-1})$ -squares of order mn.

Proposition 2.1.

Let $m>3,m\ne 6, n\le m,$ $k_1\le m-1$ and $k_2\le n-1$ be positive integers, and assume that there exist collections ${\mathcal{G}}_l$ of mutually orthogonal G_l-squares of $K_{n,n}$ for $l\in {\mathbb{Z}}_m.$ Then there exists $k=\min \{k_1,k_2\}$ mutually orthogonal $(G_0\cup G_1\cup G_2\cup \dots \cup G_{m-1})$ -squares of $K_{mn,mn}.$

Proof.

Let $L^s=(a_{ij}^s), s\in {\mathbb{Z}}_{k_1}, 0\le i,j\le m-1$ be $k_1$ mutually orthogonal Latin squares of order m on the set ${\mathbb{Z}}_m.$ For any $l\in {\mathbb{Z}}_m,$ let $L_l^s=(b_{ij}^{s,l}), s\in {\mathbb{Z}}_{k_2}, 0\le i,j\le n-1$ be k₂ mutually orthogonal G_l-squares of order n. If $k=\min \{k_1,k_2\}.$ Then, we construct $k$ mutually orthogonal $(G_0\cup G_1\cup G_2\cup \dots \cup G_{m-1})$-squares $N_s=(z_{ij}^s),s\in {\mathbb{Z}}_k$ and $0\le i,j\le mn-1.$ For given $i,j\in {\mathbb{Z}}_{mn},$ let $\lambda ,\mu ,\rho ,\sigma$ be uniquely defined by $i=\lambda n+\mu ;\lambda \in {\mathbb{Z}}_m,\mu \in {\mathbb{Z}}_n$ and $j=\rho n+\sigma ; \rho \in {\mathbb{Z}}_m, \sigma \in {\mathbb{Z}}_n.$ Then the entries $z_{ij}^s$ of $N_s$ are as follows, (1) $$z_{ij}^s =z_{\lambda n+\mu ,\rho n+\sigma }^s=n{a}_{\lambda ,\rho }^s+b_{\mu ,\sigma }^{s,\lambda }.$$(1)

We prove that $N_s$ have the desired properties. Firstly, we show that $N_s$ is a $(G_0\cup G_1\cup G_2\cup \dots \cup G_{m-1})$-square. Let $i\in {\mathbb{Z}}_{mn}$ be arbitrarily chosen. Then, let ${\overline{\lambda }}^s$ and ${\overline{\mu }}^s$ be defined by $i=n{\overline{\lambda }}^s+{\overline{\mu }}^s;{\overline{\lambda }}^s\in {\mathbb{Z}}_m,{\overline{\mu }}^s\in {\mathbb{Z}}_n.$ We are looking for all edges of the graph given by the entries $i$ in N_s. By construction we have $n{a}_{\lambda ,\rho }^s+b_{\mu ,\sigma }^{s,\lambda }=n{\overline{\lambda }}^s+{\overline{\mu }}^s.$ By the ranges of $\lambda ,\mu ,{\overline{\lambda }}^s,{\overline{\mu }}^s,$ it follows that $a_{\lambda ,\rho }^s={\overline{\lambda }}^s$ and $b_{\mu ,\sigma }^{s,\lambda }={\overline{\mu }}^s.$ For any $\lambda \in {\mathbb{Z}}_m$ there is a unique $\rho ,$ with $a_{\lambda ,\rho }^s={\overline{\lambda }}^s,$ since L^s is a Latin square. For fixed $\lambda ,\rho$ the graph induced by the vertices $n.\lambda +\mu , n.\rho +\sigma (\mu ,\sigma \in {\mathbb{Z}}_n)$ is exactly $G_{\lambda }.$$$ Since $\lambda$ is running from 0 to m – 1 the graph given by the entries i in N_s is the vertex disjoint union of $G_0\cup G_1\cup G_2\cup \dots \cup G_{m-1}.$ Secondly, we show that N_s, $s\in {\mathbb{Z}}_k$ are mutually orthogonal. Assume the contrary, $i.e.,$ there are two equal pairs of entries of N_r and N_t where 0 $\le$ r < t $\le k-1.$ That is, there are (p, q) and $(p^{\prime },q^{\prime })$ with $p,q,p^{\prime },q^{\prime }\in$ ${\mathbb{Z}}_{mn},$ $(p,q)\ne (p^{\prime },q^{\prime })$ and $(z_{p,q}^r,z_{p,q}^t)=(z_{p^{\prime },q^{\prime }}^r,z_{p^{\prime },q^{\prime }}^t)$ where $p=n.\lambda +\mu ,q=n.\rho +\sigma ,p\prime =n.\lambda \mathrm{ }\prime +\mu \prime ,$ and $q\prime =n.\rho \prime +\sigma \prime .$ Hence $z_{p,q}^r$ $=$ $z_{p^{\prime },q^{\prime }}^r$ and $z_{p,q}^t$ $=$ $z_{p^{\prime },q^{\prime }}^t$ and $n.a_{\lambda ,\rho }^r+b_{\mu ,\sigma }^{r,\lambda }$ $=n.a_{{\lambda }^{\prime },{\rho }^{\prime }}^r+b_{{\mu }^{\prime },{\sigma }^{\prime }}^{r,{\lambda }^{\prime }}, n.a_{\lambda ,\rho }^t+b_{\mu ,\sigma }^{t,\lambda }$ $=n.a_{{\lambda }^{\prime },{\rho }^{\prime }}^t+b_{{\mu }^{\prime },{\sigma }^{\prime }}^{t,{\lambda }^{\prime }}.$ It follows $b_{\mu ,\sigma }^{r,\lambda }=b_{{\mu }^{\prime },{\sigma }^{\prime }}^{r,{\lambda }^{\prime }},a_{\lambda ,\rho }^r=a_{{\lambda }^{\prime },{\rho }^{\prime }}^r, b_{\mu ,\sigma }^{t,\lambda }=b_{{\mu }^{\prime },{\sigma }^{\prime }}^{t,{\lambda }^{\prime }},a_{\lambda ,\rho }^t=a_{{\lambda }^{\prime },{\rho }^{\prime }}^t.$ Since $L^r$ and L^t are orthogonal, from $(a_{\lambda ,\rho }^r,a_{\lambda ,\rho }^t)=(a_{{\lambda }^{\prime },{\rho }^{\prime }}^r,a_{{\lambda }^{\prime },{\rho }^{\prime }}^t)$ follows that $\lambda ={\lambda }^{\prime }$ and $\rho ={\rho }^{\prime }.$ Since $L_{\lambda }^r$ and $L_{\lambda }^t$ are orthogonal, from $(b_{\mu ,\sigma }^{r,\lambda },b_{\mu ,\sigma }^{t,\lambda })=(b_{{\mu }^{\prime },{\sigma }^{\prime }}^{r,{\lambda }^{\prime }},b_{{\mu }^{\prime },{\sigma }^{\prime }}^{t,{\lambda }^{\prime }})$ follows that $\mu ={\mu }^{\prime }$ and $\sigma ={\sigma }^{\prime }, i.e.,$ $p=p^{\prime }$ and $q=q^{\prime }$ contradicting the assumption.□

Example 2.2.

For a direct application to Proposition 2.1, let $m=n=4,$ then there exists 3 mutually orthogonal $(G_0\cup G_1\cup G_2\cup G_3)$-squares of $K_{16,16},$ where $G_0\cong 4K_2,G_1\cong 4K_2,G_2\cong 2K_{1,2},$ and $G_3\cong C_4.$ Let $L^s;$ $0\le s\le 2$ be the three mutually orthogonal Latin squares of order 4 as follows: $$L^0=\left[\begin{array}{cccc}1& 0& 3& 2\\ 2& 3& 0& 1\\ 3& 2& 1& 0\\ 0& 1& 2& 3\end{array}\right], L^1=\left[\begin{array}{cccc}2& 3& 0& 1\\ 3& 2& 1& 0\\ 1& 0& 3& 2\\ 0& 1& 2& 3\end{array}\right], L^2=\left[\begin{array}{cccc}3& 2& 1& 0\\ 1& 0& 3& 2\\ 2& 3& 0& 1\\ 0& 1& 2& 3\end{array}\right].$$

Three mutually orthogonal Latin squares of order $4, {\mathcal{G}}_0=\{L_0^0,L_0^1,L_0^2\}.$ $$L_0^0=\left[\begin{array}{cccc}1& 0& 3& 2\\ 2& 3& 0& 1\\ 3& 2& 1& 0\\ 0& 1& 2& 3\end{array}\right], L_0^1=\left[\begin{array}{cccc}2& 3& 0& 1\\ 3& 2& 1& 0\\ 1& 0& 3& 2\\ 0& 1& 2& 3\end{array}\right], L_0^2=\left[\begin{array}{cccc}3& 2& 1& 0\\ 1& 0& 3& 2\\ 2& 3& 0& 1\\ 0& 1& 2& 3\end{array}\right].$$

Three mutually orthogonal Latin squares of order $4, {\mathcal{G}}_1=\{L_1^0,L_1^1,L_1^2\}.$ $$L_1^0=\left[\begin{array}{cccc}1& 0& 3& 2\\ 2& 3& 0& 1\\ 3& 2& 1& 0\\ 0& 1& 2& 3\end{array}\right], L_1^1=\left[\begin{array}{cccc}2& 3& 0& 1\\ 3& 2& 1& 0\\ 1& 0& 3& 2\\ 0& 1& 2& 3\end{array}\right], L_1^2=\left[\begin{array}{cccc}3& 2& 1& 0\\ 1& 0& 3& 2\\ 2& 3& 0& 1\\ 0& 1& 2& 3\end{array}\right].$$

Three mutually orthogonal $2K_{1,2}$-squares of order $4, {\mathcal{G}}_2=\{L_2^0,L_2^1,L_2^2\}.$ $$L_2^0=\left[\begin{array}{cccc}0& 3& 2& 1\\ 2& 1& 0& 3\\ 0& 3& 2& 1\\ 2& 1& 0& 3\end{array}\right], L_2^1=\left[\begin{array}{cccc}2& 3& 0& 1\\ 3& 2& 1& 0\\ 3& 2& 1& 0\\ 2& 3& 0& 1\end{array}\right], L_2^2=\left[\begin{array}{cccc}3& 0& 1& 2\\ 3& 0& 1& 2\\ 2& 1& 0& 3\\ 2& 1& 0& 3\end{array}\right].$$

Three mutually orthogonal C₄-squares of order $4, {\mathcal{G}}_3=\{L_3^0,L_3^1,L_3^2\}.$ $$L_3^0=\left[\begin{array}{cccc}0& 0& 1& 1\\ 0& 0& 1& 1\\ 2& 2& 3& 3\\ 2& 2& 3& 3\end{array}\right], L_3^1=\left[\begin{array}{cccc}0& 1& 0& 1\\ 2& 3& 2& 3\\ 0& 1& 0& 1\\ 2& 3& 2& 3\end{array}\right], L_3^2=\left[\begin{array}{cccc}0& 2& 2& 0\\ 3& 1& 1& 3\\ 3& 1& 1& 3\\ 0& 2& 2& 0\end{array}\right].$$

From equation (1)(1) $$z_{ij}^s =z_{\lambda n+\mu ,\rho n+\sigma }^s=n{a}_{\lambda ,\rho }^s+b_{\mu ,\sigma }^{s,\lambda }.$$(1) , $$N_0=\left(\begin{array}{cccccccccccccccc}5\hfill & 4\hfill & 7\hfill & 6\hfill & 1\hfill & 0\hfill & 3\hfill & 2\hfill & 13\hfill & 12\hfill & 15\hfill & 14\hfill & 9\hfill & 8\hfill & 11\hfill & 10\hfill \\ 6\hfill & 7\hfill & 4\hfill & 5\hfill & 2\hfill & 3\hfill & 0\hfill & 1\hfill & 14\hfill & 15\hfill & 12\hfill & 13\hfill & 10\hfill & 11\hfill & 8\hfill & 9\hfill \\ 7\hfill & 6\hfill & 5\hfill & 4\hfill & 3\hfill & 2\hfill & 1\hfill & 0\hfill & 15\hfill & 14\hfill & 13\hfill & 12\hfill & 11\hfill & 10\hfill & 9\hfill & 8\hfill \\ 4\hfill & 5\hfill & 6\hfill & 7\hfill & 0\hfill & 1\hfill & 2\hfill & 3\hfill & 12\hfill & 13\hfill & 14\hfill & 15\hfill & 8\hfill & 9\hfill & 10\hfill & 11\hfill \\ 9\hfill & 8\hfill & 11\hfill & 10\hfill & 13\hfill & 12\hfill & 15\hfill & 14\hfill & 1\hfill & 0\hfill & 3\hfill & 2\hfill & 5\hfill & 4\hfill & 7\hfill & 6\hfill \\ 10\hfill & 11\hfill & 8\hfill & 9\hfill & 14\hfill & 15\hfill & 12\hfill & 13\hfill & 2\hfill & 3\hfill & 0\hfill & 1\hfill & 6\hfill & 7\hfill & 4\hfill & 5\hfill \\ 11\hfill & 10\hfill & 9\hfill & 8\hfill & 15\hfill & 14\hfill & 13\hfill & 12\hfill & 3\hfill & 2\hfill & 1\hfill & 0\hfill & 7\hfill & 6\hfill & 5\hfill & 4\hfill \\ 8\hfill & 9\hfill & 10\hfill & 11\hfill & 12\hfill & 13\hfill & 14\hfill & 15\hfill & 0\hfill & 1\hfill & 2\hfill & 3\hfill & 4\hfill & 5\hfill & 6\hfill & 7\hfill \\ 12\hfill & 15\hfill & 14\hfill & 13\hfill & 8\hfill & 11\hfill & 10\hfill & 9\hfill & 4\hfill & 7\hfill & 6\hfill & 5\hfill & 0\hfill & 3\hfill & 2\hfill & 1\hfill \\ 14\hfill & 13\hfill & 12\hfill & 15\hfill & 10\hfill & 9\hfill & 8\hfill & 11\hfill & 6\hfill & 5\hfill & 4\hfill & 7\hfill & 2\hfill & 1\hfill & 0\hfill & 3\hfill \\ 12\hfill & 15\hfill & 14\hfill & 13\hfill & 8\hfill & 11\hfill & 10\hfill & 9\hfill & 4\hfill & 7\hfill & 6\hfill & 5\hfill & 0\hfill & 3\hfill & 2\hfill & 1\hfill \\ 14\hfill & 13\hfill & 12\hfill & 15\hfill & 10\hfill & 9\hfill & 8\hfill & 11\hfill & 6\hfill & 5\hfill & 4\hfill & 7\hfill & 2\hfill & 1\hfill & 0\hfill & 3\hfill \\ 0\hfill & 0\hfill & 1\hfill & 1\hfill & 4\hfill & 4\hfill & 5\hfill & 5\hfill & 8\hfill & 8\hfill & 9\hfill & 9\hfill & 12\hfill & 12\hfill & 13\hfill & 13\hfill \\ 0\hfill & 0\hfill & 1\hfill & 1\hfill & 4\hfill & 4\hfill & 5\hfill & 5\hfill & 8\hfill & 8\hfill & 9\hfill & 9\hfill & 12\hfill & 12\hfill & 13\hfill & 13\hfill \\ 2\hfill & 2\hfill & 3\hfill & 3\hfill & 6\hfill & 6\hfill & 7\hfill & 7\hfill & 10\hfill & 10\hfill & 11\hfill & 11\hfill & 14\hfill & 14\hfill & 15\hfill & 15\hfill \\ 2\hfill & 2\hfill & 3\hfill & 3\hfill & 6\hfill & 6\hfill & 7\hfill & 7\hfill & 10\hfill & 10\hfill & 11\hfill & 11\hfill & 14\hfill & 14\hfill & 15\hfill & 15\hfill \end{array}\right),$$ $$N_1=\left(\begin{array}{cccccccccccccccc}10\hfill & 11\hfill & 8\hfill & 9\hfill & 14\hfill & 15\hfill & 12\hfill & 13\hfill & 2\hfill & 3\hfill & 0\hfill & 1\hfill & 6\hfill & 7\hfill & 4\hfill & 5\hfill \\ 11\hfill & 10\hfill & 9\hfill & 8\hfill & 15\hfill & 14\hfill & 13\hfill & 12\hfill & 3\hfill & 2\hfill & 1\hfill & 0\hfill & 7\hfill & 6\hfill & 5\hfill & 4\hfill \\ 9\hfill & 8\hfill & 11\hfill & 10\hfill & 13\hfill & 12\hfill & 15\hfill & 14\hfill & 1\hfill & 0\hfill & 3\hfill & 2\hfill & 5\hfill & 4\hfill & 7\hfill & 6\hfill \\ 8\hfill & 9\hfill & 10\hfill & 11\hfill & 12\hfill & 13\hfill & 14\hfill & 15\hfill & 0\hfill & 1\hfill & 2\hfill & 3\hfill & 4\hfill & 5\hfill & 6\hfill & 7\hfill \\ 14\hfill & 15\hfill & 12\hfill & 13\hfill & 10\hfill & 11\hfill & 8\hfill & 9\hfill & 6\hfill & 7\hfill & 4\hfill & 5\hfill & 2\hfill & 3\hfill & 0\hfill & 1\hfill \\ 15\hfill & 14\hfill & 13\hfill & 12\hfill & 11\hfill & 10\hfill & 9\hfill & 8\hfill & 7\hfill & 6\hfill & 5\hfill & 4\hfill & 3\hfill & 2\hfill & 1\hfill & 0\hfill \\ 13\hfill & 12\hfill & 15\hfill & 14\hfill & 9\hfill & 8\hfill & 11\hfill & 10\hfill & 5\hfill & 4\hfill & 7\hfill & 6\hfill & 1\hfill & 0\hfill & 3\hfill & 2\hfill \\ 12\hfill & 13\hfill & 14\hfill & 15\hfill & 8\hfill & 9\hfill & 10\hfill & 11\hfill & 4\hfill & 5\hfill & 6\hfill & 7\hfill & 0\hfill & 1\hfill & 2\hfill & 3\hfill \\ 6\hfill & 7\hfill & 4\hfill & 5\hfill & 2\hfill & 3\hfill & 0\hfill & 1\hfill & 14\hfill & 15\hfill & 12\hfill & 13\hfill & 10\hfill & 11\hfill & 8\hfill & 9\hfill \\ 7\hfill & 6\hfill & 5\hfill & 4\hfill & 3\hfill & 2\hfill & 1\hfill & 0\hfill & 15\hfill & 14\hfill & 13\hfill & 12\hfill & 11\hfill & 10\hfill & 9\hfill & 8\hfill \\ 7\hfill & 6\hfill & 5\hfill & 4\hfill & 3\hfill & 2\hfill & 1\hfill & 0\hfill & 15\hfill & 14\hfill & 13\hfill & 12\hfill & 11\hfill & 10\hfill & 9\hfill & 8\hfill \\ 6\hfill & 7\hfill & 4\hfill & 5\hfill & 2\hfill & 3\hfill & 0\hfill & 1\hfill & 14\hfill & 15\hfill & 12\hfill & 13\hfill & 10\hfill & 11\hfill & 8\hfill & 9\hfill \\ 0\hfill & 1\hfill & 0\hfill & 1\hfill & 4\hfill & 5\hfill & 4\hfill & 5\hfill & 8\hfill & 9\hfill & 8\hfill & 9\hfill & 12\hfill & 13\hfill & 12\hfill & 13\hfill \\ 2\hfill & 3\hfill & 2\hfill & 3\hfill & 6\hfill & 7\hfill & 6\hfill & 7\hfill & 10\hfill & 11\hfill & 10\hfill & 11\hfill & 14\hfill & 15\hfill & 14\hfill & 15\hfill \\ 0\hfill & 1\hfill & 0\hfill & 1\hfill & 4\hfill & 5\hfill & 4\hfill & 5\hfill & 8\hfill & 9\hfill & 8\hfill & 9\hfill & 12\hfill & 13\hfill & 12\hfill & 13\hfill \\ 2\hfill & 3\hfill & 2\hfill & 3\hfill & 6\hfill & 7\hfill & 6\hfill & 7\hfill & 10\hfill & 11\hfill & 10\hfill & 11\hfill & 14\hfill & 15\hfill & 14\hfill & 15\hfill \end{array}\right),$$ $$N_2=\left(\begin{array}{cccccccccccccccc}15\hfill & 14\hfill & 13\hfill & 12\hfill & 11\hfill & 10\hfill & 9\hfill & 8\hfill & 7\hfill & 6\hfill & 5\hfill & 4\hfill & 3\hfill & 2\hfill & 1\hfill & 0\hfill \\ 13\hfill & 12\hfill & 15\hfill & 14\hfill & 9\hfill & 8\hfill & 11\hfill & 10\hfill & 5\hfill & 4\hfill & 7\hfill & 6\hfill & 1\hfill & 0\hfill & 3\hfill & 2\hfill \\ 14\hfill & 15\hfill & 12\hfill & 13\hfill & 10\hfill & 11\hfill & 8\hfill & 9\hfill & 6\hfill & 7\hfill & 4\hfill & 5\hfill & 2\hfill & 3\hfill & 0\hfill & 1\hfill \\ 12\hfill & 13\hfill & 14\hfill & 15\hfill & 8\hfill & 9\hfill & 10\hfill & 11\hfill & 4\hfill & 5\hfill & 6\hfill & 7\hfill & 0\hfill & 1\hfill & 2\hfill & 3\hfill \\ 7\hfill & 6\hfill & 5\hfill & 4\hfill & 3\hfill & 2\hfill & 1\hfill & 0\hfill & 15\hfill & 14\hfill & 13\hfill & 12\hfill & 11\hfill & 10\hfill & 9\hfill & 8\hfill \\ 5\hfill & 4\hfill & 7\hfill & 6\hfill & 1\hfill & 0\hfill & 3\hfill & 2\hfill & 13\hfill & 12\hfill & 15\hfill & 14\hfill & 9\hfill & 8\hfill & 11\hfill & 10\hfill \\ 6\hfill & 7\hfill & 4\hfill & 5\hfill & 2\hfill & 3\hfill & 0\hfill & 1\hfill & 14\hfill & 15\hfill & 12\hfill & 13\hfill & 10\hfill & 11\hfill & 8\hfill & 9\hfill \\ 4\hfill & 5\hfill & 6\hfill & 7\hfill & 0\hfill & 1\hfill & 2\hfill & 3\hfill & 12\hfill & 13\hfill & 14\hfill & 15\hfill & 8\hfill & 9\hfill & 10\hfill & 11\hfill \\ 11\hfill & 8\hfill & 9\hfill & 10\hfill & 15\hfill & 12\hfill & 13\hfill & 14\hfill & 3\hfill & 0\hfill & 1\hfill & 2\hfill & 7\hfill & 4\hfill & 5\hfill & 6\hfill \\ 11\hfill & 8\hfill & 9\hfill & 10\hfill & 15\hfill & 12\hfill & 13\hfill & 14\hfill & 3\hfill & 0\hfill & 1\hfill & 2\hfill & 7\hfill & 4\hfill & 5\hfill & 6\hfill \\ 10\hfill & 9\hfill & 8\hfill & 11\hfill & 14\hfill & 13\hfill & 12\hfill & 15\hfill & 2\hfill & 1\hfill & 0\hfill & 3\hfill & 6\hfill & 5\hfill & 4\hfill & 7\hfill \\ 10\hfill & 9\hfill & 8\hfill & 11\hfill & 14\hfill & 13\hfill & 12\hfill & 15\hfill & 2\hfill & 1\hfill & 0\hfill & 3\hfill & 6\hfill & 5\hfill & 4\hfill & 7\hfill \\ 0\hfill & 2\hfill & 2\hfill & 0\hfill & 4\hfill & 6\hfill & 6\hfill & 4\hfill & 8\hfill & 10\hfill & 10\hfill & 8\hfill & 12\hfill & 14\hfill & 14\hfill & 12\hfill \\ 3\hfill & 1\hfill & 1\hfill & 3\hfill & 7\hfill & 5\hfill & 5\hfill & 7\hfill & 11\hfill & 9\hfill & 9\hfill & 11\hfill & 15\hfill & 13\hfill & 13\hfill & 15\hfill \\ 3\hfill & 1\hfill & 1\hfill & 3\hfill & 7\hfill & 5\hfill & 5\hfill & 7\hfill & 11\hfill & 9\hfill & 9\hfill & 11\hfill & 15\hfill & 13\hfill & 13\hfill & 15\hfill \\ 0\hfill & 2\hfill & 2\hfill & 0\hfill & 4\hfill & 6\hfill & 6\hfill & 4\hfill & 8\hfill & 10\hfill & 10\hfill & 8\hfill & 12\hfill & 14\hfill & 14\hfill & 12\hfill \end{array}\right),$$ which are mutually orthogonal $(4K_2\cup 4K_2\cup 2K_{1,2}\cup C_4)$-squares. For more illustration, see Figure 2.

Figure 2. The graphs corresponding to the zero values in $N_0,N_1,$ and $N_2.$

3. Generalization of Kronecker product of the MOGS

The Kronecker product of two Latin squares L and M is defined as follows. If x is any symbol in L, write (x, M) for the array derived from M by replacing each entry y by the ordered pair (x, y). Then replace every occurrence of x in L by $(x,M).$

Example 3.1.

Let L and M be Latin squares of order three: $$L=\left[\begin{array}{ccc}0& 1& 2\\ 1& 2& 0\\ 2& 0& 1\end{array}\right],M=\left[\begin{array}{ccc}\alpha & \beta & \gamma \\ \beta & \gamma & \alpha \\ \gamma & \alpha & \beta \end{array}\right].$$ Hence, the Kronecker product of L and M is $$L\otimes M=\left[\begin{array}{c}\begin{array}{ccccccccc}0\alpha & 0\beta & 0\gamma & 1\alpha & 1\beta & 1\gamma & 2\alpha & 2\beta & 2\gamma \\ 0\beta & 0\gamma & 0\alpha & 1\beta & 1\gamma & 1\alpha & 2\beta & 2\gamma & 2\alpha \\ 0\gamma & 0\alpha & 0\beta & 1\gamma & 1\alpha & 1\beta & 2\gamma & 2\alpha & 2\beta \\ 1\alpha & 1\beta & 1\gamma & 2\alpha & 2\beta & 2\gamma & 0\alpha & 0\beta & 0\gamma \\ 1\beta & 1\gamma & 1\alpha & 2\beta & 2\gamma & 2\alpha & 0\beta & 0\gamma & 0\alpha \\ 1\gamma & 1\alpha & 1\beta & 2\gamma & 2\alpha & 2\beta & 0\gamma & 0\alpha & 0\beta \\ 2\alpha & 2\beta & 2\gamma & 0\alpha & 0\beta & 0\gamma & 1\alpha & 1\beta & 1\gamma \\ 2\beta & 2\gamma & 2\alpha & 0\beta & 0\gamma & 0\alpha & 1\beta & 1\gamma & 1\alpha \\ 2\gamma & 2\alpha & 2\beta & 0\gamma & 0\alpha & 0\beta & 1\gamma & 1\alpha & 1\beta \end{array}\end{array}\right].$$

From the previous example, it is clear that the Kronecker product of Latin squares is a Latin square. In general, if L is a Latin square of order l and M is a Latin square of order $m,$ then $L\otimes M$ is a Latin square of order $lm.$ Also, the Kronecker product preserves orthogonality: if L₁ is orthogonal to L₂ and M₁ is orthogonal to $M_2,$ then $L_1\otimes M_1$ is orthogonal to $L_2\otimes M_2.$ Hence, $N(lm,lm{K}_2)\ge \min \{N(l,l{K}_2),N(m,m{K}_2)\},$ see [14]. Note that a Latin square of order n represents the edge decomposition of $K_{n,n}$ by $n{K}_2.$

El-Shanawany et al. [9] generalized the Kronecker product of Latin squares as follows, if $N(m, G)\ge k_1$ and $N(n, H)\ge k_2$ and $\min \{k_1,k_2\}=k,$ then $N(mn, \mathbb{G})\ge k$ $\text{by}$ Proposition 3.2, where $\mathbb{G}\cong G\otimes H.$

Proposition 3.2.

([9]) If there are k MOGS of order m of the graph G and k MOGS of order n of the graph H, then there are k MOGS of order mn of the graph $\mathbb{G}\cong G\otimes H.$

This section deals with a generalization of the Kronecker product from MOLS to MOGS. Our main object is the generalization of a previous known result about the existence of MOGS derived from the Kronecker product of two families of MOGS (Proposition 3.2) to the existence of MOGS derived from the Kronecker product of n families of MOGS (Proposition 3.3).

Proposition 3.3.

Let $\lambda \in \{1,2,\dots ,n\}$ and there are $k_{\lambda }$ MOGS of order $m_{\lambda }$ for the graph $G_{\lambda },$ then there are $k=\min \left\{k_{\lambda }\right\}$ MOGS of order $\mu =\underset{\lambda =1}{\prod ^n}{m}_{\lambda }$ for the graph $\mathbb{G}\cong G_1\otimes G_2\otimes \dots \otimes G_n.$

Proof.

Call the $k_{\lambda }$ MOGS of order $m_{\lambda }$ are $M^{s,\lambda }=(a_{ij}^{s,\lambda }),s\in {\mathbb{Z}}_{k_{\lambda }},i,j\in {\mathbb{Z}}_{m_{\lambda }}.$ For a fixed $s\in {\mathbb{Z}}_k,$ take the Kronecker product of $M^{s,\lambda }$ where $\lambda \in \{1,2,\dots ,n\}.$ Now, we have k squares of order μ, and simply need to show that they are mutually orthogonal. For $p,q\in {\mathbb{Z}}_k,p\ne q,$ we will show that $M^{p,1}\otimes$ $M^{p,2}\otimes \dots \otimes M^{p,n}$ and $M^{q,1}\otimes$ $M^{q,2}\otimes \dots \otimes M^{q,n}$ are orthogonal graph squares of order $\mu .$ Consider an ordered pair, $((a_{ij}^{p,1},a_{ij}^{p,2},\dots ,a_{ij}^{p,n}),(a_{ij}^{q,1},a_{ij}^{q,2},\dots ,a_{ij}^{q,n})).$ We want to find a unique cell $((i_1,i_2,\dots ,i_n),(j_1,j_2,\dots ,j_n))$ such that $$\begin{array}{c}(M^{p,1}\otimes M^{p,2}\otimes \dots \otimes M^{p,n})((i_1,i_2,\dots ,i_n),(j_1,j_2,\dots ,j_n))=(a_{ij}^{p,1},a_{ij}^{p,2},\dots ,a_{ij}^{p,n})\\ (M^{q,1}\otimes M^{q,2}\otimes \dots \otimes M^{q,n})((i_1,i_2,\dots ,i_n),(j_1,j_2,\dots ,j_n))=(a_{ij}^{q,1},a_{ij}^{q,2},\dots ,a_{ij}^{q,n})\end{array}$$ This is equivalent to $$\begin{array}{c}{M}^{p,1}(i_1,j_1)=a_{ij}^{p,1},\\ M^{p,2}(i_2,j_2)=a_{ij}^{p,2},\\ ⋮\\ M^{p,n}(i_n,j_n)=a_{ij}^{p,n},\text{and}\\ M^{q,1}(i_1,j_1)=a_{ij}^{q,1},\\ M^{q,2}(i_2,j_2)=a_{ij}^{q,2},\\ ⋮\\ M^{q,n}(i_n,j_n)=a_{ij}^{q,n},\end{array}$$ for $r,s\in \{1,2,\dots ,n\},r\ne s,$ the squares $M^{p,r}(i_r,j_r)=a_{ij}^{p,r}$ and $M^{q,r}(i_r,j_r)=a_{ij}^{q,r}$ determine $(i_r,j_r)$ uniquely because $M^{p,r}$ and $M^{q,r}$ are orthogonal; and the squares $M^{p,s}(i_s,j_s)=a_{ij}^{p,s}$ and $M^{q,s}(i_s,j_s)=a_{ij}^{q,s}$ determine $(i_s,j_s)$ uniquely because $M^{p,s}$ and $M^{q,s}$ are orthogonal. The desired cell, $((i_1,i_2,\dots ,i_n),(j_1,j_2,\dots ,j_n))$ is therefore determined uniquely. Then, the previous mutually orthogonal k squares of order $\mu$ take the form $L^s=(c_{ij}^s), s\in {\mathbb{Z}}_k$ and $i,j\in {\mathbb{Z}}_{\mu }.$ For given $i,j\in {\mathbb{Z}}_{\mu },$ suppose ${\alpha }_{\lambda },{\beta }_{\lambda }\in {\mathbb{Z}}_{m_{\lambda }}$ $\text{be}$ $\text{defined}$ $\text{by}$ $i=m_n{m}_{n-1}\dots m_2{\alpha }_1+m_n{m}_{n-1}\dots m_3{\alpha }_2+\dots +m_n{\alpha }_{n-1}+{\alpha }_n \text{and}$ $j=m_n{m}_{n-1}\dots m_2{\beta }_1+m_n{m}_{n-1}\dots m_3{\beta }_2+\dots +m_n{\beta }_{n-1}+{\beta }_n.$ Then the entries $c_{ij}^s$ of $L^s$ are as follows, $c_{ij}^s=m_n{m}_{n-1}\dots m_2{a}_{{\alpha }_1,{\beta }_1}^{s,1}+m_n{m}_{n-1}\dots m_3{a}_{{\alpha }_2,{\beta }_2}^{s,2}+\dots +m_n{a}_{{\alpha }_{n-1},{\beta }_{n-1}}^{s,n-1}+a_{{\alpha }_n,{\beta }_n}^{s,n}.$ $$ For $p_{\lambda }\in {\mathbb{Z}}_{m_{\lambda }},$ $s\in {\mathbb{Z}}_k,$ we have $E(G^{p_{\lambda },s} )=\{({({\alpha }_{\lambda })}_0,{({\beta }_{\lambda })}_1):a_{{\alpha }_{\lambda },{\beta }_{\lambda }}^{s,\lambda }=M^{s,\lambda }(({\alpha }_{\lambda },{\beta }_{\lambda }))=p_{\lambda }\},$$$ then we get, $E({\mathbb{G}}^{m_n{m}_{n-1}\dots m_2{p}_1+m_n{m}_{n-1}\dots m_3{p}_2+\dots +m_n{p}_{n-1}+p_n,s})=\{(u_0,v_1)=({(m_n{m}_{n-1}\dots m_2{\alpha }_1+m_n{m}_{n-1}\dots m_3{\alpha }_2+\dots +m_n{\alpha }_{n-1}+{\alpha }_n)}_0,{(m_n{m}_{n-1}\dots m_2{\beta }_1+m_n{m}_{n-1}\dots m_3{\beta }_2+\dots +m_n{\beta }_{n-1}+{\beta }_n)}_1):L^s(u,v)=m_n{m}_{n-1}\dots m_2{p}_1+m_n{m}_{n-1}\dots m_3{p}_2+\dots +m_n{p}_{n-1}+p_n\}.$□

4. Conclusion

We have presented new propositions for constructing the MOGS. The first proposition for constructing the mutually orthogonal disjoint union of graphs squares and the second proposition for the generalization of the Kronecker product of MOGS as a generalization to the MacNeish’s Kronecker product of MOLS. Hence, MOGS can be constructed for new infinite graph classes. In future, we will try to use our results in this paper to construct new types of topological structures.