Zero-divisor graphs of unitary R-modules over commutative rings

Abstract

Let R be a commutative ring with unity $1\ne 0$ and let M be a unitary $R-$module. In this paper, we derive some completeness conditions on the zero divisor graphs of modules over commutative rings. It is shown that the weak zero divisor graph of a simple $R-$module is complete if and only if R is a field. We investigate the zero divisor graphs in finitely generated $R-$modules. We find the diameter, the girth, the clique number and the vertex degrees of the zero-divisor graphs of the rings of integer modulo n as $\mathbb{Z}-$modules.

Keywords:

• Module
• ring
• zero divisor graph of module
• complete graph
• diameter
• clique

AMS SUBJECT CLASSIFICATION:

• 13A99
• 05C12
• 05C25
• 05C78

1. Introduction

A simple graph G consists of a vertex set $V(G)\ne \varnothing$ and an edge set E(G) of unordered pairs of distinct vertices. The cardinality of V(G) is called the order of G and the cardinality of E(G) is its size. A graph G is connected if and only if there exists a path between every pair of vertices u and v. A graph on n vertices such that every pair of distinct vertices is joined by an edge is called a complete graph, denoted by K_n. A complete subgraph of G of largest order is called a maximal clique of G and its order is called the clique number of G, denoted by cl(G). The number of edges incident on a vertex v is called the degree of v and is denoted by d_v or d(v). A vertex of degree 1 is called a pendent vertex. In a connected graph G, the distance between two vertices u and v is the length of the shortest path between u and v. The diameter of a graph G is defined as $\mathit{diam}(G)=\mathit{max}\{(d(u,v)| u,v\in V(G))\},$ where d(u, v) denotes the distance between vertices u and v of G. For more definitions and terminology of graph theory, we refer to [9].

Throughout, R shall denote a commutative ring with unity $1\ne 0.$ Let Z(R) be the set of zero-divisors of R. The concept of the zero-divisor graph of a commutative ring was first introduced by Beck [4]. The zero-divisor graph $\Gamma (R)$ associated to a ring R has its vertices as elements of $Z^{*}(R)=Z(R)\backslash \left\{0\right\}$ and two vertices $x,y\in Z^{*}(R)$ are adjacent if and only if xy = 0.

We denote a unitary $R-$module by M, unless otherwise stated. For an $R-$module M and $x\in M,$ the set $[x:M]=\{r\in R:rM\subseteq Rx\},$ is clearly an ideal of R and an annihilator of the factor module M/Rx. The annihilator of M denoted by ann(M) is $[0:M].$ The concept of the zero-divisor graph has been extended to modules over rings, see for instance, [5, 10, 11]. Further, Ghalandarzadeh and Rad [6] extended the notion of the zero-divisor graph to the torsion graph associated with a module M over a ring R, whose vertices are the non-zero torsion elements of M such that two distinct vertices a and b are adjacent if and only if $(a:M)(b:M)M=0.$ The idea was extended to other graph structures, like the zero-divisor graphs of idealizations with respect to the prime modules [2], the L-total graph of an L-module [1], etc, to mention a few.

For any set X, let $\left|X\right|$ denote the cardinality of X and $X^{*}$ denote the set of the non-zero elements of X. We denote an empty set by $\varnothing$ and the complement of X shall be denoted by X^c. We denote the ring of integers by $\mathbb{Z},$ the ring of integer modulo n by ${\mathbb{Z}}_n$ and the finite field with q elements by ${\mathbb{F}}_q.$ For more definitions and terminology of module and ring theory, we refer to [3, 7].

The rest of the paper is organized as follows. In Section 2, we include some completeness conditions of the zero-divisor graph of the unitary $R-$modules. For instance, it is shown that the zero divisor graph of $M\oplus M$ is complete for every simple module M. In Section 3, we investigate some graph parameters of the zero-divisor graphs of the modules like the diameter, the girth, the clique number and the vertex degrees.

2. Graphs associated with modules over commutative rings

Throughout, we treat M as a unitary $R-$module. Let $N\subseteq M.$ We define the annihilator of N by $(0:N)=\{r\in R|\text{for}\mathrm{ }\text{all} m\in M, rm=0\}.$ For $m\in M,$ we denote the annihilator of the factor module M/Rm by $m_M.$ Thus, $m_M:=\{r\in R|rM\subseteq mR\}.$ Let z be an element in M. The following definition is due to Behboodi [5]. An element $z\in M$ is a

1. weak zero divisor, if either z = 0 or $z_{M}z{\prime }_{M}M=0$ for some $0\ne z\prime \in M$ with $z{\prime }_M\subset R;$

2. zero divisor, if either z = 0 or $0\ne z_M$ and $z_{M}z{\prime }_{M}M=0$ for some $0\ne z\prime \in M$ with $0\ne z{\prime }_M\subset R;$

3. strong zero divisor, if either z = 0 or $(0{:}_{R}M)\subset z_M$ and $z_{M}z{\prime }_{M}M=0$ for some $0\ne z\prime \in M$ with $0\ne z{\prime }_M\subset R.$

For any $R-$module M, we write $Z_w(M),$ Z(M) and $Z_s(M),$ respectively, for the set of non-zero weak zero divisors, non-zero zero divisors and non-zero strong zero divisors. Clearly, $Z_s(M)\subseteq Z(M)\subseteq Z_w(M)$ and all of these sets coincide with the set of zero divisors of R when M = R. Behboodi [5] associated three simple graphs, denoted by ${\Gamma }_w(M), \Gamma (M)$ and ${\Gamma }_s(M),$ called the weak zero-divisor graph, zero-divisor graph and strong zero-divisor graph, to an $R-$module M with vertex sets defined as $Z_w(M),$ Z(M) and $Z_s(M),$ respectively. Two distinct vertices $z_M$ and $z{\prime }_M$ being adjacent if and only if $z_{M}z{\prime }_{M}M=0.$ From the definition, clearly ${\Gamma }_w(M)\subseteq \Gamma (M)\subseteq {\Gamma }_s(M)$ as induced subgraphs.

Behboodi [5] showed that for any $R-$module M, either ${\Gamma }_w(M)=\Gamma (M)$ or $\Gamma (M)={\Gamma }_s(M)$ and also, ${\Gamma }_s(M)$ is always connected with diameter at most 3. Moreover, if ${\Gamma }_s(M)$ is not a tree, then the girth of ${\Gamma }_s(M)$ is at most 4. Further, characterized the $R-$modules M for which ${\Gamma }_w(M)=\Gamma (M)={\Gamma }_s(M)$ and showed that such a property is only enjoyed by the multiplication modules. Whenever, ${\Gamma }_w(M)=\Gamma (M)={\Gamma }_s(M),$ we shall write ${\Gamma }_z(M)$ with vertex set $Z_z(M).$ Behboodi showed that the weak zero-divisor graph of a module M is finite if and only if either M is finite or prime multiplication-like module.

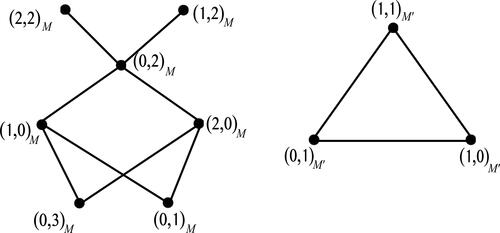
Example 2.1.

Let $R=\mathbb{Z}$ and $M={\mathbb{Z}}_3\times {\mathbb{Z}}_4.$ Then M consists of 12 elements as an $R-$module. As M is a multiplication-like module, we have ${\Gamma }_w(M)=\Gamma (M)={\Gamma }_s(M).$ Also, we have $Z_z(M)=\{{(0,1)}_M,$ ${(0,2)}_M,$ ${(0,3)}_M,$ ${(1,2)}_M,$ ${(2,0)}_M,$ ${(2,2)}_M,$ ${(1,0)}_M\}.$ Further, it can be verified that ${(0,1)}_M=3\mathbb{Z}={(0,3)}_M,{(0,2)}_M=6\mathbb{Z},{(1,2)}_M=2\mathbb{Z}={(2,2)}_M,{(2,0)}_M=4\mathbb{Z}={(1,0)}_M.$ Now, let $M\prime ={\mathbb{Z}}_2\times {\mathbb{Z}}_2.$ Then $Z_s(M\prime )=\varnothing ,Z(M\prime )=Z_w(M\prime )=M\prime -\{(0,0)\}.$ For any $z,z\prime \in M\prime -\{(0,0)\},$ we have $z_{M\prime }z{\prime }_{M\prime }M\prime =0.$ The zero divisor graphs of M and $M\prime$ are given in Figure 1.

Figure 1. ${\Gamma }_z({\mathbb{Z}}_3\times {\mathbb{Z}}_4)$ and ${\Gamma }_w({\mathbb{Z}}_2\times {\mathbb{Z}}_2)=\Gamma ({\mathbb{Z}}_2\times {\mathbb{Z}}_2).$

If X is a subset of a module M over a ring R, then the intersection of all submodules of M containing X is called the submodule generated by X (or spanned by X). If X is finite, and X generates the module M, then M is said to be finitely generated. If $X=\varnothing ,$ then X clearly generates the zero module. If X consists of a single element, say, $X=\left\{a\right\},$ then the submodule generated by X is called the cyclic (sub)module generated by a. Finally, if $\left\{M_i\right|i\in I\}$ is a family of submodules of M, then the submodule generated by $X={\cup }_{i\in I}^{}{M}_i$ is called the sum of the modules M_i. If the index set I is finite, the sum of $M_1,M_2,\dots ,M_n$ is denoted by $M_1+M_2+\dots +M_n.$ A non zero module M is said to be simple if it has no submodules other than (0) and M.

The following theorem provides a condition for the adjacency of two distinct vertices in the zero divisor graph of a finitely generated module.

Theorem 2.2.

Let $M_1,M_2,\dots ,M_k,\dots$ be a sequence of finitely generated simple $R-$modules and let $M=\underset{i\in \mathbb{N}}{\overset{}{\oplus }}{M}_i$. Then $x_M{y}_{M}M=0$ if and only if xR and yR are disjoint $R-$modules.

Proof.

Let $x_M{y}_{M}M=0.$ Assume to the contrary and let $0\ne z\in Rx\cap Ry.$ Then, the submodule generated by z is given as $<z>=M_k\subseteq Rx\cap Ry.$ So there exist subsets ${\mathbb{N}}_1$ and ${\mathbb{N}}_2$ of $\mathbb{N}$ such that $Rx=\underset{i\in {\mathbb{N}}_1}{\oplus }{M}_i$ and $Ry=\underset{j\in {\mathbb{N}}_2}{\oplus }{M}_j.$ Therefore, we can write $M=Rx\oplus (\underset{j\in {\mathbb{N}}_2}{\oplus }{M}_j)=Ry\oplus (\underset{i\in {\mathbb{N}}_1}{\oplus }{M}_i).$ In this notation, we have $$y_M=y_{Ry\oplus \left(\underset{i\in {\mathbb{N}}_1}{\oplus }{M}_i\right)}=\left(0:\underset{i\in {\mathbb{N}}_1}{\oplus }{M}_i^{\prime }\right)=\underset{i\in {\mathbb{N}}_1}{\cap }\left(0:M_i\right) \mathrm{ }\text{and} Rx\cong \underset{i\in {\mathbb{N}}_2^c}{\oplus }{M}_i^{\prime }.$$

Thus, we have $(0:Rx)$ $=(0:x)$ $=(0:\underset{i\in {\mathbb{N}}_2^c}{\oplus }{M}_i)=\underset{i\in {\mathbb{N}}_2^c}{\cap }(0:M_i).$ Since $x_M{y}_{M}M=0,$ we have $y_M\subseteq (0:x).$ This implies that $$\underset{i\in {\mathbb{N}}_1}{\cap }\left(0:M_i\right)\subseteq \left(0:\underset{i\in {\mathbb{N}}_2^c{M}_i}{\oplus }\right).$$

Now, since each $M_t, t\in \mathbb{N}$ is simple and $M_{t_1}\ncong M_{t_2}$ for all $t_1\ne t_2,$ we conclude that $(0:M_{t_1})$ and $\left(0:M_{t_2}\right)$ are coprime. Therefore, we can write (2.1) $$\underset{i\in {\mathbb{N}}_1}{\cap }\left(0:M_i\right)=\underset{i\in {\mathbb{N}}_1}{\otimes }\left(0:M_i\right)\subseteq \underset{i\in {\mathbb{N}}_2^c}{\cap }\left(0:M_i\right)\subseteq \left(0:M_t\right)\text{for}\mathrm{ }\text{all}\mathrm{ }t\in {\mathbb{N}}_2^c.$$(2.1)

This implies that for every $p\in {\mathbb{N}}_2^c,$ there exists $q\in {\mathbb{N}}_1$ such that $(0:M_q)\subseteq (0:M_p).$ Therefore, $(0:M_q)=(0:M_p)$ and so M_q = M_p. Finally, $M_k\subseteq Rx=\underset{i\in {\mathbb{N}}_2^c}{\oplus }.$ So there exists $s\in {\mathbb{N}}_2^c$ such that M_k = M_s. As in Equation (2.1)(2.1) $$\underset{i\in {\mathbb{N}}_1}{\cap }\left(0:M_i\right)=\underset{i\in {\mathbb{N}}_1}{\otimes }\left(0:M_i\right)\subseteq \underset{i\in {\mathbb{N}}_2^c}{\cap }\left(0:M_i\right)\subseteq \left(0:M_t\right)\text{for}\mathrm{ }\text{all}\mathrm{ }t\in {\mathbb{N}}_2^c.$$(2.1) , there exists $t\prime \in {\mathbb{N}}_2^c$ such that $M_k=M_s=M_t^{\prime }.$ Thus, $M_k\subseteq Ry\cap (\underset{i\in {\mathbb{N}}_1}{\oplus }{M}_i)=(0).$ This implies that z = 0, which is contradicts the hypothesis. On the other hand, since $x_M{y}_{M}M\subseteq Rx\cap Ry,$ we conclude that $Rx\cap Ry=(0),$ which implies that $x_M{y}_{M}M=0.$ □

The following lemma will be used in the sequel.

Lemma 2.3.

[Proposition 5.3.4, [8]] An $R-$module M is simple if and only if $M\cong R/\mathfrak{a}$ for some maximal ideal $\mathfrak{a}$ in R.

An $R-$module M is said to be decomposable if there exist two non-zero submodules M₁ and M₂ such that $M=M_1\oplus M_2$ and indecomposable if it is not a direct sum of two non-zero submodules. The following theorem shows that the zero divisor graph of a simple R-module is complete.

Theorem 2.4.

If M is a simple $R-$module, then ${\Gamma }_w(M\oplus M)$ is complete.

Proof.

Let M be a simple $R-$module, and let $\mathcal{M}=M\oplus M.$ By definition, ${(0,m)}_{\mathcal{M}}=(0:M)$ for every $0\ne m\in M.$ Therefore, for each $(m\prime ,m″)\in \mathcal{M},$ we have ${(m\prime ,m″)}_{\mathcal{M}}{(0,m)}_{\mathcal{M}}\mathcal{M}=0.$ Similarly, ${(m\prime ,m″)}_{\mathcal{M}}{(m,0)}_{\mathcal{M}}\mathcal{M}=0.$ Now, for each $m_1,m_2\in M-\left\{0\right\},$ we have $(0:m_1)=(0:m_2)=(0:M).$ By Lemma 2.3, we see that $(0:M)$ is a maximal ideal of R, which is contained in ${(m_1,m_2)}_{\mathcal{M}}.$ Now, if ${(m_1,m_2)}_{\mathcal{M}}\subseteq (0:M),$ we are done. Otherwise, $1\in {(m_1,m_2)}_{\mathcal{M}},$ which gives $(m_1,0)1\in (m_1,m_2)R.$ Therefore, there exists $r\in R$ such that $m_1=m_{1}r$ and $m_{2}r=0.$ Thus, $r\in (0:m_2)=(0:m_1),$ which implies that $m_{1}r=0.$ Therefore $m_1=0,$ a contradiction. Thus we have $(0:M)={(m_1,m_2)}_{\mathcal{M}},$ and so ${\Gamma }_w(M)$ is complete. □

Let $R=\mathbb{Z}$ and $M={\mathbb{Z}}_p\times {\mathbb{Z}}_p\times \cdots \times {\mathbb{Z}}_p$ ($n-$copies of ${\mathbb{Z}}_p$). Then $(z_1,z_2,$ $\dots ,z_n{)}_M$ $=p\mathbb{Z}$ if some z_i = 0 and some $z_j\ne 0$ for some $1\le i\ne j\le n$ and ${(1,1,\dots ,1)}_M=\mathbb{Z}.$ Thus, the strong zero divisor graph of M is empty and that $\Gamma (M)={\Gamma }_w(M)\cong K_{p^n-1}.$

As seen above, ${\Gamma }_w({\mathbb{Z}}_p\times {\mathbb{Z}}_p)$ is complete when $M={\mathbb{Z}}_p\times {\mathbb{Z}}_p$ is considered as a $\mathbb{Z}-$module. However, the same does not hold true in general for all non-simple modules M when the ring R is chosen arbitrarily. The following theorem restricts the choice for the ring R for a module M to have a complete zero divisor graph.

Theorem 2.5.

Let M be an $R-$module which is not simple. Then ${\Gamma }_w(M)$ is complete if and only if R is a field.

Proof.

As M is not simple, there exists an $R-$submodule $M\prime$ such that $(0)⊊M\prime ⊊M.$ Let $0\ne y\in x_M$ for some $x\in M.$ Then $yM\subseteq xR.$ This implies that $M\subseteq y^{-1}xR\subseteq xR,$ which is a contradiction. Therefore, $x_M=0.$ Thus, for all $x,y\in M-\left\{0\right\},$ we have $x_M{y}_{M}M=0.$ Conversely. assume that $x_M{y}_{M}M=0$ for all $x_M,y_M\in Z_w(M).$ Let N be a proper ideal of R. Consider $M=\frac{R}{N}\oplus R$ and let $m=({\widehat{r}}_1,r_1), m\prime =({\widehat{r}}_1^{\prime },r_1^{\prime }),$ where ${\widehat{r}}_1,{\widehat{r}}_1^{\prime }\in \frac{R}{N}$ and $r_1,r_1^{\prime }\in R.$ Choose $r\in R-\{0,1\}.$ As $N\subset R,$ we have ${(0,r)}_M\supseteq \mathit{NrR}.$ Because ${(0,r_1)}_M{(0,r_1^{\prime })}_{M}M=0$ for every $r_1,r_1^{\prime }\in R,$ we have rN = 0 for every $r\in R-\{0,1\}.$ This also implies that $(1-r)N=0$ and hence $N=rN=(0).$ □

Let M be a $\mathbb{Z}$module. Let z be a non-zero weak zero divisor in M. Then $z_M=n\mathbb{Z}$ for some $n\in \mathbb{N}.$ It is trivial to see that $|n\mathbb{Z}\cap m\mathbb{Z}|\ge 2$ for all $m\in \mathbb{N}.$ Also, $Z_w(M)=\left\{0\right\}$ if and only if M is a simple $\mathbb{Z}-$module. Since every finite module M is a finite abelian group, so we have the following proposition.

Proposition 2.6.

A vertex in a weak zero divisor graph of a finite $\mathbb{Z}-$module M represents an essential ideal if and only if M is a non-simple finite group.

Let $M={\mathbb{Z}}^{\times n}$ ($n-$ copies of $\mathbb{Z}$) be a $\mathbb{Z}-$module. Then it is easy to see that each non-zero element of M is a weak zero divisor and that for all $z,z\prime \in Z_w(M),$ we have $z_{M}z{\prime }_{M}M=0.$ Therefore, ${\Gamma }_w(M)=K_{\left|M\right|-1}.$ Now, the submodules generated by the non-zero weak zero divisors of M are the lines with integral coordinates in the hyperplane ${\mathbb{R}}^{\times n}$ intersecting at the origin only. It follows that for every non-zero weak zero divisor m of M the ideal $\{z\in Z|zM\subseteq mZ\}$ is not an essential ideal. This shows that Proposition 2.6 is not true for infinite modules.

Theorem 2.7.

Let R be an integral domain and M an $R-$module. If there exists an element $m\in M$ such that $(0:m)=0$, then ${\Gamma }_w(M\oplus R)$ is complete.

Proof.

Choose $0\ne r\in R$ and $m\in M.$ Let $z\in {(r,m)}_M.$ Then $(0,m)z=(r,m)r\prime$ for some $r\prime \in R.$ This gives $r\prime r=0,$ which implies that $r\prime =0,$ since R is a domain. This further implies that z = 0 because $mz=r\prime r$ and $(0:m)=0.$ Therefore, for each $0\ne r\in R$ and $m\in M,$ we have ${(r,m)}_M=0.$ Further, let $0\ne m\prime \in M$ and choose $z\prime \in {(0,m\prime )}_M.$ Then $(1,0)z\prime =(0,m\prime )r″$ for some $r″\in R.$ This gives $z\prime =0$ and so ${(0,m\prime )}_M=0.$ Therefore, ${\Gamma }_w(M\oplus R)$ is complete. □

Definition 2.8.

Let R be a ring and M be an $R-$module. If for every non-zero submodule N of M and an ideal A of R with NA = 0 implies MA = 0, we say that M is a prime module. This is equivalent to saying that $(0:M)=(0:N)$ for every non-zero submodule N of M. It is immediate that $(0:M)$ is a prime ideal, and it is called the affiliated prime of M. Also, if each submodule of M is of the form AM for some ideal A of R, then we say that M is a multiplication module. Moreover, if a multiplication module M satisfies $(0:M)\subset (0:M/N)$ for every non-zero submodule N of M, then M is called a multiplication-like module.

Theorem 2.9.

Let M be a multiplication module over a ring R. Then the zero divisor graph of M is empty if and only if M is a prime multiplication-like module.

Proof.

Since every multiplication module is a multiplication-like module, therefore it suffices to prove the result for multiplication-like modules. Assume that M is not a prime multiplication-like module. We will show that ${\Gamma }_w(M)$ is non-empty. As M is not a prime multiplication-like module, we have $(0:M)$ is not a prime ideal. Thus, there exist ideals $\mathfrak{a}$ and $\mathfrak{b}$ which properly contain $(0:M)$ and satisfy $\mathfrak{a}M\ne 0,\mathfrak{b}M\ne 0$ and $\mathfrak{a}\mathfrak{b}M=0.$ Thus, we can find $0\ne a\in \mathfrak{a}M$ and $0\ne b\in \mathfrak{b}M$ such that $a_M\subseteq aR\subseteq \mathfrak{a}M$ and $b_M\subseteq bR\subseteq \mathfrak{b}M.$ Then, we have $a_M{b}_M\subseteq \mathfrak{a}\mathfrak{b}M=0.$ Therefore, $\Gamma (M)\ne 0.$

On the other hand, if M is a prime multiplication-like module, then $(0:M)\subseteq m_M$ for every non-zero $m\in M,$ that is, for each non-zero $m\prime ,m″\in M,$ we have $m{\prime }_{M}m\prime {\prime }_{M}M\ne 0.$ Therefore, ${\Gamma }_w(M)=\varphi .$ □

3. Graph parameters of zero divisor graphs of modules

In the following theorem, we compute the clique number of the zero divisor graph of a multiplication module. Noting that the weak zero divisor graph, the zero divisor graph and the strong zero divisor graph all coincide in case of multiplication-like modules, we write ${\Gamma }_z(M)$ to denote the zero divisor graph of such modules.

Theorem 3.1.

Let M be an $R-$module, where $R=\mathbb{Z}$ and $M={\mathbb{Z}}_{p^t}$ for $t\in \mathbb{N}$ and a prime p. Then the clique number of ${\Gamma }_z(M)$ is equal to $p^{\frac{t}{2}}-1$ or $p^{\frac{t-1}{2}}$ according as t is even or odd.

Proof.

It follows immediately that every vertex of ${\Gamma }_z(M)$ is of the form rp for some $r\in R.$ We divide the vertex set of ${\Gamma }_z(M)$ into disjoint subsets ${\mathrm{Z}}_1,{\mathrm{Z}}_2,\dots ,{\mathrm{Z}}_{t-1},$ where ${\mathrm{Z}}_k=\left\{r{p}^k\right|p\nmid r\}.$ It is not difficult to see that the cardinality of ${\mathrm{Z}}_k$ as a subset of $V({\Gamma }_z(M))$ is equal to $(p-1)p^{n-k-1}, 1\le k\le t-1.$ Let $u=r{p}^{k_1}$ and $u\prime =r\prime p^{k_2}$ be two vertices of ${\Gamma }_z(M).$ Then $u_{M}u{\prime }_{M}M=0$ if and only if $k_1+k_2\ge n.$ Thus, for all $v,v\prime \in M_s,$ we have $v_{M}v{\prime }_{M}M=0$ for all integers $s\ge \lceil \frac{t}{2}\rceil .$ Now, assume that t is even. Then $w_{M}w{\prime }_{M}M\ne 0$ for all $w\in {\mathrm{Z}}_s^{\prime } ,1\le s\prime \le \frac{t}{2}$ and $w\prime \in {\mathrm{Z}}_{\frac{t}{2}}.$ Also, when t is odd, no two vertices are adjacent inside ${\mathrm{Z}}_{\left[\frac{t}{2}\right]}$ and every vertex of ${\mathrm{Z}}_{\left[\frac{t}{2}\right]}$ is adjacent to every vertex of ${\mathrm{Z}}_{\lceil \frac{t}{2}\rceil }.$ Therefore, it follows that $cl({\Gamma }_z(M))=p^{[\frac{t}{2}]}-1,$ when t is even and is equal to $p^{[\frac{t}{2}]},$ when t is odd. □

The girth of a graph G is defined as the length (or order) of the smallest cycle contained in G, and is denoted by gr(G). If G has no cycle, then $gr(G)=\infty .$ The following theorem characterizes the diameter, the smallest ($d_{\delta }$) and the largest ($d_{\Delta }$) vertex degree and the girth of the zero divisor graph of a $\mathbb{Z}-$module M.

Theorem 3.2.

Let p be a prime integer and $t\in \mathbb{N}-\left\{1\right\}$. Then for an $R-$module M, where $R=\mathbb{Z}$ and $M={\mathbb{Z}}_{p^t}$, the following statements hold, unless $t=p=2.$

1. $\mathit{diam}({\Gamma }_z(M)=2$

2. $d_{\delta }({\Gamma }_z(M)=1$ and $d_{\Delta }({\Gamma }_z(M)=p^{t-1}-2.$

3. $gr({\Gamma }_z(M)=\infty$ if and only if t = 4, 8, 9, otherwise $gr({\Gamma }_z(M)=3.$

Proof.

As in the proof of Theorem 3.1, we define ${\mathrm{Z}}_k=\left\{r{p}^k\right|p\nmid r\}.$ Then ${\mathrm{Z}}_1,{\mathrm{Z}}_2,\dots ,{\mathrm{Z}}_{t-1}$ gives a partition of the vertex set of ${\Gamma }_z(M)$ and ${\mathrm{Z}}_k=(p-1)p^{t-k-1}, 1\le k\le t-1.$ Now, two elements $m=r_1{p}^k$ and $m\prime =r_2{p}^l$ of M satisfy $m_{M}m{\prime }_{M}M=0$ if and only if $k+l\ge t.$ Therefore, it follows instantly that every vertex $u\in V({\Gamma }_z(M))$ is adjacent to every vertex contained in ${\mathrm{Z}}_{t-1}.$ Thus, $\mathit{diam}({\Gamma }_z(M))=2.$ Further, let $n\in {\mathrm{Z}}_1$ and choose $n\prime \in V({\Gamma }_z(M)).$ Then $n_{M}n{\prime }_{M}M=0$ if and only if $n\prime \in {\mathrm{Z}}_{t-1}.$ Thus, it follows that $\delta ({\Gamma }_z(M))=p-1$ and that $\Delta ({\Gamma }_z(M))=p^{t-1}-2.$ This proves (1) and (2).

(3) From the previous paragraph, we see that for all $a\in {\mathrm{Z}}_{t-1},d(a,b)=1$ for all vertices $b\ne a$ of ${\Gamma }_z(M).$ Also, if $c\in {\mathrm{Z}}_1,$ then $d(c,e)=1$ only if $e\in {\mathrm{Z}}_{t-1}.$ Thus, the set of elements in ${\mathrm{Z}}_{t-1}$ form the center of ${\Gamma }_z(M).$ Now, assume that ${\Gamma }_z(M)$ is a tree. Then ${\Gamma }_z(M)$ has either one or two centres. Therefore, $\left|{\mathrm{Z}}_{t-1}\right|$ must be either 1 or 2, so that $p=$ 2 or 3. Now, either $z_1{p}^2-3z_2{p}^2-z_3{p}^3-z_1{p}^2$ or $z{\prime }_2{p}^2-z{\prime }_{1}p-2z{\prime }_3{p}^2-z{\prime }_{1}p$ form a triangle in ${\Gamma }_z(M)$ for all $z_1,z_2,z_3,z{\prime }_1,z{\prime }_2,z{\prime }_3\in R$ and $p^t\notin \{4,8,9\}.$ Therefore, the result follows. □

Corollary 3.3.

$gr({\Gamma }_z(M)=\infty$ if and only if ${\Gamma }_z(M)$ is a star graph, where $M={\mathbb{Z}}_{p^t}, t\in \mathbb{N}$, is considered a $\mathbb{Z}-$module.

Let $M={\mathbb{Z}}_p\times {\mathbb{Z}}_q,$ where p and q are distinct primes, be a $\mathbb{Z}-$module. Then, it can be easily verified that ${(z_1,z_2)}_M=p\mathbb{Z},$ if $z_1=0\ne z_2;$ ${(z_1,z_2)}_M=q\mathbb{Z},$ if $z_2=0\ne z_1,$ and ${(z_1,z_2)}_M=\mathbb{Z},$ if $z_1\ne 0\ne z_2.$ Thus, ${\Gamma }_z(M)$ is complete bipartite. While one expects that if $p_1,p_2,\dots ,p_t,t\ge 3,$ are distinct primes, and $M={\mathbb{Z}}_{p_1}\times {\mathbb{Z}}_{p_2}\times \cdots \times {\mathbb{Z}}_{p_t}$ then ${\Gamma }_z(M)$ is complete $t-$ partite, but this is not a case. However, ${\Gamma }_z(M)$ contains the so expected $t-$ partite graph as a subgraph as can be seen in ${\Gamma }_z({\mathbb{Z}}_2\times {\mathbb{Z}}_3\times {\mathbb{Z}}_5)$ in which, ${(0,1,1)}_M={(0,1,2)}_M={(0,1,3)}_M={(0,1,4)}_M={(0,2,1)}_M={(0,2,2)}_M={(0,2,3)}_M={(0,2,4)}_M=2\mathbb{Z},{(1,0,1)}_M={(1,0,2)}_M={(1,0,3)}_M={(1,0,4)}_M=3\mathbb{Z},{(1,1,0)}_M={(1,2,0)}_M=5\mathbb{Z},{(0,0,1)}_M={(0,0,2)}_M={(0,0,3)}_M={(0,0,4)}_M=6\mathbb{Z},{(0,1,0)}_M={(0,2,0)}_M$ = $10\mathbb{Z}$ and ${(1,0,0)}_M=15\mathbb{Z},$ so that $\mathrm{deg}({(0,1,1)}_M)=1,\mathrm{deg}({(1,0,1)}_M)=2,\mathrm{deg}({(1,1,0)}_M)=4,\mathrm{deg}({(0,0,1)}_M)=5$ $\mathrm{deg}({(0,1,0)}_M)=9,\mathrm{deg}({(1,0,0)}_M)=14,$ thus containing six different vertex degrees. However, a complete $t-$ partite graph can possess at most t distinct vertex degrees. Therefore, ${\Gamma }_z({\mathbb{Z}}_2\times {\mathbb{Z}}_3\times {\mathbb{Z}}_5)$ is not complete $t-$ partite, but we see that the subsets ${\mathrm{V}}_1=\{{(0,0,1)}_M,$ ${(0,0,2)}_M,$ ${(0,0,3)}_M,$ ${(0,0,4)}_M\},{\mathrm{V}}_2=\{{(0,1,0)}_M,{(0,2,0)}_M\}$ and ${\mathrm{V}}_3=\left\{{(1,0,0)}_M\right\}$ of the vertex set of ${\Gamma }_z({\mathbb{Z}}_2\times {\mathbb{Z}}_3\times {\mathbb{Z}}_5)$ induce a complete $3-$ partite subgraph.

If p, q, r are distinct primes and $M={\mathbb{Z}}_p\times {\mathbb{Z}}_q\times {\mathbb{Z}}_r$ be a $\mathbb{Z}-$module, then it is always possible to partition the vertex of ${\Gamma }_z(M)$ into six disjoint sets, say, ${\mathrm{V}}_i, 1\le i\le 6,$ where ${\mathrm{V}}_i^{\prime }s$ are defined in the following way. Let $u_p,u_q,u_r$ denote the arbitrary non-zero elements in ${\mathbb{Z}}_p,{\mathbb{Z}}_q$ and ${\mathbb{Z}}_r,$ respectively. Then ${\mathrm{V}}_1=\left\{{(u_p,0,0)}_M\right\},{\mathrm{V}}_2=\left\{{(0,u_q,0)}_M\right\},{\mathrm{V}}_3=\left\{{(0,0,u_r)}_M\right\},{\mathrm{V}}_4=\left\{{(u_p,u_q,0)}_M\right\},{\mathrm{V}}_5=\left\{{(u_p,0,u_r)}_M\right\}$ and ${\mathrm{V}}_6=\left\{{(0,u_q,u_r)}_M\right\}.$ Let $x^{(i)}\in {\mathrm{V}}_i.$ Then it is an easy exercise to verify that $x_M^{(1)}=qr\mathbb{Z},x_M^{(2)}=pr\mathbb{Z},x_M^{(3)}=pq\mathbb{Z},x_M^{(4)}=r\mathbb{Z},x_M^{(5)}=q\mathbb{Z}$ and $x_M^{(6)}=p\mathbb{Z}.$ Thus, it can be easily seen that $\mathrm{deg}(x_M^{(i)}),$ for $1\le i\le 6$ is an element of the ordered set $\{p-1,q-1,r-1,pq-1,pr-1,qr-1\}.$ Moreover, the clique number of ${\Gamma }_z(M)$ is 3 and the sets ${\mathrm{V}}_4,{\mathrm{V}}_5$ and ${\mathrm{V}}_6$ induce a complete $3-$ partite subgraph. In fact, this can be generalized to the following theorem.

Theorem 3.4.

Let M be an $R-$module, where $M={\mathbb{Z}}_{p_1}\times {\mathbb{Z}}_{p_2}\times \cdots {\mathbb{Z}}_{p_t}$ and $R=\mathbb{Z},$ then

1. $cl({\Gamma }_z(M))=3.$

2. $\mathrm{deg}({(x_1,x_2,\dots ,x_t)}_M)=\frac{p_1{p}_2\dots p_t}{\Pi p_i}-1,$ where i runs over the indices of $x_i^{\prime }s$ in ${(x_1,x_2,\dots ,x_t)}_M$ which are equal to 0.

3. The set of vertices ${\mathrm{V}}_i=\left\{{(x_1,x_2,\dots ,x_{i-1},0,x_{i+1},\dots ,x_t)}_M\right|x_i\in {\mathbb{Z}}_{p_i}\}$ induces a complete $t-$ partite subgraph in ${\Gamma }_z(M).$

Theorem 3.5.

Let M and N be two $R-$modules such that the sum of their annihilators equals R. Then the following statements hold.

1. If ${\Gamma }_w(M)={\Gamma }_w(N)=\varnothing ,$ then $cl(\Gamma (M\oplus N))=2.$

2. If ${\Gamma }_w(M)=\varnothing$ and ${\Gamma }_w(N)\ne \varnothing ,$ then $cl({\Gamma }_w(M\oplus N))=cl({\Gamma }_w(N))+1.$

3. If ${\Gamma }_w(M)\ne \varnothing$ and ${\Gamma }_w(N)\ne \varnothing ,$ then $cl({\Gamma }_w(M\oplus N))$ $=cl({\Gamma }_w(M))$ $+cl(\Gamma (N))$ $+{\eta }_1{\eta }_2,$ where ${\eta }_1,{\eta }_2$ denotes the number of elements η in cliques of ${\Gamma }_w(M)$ and ${\Gamma }_w(N),$ respectively, whose square is 0.

Proof.

For any $R-$module M, let $Z_w(M)$ and $Z_w^{*}(M)$ denote the set of weak zero divisors and non-zero weak zero divisors of M. Let M and N be two $R-$modules, $m_1,m_2\in M$ and $n_1,n_2\in N$ and $M\oplus N=\mathcal{M}.$

1. Assume that $Z_w(M)=Z_w(N)=\left\{0\right\}.$ Then for each $m_1,m_2\in M$ and $n_1,n_2\in N,$ we have ${(m_1,0)}_{\mathcal{M}}{(m_2,0)}_{\mathcal{M}}\mathcal{M}\ne 0,{(0,n_1)}_{\mathcal{M}}{(0,n_2)}_{\mathcal{M}}\mathcal{M}\ne 0$ and ${(m_1,0)}_{\mathcal{M}}{(0,n_1)}_{\mathcal{M}}\mathcal{M}=0.$ Thus, $cl(\Gamma (M\oplus N))=2.$

2. As ${\Gamma }_w(N)\ne \varnothing ,$ we have $Z_w(N)\ne (0).$ Let $\mathrm{K}=\{k_1,k_2,\dots ,k_t\}$ be an induced maximal clique in ${\Gamma }_w(N).$ Then, for each $n\in Z_w^{*}(N)-\mathrm{K},$ there exists some $k_i\in \mathrm{K}$ such that $n_N{k}_i{}_{N}N\ne 0.$ Now, for each $(m,0),(0,n)\in M\oplus N,$ we have ${(m,0)}_{\mathcal{M}}{(0,n)}_{\mathcal{M}}\mathcal{M}=0$ and for all $m\prime \in M-\left\{0\right\}$ and $n\prime \in N,$ we have ${(m\prime ,0)}_{\mathcal{M}}{(m\prime ,n\prime )}_{\mathcal{M}}\mathcal{M}\ne 0.$ Thus, the vertices of the form $(m,0)$ contribute 1 to the clique number and the fact that ${\Gamma }_w(M)=\varnothing ,$ we conclude that $cl({\Gamma }_w(M\oplus N))=1+cl({\Gamma }_w(N)).$

3. Let $Z_w(M)\ne \left\{0\right\}$ and $Z_w(N)\ne \left\{0\right\}.$ Let ${\mathrm{K}}_M=\{k_1,k_2,\dots ,k_{t_1}\}$ and ${\mathrm{K}}_N=$ $\{l_1,$ $l_2,$ $\dots ,$ $l_{t_2}\}$ be the induced maximal complete subgraphs of ${\Gamma }_w(M)$ and ${\Gamma }_w(N).$ Then, for each $m\in Z_w^{*}(M)-{\mathrm{K}}_M$ and $n\in Z_w^{*}(N)-{\mathrm{K}}_N,$ we can find $k_i\in {\mathrm{K}}_M, 1\le i\le t_1$ and $k_j\in {\mathrm{K}}_N, 1\le j\le t_2$ which satisfy $(m,0)(k_i,0)M\ne 0$ and ${(0,n)}_{\mathcal{M}}{(0,k_j)}_{\mathcal{M}}\mathcal{M}\ne 0.$ Also, for every $m_1\in M-\left\{0\right\}$ and $n_1\in N-\left\{0\right\},$ there exist no $m_1^{\prime }\in M-Z_w^{*}(M)$ and $n_1^{\prime }\in N-Z_w^{*}(N)$ for which ${(m_1,n_1)}_{\mathcal{M}}{(m_1^{\prime },n_1^{\prime })}_{\mathcal{M}}\mathcal{M}=0$ holds true. Even if m₁ (or equivalently $m_1^{\prime }$) is chosen from M, then a similar statement holds true if $n_{1_N}{n}_{1_N}N\ne 0$ (or equivalently $n{\prime }_{1_N}n{\prime }_{1_N}N\ne 0$). A similar argument is valid for $n_1,n_1^{\prime }$ if chosen from N. Thus, such vertices do not contribute to the clique number. Now, for all $m\prime \in M$ and $n\prime \in N,$ we have ${(m\prime ,0)}_{\mathcal{M}}{(0,n\prime )}_{\mathcal{M}}\mathcal{M}=0,$ but however such a vertex, say $(m″,0),$ contributes to the clique if and only if $m″\in {\mathrm{K}}_M$ and $m\prime {\prime }_{M}m\prime {\prime }_{M}M=0.$ This argument adds each vertex $k\in {\mathrm{K}}_M$ and $k\prime \in {\mathrm{K}}_N$ which satisfy $k_M{k}_{M}M=0$ and $k{\prime }_{N}k{\prime }_{N}N=0$ to the clique. Therefore, the clique number of ${\Gamma }_w(M\oplus N)$ is equal to $cl({\Gamma }_w(M))+cl({\Gamma }_w(N))+{\eta }_1{\eta }_2,$ where η₁ and η₂ are the number of vertices $k^{(1)}\in {\mathrm{K}}_M$ and $k^{(2)}\in {\mathrm{K}}_N,$ respectively, which satisfy $k_M^{(1)}{k}_M^{(1)}M=0$ and $k_N^{(2)}{k}_N^{(2)}N=0$ □

Theorem 3.6.

Let R be a finite integral domain and M be an $R-$module which is not simple. Then $cl({\Gamma }_w(M))=\left|M\right|-1.$

Proof.

The proof follows by Theorem 2.5. □

Theorem 3.7.

Let $M={\mathbb{Z}}_{p_1^{a_1}{p}_2^{a_2}\dots p_t^{a_t}}$ be a $\mathbb{Z}-$module, where $p_1,p_2,\dots ,p_t$ are distinct primes. Then the clique number of ${\Gamma }_z(M)$ is equal to t, if $a_1=a_2=\cdots =a_t=1$. In case $a_i=2b_i$, then the clique number of ${\Gamma }_z(M)$ is $p_1^{b_1}{p}_2^{b_2}\dots p_t^{b_t}-1.$

Proof.

Let $n=p_1{p}_2\dots p_t.$ Define $n_i=\frac{n}{p_i}, 1\le i\le t,$ and choose $z_i\in \mathbb{Z}{n}_i.$ Then $z_{i}M{z}_{j}MM=0$ for all $i\ne j.$ Therefore, contains a clique of order t. Moreover, if $m\in \mathbb{Z}{n}_i{n}_j,$ then $x_{i}M{m}_{M}M\ne 0$ for all $x_i\in M.$ Hence, $cl({\Gamma }_z(M))=t.$ Now, let $m=p_1^{b_1}{p}_2^{b_2}\dots p_t^{b_t}.$ Then $m\in M$ and we have $m_M{m}_{M}M=0.$ Consider the submodules $\mathbb{Z}m,\mathbb{Z}2m,\dots ,\mathbb{Z}(m-1)m,$ then we have $z_{i}M{z}_{j}MM=0$ for all $z_i\in {\mathbb{Z}}_i$ and $z_j\in {\mathbb{Z}}_j,$ where $i,j=\{m,2m,\dots ,(m-1)m\}.$ Moreover, let $\mathbb{Z}k$ be a submodule of M, where $k\notin \{m,2m,\dots ,(m-1)m\}.$ Then k is of the form $p_1^{c_1}{p}_2^{c_2}\dots p_t^{c_t},$ where some c_i < b_i. Without loss of generality, let $c_1<b_1$ and let $z\in \mathbb{Z}k,$ then we get $z_{M}z{\prime }_{M}M\ne 0$ where $z\prime$ is an element of $\mathbb{Z}m.$ Therefore, the clique number is equal to $p_1^{b_1}{p}_2^{b_2}\dots p_t^{b_t}-1.$ □

Data availibility

Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.

Acknowledgments

We are grateful to the anonymous referee for his useful suggestions.

Additional information

Funding

The research of S. Pirzada is supported by the SERB-DST research project number CRG/2020/000109.