Quasi-total Roman bondage number in graphs

Abstract

A quasi-total Roman dominating function (QTRD-function) on $G=(V,E)$ is a function $f:V\to \{0,1,2\}$ such that (i) every vertex x for which f(x) = 0 is adjacent to at least one vertex v for which f(v) = 2, and (ii) if x is an isolated vertex in the subgraph induced by the set of vertices with non-zero values, then f(x) = 1. The weight of a QTRD-function is the sum of its function values over the whole set of vertices, and the quasi-total Roman domination number is the minimum weight of a QTRD-function on G. The quasi-total Roman bondage number ${\mathrm{b}}_{\mathit{qtR}}(G)$ of a graph G is the minimum number of edges that have to be deleted to G in order to increase the quasi-total Roman domination number. In this paper, we start the study of quasi-total Roman bondage in graphs. We first show that the decision problem associated with the quasi-total Roman bondage problem is NP-hard even when restricted to bipartite graphs. Then basic properties of the quasi-total Roman bondage number are provided. Finally, some sharp bounds for ${\mathrm{b}}_{\mathit{qtR}}(G)$ are also presented.

Keywords:

• Quasi-total Roman domination number
• quasi-total Roman bondage number
• complexity

MATHEMATICS SUBJECT CLASSIFICATION 2020:

• 05C05
• 05C69

1. Introduction

In this paper, G is a simple and connected graph with vertex set V(G) and edge set E(G) (briefly V and E). Two vertices are neighbors inG if they are adjacent. The open neighborhood of a vertex v is the set $N_G(v)=N(v)=\{u\in V(G)|uv\in E(G)\}$ while its closed neighborhood is the set $N_G[v]=N[v]=N(v)\cup \left\{v\right\}.$ Similarly, the open neighborhood of a set $S\subseteq V$ is the set $N(S)={\cup }_{v\in S}N(v)$ and the closed neighborhood of S is $N[S]=N(S)\cup S.$ The degree of a vertex $v\in V$ is ${\mathrm{deg}}_G(v)=|N(v)|.$ The minimum degree and the maximum degree of a graph G are denoted by $\delta =\delta (G)$ and $\Delta =\Delta (G),$ respectively. A leaf of G is a vertex of degree one, while a support vertex of G is a vertex adjacent to a leaf. A star of order $n\ge 2$ is the complete bipartite graph $K_{1,n-1}.$ We write P_n, C_n and K_n for the path, cycle and complete graph of order n, respectively. A tree T is a double star if it contains exactly two vertices that are not leaves. A double star with respectively p and q leaves attached at each support vertex is denoted by $D{S}_{p,q}.$ The complement of a graph G is the graph $\overline{G},$ where $V(\overline{G})=V(G)$ and $uv\in E(\overline{G})$ if and only if $uv\notin E(G).$

Let $v\in S\subseteq V.$ Vertex u is called a private neighbour of v with respect to S (denoted by u is an S-pn of v) if $u\in N[v]-N[S-\{v\}].$ An S-pn of v is external if it is a vertex of V – S. The set epn$(v;S)=N(v)-N[S-\{v\}]$ of all external S-pn’s of v is called the external private neighbourhood set of v with respect to S.

A set $S\subseteq V(G)$ is a (total) dominating set if every vertex in $V(G)-S(V(G))$ has at least one neighbor in S. The (total) domination number $\gamma (G)$ (${\gamma }_t(G)$) of a graph G is the minimum cardinality of a (total) dominating set of G. In 1990, Fink et al. [10] introduced the bondage number b(G) to measure the vulnerability or the stability of the domination in an interconnection network G under edge failure. They defined it as the minimum number of edges whose removal from G increases thedomination number. An edge set B for which $\gamma (G-B)>\gamma (G)$ is called a bondage set. A b(G)-set is a bondage set of G of size b(G). The concept of total bondage number $b_t(G)$ of a graph G investigated in [14] as follows. If there exists $E\prime \subseteq E(G)$ such that (i) there is no isolated vertex in $G-E\prime$ and (ii) ${\gamma }_t(G-E)>{\gamma }_t(G),$ then the edge set $E\prime$ is called a total bondage set for G. If there is at least one total bondage set for G, we define $b_t(G)=\min \left\{\right|E\prime |:E\prime \text{is a total bondage set of}G\}.$ Otherwise we put $b_t(G)=\infty .$ A $b_t(G)$-set is a total bondage set of G of size $b_t(G).$

A function $f:V(G)\to \{0,1,2\}$ is a Roman dominating function (RDF) on G if every vertex $u\in V$ for which f(u) = 0 is adjacent to at least one vertex v for which f(v) = 2. The weight of an RDF f is the value $f(V(G))=\sum _{u\in V(G)}f(u),$ and the Roman domination number ${\gamma }_R(G)$ is the minimum weight of an RDF on G. The concept of Roman domination is now well-studied in graph theory since its introduction in 2004 by Cockayne et al. [9]. The literature on Roman domination and its variations has been surveyed and detailed in two book chapters and two surveys papers [5–8].

One of the variations of Roman domination in which we are interested in this paper is the quasi-total Roman domination introduced by Cabrera-García el al. [1]. A function $f:V(G)\to \{0,1,2\}$ is a quasi-total Roman dominating function (QTRD-function), if the following hold: (i) every vertex x for which f(x) = 0 is adjacent to at least one vertex v for which f(v) = 2, and (ii) every vertex x for which f(x) = 2 must have at least one neighbor y with $f(y)\in \{1,2\}.$ The quasi-total Roman domination number of a graph G, denoted by ${\gamma }_{\mathit{qtR}}(G),$ equals the minimum weight of a QTRD-function on G. For a QTRD-function f, let $V_i=\{v\in V:f(v)=i\}$ for $i\in \{0,1,2\}.$ Since f is determined by these sets, we will simply write $f=(V_0,V_1,V_2)$ (or $f=(V_0^f,V_1^f,V_2^f)$ to refer to f). Also, a ${\gamma }_{\mathit{qtR}}(G)$-function will refer a QTRD-function on G with weight ${\gamma }_{\mathit{qtR}}(G).$ For more results on quasi-total Roman domination and related parameters we refer the reader to [2–4, 13].

The aim of this paper is to initiate the study of the quasi-total Roman bondage number $b_{\mathit{qtR}}(G)$ of a graph G defined as theminimum cardinality of all sets $E^{\prime }\subseteq E(G)$ such that ${\gamma }_{\mathit{qtR}}(G-E^{\prime })>{\gamma }_{\mathit{qtR}}(G).$ In the case that there is no such subset of edges, we define ${\mathrm{b}}_{\mathit{qtR}}(G)=0.$

We will say that a subset $E^{\prime }\subseteq E(G)$ is an $b_{\mathit{qtR}}(G)$-set if $\left|E^{\prime }\right|=b_{\mathit{qtR}}(G)$ and ${\gamma }_{\mathit{qtR}}(G-E^{\prime })>{\gamma }_{\mathit{qtR}}(G).$

In the this paper, we show that the decision problem corresponding to the problem of computing ${\mathrm{b}}_{\mathit{qtR}}(G)$ is NP-hard even when restricted to bipartite graphs. Then various properties of the quasi-total Roman bondage number are presented and some sharp bounds on it are established.

Before going further, we need to recall some results that will be useful in this work.

Proposition 1

([1, 12]). If G is a connected graph of order $n\ge 3$, then $3\le {\gamma }_{\mathit{qtR}}(G)\le n$. Moreover,

1. ${\gamma }_{\mathit{qtR}}(G)=3$ if and only if G is a graph of maximum degree n – 1.

2. ${\gamma }_{\mathit{qtR}}(G)=4$ if and only if $\gamma (G)={\gamma }_t(G)=2.$

3. ${\gamma }_{\mathit{qtR}}(G)=n$ if and only if G is a path or a cycle.

Corollary 2.

Let G be a connected graph of order $n\ge 3$. Then $b_{\mathit{qtR}}(G)=0$ if and only if G is a path or a cycle.

Proof.

If G is a path or a cycle, then ${\gamma }_{\mathit{qtR}}(G)=n$ by Proposition 1-(iii). Thus for any subset $E^{\prime }\subseteq E(G)$ we have ${\gamma }_{\mathit{qtR}}(G-E^{\prime })={\gamma }_{\mathit{qtR}}(G)$ and so $b_{\mathit{qtR}}(G)=0.$

Conversely, assume that $b_{\mathit{qtR}}(G)=0.$ It follows that there is no subset $E^{\prime }\subseteq E(G)$ such that ${\gamma }_{\mathit{qtR}}(G-E^{\prime })>{\gamma }_{\mathit{qtR}}(G).$ Thus for any subset $E^{\prime }\subseteq E(G)$ we must have ${\gamma }_{\mathit{qtR}}(G-E^{\prime })={\gamma }_{\mathit{qtR}}(G).$ In particular, we have $n={\gamma }_{\mathit{qtR}}(\overline{K_n})={\gamma }_{\mathit{qtR}}(G-E(G))={\gamma }_{\mathit{qtR}}(G).$ Proposition 1-(iii) implies that G is a path or a cycle.

2. Complexity result

Our aim in this section is to show that the decision problem associated with the quasi total Roman bondage is NP-hard even when restricted to bipartite graphs.

Quasi Total Roman Bondage (QT Roman Bondage)

Instance: A nonempty bipartite graph G and a positive integer k.

Question: Is ${\mathrm{b}}_{\mathit{qtR}}(G)\le k$ ?

We show the NP-hardness of QTR bondage problem by transforming the 3-SAT problem to it in polynomial time. Recall that the 3-SAT problem specified below was proven to be NP- complete in [11].

3-SAT problem

Instance: A collection $\mathcal{C}=\{C_1,C_2,\dots ,C_m\}$ of clauses over a finite set U of variables such that $\left|C_j\right|=3$ for $j=1,2,\dots ,m.$

Question: Is there a truth assignment for U that satisfies all the clauses in $\mathcal{C}$?

Now, we show that the problem above is NP-hard, even when restricted to bipartite graphs.

Theorem 3.

The QTR-Bondage problem is NP-hard for bipartite graphs.

Proof.

Let $U=\{u_1,u_2,\dots ,u_n\}$ and $\mathcal{C}$ =$\{C_1,C_2,\dots ,C_m\}$ be an arbitrary instance of 3-SAT problem. We will construct a bipartite graph and a positive integer k such that $\mathcal{C}$ is satisfiable if and only if $b_{\mathit{qtR}}(G)\le k.$

For each $i=1,2,\dots ,n,$ corresponding to the variable $u_i\in U,$ associate a complete bipartite graph $H_i=K_{4,4}$ with bipartite sets $X=\{x_i,y_i,z_i,w_i\}$ and $Y=\{u_i,t_i,{\overline{u}}_i,r_i\}.$ For each $j=1,2,\dots ,m,$ corresponding to the clause $C_j=\{p_j,q_j,r_j\}\in \mathcal{C},$ associate a single vertex c_j and add the edge set $c_j{u}_i$ if $u_i\in C_j$ and $c_j{\overline{u}}_i$ if ${\overline{u}}_i\in C_j.$ Finally, add a graph T with vertex set $V(T)=\{s_1,s_2,s_3,s_4,s_5,s_6\}$ and edge set $E(T)=\{s_1{s}_2,s_1{s}_4,s_2{s}_3,s_2{s}_5,s_3{s}_4,s_4{s}_5,s_5{s}_6\},$ join s₁ and s₃ to each vertex c_j with $1\le j\le m.$ Clearly, G is a bipartite graph of order $8n+m+6.$ It is easy to see that the construction can be accomplished in polynomial time. All that remains to be shown is that $\mathcal{C}$ is satisfiable if and only if $b_{\mathit{qtR}}(G)=1.$ This aim can be fulfilled by proving the following claims.

Claim 1.

${\gamma }_{\mathit{qtR}}(G)\ge 4n+4.$ Moreover, if ${\gamma }_{\mathit{qtR}}(G)=4n+4,$ then for any γ_qtR-function $f=(V_0,V_1,V_2)$ on G, $f(V(H_i))$ and $V(T)\cap V_2=\{s_2,s_5\}$ or $V(T)\cap V_2=\{s_4,s_5\}$ and $\left|\right\{u_i,\overline{u_i}\}\cap V_2|\le 1$ for $i=1,2,\dots ,n,$ while $f(c_j)=0$ for each $1\le j\le m.$

Proof

of Claim 1. Let $f=(V_0,V_1,V_2)$ be a ${\gamma }_{\mathit{qtR}}(G)$-function. By the construction of G, we have $f(V(H_i))\ge 4$ for each $i\in \{1,2,\dots ,n\}.$ Moreover, one can easily see that $f(V(T))+{\sum }_{j=1}^{m}f(c_j)\ge 4,$ and therefore ${\gamma }_{\mathit{qtR}}(G)\ge 4n+4.$

Suppose that ${\gamma }_{\mathit{qtR}}(G)=4n+4.$ Then $f(V(H_i))=4$ for each $i=1,2,\dots ,n.$ If $f(s_1)\ge 1$ (the case $f(s_3)\ge 1$ is similar), then to dominate other vertices in T we must have $f(V(T))\ge 5$ which leads to a contradiction. Hence $f(s_1)=f(s_3)=0.$ This implies that $f(s_2)=f(s_5)=2$ or $f(s_4)=f(s_5)=2,$ and ${\sum }_{i=1}^{m}f(c_j)=0.$ Finally, if $\{u_i,\overline{u_i}\}\subseteq V_2$ for some $i\in \{1,2,\dots ,n\},$ then $f(V(H_i))\ge 5,$ a contradiction again. Thus, there is at most one vertex in $\{u_i,\overline{u_i}\}$ of weight 2.$\hspace{1em}♦$

Figure 1 shows the resulting graph when $U=\{u_1,u_2,u_3,u_4\}$ and $\mathrm{C}=\{C_1,C_2,C_3\},$ where $C_1=\{u_1,u_2,{\overline{u}}_3\},C_2=\{{\overline{u}}_1,u_2,u_4\}$ and $C_3=\{{\overline{u}}_2,u_3,u_4\}.$

Figure 1. An instance of the quasi total Roman bondage number problem resulting from an instance of 3SAT. Here k = 1 and ${\gamma }_{\mathit{qtR}}(G)=20,$ where the bold vertex p means there is a QTRD f with f(p) = 2.

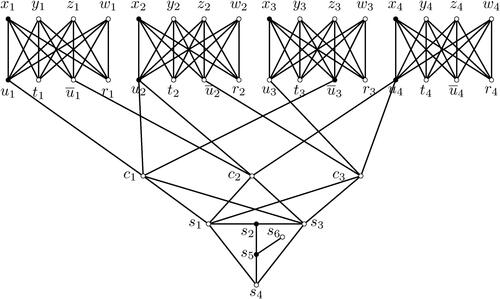
Claim 2.

${\gamma }_{\mathit{qtR}}(G)=4n+4$ if and only if $\mathcal{C}$ is satisfiable.

Proof

of Claim 2. Suppose that ${\gamma }_{\mathit{qtR}}(G)=4n+4$ and let $f=(V_1,V_1,V_2)$ be a γ_qtR-function of G. By Claim 1, $V(T)\cap V_2=\{s_2,s_5\}$ or $V(T)\cap V_2=\{s_4,s_5\},\left|\right\{u_i,\overline{u_i}\}\cap V_2|\le 1$ for $i=1,2,\dots ,n$ and $f(c_j)=0$ for each $1\le j\le m.$ Let $t:U\to \{T,F\}$ be a mapping defined by (1) $$t(u_i)=\{\begin{array}{cc}T\hfill & \text{if}f(u_i)=2\hfill \\ F\hfill & \text{otherwise}\hfill \end{array}$$(1) for $i=1,\dots ,n.$ We will show that t is a satisfying truth assignment for $\mathcal{C}.$ Since the vertex c_j is not adjacent to any member of $\{s_2,s_4,s_5\}\cup \{x_i,y_i,z_i,w_i,t_i,r_i\},$ there exists some i with $1\le i\le n$ such that c_j is quasi total Roman dominated by u_i or $\overline{u_i}.$ If c_j is dominated by u_i, then $f(u_i)=2$ and so $t(u_i)=T.$ If c_j is dominated by $\overline{u_i},$ then $f(\overline{u_i})=2$ and so $t(u_i)=F$ and so $t(\overline{u_i})=T$ by (1). Hence, in both cases the clause C_j is satisfied. The arbitrariness of j with $1\le j\le m$ shows that all the clauses in $\mathcal{C}$ are satisfied by t, that is, $\mathcal{C}$ is satisfiable.

Conversely, suppose that $\mathcal{C}$ is satisfiable, and let $t:U\to \{T,F\}$ be a satisfying truth assignment for $\mathcal{C}.$ We construct a subset D of vertices of G as follows. If $t(u_i)=T,$ then put the vertices u_i and x_i in D; if $t(u_i)=F,$ then put the vertices $\overline{u_i}$ and x_i in D. Hence $\left|D\right|=2n.$ Define the function g by g(x) = 2 for every $x\in D,g(s_2)=g(s_5)=2$ and g(y) = 0 for the remaining vertices. Since t is a satisfying truth assignment for $\mathcal{C},$ the corresponding vertex c_j in G is adjacent to at least one vertex in D. One can easy check that g is a QTR-function of G of weight $4n+4$ and so ${\gamma }_{\mathit{qtR}}(G)\le 4n+4.$ By Claim 1, ${\gamma }_{\mathit{qtR}}(G)\ge 4n+4.$ Therefore, ${\gamma }_{\mathit{qtR}}(G)=4n+4.$$\hspace{1em}♦$

Claim 3.

For any edge $e\in E(G),{\gamma }_{\mathit{qtR}}(G-e)\le 4n+5.$

Proof

of Claim 3. If $e\in E(H_i)$ for some $i=1,2,\dots ,n,$ say $e=x_i{u}_i,$ or e be an edge between some vertex of H_i and some c_j or $e\in \{s_2{s}_5,s_2{s}_3,s_5{s}_6\},$ then the function f defined by $f(y_i)=f(\overline{u_i})=2$ for $1\le i\le n,f(s_1)=f(s_4)=2,f(s_6)=1,$ is a QTRD-function of G – e of weight $4n+5.$ If $e=s_2{c}_j$ for some j, then the function f defined as above is a QTRD-function of G – e of weight $4n+5.$ If $e=s_1{s}_2$ or $e=s_1{c}_j$ for some j, then the function g defined by $g(y_i)=g(\overline{u_i})=2$ for $1\le i\le n,g(s_2)=g(s_4)=2,g(s_6)=1,$ is a QTRD-function of G – e of weight $4n+5.$ If $e\in \{s_3{s}_4,s_4{s}_5\},$ then the function h defined by $h(y_i)=h(\overline{u_i}=2$ for $1\le i\le n,h(s_2)=h(s_1)=2,h(s_6)=1,$ is a QTRD-function of G – e of weight $4n+5.$ If $e=s_1{s}_4,$ then the function l defined by $l(y_i)=l(\overline{u_i})=2$ for $1\le i\le n,l(s_2)=l(s_3)=2,l(s_6)=1,$ is a QTRD-function of G – e of weight $4n+5.$ Thus for any edge $e\in E(G),{\gamma }_{\mathit{qtR}}(G-e)\le 4n+5.$$\hspace{1em}♦$

Claim 4.

${\gamma }_{\mathit{qtR}}(G)=4n+4$ if and only if $b_{\mathit{qtR}}(G)=1.$

Proof

of Claim 4. Assume ${\gamma }_{\mathit{qtR}}(G)=4n+4$ and take $e=s_5{s}_6.$ Suppose that ${\gamma }_{\mathit{qtR}}(G-e)={\gamma }_{\mathit{qtR}}(G).$ Let $f=(V_0,V_1,V_2)$ be a ${\gamma }_{\mathit{qtR}}(G-e)$-function. As f is also a γ_qtR-function of G, by Claim 1, $T\cap V_2=\{s_2,s_5\}$ or $T\cap V_2=\{s_4,s_5\},$ which contradicts the fact that s₆ is dominated by s₅. This contradiction shows that ${\gamma }_{\mathit{qtR}}(G-e)>{\gamma }_{\mathit{qtR}}(G),$ hence $b_{\mathit{qtR}}(G)=1.$

Now assume that $b_{\mathit{qtR}}(G)=1.$ By Claim 3, we have that ${\gamma }_{\mathit{qtR}}(G)\ge 4n+4.$ Let $e\prime$ be an edge such that ${\gamma }_{\mathit{qtR}}(G-e\prime )>{\gamma }_{\mathit{qtR}}(G).$ By Claim 3, we have that ${\gamma }_{\mathit{qtR}}(G-e\prime )\le 4n+5.$ Thus, $4n+4\le {\gamma }_{\mathit{qtR}}(G)<{\gamma }_{\mathit{qtR}}(G-e\prime )\le 4n+5,$ which yields $4n+4={\gamma }_{\mathit{qtR}}(G).$$\hspace{1em}♦$

It follows from Claim 2 and 4 that $b_{\mathit{qtR}}(G)=1$ if and only if $\mathcal{C}$ is satisfiable and the theorem follows.□

3. Properties and exact values of $b_{\mathit{qtR}}(G)$

In this section we study the basic properties and exact values of $b_{\mathit{qtR}}(G)$ for some classes of graphs. First, we show that an $b_{\mathit{qtR}}(G)$-set of a connected graph with ${\gamma }_{\mathit{qtR}}(G)<n$ can increases the quasi-total Roman domination number of G by at most two.

Proposition 4.

Let G be a connected graph of order n with ${\gamma }_{\mathit{qtR}}(G)<n$. If e = uv is an edge of G, then $${\gamma }_{\mathit{qtR}}(G)\le {\gamma }_{\mathit{qtR}}(G-e)\le {\gamma }_{\mathit{qtR}}(G)+2.$$

Proof.

The lower bound is trivial because any ${\gamma }_{\mathit{qtR}}(G-e)$-function is a QTRD-function of G. To show the upper bound, let f be a ${\gamma }_{\mathit{qtR}}(G)$-function. If $2\notin \{f(u),f(v)\},$ then f is a QTRD-function of G – e implying that ${\gamma }_{\mathit{qtR}}(G-e)={\gamma }_{\mathit{qtR}}(G)$ as desired. Assume that $2\in \{f(u),f(v)\}.$ Without loss of generality, suppose that f(u) = 2. If f(v) = 0, then the function g defined on G – e by g(v) = 1 and $g(x)=f(x)$ otherwise, is a QTRD-function on G – e and thus ${\gamma }_{\mathit{qtR}}(G-e)\le \omega (g)\le \omega (f)+1={\gamma }_{\mathit{qtR}}(G)+1.$ If f(v) = 1, then let $u_1\in N_G(u)\cap V_0$ and define the function g on $V(G-e)$ by $g(u_1)=1$ and $g(x)=f(x)$ otherwise. Clearly, g is a QTRD-function on G – e implying that ${\gamma }_{\mathit{qtR}}(G-e)\le \omega (g)\le \omega (f)+1={\gamma }_{\mathit{qtR}}(G)+1.$ If f(v) = 2, then let $u_1\in N_G(u)\cap V_0$ and $v_1\in N_G(v)\cap V_0$ and define the function g on G – e by $g(u_1)=g(v_1)=1$ and $g(x)=f(x)$ otherwise. Then g is a QTRD-function on G – e such that ${\gamma }_{\mathit{qtR}}(G-e)\le \omega (g)\le \omega (f)+2={\gamma }_{\mathit{qtR}}(G)$ and the proof is complete.□

Corollary 5.

Let G be a connected graph of order n with ${\gamma }_{\mathit{qtR}}(G)<n$. If F is an $b_{\mathit{qtR}}(G)$-set, then $${\gamma }_{\mathit{qtR}}(G)+1\le {\gamma }_{\mathit{qtR}}(G-F)\le {\gamma }_{\mathit{qtR}}(G)+2.$$

Both bounds are sharp.

Proof.

By assumption, we have ${\gamma }_{\mathit{qtR}}(G-F)\ge {\gamma }_{\mathit{qtR}}(G)+1.$ To show the upper bound, let $e=uv\in F.$ Since F is an $b_{\mathit{qtR}}(G)$-set, we have ${\gamma }_{\mathit{qtR}}((G-F)+e)={\gamma }_{\mathit{qtR}}(G)$ and Proposition 4 implies that ${\gamma }_{\mathit{qtR}}(G-F)\le {\gamma }_{\mathit{qtR}}((G-F)+e)+2={\gamma }_{\mathit{qtR}}(G)+2.$

The sharpness of the upper bound can be seen for double stars $D{S}_{p,q}(q\ge p\ge 2),$ while the sharpness of the lower bound can be seen by considering the double star $D{S}_{1,q}(q\ge 2).$□

Proposition 6.

Let G be a connected graph of order $n\ge 4$ with ${\gamma }_{\mathit{qtR}}(G)=3$. Then $b_{\mathit{qtR}}(G)=\lceil \frac{t}{2}\rceil$ where t is the number of vertices of G with degree n – 1.

Proof.

By Proposition 1 we have $t\ge 1.$ Let $v_1,\dots ,v_t$ be the vertices of G with degree n – 1 and let F be a $b_{\mathit{qtR}}(G)$-set. It follows from Proposition 1 and the fact ${\gamma }_{\mathit{qtR}}(G-F)>{\gamma }_{\mathit{qtR}}(G)=3$ that $\Delta (G-F)<n-1.$ Thus F must be saturate every vertex in $\{v_1,\dots ,v_t\}$ which implies $b_{\mathit{qtR}}(G)=\left|F\right|\ge \lceil \frac{t}{2}\rceil .$

To prove the inverse inequality, let $F=\left\{v_{1}u\right\}$ for some $u\in V(G)-\left\{v_1\right\}$ if t = 1, let $F=\{v_1{v}_2,v_3{v}_4,\dots ,v_{t-1}{v}_t\}$ if t is even and let $F=\{v_1{v}_2,v_1{v}_3,v_4{v}_5,\dots ,v_{t-1}{v}_t\}$ if $t\ge 3$ is odd. Then $\Delta (G-F)<n-1$ and by Proposition 1 we have ${\gamma }_{\mathit{qtR}}(G-F)\ge 4>{\gamma }_{\mathit{qtR}}(G),$ and thus $b_{\mathit{qtR}}(G)\le \lceil \frac{t}{2}\rceil .$ Consequently, $b_{\mathit{qtR}}(G)=\lceil \frac{t}{2}\rceil .$□

Corollary 7.

For $n\ge 4,b_{\mathit{qtR}}(K_n)=\lceil \frac{n}{2}\rceil .$

Proposition 8.

Let G be a connected graph of order $n\ge 5$ with ${\gamma }_{\mathit{qtR}}(G)=4$ and $b_t(G)<\infty$. Then $b_{\mathit{qtR}}(G)\le b_t(G).$

Proof.

Let F be a $b_t(G)$-set. By definition G – F is isolated-free and ${\gamma }_t(G-F)\ge {\gamma }_t(G)+1\ge 3.$ Let $G_1,\dots ,G_t$ be the connected components of G – F. If $t\ge 3,$ then we have ${\gamma }_{\mathit{qtR}}(G-F)={\sum }_{i=1}^t{\gamma }_{\mathit{qtR}}(G_i)\ge 2t>4={\gamma }_{\mathit{qtR}}(G).$ If t = 2, then one of its component, say G₁, has order at least 3 (note that $n\ge 5$) and so ${\gamma }_{\mathit{qtR}}(G-F)={\gamma }_{\mathit{qtR}}(G_1)+{\gamma }_{\mathit{qtR}}(G_2)\ge 3+2>4={\gamma }_{\mathit{qtR}}(G).$ Assume that t = 1. Since G – F is connected and ${\gamma }_t(G-F)\ge 3,$ we deduce from Proposition 1-(ii) that ${\gamma }_{\mathit{qtR}}(G-F)\ge 5.$ Thus $b_{\mathit{qtR}}(G)\le \left|F\right|=b_t(G).$

It is shown that for $n\ge m\ge 2,b_t(K_{m,n})=m$ [14].

Corollary 9.

For $n\ge m\ge 2$ with $m+n\ge 5,$ $b_{\mathit{qtR}}(K_{m,n})=m.$

Proof.

Since ${\gamma }_{\mathit{qtR}}(K_{m,n})=4$ and $b_t(K_{m,n})<\infty ,$ we deduce from Proposition 8 that $b_{\mathit{qtR}}(K_{m,n})\le b_t(K_{m,n})=m.$ To prove the inverse inequality, let F be a $b_{\mathit{qtR}}(K_{m,n})$-set. Then ${\gamma }_{\mathit{qtR}}(K_{m,n}-F)>{\gamma }_{\mathit{qtR}}(K_{m,n})=4.$ If $K_{m,n}-F$ has an isolated vertex w, then we have $\left|F\right|\ge \mathrm{deg}(w)\ge m=b_t(K_{m,n}).$ Assume that $K_{m,n}-F$ has no isolated vertex. If $K_{m,n}-F$ is not connected, then we have ${\gamma }_t(K_{m,n}-F)\ge 4>2={\gamma }_t(K_{m,n})$ and so $\left|F\right|\ge b_t(K_{m,n}).$ If $K_{m,n}$ is connected, then we deduce from Proposition 1-(ii) and the fact ${\gamma }_{\mathit{qtR}}(K_{m,n}-F)\ge 5$ that ${\gamma }_t(K_{m,n}-F)\ge 3>2={\gamma }_t(K_{m,n})$ and so $\left|F\right|\ge b_t(K_{m,n}).$ In either case, we have $b_{\mathit{qtR}}(K_{m,n})\ge b_t(K_{m,n})=m.$ Thus $b_{\mathit{qtR}}(K_{m,n})=m.$

Theorem 10.

Let G be a connected graph of order n with ${\gamma }_{\mathit{qtR}}(G)<n$. Then $b_{\mathit{qtR}}(G)=1$ if and only if there is an edge e = uv such that for any ${\gamma }_{\mathit{qtR}}(G)$-function f, $2\in \{f(u),f(v)\}$ and one of the following hold.

1. $v\in \mathit{epn}(u,V_2)\cap V_0$ or $u\in \mathit{epn}(v,V_2)\cap V_0;$

2. either f(u) = 1 and $v\in \mathit{epn}(u,(V_1\cup V_2)-\{v\})$ or f(v) = 1 and $u\in \mathit{epn}(v,(V_1\cup V_2)-\{u\})$;

3. $f(u)=f(v)=2$ and $v\in \mathit{epn}(u,(V_1\cup V_2)-\{v\}$ or $u\in \mathit{epn}(v,(V_1\cup V_2)-\{u\}).$

Proof.

Let there exist an edge e = uv such that for any ${\gamma }_{\mathit{qtR}}(G)$-function f, $2\in \{f(u),f(v)\}$ and one of the conditions (1), (2) or (3) holds. We claim that ${\gamma }_{\mathit{qtR}}(G-e)>{\gamma }_{\mathit{qtR}}(G)$ which leads to $b_{\mathit{qtR}}(G)=1.$ Let g be a ${\gamma }_{\mathit{qtR}}(G-e)$-function. Obviously, g is a QTRD-function of G. If $2\notin \{g(u),g(v)\},$ then by the assumption g is not a ${\gamma }_{\mathit{qtR}}(G)$-function and so ${\gamma }_{\mathit{qtR}}(G-e)=\omega (g)>{\gamma }_{\mathit{qtR}}(G).$ Assume that $2\in \{g(u),g(v)\}.$ Suppose without loss of generality that g(u) = 2. First let g(v) = 0. Then v has a neighbor w in G – e with g(w) = 2 and so $v\notin epn(u,V_2)\cap V_0.$ It follows from our earlier assumption that g is not a ${\gamma }_{\mathit{qtR}}(G)$-function and so ${\gamma }_{\mathit{qtR}}(G-e)=\omega (g)>{\gamma }_{\mathit{qtR}}(G).$ Assume that g(v) = 1. Since g is a ${\gamma }_{\mathit{qtR}}(G-e)$-function and g(u) = 2, u has a neighbor w in G – e with $g(w)\ge 1$ and so $u\notin epn(v,(V_1\cup V_2)-\{u\}).$ It follows from our earlier assumption that g is not a ${\gamma }_{\mathit{qtR}}(G)$-function and so ${\gamma }_{\mathit{qtR}}(G-e)=\omega (g)>{\gamma }_{\mathit{qtR}}(G).$ Finally let g(v) = 2. Since g is a ${\gamma }_{\mathit{qtR}}(G-e)$-function with $g(u)=g(v)=2,$ u has a neighbor $u\prime$ in G – e with $g(u\prime )\ge 1$ and v has a neighbor $v\prime$ in G – e with $g(v\prime )\ge 1$ and so $v\notin epn(u,(V_1\cup V_2)-\{v\}$ and $u\notin epn(v,(V_1\cup V_2)-\{u\}).$ It follows from our earlier assumption that g is not a ${\gamma }_{\mathit{qtR}}(G)$-function and so ${\gamma }_{\mathit{qtR}}(G-e)=\omega (g)>{\gamma }_{\mathit{qtR}}(G).$ Thus $b_{\mathit{qtR}}(G)=1.$

Conversely, let $b_{\mathit{qtR}}(G)=1$ and let $F=\left\{e\right\}$ be an $b_{\mathit{qtR}}(G)$-set, that is ${\gamma }_{\mathit{qtR}}(G-e)>{\gamma }_{\mathit{qtR}}(G).$ Suppose f is an arbitrary ${\gamma }_{\mathit{qtR}}(G)$-function. If $2\notin \{f(u),f(v)\},$ then clearly f is a QTRD-function of G – e which leads to a contradiction. Thus $2\in \{f(u),f(v)\}.$ Assume without loss of generality that f(u) = 2. If f(v) = 0 and $v\notin epn(u,V_2),$ then f is a QTRD-function of G – e which leads to a contradiction again. Thus, if f(v) = 0, then $v\in \mathit{epn}(u,V_2)$ and (1) holds. If f(v) = 1 and $u\notin epn(v,(V_1\cup V_2)-\{u\}),$ then f is a QTRD-function of G – e and we get a contradiction again. Therefore, if f(v) = 1, then $u\in \mathit{epn}(v,(V_1\cup V_2)-\{u\})$ and hence (2) holds. Finally, let f(v) = 2. If $v\notin epn(u,(V_1\cup V_2)-\{v\}$ and $u\notin epn(v,(V_1\cup V_2)-\{u\}),$ then f is a QTRD-function of G – e and we get a contradiction. Thus, if f(v) = 2, then $v\in \mathit{epn}(u,(V_1\cup V_2)-\{v\})$ or $u\in \mathit{epn}(v,(V_1\cup V_2)-\{u\})$ and (3) holds. This completes the proof.

Corollary 11.

If G has a support vertex with at least three pendant edges, then $b_{\mathit{qtR}}(G)=1.$

4. Bounds on $b_{\mathit{qtR}}(G)$

In this section we provide some bounds on Quasi-total Roman bondage number of graphs.

Proposition 12.

If G is graph of order $n\ge 4$ with a strong support vertex, then $b_{\mathit{qtR}}(G)\le n-3.$

Proof.

Let v be a strong support vertex of G and $v_1,\dots ,v_t$ be the non-leaf neighbors of v. If v is adjacent to at least three leaves, then the result follows from Corollary 11. Hence assume that v is adjacent to exactly two leaves. Let $X=V(G)-(L_v\cup \{v\})$ and $F=\left\{v{v}_i\right|1\le i\le t\}.$ Clearly ${\gamma }_{\mathit{qtR}}(G-F)=3+{\gamma }_{\mathit{qtR}}(G[X]).$ If $G[X]$ has a ${\gamma }_{\mathit{qtR}}(G[X])$-function f with $f(v_i)\ge 1$ for some i, then the function g defined by g(v) = 2, $g(x)=f(x)$ for each $x\in X$ and g(x) = 0 otherwise is a QTRD-function of G implying that ${\gamma }_{\mathit{qtR}}(G-F)>{\gamma }_{\mathit{qtR}}(G).$ Hence we assume any ${\gamma }_{\mathit{qtR}}(G[X])$-function assigns 0 to each $v_i(1\le i\le t).$ Let Y be the set of vertices $u\in N(v_1)$ for which there is a ${\gamma }_{\mathit{qtR}}(G[X])$-function which assigns label 2 to u, and let $F\prime =\left\{v_{1}u\right|u\in Y\}.$ One can easily seen that ${\gamma }_{\mathit{qtR}}(G[X]-F\prime )>{\gamma }_{\mathit{qtR}}(G[X]).$ This implies that ${\gamma }_{\mathit{qtR}}(G-(F\cup F\prime ))=3+{\gamma }_{\mathit{qtR}}(G[X]-F\prime )>3+{\gamma }_{\mathit{qtR}}(G[X])={\gamma }_{\mathit{qtR}}(G-F)\ge {\gamma }_{\mathit{qtR}}(G).$ Therefore $b_{\mathit{qtR}}(T)\le |F\cup F\prime |=\left|F\right|+|F\prime |\le n-3$ and the proof is complete.□

A broom graph $B_{n,m}$ is a graph of n vertices, which have a path P with m vertices and $(n-m)$ pendant vertices. All of these vertices are adjacent to either the origin u or the terminus v of the path P.

Proposition 13.

Let G be a connected graph and xyz be a path in G such that there is a pendant path $y{z}_1\dots z_k(k\ge 1)$. Then $$b_{\mathit{qtR}}(G)\le \mathrm{deg}(x)+\mathrm{deg}(y)+\mathrm{deg}(z)-4-\mathcal{l}(x,z)$$ where $\mathcal{l}(x,z)=0$ if $xz\notin E(G)$ and $\mathcal{l}(x,z)=2$ if $xz\in E(G).$

Furthermore, this bound is sharp for broom graph $B_{m+2,m}.$

Proof.

Let F be the set of all edges incident to x, y and z with exception the edges of {yx, yz, xz}. Clearly $\left|F\right|=\mathrm{deg}(x)+\mathrm{deg}(y)+\mathrm{deg}(z)-4-\mathcal{l}(x,z).$ If $F=\left\{y{z}_1\right\},$ then G is obtained from the path $xy{z}_1\dots z_k$ by adding a pendant edge at y and clearly $b_{\mathit{qtR}}(G)=1=\mathrm{deg}(x)+\mathrm{deg}(y)+\mathrm{deg}(z)-4.$ Assume that $\left\{y{z}_1\right\}\subset F.$ Let G₁, G₂ be the components of G – F containing z₁ and y, respectively, and let $G_3=(G-F)-(V(G_1)\cup V(G_2)).$ Clearly ${\gamma }_{\mathit{qtR}}(G-F)=3+k+{\gamma }_{\mathit{qtR}}(G_3).$ Let f be a ${\gamma }_{\mathit{qtR}}(G_3)$-function and define g on G by $g(x)=g(z)=0,g(y)=2,g(z_i)=1$ for each i and $g(u)=f(u)$ for $u\in V(G_3).$ It is easy to see that g is a QTRD-function of G of weight $2+k+{\gamma }_{\mathit{qtR}}(G_3).$ Therefore $b_{\mathit{qtR}}(G)\le \mathrm{deg}(x)+\mathrm{deg}(y)+\mathrm{deg}(z)-4.$

Proposition 14.

Let G be a connected graph of order $n\ge 4$ and $(x_1{x}_2{x}_3{x}_1)$ be a triangle in G. Then $$b_{\mathit{qtR}}(G)\le \mathrm{deg}(x_1)+\mathrm{deg}(x_2)+\mathrm{deg}(x_3)-6+n-|{\cup }_{i=1}^{3}N(x_i)|.$$

Proof.

Let F be the set of all edges incident to x₁, x₂ and x₃ with exception the edges of $x_1{x}_2,x_2{x}_3$ and $x_1{x}_3.$ Clearly $\left|F\right|=\mathrm{deg}(x_1)+\mathrm{deg}(x_2)+\mathrm{deg}(x_3)-6$ and ${\gamma }_{\mathit{qtR}}(G-F)=3+{\gamma }_{\mathit{qtR}}(G[V-\{x_1,x_2,x_3\}]).$ If ${\gamma }_{\mathit{qtR}}(G-F)>{\gamma }_{\mathit{qtR}}(G),$ then we are done. Hence let ${\gamma }_{\mathit{qtR}}(G-F)={\gamma }_{\mathit{qtR}}(G).$ We deduce from ${\gamma }_{\mathit{qtR}}(G-F)={\gamma }_{\mathit{qtR}}(G)$ that no neighbor of x_i in $V(G)-\{x_1,x_2,x_3\},$ is not assigned a positive weight under any ${\gamma }_{\mathit{qtR}}(G-F)$-function for $i\in \{1,2,3\}.$ Let $w\in N(x_i)$ for some i (note that G is a connected graph of order $n\ge 4.$) Let Y be the set of vertices in $V(G)-\{x_1,x_2,x_3\}$ which assigned a positive weight under some ${\gamma }_{\mathit{qtR}}(G-F)$-function. Then $Y\subseteq V(G)-{\cup }_{i=1}^{3}N(x_i).$ Let $F\prime =\left\{wy\right|y\in N(w)\cap Y\}.$ Clearly $|F\cup F\prime |\le \mathrm{deg}(x_1)+\mathrm{deg}(x_2)+\mathrm{deg}(x_3)-6+n-|{\cup }_{i=1}^{3}N(x_i)|.$ We show that ${\gamma }_{\mathit{qtR}}(G-(F\cup F\prime ))>{\gamma }_{\mathit{qtR}}(G).$ Let f be a ${\gamma }_{\mathit{qtR}}(G-(F\cup F\prime ))$-function. Obviously $f(x_1)+f(x_2)+f(x_3)=3$ and the function f restricted to $(G-F)-\{x_1,x_2,x_3\}$ is an QTRDF of $(G-F)-\{x_1,x_2,x_3\}.$ To dominate w we must have $f(w)\ge 1$ or f(u) = 2 for some $u\in N(w)-Y.$ We deduce from our earlier assumption that the restriction of f on $(G-F)-\{x_1,x_2,x_3\}$ is not a ${\gamma }_{\mathit{qtR}}(G-F)-\{x_1,x_2,x_3\}$-function. Thus ${\gamma }_{\mathit{qtR}}(G-(F\cup F\prime ))=\omega (f)>3+{\gamma }_{\mathit{qtR}}(G-F)-\{x_1,x_2,x_3\}={\gamma }_{\mathit{qtR}}(G-F)={\gamma }_{\mathit{qtR}}(G).$ This completes the proof.

Proposition 15.

Let G be a connected graph of order $n\ge 5$ with ${\gamma }_{\mathit{qtR}}(G)=4$. Then for each two adjacent vertices u, v, $$b_{\mathit{qtR}}(G)\le \mathrm{deg}(u)+\mathrm{deg}(v)-2.$$

Proof.

Let F be the set of all edges incident to u and v with exception uv. Let $G_1,\dots ,G_t$ be the components of G – F. Assume without loss of generality that $u\in V(G_1).$ Then $G_1\simeq K_2.$ If $t\ge 4,$ then we have ${\gamma }_{\mathit{qtR}}(G-F)={\sum }_{i=1}^t{\gamma }_{\mathit{qtR}}(G_i)=2+{\sum }_{i=2}^t{\gamma }_{\mathit{qtR}}(G_i)\ge 5.$ If t = 3, then we deduce from $n\ge 5$ that $|V(G_i)|\ge 2$ for some $i\in \{2,3\},$ say i = 2. Thus ${\gamma }_{\mathit{qtR}}(G-F)={\sum }_{i=1}^3{\gamma }_{\mathit{qtR}}(G_i)\ge 2+2+{\gamma }_{\mathit{qtR}}(G_3)\ge 5.$ Assume that t = 2. Then G₂ is a connected graph of order at least three. Proposition 1 implies that ${\gamma }_{\mathit{qtR}}(G-F)={\gamma }_{\mathit{qtR}}(G_1)+{\gamma }_{\mathit{qtR}}(G_2)\ge 2+3=5.$ Thus $b_{\mathit{qtR}}(G)\le \left|F\right|=\mathrm{deg}(u)+\mathrm{deg}(v)-2.$□

Proposition 16.

Let G be a connected graph of order $n\ge 5$ different from C_n. If $g(G)\ge 5$, then $b_{\mathit{qtR}}(G)\le n-g(G).$

Proof.

Let $C=(x_1{x}_2\dots x_{g(G)}{x}_1)$ be a cycle of G on g(G) vertices. Since $g(G)\ge 5,$ we have $N(v_i)\cap N(v_j)=\varnothing$ for each $1\le i\ne j\le g(G).$ Let F₁ be the set of all edges incident with $v_1,\dots ,v_{g(G)}$ with exception the edges on C. Let f be a ${\gamma }_{\mathit{qtR}}(G-F_1)$-function. Then we have ${\gamma }_{\mathit{qtR}}(G-F_1)=g(G)+{\gamma }_{\mathit{qtR}}(G-V(C)).$ If f assigns a positive weight to a vertex $x\in N(v_i)\cap (V(G)-V(C)),$ say i = 2, then the function g defined by $g(v_2)=2,g(v_1)=g(v_3)=0$ and g(y) = 1 for $y\in \{v_4,\dots ,v_{g(G)}\},$ is a QTRD of G of weight less than $\omega (g)<\omega (f).$ Hence, we assume that there is no vertex in ${\cup }_{i=1}^{g(G)}(N(v_i)\cap (V(G)-V(C)))$ assigned a positive weight under any ${\gamma }_{\mathit{qtR}}(G-F_1)$-function. Since $G\ne C,$ we may assume that there is a vertex $x\in N(v_1)\cap (V(G)-V(C)).$ Let Y be the set of vertices in $N(x)\cap (V(G)-V(C))$ which are assigned 2 under some ${\gamma }_{\mathit{qtR}}(G-F_1)$-function, and let $F=F_1\cup \left\{xy\right|y\in Y\}.$ Clearly $\left|F\right|\le n-g(G).$ It is easy to check that $${\gamma }_{\mathit{qtR}}(G-F)>g(G)+{\gamma }_{\mathit{qtR}}(G-F_1)\ge {\gamma }_{\mathit{qtR}}(G)$$ and thus $b_{\mathit{qtR}}(G)\le n-g(G)$ as desired.□

5. Trees

In this section we provide two upper bounds on the quasi-total Roman bondage number of trees.

Proposition 17.

Let T be a tree of order $n\ge 4$ different from path P_n. Then $$b_{\mathit{qtR}}(T)\le \frac{n-2}{2},$$ with equality if and only if $T=K_{1,3}.$

Proof.

If $\text{diam}(T)=2,$ then T is a star of order at least 4 and clearly removing any edge increases the quasi-total Roman domination number yielding $b_{rI}(T)=1\le \frac{n-2}{2}$ with equality if and only if $T=K_{1,3}.$ If $\text{diam}(T)=3,$ then T is a double star of order at least 5 and removing any pendant edge incident to a support vertex with degree at least 3 increases the quasi-total Roman domination number yielding $b_{rI}(T)=1<\frac{n-2}{2}$ (notice that $n\ge 5$ because T is not a path). Hence, we assume that $\text{diam}(T)\ge 4.$ Let $P:=(u=)u_1{u}_2\dots u_k(=v)$ be a longest path in T between a leaf and a vertex of degree at least 3. Without loss of generality, assume that $\mathrm{deg}(u)=1$ and $\mathrm{deg}(v)\ge 3$ and root T at u. Let $v_1,\dots ,v_t$ be the children of v. By the choice of path P, we have $\mathrm{deg}(v_1)=\dots =\mathrm{deg}(v_t)=2,$ the maximal subtrees $T_{v_1},\dots ,T_{v_t}$ are paths and that $k\ge 3$ since $\text{diam}(T)\ge 4.$ We consider two situations.

Case 1. ${\mathrm{deg}}_T(v)\ge 4.$

Suppose $v_1,\dots ,v_s(s\le t)$ are leaf children of v, if any. If s = t, then let $F=\{v{u}_{k-1},v{v}_t\}$ and $T\prime$ be the component of T – F containing u. Then we have $\left|F\right|<\frac{n-2}{2}$ and clearly ${\gamma }_{\mathit{qtR}}(T-F)={\gamma }_{\mathit{qtR}}(T\prime )+4.$ Let f be a ${\gamma }_{\mathit{qtR}}(T\prime )$-function and define the function g on T by g(v) = 2, $g(v_1)=1,g(v_i)=0$ for $2\le i\le t,$ and $g(x)=f(x)$ for $x\in V(T\prime ).$ Obviously g is an QTRD-function of T with weight less than ${\gamma }_{\mathit{qtR}}(T\prime )+3,$ as desired. Assume that s < t. If $s\ge 2,$ then let $F=\left\{v{v}_i\right|s+1\le i\le t\}$ and $T\prime$ be the component of T – F containing v. Then we have $\left|F\right|<\frac{n-2}{2}$ and clearly ${\gamma }_{\mathit{qtR}}(T-F)={\gamma }_{\mathit{qtR}}(T\prime )+{\sum }_{i=s+1}^r|V(T_i)|.$ Let f be a ${\gamma }_{\mathit{qtR}}(T\prime )$-function such that f(v) is maximized. Since v is a strong support vertex, we must have f(v) = 2. Define the function g on T by $g(v_i)=0$ for $s+1\le i\le t,g(x)=f(x)$ for $x\in V(T\prime )$ and g(x) = 1 otherwise. Obviously g is an QTRD-function of T with weight less than ${\gamma }_{\mathit{qtR}}(T-F),$ as desired.

Assume now that $s\le 1.$ Let $F=\{v{u}_{k-1},v{v}_i|3\le i\le t\}$ and $T\prime$ be the component of T – F containing u. Clearly, $\left|F\right|<\frac{n-2}{2}$ and ${\gamma }_{\mathit{qtR}}(T-F)={\gamma }_{\mathit{qtR}}(T\prime )+|V(T_v)|.$ Let f be a ${\gamma }_{\mathit{qtR}}(T\prime )$-function and define g on T by $g(v)=2,g(v_1)=1,g(v_i)=0$ for $2\le i\le t,g(x)=f(x)$ for $x\in V(T\prime )$ and g(x) = 1 otherwise. Obviously g is an QTRD-function of T with weight less than ${\gamma }_{\mathit{qtR}}(T-F),$ as desired.

Case 2. ${\mathrm{deg}}_T(v)=3.$

Then T_v is a path. Let $T\prime$ be the component of $T-v{u}_{k-1}$ containing $u_{k-1}.$ If $T\prime$ is a star, then it is easy to see that ${\gamma }_{\mathit{qtR}}(T-v{u}_{k-1})>{\gamma }_{\mathit{qtR}}(T)$ implying that $b_{\mathit{qtR}}(T)=1<\frac{n-2}{2}.$ Hence, assume that $T\prime$ is not a star and so $|V(T\prime )|\ge 4.$ If $\mathrm{deg}(u_{k-1})=2,$ then one can easily seen that ${\gamma }_{\mathit{qtR}}(T-\{v{u}_{k-1},u_{k-1}{u}_{k-2}\})>{\gamma }_{\mathit{qtR}}(T)$ implying that $b_{\mathit{qtR}}(T)=2<\frac{n-2}{2}.$ Henceforth, we let $\mathrm{deg}(u_{k-1})\ge 3.$ By the choice of the path P, we deduce that the maximal subtree of any children of $u_{k-1}$ is a path. Let $z_1,\dots ,z_k$ be the leaf neighbors of $u_{k-1},$ if any, and $y_1(=v),\dots ,y_s$ be the other children of $u_{k-1}.$ If $u_{k-1}$ has a leaf child, then let $F=\{u_{k-1}{u}_{k-2},u_{k-1}{y}_i|1\le i\le s\}$ and if $u_{k-1}$ has no leaf child and it a has child of degree 2, say y_s, then let $F=\{u_{k-1}{u}_{k-2},u_{k-1}{y}_i|1\le i\le s-1\}$ and otherwise let $F=\left\{u_{k-1}{y}_i\right|1\le i\le s\}.$ Clearly $\left|F\right|<\frac{n-2}{2}.$ Let $T\prime$ be the component of T – F containing $u_{k-2}$ and f be a ${\gamma }_{\mathit{qtR}}(T-F)$-function. Then the function f restricted to $T\prime$ is a ${\gamma }_{\mathit{qtR}}(T\prime )$-function. In the first and second cases, by Proposition 1-(iii), we may assume that $f(u_{k-1})\ge 1$ and that f assigns 1 to each vertex of $V(T_{y_i}).$ On the other hand, any ${\gamma }_{\mathit{qtR}}(T\prime )$-function g can be extended to an QTRD-function h of T of weight less than $\omega (f)$ by defining $h(x)=g(x)$ for $x\in V(T\prime ),$ h(v) = 2, $h(v_i)=0$ for $1\le i\le t$ and h(x) = 1 otherwise. In the third case, we may assume that f assigns 1 to each vertex of $V(T_{y_i})$ for each i. Also, if g is a ${\gamma }_{\mathit{qtR}}(T\prime )$-function, then the function h defined by $h(u_{k-1})=\min \{g(u_{k-1})+1,2\},h(y_i)=2$ for $1\le i\le s,$ h(x) = 0 for $x\in {\cup }_{i=1}^s{C}_{y_i}$ and h(x) = 0 otherwise, is an QTRD-function of T of weight less than $\omega (f).$ Thus $b_{\mathit{qtR}}(T)\le \left|F\right|<\frac{n-2}{2}$ and the proof is complete.

Proposition 18.

Let T be a tree of order $n\ge 3$ different from path P_n. Then $b_{\mathit{qtR}}(T)\le \Delta -1.$

Proof.

Since T is not a path, we have $\Delta (T)\ge 3.$ If $\text{diam}(T)=2,$ then T is a star $K_{1,n-1}$ where $n\ge 4.$ Let v be the center of $K_{1,n-1}$ and u be a leaf adjacent to v. One can easily seen that ${\gamma }_{\mathit{qtR}}(T-uv)=4>3={\gamma }_{\mathit{qtR}}(K_{1,n-1}).$ If $\text{diam}(T)=3,$ then T is a double star $D{S}_{p,q}(q\ge p\ge 1)$ with $q\ge 2$ because of $T\ne P_4.$ If e is the central edge of T, then clearly ${\gamma }_{\mathit{qtR}}(T-e)\ge 5>{\gamma }_{\mathit{qtR}}(T).$ Hence, we assume that $\text{diam}(T)\ge 4.$ We consider two cases.

Case 1. $\Delta (T)=3.$

Let v be a vertex of degree 3 with neighbors $v_1,v_2,v_3$ and root T at v. If v is the only vertex of T with degree 3, then $T-v{v}_1$ is disjoint union of two paths and by Proposition 1 we have ${\gamma }_{\mathit{qtR}}(T-v{v}_1)=n>{\gamma }_{\mathit{qtR}}(T).$ Hence, we assume that T has at least two vertices of degree 3. Let u be a furthest vertex from v with degree 3 and let w be the patent of u. If $\mathrm{deg}(w)=2$ and $w\prime$ be the parent of w, then let $T\prime$ be the component of $T-\{ww\prime ,wu\}.$ Then we have ${\gamma }_{\mathit{qtR}}(T-\{ww\prime ,wu\})={\gamma }_{\mathit{qtR}}(T\prime )+1+n(T_u)$ (notice that T_u is a path). Let $f\prime$ be a ${\gamma }_{\mathit{qtR}}(T-\{ww\prime ,wu\})$-function and define the function g by $g(x)=f\prime (x)$ for $x\in V(T\prime ),$ g(u) = 2, g(x) = 0 if x is a child of u, and g(x) = 1 otherwise. Clearly g is a QTRD-function of T with weight ${\gamma }_{\mathit{qtR}}(T-\{ww\prime ,wu\})-1$ implying that $b_{\mathit{qtR}}(T)\le 2=\Delta -1.$ Hence assume that $\mathrm{deg}(w)=3.$ Let $u\prime$ be a child of w different from u and let $N(w)=\{u,u_1,u_2\}.$ By the choice of u, $T_{u_1}$ is a path. First let $\mathrm{deg}(u_1)=2.$ Let $T_1,T_2,T_3$ be the components of $T-\{wu,w{u}_2\}$ containing $u_2,w,u$ respectively. Clearly, we have ${\gamma }_{\mathit{qtR}}(T-\{wu,w{u}_2\})={\gamma }_{\mathit{qtR}}(T_1)+n(T_2)+n(T_3).$ Let $f\prime$ be a ${\gamma }_{\mathit{qtR}}(T_1)$-function and define the function g by $g(x)=f\prime (x)$ for $x\in V(T_1),$ g(u) = 2, g(x) = 0 if x is a child of u and g(x) = 1 otherwise. Obviously, g is a QTRD-function of T with weight ${\gamma }_{\mathit{qtR}}(T-\{ww\prime ,wu\})-1$ implying that $b_{\mathit{qtR}}(T)\le 2=\Delta -1.$ Now assume that $\mathrm{deg}(u_1)=3.$ Let $T_1,T_2,T_3$ be the components of $T-\{w{u}_1,w{u}_2\}$ containing $u_2,u_1,w$ respectively. Clearly, we have ${\gamma }_{\mathit{qtR}}(T-\{w{u}_1,w{u}_2\})={\gamma }_{\mathit{qtR}}(T_1)+{\gamma }_{\mathit{qtR}}(T_2)+n(T_3)-1.$ Let f₁ be a ${\gamma }_{\mathit{qtR}}(T_1)$-function and f₃ be a ${\gamma }_{\mathit{qtR}}(T_3)$-function. Without loss of generality, assume that $f_3(w)=1$ and $f_3(u)=2.$ Then the function g defined by $g(x)=f_1(x)$ for $x\in V(T_1),g(x)=f_3(x)$ for $x\in V(T_3),$ g(w) = 0 and g(x) = 1 otherwise, is a QTRD-function of T with weight ${\gamma }_{\mathit{qtR}}(T-\{ww\prime ,wu\})-1$ implying that $b_{\mathit{qtR}}(T)\le 2=\Delta -1.$

Case 2. $\Delta (T)\ge 4.$

Let v be a vertex with maximum degree Δ and let u be a furthest leaf from v. Root T at u and let w be the parent of v. Let T₁, T₂ be the components of T – vw containing w and v respectively. Since $\Delta (T_v)\ge 3,$ by Case 1, we have $b_{\mathit{qtR}}(T_v)\le \Delta -2.$ Let F be a $b_{\mathit{qtR}}(T_v)$-set. Then we have ${\gamma }_{\mathit{qtR}}(T-(F\cup \left\{vw\right\}))={\gamma }_{\mathit{qtR}}(T_1)+{\gamma }_{\mathit{qtR}}(T_2-F)>{\gamma }_{\mathit{qtR}}(T_1)+{\gamma }_{\mathit{qtR}}(T_2)\ge {\gamma }_{\mathit{qtR}}(T)$ and thus $b_{\mathit{qtR}}(T)\le \Delta -1.$ This completes the proof.□

6. Conclusion

In this manuscript, we initiate the study of quasi-total Roman bondage in graphs. We first show that the decision problem associated with the quasi-total Roman bondage problem is NP-hard even when restricted to bipartite graphs. Then we provided the basic properties of the quasi-total Roman bondage number and some sharp bounds for ${\mathrm{b}}_{\mathit{qtR}}(G).$ In particular, we prove that for any tree T of order $n\ge 4$ different from paths, ${\mathrm{b}}_{\mathit{qtR}}(T)\le \min \{\Delta (T)-1,\frac{n-2}{2}\}.$ Establishing a sharp upper bound for the quasi-total Roman bondage number of connected graph G of order $n\ge 3$ different from paths and cycles in terms of the order remains open.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Disclosure statement

No potential conflict of interest was reported by the authors.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Additional information

Funding

This work was supported by the National Natural Science Foundation of China (No. 62172116).