Total mixed domination in graphs

Abstract

For a graph $G=(V,E),$ we call a subset $S\subseteq V\cup E$ a total mixed dominating set of G if each element of $V\cup E$ is either adjacent or incident to an element of S, and the total mixed domination number of G is the minimum cardinality of a total mixed dominating set of G. In this paper, we initiate to study the total mixed domination number of a connected graph by giving some tight bounds in terms of some parameters such as order and total domination numbers of the graph and its line graph. Then we discuss on the relation between total mixed domination number of a graph and its diameter. Study of this number in trees and 2-corona graphs is our next work. Also we show that the total mixed domination number of a graph is equal to the total domination number of its total graph. Giving the total mixed domination numbers of the paths, cycles, complete bipartite graphs, complete graphs and wheels is our last work.

Keywords:

• Total mixed domination
• total domination
• total graph

MSC (2010):

• 05C69

1. Introduction

All graphs considered here are non-empty, finite, undirected and simple. For standard graph theory terminology not given here we refer to [5]. Let $G=(V,E)$ be a graph with the vertex set V of order n and the edge set E of size m. $N_G(v)$ and $N_G[v]$ denote the open neighborhood and the closed neighborhood of a vertex v, respectively, while $\delta =\delta (G)$ and $\Delta =\Delta (G)$ denote the minimum and maximum degrees of G, respectively. Also we define $N_E(v)=\{e\in E | v\in e\}$ for any vertex v, $N_G(e)=\{v\in V | v\in e\}$ and $N_E(e)=\{e\prime \in E | e\mathrm{ }\text{and}\mathrm{ }e\prime \mathrm{ }\text{are}\mathrm{ }\text{adjacent}\}$ for any edge e, and $N_{T(G)}(x)=N_G(x)\cup N_E(x)$ for any element $x\in V(G)\cup E(G)$ (T(G) denotes the total graph of G which will define after). For any two vertices u and v in a connected graph G the distance between u and v is the minimum length of a shortest (u, v)-path in G and is denoted by d(u, v). The maximum distance among all pairs of vertices of G is the diameter of G, which is denoted by diam(G). A Hamiltonian path in a graph G is a path which contains every vertex of G.

We write K_n, C_n and P_n for a complete graph, a cycle and a path of order n, respectively, while $G[S],$ W_n and $K_{n_1,n_2,\dots ,n_p}$ denote the subgraph of G induced by a subset $S\subseteq V(G)\cup E(G)$ of G, a wheel of order n + 1, and a complete p-partite graph, respectively. The complement of a graph G, denoted by $\overline{G},$ is a graph with the vertex set V(G) and for every two vertices v and w, $vw\in E(\overline{G})$ if and only if $vw\notin E(G).$ The line graph L(G) of G is a graph with the vertex set E(G) and two vertices of L(G) are adjacent when they are incident in G.

Domination in graphs is now well studied in graph theory and the literature on this subject has been surveyed and detailed in the two books by Haynes, Hedetniemi, and Slater [2, 3]. A famous type of them is total domination. The literature on the subject Total domination in graphs has been surveyed and detailed in the recent book [4] by Henning and Yeo.

Definition 1.1.

A subset $S\subset V$ of a graph G is called a total dominating set, briefly TDS, of G if each vertex of V is adjacent to a vertex in S, and the minimum cardinality of a total dominating set is called the total domination number ${\gamma }_t(G)$ of G.

Y. Zhao, L. Kang, and M. Y. Sohn in [6] introduced another domination number as follows.

Definition 1.2.

[6] A subset $S\subseteq V\cup E$ of a graph G is called a mixed dominating set, briefly MDS, of G if each element of $(V\cup E)-S$ is either adjacent or incident to an element of S, and the mixed domination number ${\gamma }_m(G)$ of G is the minimum cardinality of a mixed dominating set.

Here, we define the concepts of total mixed dominating set and total mixed domination number of a graph.

Definition 1.3.

A subset $S\subseteq V\cup E$ of a graph G with $\delta (G)\ge 1$ is a total mixed dominating set, briefly TMDS, of G if each element of $V\cup E$ is either adjacent or incident to an element of S, and the total mixed domination number ${\gamma }_{tm}(G)$ of G is the minimum cardinality of a total mixed dominating set.

The goal of this paper is to initiate studying of total mixed domination number of a graph as follows. In Sec. 2, we give some tight lower and upper bounds for the total mixed domination number of a connected graph in terms of some parameters such as the order of the graph or the total domination numbers of the graph and its line graph. Also we discuss on the relation between the total mixed domination number of a graph with its diameter. In Sec. 3, study of total mixed domination number of trees and 2-corona graphs is our first work. Then, we show that the total mixed domination number of a graph is equal to the total domination number of its total graph. In Sec. 4, we will calculate the total mixed domination number of the paths, cycles, complete bipartite graphs, complete graphs and wheels. Finally, in the last section we present some open problems that can be as some motivations for next works on this topic.

Here, we fix a notation for the vertex set, the edge set and open neighborhood of a graph which are used thorough this paper. For a graph G with the vertex set $V=\left\{v_i\right|1\le i\le n\},\mathbb{E}(G)$ or simply $\mathbb{E}$ denotes the edge set of G in which an edge $v_i{v}_j$ is denoted by e_ij. Then $V(L(G))=\mathbb{E},$ and the edge set of L(G) is the set $\{e_{ij}{e}_{ik} | e_{ij},e_{ik}\in \mathbb{E}\}.$ A min-TDS/min-TMDS of G denotes a TDS/TMDS of G with minimum cardinality. Also we agree that a vertex v dominates an edge e or an edge e dominates a vertex v mean $v\in e.$ Similarly, we agree that an edge dominates another edge means they have a common vertex.

2. Some bounds

Here, we give some tight bounds for the total mixed domination number of a connected graph in terms of some parameters such as order of the graph or the total domination numbers of the graph and its line graph. Also we discuss on the relation between the total mixed domination number of a graph and its diameter. First an observation.

Observation 2.1.

Let G be a graph with the vertex set $V=\{v_i | 1\le i\le n\}$ and $\delta (G)\ge 1.$

• A subset $S\subseteq \mathbb{E}$ is a TDS of L(G) if and only if $\{i,j | e_{ij}\in \mathbb{E}\}\cap \{i,j | e_{ij}\in S\}\ne \varnothing .$

• A TDS $S\mathrm{ }\text{of}\mathrm{ }G$ is a TMDS of G if and only if $\overline{S}$ is independent in G.

Theorem 2.2.

Let G be a connected graph with $\delta (G)\ge 1$. Then $$\max \{{\gamma }_t(G),{\gamma }_t(L(G))\}\le {\gamma }_{tm}(G)\le {\gamma }_t(L(G))+{\gamma }_t(G),$$ and the bounds are tight.

Proof.

Let G be a connected graph with the vertex set $V=\{v_1,\dots ,v_n\}$ and edge set $\mathbb{E}$ and let e_ij denote the edge $v_i{v}_j.$ Then $V(L(G))=\mathbb{E}\mathrm{ }\text{and}\mathrm{ }E(L(G))=\{e_{ij}{e}_{i^{\prime }{j}^{\prime }} | \{i,j\}\cap \{i^{\prime },j^{\prime }\}\ne \varnothing \}.$ Since the union of a TDS of G and a TDS of L(G) is a TMDS of G, we have ${\gamma }_{tm}(G)\le {\gamma }_t(L(G))+{\gamma }_t(G).$ To prove the lower bound, let S be a min-TMDS of G. If either every vertex of V is dominated by a vertex in $S\cap V,$ or every edge of $\mathbb{E}$ is dominated by an edge in $S\cap \mathbb{E},$ then $S\setminus \mathbb{E}\mathrm{ }\text{or}\mathrm{ }S\setminus V$ is a TDS of $G\mathrm{ }\text{or}\mathrm{ }L(G),$ respectively, and there is nothing to prove. Otherwise, $$\begin{array}{cc}S{\prime }_G\hfill & =(S\setminus \mathbb{E})\cup \{v_i | v_i\mathrm{ }\text{is}\mathrm{ }\text{adjacent}\mathrm{ }\text{to}\mathrm{ }\text{some}\mathrm{ }{v}_j\in S\mathrm{ }\text{such}\mathrm{ }\text{that}\mathrm{ }{N}_{T(G)}(v_j)\cap S\subseteq \mathbb{E}\}\hfill \\ \hfill & \cup \{v_i,v_j | e_{ij},e_{jk}\in S\mathrm{ }\text{but}\mathrm{ }{v}_j,v_k\notin S\}\hfill \end{array}$$ is a TDS of G with cardinality at most $\left|S\right|.$ Since also by changing the roles of $G\mathrm{ }\text{and}\mathrm{ }L(G)$ we may obtain a TDS $S{\prime }_L\mathrm{ }\text{of}\mathrm{ }L(G)$ with cardinality at most $\left|S\right|,$ we have proved $$\max \{{\gamma }_t(G),{\gamma }_t(L(G))\}\le \max \left\{\right|S{\prime }_G|,|S{\prime }_L\left|\right\}\le \left|S\right|={\gamma }_{tm}(G).$$

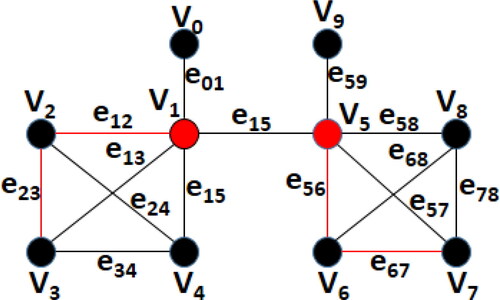
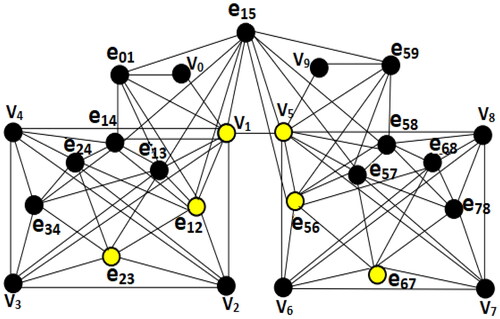
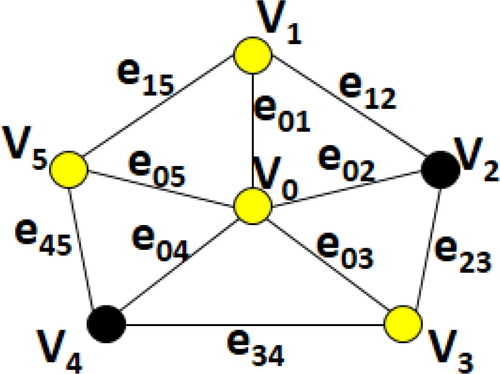
The lower bound is tight for the complete graphs $K_{3n}$ by Propositions 4.6 and 4.7 when $\max \{{\gamma }_t(G),{\gamma }_t(L(G))\}={\gamma }_t(L(G)).$ The case $\max \{{\gamma }_t(G),{\gamma }_t(L(G))\}={\gamma }_t(G)={\gamma }_{tm}(G)$ is discussed in Corollary 2.3. To show that the upper bound is tight, consider the graph G illustrated in Figure 1 with ${\gamma }_t(G)=2$ (because $\{v_1,v_5\}$ is a min-TDS) and ${\gamma }_t(L(G))=4$ by Observation 2.1 (because $\{e_{12},e_{23},e_{56},e_{67}\}$ is a TDS of L(G) and for any set $\{e_{ij},e_{jk},e_{k\ell }\}$ we have $\{i,j,k,\ell \}\ne \{0,1,\dots 9\}$). Hence it is sufficient to prove ${\gamma }_{tm}(G)=6.$ First since $\{v_1,v_5,e_{56},e_{67},e_{12},e_{23}\}$ is a TMDS of G, we have ${\gamma }_{tm}(G)\le 6.$ Let $G_1\mathrm{ }\text{and}\mathrm{ }{G}_2$ be the subgraphs of G induced by $\{v_i | 0\le i\le 4\left\}\mathrm{ }\text{and}\mathrm{ }\right\{v_i | 5\le i\le 9\},$ respectively, which are isomorphic together (see Figure 2). And let also S be a TMDS of G such that $|S\cap (V(G_2)\cup \mathbb{E}(G_2))|\ge |S\cap (V(G_1)\cup \mathbb{E}(G_1))|\ge 2.$ By the contrary, let $|S\cap (V(G_1)\cup \mathbb{E}(G_1))|=2.$ Since $N_{T(G)}(v_0)\cap S\subseteq \{v_1,e_{01}\},$ we have $S\cap (V(G_1)\cup \mathbb{E}(G_1))=\{e_{01},w\}$ for some $w\in \{v_1,v_0,e_{1j} | 2\le j\le 4\}\mathrm{ }\text{or}\mathrm{ }S\cap (V(G_1)\cup \mathbb{E}(G_1))=\{v_1,w\}$ for some $w\in \{v_j,e_{1j} | 2\le j\le 4\}\cup \{v_0,e_{01}\}.$ Hence $S\cap (V(G_1)\cup \mathbb{E}(G_1))$ is one the sets $\{e_{01},v_j\}$ for some j = 0, 1, or $\{e_{01},e_{1j}\}$ for some j = 2, 3, 4, or $\{v_1,v_j\}$ for some $j=0,2,3,4,$ or $\{v_1,e_{1j}\}$ for some $j=0,2,3,4.$ Since in each case $N_{T(G)}(e_{k\ell })\cap S=\varnothing$ for some $k,\ell \in \{2,3,4\}-\left\{j\right\},$ we conclude $|S\cap (V(G_1)\cup \mathbb{E}(G_1))|\ge 3$ and so ${\gamma }_{tm}(G)=6.$ □

Figure 1. The illustration of the graphs G (left) and L(G) (right) discussed in Theorem 2.2.

Figure 2. The set $\{v_1,v_5,e_{56},e_{67},e_{12},e_{23}\}$ is a min-TMDS of the graph G.

Figure 7. The total graph $T(P_{12})$ with a min-TDS $\{v_2,v_3,e_{56},e_{67},v_9,v_{10},v_{11}\},$ and the connected components $G_1,G_2,G_3$ that are arranged from left to right where $V(G_1)=\{v_2,v_3\},V(G_2)=\{e_{56},e_{67}\} \text{and} V(G_3)=\{v_9,v_{10},v_{11}\}.$

Corollary 2.3.

For any graph G which has a min-TDS such that its complement is an independent set, ${\gamma }_t(G)={\gamma }_{tm}(G).$

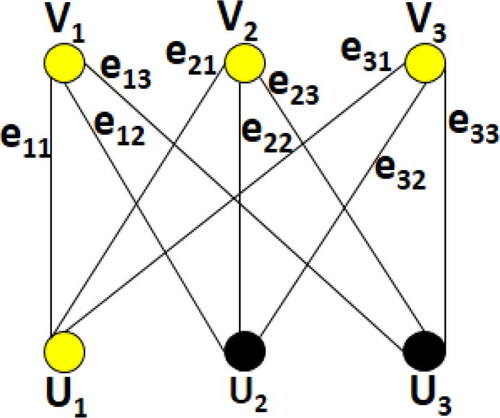
For an example, ${\gamma }_t(G)={\gamma }_{tm}(G)\mathrm{ }\text{where}\mathrm{ }G$ is the complete bipartite graph $K_{1,n}$ or its derivation $S_{1,n,n}$ (we recall that the derivation of a graph is the graph which is obtained by replacing every its edge by a path of length 2). In Figure 3, the set of yellow vertices $\{v_0,v_1,v_2,v_3\}$ is both a min-TDS and a min-TMDS of $S_{1,3,3}.$

Figure 3. The set $\{v_0,v_1,v_2,v_3\}$ is both a min-TDS and a min-TMDS of $S_{1,3,3}.$

The next theorem improves the upper bound given in Theorem 2.2 when either the line graph L(G) has a min-TDS D such that there exist less than ${\gamma }_t(G)$ disjoint maximal cliques in $L(G)\setminus D,$ or G has a min-TDS S such that the minimum size of vertex cover of $G\setminus S$ is less than ${\gamma }_t(L(G))$ (recall that a vertex cover of G is a subset $\mathit{S} \text{of} V(G)$ such that each edge of G has a vertex in S and the $\beta (G)$ denotes the minimum size of a vertex cover of G).

Theorem 2.4.

For any connected graph $G\mathrm{ }\text{with}\mathrm{ }\delta (G)\ge 1$, let c_D be the minimum number of disjoint maximal cliques in $L(G)\setminus D\mathrm{ }\text{where}\mathrm{ }D$ is a min-TDS of L(G), and let $\beta (G\setminus S)$ be the minimum size of a vertex cover of $G\setminus S\mathrm{ }\text{where}\mathrm{ }S$ is a min-TDS of G. Then, by the assumptions c_L(G) = min{c_D | D is a min-TDS of L(G)} and β_G = min{β(G\S) | S is a min-TDS of G}, $${\gamma }_{tm}(G)\le \min \{{\gamma }_t(L(G))+c_{L(G)},{\gamma }_t(G)+{\beta }_G\}.$$

Proof.

We show that the total mixed domination number of G is at most the minimum of the given set, when $G=(V,\mathbb{E})$ is a connected graph with $\delta (G)\ge 1\mathrm{ }\text{and}\mathrm{ }V=\{v_1,\dots ,v_n\},$ and e_ij denotes the edge $v_i{v}_j.$ So $E(L(G))=\{e_{ij}{e}_{ik} | e_{ij},e_{ik}\in \mathbb{E}\}.$ First we prove ${\gamma }_{tm}(G)\le {\gamma }_t(L(G))+c_{L(G)}.$ Let D be a min-TDS of L(G) such that $c_{L(G)}=c_D.$ Obviously D dominates all elements of $E(L(G))\cup \{v_i | e_{ij}\in D\mathrm{ }\text{for}\mathrm{ }\text{some}\mathrm{ }j\}.$ Let $\mathcal{C}$ be a subset of $E(L(G))$ with cardinality $c_{L(G)}$ such that every maximal clique of $L(G)\setminus D$ has exactly one vertex in $\mathcal{C},$ and let v_i be a vertex that does not dominated by D. Since $N_{L(G)}(v_i)=\left\{e_{ij}\right|v_i{v}_j\in E(G)\}$ is a maximal clique in $L(G)\setminus D,$ we are sure that v_i is dominated by the unique vertex which is in $\mathcal{C}\cap N_{L(G)}(v_i).$ Thus $D\cup \mathcal{C}$ is a TMDS of G, and so ${\gamma }_{tm}(G)\le |D\cup \mathcal{C}|={\gamma }_t(L(G))+c_{L(G)}.$ In a similar way, the inequality ${\gamma }_{tm}(G)\le {\gamma }_t(G)+{\beta }_G$ can be proved and this completes our proof. □

As we show in below, our motivation to state Theorem 2.4 is existence of graphs that the upper bound in Theorem 2.4 is better for them than the upper bound in Theorem 2.2. Let W_n be a wheel of order $n+1\ge 4$ with the vertex set $V=\{v_i | 0\le i\le n\}$ and the edge set $\mathbb{E}=\{e_{0i},e_{i(i+1)} | \text{for} 1\le i\le n\}.$ Then, since $S=\{v_0,v_1\}$ is a min-TDS of $W_n,{\gamma }_t(W_n)=2.$ On the other hand, $W_n\setminus S\cong P_{n-1}\mathrm{ }\text{implies}\mathrm{ }{\beta }_{W_n}=\beta (P_{n-1})=\lfloor \frac{n-1}{2}\rfloor .$ Hence ${\gamma }_t(W_n)+{\beta }_{W_n}=2+\lfloor \frac{n-1}{2}\rfloor =\lceil \frac{n}{2}\rceil +1.$ Since ${\gamma }_t(L(W_n))=\lceil \frac{n}{2}\rceil$ by Lemma 2.5, we have $$\begin{array}{c}\min \{{\gamma }_t(L(W_n))+c_{L(W_n)},{\gamma }_t(W_n)+{\beta }_{W_n}\}=\min \{\lceil \frac{n}{2}\rceil +c_{L(W_n)},\lceil \frac{n}{2}\rceil +1\}\hfill \\ \hfill & =\lceil \frac{n}{2}\rceil +1\hfill \\ \hfill & ={\gamma }_{tm}(W_n) (\text{by Proposition}\mathrm{ }4.8)\hfill \\ \hfill & <{\gamma }_t(L(W_n))+{\gamma }_t(W_n).\hfill \end{array}$$

Lemma 2.5.

For any wheel W_n of order $n+1\ge 4,{\gamma }_t(L(W_n))=\lceil \frac{n}{2}\rceil .$

Proof.

Let W_n be a wheel of order $n+1\ge 4$ with the vertex set $V=\{v_i | 0\le i\le n\}$ and the edge set $\mathbb{E}=\{e_{0i},e_{i(i+1)} | \text{for} 1\le i\le n\}$ (note: n + 1 is considered 1 to modulo n). Let S be a TDS of $L(W_n)\mathrm{ }\text{where}\mathrm{ }V(L(W_n))=\mathbb{E}.$ Then $\{i,i+1\}\cap \{1,2,\dots ,n\}\ne \varnothing$ for each $1\le i\le n$ because of $N_{W_n}(e_{i(i+1)})\cap S=\{v_i,v_{i+1}\}\cap S\ne \varnothing .$ Hence $\left|S\right|\ge \lceil \frac{n}{2}\rceil .$ Now since $\{e_{0(2i-1)} | 1\le i\le \lceil \frac{n}{2}\rceil \}$ is a TDS of $L(W_n),$ we have ${\gamma }_t(L(W_n))=\lceil \frac{n}{2}\rceil .$ □

Lemma 2.5 shows the upper bound in Theorem 2.4 is tight for any wheel. We know for any graph G with a non-empty edge set, ${\gamma }_{tm}(G)\ge 2$, and Corollary 2.3 characterizes graphs $G\mathrm{ }\text{satisfy}\mathrm{ }{\gamma }_{tm}(G)=2.$ The next theorem gives a sufficient condition for that the total mixed domination number of a graph be at least 3.

Theorem 2.6.

For any connected graph G of order at least $2,{\gamma }_{tm}(G)=2\mathrm{ }\mathit{implies}\mathit{diam}\mathrm{ }(G)\le 3.$

Proof.

Let $G=(V,\mathbb{E})$ be a connected graph with $\mathit{diam}(G)\ge 4$ and $\delta (G)\ge 1$ in which $V=\{v_1,\dots ,v_n\}.$ The condition $\mathit{diam}(G)\ge 4$ implies that G has a path P of length at least 4 as an induced subgraph of G. Let S be a min-TMDS of G of cardinality 2. If $\mathit{S} \text{is} \{v_i,v_j\}\mathrm{ }\text{or}\mathrm{ }\{v_i,e_{ij}\}$ for some i, j, then $N_{T(G)}(e_{pq})\cap S=\varnothing$ for some $v_p,v_q\in V(P),$ a contradiction. Also if $S=\{e_{ij},e_{jk}\}$ for some i, j, k, then $N_{T(G)}(v_{\ell })\cap S=\varnothing$ for some $v_{\ell }\in V(P)$ such that $\ell \ne i,j,k,$ a contradiction. So ${\gamma }_{tm}(G)\ne 2.$ □

Now, we present another upper bound for ${\gamma }_{tm}(G)$ in term of the order of the graph which is tight by Proposition 4.6.

Theorem 2.7.

For any connected graph G of order $n\ge 2$ which has a Hamiltonian path, ${\gamma }_{tm}(G)\le \lceil \frac{5n}{3}\rceil -n.$

Proof.

Let $P:v_1{v}_2\cdots v_n$ be a Hamiltonian path in a connected graph G of order $n\ge 2.$ Since each of the sets $$\begin{array}{c}{S}_0=\{e_{(3i+1)(3i+2)}{e}_{(3i+2)(3i+3)}\hfill \\ | 0\le i\le \lfloor \frac{n}{3}\rfloor -1\}\hfill & \text{if}\mathrm{ }n\equiv 0\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right),\hfill \\ S_1=S_0\cup \left\{e_{(n-1)n}\right\}\hfill & \text{if}\mathrm{ }n\equiv 1\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right),\hfill \\ S_2=S_0\cup \{e_{(n-2)(n-1)},e_{(n-1)n}\}\hfill & \text{if}\mathrm{ }n\equiv 2\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right),\hfill \end{array}$$ is a TMDS of G, the result holds. □

3. Trees, 2-corona graphs and total graphs

The facts that $\mathit{diam}(C_4)=2 and {\gamma }_{tm}(C_4)=3$ show that the converse of Theorem 2.6 is not true in general. But next theorem shows that it holds for trees.

Theorem 3.1.

For any tree $\mathbb{T}$ of order at least $2,{\gamma }_{tm}(\mathbb{T})=2$ if and only if $\mathit{diam}(\mathbb{T})\le 3.$

Proof.

By Theorem 2.6, it is sufficient to prove that $\mathit{diam}(\mathbb{T})\le 3\mathrm{ }\text{implies}\mathrm{ }{\gamma }_{tm}(\mathbb{T})=2.$ If $\mathit{diam}(\mathbb{T})=1,$ then $\mathbb{T}\cong K_2$ and so ${\gamma }_{tm}(\mathbb{T})=2.$ If $\mathit{diam}(\mathbb{T})=2,$ then $\mathbb{T}$ is isomorphic to the complete bipartite graph $K_{1,n-1}$ and so ${\gamma }_{tm}(\mathbb{T})=2$ by Proposition 4.4. Now let $\mathit{diam}(\mathbb{T})=3.$ Then $\mathbb{T}$ is a double star tree which is obtained by joining the central vertex v of a tree $K_{1,p}$ and the central vertex w of a tree $K_{1,q}\mathrm{ }\text{where}\mathrm{ }p+q=n-2.$ Since {v, w} is a TMDS of $\mathbb{T},$ we have ${\gamma }_{tm}(\mathbb{T})=2.$ □

Next theorem improves the upper bound given in Theorem 2.7 for trees.

Theorem 3.2.

For any tree $\mathbb{T}$ of order $n\ge 3,{\gamma }_{tm}(\mathbb{T})\le \lfloor \frac{2n}{3}\rfloor .$

Proof.

Let $\mathbb{T}=(V,\mathbb{E})$ be a tree in which $V=\{v_i | 1\le i\le n\}.$ Choose a leaf $v\mathrm{ }\text{of}\mathrm{ }\mathbb{T}$ and label each vertex of $\mathbb{T}$ with its distance from v to modulo 3. This partitions V to the three independent sets $A_0,A_1\mathrm{ }\text{and}\mathrm{ }{A}_2\mathrm{ }\text{where}\mathrm{ }{A}_i=\{u\in V | d_{\mathbb{T}}(u,v)\equiv i\hspace{0.5em}(\mathrm{mod\hspace{0.5em}}3)\}\mathrm{ }\text{for}\mathrm{ }0\le i\le 2.$ Then by the pigeonhole principle at least one of them, say A₀, contains at least one third of the vertices of $\mathbb{T},$ and so $|A_1\cup A_2|\le \lfloor \frac{2n}{3}\rfloor .$ We see that every non-leaf and every leaf $v_i\in V(\mathbb{T})-A_1\cup A_2$ is adjacent to some vertex in $A_1\cup A_2.$ If needed, we replace every leaf $v_i\in A_1\cup A_2$ by an its neighbour out of $A_1\cup A_2.$ The obtained set S by this way is a TMDS of $\mathbb{T}.$ Because obviously $N_{\mathbb{T}}(v_i)\cap S\ne \varnothing$ for each $v_i\in V(\mathbb{T}),$ and $\{v_i,v_j\}\cap S\ne \varnothing$ for each $e_{ij}\in \mathbb{E}$ (because $d_{\mathbb{T}}(v,v_i)\cancel{\equiv }{d}_{\mathbb{T}}(v,v_j)\hspace{0.5em}(\mathrm{mod\hspace{0.5em}}3)$), and so every $e_{ij}\in \mathbb{E}$ is dominated by $v_i\in S\mathrm{ }\text{or}\mathrm{ }{v}_j\in S.$ Therefore ${\gamma }_{tm}(\mathbb{T})\le \left|S\right|\le \lfloor \frac{2n}{3}\rfloor .$ □

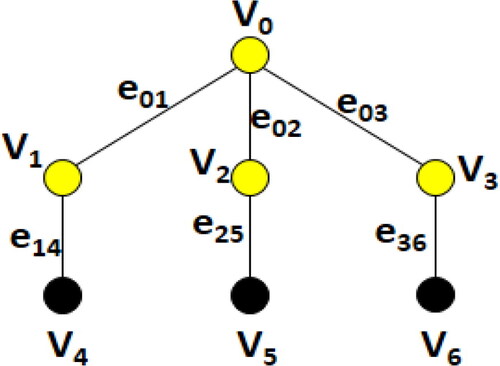
In the next theorem, we show that for every graph G of order n the total mixed domination number of $G°P_2\mathrm{ }\text{is}\mathrm{ }2n,$ where $G°P_2$ is the 2-corona of G which is obtained from G by adding a path of length 2 to each vertex of G. Figure 4 shows the graph $P_6°P_2.$

Figure 4. The set $\{v_i | 1\le i\le 12\}$ is a min-TMDS of $P_6°P_2.$

Theorem 3.3.

For any connected graph G of order $n\ge 2,{\gamma }_{tm}(G°P_2)=2n.$

Proof.

Let $G=(V,\mathbb{E})$ be a connected graph in which $V=\{v_i | 1\le i\le n\}.$ Then $V(G°P_2)=\{v_i | 1\le i\le 3n\}\mathrm{ }\text{and}E(G°P_2)=\mathbb{E}\cup \{e_{i(n+i)},e_{(n+i)(2n+i)} | 1\le i\le n\}.$ Since $\{v_i,v_{n+i} | 1\le i\le n\}$ is a TMDS of $G°P_2,$ we have ${\gamma }_{tm}(G°P_2)\le 2n.$

Now let S be a min-TMDS of $G°P_2.$ Then $\{v_{n+i},e_{(n+i)(2n+i)}\}\cap S$ contains an element w_i (because $N_{T(G°P_2)}(v_{2n+i})\cap S\ne \varnothing$) for each $1\le i\le n.$ Since also every w_i must be dominated by an element $w{\prime }_i\in N_{T(G°P_2)}(w_i)\cap S,$ and all of the elements $w_i\mathrm{ }\text{and}\mathrm{ }w{\prime }_i$ are distinct, we conclude that S includes the set $\{w_i,w{\prime }_i | 1\le i\le n\}$ of cardinality 2n, and so ${\gamma }_{tm}(G°P_2)\ge 2n,$ which completes our proof. For an example, Figure 4 shows $P_6°P_2$ with the min-TMDS $\{v_i | 1\le i\le 12\}$ of it. □

By Theorem 3.3 the upper bound in Theorem 3.2 is tight for any 2-corona $\mathbb{T}°P_2$ in which $\mathbb{T}$ is a tree of order $n\ge 3.$

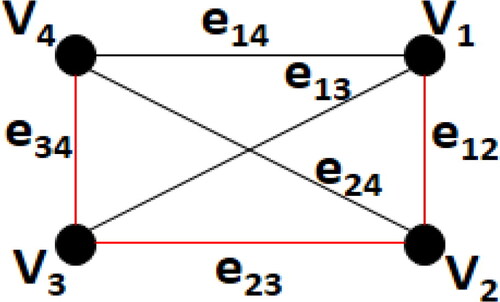
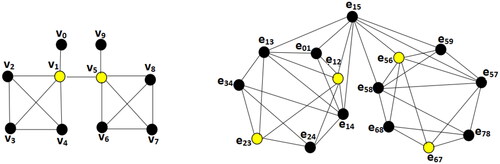
The total graph T(G) of a graph $G=(V,\mathbb{E})$ is the graph whose vertex set is $V\cup \mathbb{E}$ and two vertices are adjacent whenever they are either adjacent or incident in G [1]. It is obvious that if G has order n and size m, then T(G) has order n + m and size $3m+|E(L(G))|,$ and also T(G) contains both $G\mathrm{ }\text{and}\mathrm{ }L(G)$ as two induced subgraphs and it is the largest graph formed by adjacent and incidence relation between graph elements. See Figure 5 for an example.

Figure 5. The total graph of the graph in Figure 1 with the min-TDS $\{v_1,v_5,e_{12},e_{23},e_{56},e_{67}\}.$

It is clear that a total mixed dominating set of a graph G corresponds with a total dominating set of the total graph $T(G)\mathrm{ }\text{of}\mathrm{ }G.$ Hence we have the next theorem, and so to find the total mixed domination number of a graph we may calculate the total domination number of the total graph of the graph.

Theorem 3.4.

For any graph $G\mathrm{ }\mathit{\text{with}}\mathrm{ }\delta (G)\ge 1,{\gamma }_{tm}(G)={\gamma }_t(T(G)).$

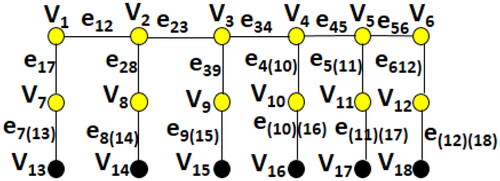
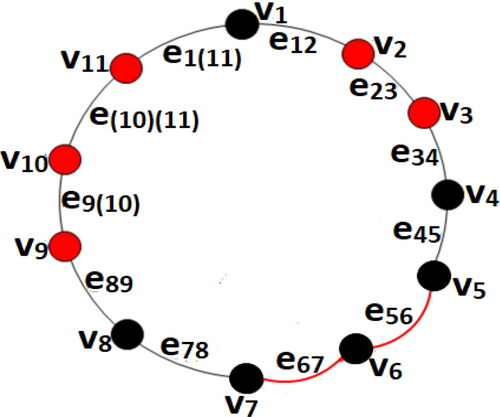
As we will see in Proposition 4.1, for an example of Theorem 3.4, while Figure 6 shows a path P12 with a min-TMDS, Figure 7 shows the total graph of the path with the same set as a min-TDS of it.

4. Some classes of graphs

In this section, we present formulas for the total mixed domination number of some known classes of graphs. The first two propositions are devoted to the paths and cycles.

Proposition 4.1.

For any path P_n of order $n\ge 2,$ $${\gamma }_{tm}(P_n)=\{\begin{array}{cc}4\lceil \frac{n}{7}\rceil -3\hfill & \mathit{\text{if}}\mathrm{ }n\equiv 1\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}7\right),\hfill \\ 4\lceil \frac{n}{7}\rceil -2\hfill & \mathit{\text{if}}\mathrm{ }n\equiv 2,3,4\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}7\right),\hfill \\ 4\lceil \frac{n}{7}\rceil -1\hfill & \mathit{\text{if}}\mathrm{ }n\equiv 5\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}7\right),\hfill \\ 4\lceil \frac{n}{7}\rceil \hfill & \mathit{\text{if}}\mathrm{ }n\equiv 0,6\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}7\right).\hfill \end{array}$$

Proof.

By Theorem 3.4, we calculate the total domination number of $T(P_n)\mathrm{ }\text{when}\mathrm{ }{P}_n=(V,\mathbb{E})$ is a path of order $n\ge 2$ in which $V=\{v_1,v_2,\cdots ,v_n\}$ and $\mathbb{E}=\{e_{i(i+1)} | 1\le i\le n-1\}.$ Then $V(T(P_n))=V\cup \mathbb{E}\mathrm{ }\text{and}\mathrm{ }E(T(P_n))=\mathbb{E}\cup E(L(P_n))\cup \{e_{i(i+1)}{v}_i,e_{i(i+1)}{v}_{i+1} | 1\le i\le n-1\}$ in which $E(L(P_n))=\{e_{i(i+1)}{e}_{(i+1)(i+2)} | 1\le i\le n-2\}.$

Claim: There exists a min-TDS $S\mathrm{ }\text{of}\mathrm{ }T(P_n)$ with the following three properties.

P.1. $V(G_i)\subseteq V$ if and only if $V(G_{i+1})\subseteq \mathbb{E}$ for each i,

P.2. $|V(G_i)|=2$ for each i, perhaps except for i = w,

P.3. $V(G_1)\subseteq V,$

in which $G_1,\cdots ,G_w$ are all connected components of the induced subgraph $T(P_n)[S]$ that are arranged from left to right in $T(P_n)$ (see Figure 7 for an example).

Figure 6. A path P₁₂ with a min-TMDS $\{v_2,v_3,e_{56},e_{67},v_9,v_{10},v_{11}\}.$

By proving the claim, each of the sets $$\begin{array}{c}{S}_0=\{v_{7i+2},v_{7i+3},e_{(7i+5)(7i+6)},\hfill \\ e_{(7i+6)(7i+7)} | 0\le i\le \lfloor \frac{n}{7}\rfloor -1\}\hfill & \text{if}\mathrm{ }n\equiv 0\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}7\right),\hfill \\ S=S_0\cup \left\{e_{(n-1)n}\right\}\hfill & \text{if}\mathrm{ }n\equiv 1\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}7\right),\hfill \\ S=S_0\cup \{v_{n-1},v_n\}\hfill & \text{if}\mathrm{ }n\equiv 2,3\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}7\right),\hfill \\ S=S_0\cup \{v_{n-2},v_{n-1}\}\hfill & \text{if}\mathrm{ }n\equiv 4\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}7\right)\hfill \\ S=S_0\cup \{v_{n-3},v_{n-2},v_{n-1}\}\hfill & \text{if}\mathrm{ }n\equiv 5\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}7\right),\hfill \\ S=S_0\cup \{v_{n-4},v_{n-3},e_{(n-2)(n-1)},e_{(n-1)n}\}\hfill & \text{if}\mathrm{ }n\equiv 6\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}7\right)\hfill \end{array}$$ will be a min-TDS of $T(P_n),$ and this completes our proof.

Proof

of the claim: Let S be a min-TDS of $T(P_n).$ We may assume for every $e\in E(T(P_n)[S]),e=v_i{v}_{i+1}\mathrm{ }or\mathrm{ }e=e_{i(i+1)}{e}_{(i+1)(i+2)}$ for some i. Because otherwise if $e=v_i{e}_{(i-1)i}\mathrm{ }or\mathrm{ }e=v_i{e}_{i(i+1)}$ for some i, then we can replace $S\mathrm{ }\text{by}\mathrm{ }(S-\{v_i\})\cup \left\{e_{i(i+1)}\right\}\mathrm{ }\text{or}\mathrm{ }(S-\{e_{i(i+1)}\})\cup \left\{v_{i+1}\right\},$ respectively, that each of them is again a min-TDS of $T(P_n).$ So we may assume that every connected component of $T(P_n)[S]$ is a path of order at least 2 whose vertex set is either a subset of V or a subset of $\mathbb{E}.$ By the minimality of S, we have $|V(G_i)|\le 4$ for each i. Our proof will be completed by showing that S satisfies the above three property.

P.1: Let $V(G_j)=\left\{v_i\right|\ell \le i\le k\}$ and $V(G_{j+1})=\left\{v_i\right|k+2\le i\le k+r\}$ for some $j,\ell ,k,r.$ Then we can replace $S\mathrm{ }\text{by}\mathrm{ }(S\setminus V(G_{j+1}))\cup \left\{e_{i(i+1)}\right|k+2\le i\le k+r\}$ which is again a min-TDS of $T(P_n).$ There is a similar proof when both of $V(G_i)\mathrm{ }\text{and}\mathrm{ }V(G_{i+1})$ are subsets of $\mathbb{E}.$

P.2: Since the case $V(G_i)\subseteq \mathbb{E}$ has a similar proof, we assume $V(G_i)\subseteq V.$ If for some $i\mathrm{ }\text{and}\mathrm{ }j,V(G_i)=\{v_j,v_{j+1},v_{j+2},v_{j+3}\},$ then we can replace $V(G_i)\mathrm{ }\text{by}\mathrm{ }\{v_{j+2},v_{j+3}\}\cup \{e_{(j-1)j},e_{j(j+1)}\}\mathrm{ }\text{or}\mathrm{ }\{v_j,v_{j+1}\}\cup \{e_{(j+2)(j+3)},e_{(j+3)(j+4)}\},$ and find the min-TDSs $(S-\{v_j,v_{j+1}\})\cup \{e_{(j-1)j},e_{j(j+1)}\}\mathrm{ }\text{or}\mathrm{ }(S-\{v_{j+2},v_{j+3}\})\cup \{e_{(j+2)(j+3)},e_{(j+3)(j+4)}\},$ respectively. Now let $V(G_i)=\{v_{j+1},v_{j+2},v_{j+3}\}$ for some $i\mathrm{ }\text{and}\mathrm{ }j.$ Then $V(G_{i+1})\subseteq \mathbb{E}$ by P.1, and $j+4=\min \{m | e_{m(m+1)}\in V(G_{i+1})\}$ by the minimality of $\left|S\right|.$ Then we can replace S by the min-TDS $(S-\{v_{j+2}\})\cup \left\{e_{(j+3)(j+4)}\right\}\mathit{ofT}(P_n).$

P.3: Since S is minimum, P.3 holds. □

Proposition 4.2.

For any cycle C_n of order $n\ge 3,$ $${\gamma }_{tm}(C_n)=\{\begin{array}{cc}4\lceil \frac{n}{7}\rceil -3\hfill & if\mathrm{ }n\equiv 1\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}7\right),\hfill \\ 4\lceil \frac{n}{7}\rceil -2\hfill & if\mathrm{ }n\equiv 2,3\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}7\right),\hfill \\ 4\lceil \frac{n}{7}\rceil -1\hfill & if\mathrm{ }n\equiv 4\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}7\right),\hfill \\ 4\lceil \frac{n}{7}\rceil \hfill & if\mathrm{ }n\equiv 0,5,6\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}7\right).\hfill \end{array}$$

Proof.

Let $C_n=(V,\mathbb{E})$ be a cycle of order $n\ge 3$ in which $V=\{v_1,v_2,\dots ,v_n\}$ and $\mathbb{E}=\{e_{i(i+1)} | 1\le i\le n\}.$ Then $V(T(C_n))=V\cup \mathbb{E}\mathrm{ }\text{and}\mathrm{ }E(T(C_n))=\{e_{i(i+1)}{v}_i,e_{i(i+1)}{v}_{i+1} | 1\le i\le n\}\cup \mathbb{E}\cup E(L(C_n))$ where $E(L(C_n))=\{e_{i(i+1)}{e}_{(i+1)(i+2)} | 1\le i\le n\}.$ In a similar way to the proof of Proposition 4.1, it can be easily verified that the sets $$\begin{array}{c}{S}_0=\{v_{7i+2},v_{7i+3},e_{(7i+5)(7i+6)},\hfill \\ e_{(7i+6)(7i+7)} | 0\le i\le \lfloor \frac{n}{7}\rfloor -1\}\hfill & \text{if}\mathrm{ }n\equiv 0\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}7\right),\hfill \\ S=S_0\cup \left\{e_{(n-1)n}\right\}\hfill & \text{if}\mathrm{ }n\equiv 1\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}7\right),\hfill \\ S=S_0\cup \{v_{n-1},v_n\}\hfill & \text{if}\mathrm{ }n\equiv 2,3\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}7\right),\hfill \\ S=S_0\cup \{v_{n-2},v_{n-1},v_n\}\hfill & \text{if}\mathrm{ }n\equiv 4\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}7\right)\hfill \\ S=S_0\cup \{v_{n-3},v_{n-2},v_{n-1},v_n\}\hfill & \text{if}\mathrm{ }n\equiv 5\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}7\right),\hfill \\ S=S_0\cup \{v_{n-4},v_{n-3},e_{(n-2)(n-1)},e_{(n-1)n}\}\hfill & \text{if}\mathrm{ }n\equiv 6\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}7\right).\hfill \end{array}$$ are min-TMDSs of C_n in each case, and this completes our proof. See Figure 8 as an example. □

Figure 8. The set $\{v_2,v_3,e_{56},e_{67},v_9,v_{10},v_{11}\}$ is a min-TMDS of C₁₁.

Propositions 4.1 and 4.2 show that the total mixed domination numbers of a cycle and a path of the same order are roughly same in the following meaning.

Corollary 4.3.

For any integer $n\ge 3,$ $${\gamma }_{tm}(C_n)=\{\begin{array}{cc}{\gamma }_{tm}(P_n)+1\hfill & if\mathrm{ }n\equiv 4,5\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}7\right),\hfill \\ {\gamma }_{tm}(P_n)\hfill & \mathit{otherwise}.\hfill \end{array}$$

In the next step, we calculate the total mixed domination number of a complete bipartite graph.

Proposition 4.4.

For any integers $n\ge m\ge 1,{\gamma }_{tm}(K_{m,n})=m+1.$

Proof.

Let $V\cup U$ be the partition of the vertex set of the complete bipartite graph $K_{m,n}$ to the independent sets $V=\{v_i | 1\le i\le m\}\mathrm{ }\text{and}\mathrm{ }U=\{u_j | 1\le j\le n\}.$ Since $V\cup \left\{u_1\right\}$ is a TMDS of $K_{m,n},$ we have ${\gamma }_{tm}(K_{m,n})\le m+1.$

Now, by the contrary, let S be a TMDS of $K_{m,n}$ with cardinality m. Since the subgraph of $K_{m,n}$ induced by V or U is isomorphic to the empty graphs $\overline{K_m}\mathrm{ }\text{or}\mathrm{ }\overline{K_n},$ respectively, we have $S⊈V\mathrm{ }\text{and}\mathrm{ }S⊈U.$ For $1\le i\le m\mathrm{ }\text{and}\mathrm{ }1\le j\le n,$ we define $R_i=\{e_{ih} | 1\le h\le n\}\mathrm{ }\text{and}\mathrm{ }{C}_j=\{e_{hj} | 1\le h\le m\}.$ Let $I=\{i | 1\le i\le m, R_i\cap S\ne \varnothing \}$ and $J=\{j | 1\le j\le n, C_j\cap S\ne \varnothing \}.$ Since $S\subseteq \mathbb{E}\mathrm{ }\text{implies}\mathrm{ }I\ne \{1,\cdots ,m\}\mathrm{ }\text{or}\mathrm{ }J\ne \{1,\cdots ,n\},$ and so for some $i\notin I$ or some $j\notin J,v_i\mathrm{ }\text{or}\mathrm{ }{u}_j$ is not dominated by S, we have $S⊈\mathbb{E}.$ Hence both of the sets $I_V=\{i | 1\le i\le m, v_i\in S\}$ and $J_U=\{j | 1\le j\le n, u_j\in S\}$ are nonempty. Because $I_V\ne \varnothing \mathrm{ }\text{and}\mathrm{ }{J}_U=\varnothing$ imply $N_{T(K_{m,n})}(v_i)\cap S=\varnothing$ for some i, and $I_V=\varnothing \mathrm{ }\text{and}\mathrm{ }{J}_U\ne \varnothing$ imply $N_{K_{m,n}}(u_j)\cap S=\varnothing$ for some j, which are contradictions. Therefore $R_i\cap S\ne \varnothing$ for each $i\notin I_V\mathrm{ }\text{or}\mathrm{ }{C}_j\cap S\ne \varnothing$ for each $j\notin J_U$ (beacause $R_i\cap S=\varnothing$ for some $i\notin I_V\mathrm{ }\text{and}\mathrm{ }{C}_j\cap S=\varnothing$ for some $j\notin J_U\mathrm{ }\text{imply}\mathrm{ }{N}_{T(K_{m,n})}(e_{ij})\cap S=\varnothing$). Hence $|S\cap (\mathbb{E}\setminus {\mathbb{E}}_{VU})|\ge \min \{n-|I_V|,m-|J_U\left|\right\}$ in which ${\mathbb{E}}_{VU}=\{e_{ij} | i\in I_V\mathrm{ }\text{and}\mathrm{ }j\in J_U\},$ and so $$\begin{array}{ccc}\left|S\right|\hfill & =\hfill & m\hfill \\ \hfill & \ge \hfill & |S\cap (\mathbb{E}\setminus {\mathbb{E}}_{VU})|+\left|I_V\right|+\left|J_U\right|\hfill \\ \hfill & \ge \hfill & \min \{n-|I_V|,m-|J_U\left|\right\}+\left|I_V\right|+\left|J_U\right|\hfill \\ \hfill & >\hfill & m,\hfill \end{array}$$ a contradiction. Therefore ${\gamma }_{tm}(K_{m,n})=m+1.$ See Figure 9 as an example. □

Figure 9. The set $\{v_1,v_2,v_3,u_1\}$ is a min-TMDS of $K_{3,3}.$

To find the total mixed domination number of a complete graph, we need next lemma.

Lemma 4.5.

Let S be a min-TMDS of a graph $G=(V,\mathbb{E})$ in which $V=\{v_1,\cdots ,v_n\}\mathrm{ }\mathit{\text{and}}\mathrm{ }\mathbb{E}=\{e_{ij} | v_i{v}_j\mathrm{ }\mathit{\text{is}}\mathrm{ }\mathit{\text{an}}\mathrm{ }\mathit{\text{edge}}\}$. If $A=\{v_i | v_i\notin S, e_{ij}\in S\mathrm{ }\mathit{\text{for}}\mathrm{ }\mathit{\text{some}}\mathrm{ }j\}$, then $$|S\cap \mathbb{E}|\ge \{\begin{array}{cc}\lfloor \frac{2\left|A\right|}{3}\rfloor \hfill & if\mathrm{ }\left|A\right|\equiv 0\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right),\hfill \\ \lfloor \frac{2\left|A\right|}{3}\rfloor +1\hfill & if\mathrm{ }\left|A\right|\cancel{\equiv }0\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right).\hfill \end{array}$$

Proof.

Let $G=(V,\mathbb{E})$ be a graph in which $V=\{v_1,\dots ,v_n\}\mathrm{ }\text{and}\mathrm{ }\mathbb{E}=\{e_{ij} | v_i{v}_j\mathrm{ }\text{is}\mathrm{ }\text{an}\mathrm{ }\text{edge}\}.$ Let S be a min-TMDS of G and let $A=\{v_i | v_i\notin S, e_{ij}\in S\mathrm{ }\text{for}\mathrm{ }\text{some}\mathrm{ }j\}.$ For any $B\subseteq A,$ we define ${\mathbb{E}}_B=\{e_{ij}\in S | \{v_i,v_j\}\cap B\ne \varnothing \}.$ If $N_G(v_i)\cap A=\varnothing$ for each $v_i\in A,$ then ${\mathbb{E}}_A\mathrm{ }\text{and}\mathrm{ }A$ have same cardinality, and so $|S\cap \mathbb{E}|\ge \left|{\mathbb{E}}_A\right|=\left|A\right|\ge \lfloor \frac{2\left|A\right|}{3}\rfloor +1,$ as desired. Therefore, we assume that there exist two vertices $v_i,v_j\in A\mathrm{ }\text{while}\mathrm{ }{e}_{ij}\in S,$ and continue our proof by induction on $\left|A\right|.$ It can be easily verified that for any $B\subseteq A$ with cardinality at most 2, the following inequality (4.0.1)(4.0.1) $$\left|{\mathbb{E}}_B\right|\ge \{\begin{array}{cc}\lfloor \frac{2\left|B\right|}{3}\rfloor \hfill & \text{if}\mathrm{ }\left|B\right|\equiv 0\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right),\hfill \\ \lfloor \frac{2\left|B\right|}{3}\rfloor +1\hfill & \text{if}\mathrm{ }\left|B\right|\cancel{\equiv }0\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right).\hfill \end{array}$$(4.0.1) holds, and we assume it holds for any set of cardinality less than $\left|A\right|.$ Then we may assume $e_{i\ell }\in N_{T(G)}(e_{ij})\cap S$ for some $\ell \ne j.$ By using the induction hypothesis for the set $B=A\setminus \{v_i,v_j,v_{\ell }\},$ which has cardinality $m-3\mathrm{ }\text{or}\mathrm{ }m-2,$ we have (4.0.1) $$\left|{\mathbb{E}}_B\right|\ge \{\begin{array}{cc}\lfloor \frac{2\left|B\right|}{3}\rfloor \hfill & \text{if}\mathrm{ }\left|B\right|\equiv 0\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right),\hfill \\ \lfloor \frac{2\left|B\right|}{3}\rfloor +1\hfill & \text{if}\mathrm{ }\left|B\right|\cancel{\equiv }0\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right).\hfill \end{array}$$(4.0.1) Now by inequality (4.0.1)(4.0.1) $$\left|{\mathbb{E}}_B\right|\ge \{\begin{array}{cc}\lfloor \frac{2\left|B\right|}{3}\rfloor \hfill & \text{if}\mathrm{ }\left|B\right|\equiv 0\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right),\hfill \\ \lfloor \frac{2\left|B\right|}{3}\rfloor +1\hfill & \text{if}\mathrm{ }\left|B\right|\cancel{\equiv }0\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right).\hfill \end{array}$$(4.0.1) and the fact that $\left|{\mathbb{E}}_A\right|\ge |{\mathbb{E}}_B\cup \{e_{ij},e_{i\ell }\left\}\right|=\left|{\mathbb{E}}_B\right|+2,$ our proof will be completed. □

Proposition 4.6.

For any complete graph K_n of order $n\ge 2,{\gamma }_{tm}(K_n)=\lceil \frac{5n}{3}\rceil -n.$

Proof.

Let K_n be a complete graph with the vertex set $V=\{v_1,v_2,\cdots ,v_n\}$ and the edge set $\mathbb{E}.$ First we notice $$\lceil \frac{5n}{3}\rceil -n=\{\begin{array}{cc}\lfloor \frac{2n}{3}\rfloor \hfill & \text{if}\mathrm{ }n\equiv 0\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right),\hfill \\ \lfloor \frac{2n}{3}\rfloor +1\hfill & \text{if}\mathrm{ }n\equiv 1,2\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right).\hfill \end{array}$$ By Propositions 4.1 and 4.2, we may assume $n\ge 4.$ For any arbitrary TMDS $S\mathrm{ }\text{of}\mathrm{ }{K}_n$ we show (4.0.2) $$\left|S\right|\ge \{\begin{array}{cc}\lfloor \frac{2n}{3}\rfloor \hfill & \text{if}\mathrm{ }n\equiv 0\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right),\hfill \\ \lfloor \frac{2n}{3}\rfloor +1\hfill & \text{if}\mathrm{ }n\equiv 1,2\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right).\hfill \end{array}$$(4.0.2) If $S\cap \mathbb{E}=\varnothing ,$ then $\left|S\right|\ge n-1\ge \lfloor \frac{2n}{3}\rfloor +1,$ and there is nothing to prove (because otherwise, for any two vertices $v_i\mathrm{ }\text{and}\mathrm{ }{v}_j$ out of S, the edge e_ij can not be dominated by S). Also if $S\cap V=\varnothing ,$ then there exists an edge $e_{i{k}_i}\in S$ for dominating $v_i\mathrm{ }\text{by}\mathrm{ }S,$ and so inequality (4.0.2)(4.0.2) $$\left|S\right|\ge \{\begin{array}{cc}\lfloor \frac{2n}{3}\rfloor \hfill & \text{if}\mathrm{ }n\equiv 0\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right),\hfill \\ \lfloor \frac{2n}{3}\rfloor +1\hfill & \text{if}\mathrm{ }n\equiv 1,2\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right).\hfill \end{array}$$(4.0.2) holds by Lemma 4.5. Therefore we assume $S\cap V\ne \varnothing \mathrm{ }\text{and}\mathrm{ }S\cap \mathbb{E}\ne \varnothing .$ Let $|S\cap V|=\ell \ge 1.$ Then the set $$A=\{v_i | v_i\in V-S\mathrm{ }\text{and}\mathrm{ }{e}_{ij}\in S\mathrm{ }\text{for}\mathrm{ }\text{some}\mathrm{ }j\}$$ has cardinality at least $n-\ell -1$ (because otherwise, for any two vertices $v_i,v_i\in V-S,$ the edge e_ij does not dominate by S), and so $$|S\cap \mathbb{E}|\ge \{\begin{array}{cc}\lfloor \frac{2(n-\ell -1)}{3}\rfloor \hfill & \text{if}\mathrm{ }n\equiv \ell +1\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right),\hfill \\ \lfloor \frac{2(n-\ell -1)}{3}\rfloor +1\hfill & \text{if}\mathrm{ }n\equiv \ell ,\ell +2\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right),\hfill \end{array}$$ by Lemma 4.5. Hence $$\left|S\right|=|S\cap V|+|S\cap \mathbb{E}|\ge \{\begin{array}{cc}\lfloor \frac{2n+\ell -2}{3}\rfloor \hfill & \text{if}\mathrm{ }n\equiv \ell +1\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right),\hfill \\ \lfloor \frac{2n+\ell -2}{3}\rfloor +1\hfill & \text{if}\mathrm{ }n\equiv \ell ,\ell +2\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right),\hfill \end{array}$$ which implies $$\left|S\right|\ge \{\begin{array}{cc}\lfloor \frac{2n}{3}\rfloor \hfill & \text{if}\mathrm{ }n\equiv 0\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right),\hfill \\ \lfloor \frac{2n}{3}\rfloor +1\hfill & \text{if}\mathrm{ }n\equiv 1\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right),\hfill \\ \lfloor \frac{2n}{3}\rfloor +1\hfill & \text{if}\mathrm{ }n\equiv 2\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right)\mathrm{ }\text{and}\mathrm{ }\ell \ne 1.\hfill \end{array}$$

Now we discuse on the only remained case $n\equiv 2\hspace{0.5em}(\mathrm{mod\hspace{0.5em}}3)\mathrm{ }\text{and}\mathrm{ }\ell =1.$ Let $S\cap V=\left\{v_n\right\}\mathrm{ }\text{and}\mathrm{ }{\mathbb{E}}_A=\{e_{ij}\in S | \{v_i,v_j\}\cap A\ne \varnothing \}.$ Then $n-2\le \left|A\right|\le n-1,$ and $$\left|{\mathbb{E}}_A\right|\ge \{\begin{array}{cc}\lfloor \frac{2(n-2)}{3}\rfloor \hfill & \text{if}\mathrm{ }\left|A\right|=n-2\equiv 0\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right),\hfill \\ \lfloor \frac{2(n-1)}{3}\rfloor +1\hfill & \text{if}\mathrm{ }\left|A\right|=n-1\equiv 1\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right).\hfill \end{array}$$ Since $\left|A\right|=n-1\mathrm{ }\text{implies}\mathrm{ }\left|S\right|=|S\cap V|+|S\cap \mathbb{E}|\ge 1+\left|{\mathbb{E}}_A\right|\ge \lfloor \frac{2n}{3}\rfloor +1,$ as desired, we assume $\left|A\right|=n-2.$ For some $p\ne n,$ let $e_{pn}\in S$ be an edge that dominates v_n. Then $v_p\in A\mathrm{ }\text{and}\mathrm{ }{e}_{pn}\in {\mathbb{E}}_A,$ and so $\left|A\setminus \right\{v_p\left\}\right|=n-3\equiv 2\hspace{0.5em}(\mathrm{mod\hspace{0.5em}}3).$ Hence $\left|{\mathbb{E}}_{A\setminus \left\{v_p\right\}}\right|\ge \lfloor \frac{2(n-3)}{3}\rfloor +1$ by (4.0.1). Now the facts $e_{pn}\notin {\mathbb{E}}_{A\setminus \left\{v_p\right\}}\mathrm{ }\text{and}\mathrm{ }{\mathbb{E}}_{A\setminus \left\{v_p\right\}}\cup \{e_{pn},v_n\}\subseteq S \text{imply} \left|S\right|\ge \left|{\mathbb{E}}_{A\setminus \left\{v_p\right\}}\right|+2\ge \lfloor \frac{2n}{3}\rfloor +1,$ as desired. On the other hand, since each of the sets $$\begin{array}{c}{S}_0=\{e_{(3i+1)(3i+2)},e_{(3i+2)(3i+3)}\hfill \\ | 0\le i\le k-1\}\hfill & \text{if}\mathrm{ }n\equiv 0\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right),\hfill \\ S_1=S_0\cup \left\{e_{(3k)(3k+1)}\right\}\hfill & \text{if}\mathrm{ }n\equiv 1\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right),\hfill \\ S_2=S_0\cup \left\{e_{(3k)(3k+1)}\right\},e_{(3k+1)(3k+2)}\}\hfill & \text{if}\mathrm{ }n\equiv 2\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right),\hfill \end{array}$$ is a TMDS of K_n with the minimum cardinality when $k=\lfloor \frac{n}{3}\rfloor ,$ we have proved $${\gamma }_{tm}(K_n)=\{\begin{array}{cc}\lfloor \frac{2n}{3}\rfloor \hfill & \text{if}\mathrm{ }n\equiv 0\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right),\hfill \\ \lfloor \frac{2n}{3}\rfloor +1\hfill & \text{if}\mathrm{ }n\equiv 1,2\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right).\hfill \end{array}$$ For an example, see Figure 10. □

Figure 10. The set $\{e_{12},e_{23},e_{34}\}$ is a min-TMDS of K₄.

Before giving the total mixed domination number of a wheel, as we promise in the proof of Theorem 2.2, we show that the lower bound in Theorem 2.2 is tight by Propositions 4.6 and 4.7.

Proposition 4.7.

For any complete graph K_n of order $n\ge 4,{\gamma }_t(L(K_n))=\lfloor \frac{2n}{3}\rfloor .$

Proof.

Let $K_n=(V,\mathbb{E})$ be a complete graph of order $n\ge 4$ with the vertex set $V=\{v_1,\dots ,v_n\}$ and edge set $\mathbb{E}.$ Then $V(L(K_n))=\mathbb{E}.$ For any TDS $S\mathrm{ }\text{of}\mathrm{ }L(K_n),$ let I be the set of all indices of the vertices of S. Obviously for any three indices $1\le i<j<k\le n,\left|\right\{i,j,k\}\cap I|\ge 2$ because for any $i,j\notin I,$ the vertex e_ij can not be dominated by S. Thus $\left|S\right|\ge \lfloor \frac{2n}{3}\rfloor ,$ and since the sets $$\begin{array}{cc}{S}_0=S_2\cup \left\{e_{(n-2)(n-1)}\right\}\hfill & \text{if}\mathrm{ }n\equiv 0\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right),\hfill \\ S_1=\{e_{(3i+1)(3i+2)},e_{(3i+2)(3i+3)},\hfill \\ | 0\le i\le \lfloor \frac{n}{3}\rfloor -1\}\hfill & \text{if}\mathrm{ }n\equiv 1\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right),\hfill \\ S_2=S_1\cup \left\{e_{(n-2)(n-1)}\right\}\hfill & \text{if}\mathrm{ }n\equiv 2\hspace{0.5em}\left(\mathrm{mod\hspace{0.5em}}3\right),\hfill \end{array}$$ are TDSs of $L(K_n)$ in each of the cases, the result holds. □

Proposition 4.8.

For any wheel W_n of order $n+1\ge 4,{\gamma }_{tm}(W_n)=\lceil \frac{n}{2}\rceil +1.$

Proof.

Let $W_n=(V,\mathbb{E})$ be a wheel of order $n+1\ge 4$ with the vertex set $V=\{v_i | 0\le i\le n\}$ and edge set $\mathbb{E}=\{e_{0i},e_{i(i+1)} | 1\le i\le n\}.$ Since $S=\left\{v_0\right\}\cup \{v_{2i-1} | 1\le i\le \lceil \frac{n}{2}\rceil \}$ is a TMDS of W_n, we have ${\gamma }_{tm}(W_n)\le \lceil \frac{n}{2}\rceil +1.$

In the sequel, we show ${\gamma }_{tm}(W_n)\ge \lceil \frac{n}{2}\rceil +1.$ Let S be an arbitrary TMDS of W_n. If $S\cap \mathbb{E}=\varnothing ,$ then, since $N(e_{i(i+1)})\cap S\ne \varnothing$ for each $1\le i\le n,S\cap \{v_i,v_{i+1}\}\ne \varnothing ,$ and so $\left|S\right|\ge \lceil \frac{n}{2}\rceil .$ Since we have nothing to prove when $\{v_1,\dots ,v_n\}\subseteq S,$ we assume $v_i\notin S$ for some $1\le i\le n.$ This implies $v_0\in S$ (because $S\mathrm{ }\text{dominates}\mathrm{ }{e}_{0i}\mathrm{ }\text{and}\mathrm{ }S\cap \mathbb{E}=\varnothing$), and so $\left|S\right|\ge \lceil \frac{n}{2}\rceil +1.$ Now let $S\cap V=\varnothing .$ Then, for dominating every vertex $v_i\in V\mathrm{ }\text{by}\mathrm{ }S,$ there exists an edge $e_{pi}\in S$ for some $p\ne i.$ By knowing $N_{W_n}(e_{pi})=\{v_p,v_i\},$ we conclude S has cardinality at least $\lceil \frac{n+1}{2}\rceil$ which is $\lceil \frac{n}{2}\rceil +1$ for even n and is $\lceil \frac{n}{2}\rceil$ for odd n. Since the subgraph of W_n induced by S is connected and $S\subseteq \mathbb{E},$ we obtain $\left|\right\{v_i | e_{ij}\in S\mathrm{ }\text{for}\mathrm{ }\text{some}\mathrm{ }j\}|<n+1\mathrm{ }if\mathrm{ }|S|=\lceil \frac{n+1}{2}\rceil \mathrm{ }\text{and}\mathrm{ }n$ is odd, a contradiction. Thus $\left|S\right|\ge \lceil \frac{n+1}{2}\rceil +1=\lceil \frac{n}{2}\rceil +1$ for odd n.

Thus $S\cap V\ne \varnothing \mathrm{ }\text{and}\mathrm{ }S\cap \mathbb{E}\ne \varnothing .$ By assumption $|S\cap V|=\ell$ it is sufficient to prove $|S\cap \mathbb{E}|\ge \lceil \frac{n}{2}\rceil -\ell +1.$ Let ${\mathbb{E}}_0=\{e_{i(i+1)} | \left|\right\{v_i,v_{i+1}\}\cap S|=0\mathrm{ }\text{for}\mathrm{ }1\le i\le n\}.$ Since every $e_{i(i+1)}\in {\mathbb{E}}_0$ must be dominated by an edge $e_{pq}\in S$ in which $\left|\right\{p,q\}\cap \{i,i+1\left\}\right|=1,$ the set ${\mathbb{E}}_{00}=\{e_{pq}\in S | e_{pq}\text{dominates}\mathrm{ }\text{an}\mathrm{ }\text{edge}\mathrm{ }{e}_{i(i+1)}\in {\mathbb{E}}_0\}$ is not empty, and more $\left|{\mathbb{E}}_{00}\right|\ge \lceil \frac{\left|{\mathbb{E}}_0\right|}{2}\rceil$ because every $e_{pq}\in {\mathbb{E}}_{00}$ is adjacent to at most two edges in ${\mathbb{E}}_0.$ Let ${\mathbb{E}}_1=\{e_{i(i+1)} | \left|\right\{v_i,v_{i+1}\}\cap S|\ne 0\text{for}\mathrm{ }1\le i\le n\}.$ If $v_0\in S,$ then $\left|{\mathbb{E}}_1\right|\le 2(\ell -1),$ and so $\left|{\mathbb{E}}_0\right|\ge n-2\ell +2$ which implies $|S\cap \mathbb{E}|\ge \lceil \frac{\left|{\mathbb{E}}_0\right|}{2}\rceil =\lceil \frac{n-2\ell +2}{2}\rceil =\lceil \frac{n}{2}\rceil -\ell +1,$ as desired.

Therefore we may assume $v_0\notin S.$ Then $\left|{\mathbb{E}}_1\right|\le 2\ell$ and so $\left|{\mathbb{E}}_0\right|\ge n-2\ell .$ Let $\left|{\mathbb{E}}_0\right|\le n-2\ell +1$ by the contrary. Hence $2\ell -1\le \left|{\mathbb{E}}_1\right|\le 2\ell .$ Since by the assumption $\left|{\mathbb{E}}_1\right|=2\ell$ we reach to this contradiction that the subgraph of W_n induced by $S\cap V\mathrm{ }\text{contains}\mathrm{ }\ell$ isolated vertices, we may assume $\left|{\mathbb{E}}_1\right|=2\ell -1.$ Again, since the subgraph of W_n induced by $S\cap V$ does not have isolated vertex, we must have $\ell =2,$ and so $\left|{\mathbb{E}}_0\right|=n-2\ell +1=n-3.$ Since obviousely $|S\cap \mathbb{E}|\ge \lceil \frac{\left|{\mathbb{E}}_0\right|}{2}\rceil =\lceil \frac{n}{2}\rceil -\ell +1$ for even n, let n be odd. Without loss of generality, we assume $S\cap V=\{v_1,v_2\},$ and so ${\mathbb{E}}_0=\{e_{i(i+1)} | 3\le i\le n-1\}.$

By the contrary let $|S\cap \mathbb{E}|=\frac{n-3}{2}.$ Since there is nothing to prove for n = 3 by Proposition 4.6, we assume $n\ge 5.$ For n = 5, since v₄ does not dominated by $S-\mathbb{E},|S\cap \mathbb{E}|=1\mathrm{ }\text{implies}\mathrm{ }S\cap \mathbb{E}=\left\{e_{i4}\right\}$ for some $i\ne 4,$ that is, $S=\{v_1,v_2,e_{i4}\}.$ But since $e_{i4}$ does not dominated by S, we reach contradiction. Thus $|S\cap \mathbb{E}|>\frac{n-3}{2}=1$ and so ${\gamma }_{tm}(W_5)=\lceil \frac{5}{2}\rceil +1=4.$ Therefore, in the sequel, we assume $n\ge 7.$ If $S\cap \mathbb{E}\subseteq {\mathbb{E}}_0,$ then $S\cap \mathbb{E}={\mathbb{E}}_0-\{e_{(2i)(2i+1)} | 2\le i\le \frac{n-1}{2}\}\mathrm{ }\text{or}S\cap \mathbb{E}=\{e_{\left(2i\right)(2i+1)} | 2\le i\le \frac{n-3}{2}\}\cup \left\{\alpha \right\}$ where $\mathrm{ }\alpha \in \{e_{(n-2)(n-1)},e_{(n-1)n}\},$ which imply one of the edges $e_{0n}\mathrm{ }\text{or}\mathrm{ }{e}_{03}$ does not respectively dominated by S, a contradiction. Thus $|S\cap \{e_{0i} | 1\le i\le n\}|=m\ge 1.$ Let also $V^{\prime }=V-N_G(\{v_1,v_2\})=\{v_4,\dots ,v_{n-1}\},{\mathbb{E}}_0^{\prime }=\{e_{i(i+1)}\in S\cap {\mathbb{E}}_0 | \{e_{0i},e_{0(i+1)}\}\cap S\ne \varnothing \}\mathrm{ }\text{and}\mathrm{ }{\mathbb{E}}_0^{″}={\mathbb{E}}_0-{\mathbb{E}}_0^{\prime }.$ So (4.0.3) $$|S\cap {\mathbb{E}}_0|=\frac{n-3}{2}-m=\left|{\mathbb{E}}_0^{\prime }\right|+\left|{\mathbb{E}}_0^{″}\right|.$$(4.0.3) Since $N_{W_n}(e_{i(i+1)})=\{v_i,v_{i+1}\}\mathrm{ }\text{for}\mathrm{ }{e}_{i(i+1)}\in \mathbb{E}{\prime }_0\mathrm{ }\text{and}\mathrm{ }|N(e_{0j})\cap \{v_i,v_{i+1}\left\}\right|=1\mathrm{ }\text{when}\mathrm{ }{e}_{0j}\in \{e_{0i},e_{0(i+1)}\}\subset S,$ we have $|N_{T(W_n)}(S\cap {\mathbb{E}}_0^{\prime })\cap V^{\prime }|\le m+\left|\mathbb{E}{\prime }_0\right|.$ Since the subgraph $W_n[{\mathbb{E}}_0^{″}]\mathrm{ }\text{of}{W}_n$ induced by ${\mathbb{E}}_0^{″}$ dominates the most number of vertices in $V\prime$ when it has as possible as the most number of the complete graphs K₂ as induced subgraphs, we conclude that at least two edges of ${\mathbb{E}}_0^{″}$ are needed for dominating every three vertices of $V\prime \mathrm{ }\text{by}\mathrm{ }{\mathbb{E}}_0^{″},$ and so $|N_{T(W_n)}(S\cap {\mathbb{E}}_0^{″})\cap V^{\prime }|\le \frac{3\left|{\mathbb{E}}_0^{″}\right|}{2}.$ Hence (4.0.4) $$|N_{T(W_n)}(S\cap {\mathbb{E}}_0)\cap V^{\prime }|\le m+\left|\mathbb{E}{\prime }_0\right|+\frac{3\left|{\mathbb{E}}_0^{″}\right|}{2}.$$(4.0.4) Now by knowing $V^{\prime }\subseteq N_{T(W_n)}(S\cap {\mathbb{E}}_0)$ which implies $|N_{T(W_n)}(S\cap {\mathbb{E}}_0)|\ge \left|V^{\prime }\right|=n-4,$ and by the relations (4.0.3)(4.0.3) $$|S\cap {\mathbb{E}}_0|=\frac{n-3}{2}-m=\left|{\mathbb{E}}_0^{\prime }\right|+\left|{\mathbb{E}}_0^{″}\right|.$$(4.0.3) and (4.0.4)(4.0.4) $$|N_{T(W_n)}(S\cap {\mathbb{E}}_0)\cap V^{\prime }|\le m+\left|\mathbb{E}{\prime }_0\right|+\frac{3\left|{\mathbb{E}}_0^{″}\right|}{2}.$$(4.0.4) , we obtain $\left|{\mathbb{E}}_0^{″}\right|\ge n-5,$ and so m = 1. Then $|S\cap {\mathbb{E}}_0|=\frac{n-3}{2}-1=\frac{n-5}{2}.$ Thus the number of vertices of $V\prime$ dominated by $S\cap {\mathbb{E}}_0$ is at most $\frac{3(n-5)}{4}+1$ which is less than $n-4=|V\prime |\mathrm{ }\text{when}\mathrm{ }n\ge 7.$ Therefore $|S\cap \mathbb{E}|\ge \frac{n-3}{2}+1=\frac{n-1}{2}=\lceil \frac{n}{2}\rceil -\ell +1,$ as desired. See Figure 11 for an example. □

Figure 11. The set $\{v_0,v_1,v_3,v_5\}$ is a min-TMDS of W₅.

5. Some open problems

Problem 5.1.

1. For any graph G, is it true that ${\gamma }_{tm}(G)={\gamma }_t(G)$ if and only if it has a min-TDS such that its complement is an independent set of G?

2. Find some families of non-complete graphs $G\mathrm{ }\mathit{\text{satisfy}}{\gamma }_{tm}(G)={\gamma }_t(L(G)).$

3. Find some families of connected graphs $G\mathrm{ }\mathit{\text{satisfy}}{\gamma }_{tm}(G)={\gamma }_t(L(G))+{\gamma }_t(G).$

It can be easily verified that Theorem 2.7 is true for any connected graph of order at most 5. So the existence of a Hamiltonian path in a graph is not a necessary condition in the theorem, and naturally the following problem arises.

Problem 5.2.

Find some other family of graphs G of order $n\mathrm{ }\text{satisfy}\mathrm{ }{\gamma }_{tm}(G)\le \lceil \frac{5n}{3}\rceil -n.$

We know ${\gamma }_{tm}(G)>{\gamma }_t(G)$ for almost all graphs. As we saw in some graphs such as complete graphs and wheels, ${\gamma }_{tm}(G)-{\gamma }_t(G)\to \infty \mathrm{ }\text{when}\mathrm{ }n\to \infty$ for many graphs G. So, we end our paper with the following important problem.

Problem 5.3.

Find some real number $\alpha >1$ such that for any graph $G,{\gamma }_{tm}(G)\ge \alpha {\gamma }_t(G).$