?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.Abstract
A subset is called an h-extra r-component cut of G if G – F is disconnected and there are at least r components, each component has at least h + 1 vertices. The cardinality of a minimum h-extra r-component cut of G, denoted by
is the h-extra r-component connectivity of G. In this paper, we introduce a novel connectivity called the g-good r-component connectivity. For
if G – F is disconnected and there are at least r components and each vertex
has at least g neighbors, then F is called a g-good r-component cut of G; the g-good r-component connectivity of G, denoted by
is the minimum cardinality of a g-good r-component cut of G. In this work, we prove that
for
and
for
where Qn is n-dimension hypercube.
1. Introduction
The topological structure of a computer interconnection network can be represented by a graph, where vertices represent processors and edges represent communication links between processors. To evaluate the reliability and fault tolerance of a network in communication, many related concepts and graph parameters have been put forward. The connectivity of graph is an important parameter reflecting the strength between two nodes in an interconnection network. The traditional connectivity of a graph is the minimum number of vertices whose removal leaves the remaining graph disconnected or trivial. Note that, in the event of a random node failure, it is very unlikely that all of the nodes adjacent to a single node fail simultaneously. Thus, the traditional connectivity has certain limitations and underestimates the resilience of the network. To measure the fault tolerance of an interconnection network more accurately, Harary [Citation8] introduced the concept of the conditional connectivity by placing some requirements on the components of G – F for
Here are some of the most studied conditional connectivity: g-good neighbor connectivity, h-extra connectivity and r-component connectivity. For a faulty set if F is called a g-good neighbor cut of G, then G – F is disconnected and each vertex
has at least g neighbors. The minimum cardinality of g-good neighbor cuts is said to be the g-good neighbor connectivity of G, denoted by
The relevant results of the g-good neighbor connectivity can be referred to [Citation11, Citation12, Citation14, Citation16, Citation19]. It was stated in [Citation15] that introduced the concept of the g-extra connectivity, and Fàbrega and Fiol [Citation4, Citation5] gave a result regarding this concept. An h-extra cut of G is a set of vertices whose deletion results in G – F is disconnected and each remaining component has more than h vertices. The h-extra connectivity of a graph G, denoted by κh, is the minimum cardinality of h-extra cuts of G. Recent results of the h-extra connectivity can be referred to [Citation6, Citation7, Citation13, Citation23, Citation26]. Let G be a non-complete graph and r be a positive integer. A r-component cut of G is a set of vertices whose deletion results in at least r components. The r-component connectivity
of a graph G is the cardinality of the smallest r-component cut of G. For more research on the r-component connectivity, we refer to [Citation2, Citation3, Citation9, Citation17, Citation20, Citation24].
The above mentioned conditional connectivity is only a condition that restricts the components of G – F. In some cases, we need to have various restrictions on the components of G – F. Recently, Li et al. [Citation10] introduced the h-extra r-component connectivity, and the authors prove that for
and
for
For two integers
and
a subset
is called an h-extra r-component cut of G if there are at least r connected components in G – F and each component has at least h + 1 vertices. The minimum cardinality of h-extra r-component cuts of G, if exists, is the h-extra r-component connectivity of G, denoted by
At present, there are few results on the h-extra r-component connectivity.
In this paper, we give the concept of the g-good r-component connectivity.
Definition 1.1.
Let G be a connected graph, for if G – F is disconnected and there are at last r components and each vertex
has at least g neighbors, then F is called a g-good r-component cut of G. The g-good r-component connectivity of G, denoted by
is the minimum cardinality of g-good r-component cuts of G.
In this work, we prove that for
and
for
where Qn is n-dimension hypercube.
2. Preliminaries
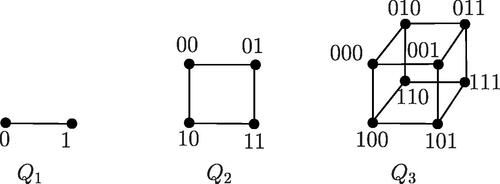
Hypercube is a very well-known and fundamental computer network model. An n-dimension hypercube Qn has vertices and
edges. Each vertex in Qn is represented as an n-bit binary ({0, 1}) string and two vertices are adjacent if and only if they differ exactly in one position. We set
be the subgraph of Qn induced by the bit n being i, where i = 0, 1. Obviously,
is isomorphic to
for i = 0, 1. For each vertex in
(respectively,
), there is a neighbor in
(respectively,
), which is called the outer neighbor. Note that Qn is a bipartite graph, so there is no odd cycles in Qn. See .
Given a graph G, let V(G), E(G), and (u, v) denote the set of vertices, the set of edges, and the edge whose end vertices are u and v. For an integer the path Pn is a graph of order n and size n – 1 whose vertices can be labeled by
For an integer
the cycle Cn is a graph of order n and size n which can be represented by
The degree of vertex u in graph G is the number of neighbors, denoted by d(v). The neighbors of a vertex u in G is denoted by
For a set
the neighbors in
of vertices in U are called the neighbors of U, denoted by
Terminologies not given here can be referred to [Citation1].
Here are some lemmas that will be used in this paper.
Lemma 2.1
[Citation18, Citation22]. For any integer , the minimum number of vertices adjacent to t vertices in Qn is
. For any integer
, the minimum number of vertices adjacent to t vertices in Qn is
Lemma 2.2
[Citation25]. If for
, then
is either connected or disconnected with a large connected component and remaining small components containing at most two vertices in total.
Lemma 2.3
[Citation25]. If for
, then
is either connected or disconnected with a large connected component and remaining small components containing at most four vertices in total.
Lemma 2.4
[Citation21]. For and any
, if
and
, then
, where
is as defined in Lemma 2.1.
Lemma 2.5.
Let Ca and Cb be cycles with length 4 in Qn. If and
, then
Proof.
Let and
By the structure of Qn, for any two vertices x and y have either two common neighbors or no common neighbors. If x1 and y1 have two common neighbors, then x1 and y2 or y4 have no common neighbor, otherwise, there is a cycle with length 5. Moreover, x1 and y3 also have no common neighbor, otherwise, there is a cycle with length 7. Similarly to xi and yi for
So
□
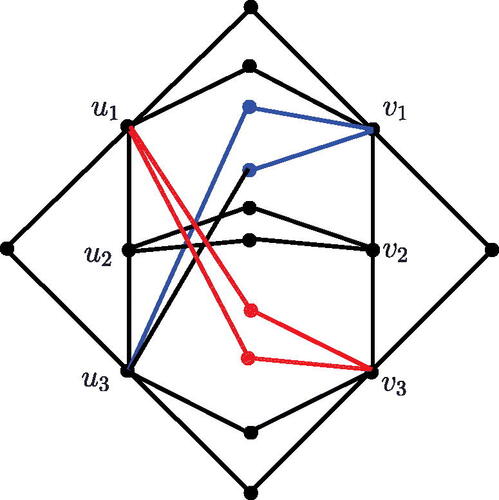
Lemma 2.6.
For and
. Let
and
. If
and
, then
Proof.
Since Qn has no odd cycle, adjacent vertices have no common neighbor. By the structure of Qn, for any two vertices u and v, they have either two common neighbors or no common neighbor. Since v2(respectively, u2) is a common neighbor of v1 and v3(respectively, u1 and u3), it follows that v1 and v3(respectively, u1 and u3) have another common neighbor. Considering the following cases:
Case 1. u1 and v1 have two common neighbors.
Since u1 and v1 have two common neighbors, we know that u1 have at most two common neighbors with v3 and u1, respectively. u1 and v2 have no common neighbor, otherwise, there is a cycle with length 5. Moreover, u2 has no common neighbor with v1 and v3, otherwise, there is a cycle with length 5, and u2 have at most two common neighbors with v2. Similarly, u3 have at most two common neighbors with v1 and v3, respectively. And u3 have no common neighbor with v2, otherwise, there is a cycle with length 5. By the above discussion, we can get the path and
have at most 10 common neighbors. Thus
Case 2. u1 and v2 have two common neighbors.
If u1 and v2 have two common neighbors, then u1 have no common neighbor with v1 and v3, otherwise, there is a cycle with length 5. Vertex u2 have at most two common neighbors with v1, then u2 have no common neighbor with v2, otherwise, there is a cycle with length 5. Moreover, u2 have at most two common neighbors with v3. Vertex u3 have no common neighbor with v1 and v3, otherwise, there is a cycle with length 7. And u3 have at most two common neighbors with v2. After the above discussion, we can get the path and
have at most 8 common neighbors. Thus
Case 3. u1 and v3 have two common neighbors.
The proof of this case is the same as the proof of Case 1.
Case 4. u2 and v1 or u2 and v3 have two common neighbors.
The proof for this case is the same as the proof for the Case 2.
Case 5. u2 and v2 have two common neighbors.
Since u2 and v2 have two common neighbors, we have u2 and v1 or u2 and v3 have no common neighbor, otherwise, there is a cycle with length 5. After a simple check, u1 have at most two common neighbors with v1 and v3. Similarly, u3 have at most two common neighbors with v3 and v1. Thus
Case 6. u3 and v1 or u3 and v2 or u3 and v3 have two common neighbors.
The proof of this case is the same as the proof of Case 1, Case 2 and Case 3, respectively. □
3. g-good r-component connectivity
In this section, we will show the 2-good 3-component connectivity of hypercubes.
Lemma 3.1.
Let Qn be an n-dimension hypercube. Then for
Proof.
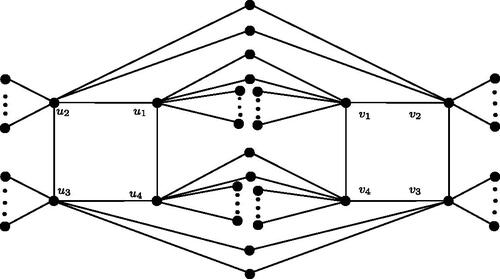
Let and
be cycles in Qn. Without loss generality, suppose that
and
ui and vi have two common neighbors for
We set
then
see . There are at least three components in
For any vertex v in cycle
or
d(v) = 2. Let
If u and u1 have common neighbors, then u and u2 or u4 have no common neighbors, otherwise, there would be a cycle with length 5 in Qn. Since
and
we have
Since Qn is n-regular and
it follows that u has at least two neighbors. So
for
□
Lemma 3.2.
Let Qn be an n-dimension hypercube. Then for
Proof.
Let F be a 2-good 3-component cut of Qn and Let
and
Then
Without loss of generality, suppose that
Since
we have
for
By Lemma 2.3, we consider the following cases:
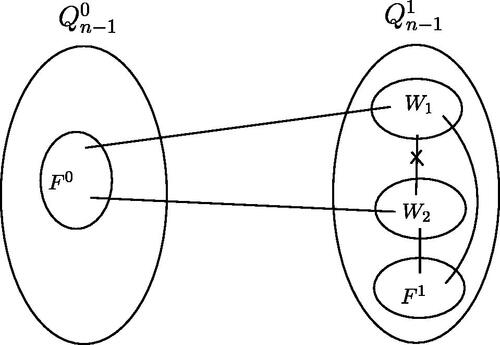
Case 1. is connected.
Since F is a 2-good 3-component cut, we have is disconnected and
exists two connected components, denoted by W1 and W2. There is no cycle with length 3 in Qn, so W1 and W2 contain at least a cycle with length 4. By the structure of Qn, each vertex in
has an outer neighbor in
thus
It is clear that
and
so
see . Let
and
for
We have
for
and
Since
it follows that
for
by Lemma 2.4. According to Lemma 2.1,
for
and
for
when
The minimum value of these two quadratic functions
and
is min
for
The quadratic gets the minimum value if and only if
In this case, W1 and W2 are exactly two cycles with length 4 in
By Lemma 2.5, we have
It follows that
and a contradiction is obtained.
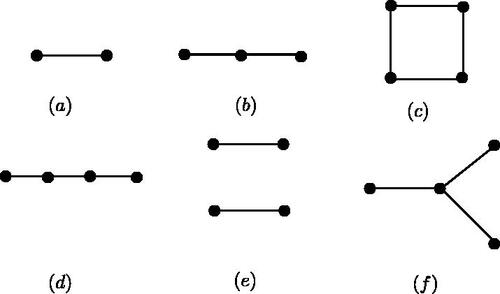
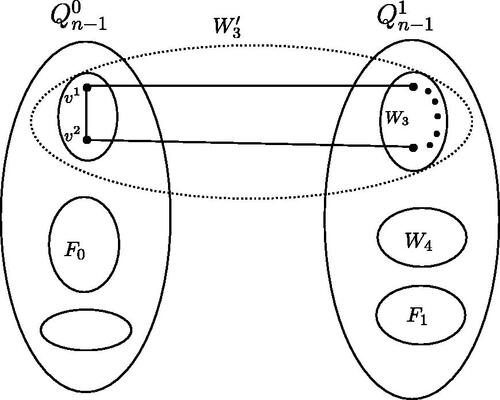
Case 2. is disconnected with a large connected component and remaining small components containing at most four vertices in total.
Since F is a 2-good 3-component cut and each vertex in only has one outer neighbor in
the connected components of
contain no isolated vertices. The graphs with no isolated vertices induced by at most 4 vertices are shown in . We divide into the following four cases for discussion.
Subcase 2.1. is disconnected with a large connected component and a path P2 (), denoted by
There are at least two connected components in one of which contains the outer neighbors of v1 and v2, denoted by W3, and another connected component which is also the connected component of
denoted by W4. Let
and
is a connected component of
see . It is obvious that
and
so
Let
and
Since each vertex in
has an outer neighbor in
we have
So
The following discussion is similar to Case 1, where the quadratic function
gets the minimum value at
Then connected components W3 and W4 are cycles with length 4 in
By Lemma 2.5, we have
It follows that
and a contradiction is obtained.
Subcase 2.2. is disconnected with a large connected component and a path P3 (), denoted by
In there are at least two connected components, denoted by W5 and W6. Without loss of generality, suppose that W5 contains outer neighbors of v3, v4 and v5. Since
it follows that
It is the same as the discussion in Subcase 2.1, and a contradiction is obtained.
Subcase 2.3. is disconnected with a large connected component and a cycle with length 4 (), denoted by
There are at least two connected components in denoted by W7 and W8. If C is a connected component of
then
So
Then from the same reason as Subcase 2.1, we get a contradiction. If C is not a connected component of
then
So
It is the same as the discussion in Subcase 2.1, and a contradiction is obtained.
Subcase 2.4. is disconnected with a large connected component and a path P4 (), denoted by
There are at least two connected components in denoted by W7 and W8. Hence we have
it follows that
It is similar to the above discussion in Subcase 2.1 and a contradiction is obtained. The proof is the same as the other two subgraphs ( and ), we just prove the path P4. □
By Lemma 3.1 and Lemma 3.2, the following theorem is established.
Theorem 3.3.
Let Qn be an n-dimension hypercube. Then for
4. g-extra r-component connectivity
Lemma 4.1.
Let Qn be an n-dimension hypercube. Then for
Proof.
Let
and
Let
Then
see . There are at least three connected components in
two of which are paths with length 3, denoted by
and
respectively. Since Qn is bipartite, there is no odd cycle in Qn. For any
When
w has two common neighbors with
and v3. It follows that w has a neighbor
in
because the regularity of Qn is
The vertex
has at most two common neighbors with u2 and v2, respectively. Then
we have
have at least 5 neighbors in
So every connected component of
has at least three vertices, thus
for
□
Lemma 4.2.
Let Qn be an n-dimension hypercube. Then for
Proof.
Suppose that F is a 2-extra 3-component cut and Let
and
Without loss of generality, suppose that
Since
we have
By Lemma 2.2, we consider the following cases:
Case 1. is connected.
Since F is a 2-extra 3-component cut, we have is disconnected and exists two connected components in
denoted by S1 and S2. It is clear that
Since
and
it follows that
Let
and
for
We have
for
and
Since
it follows that
for
by Lemma 2.4. By Lemma 2.1,
for
and
for
when
The minimum value of these two quadratic functions
and
is min
for
The quadratic gets the minimum value if and only if
In this case, S1 and S2 are paths with length 3 in
By Lemma 2.6, we have
Hence
and a contradiction is obtained.
Case 2. is disconnected with a large connected component and remaining small components containing at most two vertices in total.
Subcase 2.1. is disconnected with a large connected component and an isolated vertex, denoted by v1.
In there are at least two connected components, denoted by S3 and S4. Since
it follows that
It is similar to Case 1, and a contradiction is obtained.
Subcase 2.2. is disconnected with a large connected component and two isolated vertices, denoted by v2 and v3.
There are at least two connected components in denoted by S5 and S6. Since
it follows that
It is similar to Case 1 and a contradiction is obtained.
Subcase 2.3. is disconnected with a large connected component and a path P2, denoted by
This proof is the same as Subcase 2.2. □
By Lemma 4.1 and Lemma 4.2, we have the following result.
Theorem 4.3.
Let Qn be an n-dimension hypercube. Then for
5. Concluding remarks
In this paper, we obtain when
and
when
These questions still remain open, we can consider more general results like
and
Other forms of the novel connectivity can also be considered, which are valuable for measuring the fault tolerance of interconnection networks.
Disclosure statement
No potential conflict of interest was reported by the authors.
Data availability
The data used to support the findings of this study are available from the corresponding author upon request.
Additional information
Funding
References
- Bondy, J. A, Murty, U. S. R. (2008). Graph Theory. Berlin: Springer-Verlag.
- Chang, J. M., Pai, K. J., Wu, R. Y, Yang, J. S. (2019). The 4-component connectivity of alternating group networks. Theor. Comput. Sci. 766: 38–45.
- Cheng, E., Qiu, K, Shen, Z. (2014). Connectivity results of hierarchical cubic networks as associated with linearly many faults. IEEE International Conference on Computational Science and Engineering, pp. 1213–1220.
- Fàbrega, J, Fiol, M. A. (1994). Extra connectivity of graphs with large girth. Discrete Math. 127(1-3): 163–170.
- Fàbrega, J, Fiol, M. A. (1996). On the extra connectivity of graphs. Discrete Math. 155(1-3): 49–57.
- Guo, J, Lu, M. (2016). The extra connectivity of bubble-sort star graphs. Theor. Comput. Sci. 645: 91–99.
- Han, W. P, Wang, S. Y. (2015). The g-extra conditional diagnosability of folded hypercubes. Appl. Math. Sci. 9: 346–357.
- Harary, F. (1983). Conditional connectivity. Networks 13(3): 347–357.
- Hsu, L. H., Cheng, E., Lipták, L., Tan, J. J. M., Lin, C. K, Ho, T. Y. (2012). Component connectivity of the hypercubes. Int. J. Comput. Math. 89 (2): 137–145.
- Li, B., Lan, J. F., Ning, W. T., Tian, Y. C., Zhang, X, Zhu, Q. (2021). h-extra r-component connectivity of interconnection networks with application to hypercubes. Theor. Comput. Sci. 895: 68–74.
- Li, D, Lu, M. (2017). The g-good-neighbor conditional diagnosability of star graphs under the PMC and MM* model. Theor. Comput. Sci. 674: 53–59.
- Lin, L., Xu, L., Wang, D, Zhou, S. (2018). The g-good-neighbor conditional diagnosability of arrangement graphs. IEEE Trans. Depend. Secure Comput. 15(3): 542–548.
- Lin, L., Xu, L, Zhou, S. (2015). Conditional diagnosability and strong diagnosability of split-star networks under the PMC model. Theor. Comput. Sci. 562: 565–580.
- Peng, S. L., Lin, C. K., Tan, J. M, Hsu, L. H. (2012). The g-good-neighbor conditional diagnosability of hypercube under PMC model. Appl. Math. Comput. 218: 10406–10412.
- Preparata, F. P., Metze, G, Chien, R. T. (1967). On the connection assignment problem of diagnosable systems. IEEE Trans. Electron. Comput. EC-16(6): 848–854.
- Ren, Y, Wang, S. (2017). The g-good-neighbor diagnosability of locally twisted cubes. Theor. Comput. Sci. 697: 91–97.
- Sampathkumar, E. (1984). Connectivity of a graph-a generalization. J. Comb. Inf. Syst. Sci. 9: 71–78.
- Somani, A. K, Peleg, O. (1996). On diagnosability of large fault sets in regular topology-based computer systems. IEEE Trans. Comput. 45 (8): 892–903.
- Wei, Y, Xu, M. (2018). The 1, 2-good-neighbor conditional diagnosabilities of regular graphs. Appl. Math. Comput. 334: 295–310.
- Xu, L., Zhou, S, Yang, W. (2020). Component connectivity of Cayley graphs generated by transposition trees. Int. J. Parallel Emerg. Distrib. Syst. 35(1): 103–110.
- Yang, W, Meng, J. (2010). Extraconnectivity of hypercubes(ii). Australas. J. Comb. 47: 189–195.
- Yang, X., Cao, J., Megson, G. M, Luo, J. (2006). Minimun neighborhood in a generalized cube. Inf. Process. Lett. 97 (3): 88–93.
- Zhang, M. M, Zhou, J. X. (2015). On g-extra connectivity of folded hypercubes. Theor. Comput. Sci 593: 146–153.
- Zhao, S., Yang, W, Zhang, S. (2016). Component connectivity of hypercubes. Theor. Comput. Sci. 640: 115–118.
- Zhu, Q., Wang, X, Cheng, G. (2013). Reliability evaluation of bc networks. IEEE Trans. Comput. 62 (11): 2337–2340.
- Zhu, Q, Zhang, X. (2017). The h-extra conditional diagnosability of hypercubes under the PMC model and MM* model. Int. J. Comput. Math. Comput. Syst. Theory 1(1-4): 141–150.