Domination parameters of generalized Sierpiński graphs

Abstract

In this paper, we obtain the Italian domination number, perfect Italian domination number and double Roman domination number of generalized Sierpiński graph $S(G,2),$ where G is a cycle C_n, $n\ge 4,$ a complete bipartite graph $K_{1,q}$ or $K_{2,q},q\ge 2$ and a bistar $B_{m,n},m,n\ge 3.$

Keywords:

• Italian domination
• perfect Italian domination
• double Roman domination
• generalized Sierpiński graphs

AMS Subject Classification:

• 05C69
• 05C76

1. Introduction

Let G be a simple graph with vertex set V(G) and edge set E(G). If there is no ambiguity in the choice of G, then we write V(G) and E(G) as V and E, respectively. The number of vertices and edges of the graph G are denoted by n(G) and m(G), respectively. The open neighbourhood of a vertex $v\in V$ is the set $N(v)=\{u:uv\in E\}$ and the vertices in N(v) are called the neighbours of v. $|N(v)|$ is called the degree of the vertex v in G and is denoted by $d_G(v),$ or simply d(v). The vertices with degree one are called leaves, whereas the vertices with degree $n-1$ are called universal vertices. Let C_n denote a cycle on n vertices and $K_{p,q}$ denote a complete bipartite graph on p + q vertices, where one partition contains p vertices and other partition contains q vertices. The bistar $B_{m,n}$ is the graph obtained by joining the center vertices of $K_{1,m}$ and $K_{1,n}$ by an edge.

Let f be a function defined on the vertex set of a graph G. The weight of f is defined as $f(V)=\sum _{v\in V}f(v).$ A Roman dominating function on G is a function $f:V(G)\to \{0,1,2\}$ such that every vertex $u\in V$ with $f(u)=0$ has at least a neighbor $v\in N_G(u)$ satisfying $f(v)=2.$ The Roman domination number of G, denoted by ${\gamma }_R(G),$ is the minimum weight among all Roman dominating functions on G. Cockayne, Dreyer, S. M. Hedetniemi and S. T. Hedetniemi [14] introduced the concept of Roman Domination in graphs, and since then a lot of related variations and generalizations have been studied (see [7, 11–13]).

An Italian dominating function – IDF (perfect Italian dominating function – PID-function) of a graph G is a function $f:V(G)\to \{0,1,2\}$ satisfying the condition that for every $v\in V$ with $f(v)=0,$ we have $\sum _{u\in N(v)}f(u)\ge 2$ ($\sum _{u\in N(v)}f(u)=2$), i.e., either v is adjacent to at least one vertex u with $f(u)=2$ or at least two vertices x and y with $f(x)=f(y)=1$ (i.e., all the neighbours of v are assigned the weight 0 by f except for exactly one vertex u for which $f(u)=2$ or for exactly two vertices u and w for which $f(u)=f(w)=1$). The Italian domination number, ${\gamma }_I(G)$ (perfect Italian domination number, ${\gamma }_I^p(G)$) is the minimum weight of an Italian dominating function [24] (perfect Italian dominating function [23]). The Italian dominating function with weight ${\gamma }_I(G)$ is called a γ_I-function [10]. The sum of the weights of the vertices of H is denoted by f(H), where H is any subgraph of G. i.e., $f(H)=\sum _{u\in V(H)}f(u).$ The study of Italian domination was initiated by Chellai et al. in [10] and they called Italian domination as Roman $\left\{2\right\}$-domination. Italian domination is fairly a new concept and there are only a handful of papers on Italian domination. Interested readers may refer to [2, 17, 18, 20, 22, 24, 26, 28] and [35]. In [29], the exact value of perfect Italian domination number for Cartesian product of some special graphs is obtained. A relation between the Roman domination number and the perfect Italian domination number of a graph G is obtained and the corresponding realization problem is also solved. In [32], the authors characterize the graphs G with ${\gamma }_I^p(G)$ equal to 2 and 3 and determined the exact value of the parameter for several simple-structured graphs. It is also proved that it is NP-complete to decide whether a given bipartite graph admits a perfect Italian dominating function of weight k.

Given a graph $G=(V,E),$ a function $f:V\to \{0,1,2,3\}$ having the property that if f(v) = 0, then there exist $v_1,v_2\in N(v)$ such that $f(v_1)=f(v_2)=2$ or there exists $w\in N(v)$ such that f(w) = 3, and if f(v) = 1, then there exists $w\in N(v)$ such that $f(w)\ge 2$ is called a double Roman dominating function (DRDF). The double Roman domination number, ${\gamma }_{dR}(G),$ is the minimum among the weights of DRDFs on G. If $f:V\to \{0,1,2,3\}$ is a function defined on V(G), then $\{v\in V(G):f(v)=i\}$ is denoted by $V_i^f.$ (If there is no ambiguity, $V_i^f$ is written as V_i [9]. The study of double Roman domination was initiated by R. A. Beeler, T. W. Haynes and S. T. Hedetniemi in [9]. Interested readers may refer [3–6, 21, 34, 36] and [38]. Domination parameters in some classes of graphs have been studied by several authors (see [15, 16]).

Let $G=(V,E)$ be a non-empty graph of order $n\ge 2,$ and t a positive integer. Let V^t be the set of words of length t on alphabet V. A word u of length t is denoted by $u_1{u}_2\dots u_t.$ The graph $S(K_n,t),t\ge 1,$ was introduced by Klavžar and Milutinović in [30] and was later called as Sierpiński graphs in [31]. $S(K_n,t)$ has vertex set V^t and $\{u,v\}$ is an edge if and only if there exists $i\in \{1,2,\dots ,t\}$ such that: (i) $u_j=v_j,$ if $j<i;$ (ii) $u_i\ne v_i;$ (iii) $u_j=v_i$ and $v_j=u_i,$ if $j>i.$ The vertices of the form $\mathit{uuu}\dots u$ are called extreme vertices of $S(K_n,t).$

The generalized Sierpiński graph of a graph G, denoted by S(G, t), is a graph with vertex set V^t and edge set $\left\{\right\{w{u}_i{u}_j^{r-1},w{u}_j{u}_i^{r-1}\}:\{u_i,u_j\}\in E,i\ne j;r\in \{1,2,\dots ,t\};w\in V^{t-r}\}$ [19]. Note that $S(G,1)$ is G itself. If $V=\{1,2,\dots ,n\}$ is the vertex set of G, then in $S(G,2)$ $V_i=\{ij:j=1,2,\dots ,n\}$ induces a copy of G for each $i\in \{1,2,\dots ,n\}.$ The subgraph induced by V_i is denoted by Gⁱ, for $i\in \{1,2,\dots ,n\}.$ Figure 1 gives $S(C_5,1)$ and $S(C_5,2).$

Figure 1. Sierpiński graphs $S(C_5,t),t=1,2.$

The value of various domination parameters of Sierpiński graphs were studied in [6, 27, 33] and [37]. The reader may refer to the survey paper [25]. For any graph theoretic terminology and notations not mentioned here, the readers may refer to [8].

The following results are useful in this paper.

Theorem 1.1.

[10] For a cycle C_n and a path P_n, ${\gamma }_I(C_n)=\lceil \frac{n}{2}\rceil ,{\gamma }_I(P_n)=\lceil \frac{n+1}{2}\rceil .$

Theorem 1.2.

[32] For a cycle C_n, ${\gamma }_I^p(C_n)=\lceil \frac{n}{2}\rceil .$

Proposition 1.3.

[9] In a double Roman dominating function of weight ${\gamma }_{dR}(G)$, no vertex needs to be assigned the value 1.

Proposition 1.4.

[1] For $n\ge 3,$ $${\gamma }_{dR}(C_n)=\{\begin{array}{ll}n& ifn\equiv 0,2,3,4(\mathit{mod}6),\\ n+1& ifn\equiv 1,5(\mathit{mod}6).\end{array}$$

Proposition 1.5.

[1] For $n\ge 1,$ $${\gamma }_{dR}(P_n)=\{\begin{array}{ll}n& ifn\equiv 0(\mathit{mod}3),\\ n+1& ifn\equiv 1or2(\mathit{mod}3).\end{array}$$

In this paper, we obtain the exact values of the Italian domination number, the perfect Italian domination number and the double Roman domination number of the generalized Sierpiński graph $S(G,2),$ where G is a cycle C_n, $n\ge 4,$ a complete bipartite graph $K_{1,q}$ or $K_{2,q},q\ge 2$ and a bistar $B_{m,n},m,n\ge 3.$

2. Main Results

For n = 3, $C_n\cong K_3$ and ${\gamma }_I(S(K_n,2)),{\gamma }_I^p(S(K_n,2))$ and ${\gamma }_{dR}(S(K_n,2))$ were discussed in [27, 28] and [6], respectively. Hence, in this section, we consider C_n, for $n\ge 4$ only.

Theorem 2.1.

The Italian domination number of the generalized Sierpiński graph $S(C_n,2)$ is ${\gamma }_I(S(C_n,2))=n\lceil \frac{n}{2}\rceil$, for $n\ge 4.$

Proof.

Let $V(C_n)=\{v_1,v_2,\dots ,v_n\}.$ Then $S(C_n,2)$ has the vertex set $\{v_i{v}_j:i,j\in \{1,2,\dots ,n\left\}\right\}$ and edge set $\{(v_i{v}_j,v_i{v}_k):v_j{v}_k\in E(C_n)\}\cup \{(v_i{v}_j,v_j{v}_i):v_i{v}_j\in E(C_n)\}.$ In $S(C_n,2)$ there are n copies of C_n and we know that ${\gamma }_I(C_n)=\lceil \frac{n}{2}\rceil .$ Therefore, if we take a γ_I-function in each copy of C_n, we get an IDF of $S(C_n,2),$ so that ${\gamma }_I(S(C_n,2))\le n\lceil \frac{n}{2}\rceil .$

For the reverse inequality, note that in $C_n^i,v_i{v}_i$ is the extreme vertex and $v_i{v}_{i-1}$ and $v_i{v}_{i+1}$ are the vertices which are adjacent to $C_n^{i-1}$ and $C_n^{i+1},$ respectively. The vertices other than $v_i{v}_{i-1},v_i{v}_i,v_i{v}_{i+1}$ form a path on $n-3$ vertices, say $P_{n-3}^i.$ Therefore, $f(P_{n-3}^i-\{v_i{v}_{i-2},v_i{v}_{i+2}\})\ge \lceil \frac{n-5+1}{2}\rceil =\lceil \frac{n-4}{2}\rceil .$ To Italian dominate $v_i{v}_{i-2},v_i{v}_i,v_i{v}_{i+2}$ (which do not have any adjacency outside $C_n^i$) we need minimum weight 2. Therefore, $f(C_n^i)\ge \lceil \frac{n-4}{2}\rceil +2=\lceil \frac{n}{2}\rceil$ so that ${\gamma }_I(S(C_n,2))\ge n\lceil \frac{n}{2}\rceil .$ Hence, ${\gamma }_I(S(C_n,2))=n\lceil \frac{n}{2}\rceil .$ □

Corollary 2.2.

The perfect Italian domination number of the generalized Sierpiński graph $S(C_n,2)$ is ${\gamma }_I^p(S(C_n,2))=n\lceil \frac{n}{2}\rceil$, for $n\ge 4.$

Proof.

We know that ${\gamma }_I^p(C_n)=\lceil \frac{n}{2}\rceil .$ The proof is similar to that of Theorem 2.1. □

Lemma 2.3.

If P_n is a path on n vertices, where n is a multiple of 3, then the weight of a γ_dR-function assigned to the end vertices is always zero.

Proof.

Let P_n be the path $v_1{v}_2\dots v_n.$ Let f be any γ_dR-function with $f(v_1)=1.$ Then v₁ cannot double Roman dominate any other vertex. Hence, $f(P_n-v_1)\ge n-1+1=n,$ so that $f(P_n)\ge n+1$ which is a contradiction.

Now let f be a γ_dR-function with $f(v_1)=2.$ If $f(v_2)\le 1,$ then none of the vertices of $P_n-\{v_1,v_2\}$ are double Roman dominated by vertices outside $P_n-\{v_1,v_2\}.$ Consequently, $f(P_n-\{v_1,v_2\})\ge n-2+1=n-1,$ so that $f(P_n)\ge n-1+2=n+1,$ which is a contradiction. If $f(v_2)>1$ then we can find a DRDF g as follows. $g(v_1)=0,g(v_2)=3$ and $g(v_i)=f(v_i)$ for $i=3,4,\dots ,n.$ Clearly, g is a DRDF with weight less than that of f, which is also a contradiction. Hence, we conclude that $f(v_1)\ne 2.$

Similarly, the case when $f(v_1)=3$ also leads to a contradiction and so $f(v_1)=0.$ In the same manner, we can also prove that $f(v_n)=0.$ □

Lemma 2.4.

If C_n is a cycle, where n is an odd multiple of 3 then in any γ_dR-function, no vertex is assigned the weight 2.

Proof.

Let C_n be a cycle $v_1{v}_2\dots v_n$ and let f be a γ_dR-function with at least one vertex assigned the weight 2. For definiteness, let $f(v_1)=2.$ If $f(v_2)$ is non-zero, then $f(v_1)+f(v_2)\ge 4$ and $f(C_n-\{v_1,v_2,v_3,v_n\})\ge n-4+1=n-3,$ so that $f(C_n)\ge n-3+4=n+1$ which is a contradiction. If $f(v_2)=0,$ then $f(v_3)$ must be non-zero. If $f(v_3)=3$ then $f(v_1)+f(v_3)=5$ and $f(C_n-\{v_1,v_2,v_3,v_4,v_n\})\ge n-5+1=n-4$ so that $f(C_n)\ge n-4+5=n+1$ which is also a contradiction. Hence, $f(v_3)=2.$ Continuing this argument, we get $f(v_i)=0$ or 2 according as i is even or odd, respectively, so that $f(C_n)=n+1$ which is a contradiction. Hence, the result follows. □

Theorem 2.5.

The double Roman domination number of the generalized Sierpiński graph $S(C_n,2)$ is $${\gamma }_{dR}(S(C_n,2))=\{\begin{array}{ll}{n}^2-\frac{n}{2}& ifn=3k,k\ge 1is\mathit{even},\\ n^2-\frac{n}{3}& ifn=3k,k\ge 1is\mathit{odd},\\ n(n-1)& ifn=3k+1,k\ge 1,\\ n^2& ifn=3k+2,k\ge 1.\end{array}$$

Proof.

Let $V(C_n)=\{v_1,v_2,\dots ,v_n\}.$ Then $S(C_n,2)$ has the vertex set $\{v_i{v}_j:i,j\in \{1,2,\dots ,n\left\}\right\}$ and edge set $\{(v_i{v}_j,v_i{v}_k):v_j{v}_k\in E(C_n)\}\cup \{(v_i{v}_j,v_j{v}_i):v_i{v}_j\in E(C_n)\}.$ We consider the following cases.

Case 1: $n=3k,k\ge 1$ is even.

Define the following function on $S(C_n,2).$ $$f(v_i{v}_j)=\{\begin{array}{l}3ifi=2,4,\dots ,n;j=i+3l(\mathit{mod}n);l=1,2,\dots ,k-1,\\ 2ifi=1,3,\dots ,n-1;j=i+1+2l(\mathit{mod}n),\\ l\ge 0\mathit{and}i=j=2,4,\dots ,n,\\ 0\mathit{otherwise}.\end{array}$$ Clearly, f is a DRDF and $f(V)=3\frac{n}{2}(k-1)+2\frac{n}{2}\frac{n}{2}+2\frac{n}{2}=n^2-\frac{n}{2}.$ Hence, ${\gamma }_{dR}(S(C_n,2))\le n^2-\frac{n}{2}.$

For the reverse inequality, note that in each $C_n^i,v_i{v}_i$ is the extreme vertex and $v_i{v}_{i-1}$ and $v_i{v}_{i+1}$ are the only vertices adjacent to other copies of C_n. The remaining vertices (other than $v_i{v}_{i-1},v_i{v}_i,v_i{v}_{i+1}$) form a path on $n-3$ vertices, say $P_{n-3}^i.$ Let f be any DRDF of $S(C_n,2).$ If $f(v_i{v}_{i-1})+f(v_i{v}_{i+1})=0,$ then $f(v_i{v}_i)\ge 2$ and $f(P_{n-3}^i)\ge n-3,$ so that $f(C_n^i)\ge n-3+2=n-1.$ If $f(v_i{v}_{i-1})+f(v_i{v}_{i+1})=2,$ then one of $f(v_i{v}_{i-1})$ and $f(v_i{v}_{i+1})$ must be 2. For definiteness, let $f(v_i{v}_{i+1})=2.$ Then $f(P_{n-3}^i-v_i{v}_{i+2})\ge n-4+1=n-3.$ In this case, $f(v_i{v}_i)\ge 2$ so that $f(C_n^i)\ge n-3+2+2=n+1.$ If $f(v_i{v}_{i-1})+f(v_i{v}_{i+1})=3,$ then one of $f(v_i{v}_{i-1})$ and $f(v_i{v}_{i+1})$ is 3. For definiteness, let $f(v_i{v}_{i+1})=3.$ Then $f(P_{n-3}^i-v_i{v}_{i+2})\ge n-4+1=n-3$ so that $f(C_n^i)\ge n.$ If $f(v_i{v}_{i-1})+f(v_i{v}_{i+1})\ge 4$ then $f(P_{n-3}^i-v_i{v}_{i-2},v_i{v}_{i+2})\ge n-5+1=n-4$ so that $f(C_n^i)\ge n.$ Thus, in all cases, $f(C_n^i)\ge n-1$ and if $f(C_n^i)=n-1$ then $f(P_{n-3}^i)=n-3,f(v_i{v}_{i-1})=f(v_i{v}_{i+1})=0$ and $f(v_i{v}_i)=2.$ We claim that if $f(C_n^{i_0})=n-1$ then $f(C_n^{i_0+1})\ge n.$ Since $f(P_{n-3}^{i_0})=n-3,$ then $f(v_{i_o}{v}_{i_0-2})=f(v_{i_0}{v}_{i_0+2})=0$ by Lemma 2.3. Therefore, since $f(v_{i_o}{v}_{i_0-1})=f(v_{i_0}{v}_{i_0+1})=0,$ to double Roman dominate $v_{i_0}{v}_{i_0+1},f(v_{i_0+1}{v}_{i_0})\ge 2$ so that $f(C_n^{i_0+1})\ge n.$ Thus if $f(C_n^{i_0})=n-1$ then $f(C_n^{i_0+1})\ge n$ so that $f(S(C_n,2))\ge n\frac{n}{2}+(n-1)\frac{n}{2}=n^2-\frac{n}{2}.$

Case 2: $n=3k,$ $k\ge 1$ is odd.

As in case 1, for any γ_dR-function f of $S(C_n,2)$ $f(C_n^i)\ge n-1$ for each $i=1,2,\dots ,n.$ We claim that if $f(C_n^{i_0})=n-1,$ then both $f(C_n^{i_0-1})$ and $f(C_n^{i_0+1})$ is at least n. If $f(C_n^{i_0})=n-1,$ then $f(v_{i_0}{v}_{i_0})=2$ and $f(v_{i_o}{v}_{i_0-1})=f(v_{i_0}{v}_{i_0+1})=0.$ So to double Roman dominate $v_{i_0}{v}_{i_0+1},f(v_{i_0+1}{v}_{i_0})$ must be at least 2. If $f(v_{i_0+1}{v}_{i_0})=2,$ then $f(C_n^{i_0+1})\ge n+1$ by Lemma 2.4 and so $f(v_{i_0+1}{v}_{i_0})=3.$ If $f(v_{i_0+1}{v}_{i_0})=3$ then $f(v_{i_0+1}{v}_{i_0+2})$ must be zero in order to make $f(C_n^{i_0+1})=n.$ i.e., the only vertex which is outside $C_n^{i_0+1}$ and double Roman dominated by vertices in $C_n^{i_0+1}$ is $v_{i_0}{v}_{i_0+1}.$ Similarly, $f(v_{i_0-1}{v}_{i_0})=3,f(C_n^{i_0-1})=n$ and the only vertex which is outside $C_n^{i_0-1}$ and double Roman dominated by vertices in $C_n^{i_0-1}$ is $v_{i_0}{v}_{i_0-1}.$ Thus, for three consecutive copies of C_n, at most one copy can have weight $n-1$ and hence $f(S(C_n,2))\ge n^2-\frac{n}{3}.$

Case 3: $n=3k+1,k\ge 1.$

Define the following function on $S(C_n,2)$ $$f(v_i{v}_j)=\{\begin{array}{l}3ifi\in \{1,2,\dots ,n\}\mathit{and}j=i+1+3l(\mathit{mod}n);\\ l=0,1,\dots ,k-1,\\ 0\mathit{otherwise}.\end{array}$$ Clearly, f is a DRDF and $f(V)=n3k=n(n-1).$ Hence, ${\gamma }_{dR}(S(C_n,2))\le n(n-1).$

For the reverse inequality, note that $f(C_n^i)\ge n-1$ for all $i\in \{1,2,\dots ,n\}$ as in above cases and hence $f(S(C_n,2))\ge n(n-1).$

Case 4: $n=3k+2,k\ge 1.$

Define the following function on $S(C_n,2).$ $$f(v_i{v}_j)=\{\begin{array}{l}3ifi\in \{1,2,\dots ,n\},j=i+1+3l(\mathit{mod}n),\\ l=0,1,\dots ,k-1,\\ 2ifi\in \{1,2,\dots ,n\},j=i-3(\mathit{mod}n),\\ 0\mathit{otherwise}.\end{array}$$ Clearly, f is a DRDF and $f(V)=n(3k+2)=n^2.$ Hence, ${\gamma }_{dR}(S(C_n,2))\le n^2.$

For the reverse inequality, the proof is similar to case 3 except when $f(v_i{v}_{i-1})+f(v_i{v}_{i+1})\ge 4.$ If $f(v_i{v}_{i-1})+f(v_i{v}_{i+1})=4,$ then $f(v_i{v}_{i-1})=f(v_i{v}_{i+1})=2$ and hence $P_{n-3}^i\cup \{v_i{v}_{i-1},v_i{v}_{i+1}\}$ can be considered as a path on $n-1$ vertices of which none of the vertices are double Roman dominated by vertices from copies of C_n other than $C_n^i.$ Consequently, $f(C_n^i)\ge f(P_{n-3}^i\cup \{v_i{v}_{i-1},v_i{v}_{i+1}\})\ge n-1+1=n.$ If $f(v_i{v}_{i-1})+f(v_i{v}_{i+1})\ge 5,$ then $f(P_{n-3}^i\cup \{v_i{v}_{i-2},v_i{v}_{i+2}\})\ge n-5$ and so $f(C_n^i)\ge n.$ Thus in all cases, $f(C_n^i)\ge n$ and hence $f(S(C_n,2))\ge n^2.$ □

When p = 1 and q = 1 $K_{p,q}$ is K₂ and it is proved in [28] that ${\gamma }_I(S(K_n,2))=2n-1.$ Therefore, ${\gamma }_I(S(K_{1,1},2))=3$ and also ${\gamma }_I^p(S(K_{1,1},2))=3.$ Also in [6], it is found that ${\gamma }_{dR}(S(K_n,2))=3n-1$ and hence ${\gamma }_{dR}(S(K_{1,1},2))=5.$ When p = 1 and q = 2 then $K_{p,q}=P_3$ and it is a simple observation that ${\gamma }_I(S(P_3,2))=5,{\gamma }_I^p(S(P_3,2))=6$ and ${\gamma }_{dR}(S(P_3,2))=8.$ Hence, in the following theorems, we consider the case p = 1 and $q\ge 3.$

Theorem 2.6.

The Italian domination number of the generalized Sierpiński graph $S(K_{1,q},2)$ is ${\gamma }_I(S(K_{1,q},2))=2q+1,q\ge 3.$

Proof.

Let $v_1,v_2,\dots ,v_{q+1}$ be the vertices of $K_{1,q}$ where v₁ is the universal vertex. Define the following function on $S(K_{1,q},2)$ as follows. $$f(v)=\{\begin{array}{l}2ifv=v_i{v}_1,i=2,3,\dots ,q+1,\\ 1ifv=v_1{v}_1,\\ 0\mathit{otherwise}.\end{array}$$ Clearly, f is an IDF and $f(V)=2q+1$ and hence, ${\gamma }_I(S(K_{1,q},2))\le 2q+1.$

Since $q\ge 3,$ each copy of $K_{1,q}^i$ for $i=2,3,\dots ,q+1,$ contains three or more leaves. So to Italian dominate these vertices we need to assign weight at least 2 to the vertex $v_i{v}_1.$ Now in $K_{1,q}^1,$ the vertices $v_1{v}_j,j=2,3,\dots ,q+1$ are Italian dominated by $v_j{v}_1.$ So the only vertex which is not Italian dominated in $K_{1,q}^1$ is $v_1{v}_1.$ Hence, we have to assign weight 1 to $v_1{v}_1,$ so that, ${\gamma }_I(S(K_{1,q},2))\ge 2q+1.$ Therefore, ${\gamma }_I(S(K_{1,q},2))=2q+1.$ □

Theorem 2.7.

The perfect Italian domination number of the generalized Sierpiński graph $S(K_{1,q},2)$ is ${\gamma }_I^p(S(K_{1,q},2))=2(q+1),q\ge 3.$

Proof.

Let $v_1,v_2,\dots ,v_{q+1}$ be the vertices of $K_{1,q}$ where v₁ is the universal vertex. Define the following function on $S(K_{1,q},2)$ as follows. $$f(v)=\{\begin{array}{l}2ifv=v_i{v}_1,i=2,3,\dots ,q+1,\mathit{and}v=v_1{v}_2,\\ 0\mathit{otherwise}.\end{array}$$ Clearly, f is a PID function and $f(V)=2q+2=2(q+1).$ Therefore, ${\gamma }_I^p(S(K_{1,q},2))\le 2(q+1).$

In each $K_{1,q}^i$ for $i=2,3,\dots ,q+1,$ there are q vertices which are not adjacent to vertices of other copies of $K_{1,q}.$ Hence, for any ${\gamma }_I^p$-function f of $S(K_{1,q},2),f(K_{1,q}^i)\ge 2,i=2,3,\dots ,q+1.$ Also, it is optimum to assign the weight 2 to $v_i{v}_1$ where $i=2,3,\dots ,q+1.$ Now, the only vertex which is not perfect Italian dominated is $v_1{v}_1.$ We cannot give the weight 1 to $v_1{v}_1,$ since, in this case $\sum _{u\in N(v_1{v}_i)}f(u)=3,$ for $i=2,3,\dots ,q+1.$ Hence, we have to give weight to the vertices of $K_{1,q}^1,$ so that $\sum _{u\in N(v_1{v}_1)}f(u)=2,$ which results in $f(K_{1,q}^1)=2.$ Therefore, ${\gamma }_I^p(S(K_{1,q},2))\ge 2q+2=2(q+1).$ Hence, ${\gamma }_I^p(S(K_{1,q},2))=2(q+1).$ □

Theorem 2.8.

The double Roman domination number of the generalized Sierpiński graph $S(K_{1,q},2)$ is ${\gamma }_{dR}(S(K_{1,q},2))=3q+2,q\ge 3.$

Proof.

The proof is similar to that of Theorem 2.6 with the difference that the weights 2 and 1 are replaced by 3 and 2, respectively. □

When $p=q=2,K_{p,q}=C_4$ and it is discussed in the section 2.

Theorem 2.9.

The Italian domination number of the generalized Sierpiński graph $S(K_{2,q},2)$ is ${\gamma }_I(S(K_{2,q},2))=2(q+2)$ for p = 2, $q\ge 3.$

Proof.

Let $V(K_{2,q})=\{v_1,v_2,\dots ,v_{q+2}\}$ be the vertex set of $K_{2,q}$ and $d(v_1)=d(v_2)=q.$ Define the following function on $S(K_{2,q},2)$ as follows. $$f(v)=\{\begin{array}{l}1ifv=v_i{v}_1,v_i{v}_2,i\in \{1,2,\dots ,q+2\},\\ 0\mathit{otherwise}.\end{array}$$ It can be easily verified that f is an IDF and $f(V)=2(q+2).$ Therefore, ${\gamma }_I(S(K_{2,q},2))\le 2(q+2).$

In each $K_{2,q}^i$ there are at least two vertices which are not adjacent to vertices of other copies of $K_{2,q}.$ So to Italian dominate $K_{2,q}^i$ we need at least weight 2. Therefore, ${\gamma }_I(S(K_{2,q},2))\ge 2(q+2).$ Hence, ${\gamma }_I(S(K_{2,q},2))=2(q+2).$ □

Proposition 2.10.

The perfect Italian domination number of generalized Sierpiński graph $S(K_{2,3},2)$ is ${\gamma }_I^p(S(K_{2,3},2))=11.$

Proof.

Let $\{v_1,v_2,v_3,v_4,v_5\}$ be the vertex set of $K_{2,3}$ where $\{v_1,v_2\}$ and $\{v_3,v_4,v_5\}$ are the partite sets of the vertex set. Define a function f on $S(K_{2,3},2)$ as follows. 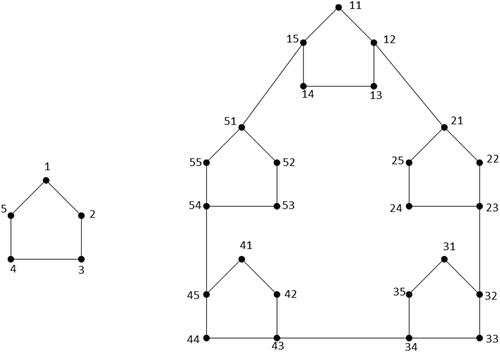$$f(v)=\{\begin{array}{l}2ifv=v_2{v}_5,v_5{v}_1,\\ 1if{v}_i{v}_j,i=3,4,j=1,2,\mathit{and}v=v_1{v}_3,v_1{v}_4,v_2{v}_2,\\ 0\mathit{otherwise}.\end{array}$$ It can be easily verified that f is a PID- function and $f(V)=11$ so that ${\gamma }_I^p(S(K_{2,3},2))\le 11.$ (This labeling is illustrated in Figure 2.)

Figure 2. Illustration of $S(K_{2,3},2).$

In each copy of $K_{2,3}$ there are at least 2 vertices which are not adjacent to the vertices of other copies of $K_{2,3}.$ Hence to perfect Italian dominate each $K_{2,3}^i$ we need minimum weight 2. If possible, assume that $f(K_{2,3}^i)=2$ for every $i=1,2,3,4,5.$ In particular, $f(K_{2,3}^1)=2.$ Since $v_1{v}_1$ and $v_1{v}_2$ are not adjacent to any vertices of other copies of $K_{2,3},$ these vertices must be perfect Italian dominated by the vertices of $K_{2,3}^1.$ Then, one of the following cases may arise.

Case 1: $f(v_1{v}_1)=f(v_1{v}_2)=1.$

Since $f(K_{2,3}^1)=2,f(v_1{v}_j)=0.$ Since f is a PID function $\sum _{u\in N(v_1{v}_j)}f(v_1{v}_j)=2$ and hence $f(v_j{v}_1)=0$ for $j=3,4,5.$ Now, to perfect Italian dominate $v_j{v}_1,$ we must have ${\sum }_{k=3}^{5}f(v_j{v}_k)=2,j=3,4,5.$ This implies, there exists at least one vertex $v_j{v}_k$ with $f(v_j{v}_k)=0.$ To perfect Italian dominate this $v_j{v}_k,$ we must have $f(v_j{v}_2)=2,$ which is a contradiction to the fact that $f(K_{2,3}^j)=2.$

Case 2: ${\sum }_{j=3}^{5}f(v_1{v}_j)=2.$

Then for the vertices $v_1{v}_3,v_1{v}_4$ and $v_1{v}_5$ either two vertices have weight 1 or one vertex has weight 2.

Subcase(a): Two vertices have weight 1 and the third vertex has weight 0.

For definiteness, let $f(v_1{v}_3)=f(v_1{v}_4)=1$ and $f(v_1{v}_5)=0.$ Now, to perfect Italian dominate $v_1{v}_5$ we must have $f(v_5{v}_1)=2.$ Since $f(K_{2,3}^5)=2,f(v_5{v}_2)=0.$ To perfect Italian dominate $v_5{v}_2$ we must have $f(v_2{v}_5)=2.$ Since $f(K_{2,3}^2)=2,f(v_2{v}_3)=f(v_2{v}_4)=0.$ To perfect Italian dominate $v_2{v}_3$ and $v_2{v}_4$ we must have $f(v_3{v}_2)=f(v_4{v}_2)=2.$ But the vertices $v_3{v}_1$ and $v_4{v}_1$ are not perfect Italian dominated. To perfect Italian dominate these vertices we need more weight, which contradicts the fact that $f(K_{2,3}^i)=2$ for all i.

Subcase(b): One vertex has weight 2 and other vertices have weight 0.

For definiteness, let $f(v_1{v}_3)=2,$ and $f(v_1{v}_i)=0,$ for $i=1,2,4,5.$ To perfect Italian dominate $v_1{v}_4$ and $v_1{v}_5$ we must have $f(v_4{v}_1)=f(v_5{v}_1)=2.$ Since $f(K_{2,3}^4)=f(K_{2,3}^5)=2,$ we have $f(v_4{v}_2)=f(v_5{v}_2)=0.$ To perfect Italian dominate $v_4{v}_2$ and $v_5{v}_2$ we must have $f(v_2{v}_4)=f(v_2{v}_5)=2,$ which is a contradiction to the fact that $f(K_{2,3}^2)=2.$

Therefore, ${\gamma }_I^p(S(K_{2,3},2))\ge 11.$ Hence, ${\gamma }_I^p(S(K_{2,3}2))=11.$ □

Theorem 2.11.

The perfect Italian domination number of the generalized Sierpiński graph $S(K_{2,q},2)$ is ${\gamma }_I^p(S(K_{2,q},2))=2(q+3)$, for $p=2,q\ge 4.$

Proof.

Let $V(K_{2,q})=\{v_1,v_2,\dots ,v_{q+2}\}$ be the vertex set of $K_{2,q}$ where $\{v_1,v_2\}$ and $\{v_3,v_4,\dots ,v_{q+2}\}$ are the partite sets of $K_{2,q}.$ Define a function on $S(K_{2,q},2)$ as follows. $$f(v)=\{\begin{array}{l}2ifv=v_i{v}_3,i=1,2,\\ 1ifv=v_i{v}_1,v_i{v}_2,i=3,4,\dots ,q+2,v=v_i{v}_1,i=1,2,\\ 0\mathit{otherwise}.\end{array}$$ Clearly, f is a PID-function and $f(V)=2(q+3)$ so that ${\gamma }_I^p(S(K_{2,q},2))\le 2(q+3).$

Since in each copy of $K_{2,q}^i$ there are at least two vertices which are not adjacent to vertices of other copies of $K_{2,q},$ we need at least weight 2 to perfect Italian dominate each $K_{2,q}^i.$ If there are two copies of $K_{2,q}$ with $f(K_{2,q}^i)=3,$ then $f(S(K_{2,q},2))=2(q+3).$ Therefore, if possible assume that, there exists exactly one copy of $K_{2,q}$ with $f(K_{2,q}^i)=3$ and all other copies have weight 2. Then either $f(K_{2,q}^1)=2$ or $f(K_{2,q}^2)=2.$ For definiteness, let $f(K_{2,q}^1)=2.$ Since both $v_1{v}_1$ and $v_1{v}_2$ are perfect Italian dominated by the vertices of $K_{2,q}^1,$ one of the following cases arises.

Case 1: $f(v_1{v}_1)=f(v_1{v}_2)=1.$

Since $f(K_{2,q}^1)=2,f(v_1{v}_j)=0$ for $j=3,4,\dots ,q+2.$ Since f is a perfect Italian dominating function $\sum _{u\in N(v_1{v}_j)}f(u)=2$ so that $f(v_j{v}_1)=0$ for $j=3,4,\dots ,q+2.$ To perfect Italian dominate $v_j{v}_1,$ we must have $\sum _{u\in N(v_j{v}_1)}f(u)=2.$ This implies, there exists at least two vertices $v_j{v}_k$ such that $f(v_j{v}_k)=0$ for $j,k=3,4,\dots ,q+2,$ and hence $f(v_j{v}_2)=0,$ which implies $f(K_{2,q}^i)=4$ for $i=3,4,\dots ,q+2,$ which is a contradiction.

Case 2: ${\sum }_{j=3}^{q+2}f(v_1{v}_j)=2.$

Then for the vertices $v_1{v}_3,v_1{v}_4,\dots ,v_1{v}_{q+2}$ either two vertices have weight 1 or one vertex has weight 2.

Subcase (a): $f(v_1{v}_j)=1$ for exactly two $j\prime s,$ and $f(v_1{v}_j)=0$ for all other $j\prime s,j=3,4,\dots ,q+2.$

For definiteness, let $f(v_1{v}_3)=f(v_1{v}_4)=1.$ Since $f(K_{2,q}^1)=2,f(v_1{v}_j)=0$ for $j=5,6,\dots ,q+2.$ To perfect Italian dominate $v_1{v}_j$ for $j=5,6,\dots ,q+2$ we must have $f(v_j{v}_1)=2.$ Since $f(K_{2,q}^j)=2,f(v_j{v}_2)=0.$ To perfect Italian dominate $v_j{v}_2$ we must have $f(v_2{v}_j)=2,$ for $j=5,6,\dots ,q+2.$ This implies, $f(K_{2,q})>4,$ which is a contradiction.

Subcase (b): $f(v_1{v}_j)=2$ for exactly one j and $f(v_1{v}_j)=0$ for all other $j\prime s,j=3,4,\dots ,q+2.$

For definiteness, let $f(v_1{v}_3)=2$ and $f(v_1{v}_j)=0$ for $j=4,5,\dots ,q+2.$ To perfect Italian dominate $v_1{v}_j$ we must have $f(v_j{v}_1)=2.$ Since $f(K_{2,q}^j)=2$ we must have $f(v_j{v}_2)=0.$ To perfect Italian dominate $v_j{v}_2$ we must have $f(v_2{v}_j)=2.$ This implies that $f(K_{2,q}^2)>6,$ which is a contradiction.

Therefore, ${\gamma }_I^p(S(K_{2,q},2))\ge 2q+6.$ Hence, ${\gamma }_I^p(S(K_{2,q},2))=2(q+3).$ □

Theorem 2.12.

The double Roman domination number of generalized Sierpiński graph $S(K_{2,3},2)$ is ${\gamma }_{dR}(S(K_{2,3},2))=18.$

Proof.

Let $\{v_1,v_2,v_3,v_4,v_5\}$ be the vertex set of $K_{2,3}$ where $\{v_1,v_2\}$ and $\{v_3,v_4,v_5\}$ are the partite sets of the vertex set. Define a function f as follows. $$f(v)=\{\begin{array}{l}3ifv=v_1{v}_3,v_2{v}_4,v_2{v}_5,v_3{v}_2,v_4{v}_1,v_5{v}_1,\\ 0\mathit{otherwise}.\end{array}$$ Clearly, f is a DRDF and ${\gamma }_{dR}(S(K_{2,3},2))\le 18.$

To prove the reverse inequality, note that in each copy of $K_{2,3}$ in $S(K_{2,3},2)$ there are at least two vertices which are not adjacent to other copies of $K_{2,3}.$ Hence, for any γ_dR-function f of $S(K_{2,3},2),f(K_{2,3}^i)\ge 3$ for all $i\in \{1,2,\dots ,5\}$ so that $f(S(K_{2,3},2))\ge 15.$ Therefore, in order to prove ${\gamma }_{dR}(S(K_{2,3},2))=18,$ we need only to prove that there does not exist any DRDF with weight 15, 16 or 17.

Claim 1: There does not exist a DRDF f with $f(S(K_{2,3},2))=15.$

Proof of Claim 1:

If there exists a DRDF f with $f(S(K_{2,3},2))=15,$ then $f(v_1{v}_j)=3$ for exactly one $j=3,4,5.$ For definiteness, let $f(v_1{v}_3)=3.$ Now to double Roman dominate $v_1{v}_4$ and $v_1{v}_5,f(v_4{v}_1)$ and $f(v_5{v}_1)$ must be three. Since, $f(K_{2,3}^4)=f(K_{2,3}^5)=3,v_4{v}_2$ and $v_5{v}_2$ should be double Roman dominated by $v_2{v}_4$ and $v_2{v}_5$ respectively which makes $f(K_{2,3}^2)\ge 6$ which is a contradiction.

Claim 2: There does not exist a DRDF f with $f(S(K_{2,3},2))=16.$

Proof of Claim 2:

If there exists a DRDF f with $f(S(K_{2,3},2))=16,$ then $f(K_{2,3}^{i_0})=4$ for exactly one i₀ with $1\le i_0\le 5$ and $f(K_{2,3}^i)=3,$ for every $i\in \{1,2,\dots ,5\},i\ne i_0.$ Then at least one among $f(K_{2,3}^1)$ and $f(K_{2,3}^2)$ must be 3. For definiteness, let $f(K_{2,3}^1)=3.$ Since $f(K_{2,3}^j)\le 4,$ for every $j=2,3,4,5,$ we get the same contradiction as in the proof of claim 1.

Claim 3: There does not exist a DRDF f with $f(S(K_{2,3},2))=17.$

Proof of Claim 3:

If there exists a DRDF f with $f(S(K_{2,3},2))=17,$ then the following two cases arise.

1. $f(K_{2,3}^{i_0})=5$ for exactly one i₀ with $1\le i_0\le 5$ and $f(K_{2,3}^i)=3,$ for every $i\in \{1,2,\dots ,5\},i\ne i_0.$

2. $f(K_{2,3}^i)=4$ for exactly two $i\prime s$ say i₀, j₀ with $1\le i_0,j_0\le 5$ and $f(K_{2,3}^i)=3,$ for every $i\in \{1,2,\dots ,5\},i\ne i_0,j_0.$

In case (i) at least one among $f(K_{2,3}^1)$ and $f(K_{2,3}^2)$ must be 3. For definiteness, $f(K_{2,3}^1)=3.$ Then as in the proof of claim 1 we may take $f(v_1{v}_3)=f(v_4{v}_2)=f(v_5{v}_2)=3.$ If $f(K_{2,3}^4)=f(K_{2,3}^5)=3,$ then we get the same contradiction as in the proof of claim 1. Hence one among $f(K_{2,3}^4)$ and $f(K_{2,3}^5)$ must be 5. For definiteness let $f(K_{2,3}^4)=5.$ Since $f(K_{2,3}^5)=3,$ to double Roman dominate $v_5{v}_2,f(v_2{v}_5)=3.$ But $v_2{v}_4$ is not get double Roman dominated and hence $f(K_{2,3}^2)\ge 3,$ which is a contradiction. Hence, we conclude that ${\gamma }_{dR}(S(K_{2,3},2))\ge 18.$ □

Now we obtain the Italian domination number, perfect Italian domination number and double Roman domination number of Sierpiński graph of bistar $B_{m,n},$ when t = 2.

Theorem 2.13.

The Italian domination number of the generalized Sierpiński graph $S(B_{m,n},2)$ is ${\gamma }_I(S(B_{m,n},2))=4(m+n+1),m,n\ge 3.$

Proof.

Let $V(B_{m,n})=\{v_1,v_2,\dots ,v_m,v_{m+1},v_{m+2},\dots ,v_{m+n},v_{m+n+1},v_{m+n+2}\}$ be the vertex set of $B_{m,n}.$ Let $d(v_{m+n+1})=m+1,d(v_{m+n+2})=n+1.$ Define a function f on $B_{m,n}$ as follows. $$f(v)=\{\begin{array}{l}2ifv=v_{m+n+1}{v}_{m+n+2},v_{m+n+2}{v}_{m+n+1}or\\ v=v_i{v}_{m+n+1},v_i{v}_{m+n+2},i\in \{1,2,\dots ,m+n\},\\ 0\mathit{otherwise}.\end{array}$$ Clearly, f is an IDF and $f(V)=4(m+n)+4=4(m+n+1)$ so that ${\gamma }_I(S(B_{m,n},2))\le 4(m+n+1).$

In each $B_{m,n}^i$ for $i\in \{1,2,\dots ,m+n\}$ there are m + n leaves. To Italian dominate these copies we need at least weight 4. For that, it is optimum to assign weight 2 to the vertices $v_i{v}_{m+n+1}$ and $v_i{v}_{m+n+2}.$ In $B_{m,n}^{m+n+1}$ and $B_{m,n}^{m+n+2}$ there are only n and m leaves, respectively. To Italian dominate these vertices we need at least weight 2. Therefore, ${\gamma }_I(S(B_{m,n},2))\ge 4(m+n)+2+2=4(m+n+1).$ Hence, ${\gamma }_I(S(B_{m,n},2))=4(m+n+1).$ □

Corollary 2.14.

The perfect Italian domination number of the generalized Sierpiński graph $S(B_{m,n},2)$ is ${\gamma }_I^p(S(B_{m,n},2))=4(m+n+1).$

Proof.

In the proof of the above theorem we have defined an Italian dominating function with the property that every vertex with weight 0 is adjacent to exactly one vertex with weight 2. Therefore, ${\gamma }_I^p(S(B_{m,n},2))\le 4(m+n+1).$ We know that ${\gamma }_I(S(B_{m,n},2))\le {\gamma }_I^p(S(B_{m,n},2)).$ Hence, ${\gamma }_I^p(S(B_{n,n},2))=4(m+n+1).$ □

Theorem 2.15.

The double Roman domination number of the generalized Sierpiński graph $S(B_{m,n},2)$ is ${\gamma }_{dR}(S(B_{m,n},2))=6(m+n+1),m,n\ge 3.$

Proof.

The proof is similar to that of Theorem 2.13 with the difference that the weight 2 is replaced by 3. □