?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.Abstract
In general, determining the domination number and the feedback vertex number
of a claw-free graph (even a line graph) is NP-hard. In contrast, the situation becomes different for the complement of a line graph. In this paper, it is shown that
for a claw-free G with
and thus determining the domination number of the complement of a claw-free G with
is polynomial, where
is the independence number of G. Furthermore, if a graph G is not a star, has no isolated vertex and isolated edge, then
where J(G) is the complement of the line graph L(G) of G. If a graph G is not a star, and has no isolated vertex,
provided
For the case when
is also given. Thereby, we are able to show that determining
is polynomial.
1. Introduction
All graphs considered here are finite, undirected and simple. We refer to [Citation6] for unexplained terminology and notation. Let be a graph. The order
and size
are denoted by n and m, respectively. The degree and the neighborhood of a vertex v are denoted by
and
respectively. The complement of G is denoted by
The maximum degree of G is denoted by
As usual, we use Kn, Cn, and Pn that denote the complete graph, the cycle, and the path of order n, respectively. For two positive integers, r, s, and denote the complete bipartite graph with r vertices in one part and s vertices in the other part. In particular,
is called a star if
Let G and H be two graphs. Their union and intersection are denoted by and
respectively. If G and H are disjoint, then
is denoted by G + H, and the join
is the graph obtained from G + H by joining each vertex of G to all vertices of H. Furthermore, for an integer
if
and
for any distinct
is denoted by kG.
The line graph L(G) of a graph G, is the graph with in which two vertices are adjacent if and only if they are adjacent in G. We refer to [Citation4] for some related result on line graphs. In [Citation10], Chartrand et al. called the complement of line graph as the jump graph of a graph G, denoted by J(G). They presented some sufficient conditions for a jump graph to be hamiltonian. Wu and Meng [Citation29] gave a simple characterization of hamiltonian jump graphs, and confirmed the validity of a conjecture and disproved a conjecture in [Citation10]. We refer to [Citation2, Citation11, Citation18, Citation28] for more works on complements of line graphs.
For a given graph F, a graph G is called F-free if no induced subgraph of G is isomorphic to F. In particular, a -free graph is called a claw-free graph. It is well-known that a line graph is a claw-free graph, and thus the complement of a line graph is the complement of a claw-free graph. Note also that the complement of a triangle-free graph is claw-free. For simplicity, we use
to denote that H is a subgraph of G or H is isomorphic to a subgraph G. Let
be a set of graphs. We use
to denote that G is isomorphic to a member of
Let and
The subgraph induced by S, denoted by
is the graph with S as its vertex set, in which two vertices are adjacent if and only if they are adjacent in G. The subgraph induced by M, denoted by
is the graph with M as its edge set, and with vertex set composed of all vertices incident with an edge of M in G. We call M a matching of G if no two elements of M is adjacent in G. The matching number of G, denoted by
is the cardinality of a maximum matching of G. A set S is called a clique (resp. independent set) of G if any two vertices of S are adjacent (resp. nonadjacent) in G. The clique number
(resp. independence number
is the cardinality of a maximum clique (a maximum independent set) of G.
A set S is a dominating set of a graph G if every vertex in is adjacent to at least one vertex of S in G. The domination number of G, denoted by
is the cardinality of a minimum dominating set of G. The independent domination number of a graph G, denoted by i(G), is the cardinality of a minimum maximal independent set of G.
Poljak [Citation24] showed that finding a maximum clique problem is NP-complete for claw-free graphs. In contrast, Minty [Citation22] and Sbihi [Citation26] showed that there is a polynomial algorithm to find an independent set of maximum weight in a weighted claw-free graph, and so there is a polynomial algorithm to determine Johnson [Citation13] was the first person to show that the determination of the domination number
of a graph is NP-complete. Later, Hedetniemi and Lasker [Citation15] showed the determination of the domination number
of a claw-free graph is NP-complete.
In contrast, we show that for a claw-free G with
and thus determining the domination number of the complement of a claw-free G with
is polynomial. Furthermore, if G is a graph without the isolated vertex and isolated edge and is not a star, then
where J(G) is the complement of the line graph L(G) of G.
Given a graph G, an interesting question is that how many vertices must be removed so that no cycles remain? In this context, the number is called the decycling number of G, and was originally explored by Beineke and Vandell [Citation8]. Of course, what remains is an induced forest of G. As it happens, Erdős, Saks, and Sós considered the more restricted problem of the maximum order of an induced tree in G [Citation12]. The same concept was also studied earlier in the context of electronics where cycles cause interference-hence the alternative but less natural name of vertex feedback. In general, we call this vertex set a feedback vertex set. A set
is called a feedback vertex set of G if G – S is a forest of G. The feedback vertex number of G, denoted by
is the cardinality of a minimum feedback set of G. The forest number f(G) of G is
In general, it is NP-hard to determine the feedback vertex number of a graph G [Citation16]. However, it becomes polynomial for specific families of graphs such as interval graph [Citation20], permutation graphs [Citation7], graphs with maximum degree 3 [Citation27]. Bau and Beineke [Citation3] provided a review of some earlier results and open problems on the decycling number of graphs. We refer to [Citation5, Citation9, Citation17, Citation19] for some recent results on it.
It is not hard to see that for a graph G,
Thus, with equality if and only if G has a Hamilton path, where n is the order of G. Furthermore, determining the feedback number (or the forest number) of a line graph (claw-free) is NP-hard since it is NP-complete to determine whether a graph G has a Hamilton path [Citation6]. It is also well-known that determining the feedback vertex number of a bipartite (triangle-free) graph (their complements are claw-free) is NP-complete [Citation30].
The situation becomes different for the complements of line graphs. In Section 3, we show that for a graph G if
or
For a graph without isolated vertices and with
and
we have
with the left side of equality if and only if G contains a subgraph
For the case when
is also determined.
2. Domination number
Ore [Citation23] proved that for for a graph G of order n without isolated vertices. McCuaig and Shepherd [Citation21] showed that
for a connected graph with exception of seven graphs. Reed [Citation25] proved that
Allan and Laskar [Citation1] proved that
for a claw-free G. Gernert [Citation14] proved that if G is 2-connected and claw-free of order n, then
and the bound is sharp, since
Theorem 2.1.
Let be a fixed integer. If G is a
-free graph with
, then
. In particular,
for a claw-free G with
Proof.
Let be an independent set of G. Take a vertex
Since G is
-free, v cannot be adjacent to each element of S in G, implying that v is adjacent to at least one element of S in
This shows that S is a dominating set of
and thus
□
Note that for a graph G, if and only if
is a triangle-free graph. In general,
can be arbitrarily large for a triangle-free graph
For example, if
then
thus
A matching M of G is called an induced matching if If G has an isolated edge then, trivially,
If G is a star of size m then
and thus
The following theorem says that for any graph G, one can find a minimum dominating set of J(G) in polynomial time.
Theorem 2.2.
Let G be a graph without isolated vertices and isolated edges. If G is not a star, then
Moreover, if and only if one of the following holds:
G has an induced matching of size of 2,
there exists a vertex of degree 2, whose two neighbors are not adjacent in G.
Proof.
Since G has no isolated edge,
If G has a triangle, then the three edges of the triangle form a dominating set of J(G), and thus So, assume that G has no triangle. Since G is not a star,
If
then any matching of cardinality three forms a dominating set of J(G). So, now we consider the remaining case when
and let
be a matching of G. If there is no edge adjacent to both e1 and e2 in G, then M is a dominating set of J(G). So, now take an edge e3 adjacent to both e1 and e2 in G. Since G has no triangle, any edge
is not adjacent to some element of
implying that
is a dominating set of J(G). Summing up the above,
We proceed to show the second half of the statement.
Sufficiency. Let be an induced matching of size 2. Any edge
cannot be adjacent to both of e1 and e2. Hence e is adjacent to one of e1 and e2 in J(G), and thus
Now assume that there exists a vertex u with
such that
Set
Clearly, it is easy to see that every edge
is adjacent to one of e1 and e2 in J(G). Again, we have
Necessity. Let and
be a dominating set of J(G). We consider two cases. If e1 and e2 are not adjacent, then
is an induced matching of G. Otherwise, an edge e3 is adjacent to both e1 and e2 in G, implying that e is adjacent to neither e1 nor e2 in J(G), contradicting that
is a dominating set of J(G). Assume that e1 and e2 are adjacent in G and let
and
Since S is a dominating set of J(G), it is easy to see that
and
□
3. Forest number
In this section, we determine the forest number of the complement of a line graph. Since an isolated vertex does not affect the number of vertices in the complement of the line graph, we only consider the case where the graph G does not contain isolated vertex. Note that we will use e(G) to represent the number of edges of graph G in the rest of the article. We begin with a simple observation.
Observation 3.1.
If H is a subgraph of a graph G, then J(H) is an induced subgraph of J(G).
Lemma 3.2.
If G is a graph with , then J(G) is a forest.
Proof.
Since or
If
then
J(G) is a independent set with Δ vertices. If
then J(G) is the union of a star of Δ vertices and a isolated vertex. Combining the above, we conclude that J(G) is a forest if
□
Corollary 3.3.
For any graph G with
Lemma 3.4.
Let G be a graph with or
. If J(G) is a forest, then
Proof.
If and J(G) is a forest, then
and thus
Now we consider the case when
We assume that
Let v be a vertex of maximum degree in G, and
the edges incident with v in G. Take two edges
of G not incident with v. We consider two cases.
Case 1.
and
are not adjacent.
Since there exists an edge ek that is adjacent to neither
nor
in G. Then
induces a triangle in J(G).
Case 2.
and
are adjacent.
Since there exist two edges ei and ej, each of which is adjacent to neither
nor
in G. It can be seen that
induces a 4-cycle in J(G). □
The following result is an immediate consequence of the above lemmas.
Corollary 3.5.
If G is a graph with or
, then J(G) is a forest if and only if G has at most
edges.
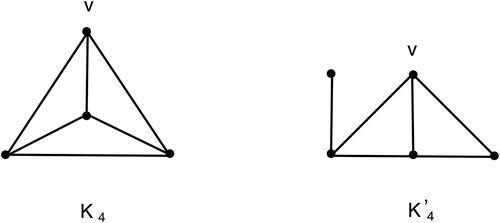
Lemma 3.6.
If G is a graph with , then J(G) is a forest if and only if G has at most three edges or is
Proof.
If then by Lemma 3.2, J(G) is a forest. It is straightforward to check that J(G) is forest for each
since
and
Conversely, assume that J(G) is a forest. Since is the set of all graphs with e(G) = 4 and
we have
If
then either
or G is a subgraph of
Let
be a matching of G. Clearly,
induces a triangle in J(G). In the latter case, J(G) contains C4. □
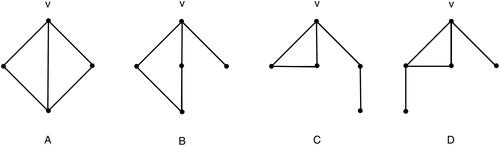
Let where
are the graphs as shown in .
Lemma 3.7.
If G is a graph with , then J(G) is a forest if and only if G has at most four edges or
or
}, as shown in .
Proof.
If then by Lemma 3.2, J(G) is a forest. One can check that both
and
are forests. Since
or
by Lemma 3.1, J(G) is also a forest.
Assume that J(G) is a forest and
Claim 1.
If e(G) = 5,
Let with
and
Let e1 and e2 be two edges of G not incident with v in G. First assume that e1 and e2 are not adjacent in G. If
as depicted in , then there exists an edge vvi which is adjacent to neither e1 nor e2. So,
induces a triangle of J(G), and thus
Next assume that e1 and e2 are adjacent in G, and let
If
J(G) contains C4. If
then
Summing up the above,
Claim 2.
If e(G) = 6,
Let with
and
Let e1, e2 and e3 be the three edges of G not incident with v in G. By the result of Claim 1,
for each
Otherwise G contains cycles. It follows that
Finally, we complete the whole proof by showing that is not possible. Suppose
with e(H) = 7. By Lemma 3.1, J(H) is a forest and further
is also a forest for any
By Claim 2,
if possible isolated vertices of H – e are deleted. If
then by
and thus J(H) contains a triangle, a contradiction. If
then J(H) contains C6. The proof is complete. □
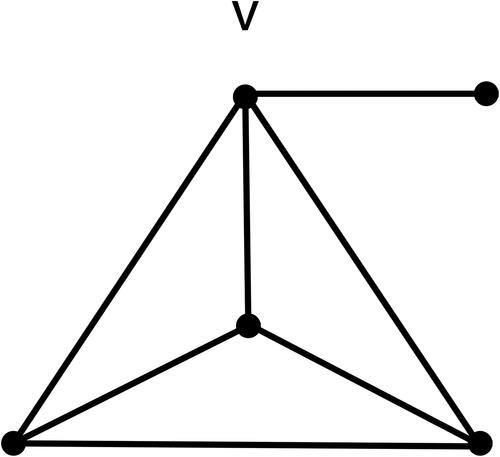
Let }, as given in .
Lemma 3.8.
If G is a graph with , then J(G) is a forest if and only if G has at most five edges or
or
Proof.
If then by Lemma 3.2, J(G) is a forest. It is straightforward to check that J(G) is a forest for each
Assume that J(G) is a forest and
Claim 1.
If e(G) = 6, then
Let with
and
Let e1 and e2 be two edges of G not incident with v in G. First assume that e1 and e2 are not adjacent in G. If
then there exists an edge vvi which is adjacent to neither e1 nor e2. So,
induces a triangle in J(G), and thus
Next assume that e1 and e2 are adjacent in G. If
then there exists two edges vvi, vvj each of which is adjacent to neither e1 nor e2. So,
induces a C4 in J(G), and thus
Claim 2.
If e(G) = 7, then
Let with
and
Let e1, e2 and e3 be the three edges of G not incident with v in G. By Claim 1 when
for each
It follows that
However,
contains C5 and
contains C6. This shows that
().
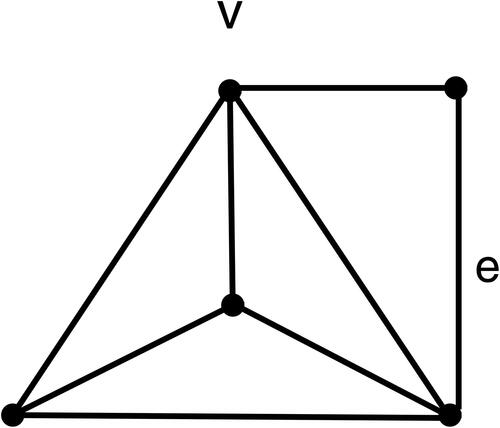
Finally, we complete the proof by showing that is impossible. Suppose
and
with e(H) = 8. By Lemma 3.1, J(H) is a forest and further
is also a forest for any
By Claim 2,
(see ) if possible isolated vertices of H – e are deleted. It follows that H is isomorphic to the graph shown in . It is easy to check that J(H) contains C5, a contradiction. The proof is complete. □
Now we are ready to give our main theorem. The jump graph of a graph G is determined in terms of its maximum degree.
Theorem 3.9.
For any graph G, we have
Proof.
If then
and
So, J(G) is itself a forest, and
Next assume that By Corollary 3.3,
We assume that
Let H be a subgraph of G with
such that J(H) is a forest, subject to this, e(H) is maximum. By Lemma 3.1,
If or
then by Corollary 3.5,
Since
we have
and
Thus,
Since J(H) is a forest, by Lemmas 3.6-3.8,
If
then by
we have
Moreover, by Lemmas 3.6-3.8,
with
Now assume that Since J(H) is a forest and
by Lemmas 3.6-3.8,
Since
If
then by Lemmas 3.6-3.8,
and
or
or
and
Next suppose that If
then by Lemma 3.7,
and
Since
by Lemma 3.8,
If
then
and by Lemma 3.8,
□
Acknowledgments
The authors would like to thank the anonymous referees for their valuable comments and suggestions.
Data availability
No data were used for the research described in the article.
Additional information
Funding
References
- Allan, R. B, Laskar, R. (1978). On domination and independent domination numbers of a graph. Discrete Math. 23(2): 73–76.
- An, X, Wu, B. (2007). Hamiltonicity of complements of middle graphs. Discrete Math. 307(9-10): 1178–1184.
- Bau, S, Beineke, L. W. (2002). The decycling number of graphs. Australas. J. Comb. 25: 285–298.
- Beineke, L. W, Bagga, J. S. (2021). Line Graphs and Line Digraphs. Switzerland: Springer.
- Bonamy, M., Dabrowski, K. K., Feghali, C., Johnson, M, Paulusma, D. (2018). Independent feedback vertex sets for graphs of bounded diameter. Inform. Process. Lett. 131: 26–32.
- Bondy, J. A, Murty, U. S. R. (2008). Graph Theory. GTM 244, London: Springer.
- Brandstädt, A. (1992). On improved time bounds for permutation graphs problem 18th International Workshop on Graph-Theoretic Concepts in Computer Science, WG92. In: Lecture Notes in Comput. Sci., vol. 657, Springer, Berlin, pp. 1–10.
- Beineke, L. W, Vandell, R. C. (1997). Decycling graphs. J. Graph Theory 25(1): 59–77.
- Chang, H., Fu, H. L, Lien, M. Y. (2013). The decycling number of outerplanar graphs. J. Comb. Optim. 25(4): 536–542.
- Chartrand, G., Hevia, H., Jarrett, E. B, Schultz, M. (1997). Subgraph distances in graphs defind by edge transfers. Discrete Math. 170(1–3): 63–79.
- Chen, X., Liu, J., Xie, D, Meng, J. (2016). Edge connectivity and super edge-connectivity of jump graphs. Inform. Optim. Sci. 37(2): 233–246.
- Erdös, P., Saks, M, Sós, V. T. (1986). Maximum induced trees in graphs. J. Combin. Theory Ser. B. 41(1): 61–79.
- Garey, M. R, Johnson, D. S. (1979). Computers and Intractability: A Guide to the Theory of NP-Completeness. New York: W. H. Freeman.
- Gernert, D. (1989). Forbidden and unavoidable subgraphs. Ars Combin. 27: 165–176.
- Hedetniemi, S. T, Laskar, R. (1986). Recent results and open problems in domination theory. In Applications of Discrete Mathematics (Clemson, SC, 1986). Philadelphia, PA: SIAM, pp. 205–218.
- Karp, R. M. (1972). Reducibility among combinatorial problems. In: Complexity of Computer Computations (Miller, R. E., Thatcher, J. W. ed.). New York: Plenum Press, pp. 85–103.
- Kuo, C. J., Hsu, C. C., Lin, H. R, Lin, K. K. (2009). An efficient algorithm for minimum feedback vertex sets in rotator graphs. Inform. Process. Lett. 109(9): 450–453.
- Liu, X., An, X, Wu, B. (2009). On perf eu; ct matchings of complements of line graphs. Ars Combin. 90: 45–54.
- Gao, L., Xu, X., Wang, J., Zhu, D, Yang, Y. (2015). The decycling number of generalized Petersen graphs. Discrete Appl. Math. 181: 297–300.
- Lu, C. L, Tang, C. Y. (1997). A linear-time algorithm for the weighted feedback vertex problem on interval graphs. Inform. Process. Lett. 61(2): 107–111.
- McCuaig, W, Shepherd, B. (1989). Domination in graphs with minimum degree two. J. Graph Theory 13(6): 749–762.
- Minty, G. J. (1980). On maximal independent sets of vertices in claw-free graphs. J. Combin. Theory Ser. B. 28(3): 284–304.
- Ore, O. (1962). Theory of Graphs. Amer. Math. Soc. Colloq. Publ., Vol. 38 (Amer. Math. Soc., Providence, RI).
- Poljak, S. (1974). A note on stable sets and coloring of graphs. Comment. Math. Univ. Carolin. 15: 307–309.
- Reed, B. (1996). Paths, stars, and number three. Combinator. Probab. Comp. 5(3): 277–295.
- Sbihi, N. (1980). Algorithmes de recherche d’un stable de cardinalite maximum dans nn graphe sans etoile. Discrete Math. 29(1): 53–76.
- Ueno, S., Kajitani, Y, Gotoh, S. (1988). On the nonseparating independent set problem and feedback set problem for graphs with no vertex degree exceeding three. Discrete Math. 38: 355–360.
- Wu, B., Liu, X, Guo, X. (2008). Super-connected and hyper-connected jump graphs. Int. J. Comput. Math. 85(12): 1765–1769.
- Wu, B, Meng, J. (2004). Hamiltonian jump graphs. Discrete Math. 289(1–3): 95–106.
- Yannakakis, M. (1981). Node-deletion problem on bipartite graphs. SIAM J. Comput. 10(2): 310–327.