Twin g-noncommuting graph of a finite group

Abstract

In this paper, we introduce the twin g-noncommuting graph of a finite group that is developed by combining the concepts of the g-noncommuting graph and the twin noncommuting graph of a finite group. The twin g-noncommuting graph of a finite group G, denoted by ${\ddot{\Gamma }}_G^g,$ is constructed by considering the twin vertex set as one vertex and the adjacency of the two vertices are determined from their adjacency on the g-noncommuting graph. Furthermore, we choose dihedral group, whose representation of the twin g-noncommuting graph is determined. In addition, we determine the clique number of the twin g-noncommuting graph of dihedral group.

Keywords:

• g-noncommuting graph
• twin noncommuting graph
• twin g-noncommuting graph
• dihedral group
• clique number

MATHEMATICS SUBJECT CLASSIFICATION:

• 05C25
• 20A05

1. Introduction

Combining graph theory with abstract algebra is an interesting topic of study. One of the studies in abstract algebra is a group theory. A finite group can be represented as a graph by considering the group elements as vertices and the adjacency of two vertices is determined from the operation on the group. There are many researches that associated a graph and a finite group, such as the noncommuting graph by Abdollahi et al. [1], the power graph by Cameron and Ghosh [2], the conjugate graph by Erfanian and Tolue [5], the coprime graph by Ma et al. [9], and the noncentralizer graph by Tolue [13]. The research on graph that represented of certain group such as the identity graph of a cyclic group by Yalcin and Kirgil [16], the noncommuting graph of dihedral group by Khasraw et al. [8], and the coprime graph of generalized quaternion group by Zahidah et al. [17].

The concept of the noncommuting graph of a finite group is interesting to study in detail. In 1975, Paul Erd $\ddot{o}$ s had first introduced a graph associated to a group that is denoted by Γ_G, before this concept was developed by Moghaddamfar et al. [10] in terms of the noncommuting graph. Tolue et al. [15] generalized the noncommuting graph to the g-noncommuting graph, denoted by ${\Gamma }_G^g,$ which is a graph with the vertex set G and two distinct vertices x and y are adjacent if and only if $[x,y]\ne g$ and $[x,y]\ne g^{-1}.$

In graph theory, two vertices a and b in a connected graph Γ are called twins if a and b have the same neighbors in $V(\Gamma )\backslash \{a,b\}$ [12]. From that definition, Tolue [14] investigated the twin vertices of the noncommuting graph and yielded the concept of the twin noncommuting graph of a finite group. The twin noncommuting of a finite group is constructed by considering the twin vertex set as one vertex and the adjacency of the two vertices are determined from their adjacency on the noncommuting graph. Moreover, Tolue [14] also discussed the clique number of the twin noncommuting graph of a finite group. Based on these results, it is interesting to combine the concepts of the g-noncommuting graph and the twin noncommuting graph of a finite group that later is called by the twin g-noncommuting graph of a finite group. Moreover, in this paper we construct and determine the clique number of the twin g-noncommuting graph of dihedral group.

Throughout the paper, graphs are simple, undirected, and without loops. All of the notations and terminologies about graphs can be found in [3, 13], and for the groups in [4, 6, 7].

2. Twin g-noncommuting graph of a finite group

In this part, we introduce some definitions related to the twin g-noncommuting graph of a finite group. Let G be a finite group with the identity element e and ${\Gamma }_G^g$ be the g-noncommuting graph of a group G for fixed element $g\in G\backslash \left\{e\right\}.$ Let $x,y\in G,$ note that $[x,y]=x^{-1}{y}^{-1}xy$ is the commutator of x and y of G and $K(G)=\{[x,y]:\forall x,y\in G\}$ [7]. Let Γ be a graph and $x\in V(\Gamma ),$ Tolue in [14] defined $N(x)=\{y\in V(\Gamma ):d(x,y)=1\}$ is the vertex set that is adjacent to x. A vertex $u\in V(\Gamma )$ is called a dominant vertex if $d(u,v)=1$ for any other vertices $v\in V(\Gamma ).$

Definition 2.1.

Let G be a finite group and $x\in G$. The set of elements of the group G whose commutator with x is g or $g^{-1}$, denoted by $L_g(x)$, is defined as $L_g(x)=\{y\in G:[x,y]=g\mathrm{ }\text{or}\mathrm{ }[x,y]=g^{-1}\}$ where g is a non-identity element of G.

Let G be a finite group with the identity element e and ${\Gamma }_G^g$ be the g-noncommuting graph of G for $g\in G.$ According to [15], ${\Gamma }_G^e$ is not a connected graph, hence in this paper we only discuss about ${\Gamma }_G^g$ for $g\in G\backslash \left\{e\right\}=G^{*}.$ Meanwhile, based on Definition 2.1 we know that on ${\Gamma }_G^g,$ the set $L_g(x)\cup \left\{x\right\}$ where $x\in V({\Gamma }_G^g)$ is the vertex set that is not adjacent to x. Consequently, the vertex set that is adjacent to x of ${\Gamma }_G^g$ for $g\in G^{*}$ is $N(x)=G\backslash (L_g(x)\cup \{x\}).$

Definition 2.2.

Let G be a finite group and ${\Gamma }_G^g$ be the g-noncommuting graph of G for $g\in G^{*}$. Let $a\in V({\Gamma }_G^g)$, we denote the twin vertex set of a on ${\Gamma }_G^g$ as $\ddot{\overline{a}}=\left\{b\in G:L_g(a)\cup \{a,b\}=L_g(b)\cup \{a,b\}\right\}.$

The twin vertex set on the g-noncommuting graph in Definition 2.2 is used to bring out the concept of the twin g-noncommuting graph as follows.

Definition 2.3.

Let G be a finite group, ${\Gamma }_G^g$ be the g-noncommuting graph of G for $g\in G^{*}$, and $\ddot{\overline{x}}$ be the twin vertex set of x on ${\Gamma }_G^g$. The twin g-noncommuting graph of G for $g\in G^{*}$, denoted by ${\ddot{\Gamma }}_G^g$, is a graph with the vertex set $V({\ddot{\Gamma }}_G^g)=\left\{\ddot{\overline{x}}|x\in V({\Gamma }_G^g\right\}$ and two distinct vertices $\ddot{\overline{x}}$ and $\ddot{\overline{y}}$ are adjacent if and only if $xy\in E({\Gamma }_G^g).$

If G is a finite abelian group, then ${\Gamma }_G^g$ is a complete graph [11]. Consequently, if G is a finite abelian group, then ${\ddot{\Gamma }}_G^g$ is a trivial graph. Moreover, ${\Gamma }_G^g$ is a regular graph if and only if $g\notin K(G)$ [11], so we get a corollary as follows.

Corollary 2.1.

Let G be a finite non-abelian group with the identity element e. The twin g-noncommuting graph of G for $g\in G^{*}$ is a trivial graph if and only if $g\notin K(G).$

Let G be a finite non-abelian group with the identity element e. Obviously ${\ddot{\Gamma }}_G^g\cong {\ddot{\Gamma }}_G^{g^{-1}}$ and $e\in K(G).$ Furthermore, in the following results we consider ${\ddot{\Gamma }}_G^g$ for a finite non-abelian group G and $g\in K(G)\backslash \left\{e\right\}=K^{*}(G).$

Lemma 2.1.

If ${\ddot{\Gamma }}_G^g$ is a twin g-noncommuting graph of a non-abelian group G for $g\in K^{*}(G)$, then $\ddot{\overline{e}}$ is a dominant vertex on ${\ddot{\Gamma }}_G^g.$

Proof.

For any $\ddot{\overline{x}}\in V({\ddot{\Gamma }}_G^g)$ and certain $\ddot{\overline{e}}\in V({\ddot{\Gamma }}_G^g)$ where $\ddot{\overline{e}}\ne \ddot{\overline{x}}$ implies $[x,e]=e\ne g,g^{-1}.$ It means $\ddot{\overline{e}}$ is adjacent to any $\ddot{\overline{x}}$ on ${\ddot{\Gamma }}_G^g.$ ■

Proposition 2.1.

If ${\ddot{\Gamma }}_G^g$ is a twin g-noncommuting graph of a non-abelian group G for $g\in K^{*}(G)$, then ${\ddot{\Gamma }}_G^g$ is a connected graph with diameter two.

Proof.

Let $\ddot{\overline{x}}$ and $\ddot{\overline{y}}$ be two distinct vertices on ${\ddot{\Gamma }}_G^g.$ Then the following two cases occur.

1. If $\ddot{\overline{x}}$ and $\ddot{\overline{y}}$ are adjacent on ${\ddot{\Gamma }}_G^g,$ then $d(\ddot{\overline{x}},\ddot{\overline{y}})=1.$

2. If $\ddot{\overline{x}}$ and $\ddot{\overline{y}}$ are not adjacent on ${\ddot{\Gamma }}_G^g,$ then based on Lemma 2.1, $\ddot{\overline{x}}$ and $\ddot{\overline{y}}$ are adjacent to $\ddot{\overline{e}}\in V({\ddot{\Gamma }}_G^g)$ respectively, so $d(\ddot{\overline{x}},\ddot{\overline{y}})=d(\ddot{\overline{x}},\ddot{\overline{e}})+d(\ddot{\overline{y}},\ddot{\overline{e}})=2.$

Since the distance among the vertices either one or two, then the diameter of ${\ddot{\Gamma }}_G^g$ is two. $■$

Lemma 2.2.

If ${\ddot{\Gamma }}_G^g$ is a twin g-noncommuting graph of a non-abelian group G for $g\in K^{*}(G)$, then ${\ddot{\Gamma }}_G^g$ is not a complete graph.

Proof.

Suppose ${\ddot{\Gamma }}_G^g$ is a complete graph K_n of order n, then every pair of distinct vertices $\ddot{\overline{x}}$ and $\ddot{\overline{y}}$ are adjacent on ${\ddot{\Gamma }}_G^g$ or in other words $[x,y]\ne g$ and $g^{-1}.$ It means for all $\ddot{\overline{x}},\ddot{\overline{y}}\in V({\ddot{\Gamma }}_G^g)$ implies $[x,y]\notin K(G),$ which is a contradiction. $■$

Proposition 2.2.

If ${\ddot{\Gamma }}_G^g$ is a twin g-noncommuting graph of a non-abelian group G for $g\in K^{*}(G)$, then ${\ddot{\Gamma }}_G^g$ is not a cycle graph.

Proof.

There are two cases, i.e.

1. Based on Lemma 2.2, it is clear that ${\ddot{\Gamma }}_G^g\ne K_3=C_3.$

2. Suppose ${\ddot{\Gamma }}_G^g\cong C_n$ where n > 3. Note that for all $x\in Z(G)$ and $y\in G\backslash Z(G)$ we get $[x,y]=e$ implies $\mathrm{deg}(\ddot{\overline{x}})=n-1>2$ on ${\ddot{\Gamma }}_G^g.$ This is contrary to the fact that the degree of any vertices on a cyclic graph is two. $■$

3. The twin g-noncommuting graph of the dihedral group

The Dihedral group of order 2n, is denoted by $D_{2n},$ can be represented as $D_{2n}=<a,b\hspace{0.17em}|\hspace{0.17em}{a}^n=b^2=e,\mathit{bab}=a^{-1}>$ for $n\in \mathbb{N},n \ge 3,$ and e is the identity element of $D_{2n}$ [12]. We can see that $Z(D_{2n})=\left\{e\right\}$ and $K(D_{2n})=<a>$ where n is an odd number. If n is an even number, we have $Z(D_{2n})=\left\{e,a^{\frac{n}{2}}\right\}$ and $K(D_{2n})=<a^2>.$ Before we discuss the twin g-noncommuting graph of $D_{2n},$ we introduce a special graph as follows.

Definition 3.1.

Let k be a non-negative integer, Ω_k be a k-regular graph, i.e a graph that each vertex has the same degree k and given two distinct vertices u and v where $u,v\notin V({\Omega }_k)$. A graph ${\mathcal{A}}_k$ is defined as a graph with the vertex set $V({\mathcal{A}}_k)=V({\Omega }_k)\cup \left\{u,v\right\}$ and the edge set $E({\mathcal{A}}_k)=E({\Omega }_k)\cup \left\{uw:w\in V({\Omega }_k)\cup \left\{v\right\}\right\}.$

Let Ω_k be a k-regular graph for a non-negative integer k and has order n. A graph ${\mathcal{A}}_k$ is a connected graph, consisting of a unique end vertex and a unique dominant vertex. Consequently, the maximal degree of vertex on ${\mathcal{A}}_k$ is n + 1. Therefore, we know that the order and the size of ${\mathcal{A}}_k$ are n + 2 and $\frac{nk}{2}+n+1$ respectively. Furthermore, in this paper, $D_{2n}$ can be written as $D_{2n}=\left\{e,a,a^2,\dots ,a^{n-1},b,ab,a^{2}b,\dots ,a^{n-1}b\right\}$ and for all $a^p,a^q\in D_{2n}$ where $p,q=1,2,\dots ,n$ and $p\ne q$ implies $[a^p,a^q]=e.$ For simplicity, we denote $K(D_{2n})\backslash \left\{e\right\}=K^{*}.$

Lemma 3.1.

Let ${\Gamma }_{D_{2n}}^g$ be the g-noncommuting graph of $D_{2n}$ for $g\in K^{*}$ and define $S_1=\left\{a^i:i=1,2,\dots ,n\right\}\subseteq V({\Gamma }_{D_{2n}}^g).$

1. If n is an odd number and $g=a^{2j}\in K(D_{2n})$ for $j=1,2,\dots ,\frac{n-1}{2}$, then $\stackrel{..}{\overline{a^j}}=\left\{a^j,a^{n-j}\right\}$ and $\ddot{\overline{e}}=S_1\backslash \stackrel{..}{\overline{a^j}}$ are twin vertex sets in S₁.

2. If $n \ge 6$ is an even number and $g=a^{2j}\in K(D_{2n})$ for $j=1,2,\dots ,\lfloor \frac{n-1}{4}\rfloor$, then $\stackrel{..}{\overline{a^j}}=\left\{a^j,a^{n-j},a^{\frac{n}{2}-j},a^{\frac{n}{2}+j}\right\}$ and $\ddot{\overline{e}}=S_1\backslash \stackrel{..}{\overline{a^j}}$ are twin vertex sets in S₁.

3. If $n=4j$ and $g=a^{2j}\in K(D_{2n})$ for $j\in \mathbb{N}$, then $\stackrel{..}{\overline{a^j}}=\left\{a^j,a^{n-j}\right\}$ and $\ddot{\overline{e}}=S_1\backslash \stackrel{..}{\overline{a^j}}$ are twin vertex sets in S₁.

Proof.

1. Let n is an odd number and $g=a^{2j}\in K(D_{2n})$ for $j=1,2,\dots ,\frac{n-1}{2}.$

   1. If $[a^{r}b,a^i]=g=a^{2j}$ for all $r=1,2,\dots ,n,$ then i = j.

   2. If $[a^{r}b,a^i]=g^{-1}=a^{n-2j}$ for all $r=1,2,\dots ,n,$ then $i=n-j.$

Hence, we have $L_g(a^j)=L_g(a^{n-j})=\left\{a^{r}b:r=1,2,\dots ,n\right\}$ and $L_g(e)=L_g(a^k)=\varnothing$ for all $k=1,2,\dots ,n-1,k\ne j,n-j.$ According to Definition 2.2, the twin vertex sets in S₁ are $\stackrel{..}{\overline{a^j}}=\left\{a^j,a^{n-j}\right\}$ and $\ddot{\overline{e}}=S_1\backslash \stackrel{..}{\overline{a^j}}.$

• ii. Let $n \ge 6$ is an even number and $g=a^{2j}\in K(D_{2n})$ for $j=1,2,\dots ,\lfloor \frac{n-1}{4}\rfloor .$

  1. If $[a^{r}b,a^i]=g=a^{2j}$ for all $r=1,2,\dots ,n,$ then i = j or $i=\frac{n}{2}+j.$

  2. If $[a^{r}b,a^i]=g^{-1}=a^{n-2j}$ for all $r=1,2,\dots ,n,$ then $i=\frac{n}{2}-j$ or $i=n-j.$

Hence, we have $L_g(a^j)=L_g(a^{n-j})=L_g\left(a^{\frac{n}{2}-j}\right)=L_g\left(a^{\frac{n}{2}+j}\right)=\left\{a^{r}b:r=1,2,\dots ,n\right\}$ and $L_g(e)=L_g(a^k)=\varnothing$ for all $k=1,2,\dots ,n-1,k\ne j,n-j,\frac{n}{2}-j,\frac{n}{2}+j.$ According to Definition 2.2, the twin vertex sets in S₁ are $\stackrel{..}{\overline{a^j}}=\left\{a^j,a^{n-j},a^{\frac{n}{2}-j},a^{\frac{n}{2}+j}\right\}$ and $\ddot{\overline{e}}=S_1\backslash \stackrel{..}{\overline{a^j}}.$

• iii. For $n=4j$ and $g=a^{2j}\in K(D_{2n})$ for $j\in \mathbb{N}.$ If $[a^{r}b,a^i]=g=g^{-1}=a^{2j}$ for all $r=1,2,\dots ,n,$ then i = j or $i=n-j.$ Hence, we have $L_g(a^j)=L_g(a^{n-j})=\left\{a^{r}b:r=1,2,\dots ,n\right\}$ and $L_g(e)=L_g(a^k)=\varnothing$ for all $k=1,2,\dots ,n-1,k\ne j,n-j.$ According to Definition 2.2, the twin vertex sets in S₁ are $\stackrel{..}{\overline{a^j}}=\left\{a^j,a^{n-j}\right\}$ and $\ddot{\overline{e}}=S_1\backslash \stackrel{..}{\overline{a^j}}.$ $■$

Lemma 3.2.

Let ${\Gamma }_{D_{2n}}^g$ be the g-noncommuting graph of $D_{2n}$ for $g\in K^{*}$ and define $S_2=\left\{a^{k}b:k=1,2,\dots ,n\right\}\subseteq V({\Gamma }_{D_{2n}}^g).$

1. Let n is an odd number and $g=a^{2j}\in K(D_{2n})$ for $j=1,2,\dots ,\frac{n-1}{2}.$

   1. If $n=3j$ and j is an odd number, then $\stackrel{..}{\overline{a^{m}b}}=\left\{a^{m}b,a^{m+j}b,a^{m+2j}b\right\}$ for $m=1,2,\dots ,j$ are twin vertex sets in S₂.

   2. If $n\ne 3j$, then $\stackrel{..}{\overline{a^{k}b}}=\left\{a^{k}b\right\}$ for $k=1,2,\dots ,n$ are twin vertex sets in S₂.

2. Let $n \ge 6$ is an even number and $g=a^{2j}\in K(D_{2n})$ for $j=1,2,\dots ,\lfloor \frac{n-1}{4}\rfloor .$

   1. If $n=8j$, then $\stackrel{..}{\overline{a^{r}b}}=\left\{a^{r}b,a^{r+2j}b,a^{r+4j}b,a^{r+6j}b\right\}$ for $r=1,2,\dots ,2j$ are twin vertex sets in S2.

   2. If $n\ne 8j$, then $\stackrel{..}{\overline{a^{q}b}}=\left\{a^{q}b,a^{\frac{n}{2}+q}b\right\}$ for $q=1,2,\dots ,\frac{n}{2}$ are twin vertex sets in S2.

3. Let $n=4j$ and $g=a^{2j}\in K(D_{2n})$ for $j\in \mathbb{N}$. Then $\stackrel{..}{\overline{a^{r}b}}=\left\{a^{r}b,a^{r+2j}b\right\}$ for $r=1,2,\dots ,2j$ are twin vertex sets in S₂.

Proof.

1. Let n is an odd number and $g=a^{2j}\in K(D_{2n})$ for $j=1,2,\dots ,\frac{n-1}{2}.$

   1. If $[a^{k}b,a^i]=g=a^{2j}$ for all $k=1,2,\dots ,n,$ then i = j.

   2. If $[a^{k}b,a^i]=g^{-1}=a^{n-2j}$ for all $k=1,2,\dots ,n,$ then $i=n-j.$

   3. If $[a^{k}b,a^{l}b]=g=a^{2j}$ for $k=1,2,\dots ,n$ and $k\ne l,$ then $l=n-j+k.$

   4. If $[a^{k}b,a^{l}b]=g^{-1}=a^{n-2j}$ for $k=1,2,\dots ,n$ and $k\ne l,$ then $l=j+k.$

   Hence, for any $a^{k}b\in V({\Gamma }_{D_{2n}}^g)$ for $k=1,2,\dots ,n$ implies $$L_g(a^{k}b)=\left\{a^j,a^{n-j},a^{j+k}b,a^{n-j+k}b\right\}.$$

   1. If $n=3j$ and j is an odd number, then for any $a^{k}b\in V({\Gamma }_{D_{2n}}^g)$ for $k=1,2,\dots ,n$ implies $L_g(a^{k}b)\cup \left\{a^{k}b\right\}=L_g(a^{j+k}b)\cup \left\{a^{j+k}b\right\}=L_g(a^{2j+k}b)\cup \left\{a^{2j+k}b\right\}$ and on another hand we know that $a^{j+k}b,a^{2j+k}b\in L_g(a^{k}b).$ According to Definition 2.2, the twin vertex sets in S₂ are $\stackrel{..}{\overline{a^{m}b}}=\left\{a^{m}b,a^{m+j}b,a^{m+2j}b\right\}\mathrm{ }\text{for}\mathrm{ }m=1,2,\dots ,j.$

   2. If $n\ne 3j,$ then for all two distinct vertices a^kb and a^lb, where $k,l=1,2,\dots ,n$ and $k\ne l,$ implies $L_g(a^{k}b)\cup \left\{a^{k}b,a^{l}b\right\}\ne L_g(a^{l}b)\cup \left\{a^{k}b,a^{l}b\right\}.$ According to Definition 2.2, the twin vertex sets in S₂ are $\stackrel{..}{\overline{a^{k}b}}=\left\{a^{k}b\right\}\mathrm{ }\text{for}\mathrm{ }k=1,2,\dots ,n.$

2. Let $n \ge 6$ is an even number and $g=a^{2j}\in K(D_{2n})$ for $j=1,2,\dots ,\lfloor \frac{n-1}{4}\rfloor .$

   1. If $[a^{k}b,a^i]=g=a^{2j}$ for all $k=1,2,\dots ,n,$ then i = j or $i=\frac{n}{2}+j.$

   2. If $[a^{k}b,a^i]=g^{-1}=a^{n-2j}$ for all $k=1,2,\dots ,n,$ then $i=\frac{n}{2}-j$ or $i=n-j.$

   3. If $[a^{k}b,a^{l}b]=g=a^{2j}$ for $k=1,2,\dots ,n$ and $k\ne l,$ then $l=n-j+k$ or $l=\frac{n}{2}-j+k.$

   4. If $[a^{k}b,a^{l}b]=g^{-1}=a^{n-2j}$ for $k=1,2,\dots ,n$ and $k\ne l,$ then $l=j+k$ or $l=\frac{n}{2}+j+k.$

   Hence, for all $a^{k}b\in V({\Gamma }_{D_{2n}}^g)$ for $k=1,2,\dots ,n$ implies $$L_g(a^{k}b)=\left\{a^j,a^{n-j},a^{\frac{n}{2}-j},a^{\frac{n}{2}+j},a^{j+k}b,a^{n-j+k}b,a^{\frac{n}{2}-j+k}b,a^{\frac{n}{2}+j+k}b\right\}.$$

   1. If $n=8j,$ then for all $a^{k}b\in V({\Gamma }_{D_{2n}}^g)$ where $k=1,2,\dots ,n$ implies $L_g(a^{k}b)=L_g(a^{2j+k}b)=L_g(a^{4j+k}b)=L_g(a^{6j+k}b).$ According to Definition 2.2, the twin vertex sets in S₂ are $$\stackrel{..}{\overline{a^{r}b}}=\left\{a^{r}b,a^{r+2j}b,a^{r+4j}b,a^{r+6j}b\right\}\mathrm{ }\text{for}\mathrm{ }r=1,2,\dots ,2j.$$

   2. If $n\ne 8j,$ then for all $a^{k}b\in V({\Gamma }_{D_{2n}}^g)$ where $k=1,2,\dots ,n$ implies $L_g(a^{k}b)=L_g\left(a^{\frac{n}{2}+k}b\right).$ According to Definition 2.2, the twin vertex sets in S₂ are $\stackrel{..}{\overline{a^{q}b}}=\left\{a^{q}b,a^{\frac{n}{2}+q}b\right\}\mathrm{ }\text{for}\mathrm{ }q=1,2,\dots ,\frac{n}{2}.$

3. If $n=4j$ and $g=a^{2j}\in K(D_{2n})$ for $j\in \mathbb{N}.$

   1. If $[a^{k}b,a^i]=g=g^{-1}=a^{2j}$ for all $k=1,2,\dots ,n,$ then i = j or $i=n-j.$

   2. If $[a^{k}b,a^{l}b]=g=g^{-1}=a^{n-2j}$ for $k=1,2,\dots ,n$ and $k\ne l,$ then $l=n-j+k$ or $l=j+k.$

Therefore, for all $a^{k}b\in V({\Gamma }_{D_{2n}}^g)$ where $k=1,2,\dots ,n$ implies $L_g(a^{k}b)=\left\{a^j,a^{n-j},a^{j+k}b,a^{n-j+k}b\right\}$ such that $L_g(a^{k}b)=L_g(a^{2j+k}b).$ According to Definition 2.2, the twin vertex sets in S₂ are $\stackrel{..}{\overline{a^{r}b}}=\left\{a^{r}b,a^{r+2j}b\right\}\mathrm{ }\text{for}\mathrm{ }r=1,2,\dots ,2j.$ ▪

Referring to Lemma 3.1 and Lemma 3.2, the construction of the twin g-noncommmuting graph of $D_{2n}$ for $g\in K^{*}$ is served in the following theorems.

Theorem 3.1.

Let ${\ddot{\Gamma }}_{D_{2n}}^g$ be the twin g-noncommuting graph of $D_{2n}$ for $g\in K^{*}$. Let n be an odd number and $g=a^{2j}$ for $j=1,2,\dots ,\frac{n-1}{2}.$

1. If $n=3j$ and j is an odd number, then ${\ddot{\Gamma }}_{D_{2n}}^g$ is ${\mathcal{A}}_{j-1}$ of order j + 2.

2. If $n\ne 3j$, then ${\ddot{\Gamma }}_{D_{2n}}^g$ is ${\mathcal{A}}_{n-3}$ of order n + 2.

Proof.

Let n is an odd number and $g=a^{2j}\in K(D_{2n})$ for $j=1,2,\dots ,\frac{n-1}{2}.$

1. Let $n=3j$ and j is an odd number. According to Lemma 3.1 and Lemma 3.2, the vertex set of ${\ddot{\Gamma }}_{D_{2n}}^g$ is $V({\ddot{\Gamma }}_{D_{2n}}^g)=\left\{\ddot{\overline{e}},\stackrel{..}{\overline{a^j}},\stackrel{..}{\overline{ab}},\stackrel{..}{\overline{a^{2}b}},\dots ,\stackrel{..}{\overline{a^{j}b}}\right\}.$ Then, there are three cases to investigate the adjacency of any vertices on ${\ddot{\Gamma }}_{D_{2n}}^g,$

   1. Based on Lemma 2.1, $\ddot{\overline{e}}$ is a dominant vertex on ${\ddot{\Gamma }}_{D_{2n}}^g.$

   2. Since for all $m=1,2,\dots ,j$ implies $[a^{m}b,a^j]=a^{2j}=g,$ then for all $m=1,2,\dots ,j,\stackrel{..}{\overline{a^{m}b}}$ is not adjacent to $\stackrel{..}{\overline{a^j}}.$

   3. The adjacency of vertex in $H=\left\{\stackrel{..}{\overline{a^{m}b}}:m=1,2,\dots ,j\right\}\subseteq V({\ddot{\Gamma }}_{D_{2n}}^g).$ Since $[a^{m_1}b,a^{m_2}b]=a^{2(m_1-m_2)}\ne a^{2j}=g$ and $[a^{m_1}b,a^{m_2}b]=a^{2(m_1-m_2)}\ne a^{n-2j}=g^{-1}$ for $m_1,m_2=1,2,\dots ,j$ and $m_1\ne m_2,$ then every two distinct vertices in H are adjacent. Consequently, the induced subgraph by H on ${\ddot{\Gamma }}_{D_{2n}}^g$ is ${\Omega }_{j-1}.$

Based on three cases above and Definition 3.1, ${\ddot{\Gamma }}_{D_{2n}}^g$ is ${\mathcal{A}}_{j-1}$ of order j + 2.

• ii. Let $n\ne 3j,$ According to Lemma 3.1 and Lemma 3.2, the vertex set of ${\ddot{\Gamma }}_{D_{2n}}^g$ is $V({\ddot{\Gamma }}_{D_{2n}}^g)=\left\{\ddot{\overline{e}},\stackrel{..}{\overline{a^j}},\ddot{\overline{b}},\stackrel{..}{\overline{ab}},\stackrel{..}{\overline{a^{2}b}},\dots ,\stackrel{..}{\overline{a^{n-1}}b}\right\}.$ Then, there are three cases to investigate the adjacency of any vertices on ${\ddot{\Gamma }}_{D_{2n}}^g,$

  1. Based on Lemma 2.1, $\ddot{\overline{e}}$ is a dominant vertex on ${\ddot{\Gamma }}_{D_{2n}}^g.$

  2. Since for all $k=1,2,\dots ,n$ implies $[a^{k}b,a^j]=a^{2j}=g,$ then for all $k=1,2,\dots ,n,\stackrel{..}{\overline{a^{k}b}}$ is not adjacent to $\stackrel{..}{\overline{a^j}}.$

  3. The adjacency of vertex in $H=\left\{\stackrel{..}{\overline{a^{k}b}}:k=1,2,\dots ,n\right\}\subseteq V({\ddot{\Gamma }}_{D_{2n}}^g).$ According to Lemma 3.2, $\stackrel{..}{\overline{a^{k}b}}$ is adjacent to any vertices in H, except $\stackrel{..}{\overline{a^{j+k}b}}$ and $\stackrel{..}{\overline{a^{n-j+k}b}}.$ Consequently, the induced subgraph by H on ${\ddot{\Gamma }}_{D_{2n}}^g$ is ${\Omega }_{n-3}.$

Based on three cases above and Definition 3.1, ${\ddot{\Gamma }}_{D_{2n}}^g$ is ${\mathcal{A}}_{n-3}$ of order n + 2.▪

Corollary 3.1.

Let ${\ddot{\Gamma }}_{D_{2n}}^g$ be the twin g-noncommuting graph of $D_{2n}$ for $g\in K^{*}.$

1. If $n=3j$ and j is an odd number, then the induced subgraph by $S=\left\{\stackrel{..}{\overline{a^{m}b}}:m=1,2,\dots ,j\right\}\subseteq V({\ddot{\Gamma }}_{D_{2(3j)}}^{2j})$ is a complete subgraph of ${\ddot{\Gamma }}_{D_{2(3j)}}^{2j}$ for an odd natural number j.

2. If n is an odd non-prime number and $g=a^m\in K(D_{2n})$ for $m\in \left\{1,2\right\},$ then the induced subgraph by $S=\left\{\stackrel{..}{\overline{a^{l}b}},\stackrel{..}{\overline{a^{l+m}b}},\stackrel{..}{\overline{a^{l+2m}b}},\dots ,\stackrel{..}{\overline{a^{l+(\frac{n¯3}{2})m}b}}\right\}$ where $l=1,2,\dots ,n$ is a complete subgraph of ${\ddot{\Gamma }}_{D_{2n}}^{a^m}.$

3. If $n\ge 5$ is a prime number and $g=a^{2j}\in K(D_{2n})$ for $j=1,2,\dots ,\frac{n-1}{2},$ then the induced subgraph by $S=\left\{\stackrel{..}{\overline{a^{2j+l}b}},\stackrel{..}{\overline{a^{4j+l}b}},\stackrel{..}{\overline{a^{6j+l}b}},\dots ,\stackrel{..}{\overline{a^{(n¯1)j+l}b}}\right\}$ where $l=1,2,\dots ,n$ is a complete subgraph of ${\ddot{\Gamma }}_{D_{2n}}^{2j}.$

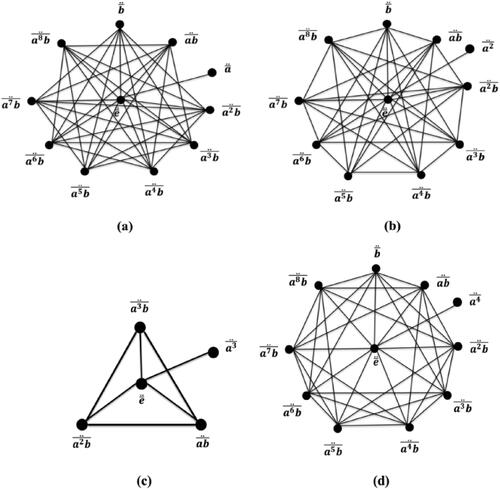
Example 1.

Some constructions of the twin g-noncommuting graph of D₁₈ for $g\in K^{*}$ can be seen in Figure 1.

Figure 1. Graph (a) ${\ddot{\Gamma }}_{D_{18}}^{a^2},$ (b) ${\ddot{\Gamma }}_{D_{18}}^{a^4},$ (c) ${\ddot{\Gamma }}_{D_{18}}^{a^6},$ (d) ${\ddot{\Gamma }}_{D_{18}}^{a^8}.$

Theorem 3.2.

Let ${\ddot{\Gamma }}_{D_{2n}}^g$ be the twin g-noncommuting graph of $D_{2n}$ for $g\in K^{*}.$

1. If $n=4j$ and $g=a^{2j}\in K(D_{2n})$ for $j\in \mathbb{N}$, then ${\ddot{\Gamma }}_{D_{2n}}^g$ is ${\mathcal{A}}_{2j-2}$ of order $2j+2.$

2. If $n=6j$ and $g=a^{2j}\in K(D_{2n})$ for $j\in \mathbb{N}$, then ${\ddot{\Gamma }}_{D_{2n}}^g$ is ${\mathcal{A}}_{3j-3}$ of order $3j+2.$

3. If $n=8j$ and $g=a^{2j}\in K(D_{2n})$ for $j\in \mathbb{N}$, then ${\ddot{\Gamma }}_{D_{2n}}^g$ is ${\mathcal{A}}_{2j-2}$ of order $2j+2.$

4. If $n=2p$ and $g=a^{2j}\in K(D_{2n})$ for $j\in \mathbb{N}$, where $p \ge 5$ is a prime number and $j=1,2,\dots ,\frac{p-1}{2}$, then ${\ddot{\Gamma }}_{D_{2n}}^g$ is ${\mathcal{A}}_{p-3}$ of order p + 2.

Proof.

1. Let $n=4j$ and $g=a^{2j}\in K(D_{2n})$ for $j\in \mathbb{N}.$ According to Lemma 3.1 and Lemma 3.2, the vertex set of ${\ddot{\Gamma }}_{D_{2n}}^g$ is $V({\ddot{\Gamma }}_{D_{2n}}^g)=\left\{\ddot{\overline{e}},\stackrel{..}{\overline{a^j}},\stackrel{..}{\overline{ab}},\stackrel{..}{\overline{a^{2}b}},\dots ,\stackrel{..}{\overline{a^{2j}b}}\right\}.$ Then, there are three cases to investigate the adjacency of any vertices on ${\ddot{\Gamma }}_{D_{2n}}^g,$

   1. Based on Lemma 2.1, $\ddot{\overline{e}}$ is a dominant vertex on ${\ddot{\Gamma }}_{D_{2n}}^g.$

   2. Since for all $r=1,2,\dots ,2j$ implies $[a^{r}b,a^j]=a^{2j}=g,$ then for all $r=1,2,\dots ,2j,\stackrel{..}{\overline{a^{r}b}}$ is not adjacent to $\stackrel{..}{\overline{a^j}}.$

   3. The adjacency of vertices in $H=\left\{\stackrel{..}{\overline{a^{r}b}}:r=1,2,\dots ,2j\right\}\subseteq V({\ddot{\Gamma }}_{D_{2n}}^g).$ According to Lemma 3.2, for all $k=1,2,\dots ,n$ implies $L_g(a^{k}b)=\left\{a^j,a^{3j},a^{k+j}b,a^{k+3j}b\right\}$ and $\stackrel{..}{\overline{a^{k+j}b}}=\left\{a^{k+j}b,a^{k+3j}b\right\}.$ Therefore, $\stackrel{..}{\overline{a^{r}b}}$ for $r=1,2,\dots ,2j$ is adjacent to any vertices in H, except $\stackrel{..}{\overline{a^{r+j}b}}.$ Consequently, the induced subgraph by H on ${\ddot{\Gamma }}_{D_{2n}}^g$ is ${\Omega }_{2j-2}.$

Based on three cases above and Definition 3.1, if $n=4j$ and $g=a^{2j}\in K(D_{2n})$ for $j\in \mathbb{N},$ then ${\ddot{\Gamma }}_{D_{2n}}^g$ is ${\mathcal{A}}_{2j-2}$ of order j + 2.

• ii. Let $n=6j$ and $g=a^{2j}\in K(D_{2n})$ for $j\in \mathbb{N}.$ According to Lemma 3.1 and Lemma 3.2, the vertex set of ${\ddot{\Gamma }}_{D_{2n}}^g$ is $V({\ddot{\Gamma }}_{D_{2n}}^g)=\left\{\ddot{\overline{e}},\stackrel{..}{\overline{a^j}},\stackrel{..}{\overline{ab}},\stackrel{..}{\overline{a^{2}b}},\dots ,\stackrel{..}{\overline{a^{3j}b}}\right\}.$ Then, there are three cases to investigate the adjacency of any vertices on ${\ddot{\Gamma }}_{D_{2n}}^g,$

  1. Based on Lemma 2.1, $\ddot{\overline{e}}$ is a dominant vertex on ${\ddot{\Gamma }}_{D_{2n}}^g.$

  2. Since for all $k=1,2,\dots ,3j$ implies $[a^{k}b,a^j]=a^{2j}=g,$ then for all $k=1,2,\dots ,3j,\stackrel{..}{\overline{a^{k}b}}$ is not adjacent to $\stackrel{..}{\overline{a^j}}.$

  3. The adjacency of vertices in $H=\left\{\stackrel{..}{\overline{a^{k}b}}:k=1,2,\dots ,3j\right\}\subseteq V({\ddot{\Gamma }}_{D_{2n}}^g).$ According to Lemma 3.2, for all $l=1,2,\dots ,n$ implies $L_g(a^{l}b)=\left\{a^j,a^{2j},a^{4j},a^{5j},a^{j+l}b,a^{k+3j}b,a^{2j+l},a^{4j+l}\right\}$ and $\stackrel{..}{\overline{a^{j+l}b}}=\left\{a^{j+l}b,a^{4j+l}\right\},\stackrel{..}{\overline{a^{5j+l}b}}=\left\{a^{2j+l}b,a^{5j+l}b\right\}.$ Therefore, $\stackrel{..}{\overline{a^{k}b}}$ for $k=1,2,\dots ,3j$ is adjacent to any vertices in H, except $\stackrel{..}{\overline{a^{j+k}b}}$ and $\stackrel{..}{\overline{a^{5j+k}b}}.$ Consequently, the induced subgraph by H on ${\ddot{\Gamma }}_{D_{2n}}^g$ is ${\Omega }_{3j-3}.$

Based on the above three cases and Definition 3.1, if $n=6j$ and $g=a^{2j}\in K(D_{2n})$ for $j\in \mathbb{N},$ then ${\ddot{\Gamma }}_{D_{2n}}^g$ is ${\mathcal{A}}_{3j-3}$ of order $3j+2.$

• iii. Let $n=8j$ and $g=a^{2j}\in K(D_{2n})$ for $j\in \mathbb{N}.$ According to Lemma 3.1 and Lemma 3.2, the vertex set of ${\ddot{\Gamma }}_{D_{2n}}^g$ is $V({\ddot{\Gamma }}_{D_{2n}}^g)=\left\{\ddot{\overline{e}},\stackrel{..}{\overline{a^j}},\stackrel{..}{\overline{ab}},\stackrel{..}{\overline{a^{2}b}},\dots ,\stackrel{..}{\overline{a^{2j}b}}\right\}.$ Then, there are three cases to investigate the adjacency of any vertices on ${\ddot{\Gamma }}_{D_{2n}}^g,$

  1. Based on Lemma 2.1, $\ddot{\overline{e}}$ is a dominant vertex on ${\ddot{\Gamma }}_{D_{2n}}^g.$

  2. Since for all $r=1,2,\dots ,2j$ implies $[a^{r}b,a^j]=a^{2j}=g,$ then for all $r=1,2,\dots ,2j,\stackrel{..}{\overline{a^{r}b}}$ is not adjacent to $\stackrel{..}{\overline{a^j}}.$

  3. The adjacency of vertices in $H=\left\{\stackrel{..}{\overline{a^{r}b}}:r=1,2,\dots ,2j\right\}\subseteq V({\ddot{\Gamma }}_{D_{2n}}^g).$ According to Lemma 3.2, for all $k=1,2,\dots ,n$ implies $L_g(a^{k}b)=\left\{a^j,a^{3j},a^{5j},a^{7j},a^{j+k}b,a^{7j+k}b,a^{3j+k},a^{5j+k}\right\}$ and $\stackrel{..}{\overline{a^{j+k}b}}=\left\{a^{j+k}b,a^{3j+k}b,a^{5j+k}b,a^{7j+k}b\right\}.$ Therefore, $\stackrel{..}{\overline{a^{r}b}}$ for $r=1,2,\dots ,2j$ is adjacent to any vertices in H, except $\stackrel{..}{\overline{a^{r+j}b}}.$ Consequently, the induced subgraph by H on ${\ddot{\Gamma }}_{D_{2n}}^g$ is ${\Omega }_{2j-2}.$

Based on three cases above and Definition 3.1, if $n=8j$ and $g=a^{2j}\in K(D_{2n})$ for $j\in \mathbb{N},$ then ${\ddot{\Gamma }}_{D_{2n}}^g$ is ${\mathcal{A}}_{2j-2}$ of order $2j+2.$

• iv. Let $n=2p$ and $g=a^{2j}\in K(D_{2n})$ for $j\in \mathbb{N},$ where $p \ge 5$ is prime number and $j=1,2,\dots ,\frac{p-1}{2}.$ According to Lemma 3.1 and Lemma 3.2, the vertex set of ${\ddot{\Gamma }}_{D_{2n}}^g$ is $V({\ddot{\Gamma }}_{D_{2n}}^g)=\left\{\ddot{\overline{e}},\stackrel{..}{\overline{a^j}},\stackrel{..}{\overline{ab}},\stackrel{..}{\overline{a^{2}b}},\dots ,\stackrel{..}{\overline{a^{p}b}}\right\}.$ Then, there are three cases to investigate the adjacency of any vertices on ${\ddot{\Gamma }}_{D_{2n}}^g,$

  1. Based on Lemma 2.1, $\ddot{\overline{e}}$ is a dominant vertex on ${\ddot{\Gamma }}_{D_{2n}}^g.$

  2. Since for all $k=1,2,\dots ,p$ implies $[a^{k}b,a^j]=a^{2j}=g,$ then for all $k=1,2,\dots ,p,\stackrel{..}{\overline{a^{k}b}}$ is not adjacent to $\stackrel{..}{\overline{a^j}}.$

  3. The adjacency of vertices in $H=\left\{\stackrel{..}{\overline{a^{k}b}}:k=1,2,\dots ,p\right\}\subseteq V({\ddot{\Gamma }}_{D_{2n}}^g).$ According to Lemma 3.2, for all $l=1,2,\dots ,n$ implies $L_g(a^{l}b)=\left\{a^j,a^{n-j},a^{p-j},a^{p+j},a^{j+l}b,a^{n-j+l}b,a^{p-j+l}b,a^{p+j+l}b\right\},$

$\stackrel{..}{\overline{a^{j+l}b}}=\left\{a^{j+l}b,a^{p+j+l}b\right\},$ and $\stackrel{..}{\overline{a^{p-j+l}b}}=\left\{a^{n-j+l}b,a^{p-j+l}b\right\}.$ Therefore, $\stackrel{..}{\overline{a^{k}b}}$ for $k=1,2,\dots ,p$ is adjacent to any vertices in H, except $\stackrel{..}{\overline{a^{k+j}b}}$ and $\stackrel{..}{\overline{a^{p+(k-j)}b}}.$ Consequently, the induced subgraph by H on ${\ddot{\Gamma }}_{D_{2n}}^g$ is ${\Omega }_{p-3}.$

Based on three cases above and Definition 3.1, if $n=2p$ and $g=a^{2j}\in K(D_{2n})$ for $j\in \mathbb{N},$ where $p \ge 5$ is a prime number and $j=1,2,\dots ,\frac{p-1}{2},$ then ${\ddot{\Gamma }}_{D_{2n}}^g$ is ${\mathcal{A}}_{p-3}$ of order p + 2.▪

Corollary 3.2.

If n = mj and $g=a^{2j}\in K(D_{2n})$ where $j\in \mathbb{N}$ and $m=\left\{4,6\right\}$, then the induced subgraph by $\left\{\stackrel{..}{\overline{a^{j+l}b}},\stackrel{..}{\overline{a^{j+1+l}b}},\dots ,\stackrel{..}{\overline{a^{2j-1+l}b}}\right\}$ where $l=1,2,\dots ,\frac{mj}{2}$ is a complete subgraph of ${\ddot{\Gamma }}_{D_{2n}}^{2j}.$

Corollary 3.3.

Let ${\ddot{\Gamma }}_{D_{2n}}^g$ be the twin g-noncommuting graph of $D_{2n}$ for $g=K^{*}$. Then

1. ${\ddot{\Gamma }}_{D_{2(4j)}}^{a^{2j}}\cong {\ddot{\Gamma }}_{D_{2(8j)}}^{a^{2j}}$ for $j\in \mathbb{N}$

2. If $n \ge 5$ is a prime number, then ${\ddot{\Gamma }}_{D_{2n}}^{a^{2j}}\cong {\ddot{\Gamma }}_{D_{2(2n)}}^{a^{2j}}$ for $j=1,2,\dots ,\frac{n-1}{2}.$

4. The clique number of the twin g-noncommuting graph of the dihedral group

In this part, we discuss related to the clique number of the twin g-noncommuting graph of dihedral group. Referring to Definition 3.1 we have that graph ${\mathcal{A}}_k=({\Omega }_k\cup K_1)+K_1,$ where K₁ is a trivial graph. Hence, we get clique number of ${\mathcal{A}}_k$ as follows.

Corollary 4.1.

Let Ω_k be a k-regular graph, then $\omega ({\mathcal{A}}_k)=\omega ({\Omega }_k)+1.$

Henceforth, we observe the clique number of the twin g-noncommuting graph of dihedral group regarding to the previous section. Note that notation ${\ddot{\Gamma }}_{D_{2n}}^g$ claims the twin g-noncommuting graph of $D_{2n}$ for $g\in K(D_{2n})\backslash \left\{e\right\}=K^{*}.$ A vertex $\stackrel{..}{\overline{a^j}}\in V({\ddot{\Gamma }}_{D_{2n}}^g)$ is an end vertex, so it is not possible to be a vertex candidate for clique on ${\ddot{\Gamma }}_{D_{2n}}^g.$ Meanwhile a vertex $\ddot{\overline{e}}\in V({\ddot{\Gamma }}_{D_{2n}}^g)$ is a dominant vertex, so $\ddot{\overline{e}}$ is a vertex candidate for clique on ${\ddot{\Gamma }}_{D_{2n}}^g.$ Based on these two conditions, the largest clique’s proof in this section only observe to the adjacency of the twin vertex sets in $S_2=\left\{a^{k}b:k=1,2,\dots ,n\right\}$ in Lemma 3.2.

Theorem 4.1.

If $n=3j$ and $g=a^{2j}\in K(D_{2n})$ for $j\in \mathbb{N}$ and j is an odd number, then $\omega ({\ddot{\Gamma }}_{D_{2(3j)}}^{a^{2j}})=j+1.$

Proof.

According to Corollary 3.1, the induced subgraph by $S=\left\{\stackrel{..}{\overline{a^{m}b}}:m=1,2,\dots ,j\right\}\subseteq V({\ddot{\Gamma }}_{D_{2(3j)}}^{a^{2j}})$ is a complete subgraph. It means the spanning vertex set of a clique Δ on ${\ddot{\Gamma }}_{D_{2(3j)}}^{a^{2j}}$ is $V(\Delta )=S\cup \left\{\ddot{\overline{e}}\right\}$ where $|V(\Delta )|=j+1.$ In another hand, we know that $\left|V({\ddot{\Gamma }}_{D_{2(3j)}}^{a^{2j}})\right|=j+2$ and based on Lemma 2.2, ${\ddot{\Gamma }}_{D_{2(3j)}}^{a^{2j}}$ is not a complete graph. Consequently, a clique Δ is the largest clique on ${\ddot{\Gamma }}_{D_{2(3j)}}^{a^{2j}}$ (see Figure 1c ${\ddot{\Gamma }}_{D_{18}}^{a^6}$ as an evidence of this theorem for j = 3).▪

Theorem 4.2.

If n is an odd non-prime number and $g=a,a^2\in K(D_{2n})$, then $\omega ({\ddot{\Gamma }}_{D_{2n}}^g)=\frac{n+1}{2}.$

Proof.

Let n is an odd non-prime number.

1. Let $g=a\in K(D_{2n})$ and $g^{-1}=a^{n-1}\in K(D_{2n}).$ According to Corollary 3.1, the spanning vertex set of a clique Δ on ${\ddot{\Gamma }}_{D_{2n}}^g$ is $V(\Delta )=\left\{\ddot{\overline{e}}\right\}\cup H$ where $H=\left\{\stackrel{..}{\overline{a^{l}b}},\stackrel{..}{\overline{a^{l+1}b}},\dots ,\stackrel{..}{\overline{a^{l+\frac{n-3}{2}}b}}\right\}$ and $l=1,2,\dots ,n.$ Consequently, $|V(\Delta )|=\frac{n+1}{2}$ and vertices on H are sequential.

Hereafter, suppose there is another clique Λ where $V(\Lambda )\subseteq V({\ddot{\Gamma }}_{D_{2n}}^g)$ and $V(\Lambda )>V(\Delta ).$ Without loss of generality, let $V(\Lambda )=V(\Delta )\cup \left\{\stackrel{..}{\overline{a^{m}b}}\right\}$ for $m\in \left\{l+\frac{n-3}{2}+r:r=1,2,\dots ,\frac{n+1}{2}\right\},$ then there are two cases for m,

1. If $m\in \left\{l+\frac{n-3}{2}+s:s=1,2,\dots ,\frac{n-1}{2}\right\},$ then $\stackrel{..}{\overline{a^{m}b}}\in V(\Lambda )$ is not adjacent to $\stackrel{..}{\overline{a^{m-(\frac{n-1}{2})}b}}\in V(\Lambda )$ since $[a^{m}b,a^{m-\frac{n-1}{2}}b]=a^{n-1}=g^{-1}$ which is a contradiction.

2. If $m=l+n-1,$ then $\stackrel{..}{\overline{a^{m}b}}\in V(\Lambda )$ is not adjacent to $\stackrel{..}{\overline{a^{l+(\frac{n-3}{2})}b}}\in V(\Lambda )$ since $[a^{m}b,a^{l+\frac{n-3}{2}}b]=[a^{l+n-1}b,a^{l+\frac{n-3}{2}}b]=a=g$ which is a contradiction.

Based on two cases above, Λ is not a clique of ${\ddot{\Gamma }}_{D_{2n}}^g.$ Hence, clique Δ is the largest clique of ${\ddot{\Gamma }}_{D_{2n}}^g,$ thus $\omega ({\ddot{\Gamma }}_{D_{2n}}^g)=\frac{n+1}{2}$.

• ii. Let $g=a^2\in K(D_{2n})$ and $g^{-1}=a^{n-2}\in K(D_{2n}).$ According to Corollary 3.1, the spanning vertex set of a clique Δ on ${\ddot{\Gamma }}_{D_{2n}}^g$ is $V(\Delta )=\left\{\ddot{\overline{e}}\right\}\cup H$ where $H=\left\{\stackrel{..}{\overline{a^{l}b}},\stackrel{..}{\overline{a^{l+2}b}},\stackrel{..}{\overline{a^{l+4}b}},\dots ,\stackrel{..}{\overline{a^{l+n¯3}b}}\right\}$ and $l=1,2,\dots ,n.$ Consequently, $|V(\Delta )|=\frac{n+1}{2}$ and vertices on H are sequential.

Hereafter, suppose there is another clique Λ where $V(\Lambda )\subseteq V({\ddot{\Gamma }}_{D_{2n}}^g)$ and $V(\Lambda )>V(\Delta ).$ Without loss of generality, let $V(\Lambda )=V(\Delta )\cup \left\{\stackrel{..}{\overline{a^{m}b}}\right\}$ for $m\in \left\{l+(2r-1):r=1,2,\dots ,\frac{n-1}{2}\right\}\cup \left\{l+n-1\right\},$ then there are two cases for m,

1. If $m\in \left\{l+(2r-1):r=1,2,\dots ,\frac{n-1}{2}\right\},$ then $\stackrel{..}{\overline{a^{m}b}}\in V(\Lambda )$ is not adjacent to $\stackrel{..}{\overline{a^{m+1}b}}\in V(\Lambda )$ since $[a^{m}b,a^{m+1}b]=a^{n-2}=g^{-1}$ which is a contradiction.

2. If $m=l+n-1,$ then $\stackrel{..}{\overline{a^{m}b}}\in V(\Lambda )$ is not adjacent to $\stackrel{..}{\overline{a^{l}b}}\in V(\Lambda )$ since $[a^{m}b,a^{l}b]=[a^{l+n-1}b,a^{l}b]=a^{n-2}=g^{-1}$ which is a contradiction.

Based on two cases above, Λ is not a clique of ${\ddot{\Gamma }}_{D_{2n}}^g.$ Hence, clique Δ is the largest clique of ${\ddot{\Gamma }}_{D_{2n}}^g,$ thus $\omega ({\ddot{\Gamma }}_{D_{2n}}^g)=\frac{n+1}{2}.$▪

Theorem 4.3.

If $n \ge 5$ is a prime number and $g=a^{2j}\in K(D_{2n})$ for $j=1,2,\dots ,\frac{n-1}{2}$, then $\omega ({\ddot{\Gamma }}_{D_{2n}}^g)=\frac{n+1}{2}.$

Proof.

According to Corollary 3.1, the spanning vertex set of a clique Δ on ${\ddot{\Gamma }}_{D_{2n}}^g$ is $V(\Delta )=\left\{\ddot{\overline{e}}\right\}\cup H$ where $H=\left\{\stackrel{..}{\overline{a^{2j+l}b}},\stackrel{..}{\overline{a^{4j+l}b}},\stackrel{..}{\overline{a^{6j+l}b}},\dots ,\stackrel{..}{\overline{a^{(n-1)j+l}b}}\right\}$ and $l=1,2,\dots ,n.$ Consequently, $|V(\Delta )|=\frac{n+1}{2}$ and vertices on H are sequential.

Hereafter, suppose there is another clique Λ where $V(\Lambda )\subseteq V({\ddot{\Gamma }}_{D_{2n}}^g)$ and $V(\Lambda )>V(\Delta ).$ Without loss of generality, let $V(\Lambda )=V(\Delta )\cup \left\{\stackrel{..}{\overline{a^{m}b}}\right\}$ for $m\in \left\{r+l:r=j,3j,5j,\dots ,nj\right\},$ then there are two cases for m,

1. If $m\in \left\{r+l:r=j,3j,5j,\dots ,(n-2)j\right\},$ then $\stackrel{..}{\overline{a^{m}b}}\in V(\Lambda )$ is not adjacent to $\stackrel{..}{\overline{a^{m+j}b}}\in V(\Lambda )$ since $[a^{m}b,a^{m+j}b]=a^{n-2j}=g^{-1}$ which is a contradiction.

2. If $m=nj+l,$ then $\stackrel{..}{\overline{a^{m}b}}\in V(\Lambda )$ is not adjacent to $\stackrel{..}{\overline{a^{(n-1)j+l}b}}\in V(\Lambda )$ since $[a^{m}b,a^{(n-1)j+l}b]=[a^{nj+l}b,a^{(n-1)j+l}b]=a^{2j}=g^{-1}$ which is a contradiction.

Based on two cases above, Λ is not a clique of ${\ddot{\Gamma }}_{D_{2n}}^g.$ Hence, clique Δ is the largest clique of ${\ddot{\Gamma }}_{D_{2n}}^g,$ thus $\omega ({\ddot{\Gamma }}_{D_{2n}}^g)=\frac{n+1}{2}.$ $■$

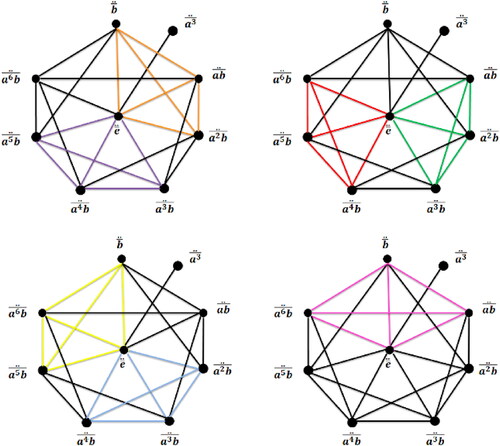
Example 2.

All possibilities of the largest clique of twin g-noncommuting graph of dihedral group for n = 7 can be seen in Figure 2.

Figure 2. All possibilities of the largest clique of ${\ddot{\Gamma }}_{D_{14}}^{a^6}.$

Theorem 4.4.

If $n=4j$ and $g=a^{2j}\in K(D_{2n})$ for $j\in \mathbb{N}$, then $\omega ({\ddot{\Gamma }}_{D_{2(4j)}}^{a^{2j}})=j+1.$

Proof.

Let $S=\left\{\stackrel{..}{\overline{a^{r}b}}:r=1,2,\dots ,2j\right\}\subseteq V({\ddot{\Gamma }}_{D_{2(4j)}}^{a^{2j}}),$ then there are two cases,

1. If j = 1, then ${\ddot{\Gamma }}_{D_8}^{a^{2j}}$ is ${\mathcal{A}}_0$ i.e, a star graph. Thus, obviously the clique number of ${\ddot{\Gamma }}_{D_8}^{a^{2j}}$ is 2.

2. If j > 1, then according to Corollary 3.2, the spanning vertex set of a clique Δ on ${\ddot{\Gamma }}_{D_{2(4j)}}^{a^{2j}}$ is $V(\Delta )=\left\{\ddot{\overline{e}}\right\}\cup H$ where $H=\left\{\stackrel{..}{\overline{a^{j+l}b}},\stackrel{..}{\overline{a^{j+1+l}b}},\dots ,\stackrel{..}{\overline{a^{2j-1+l}b}}\right\}$ and $l=1,2,\dots ,2j.$ Consequently, $|V(\Delta )|=j+1$ and vertices on H are sequential.

Hereafter, suppose there is another clique Λ where $V(\Lambda )\subseteq V({\ddot{\Gamma }}_{D_{2(4j)}}^{a^{2j}})$ and $V(\Lambda )>V(\Delta ).$ Without loss of generality, let $V(\Lambda )=V(\Delta )\cup \left\{\stackrel{..}{\overline{a^{m}b}}\right\}$ for $m\in \left\{r+l:r=1,2,\dots ,j-1\right\}\cup \left\{2j+l\right\}.$ Then there are two cases for m,

• case 1. If $m\in \left\{r+l:r=1,2,\dots ,j-1\right\},$ then $\stackrel{..}{\overline{a^{m}b}}\in V(\Lambda )$ is not adjacent to $\stackrel{..}{\overline{a^{m+j}b}}\in V(\Lambda )$ since $[a^{m}b,a^{j+m}b]=a^{2j}=g^{-1}$ which is a contradiction.

• case 2. If $m=2j+l,$ then $\stackrel{..}{\overline{a^{m}b}}\in V(\Lambda )$ is not adjacent to $\stackrel{..}{\overline{a^{j+l}b}}\in V(\Lambda )$ since $[a^{m}b,a^{j+l}b]=[a^{2j+l}b,a^{j+l}b]=a^{2j}=g^{-1}$ which is a contradiction.

Based on two cases above, Λ is not a clique of ${\ddot{\Gamma }}_{D_{2(4j)}}^{a^{2j}}.$ Hence, clique Δ is the largest clique of ${\ddot{\Gamma }}_{D_{2(4j)}}^{a^{2j}},$ thus $\omega ({\ddot{\Gamma }}_{D_{2(4j)}}^{a^{2j}})=j+1.$ $■$

Corollary 4.2.

If $n=8j$ and $g=a^{2j}\in K(D_{2n})$ for $j\in \mathbb{N}$, then $\omega ({\ddot{\Gamma }}_{D_{2(8j)}}^{a^{2j}})=j+1.$

Theorem 4.5.

If $n=6j$ and $g=a^{2j}\in K(D_{2n})$ for $j\in \mathbb{N}$, then $\omega ({\ddot{\Gamma }}_{D_{2(6j)}}^{a^{2j}})=j+1.$

Proof.

According to Corollary 3.2, then the spanning vertex set of a clique Δ on ${\ddot{\Gamma }}_{D_{2(6j)}}^{a^{2j}}$ is $V(\Delta )=\left\{\ddot{\overline{e}}\right\}\cup H$ where $H=\left\{\stackrel{..}{\overline{a^{j+l}b}},\stackrel{..}{\overline{a^{j+1+l}b}},\dots ,\stackrel{..}{\overline{a^{2j-1+l}b}}\right\}$ and $l=1,2,\dots ,3j.$ Consequently, $|V(\Delta )|=j+1$ and vertices on H are sequential.

Hereafter, suppose there is another clique Λ where $V(\Lambda )\subseteq V({\ddot{\Gamma }}_{D_{2(6j)}}^{a^{2j}})$ and $V(\Lambda )>V(\Delta ).$ Without loss of generality, let $V(\Lambda )=V(\Delta )\cup \left\{\stackrel{..}{\overline{a^{m}b}}\right\}$ for $m\in \left\{r+l:r=0,1,2,\dots ,j-1\right\}\cup \left\{s+l:s=2j,2j+1,\dots ,3j-1\right\}.$ Then there are two cases for m,

1. If $m\in \left\{r+l:r=0,1,2,\dots ,j-1\right\},$ then $\stackrel{..}{\overline{a^{m}b}}\in V(\Lambda )$ is not adjacent to $\stackrel{..}{\overline{a^{m+j}b}}\in V(\Lambda )$ since $[a^{m+j}b,a^{m}b]=a^{2j}=g$ which is a contradiction.

2. If $m\in \left\{s+l:s=2j,2j+1,\dots ,3j-1\right\},$ then $\stackrel{..}{\overline{a^{m}b}}\in V(\Lambda )$ is not adjacent to $\stackrel{..}{\overline{a^{m-j}b}}\in V(\Lambda )$ since $[a^{m-j}b,a^{m}b]=a^{n-2j}=g^{-1}$ which is a contradiction.

Based on two cases above, Λ is not a clique of ${\ddot{\Gamma }}_{D_{2(6j)}}^{a^{2j}}.$ Hence, clique Δ is the largest clique of ${\ddot{\Gamma }}_{D_{2(6j)}}^{a^{2j}},$ thus $\omega ({\ddot{\Gamma }}_{D_{2(6j)}}^{a^{2j}})=j+1.$ $■$

Corollary 4.3.

If $n=3j$ and $g=a^{2j}\in K(D_{2n})$ for $j\in \mathbb{N}$, then $\omega ({\ddot{\Gamma }}_{D_{2(3j)}}^{a^{2j}})=j+1.$

5. Conclusion

In this research, we have built up the new concept of twin g-noncommuting graph of a group. We also have constructed the twin g-noncommuting graph of the dihedral group. Furthermore, we have determined the clique number of the twin g-noncommuting graph of the dihedral group.

Disclosure statement

The authors report there are no competing interests to declare.

Data availability statement

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.