Further results on independent double roman trees

Abstract

A double Roman dominating function (DRDF) on a graph $G=(V,E)$ is a function $f:V\to \{0,1,2,3\}$ such that every vertex u with f(u) = 0 is adjacent to at least one vertex assigned a 3 or to at least two vertices assigned a 2, and every vertex v with f(v) = 1 is adjacent to at least one vertex assigned 2 or 3. The weight of a DRDF is the sum of its function values over all vertices. A DRDF f is an independent double Roman dominating function (IDRDF) if the set of vertices assigned 1, 2 and 3 is independent. The independent double Roman domination number $i_{dR}(G),$ is the minimum weight over all IDRDFs of G. Every graph G satisfies $i_{dR}(G)\le 3i(G),$ where i(G) is the independent domination number. In this paper, we give a characterization of all trees T with $i_{dR}(T)=3i(T).$

Keywords:

• Independent double Roman domination
• independent domination
• trees

AMS SUBJECT CLASSIFICATION:

• 05C69
• 05C05

1. Introduction

Let $G=(V,E)$ be a simple graph. The open neighborhood of a vertex $v\in V$ is the set $N(v)=\left\{u\right|uv\in E\}$ and its closed neighborhood is the set $N[v]=N(v)\cup \left\{v\right\}.$ The degree of a vertex $u\in V$ is ${\mathrm{deg}}_G(u)=|N(u)|.$ A vertex with exactly one neighbor is called a leaf, and its neighbor a support vertex. The set of leaves and support vertices of G are denoted by L(G) and S(G), respectively. For any set S of vertices and a vertex $u\in S,$ the external private neighborhood of u with respect to S is defined as $\text{epn}(u,S)=\left\{v\in V-S\mathrm{ }|\mathrm{ }N(v)\cap S=\left\{u\right\}\right\}.$ The distance between two vertices u and v, denoted d(u, v), is the length of a shortest path from u to v. The diameter diam(G) of a graph G is the maximum distance over all pairs of vertices of G. A path of length $\text{diam}(G),$ is called a diametrical path. A tree is an acyclic connected graph. A star $K_{1,n-1}$ is a tree of order $n\ge 2$ having n – 1 leaves, and a double star is a tree that contains exactly two vertices that are not leaves. A double star with respectively p and q leaves attached at each support vertex is denoted by $D{S}_{p,q}.$

A set $S\subseteq V$ is independent if no two vertices in S are adjacent. A set S of vertices in a graph G is an independent dominating set of G if S is independent and every vertex not in S is adjacent to a vertex in S. The independent domination number i(G) equals the minimum cardinality of a maximal independent set in G.

In 2004, Cockayne et al. [8] introduced the concept of Roman domination which is now well studied, where several variations have been defined. Among these variations, we will be interested in double Roman domination introduced in 2016 by Beeler et al. [4]. For more details on Roman domination and its variations we refer the reader to the recent papers [1–3,9] and the recent book chapters and survey [5–7].

A double Roman dominating function is defined as follows. A double Roman dominating function (DRDF) on G is a function $f:V\to \{0,1,2,3\}$ satisfying the condition that for every vertex u: (i) if f(u) = 0, then there exists a vertex $v\in N(u)$ such that f(v) = 3 or two vertices $x,y\in N(u)$ such that $f(x)=f(y)=2;$ (ii) if f(u) = 1, then there exists a vertex $v\in N(u)$ such that $f(v)\ge 2.$ For a DRDF f, let $V_i=\{v\in V|f(v)=i\}$ for $i=0,1,2,3.$ Since these four sets determine f, we can equivalently write $f=(V_0,V_1,V_2,V_3).$

Recently, Maimani et al. [11] considered double Roman dominating functions $f=(V_0,V_1,V_2,V_3)$ for which $V_1\cup V_2\cup V_3$ is independent, and called them independent double Roman dominating functions (IDRDFs). The independent double Roman domination number $i_{dR}(G),$ is the minimum weight of an IDRDF on G. A function f on G is an $i_{dR}(G)$-function if f is an IDRDF and $w(f)=i_{dR}(G).$ For more details see [10,12,13].

It was observed in [11] that for every graph G, $i_{dR}(G)\le 3i(G),$ where graphs G attaining equality have been called independent double Roman graphs. Moreover, the authors posed the problem of characterizing such graphs.

Our goal in this paper is to provide a constructive characterization of independent double Roman trees.

2. Preliminary

In this section, we present some results and definitions that will be useful for our work. We first mention that Maimani et al. [11] pointed out that for every graph G there exists an $i_{dR}(G)$-function $f=(V_0,V_1,V_2,V_3)$ such that $V_1=\varnothing .$ For sake of simplicity, we consider only the $i_{dR}(G)$-functions $f=(V_0,V_1,V_2,V_3)$ such that $V_1=\varnothing ,$ and we simply write $(V_0,V_2,V_3).$

The following result gives a necessary and sufficient condition for graphs G with $i_{dR}(G)=3i(G).$

Proposition 1.

For every graph G, $i_{dR}(G)=3i(G)$ if and only if there exists an $i_{dR}(G)$-function $f=(V_0,V_2,V_3)$, such that $V_2=\varnothing .$

Proof.

Assume that $i_{dR}(G)=3i(G)$ and let S be an i(G)-set. Clearly, $f=(V(G)-S,\varnothing ,S)$ is an $i_{dR}(G)$-function with $V_2=\varnothing .$

Conversely, if $f=(V_0,\varnothing ,V_3)$ is an $i_{dR}(G)$-function, then V₃ is a maximal independent set of G, and thus $3\left|V_3\right|=i_{dR}(G)\le 3i(G)\le 3\left|V_3\right|.$ Hence $i_{dR}(G)=3i(G).$□

The following observations can be easily derived from Proposition 1. We omit the proofs.

Observation 2.

If $i_{dR}(G)=3i(G)$, then for every $i_{dR}(G)$-function $f=(V_0,\varnothing ,V_3),$ $\mathit{epn}(v,V_3)\ne \varnothing$ for every vertex $v\in V_3.$

Observation 3.

If G is a graph such that $i_{dR}(G)=3i(G)$, then the set of support vertices of G is an independent set.

Observation 4.

If G is a graph such that $i_{dR}(G)=3i(G)$, then there exists an $i_{dR}(G)$-function $f=(V_0,\varnothing ,V_3)$, such that each support vertex of G is in V₃ and every leaf is in $V_0.$

Lemma 5.

Let w be a vertex of a tree T_w such that every leaf of T_w (except possibly w) is at distance two from w (Figure 1). Let u be a vertex of a nontrivial tree T_u and let T be the tree obtained by T_w and T_u by adding edge uw. Then $i(T)=i(T_u)+{\mathrm{deg}}_{T_w}(w).$

Figure 1. Two examples of a tree T_w used in Lemma 5.

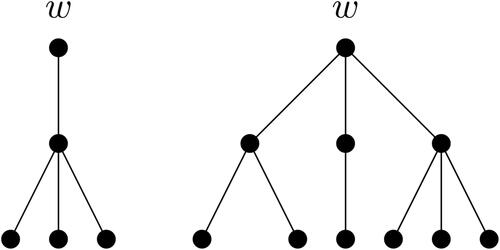
Proof.

If R is an $i(T_u)$-set, then $R\cup S(T_w)$ is a maximal independent set of T, and thus $i(T)\le i(T_u)+\left|S(T_w)\right|=i(T_u)+{\mathrm{deg}}_{T_w}(w).$ Now, among all i(T)-sets, let D be one such that $|D\cap S(T_w)|$ is maximum. We claim that $S(T_w)\subset D.$ Suppose, to the contrary, that $S(T_w)\cancel{\subset }D.$ Clearly $\left|D\cap V(T_w)\right|\ge \left|S(T_w)\right|.$ Assume first that $w\notin D.$ By the assumption, there is a vertex $x\in S(T_w)$ such that $x\notin D.$ Then D contains all leaves adjacent to x, but replacing such leaves in D by x provides an i(T)-set containing more vertices of $S(T_w),$ a contradiction. Suppose now that $w\in D.$ Then $L(T_w)\subset D.$ If $\left|N(u)\cap D\right|\ge 2,$ then $S(T_w)\cup D-(L(T_w)\cup \{w\})$ is a maximal independent set of T smaller than D, a contradiction. Hence $\left|N(u)\cap D\right|=1,$ that is w is the only neighbor of u in D. Then $S(T_w)\cup \left\{u\right\}\cup D-(L(T_w)\cup \{w\})$ is an i(T)-set containing more vertices of $S(T_w)$ than D, a contradiction. Hence $S(T_w)\subset D,$ and thus $D-S(T_w)$ is maximal independent of $T_u.$ Therefore $i(T_u)\le i(T)-\left|S(T_w)\right|,$ and so $i(T)=i(T_u)+{\mathrm{deg}}_{T_w}(w).$ □

Definition 6.

For a vertex x of G, an almost independent double Roman dominating function (almost IDRDF) relative to x is a function $f:V\to \{0,2,3\}$ such that:

1. $V_2\cup V_3$ is an independent set,

2. f(x) = 0 and x owns a neighbor w such that $f(w)>0,$

3. every vertex of $V(G)-\left\{x\right\}$ is double Roman dominated under f.

Let $i_{dR}(G;x)=\min \{f(V):$ f is an almost IDRDF on G relative to $x\}.$ An $i_{dR}(G;x)$-function is an almost IDRDF f of G relative to a vertex x with weight $i_{dR}(G;x).$ It is worth mentioning that any $i_{dR}(G;x)$-function f is an IDRDF on G – x and thus $i_{dR}(G-x)\le i_{dR}(G;x).$ We note that for a vertex x of G, $i_{dR}(G;x)$ may be greater or smaller than $i_{dR}(G).$ Indeed, let T be the tree obtained from a star $K_{1,4}$ centered at u by subdividing three edges exactly once. Let v be the unique leaf neighbor of u in T. Then $i_{dR}(T)=9$ while $i_{dR}(T;v)=8$ and $i_{dR}(T;u)=11.$ In addition, we define the following sets:

• $W_G=\{v\in V:i_{dR}(G-v)=i_{dR}(G;v)\}.$

• $W_G^1=\{v\in V:i_{dR}(G;v)\ge i_{dR}(G)\}.$

• $W_G^2=\{v\in V:f(v)\ne 0$ for every $i_{dR}(G)$-function $f\}.$

We also define the following families of trees:

• $\mathcal{F}$ denotes the family of trees T rooted at a vertex of degree at least two such that every leaf is at distance two from the root and $2\left|L(T)\right|+2>3\left|S(T)\right|.$

• ${\mathcal{F}}_0$ denotes the family of trees T rooted at a vertex of degree at least two such that every leaf is at distance two from the root and $2\left|L(T)\right|+2=3\left|S(T)\right|.$

• ${\mathcal{F}}_1$ denotes the family of trees T rooted at a vertex of degree at least two such that every leaf is at distance two from the root and $2\left|L(T)\right|+2<3\left|S(T)\right|.$

3. Main result

In the aim to characterize independent double Roman trees, let $\mathcal{T}$ be the family of unlabeled trees T that can be obtained from a sequence $T_1,T_2,\dots ,T_j(j\ge 1)$ such that T₁ is a star $K_{1,r},$ with $r\ge 1$ and for every $j\ge 2,T_{i+1}$ can be obtained from T_i by one of the following operations.

• Operation ${\mathcal{O}}_1$: Let $w\in V(T_i).$ Then $T_{i+1}$ is obtained from T_i by adding the star $K_{1,s}$ for $s\ge 2$ and joining w to a leaf u of the star.

• Operation ${\mathcal{O}}_2$: Let $w\in V(T_i).$ Then $T_{i+1}$ is obtained from T_i by adding a tree $H\in \mathcal{F}$ and joining w to the root of H.

• Operation ${\mathcal{O}}_3$: Let $w\in W_{T_i}^1$ such that $i_{dR}(T_i)\le i_{dR}(T_i-w)+1.$ Then $T_{i+1}$ is obtained from T_i by adding a tree $H\in {\mathcal{F}}_0$ and joining w to the root of H.

• Operation ${\mathcal{O}}_4$: Let $H\in {\mathcal{F}}_1$ rooted at x and let $w\in W_{T_i}^2\cap W_{T_i}.$ If $i_{dR}(T_i)+3\left|S(H)\right|-2-2\left|L(H)\right|\le i_{dR}(T_i;w),$ then $T_{i+1}$ is obtained from T_i by adding the edge wx.

• Operation ${\mathcal{O}}_5$: Let $H\in {\mathcal{F}}_1$ rooted at x and let $w\in W_{T_i}^2-W_{T_i}.$ If $i_{dR}(T_i)+3\left|S(H)\right|-2-2\left|L(H)\right|\le i_{dR}(T_i-w)+1,$ then $T_{i+1}$ is obtained from T_i by adding the edge wx.

In the proofs of the next lemmas, $f_{i+1}$ is an $i_{dR}(T_{i+1})$-function and f_i is the restriction of $f_{i+1}$ to $T_i.$

Lemma 7.

If $i_{dR}(T_i)=3i(T_i)$ and $T_{i+1}$ is obtained from T_i by Operation ${\mathcal{O}}_1,$ then $i_{dR}(T_{i+1})=3i(T_{i+1}).$

Proof.

Let y be the center vertex of the added star $K_{1,s}.$ By Lemma 5, $i(T_{i+1})=i(T_i)+1.$ Also, $i_{dR}(T_{i+1})\le i_{dR}(T_i)+3$ since any $i_{dR}(T_i)$-function can be extended to an IDRDF of $T_{i+1}$ by assigning a 3 to y and a 0 to every neighbor of y.

On the other hand, if $f_{i+1}(u)=0,$ then f_i is an IDRDF of T_i of weight $i_{dR}(T_{i+1})-3.$ If $f_{i+1}(u)=2,$ then ${\sum }_{x\in N[y]}{f}_{i+1}(x)\ge 4$ and $f_{i+1}(w)=0.$ In this case, there is a neighbor $w^{\prime }$ of w in $T_i$ such that $f_{i+1}(w^{\prime })>0$ and the minimality of $f_{i+1}$ implies that $f_{i+1}(w^{\prime })=2.$ It follows that the function g defined on $V(T_i)$ by $g(w^{\prime })=3$ and $g(x)=f_{i+1}(x)$ for each $x\in V(T_i)-\left\{w^{\prime }\right\}$ is an IDRDF of T_i of weight $i_{dR}(T_{i+1})-3.$ Finally, assume that $f_{i+1}(u)=3.$ Then ${\sum }_{x\in N[y]}{f}_{i+1}(x)\ge 5$ and $f_{i+1}(w)=0.$ Also, the minimality of $f_{i+1}$ implies that $f_{i+1}(x)=0$ for every neighbor x of w in $T_i.$ So, the function g defined on $V(T_i)$ by g(w) = 2 and $g(x)=f_{i+1}(x)$ for each $x\in V(T_i)-\left\{w\right\}$ is an IDRDF of T_i of weight $i_{dR}(T_{i+1})-3.$ In any case, $i_{dR}(T_i)\le i_{dR}(T_{i+1})-3,$ and thus $i_{dR}(T_{i+1})=i_{dR}(T_i)+3.$ Now since $i_{dR}(T_i)=3i(T_i)$ and $i(T_{i+1})=i(T_i)+1,$ we obtain $i_{dR}(T_{i+1})=3i(T_{i+1}).$ □

Lemma 8.

If $i_{dR}(T_i)=3i(T_i)$ and $T_{i+1}$ is obtained from T_i by Operation ${\mathcal{O}}_2,$ then $i_{dR}(T_{i+1})=3i(T_{i+1}).$

Proof.

Let x be the root of the tree $H\in \mathcal{F}.$ By Lemma 5, $i(T_{i+1})=i(T_i)+\left|S(H)\right|.$ Also, it is clear that $i_{dR}(T_{i+1})\le i_{dR}(T_i)+3\left|S(H)\right|.$ In the next we shall prove that $i_{dR}(T_i)\le i_{dR}(T_{i+1})-3\left|S(H)\right|.$ We first note that since $H\in \mathcal{F},{\sum }_{u\in V(H)}{f}_{i+1}(u)\ge 3\left|S(H)\right|.$ If $f_{i+1}(x)=0,$ then f_i is an IDRDF of T_i of weight $i_{dR}(T_{i+1})-3\left|S(H)\right|.$ If $f_{i+1}(x)=2,$ then $f_{i+1}(w)=0$ and each leaf of H is assigned a 2. The minimality of $f_{i+1}$ and the fact that $f_{i+1}(V(H))=2+2\left|L(H)\right|>3\left|S(H)\right|$ (since $H\in \mathcal{F}$), we deduce that there is a $w^{\prime }\in N_{T_i}(w)$ such that $f_{i+1}(w^{\prime })=2.$ So, the function g defined on $V(T_i)$ by $g(w^{\prime })=3$ and $g(u)=f_{i+1}(u)$ for each $u\in V(T_i)-\left\{w^{\prime }\right\}$ is an IDRDF of T_i of weight at most $i_{dR}(T_{i+1})-3\left|S(H)\right|.$ Finally, if $f_{i+1}(x)=3,$ then $f_{i+1}(w)=0$ and the minimality of $f_{i+1}$ leads to $f_{i+1}(u)=0$ for each $u\in N_{T_i}(w).$ Moreover, since $f_{i+1}(V(H))=3+2\left|L(H)\right|\ge 3\left|S(H)\right|+2,$ then the function g defined on $V(T_i)$ by g(w) = 2 and $g(u)=f_{i+1}(u)$ for each $u\in V(T_i)-\left\{w\right\}$ is an IDRDF of T_i of weight at most $i_{dR}(T_{i+1})-3\left|S(H)\right|.$ In any case, $i_{dR}(T_i)\le i_{dR}(T_{i+1})-3\left|S(H)\right|$ and the desired inequality follows. Now, using the facts that $i_{dR}(T_i)=3i(T_i)$ and $i(T_{i+1})=i(T_i)+\left|S(H)\right|,$ we conclude that $i_{dR}(T_{i+1})=3i(T_{i+1}).$ □

Lemma 9.

If $i_{dR}(T_i)=3i(T_i)$ and $T_{i+1}$ is obtained from T_i by Operation ${\mathcal{O}}_3,$ then $i_{dR}(T_{i+1})=3i(T_{i+1}).$

Proof.

Let $w\in W_{T_i}^1$ such that $i_{dR}(T_i)\le i_{dR}(T_i-w)+1,$ and let $H\in {\mathcal{F}}_0$ a tree rooted in x attached at w by the edge xw. By Lemma 5, $i(T_{i+1})=i(T_i)+\left|S(H)\right|.$ Also, it is clear that $i_{dR}(T_{i+1})\le i_{dR}(T_i)+3\left|S(H)\right|.$ Now, let us show that $i_{dR}(T_i)\le i_{dR}(T_{i+1})-3\left|S(H)\right|.$ If $f_{i+1}(w)>0,$ then clearly f_i is an IDRDF of T_i of weight $i_{dR}(T_{i+1})-3\left|S(H)\right|\ge i_{dR}(T_i).$ Thus, we assume that $f_{i+1}(w)=0.$ If $f_{i+1}(x)=2,$ then w has a neighbor $w^{\prime }$ in T_i assigned a 2 under $f_{i+1}.$ It follows that f_i is an almost IDRDF of T_i of weight $w(f_i)=i_{dR}(T_{i+1})-f_{i+1}(H)=i_{dR}(T_{i+1})-2-2\left|L(H)\right|=i_{dR}(T_{i+1})-3\left|S(H)\right|.$ Since $w\in W_{T_i}^1,$ we arrive at $$i_{dR}(T_i)\le i_{dR}(T_i;w)\le w(f_i)=i_{dR}(T_{i+1})-3\left|S(H)\right|.$$ Finally, if $f_{i+1}(x)=3,$ then f_i is an IDRDF of $T_i-w$ of weight $$\begin{array}{c}w(f_i)=i_{dR}(T_{i+1})-f_{i+1}(H)\\ =i_{dR}(T_{i+1})-3-2\left|L(H)\right|=i_{dR}(T_{i+1})-3\left|S(H)\right|-1.\end{array}$$ Since $i_{dR}(T_i)\le i_{dR}(T_i-w)+1,$ we arrive at $$i_{dR}(T_i)\le i_{dR}(T_i-w)+1\le w(f_i)+1=i_{dR}(T_{i+1})-3\left|S(H)\right|.$$ In all cases, $i_{dR}(T_{i+1})=i_{dR}(T_i)+3\left|S(H)\right|=3i(T_i)+3\left|S(H)\right|=3i(T_{i+1}).$ □

Lemma 10.

If $i_{dR}(T_i)=3i(T_i)$ and $T_{i+1}$ is obtained from T_i by Operation ${\mathcal{O}}_4$ or ${\mathcal{O}}_5,$ then $i_{dR}(T_{i+1})=3i(T_{i+1}).$

Proof.

Let $H\in {\mathcal{F}}_1$ be a tree rooted at x and let $w\in W_{T_i}^2$ such that $i_{dR}(T_i)+3\left|S(H)\right|-2-2\left|L(H)\right|\le \min \{i_{dR}(T_i-w)+1,i_{dR}(T_i;w)\}.$ By Lemma 5, $i(T_{i+1})=i(T_i)+\left|S(H)\right|.$ Also, it is clear that $i_{dR}(T_{i+1})\le i_{dR}(T_i)+3\left|S(H)\right|.$ Now, let us show that $i_{dR}(T_i)\le i_{dR}(T_{i+1})-3\left|S(H)\right|.$ If $f_{i+1}(w)>0,$ then f_i is an IDRDF of T_i of weight $i_{dR}(T_{i+1})-3\left|S(H)\right|\ge i_{dR}(T_i).$ So, assume that $f_{i+1}(w)=0.$ If $f_{i+1}(x)=3,$ then f_i is an IDRDF of $T_i-w$ of weight $$\begin{array}{c}w(f_i)=i_{dR}(T_{i+1})-f_{i+1}(H)\\ =i_{dR}(T_{i+1})-3-2\left|L(H)\right|.\end{array}$$ Hence $i_{dR}(T_i-w)\le i_{dR}(T_{i+1})-3-2\left|L(H)\right|.$ Since $i_{dR}(T_i)+3\left|S(H)\right|-2-2\left|L(H)\right|\le i_{dR}(T_i-w)+1,$ we arrive at $$\begin{array}{c}{i}_{dR}(T_i)+3\left|S(H)\right|-2-2\left|L(H)\right|\le i_{dR}(T_i-w)+1\\ \le i_{dR}(T_{i+1})-3-2\left|L(H)\right|+1\\ =i_{dR}(T_{i+1})-2-2\left|L(H)\right|,\end{array}$$ and therefore $i_{dR}(T_i)\le i_{dR}(T_{i+1})-3\left|S(H)\right|.$

If $f_{i+1}(x)=2,$ then clearly f_i is an almost IDRDF of T_i of weight $w(f_i)=i_{dR}(T_{i+1})-2-2\left|L(H)\right|.$ Since $i_{dR}(T_i)+3\left|S(H)\right|-2-2\left|L(H)\right|\le i_{dR}(T_i;w),$ we arrive at $$i_{dR}(T_i)+3\left|S(H)\right|-2-2\left|L(H)\right|\le i_{dR}(T_i;w)\le i_{dR}(T_{i+1})-2-2\left|L(H)\right|,$$ and therefore $i_{dR}(T_i)\le i_{dR}(T_{i+1})-3\left|S(H)\right|.$ In all cases, $i_{dR}(T_{i+1})=i_{dR}(T_i)+3\left|S(H)\right|=3i(T_{i+1}).$ □

Now we are ready to state our main result.

Theorem 11.

For a tree T, $i_{dR}(T)=3i(T)$ if and only if $T\in \mathcal{T}.$

Proof.

Assume that $T\in \mathcal{T}.$ Then there is a sequence of trees $T_1,T_2,\dots ,T_k(k\ge 1)$ such that $T_1=K_{1,r}(r\ge 1),$ and if $k\ge 2,$ then $T_{i+1}$ can be obtained recursively from T_i by one of Operations ${\mathcal{O}}_1,\dots ,{\mathcal{O}}_5$ for $i\in \{1,2,\dots ,k-1\}.$ We use the induction on the number of operations performed to construct T. Clearly, if k = 1, then the result is true. Suppose that result is true for each tree $T\in \mathcal{T}$ that can be obtained by a sequence of operations of length k – 1 and let $T^{\prime }=T_{k-1}.$ By induction, $i_{dR}(T^{\prime })=3i(T^{\prime }).$ Since $T=T_k$ is obtained from $T^{\prime }$ by using one of operations ${\mathcal{O}}_1,\dots ,{\mathcal{O}}_5,$ it follows from Lemmas 7, 8, 9 and 10 that $i_{dR}(T)=3i(T).$

Conversely, let $i_{dR}(T)=3i(T).$ We proceed by induction on the independent domination number i(T). If i(T) = 1, then T is a star of order at least two and thus $T\in \mathcal{T}.$ Let $i(T)\ge 2$ and suppose the result is true for all trees $T^{\prime }$ with $i(T^{\prime })<i(T).$ Since i(T) > 1, we have $\text{diam}(T)\ge 3.$ Moreover, Observation 3 implies that $\text{diam}(T)\ne 3,$ and thus $\text{diam}(T)\ge 4.$

Let $x{x}_1{x}_2\hspace{0.5em}\dots \hspace{0.5em}{x}_d(d\ge 5)$ be a diametral path in T. Assume that T_i is the component of $T-x_2{x}_3$ containing $x_{i+1}$ for i = 1, 2. Note that T₂ is nontrivial because $\text{diam}(T)\ge 4.$

Suppose that ${\mathrm{deg}}_T(x_2)=2.$ By Lemma 5, we have $i(T)=i(T_2)+1.$ Also, we have $i_{dR}(T)\le i_{dR}(T_2)+3.$ It follows that $$i_{dR}(T)\le i_{dR}(T_2)+3\le 3i(T_2)+3=3i(T)=i_{dR}(T),$$ and thus $i_{dR}(T_2)=3i(T_2).$ Since $i(T_2)<i(T),$ we deduce from the induction hypothesis that $T_2\in \mathcal{T}.$ Consequently, $T\in \mathcal{T}$ because it can be obtained from T₂ by Operation ${\mathcal{O}}_1.$ Henceforth, we can assume that ${\mathrm{deg}}_T(x_2)\ge 3.$ By Observation 3, x₂ is not a support vertex and thus every leaf of T₁ is at distance two from x₂. Therefore $T_1\in \mathcal{F}\cup {\mathcal{F}}_0\cup {\mathcal{F}}_1.$ Let ${\mathrm{deg}}_T(x_2)=k.$ By Lemma 5, $i(T)=i(T_2)+(k-1).$ In the sequel, we shall show that $i_{dR}(T)=i_{dR}(T_2)+3(k-1).$ First, $i_{dR}(T)\le i_{dR}(T_2)+3(k-1),$ since every $i_{dR}(T_2)$-function can be extended to an IDRDF of T by assigning a 3 to every support vertex of T₁ and a 0 to the remaining of vertices of $T_1.$ Now, assume that $i_{dR}(T)<i_{dR}(T_2)+3(k-1).$ Then $$3i(T)=i_{dR}(T)<i_{dR}(T_2)+3(k-1)\le 3i(T_2)+3(k-1)=3i(T),$$ a contradiction. Therefore $i_{dR}(T)=i_{dR}(T_2)+3(k-1)$ and thus $i_{dR}(T_2)=3i(T_2).$ Since $i(T_2)<i(T),$ we deduce from the induction hypothesis that $T_2\in \mathcal{T}.$ We now consider the following cases.

• Case 1. $2\left|L(T_1)\right|+2>3\left|S(T_1)\right|.$

  Thus $T_1\in \mathcal{F}.$ Therefore $T\in \mathcal{T}$ because it can be obtained from T₂ by Operation ${\mathcal{O}}_2.$

• Case 2. $2\left|L(T_1)\right|+2=3\left|S(T_1)\right|.$

  Thus $T_1\in {\mathcal{F}}_0.$ Assume that $x_3\notin W_{T_2}^1$ and let h₁ be an $i_{dR}(T_2;x_3)$-function. Clearly, $i_{dR}(T_2;x_3)<i_{dR}(T_2).$ We define the function g₁ on V(T) by $g_1(u)=h_1(u)$ for each $u\in T_2,g_1(u)=2$ for each $u\in \left\{x_2\right\}\cup L(T_1)$ and $g_1(u)=0$ for each $u\in S(T_1).$ Then g₁ is an IDRDF of T yielding $w(g_1)=i_{dR}(T_2;x_3)+2+2\left|L(T_1)\right|<i_{dR}(T_2)+3\left|S(T_1)\right|,$ a contradiction. Hence $x_3\in W_{T_2}^1.$ Suppose now that $i_{dR}(T_2)>i_{dR}(T_2-x_3)+1,$ and let h₂ be an $i_{dR}(T-x_3)$-function. Define the function g₂ on V(T) by $g_2(x_3)=0,g_2(u)=h_2(u)$ for each $u\in V(T_2)-\left\{x_3\right\},g_2(x_2)=3,g_2(u)=2$ for every $u\in L(T_1)$ and $g_2(u)=0$ for every $u\in S(T_1).$ Clearly, g₂ is an IDRDF of $T$ of weight $i_{dR}(T_2-x_3)+3+2\left|L(T_1)\right|.$ Consequently, $$\begin{array}{c}{i}_{dR}(T)\le i_{dR}(T_2-x_3)+3+2\left|L(T_1)\right|<i_{dR}(T_2)+2+2\left|L(T_1)\right|\\ =i_{dR}(T_2)+3\left|S(T_1)\right|=i_{dR}(T),\end{array}$$ a contradiction. Thus $i_{dR}(T_2)\le i_{dR}(T_2-x_3)+1.$ Consequently, $T\in \mathcal{T}$ since it can be obtained from T₂ by Operation ${\mathcal{O}}_3.$

• Case 3. $2\left|L(T_1)\right|+2<3\left|S(T_1)\right|.$

  Thus $T_1\in {\mathcal{F}}_1.$ If $x_3\notin W_{T_2}^2$ and h₃ be an $i_{dR}(T_2)$-function such that $h_3(x_3)=0,$ then h₃ can be extended to an IDRDF of T by assigning a 2 to x₂ and to every leaf in $L(T_1),$ and a 0 to every support vertex of T₁ and this implies that $i_{dR}(T)\le i_{dR}(T_2)+2\left|L(T_1)\right|+2<i_{dR}(T_2)+3\left|S(T_1)\right|,$ a contradiction. Thus $x_3\in W_{T_2}^2.$ Suppose now that $i_{dR}(T_2)+3\left|S(T_1)\right|-2-2\left|L(T_1)\right|>\min \{i_{dR}(T_2;x_3),i_{dR}(T_2-x_3)+1\}.$

• Subcase 3.1. $i_{dR}(T_2)+3\left|S(T_1)\right|-2-2\left|L(T_1)\right|>i_{dR}(T_2;x_3).$ Let h₄ be an $i_{dR}(T_2;x_3)$-function. Then the function g₄ defined by $g_4(u)=h_4(u)$ for each $u\in V(T_2),g_4(u)=2$ for each $u\in \left\{x_2\right\}\cup L(T_1)$ and $g_4(u)=0$ for each $u\in S(T_1)$ is an IDRDF of T of weight $i_{dR}(T_2;x_3)+2+2\left|L(T_1)\right|.$ Consequently, $$\begin{array}{c}{i}_{dR}(T)\le i_{dR}(T_2;x_3)+2+2\left|L(T_1)\right|\\ <(i_{dR}(T_2)+3\left|S(T_1)\right|-2-2\left|L(T_1)\right|)+2+2\left|L(T_1)\right|\\ =i_{dR}(T_2)+3\left|S(T_1)\right|=i_{dR}(T),\end{array}$$ a contradiction.

• Subcase 3.2. $i_{dR}(T_2)+3\left|S(T_1)\right|-2-2\left|L(T_1)\right|>i_{dR}(T_1-x_3)+1.$

  Let h₅ be an $i_{dR}(T-x_3)$-function. Then the function g₅ defined by $g_5(u)=h_5(u)$ for every $u\in V(T_2)-\left\{x_3\right\},g_5(x_3)=0,$ $g_5(x_2)=3,g_5(u)=2$ for all $u\in L(T_1)$ and $g_5(u)=0$ for all $u\in S(T_1).$ Clearly g₅ is an IDRDF of T of weight $i_{dR}(T_1-x_3)+3+2\left|L(T_1)\right|.$ Consequently, $$\begin{array}{c}{i}_{dR}(T)\le i_{dR}(T_1-x_3)+1+2+2\left|L(T_1)\right|\\ <(i_{dR}(T_2)+3\left|S(T_1)\right|-2-2\left|L(T_1)\right|)+2+2\left|L(T_1)\right|\\ =i_{dR}(T_2)+3\left|S(T_1)\right|=i_{dR}(T),\end{array}$$ a contradiction.

Therefore $i_{dR}(T_2)+3\left|S(T_1)\right|-2-2\left|L(T_1)\right|\le \min \{i_{dR}(T_2:x_3),i_{dR}(T_2-x_3)+1\}.$ It follows that $T\in \mathcal{T},$ since it can be obtained from T₂ by either Operation ${\mathcal{O}}_4$ (if $x_3\in W_{T_2}$) or Operation ${\mathcal{O}}_5$ (if $x_3\notin W_{T_2}$). This completes the proof. □

Acknowledgments

H. Abdollahzadeh Ahangar was supported by the Babol Noshirvani University of Technology under research Grant Number BNUT/385001/1401.