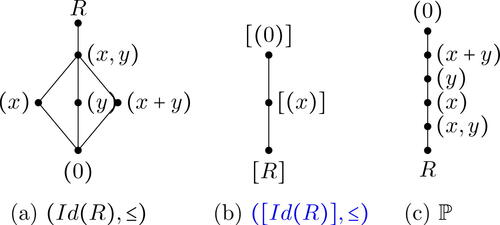On graphs with equal coprime index and clique number

Abstract

Recently, Katre et al. introduced the concept of the coprime index of a graph. They asked to characterize the graphs for which the coprime index is the same as the clique number. In this paper, we partially solve this problem. In fact, we prove that the clique number and the coprime index of a zero-divisor graph of an ordered set and the zero-divisor graph of a ring ${\mathbb{Z}}_{p^n}$ coincide. Also, it is proved that the annihilating ideal graphs, the co-annihilating ideal graphs and the comaximal ideal graphs of commutative rings can be realized as the zero-divisor graphs of specially constructed posets. Hence the coprime index and the clique number coincide for these graphs as well.

KEYWORDS:

• Coprime labeling
• coprime index
• edge clique cover
• intersection number
• zero-divisor graphs
• annihilating ideal graphs
• co-annihilating ideal graphs

MATHEMATICS SUBJECT CLASSIFICATION:

• 05C15
• 05C78
• 06A07
• 13A70

1 Introduction

Graph labeling is a very active area of research. Many researchers studied several types of graph labelings. For an excellent survey on graph labelings, we refer to Gallian [12]. Recently, Katre et al. [16] studied another labeling known as coprime labeling.

Definition 1.1.

(Katre et al. [16]) Let $G=(V,E)$ be a graph of order n. An injection $f:V\to \{2,3,4,\dots \}$ is called a coprime labeling of G if for any two vertices $u,v\in V$, u and v are adjacent if and only if f(u) and f(v) are coprime. A graph that admits a coprime labeling is called a coprime graph. A prime number p is said to be used by the coprime labeling f if p divides f(v) for some $v\in V$. Let $\mu (G,f)$ be the number of primes used by the coprime labeling f. Then $\mu (G)=\min \{\mu (G,f) : f \text{isacoprimelabelingof} G\}$ is called the coprime index of G.

It is known that every graph G is a coprime graph (cf. [16, Theorem 2.3]). Further, the coprime index of a graph G is nothing but the edge clique covering number of the complement of G (cf. [16, Theorem 2.10]). Note that finding the edge clique covering number of a graph G is NP-complete; see [13]. By an edge clique cover of a graph G, we mean a collection of cliques $C_1,C_2,\dots ,C_k$ such that ${\cup }_{i=1}^{k}E(C_i)=E(G)$. The minimum cardinality of an edge clique cover of G is called the edge clique covering number of G and is denoted by ${\theta }_{\mathrm{e}}(G)$. The best bound for ${\theta }_{\mathrm{e}}(G)$ is due to Erdös, Goodman, and Posa [11] which states that if G is any graph of order n, then ${\theta }_{\mathrm{e}}(G)\le$ $\lfloor n^2/4\rfloor$, and this bound is attained.

The edge clique covering number of a graph G is in fact the intersection number of G, that is, $i(G)={\theta }_{\mathrm{e}}(G)$; see Fred Roberts [21, Theorem 5]. The intersection number of G, denoted by i(G), is the minimum cardinality of a set X such that G is the intersection graph of a family of subsets of X.

Looking at the relations between the coprime index and the edge clique covering number, it is clear that finding the coprime index of a graph is a tough problem.

The clique number $\omega (G)$ of a graph G is the size of the largest complete subgraph of G. The chromatic number $\chi (G)$ of a graph G is the minimum number of colors required to color the vertices of G such that no two adjacent vertices receive the same color.

The following are some observations.

Observation 1.2.

[16, Observations 2.6, 2.7, 2.8]

1. $\mu (K_n)=n$.

2. If H is an induced subgraph of a graph G, then $\mu (H)\le \mu (G)$.

3. $\omega (G)\le \mu (G)$.

In view of Observation 1.2 (3), Katre et al. [16] raised the following problem.

Problem 1.3.

[16, Problem 2.9] Characterize graphs G for which $\omega (G)=\mu (G)$.

In this paper, we partially solve this problem. In fact, we prove that the clique number and the coprime index of a zero-divisor graph of an ordered set and the zero-divisor graph of a ring ${\mathbb{Z}}_{p^n}$ coincide. Also, it is proved that the annihilating ideal graphs, the co-annihilating ideal graphs and the comaximal ideal graphs of commutative rings can be realized as the zero-divisor graphs of specially constructed posets. Hence the coprime index and the clique number coincide for these graphs as well.

In the first result, we prove that the coprime index of a graph and its reduced graph remain the same. The reduced graph usually has less number of vertices. So this technique is useful and effective.

Definition 1.4.

[7, Definition 2.1] Let G be a simple graph. Consider an equivalence relation ∼ on G: $u\sim v$ if and only if $N(u)=N(v)$, where $N(x)=\{y\in V(G)\mid xy\text{isanedgeinG}\}$. The reduced graph of G, denoted by G_red, is the simple graph whose vertex set is $V(G_{\mathit{red}})=\{[v]:v\in V(G)\}$, and two distinct equivalence classes $[u]$ and $[v]$ are adjacent in G_red if and only if u and v are adjacent in G.

A graph G and its reduced graph G_red are shown in Figure 3. It is easily observed that G_red is isomorphic to an induced subgraph of G. Henceforth, we abuse the notation and will say that G_red is an induced subgraph of G. Clearly, if the graphs G and H are isomorphic, then $\mu (G)=\mu (H)$.

Theorem 1.5.

Let G be a finite simple graph of order n and G_red be its reduced graph. Then $\mu (G)=\mu (G_{\mathit{red}})$.

Proof.

Since G_red is an induced subgraph of G, $\mu (G_{\mathit{red}})\le \mu (G)$. Hence, it is enough to prove that $\mu (G)\le \mu (G_{\mathit{red}})$. For this, let $\mu (G_{\mathit{red}})=\mu (G_{\mathit{red}},f)=m$, where $f:V(G_{\mathit{red}})\to \{2,3,4,\dots \}$ be a coprime labeling of G_red. Now, we define the coprime labeling $\overline{f}$ of G using f. Let $[x_1],[x_2],\dots ,[x_k]$ be the k distinct vertices of G_red. Clearly, $V(G)={\cup }_{i=1}^k.[x_i]$. Let $[x_i]=\{y_{ij}:j=1,2,\dots ,k_i=|[x_i]\left|\right\}$. Therefore, $V(G)=\{y_{ij}:i=1,2,\dots ,k$ and $j=1,2,\dots ,k_i\}$.

Define a map $\overline{f}:V(G)\to \{2,3,4,\dots \}$ by $\overline{f}(y_{ij})={(f([x_i]))}^j$. Clearly, $\overline{f}$ is an injective map, as f is injective. It is easy to observe that y_ij and y_rs are adjacent in G if and only if $[x_i]$ and $[x_r]$ are adjacent in G_red if and only if $f([x_i])$ and $f([x_r])$ are coprime (as f is a coprime labeling of G_red) if and only if ${(f([x_i]))}^j$ and ${(f([x_r]))}^s$ are coprime if and only if $\overline{f}(y_{ij})$ and $\overline{f}(y_{rs})$ are coprime. This proves $\overline{f}$ is a coprime labeling of G. Thus, $\mu (G)\le \mu (G_{\mathit{red}})$. Hence, $\mu (G)=\mu (G_{\mathit{red}})$. □

Proposition 1.6.

[7, Proposision 2.4] G is a complete r-partite graph if and only if G_red is the complete graph K_r.

In [16], Katre et al. observed that, $\mu (K_n)=n$. In view of Theorem 1.5 and Proposition 1.6, we have the following corollary.

Corollary 1.7.

Let G be a complete r-partite graph. Then $\mu (G)=r$.

In [16], Katre et al. observed that the clique number $\omega (G)$ is less than or equal to the coprime index $\mu (G)$ of G. We sharpen this lower bound of the coprime index $\mu (G)$ in the following result.

Theorem 1.8.

Let G be a finite simple graph. Then $\omega (G)\le \chi (G)\le \mu (G)$.

Proof.

It is well known that $\omega (G)\le \chi (G)$. We want to prove that $\chi (G)\le \mu (G)$. Let $\mu (G)=\mu (G,f)=m$ and let $p_1,p_2,\dots ,p_m$ be the m distinct primes used by the coprime labeling f of G. To prove $\chi (G)\le \mu (G)$, it is enough to prove that $\chi (G)\le m$. For this, define the set $V_1=\{v\in V : p_1 \text{divides} f(v)\}$, and the set $V_k=\{v\in V\setminus ({\cup }_{j=1}^{k-1}{V}_j) : p_k \text{divides} f(v)\}$ for $k\in \{2,3,\dots m\}$. Clearly, $V={\cup }_{i=1}^m.V_i$. We assign m different colors to these V_i’s. Now, we prove that, this is a proper coloring of G. For this, if x and y are adjacent in G, then f(x) and f(y) are coprime (as f is a coprime labeling of G). This implies x and y cannot be contained in the same V_i. So x and y have different colors. Hence, this is a proper coloring with m colors. Thus, $\chi (G)\le m$. This proves $\omega (G)\le \chi (G)\le \mu (G)$. □

Definition 1.9.

(Anderson and Livingston [5]) Let R be a commutative ring with identity. The zero-divisor graph $\Gamma (R)$ of R is a simple graph with the vertex set $Z^{*}(R)=Z(R)\setminus \left\{0\right\}$, the set of non-zero zero-divisors of R, and two distinct vertices x, y are adjacent if and only if xy = 0.

Notation 1.10.

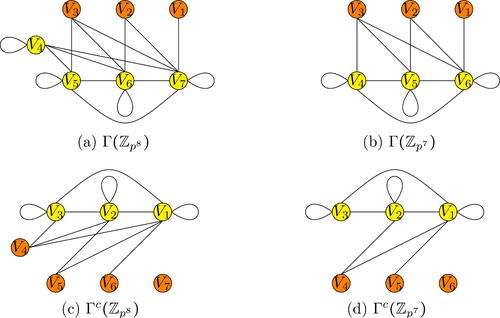
(Pirzada et al. [20]) Let p be a prime number. Consider the partition of the vertex set $V(\Gamma ({\mathbb{Z}}_{p^n}))$ into $V_1,V_2,\dots ,V_{n-1}$, where $V_i=\{{\mathcal{l}}_i{p}^i:p\nmid {\mathcal{l}}_i\},1\le i\le n-1$. Then $\left|V_i\right|=(p-1)p^{n-i-1}$.

Rewrite the elements of V_i as $V_i=\{x_{i1},x_{i2},\dots ,x_{i{k}_i}\}$, where $k_i=\left|V_i\right|=(p-1)p^{n-i-1}$. Then the elements $x_{i_1{j}_1}$ and $x_{i_2{j}_2}$ are adjacent in $\Gamma ({\mathbb{Z}}_{p^n})$ if and only if $i_1+i_2\ge n$. Also, the elements $x_{i_1{j}_1}$ and $x_{i_2{j}_2}$ are adjacent in the complement graph ${\Gamma }^c({\mathbb{Z}}_{p^n})$ if and only if $i_1+i_2<n$. The zero-divisor graphs $\Gamma ({\mathbb{Z}}_{p^n})$ and their complements ${\Gamma }^c({\mathbb{Z}}_{p^n})$ for n = 8 and n = 7 are shown in Figure 1. In the figures, a loop at V_i denotes that any two vertices of V_i are adjacent, that is, the vertices of V_i induce a complete graph on $\left|V_i\right|$ vertices and V_i is adjacent to V_j denotes that each vertex of V_i is adjacent to every vertex of V_j, that is, $V_i+V_j$ is a graph join. The join G + H of two graphs G and H is a graph formed from disjoint copies of G and H by connecting each vertex of G to each vertex of H.

Fig. 1 Zero-divisor graphs and their complements.

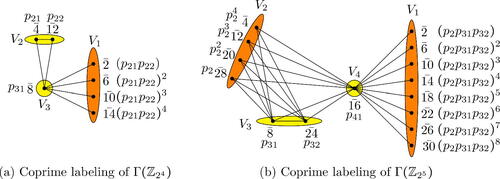
We illustrate the coprime labelings of $\Gamma ({\mathbb{Z}}_{2^4})$ and $\Gamma ({\mathbb{Z}}_{2^5})$ in Figure 2. The primes used in the coprime labeling of $\Gamma ({\mathbb{Z}}_{2^4})$ are p₂₁, p₂₂ and p₃₁. Hence, $\mu (\Gamma ({\mathbb{Z}}_{2^4}))=3=\omega (\Gamma ({\mathbb{Z}}_{2^4}))$. Also, the primes used in the coprime labeling of $\Gamma ({\mathbb{Z}}_{2^5})$ are $p_2,p_{31},p_{32}$ and p₄₁. Therefore, $\mu (\Gamma ({\mathbb{Z}}_{2^5}))=4=\omega (\Gamma ({\mathbb{Z}}_{2^5}))$. The following result is essentially proved in [8, Proposition 2.3] and [20, Theorem 2].

Fig. 2 Coprime labeling of zero-divisor graphs.

Theorem 1.11.

([8, Proposition 2.3], [20, Theorem 2]) Let $\Gamma ({\mathbb{Z}}_{p^n})$ be the zero-divisor graph of a ring ${\mathbb{Z}}_{p^n}$, where p is a prime. Then $\chi (\Gamma ({\mathbb{Z}}_{p^n}))=\omega (\Gamma ({\mathbb{Z}}_{p^n}))=\{\begin{array}{cc}{p}^{\frac{n}{2}}-1\hfill & \text{if} n \text{iseven};\hfill \\ p^{\frac{n-1}{2}}\hfill & \text{if} n \text{isodd}.\hfill \end{array}$

With this preparation, we prove our first main result.

Theorem 1.12.

Let $\Gamma ({\mathbb{Z}}_{p^n})$ be the zero-divisor graph of a ring ${\mathbb{Z}}_{p^n}$, where p is a prime. Then $\mu (\Gamma ({\mathbb{Z}}_{p^n}))=\chi (\Gamma ({\mathbb{Z}}_{p^n}))=\omega (\Gamma ({\mathbb{Z}}_{p^n}))=\{\begin{array}{cc}{p}^{\frac{n}{2}}-1\hfill & \text{if} n \text{iseven};\hfill \\ p^{\frac{n-1}{2}}\hfill & \text{if} n \text{isodd}.\hfill \end{array}$

Proof.

Consider the partition $V_i ; i=1,2,\dots ,n-1$ of $V(\Gamma ({\mathbb{Z}}_{p^n}))$ as defined in Notation 1.10.

Let $V_i=\{x_{i1},x_{i2},\dots ,x_{i{k}_i}\}$, where $k_i=\left|V_i\right|=(p-1)p^{n-i-1}$. We have the following two main cases on the values of n.

Case A: Let n be an even number.

Consider a map $f:V(\Gamma ({\mathbb{Z}}_{p^n}))\to \{2,3,4,\dots \}$ as follows: $$f(x_{ij})=\{\begin{array}{c}{p}_{ij}\hfill \\ \text{for} \frac{n}{2}\le i\le n-1,1\le j\le k_i;\hfill \\ {(\prod _{\mathcal{l}=1}^{k_{\frac{n}{2}}}{p}_{\frac{n}{2}\mathcal{l}})}^j\hfill \\ \text{for} i=\frac{n}{2}-1,1\le j\le k_{(\frac{n}{2}-1)};\hfill \\ \left[\right(\prod _{\mathcal{l}=1}^{k_{\frac{n}{2}}}{p}_{\frac{n}{2}\mathcal{l}}\left)\right(\prod _{\mathcal{l}=1}^{k_{(\frac{n}{2}+1)}}{p}_{(\frac{n}{2}+1)\mathcal{l}})\hfill \\ \dots (\prod _{\mathcal{l}=1}^{k_{n-i-1}}{p}_{(n-i-1)\mathcal{l}}){]}^j\hfill \\ \text{for} 1\le i\le (\frac{n}{2}-2),1\le j\le k_i,\hfill \end{array}$$where p_ij are distinct primes. Now, we prove that f is a coprime labeling of $\Gamma ({\mathbb{Z}}_{p^n})$. For this, let $u,v\in V(\Gamma ({\mathbb{Z}}_{p^n}))$ be distinct vertices of $\Gamma ({\mathbb{Z}}_{p^n})$. We study the following three sub-cases.

Sub-case A-I: If $u\in V_{i_1},v\in V_{i_2}$ for some $1\le i_1\le i_2\le \frac{n}{2}-1$, then $u=x_{i_1{j}_1}$, $v=x_{i_2{j}_2}$ for some $1\le j_1\le k_{i_1},1\le j_2\le k_{i_2}$ (see Notation 1.10). Clearly, $i_1+i_2<n$. This implies that u and v are not adjacent in $\Gamma ({\mathbb{Z}}_{p^n})$. Clearly, the primes $p_{\frac{n}{2}\mathcal{l}}$ divide both $f(u)=f(x_{i_1{j}_1})$ and $f(v)=f(x_{i_2{j}_2})$, for $1\le \mathcal{l}\le k_{\frac{n}{2}}$. Therefore, f(u) and f(v) are not coprime.

Sub-case A-II: If $u\in V_{i_1},v\in V_{i_2}$ for some $\frac{n}{2}\le i_1\le i_2\le n-1$, then $u=x_{i_1{j}_1}$, $v=x_{i_2{j}_2}$ for some $1\le j_1\le k_{i_1},1\le j_2\le k_{i_2}$. Clearly, $i_1+i_2\ge n$. This gives u and v are adjacent in $\Gamma ({\mathbb{Z}}_{p^n})$. By the definition of f, $f(u)=f(x_{i_1{j}_1})=p_{i_1{j}_1}$ and $f(v)=f(x_{i_2{j}_2})=p_{i_2{j}_2}$. As u and v are distinct vertices, $p_{i_1{j}_1}\ne p_{i_2{j}_2}$. This implies f(u) and f(v) are coprime.

Sub-case A-III: If $u\in V_{i_1},v\in V_{i_2}$ for some $1\le i_1\le \frac{n}{2}-1,\frac{n}{2}\le i_2\le n-1$, then $u=x_{i_1{j}_1},v=x_{i_2{j}_2}$ for some $1\le j_1\le k_{i_1},1\le j_2\le k_{i_2}$. In this case, $u=x_{i_1{j}_1}$ and $v=x_{i_2{j}_2}$ are adjacent if and only if $i_1+i_2\ge n$. If $i_1+i_2\ge n$, then $i_2\ge n-i_1>n-i_1-1$. By the definition of f, the primes $p_{i_2\mathcal{l}}$ does not divide $f(x_{i_1{j}_1})$, for all $1\le \mathcal{l}\le k_{i_2}$. In particular, the prime $p_{i_2{j}_2}$ does not divide $f(x_{i_1{j}_1})$. As $f(x_{i_2{j}_2})=p_{i_2{j}_2}$, we have $f(x_{i_1{j}_1})$ and $f(x_{i_2{j}_2})$ are coprime. Hence, f(u) and f(v) are coprime. If $i_1+i_2<n$, then u and v are not adjacent and $i_2<n-i_1$ ($i_2\le n-i_1-1$). By the definition of f, $p_{i_2{j}_2}$ divides both $f(x_{i_1{j}_1})$ and $f(x_{i_2{j}_2})$. Therefore, f(u) and f(v) are not coprime.

Thus, f is a coprime labeling of $\Gamma ({\mathbb{Z}}_{p^n})$.

The number of distinct primes used in the coprime labeling $f=\left|V_{\frac{n}{2}}\right|+\left|V_{\frac{n}{2}+1}\right|+\dots +\left|V_{n-1}\right|=(p-1)p^{n-\frac{n}{2}-1}+(p-1)p^{n-(\frac{n}{2}+1)-1}+\dots +(p-1)p^{n-(n-1)-1}=(p-1)p^{\frac{n}{2}-1}+(p-1)p^{\frac{n}{2}-2}+\dots +(p-1)=(p-1)\{p^{\frac{n}{2}-1}+p^{\frac{n}{2}-2}+\dots +1\}=p^{\frac{n}{2}}-1=\omega (\Gamma ({\mathbb{Z}}_{p^n}))$. This implies $\mu (\Gamma ({\mathbb{Z}}_{p^n}))\le \omega (\Gamma ({\mathbb{Z}}_{p^n}))$. Therefore, by Theorem 1.8, $\mu (\Gamma ({\mathbb{Z}}_{p^n}))=\chi (\Gamma ({\mathbb{Z}}_{p^n}))=\omega (\Gamma ({\mathbb{Z}}_{p^n}))=p^{\frac{n}{2}}-1$.

Case B: Let n be an odd number.

Consider a map $f:V(\Gamma ({\mathbb{Z}}_{p^n}))\to \{2,3,4,\dots \}$ as follows: $$f(x_{ij})=\{\begin{array}{c}{p}_{ij}\hfill \\ \text{for} \lfloor \frac{n}{2}\rfloor +1\le i\le n-1,1\le j\le k_i;\hfill \\ {(p_{\lfloor \frac{n}{2}\rfloor })}^j\hfill \\ \text{for} i=\lfloor \frac{n}{2}\rfloor ,1\le j\le k_{\lfloor \frac{n}{2}\rfloor };\hfill \\ {[(p_{\lfloor \frac{n}{2}\rfloor })(\prod _{\mathcal{l}=1}^{k_{(\lfloor \frac{n}{2}\rfloor +1)}}{p}_{(\lfloor \frac{n}{2}\rfloor +1)\mathcal{l}})\dots (\prod _{\mathcal{l}=1}^{k_{n-i-1}}{p}_{(n-i-1)\mathcal{l}})]}^j\hfill \\ \text{for} 1\le i\le (\lfloor \frac{n}{2}\rfloor -1),1\le j\le k_i,\hfill \end{array}$$where p_ij and $p_{\lfloor \frac{n}{2}\rfloor }$ are distinct primes. Now, we prove that f is a coprime labeling of $\Gamma ({\mathbb{Z}}_{p^n})$. For this, let $u,v\in V(\Gamma ({\mathbb{Z}}_{p^n}))$ be distinct vertices of $\Gamma ({\mathbb{Z}}_{p^n})$. We study the following three sub-cases.

Sub-case B-I: If $u\in V_{i_1},v\in V_{i_2}$ for some $1\le i_1\le i_2\le \lfloor \frac{n}{2}\rfloor$, then $u=x_{i_1{j}_1},v=x_{i_2{j}_2}$ for some $1\le j_1\le k_{i_1},1\le j_2\le k_{i_2}$. Clearly, $i_1+i_2<n$. Hence u and v are not adjacent in $\Gamma ({\mathbb{Z}}_{p^n})$. Clearly, the prime $p_{\lfloor \frac{n}{2}\rfloor }$ divides both $f(u)=f(x_{i_1{j}_1})$ and $f(v)=f(x_{i_2{j}_2})$. Therefore, f(u) and f(v) are not coprime.

Sub-case B-II: If $u\in V_{i_1},v\in V_{i_2}$ for some $\lfloor \frac{n}{2}\rfloor +1\le i_1\le i_2\le n-1$, then $u=x_{i_1{j}_1},v=x_{i_2{j}_2}$ for some $1\le j_1\le k_{i_1},1\le j_2\le k_{i_2}$. Clearly, $i_1+i_2\ge n$. Hence u and v are adjacent in $\Gamma ({\mathbb{Z}}_{p^n})$. By the definition of f, $f(u)=f(x_{i_1{j}_1})=p_{i_1{j}_1}$ and $f(v)=f(x_{i_2{j}_2})=p_{i_2{j}_2}$. As u and v are distinct vertices, $p_{i_1{j}_1}\ne p_{i_2{j}_2}$. This implies f(u) and f(v) are coprime.

Sub-case B-III: If $u\in V_{i_1},v\in V_{i_2}$ for some $1\le i_1\le \lfloor \frac{n}{2}\rfloor ,\lfloor \frac{n}{2}\rfloor +1\le i_2\le n-1$, then $u=x_{i_1{j}_1}$, $v=x_{i_2{j}_2}$ for some $1\le j_1\le k_{i_1},1\le j_2\le k_{i_2}$. In this case, $u=x_{i_1{j}_1}$ and $v=x_{i_2{j}_2}$ are adjacent if and only if $i_1+i_2\ge n$. If $i_1+i_2\ge n$, then $i_2\ge n-i_1>n-i_1-1$. By the definition of f, the primes $p_{i_2\mathcal{l}}$ does not divide $f(x_{i_1{j}_1})$, for all $1\le \mathcal{l}\le k_{i_2}$. In particular, the prime $p_{i_2{j}_2}$ does not divide $f(x_{i_1{j}_1})$. As $f(x_{i_2{j}_2})=p_{i_2{j}_2}$, we have $f(x_{i_1{j}_1})$ and $f(x_{i_2{j}_2})$ are coprime. Hence, f(u) and f(v) are coprime. If $i_1+i_2<n$, then u and v are not adjacent and $i_2<n-i_1$ ($i_2\le n-i_1-1$). By the definition of f, $p_{i_2{j}_2}$ divides both $f(x_{i_1{j}_1})$ and $f(x_{i_2{j}_2})$. Therefore, f(u) and f(v) are not coprime.

Thus, f is a coprime labeling of $\Gamma ({\mathbb{Z}}_{p^n})$.

The number of distinct primes used in the coprime labeling $f=\left|V_{\lfloor \frac{n}{2}\rfloor +1}\right|+\left|V_{\lfloor \frac{n}{2}\rfloor +2}\right|+\dots +\left|V_{n-1}\right|+1=(p-1)p^{n-(\lfloor \frac{n}{2}\rfloor +1)-1}+(p-1)p^{n-(\lfloor \frac{n}{2}\rfloor +2)-1}+\dots$ $+(p-1)p^{n-(n-1)-1}+1=(p-1)p^{n-(\frac{n-1}{2}+1)-1}+(p-1)p^{n-(\frac{n-1}{2}+2)-1}+\dots$ $+(p-1)p^{n-(n-1)-1}+1=(p-1)p^{(\frac{n-3}{2})}+(p-1)p^{(\frac{n-5}{2})}+\dots +(p-1)+1=(p-1)\{p^{(\frac{n-3}{2})}+p^{(\frac{n-5}{2})}+\dots +1\}$.

$+1=p^{\frac{n-1}{2}}-1+1=p^{\frac{n-1}{2}}=\omega (\Gamma ({\mathbb{Z}}_{p^n}))$ This implies that $\mu (\Gamma ({\mathbb{Z}}_{p^n}))\le \omega (\Gamma ({\mathbb{Z}}_{p^n}))$. Therefore, by Theorem 1.8, $\mu (\Gamma ({\mathbb{Z}}_{p^n}))=\chi (\Gamma ({\mathbb{Z}}_{p^n}))=\omega (\Gamma ({\mathbb{Z}}_{p^n}))=p^{\frac{n-1}{2}}$. □

Definition 1.13.

[1, Definition 2.1] An independent set in a graph G is a subset I of the vertex set V(G) of G such that no two vertices of I are adjacent. The independence number of G, denoted by $\alpha (G)$, is defined as the cardinality of a maximum independent set of G.

Theorem 1.14.

[1, Theorem 2] Let $\Gamma ({\mathbb{Z}}_{p^n})$ be the zero-divisor graph of a ring ${\mathbb{Z}}_{p^n}$, where p is a prime. Then $\alpha (\Gamma ({\mathbb{Z}}_{p^n}))=\{\begin{array}{cc}{p}^{n-1}-p^{\frac{n}{2}}+1\hfill & \text{if} n \text{is even};\hfill \\ p^{\frac{n-1}{2}}(p^{\frac{n-1}{2}}-1)\hfill & \text{if} n \text{is odd}.\hfill \end{array}$

The details of the proof of Theorem 1.15 can be obtained on similar lines as that of Theorem 1.11. Hence we skipped the detailed proof. The coprime labeling is given.

Theorem 1.15.

Let ${\Gamma }^c({\mathbb{Z}}_{p^n})$ be the complement of the zero-divisor graph of a ring ${\mathbb{Z}}_{p^n}$, where p is a prime. Then $\mu ({\Gamma }^c({\mathbb{Z}}_{p^n}))=\chi ({\Gamma }^c({\mathbb{Z}}_{p^n}))=\omega ({\Gamma }^c({\mathbb{Z}}_{p^n}))=\{\begin{array}{cc}{p}^{n-1}-p^{\frac{n}{2}}+1\hfill & \text{if} n \text{is even};\hfill \\ p^{\frac{n-1}{2}}(p^{\frac{n-1}{2}}-1)\hfill & \text{if} n \text{is odd}.\hfill \end{array}$

Proof.

Case A: Let n be an even number.

Consider a map $f:V({\Gamma }^c({\mathbb{Z}}_{p^n}))\to \{2,3,4,\dots \}$ as follows: $$f(x_{ij})=\{\begin{array}{c}{p}_{ij}\hfill \\ \text{for} 1\le i\le (\frac{n}{2}-1),1\le j\le k_i;\hfill \\ {(p_{\frac{n}{2}})}^j\hfill \\ \text{for} i=\frac{n}{2},1\le j\le k_{\frac{n}{2}};\hfill \\ {[(p_{\frac{n}{2}})(\prod _{\mathcal{l}=1}^{k_{(\frac{n}{2}-1)}}{p}_{(\frac{n}{2}-1)\mathcal{l}})\dots (\prod _{\mathcal{l}=1}^{k_{n-i}}{p}_{(n-i)\mathcal{l}})]}^j\hfill \\ \text{for} \frac{n}{2}+1\le i\le n-1,1\le j\le k_i,\hfill \end{array}$$where p_ij and $p_{\frac{n}{2}}$ are distinct primes. Then, f is a coprime labeling of ${\Gamma }^c({\mathbb{Z}}_{p^n})$.

The number of distinct primes used in the coprime labeling $f=\left|V_1\right|+\left|V_2\right|+\dots +\left|V_{\frac{n}{2}-1}\right|+1=(p-1)p^{n-2}+(p-1)p^{n-3}+\dots +(p-1)p^{\frac{n}{2}}+1=(p-1)\{p^{n-2}+p^{n-3}+\dots +p^{\frac{n}{2}}\}+1=p^{n-1}-p^{\frac{n}{2}}+1=\alpha (\Gamma ({\mathbb{Z}}_{p^n}))=\omega ({\Gamma }^c({\mathbb{Z}}_{p^n})).$

Case B: Let n be an odd number.

Consider a map $f:V({\Gamma }^c({\mathbb{Z}}_{p^n}))\to \{2,3,4,\dots \}$ as follows: $$f(x_{ij})=\{\begin{array}{c}{p}_{ij}\hfill \\ \text{for} 1\le i\le \lfloor \frac{n}{2}\rfloor ,1\le j\le k_i;\hfill \\ {(\prod _{\mathcal{l}=1}^{k\lfloor \frac{n}{2}\rfloor }{p}_{\lfloor \frac{n}{2}\rfloor \mathcal{l}})}^j\hfill \\ \text{for} i=\lfloor \frac{n}{2}\rfloor +1,1\le j\le k_{(\lfloor \frac{n}{2}\rfloor +1)};\hfill \\ {[(\prod _{\mathcal{l}=1}^{k_{⏧\frac{n}{2}⏧}}{p}_{\lfloor \frac{n}{2}\rfloor \mathcal{l}})(\prod _{\mathcal{l}=1}^{k_{(\lfloor \frac{n}{2}\rfloor -1)}}{p}_{(\lfloor \frac{n}{2}\rfloor -1)\mathcal{l}})\dots (\prod _{\mathcal{l}=1}^{k_{n-i}}{p}_{(n-i)\mathcal{l}})]}^j\hfill \\ \text{for}\lfloor \frac{n}{2}\rfloor +2\le i\le n-1,1\le j\le k_i\hfill \end{array}$$where p_ij are distinct primes. Then, f is a coprime labeling of ${\Gamma }^c({\mathbb{Z}}_{p^n})$.

The number of distinct primes used in the coprime labeling $f=\left|V_1\right|+\left|V_2\right|+\dots +\left|V_{\lfloor \frac{n}{2}\rfloor }\right|=(p-1)p^{n-2}+(p-1)p^{n-3}+\dots +(p-1)p^{n-\lfloor \frac{n}{2}\rfloor -1}+1=(p-1)\{p^{n-2}+p^{n-3}+\dots +p^{n-(\frac{n-1}{2})-1}\}=(p-1)\{p^{n-2}+p^{n-3}+\dots +p^{\frac{n-1}{2}}\}=p^{n-1}-p^{\frac{n-1}{2}}=p^{\frac{n-1}{2}}\{p^{\frac{n-1}{2}}-1\}=\alpha (\Gamma ({\mathbb{Z}}_{p^n}))=\omega ({\Gamma }^c({\mathbb{Z}}_{p^n})).$ □

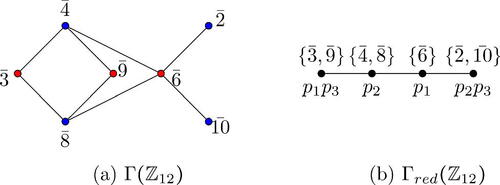
Remark 1.16.

(1) Note that $\omega (\Gamma ({\mathbb{Z}}_n))=\mu (\Gamma ({\mathbb{Z}}_n))$ may not be true, if $n\ne p^n$. In fact, it is not true for $n=12=2^2·3$. Consider the ring ${\mathbb{Z}}_{12}$. The zero-divisor graph $\Gamma ({\mathbb{Z}}_{12})$ and its reduced graph ${\Gamma }_{\mathit{red}}({\mathbb{Z}}_{12})$ are shown in Figure 3. Clearly, $\chi (\Gamma ({\mathbb{Z}}_{12}))=\omega (\Gamma ({\mathbb{Z}}_{12}))=2$. Define the function $f:V({\Gamma }_{\mathit{red}}({\mathbb{Z}}_{12}))\to \{2,3,\dots \}$ such that $f(\{\overline{3},\overline{9}\})=p_1{p}_3, f(\{\overline{4},\overline{8}\})=p_2, f(\{\overline{6}\})=p_1, f(\{\overline{2},\overline{10}\})=p_2{p}_3$, where $p_1,p_2,p_3$ are distinct primes. It is easy to verify that f is a coprime labeling of ${\Gamma }_{\mathit{red}}({\mathbb{Z}}_{12})$ and $\mu ({\Gamma }_{\mathit{red}}({\mathbb{Z}}_{12}))=3$. Hence, by Theorem 1.5, $\mu (\Gamma ({\mathbb{Z}}_{12}))=\mu ({\Gamma }_{\mathit{red}}({\mathbb{Z}}_{12}))=3$. Thus, $\omega (\Gamma ({\mathbb{Z}}_{12}))\ne \mu (\Gamma ({\mathbb{Z}}_{12}))$.

Fig. 3 Zero-divisor graph of ${\mathbb{Z}}_{12}$ and its reduced graph.

(2) Also, $\omega ({\Gamma }^c({\mathbb{Z}}_n))=\mu ({\Gamma }^c({\mathbb{Z}}_n))$ may not be true, if $n\ne p^n$. Consider the same example. Clearly, $\omega ({\Gamma }^c({\mathbb{Z}}_{12}))=4$. It is easy to check that ${\theta }_1((\Gamma ({\mathbb{Z}}_{12}))=8$. Therefore, $\mu ({\Gamma }^c({\mathbb{Z}}_{12}))=8$. Thus, $\omega ({\Gamma }^c({\mathbb{Z}}_{12}))\ne \mu ({\Gamma }^c({\mathbb{Z}}_{12}))$.

(3) Using similar techniques used in Theorems 1.12 and 1.15, it can be proved that the coprime index and the clique number coincide for the zero-divisor graph and the complement of the zero-divisor graph of a finite commutative special principal ideal ring.

We need the following definitions given in [10].

Let P be a poset. Given any $A\subseteq P$, the upper cone of A is given by $A^u=\{b\in P$ $:$ $a\le b$ for every $a\in A\}$ and the lower cone of A is given by $A^{\mathcal{l}}=\{b\in P$ $:$ $b\le a$ for every $a\in A\}$. If $a\in P$, then the sets ${\left\{a\right\}}^u$ and ${\left\{a\right\}}^{\mathcal{l}}$ will be denoted by a ${}^u$ and $a^{\mathcal{l}}$, respectively. By $A^{u\mathcal{l}}$, we mean ${\left\{A^u\right\}}^{\mathcal{l}}$. Dually, we have the notion of $A^{\mathcal{l}u}$.

Suppose that P is a poset with 0. If $\varnothing \ne A\subseteq P$, then the annihilator of A is given by $A^{\perp }=\{b\in P:{\{a,b\}}^{\mathcal{l}}=\{0\} \text{for} \text{all} a\in A\}$, and if $A=\left\{a\right\}$, then we write $a^{\perp }=A^{\perp }$. An element $a\in P$ is an atom if a > 0 and $\{b\in P$ $:$ $0<b<a\}=\varnothing$, and P is called atomic if for every $b\in P\setminus \left\{0\right\}$, there exists an atom $a\in P$ such that $a\le b$.

The direct product of posets $P_1,\dots ,P_n$ is the poset $\mathbf{P}={\prod }_{i=1}^n{P}_i$ with $\le$ defined such that $a\le b$ in P if and only if $a_i\le b_i$ (in P_i) for every $i\in \{1,\dots ,n\}$, where $a=(a_1,a_2,\dots ,a_n), b=(b_1,b_2,\dots ,b_n)$. For any $\varnothing \ne A\subseteq {\prod }_{i=1}^n{P}_i$, note that $A^u=\{b\in {\prod }_{i=1}^n{P}_i$ $:$ $a_i\le b_i$ for every $a\in A$ and $i\in \{1,\dots ,n\}\}$. Similarly, $A^{\mathcal{l}}=\{b\in {\prod }_{i=1}^n{P}_i$ $:$ $b_i\le a_i$ for every $a\in A$ and $i\in \{1,\dots ,n\}\}$.

Let $\mathbf{P}={\prod }_{i=1}^n{P}_i,(n\ge 2)$, where P_i’s are finite bounded posets such that $Z(P_i)=\left\{0\right\},\forall i$. Since P_i’s are finite bounded poset, P_i’s are atomic. Note that $Z(P_i)=0$ if and only if P_i has the unique atom. Further, assume that $q_i^{}\in P_i$ is the unique atom P_i for every i. It is not difficult to prove that $(q_1^{},0,\dots ,0),(0,q_2^{},0,\dots ,0),$ $\dots ,(0,\dots ,0,q_n^{})$ are the only n atoms of $\mathbf{P}$.

A poset P is called bounded if P has both the least element 0 and the greatest element 1.

Let P be a poset with 0. Define a zero-divisor of P to be any element of the set $Z(P)=\{a\in P$ $|$ there exists $b\in P\setminus \left\{0\right\}$ such that ${\{a,b\}}^{\mathcal{l}}=\left\{0\right\}\}$. As in [19], the zero-divisor graph of P is the graph G(P) whose vertices are the elements of $Z(P)\setminus \left\{0\right\}$ such that two vertices a and b are adjacent if and only if ${\{a,b\}}^{\mathcal{l}}=\left\{0\right\}$.

We set $\mathcal{D}=P\setminus Z(P)$. The elements $d\in \mathcal{D}$ are the dense elements of P. The zero-divisor graph $G^{*}(P)$ of P with vertex set is $P\setminus \{0,1\}$ and a and b are adjacent if and only if ${\{a,b\}}^{\mathcal{l}}=\left\{0\right\}$.

Throughout, P denotes a poset with 0 and q_i, $i\in \{1,2,\dots ,n\}$ are all atoms of P, where $n\ge 1$.

Afkhami et al. [3] partitioned the set $P\setminus \left\{0\right\}$ as follows.

Let $1\le i_1<i_2<\dots <i_k\le n$. The notation $P_{i_1{i}_2\dots i_k}$ stands for the set: $$\{x\in P : x\in {(\underset{s=1}{\overset{k}{\cap }}\{q_{i_s}\}}^u)\backslash {(\underset{j\in \{1,2,\dots ,n\}\backslash \{i_1,i_2,\dots ,i_k\}}{\cup }\{q_j\}}^u)\}.$$

In [3], the following observations are proved.

1. Let $\{i_1,\dots ,i_k\}$ and $\{j_1,\dots ,j_{k\prime }\}$ be the index sets of $P_{i_1{i}_2\dots i_k}$ and $P_{j_1{j}_2\dots j_{k\prime }}$, respectively. Then $(P_{i_1{i}_2\dots i_k})\cap (P_{j_1{j}_2\dots j_{k\prime }})=\varnothing$, if $\{i_1,\dots ,i_k\}\ne \{j_1,\dots ,j_{k\prime }\}$.

2. $P\backslash \left\{0\right\}={\cup }_{\stackrel{k=1,}{1\le i_1<i_2<\cdots <i_k\le n}}^n.P_{i_1{i}_2\dots i_k}$.

From the above two properties, it is clear that the sets $P_{i_1{i}_2\dots i_k}$ forms a partition of $P\setminus \left\{0\right\}$. In fact, one can see that a relation $\approx$ on $P\setminus \left\{0\right\}$ defined as follows: $x\approx y$ if and only if $x,y\in P_{i_1{i}_2\dots i_k}$ for some partition $P_{i_1{i}_2\dots i_k}$ of $P\setminus \left\{0\right\}$ is an equivalence relation.

The following discussion can be found in [17].

The set of equivalence classes under $\approx$ of $P\setminus \left\{0\right\}$ will be denoted by $[P]\prime =\{ P_{i_1{i}_2\dots i_k}:\{i_1,i_2\dots ,i_k\}\subseteq \{1,2,\dots ,n\} \text{and}{P}_{i_1{i}_2\dots i_k}\ne \varnothing \}$. Now, we set $[P]=[P]\prime \cup P_0$. We define relation $\le$ on $[P]$ as follows. $P_{i_1{i}_2\dots i_k}\le P_{j_1{j}_2\dots j_m}$ if and only if $b^{\perp }\subseteq a^{\perp }$, for some $a\in P_{i_1{i}_2\dots i_k}$ and for some $b\in P_{j_1{j}_2\dots j_m}$, where $P_{i_1{i}_2\dots i_k}, P_{j_1{j}_2\dots j_m}\in [P]\prime$ and $P_0\le P_{i_1{i}_2\dots i_k}$ for all $\{i_1,i_2,\dots ,i_k\}\subseteq \{1,2,\dots ,n\}$. It is not very difficult to prove that $([P], \le )$ is a poset. The least element of $([P],\le )$ is P₀, and if P has the greatest element 1, then the greatest element of the poset $([P],\le )$ is $P_{12\dots n}$. Sometimes, we abuse the notation and write $P_{i_1{i}_2\dots i_k}$ as P_I, where $I=\{i_1,i_2,\dots ,i_k\}$

Since $[P]$ is a poset with the least element $[0]=P_0$, and except $[d]$ (where $d\in \mathcal{D}$), every element of $[P]$ is a zero-divisor. Note that $\mathcal{D}$ may be empty. Hence the zero-divisor graphs $G([P])$ and $G^{*}([P])$ of the poset $[P]$ are same, that is, $G([P])=G^{*}([P])$. Hence afterwards, we write $G^{*}([P])$ for the zero-divisor graph of $[P]$. Clearly, a and b are adjacent in G(P) if and only if $[a]$ and $[b]$ are adjacent in $G^{*}([P])$. More about the inter-relationship between the properties of G(P) and $G^{*}([P])$ are mentioned in Lemma 1.17.

The following statements are essentially proved in [17] and will be used frequently in the sequel.

Lemma 1.17.

[17, Lemma 2.11] The following statements are true.

1. If $q_1,q_2,\dots ,q_n$ are distinct atoms of $P$, then $P_1,\dots ,P_n$ are distinct atoms of $[P]$.

2. The elements $P_{i_1{i}_2\dots i_k}\le P_{j_1{j}_2\dots j_m}$ in $[P]$ if and only if $\{i_1,i_2,\dots ,i_k\}\subseteq \{j_1,j_2,\dots ,j_m\}$.

3. The elements $P_{i_1{i}_2\dots i_k}$ and $P_{j_1{j}_2\dots j_m}$ are adjacent in $G^{*}([P])$ if and only if $\{i_1,i_2,\dots ,i_k\}\cap \{j_1,j_2,\dots ,j_m\}=\varnothing$. Further, $a\in V(G^{*}(P))$ if and only if $[a]\in V(G^{*}([P]))$.

4. Let $P_{i_1{i}_2\dots i_k}\in V(G^{*}([P]))$. Then for any $x,y\in P_{i_1{i}_2\dots i_k},{\{x,y\}}^{\mathcal{l}}\ne \left\{0\right\}$ in $P$. Hence, the vertices of $P_{i_1{i}_2\dots i_k}$ forms an independent set in $G^{*}(P)$. Further, if ${\{P_{i_1{i}_2\dots i_k},P_{j_1{j}_2\dots j_m}\}}^{\mathcal{l}}=\{[0]\}$ in $[P]$, then for any $x\in P_{i_1{i}_2\dots i_k}$ and for any $y\in P_{j_1{j}_2\dots j_m},{\{x,y\}}^{\mathcal{l}}=\left\{0\right\}$ in $P$. In particular, $P_{i_1{i}_2\dots i_k}$ and $P_{j_1{j}_2\dots j_m}$ are adjacent in $G^{*}([P])$ with $\left|P_{i_1{i}_2\dots i_k}\right|=r,\left|P_{j_1{j}_2\dots j_m}\right|=s$, then the vertices of $P_{i_1{i}_2\dots i_k}$ and $P_{j_1{j}_2\dots j_m}$ forms an induced complete bipartite subgraph $K_{r,s}$ of $G^{*}(P)$.

Theorem 1.18.

(Joshi [15, Corollary 2.11]) Let G(P) be the zero-divisor graph of an atomic poset P. Then $\chi (G(P))=\omega (G(P))=n$, where n is the finite number of atoms of P.

Theorem 1.19.

Let P be a finite poset with 0 and G(P) be its zero-divisor graph. Then $\mu (G(P))=\chi (G(P))=\omega (G(P))=$ Number of atoms of P.

Proof.

Let $q_1,q_2,\dots ,q_n$ be the all n atoms of P. Hence, $[P]$ will also have exactly n atoms $P_1,P_2,\dots ,P_n$. Then $V(G([P]))=\{P_I:(\varnothing \ne )I⊊\{1,2,\dots n\},P_I\ne \varnothing \}$. Since the zero-divisor graph $G([P])$ is nothing but the ${(G(P))}_{\mathit{red}}$ and $\chi (G([P]))=n$. Therefore, to prove $\chi (G(P))=\mu (G(P))$, it is enough to prove that $\mu (G([P]))=n$. Define a map $f:V(G([P]))\to \{2,3,4,\dots \}$ by $f(P_I)=\prod _{i\in I}{p}_i$, where $p_1,p_2,\dots ,p_n$ are distinct primes. We show that f is a coprime labeling of $G([P])$. By Lemma 1.17(3), P_I and P_J are adjacent in $G([P])$ if and only if $I\cap J=\varnothing$ if and only if $\prod _{i\in I}{p}_i$ and $\prod _{j\in J}{p}_j$ are coprime if and only if $f(P_I)$ and $f(P_J)$ are coprime. This proves f is a coprime labeling of $G([P])$ and $\mu (G([P]))=n$, i.e., $\mu (G([P]))=n=\mu (G(P))$, by Theorem 1.5. The result follows from Theorem 1.18. □

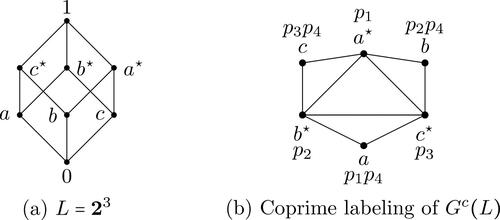
Remark 1.20.

Note that $\mu (G^c(P))=\omega (G^c(P))$ may not be true. Consider the Boolean lattice $L={\mathbf{2}}^3$ given in Figure 4. It is easy to check that $\omega (G^c(L))=3$, however, $\mu (G^c(L))=4$.

Fig. 4 Coprime labeling of the complement of zero-divisor graph.

Definition 1.21.

(West [23]) The disjoint union of graphs is an operation that combines two or more graphs to form a larger graph. It is analogous to the disjoint union of sets and is constructed by making the vertex set of the result be the disjoint union of the vertex sets of the given graphs and by making the edge set of the result be the disjoint union of the edge sets of the given graphs. Any disjoint union of two or more nonempty graphs is necessarily disconnected. If G and H are two graphs, then $G\cup H$ denotes their disjoint union.

Remark 1.22.

It is easy to observe that for any graph G, $\mu (G\cup I_m)=\mu (G)$, where I_m is an independent set with m vertices. In particular, $\mu (G^{*}(P))=\mu (G(P)\cup I_m)=\mu (G(P))$.

2 Applications

In this section, we show that various graphs associated with commutative rings with identity can be studied via zero-divisor graphs of specially constructed posets.

I. Zero-divisor graphs of finite reduced commutative rings

In [10], it is observed that if R is a reduced Artinian ring with exactly k prime ideals, then there exist fields $F_1,\dots ,F_k$ such that $R\cong F_1\times \cdots \times F_k$. Further, it is proved that the ring-theoretic zero-divisor graph $\Gamma (R)=\Gamma ({\prod }_{i=1}^k{F}_i)$ equals the poset-theoretic zero-divisor graph of R (R treated as a poset under the partial order given in [10, Lemma 3.3]), that is, $\Gamma ({\prod }_{i=1}^k{F}_i)=G({\prod }_{i=1}^k{F}_i)$ (cf. [18, Remark 3.4]).

Corollary 2.1. Let R be a finite reduced commutative ring with identity and $\Gamma (R)$ be its zero-divisor graph. Then $\mu (\Gamma (R))=\chi (\Gamma (R))=\omega (\Gamma (R))=$ Number of prime ideals of R.

II. Annihilating ideal graphs, Co-annihilating ideal graphs and Comaximal ideal graphs of commutative rings

Let R be a commutative ring with identity that is not an integral domain. An ideal I of a ring R is called an annihilating ideal if there exists $r\in R\setminus \left\{0\right\}$ such that $Ir=(0)$.

Definition 2.2.

(Visweswaran and Patel [22]) Let R be a commutative ring with identity. Associate a simple undirected graph with R, called as the annihilating ideal graph $\mathbb{A}\mathbb{G}(R)$ of R, where the vertices of $\mathbb{A}\mathbb{G}(R)$ are nonzero annihilating ideals of R and two vertices I and J are adjacent if and only if I + J is also an annihilating ideal of R.

The following is the modified definition of an annihilating ideal graph. The modified annihilating ideal graph $\mathbb{A}{\mathbb{G}}^{*}(R)$ be a simple undirected graph with vertex set $V(\mathbb{A}{\mathbb{G}}^{*}(R))$ is set of all nonzero proper ideals of R and two distinct vertices I, J are joined if and only if I + J is also an annihilating ideal of R. By [2, Lemma 2.1], I – J is an edge of $\mathbb{A}\mathbb{G}(R)$ if and only if $\mathit{Ann}(I) \cap \mathit{Ann}(J)\ne (0)$.

Let Id(R) be the set of all ideals of R. Consider an equivalence relation $\simeq$ on Id(R) such that $I\simeq J$ if and only if $\mathit{Ann}(I)=\mathit{Ann}(J)$. The equivalence class of an ideal I is the set $\{J\in Id(R)$ $:$ $I\simeq J\}$, denoted by $[I]$. The set of all equivalence classes of Id(R) is $\{ [I]$ $:$ $I\in Id(R) \}$, denoted by $[Id(R)]$. It is easy to observe that $[(0)]=\{(0)\}$ and $\mathit{Ann}(I)=(0)$, if $I\in [R]$.

Now, we define a relation $\le$ on $[Id(R)]$ such that $[I]\le [J]$ if and only if $\mathit{Ann}(I)\subseteq \mathit{Ann}(J)$. It is relatively easy to prove that $\le$ is a partial order on $[Id(R)]$. Thus, $([Id(R)],\le )$ is a poset. Since $\mathit{Ann}((0))=R$ and $\mathit{Ann}(R)=(0)$, then $[(0)]$ is the $\mathbf{1}$ and $[R]$ is the $\mathbf{0}$ of $([Id(R)],\le )$.

We construct a poset $\mathbb{P}$ from the poset $([Id(R)],\le )$. The elements $[(0)]$ and $[R]$ of the poset $([Id(R)],\le )$ are denoted by (0) and R respectively, in the poset $\mathbb{P}$. For any element $[I]\notin \{[(0)],[R]\}$ of $([Id(R)],\le )$, we replace the element $[I]$ of $([Id(R)],\le )$ by the chain of elements of the equivalence class $[I]$ in $\mathbb{P}$ whose length is equal to $|[I]|$ in some pre-determined well-order. Note that the element $[R]$ of $([Id(R)],\le )$ is replaced by the one element chain, namely R, in $\mathbb{P}$ irrespective of the cardinality of $[R]$. Clearly, every element $I\notin \{\mathbf{0},\mathbf{1}\}$ is an annihilating ideal of R. We call this poset the corresponding poset of the ring R.

We illustrate the above discussion with an example. Let $R=\frac{F_2[x,y]}{{(x,y)}^2}$, where F₂ is the field of two elements. We can check that, $Id(R)=\{(0),(x),(y),(x+y),(x,y),R\}$. Also, $[(x)]=[(y)]=[(x+y)]=[(x,y)]$. This gives, $[Id(R)]=\{[(0)],[(x)],[R]\}$. The Hasse diagrams of the ideal lattice $(Id(R),\le ),([Id(R)],\le )$ and the constructed poset $\mathbb{P}$ are shown in Figure 5.

Fig. 5 The ideal lattice and the corresponding poset.

From the construction mentioned above, the greatest element $\mathbf{1}$ and the least element $\mathbf{0}$ of a poset $\mathbb{P}$ are the ideals (0) and R, respectively. Let $I,J\in \mathbb{P}$. Clearly, I and J are comparable in $\mathbb{P}$ if and only if either I and J in the same equivalence class, or $[I]$ and $[J]$ are comparable in $([Id(R)],\le )$.

Remark 2.3.

(1) We observe that $\mathbb{P}$ is a meet-semi lattice. For this, let $I,J\in \mathbb{P}$. Since $[I+J]=\inf \{[I],[J]\}$, we have $([Id(R)],\le )$ is a meet-semi lattice. Further, the poset $\mathbb{P}$ is constructed from $([Id(R)],\le )$ by replacing the elements of $([Id(R)],\le )$ by the chains. Hence $\mathbb{P}$ is a meet-semi lattice.

(2) Let R be an Artinian ring. Hence $\mathit{Ann}(I)\cancel{=}(0)$ for every proper ideal I of R. Then the number of atoms of $\mathbb{P}$ is equal to the number of maximal ideals of R. For this, we prove that $[Id(R)]$ has $|\mathrm{Max}(R)|$ number of atoms given by $\{[M] : M\in \mathrm{Max}(R)\}$. Let $M_i,M_j\in \mathrm{Max}(R)$. Then $\mathit{Ann}(M_i+M_j)=\mathit{Ann}(R)=(0)=\mathit{Ann}(M_i)\cap \mathit{Ann}(M_j)$. Hence $\mathit{Ann}(M_i)⊈\mathit{Ann}(M_j)$ and $\mathit{Ann}(M_j)⊈\mathit{Ann}(M_i)$. Therefore, $[M_i]\nleqq [M_j]$ and $[M_j]\nleqq [M_i]$. Also, for any $(R\ne )I\in Id(R),I\subseteq M$ for some $M\in \mathrm{Max}(R)$. Therefore, $\mathit{Ann}(M)\subseteq \mathit{Ann}(I)$. Hence $[R]\cancel{=}[M]\le [I]$. This proves $\{[M] : M\in \mathrm{Max}(R)\}$ are all distinct atoms of $[Id(R)]$. Thus, by the construction of $\mathbb{P}$, the number of atoms of $\mathbb{P}$ is equal to the number of maximal ideals of R.

The elements I and J are adjacent in $G^{*}(\mathbb{P})$ if and only if ${\{I,J\}}^{\mathcal{l}}=\left\{0\right\}$ for $I,J\in V(G^{*}(\mathbb{P}))$. By Remark 2.3, I and J are adjacent in $G^{*}(\mathbb{P})$ if and only if $\mathit{Ann}(I)\cap \mathit{Ann}(J)=\mathit{Ann}(R)=(0)$. Note that, we can easily verify $\mathbb{A}\mathbb{G}(R)=G^{*c}(\mathbb{P})$ for the above example. With this preparation, we prove that the complement of an annihilating ideal graph of R is nothing but the zero-divisor graph of $\mathbb{P}$.

Lemma 2.4.

Let R be a commutative ring with identity that is not an integral domain, and let $\mathbb{P}$ be the corresponding poset of R. Then $\mathbb{A}{\mathbb{G}}^c(R)=G^{*}(\mathbb{P})$.

Proof.

First we prove that the vertex set of $\mathbb{A}{\mathbb{G}}^c(R)$ and $G^{*}(\mathbb{P})$ are equal. For this, let $I\in V(\mathbb{A}{\mathbb{G}}^c(R))$. Then I is an annihilating ideal of R, and I is an element of $\mathbb{P}$. Clearly, $I\notin [(0)]$ and $I\notin [R]$. This gives that $I\notin \{\mathbf{0},\mathbf{1}\}$. Therefore $I\in V(G^{*}(\mathbb{P}))$. This proves $V(\mathbb{A}{\mathbb{G}}^c(R))\subseteq V(G^{*}(\mathbb{P}))$.

Now, assume that $I\in V(G^{*}(\mathbb{P}))$. Clearly, $I\notin \{\mathbf{0},\mathbf{1}\}$. By the construction of $\mathbb{P}$, we have $[I]\ne [(0)]$ and $[I]\ne [R]$. Thus $\mathit{Ann}(I)\ne \mathit{Ann}(R)$ and $\mathit{Ann}(I)\ne \mathit{Ann}((0))$. This gives $\mathit{Ann}(R)=(0)⊊\mathit{Ann}(I)⊊R=\mathit{Ann}((0))$. As already observed $I\notin \{\mathbf{0},\mathbf{1}\}$ is an annihilating ideal of R, $I\in V(\mathbb{A}{\mathbb{G}}^c(R))$. This proves $V(G^{*}(\mathbb{P}))\subseteq V(\mathbb{A}{\mathbb{G}}^c(R))$. Thus, $V(\mathbb{A}{\mathbb{G}}^c(R))=V(G^{*}(\mathbb{P}))$.

Now, we prove that I and J are adjacent in $\mathbb{A}{\mathbb{G}}^c(R)$ if and only if I and J is adjacent in $G^{*}(\mathbb{P})$. For this, suppose that I and J are adjacent in $\mathbb{A}{\mathbb{G}}^c(R)$. By (1), I – J is an edge of $\mathbb{A}{\mathbb{G}}^c(R)$ if and only if $\mathit{Ann}(I)\cap \mathit{Ann}(J)=(0)=\mathit{Ann}(I+J)$. This implies $\inf \{I,J\}=I\wedge J=R$, where R is the zero of the meet-semi lattice $\mathbb{P}$. Thus, I and J are adjacent in $G^{*}(\mathbb{P})$.

Assume that I and J are adjacent in $G^{*}(\mathbb{P})$. This implies $\mathit{Ann}(I)\cap \mathit{Ann}(J)=(0)$. Thus, I and J are adjacent in $\mathbb{A}{\mathbb{G}}^c(R)$. This proves $\mathbb{A}{\mathbb{G}}^c(R)=G^{*}(\mathbb{P})$. □

Definition 2.5.

(Akbari et al. [4]) The co-annihilating-ideal graph of R, denoted by $\mathbb{C}\mathbb{A}{\mathbb{G}}^{*}(R)$, is a graph whose vertex set is the set of all nonzero proper ideals of R and two distinct vertices I and J are adjacent whenever Ann $(I)\cap$ Ann $(J)=(0)$.

Definition 2.6.

(Ye and Wu [24]) Let R be a commutative ring with identity. We associate a simple undirected graph with R, called the comaximal ideal graph $\mathbb{C}\mathbb{G}(R)$ of R, where the vertices of $\mathbb{C}\mathbb{G}(R)$ are the proper ideals of R that are not contained in the Jacobson radical J(R) of R and two vertices I and J are adjacent if and only if I + J = R.

The following is the modified definition of the comaximal ideal graph. The modified comaximal ideal graph $\mathbb{C}{\mathbb{G}}^{*}(R)$ is the graph with the vertex set as the nonzero proper ideals of R and two vertices I and J are adjacent if and only if I and J are comaximal. Clearly, one can see that the comaximal ideal graph $\mathbb{C}\mathbb{G}(R)$ is the subgraph of the modified comaximal ideal graph $\mathbb{C}{\mathbb{G}}^{*}(R)$. Moreover, $\mathbb{C}{\mathbb{G}}^{*}(R)=\mathbb{C}\mathbb{G}(R)\cup I_m$, where $m=|J(R)|-1$.

Corollary 2.7.

[4, Corollary 1.2] If R is an Artinian ring, then $\mathbb{C}{\mathbb{G}}^{*}(R)=\mathbb{C}\mathbb{G}(R)\cup I_m=\mathbb{C}\mathbb{A}{\mathbb{G}}^{*}(R)=\mathbb{A}{\mathbb{G}}^{*c}(R)=\mathbb{A}{\mathbb{G}}^c(R)$, where $m=|J(R)|-1$.

By Theorem 1.19, Remarks 1.22, 2.3(2), Lemma 2.4, Corollary 2.7, we have:

Corollary 2.8.

Let R be an Artinian ring with finitely many ideals. Then $\mu (\mathbb{C}\mathbb{G}(R))=\mu (\mathbb{C}\mathbb{A}{\mathbb{G}}^{*}(R))=\mu (\mathbb{A}{\mathbb{G}}^{*c}(R))=|\mathrm{Max}(R)|$.

III. Intersection graphs of ideals of Artinian principal ideal rings

Let R be a commutative ring with identity. Then the intersection graph of ideals $\mathbb{I}\mathbb{G}(R)$ of R is the graph whose vertices are the nonzero proper ideals of R such that distinct vertices I and J are adjacent if and only if $I\cap J\ne \left\{0\right\}$; see [9]. The vertex set of the zero-divisor graph $G^{*}(Id(R))$ of a lattice Id(R) is $Id(R)\setminus \{0_{Id(R)},1_{Id(R)}\}$, that is, the set of nonzero proper ideals of R. Therefore $V(\mathbb{I}\mathbb{G}(R))=V(G^{*}(Id(R)))=V(G^{*c}(Id(R)))$. The ideals I and J are adjacent in $G^{*}(Id(R))$ if and only if $I\wedge J=0_{Id(R)}$, that is, the ideals I and J are adjacent in $G^{*}(Id(R))$ if and only if $I\cap J=(0)$. The ideals I and J are adjacent in $G^{*c}(Id(R))$ if and only if $I\cap J\ne (0)$. Hence the following result.

Lemma 2.9.

Let R be a commutative ring with identity. Then $\mathbb{I}\mathbb{G}(R)=G^{*c}(Id(R))$.

The following discussion can be found in [10].

Let R be a commutative ring with identity. Recall that R is a special principal ideal ring (SPIR for brevity) if R is a local Artinian principal ideal ring (cf. [14]). If R is an SPIR with maximal ideal M, then there exists $n\in \mathbb{N}$ such that $M^n=\left\{0\right\},M^{n-1}\ne \left\{0\right\}$, and if I is an ideal of R, then $I=M^i$ for some $i\in \{0,1,\dots ,n\}$ ([14, Proposition 4]). In this case, M is nilpotent with an index of nilpotency equal to n, and the lattice of ideals of R is isomorphic to the chain C of length n (chain of n + 1 elements). By [14, Lemma 10], R is an Artinian principal ideal ring if and only if there exist SPIRs $R_1,\dots ,R_n$ such that $R\cong R_1\times \cdots \times R_n$ (it is also a straightforward consequence of the structure theorem of Artinian rings in [6, Theorem 8.7]). Thus, Id(R) of an Artinian principal ideal ring is product of chains $\mathbf{C}={\prod }_{i=1}^n{C}_i$ (C_i is chain of length n_i), where $R\cong R_1\times \cdots \times R_n$, nilpotency index of maximal ideal M_i of R_i is n_i. By Lemma 2.9 and from the above discussion, we have the following corollary.

Corollary 2.10.

Let R be an Artinian principal ideal ring. Then $\mu (\mathbb{I}{\mathbb{G}}^c(R))=|\mathrm{Max}(R)|$.

Acknowledgments

The authors are grateful to the referees for their suggestions which improved the presentation of the paper.

Additional information

Funding

The second author is financially supported by the Council of Scientific and Industrial Research(CSIR), New Delhi, via Senior Research Fellowship Award Letter No. 09/137(0620)/2019-EMR-I.