Additively graceful signed graphs

Abstract

Let $S=(V,E,\sigma )$ be a signed graph of order p and size q. Let $E^{+}:\{e\in E:\sigma (e)=+\},E^{-}=\{e\in E:\sigma (e)=-\},\left|E^{+}\right|=m$ and $\left|E^{-}\right|=n.$ Let $f:V\to \{0,1,2,\dots +\lceil \frac{n+1}{2}\rceil \}$ be an injective function and let $$g_f(uv)=\{\begin{array}{cc}|f(u)-f(v)|\hfill & \text{ if }uv\in E^{+}\hfill \\ f(u)+f(v)\hfill & \text{ if }uv\in E^{-}\hfill \end{array}$$

The function f is called an additively graceful labeling of S if $g_f(E^{+})=\{1,2,\dots ,m\}$ and $g_f(E^{-})=\{1,2,\dots ,n\}.$ In this paper we investigate the existence of additively graceful labeling of several classes of signed graphs.

KEYWORDS:

• Signed graph
• graceful graph
• additively graceful graph

AMS SUBJECT OF CLASSIFICATION:

• 05C 22
• 05C 78

1 Introduction

Unless mentioned otherwise, for standard terminology and notation in graph theory we follow West [7] and those for signed graphs (or, ‘sigraphs’ in short) we refer the reader to Chartrand [2] and Zaslavsky [8, 9].

A (p, q)-sigraph is an ordered pair $S=(G,s)$ where $G=(V,E)$ is a simple (p, q)-graph, called its underlying graph, and $s:E\to \{+,-\}$ is a function, called its signing function. Let $E^{+}(S)$ and $E^{-}(S)$ denote respectively the set of positive and the set of negative edges of S so that $E^{+}(S)\cup E^{-}(S)=:E(S)$ is the edge set of S. Further, if $|E^{+}(S)|=m$ and $|E^{-}(S)|=n$ such that m + n = q then S is called a (p, m, n)-sigraph. An all-positive sigraph S is one in which $E^{+}(S)=E(S)$ and an all-negative sigraph is one in which $E^{-}(S)=E(S)$. A sigraph is said to be homogeneous if it is either all-positive or all-negative, and heterogeneous otherwise.

An injection $f:V\to \{0,1,\dots ,q\}$ is said to be a graceful labeling if the induced edge function g_f defined by $g_f(uv)=|f(u)-f(v)|$ is a bijection from E to $\{1,2,\dots ,q\}$. The graph which admits such a labeling is called a graceful graph (see [4, 6]). Several classes of graceful and nongraceful graphs have been reported in the literature. For more details see Gallian [3].

Let $S=(V,E,\sigma )$ be a signed graph. Let $f:V\to \{1,2,\dots ,q\}$ be an injection and let g_f be defined on V by $g_f(uv)=\sigma (uv)|f(u)-f(v)|.$ If $g_f(E^{+})=\{1,2,\dots ,m\}$ and $g_f(E^{-})=\{-1,-2,\dots ,-n\},$ then f is called a graceful labeling of S. A sigraph S which admits such a labeling is called a graceful sigraph [4, 6].

Hegde [5] introduced the notion of additively graceful graph as follows: A (p, q)-graph $G=(V,E)$ with $q\ge 1$ and $p\ge 2$ is said to be additively graceful if it admits a labeling $f:V\to \{0,1,\dots ,\lceil \frac{(q+1)}{2}\rceil \}$ such that the edge induced labels defined by $f^{+}(uv)=f(u)+f(v)$ are all distinct, and $f^{+}:E\to \{1,2,\dots ,q\}$ is a bijection. He has characterized some additively graceful graphs, given a lower bound on number of edges of an additively graceful graph and some necessary or sufficient conditions for a graph to be additively graceful.

We extend this notion of additively graceful graphs to the realm of sigraphs as follows:

Definition 1.1.

Let $S=(V,E,\sigma )$ be a signed graph of order p and size q. Let $E^{+}:\{e\in E:\sigma (e)=+\},E^{-}=\{e\in E:\sigma (e)=-\},\left|E^{+}\right|=m$ and $\left|E^{-}\right|=n.$ Let $f:V\to \{0,1,2,\dots +\lceil \frac{n+1}{2}\rceil \}$ be an injective function and let $$g_f(uv)=\{\begin{array}{cc}|f(u)-f(v)|\hfill & \text{ if }uv\in E^{+}\hfill \\ f(u)+f(v)\hfill & \text{ if }uv\in E^{-}\hfill \end{array}$$

The function f is called an additively graceful labeling of S if $g_f(E^{+})=\{1,2,\dots ,m\}$ and $g_f(E^{-})=\{1,2,\dots ,n\}.$

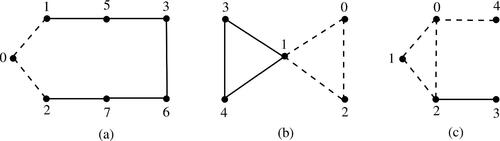
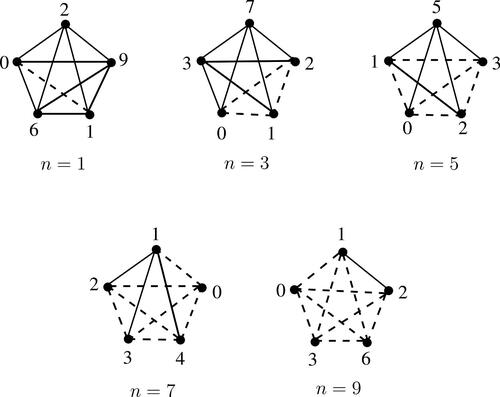
Example 1.2.

Figure 1 gives examples of additively graceful sigraphs. In the figure, dashed lines are negative edges and solid lines are positive edges.

Fig. 1 Additively graceful sigraphs

One can easily see that when n = 0, f is a graceful labeling of S, and when m = 0, f is an additively graceful labeling of S. We need the following theorems on graceful graphs and additively graceful graphs.

Theorem 1.3.

[4, 6] The complete graph K_n of order n is graceful if and only if $n\le 4$.

Theorem 1.4.

[4, 6] If G is an Eulerian (p, q)-graph with $q\equiv 1 \text{or} 2(\mathrm{mod}4)$ then G is not graceful.

Theorem 1.5.

[4] A necessary condition for a (p, q)-graph $G=(V,E)$ to be graceful is that it be possible to partition its vertex set $V:=V(G)$ into two subsets V_o and V_e such that there are exactly $\lceil q/2\rceil$ edges each of which joins a vertex of V_o with one of V_e.

Theorem 1.6.

[5] If G is an additively graceful (p, q)-graph then $q\ge 2p-4$ and this bound is the best possible.

Theorem 1.7.

[5] The complete graph K_p is additively graceful if and only if $2\le p\le 4$.

Theorem 1.8.

[5] An additively graceful graph is either K₂ or $K_{1,2}$ or has a triangle.

Theorem 1.9.

[5] If an Eulerian (p, q)-graph G is additively graceful then $q\equiv 0 \text{or} 3(\mathrm{mod}4)$.

Theorem 1.10.

[5] A unicyclic graph G is additively graceful if and only if G is isomorphic to either C₃ or to the graph obtained by joining a unique vertex to any one vertex of C₃.

In this paper we present several basic results on additively graceful sigraphs.

2 Basic results

Theorem 2.1.

Let S be an additively graceful sigraph with labeling f. Then there exists a partition of V(G) into V_o and V_e such that $m^{+}(V_o,V_e)=\lfloor \frac{m+1}{2}\rfloor$ and $m^{-}(V_o,V_e)=\lfloor \frac{n+1}{2}\rfloor$ where $m^{+}(V_o,V_e)$ and $m^{-}(V_o,V_e)$ are the number of positive and negative edges of S respectively each of which joins a vertex of V_o with one of V_e.

Proof.

Let $V_o=\{u\in V(S):f(u)\text{is odd}\}$ and $V_e=V(S)-V_o$. Therefore every edge receiving an odd label must join a vertex of V_o with one of V_e. Since the number of edges of S with odd positive labels is $\lfloor \frac{m+1}{2}\rfloor$ and the number of edges of S with odd negative labels is $\lfloor \frac{n+1}{2}\rfloor$, it follows that $m^{+}(V_o,V_e)=\lfloor \frac{m+1}{2}\rfloor$ and $m^{-}(V_o,V_e)=\lfloor \frac{n+1}{2}\rfloor$. □

Theorem 2.2.

Let S be a (p, m, n) additively graceful sigraph with labeling f. If n is odd, then $2m+n\ge 2p-3$ and if n is even, then $2m+n\ge 2p-4$ and the bounds are sharp.

Proof.

Since the highest vertex label is $m+\lceil \frac{n+1}{2}\rceil$, we have $$p-1\le m+\lceil \frac{n+1}{2}\rceil .$$

Now we have the following two cases:

Case 1:

n is odd.

Then $$p-1\le m+\frac{n+1}{2}.$$

Hence $$2p-2\le 2m+n+1.$$

Therefore $$2m+n\ge 2p-3.$$

The bound is sharp for the following infinite family of graphs when n is odd. Let $P:x,v_0,v_1,v_2,\dots ,v_{q-1}$ be a path of length q with one negative edge xv₀. Assign x the label 0. When i is even, assign v_i the label $1+\frac{i}{2}$ and if i is odd v_i is labeled $q-\frac{i-1}{2}$.

Case 2:

n is even.

Then $$p-1\le m+\frac{n}{2}+1.$$

Hence $$p-2\le \frac{2m+n}{2}.$$

Therefore $$2m+n\ge 2p-4.$$When n is even, the bound is sharp for the following infinite family of graphs. Consider the path $P:x,y,v_0,v_1,v_2,\dots ,v_{q-2}$ of length q where the edges xy and yv₀ are negative. Assign x and y the labels 1 and 0, respectively. For i even, assign v_i the label $2+\frac{i}{2}$ and for i odd, v_i is labeled $q-\frac{i-1}{2}$.

The result follows from Case 1 and Case 2. □

Corollary 2.3.

If S is an all negative sigraph which admits an additively graceful labeling then $n\ge 2p-4$.

Lemma 2.4.

If a sigraph S is additively graceful, then the sum of all edge labels of any circuit C in S is even.

Proof.

Let S be an additively graceful sigraph with an additively graceful labeling f. Let $P_1,P_2,\dots ,P_k$ and $Q_1,Q_2,\dots ,Q_k$ denote the positive and the negative sections of C respectively. For $1\le i\le k$, let $P_i=(a_{i,1},a_{i,2},\dots ,a_{i,r_i}),Q_i=(b_{i,1},b_{i,2},\dots ,b_{i,s_i})$. Where $a_{i,j},j=1,2,\dots ,r_i$ denote the vertices of the positive section P_i and $b_{i,t}$, $t=1,2,\dots ,s_i$ denote the vertices of the negative section Q_i. Let $a_{i,r_i}=b_{i,1}$ for $1\le i\le k$ and $b_{i,s_i}=a_{(i+1),1}$ for $1\le i\le k-1$. Since C is a cycle, we have $b_{k,s_k}=a_{1,1}$.

The sum of the edge labels on P_i and Q_i for $1\le i\le k$ is respectively, $$\sum _{j=1}^{r_i-1}|f(a_{i,j})-f(a_{i,(j+1)})|\equiv \left[f(a_{i,1})-f(a_{i,r_i})\right](\mathrm{mod} 2)$$and $$\sum _{j=1}^{s_i-1}\left[f(b_{i,j})+f(b_{i,(j+1)})\right]\equiv \left[f(b_{i,1})+f(b_{i,s_i})\right](\mathrm{mod} 2).$$

Hence if T denotes the sum of the edge labels of the edges of C, then $$\begin{array}{c}T\equiv \left\{\sum _{i=1}^k[f(a_{i,1})-f(a_{i,r_i})]+\sum _{i=1}^k[f(b_{i,1})+f(b_{i,s_i})]\right\}(\mathrm{mod} 2)\\ \equiv \{\sum _{i=1}^k[f(a_{i,1})-f(a_{i,r_i})]+\sum _{i=1}^{k-1}[f(a_{i,r_i})+f(a_{i+1,1})]\\ \hspace{1em}+[f(a_{k,r_k})+f(a_{1,1})]\}(\mathrm{mod} 2)\\ \equiv 2\left(f(a_{1,1})+f(a_{2,1})+\dots +f(a_{k-1,1})+f(a_{k,1})\right)(\mathrm{mod} 2)\\ \equiv 0(\mathrm{mod} 2).\end{array}$$

Therefore T is even. □

We have the following result from [4] as a corollary.

Corollary 2.5.

Let $G=(V,E)$ be a graph and $f:V\to \mathbb{N}$ be any function. Let $g_f(uv)=|f(u)-f(v)|$ for any edge uv of G. Then the sum of the edge labels of all the edges on any circuit of G is even.

Theorem 2.6.

The sigraph S obtained from the $(3,m,n)$-signed cycle $Z_3=(v_1,v_2,v_3,v_1)$ by adding k positive pendent edges $v_3{w}_1,v_3{w}_2,\dots ,$ $v_3{w}_k$ is additively graceful.

Proof.

There are three possibilities for the number of negative edges n in Z₃.

Case 1:

$n=3.$

Define $f:V(S)\to \{0,1,\dots ,k+2\}$ by $f(v_i)=i-1$ for i = 1, 2, 3 and $f(w_i)=i+2$ for $1\le i\le k$. This gives an additively graceful labeling of S.

Case 2:

$n=2.$ we have three sub-cases.

Case 2.1:

The edges $v_1{v}_2$ and $v_2{v}_3$ are negative.

Define $f:V(S)\to \{0,1,\dots ,k+3\}$ by $f(v_i)=i-1$ for i = 1, 2, 3 and $f(w_i)=i+3$ for $1\le i\le k$. This gives an additively graceful labeling of S.

Case 2.2:

The edges $v_1{v}_2$ and $v_1{v}_3$ are negative.

This sigraph is isomorphic to the one in Case 2.1 above and hence is additively graceful.

Case 2.3:

The edges $v_2{v}_3$ and $v_1{v}_3$ are negative.

This sigraph is not additively graceful. If it were, then the vertices $v_1,v_2,v_3$ would necessarily be labeled with the labels 2,1,0 respectively or with labels 1,2,0, respectively. Hence edge label 2 cannot be obtained on any of the pendent edges.

Case 3:

$n=1.$

Here also we have three sub-cases.

Case 3.1:

$v_1{v}_2$ is the negative edge.

Define $f:V(S)\to \{0,1,\dots ,k+3\}$ by $f(v_i)=i-1$ for i = 1, 2; $f(v_3)=k+2$ and $f(w_i)=i+1$ for $1\le i\le k$. This gives an additively graceful labeling of S.

Case 3.2:

$v_1{v}_3$ is the negative edge.

Define $f:V(S)\to \{0,1,\dots ,k+3\}$ by $f(v_i)=i$ for i = 1, 2; $f(v_3)=0$ and $f(w_i)=i+2$ for $1\le i\le k$. This gives an additively graceful labeling of S.

Case 3.3:

The edges $v_2{v}_3$ is negative.

This sigraph is isomorphic to the one in Case 3.2 above and hence is additively graceful. □

Theorem 2.7.

Let S be an additively graceful sigraph and let H be the subgraph induced by the set of all negative edges of S. The connected component of H which contains the vertex labeled by 0 is either a star or contains a triangle.

Proof.

Let C be the connected component of H which contains the vertex labeled by 0. Suppose C does not contain a triangle. Let u be a vertex of C with label 0 and let v₁ and v₂ be vertices adjacent to u in C with labels 1 and 2, respectively. Since $v_1{v}_2$ is not an edge in C, there exists a vertex v₃ with label 3 adjacent to u in C. Similarly if 4 is an edge label in C, then since $v_1{v}_3$ is not adjacent in C, there exists a vertex v₄ with label 4 adjacent to u in C. Also if 5 is an edge label of C, then since neither $v_1{v}_4$ nor $v_2{v}_3$ is an edge in C, there exists a vertex v₅ labeled 5 adjacent to u in C. Proceeding in this manner, we get that C is a star. □

3 Some additively graceful sigraphs

In this section, we present some results on additively graceful labeling of sigraphs on complete graphs, complete bipartite graphs and Eulerian graphs.

Theorem 3.1.

Let S be a (p, m, n)-Eulerian sigraph. A necessary condition for S to be additively graceful is that $m^2+n^2+m+n\equiv 0(\mathrm{mod}4)$.

Proof.

Let f be an additively graceful labeling of a (p, m, n)-Eulerian sigraph. Then the m positive edges are labeled as $1,2,\dots ,m$ and n negative edges are labeled as $1,2,\dots ,n$. Since sum of the edge labels along the Eulerian circuit is even, by Lemma 2.4, we have $\frac{m(m+1)}{2}+\frac{n(n+1)}{2}\equiv 0(\mathrm{mod}2).$ Hence $m^2+n^2+m+n\equiv 0(\mathrm{mod}4)$. □

Corollary 3.2.

If a (k, m, n)-signed cycle $Z_k, k=m+n\ge 3$ is additively graceful, then $m^2+n^2+m+n\equiv 0(\mathrm{mod}4)$.

Corollary 3.3.

If the signed cycle $Z_k,k=m+n\ge 3$ is such that $k\equiv 1(\mathrm{mod}4)$, then Z_k is not an additively graceful sigraph.

We have the following result from [1, 4, 6] as a corollary.

Corollary 3.4.

If S is a graceful Eulerian all-positive (p, m)-sigraph, then $m\equiv 0 \text{or} 3(\mathrm{mod}4)$.

We have the following result from [5] as a corollary.

Corollary 3.5.

If S is an additively graceful Eulerian all-negative (p, n)-sigraph, then $n\equiv 0 \text{or} 3(\mathrm{mod}4)$.

Theorem 3.6.

Let $p\ge 5$ be a positive integer such that none of p, p–2, p–4 is a perfect square. Then no sigraph on K_p is additively graceful.

Proof.

Suppose there exists a sigraph S on K_p which is additively graceful. By Theorem 2.1, there exists a partition of the vertex set V(S) into two subsets V_o and V_e such that $\left|V_o\right|=a,\left|V_e\right|=b$, a + b = p and $$ab=\lfloor \frac{m+1}{2}\rfloor +\lfloor \frac{n+1}{2}\rfloor .$$

For different parities of m and n we have the following three cases:

Case 1:

m and n are odd.

In this case, we have $$ab=\frac{m+1}{2}+\frac{n+1}{2}=\frac{m+n+2}{2}.$$

Hence $$2ab=m+n+2=\frac{p(p-1)}{2}+2.$$

Now $$|a-b|=\sqrt{{(a+b)}^2-4ab}=\sqrt{p-4}.$$

Since a–b is an integer it follows that p–4 is a perfect square, which is a contradiction.

Case 2:

One of m and n is odd and the other is even.

Without loss of generality, we assume that m is even and n is odd. In this case, we have $$ab=\frac{m}{2}+\frac{n+1}{2}=\frac{m+n+1}{2}.$$

Hence $$2ab=m+n+1=\frac{p(p-1)}{2}+1.$$

Now $$|a-b|=\sqrt{{(a+b)}^2-4ab}=\sqrt{p-2}.$$

Since a–b is an integer it follows that p–2 is a perfect square, which is a contradiction.

Case 3:

m and n are even.

In this case, we have $$ab=\frac{m}{2}+\frac{n}{2}=\frac{m+n}{2}.$$

Hence $$2ab=m+n=\frac{p(p-1)}{2}.$$

Now $$|a-b|=\sqrt{{(a+b)}^2-4ab}=\sqrt{p}$$

Since a–b is an integer it follows that p is a perfect square, which is a contradiction. □

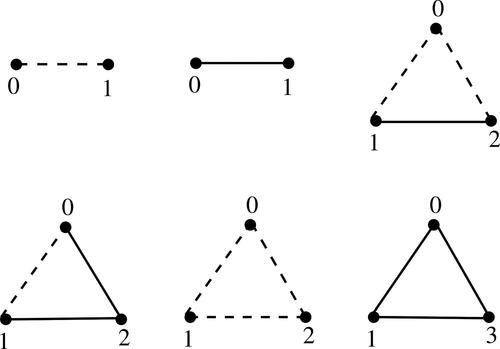
Lemma 3.7.

All sigraphs on $K_p,p\le 3$ are additively graceful.

Proof.

The additively graceful labeling of all sigraphs on $K_p,p\le 3$ are shown in Figure 2 □

Fig. 2 Additively graceful sigraphs on K₂ and K₃

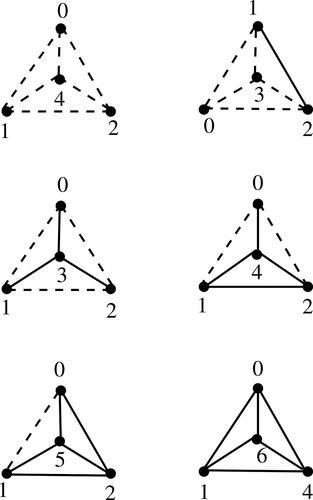
Lemma 3.8.

A (p, m, n)-sigraph S on K₄ is additively graceful if and only if either n = 0 or the subgraph H induced by the set of all negative edges is isomorphic to K₄, $K_4-e$, K₃, P₃ or P₂.

Proof.

If H is isomorphic to K₄, $K_4-e$, K₃, P₃ or P₂, then the labeling of S is given in Figure 3.

Fig. 3 Additively graceful sigraphs on K₄

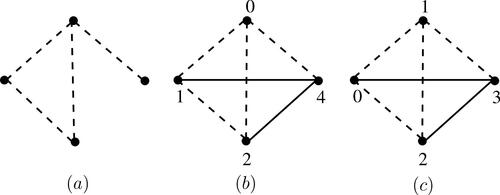
Conversely, suppose S is additively graceful. If n = 0, then there is nothing to prove. Hence we assume that n > 0. We claim that $n\ne 4$. Suppose n = 4. It follows from Theorem 2.7 that H is isomorphic to the graph given in Figure 4(a). There are exactly two possible labelings which give the set of induced edge labels $\{1,2,3,4\}$ for the negative edges in H and this labeling is given in Figure 4(b,c) . The set of induced positive edge labels is not equal to {1, 2}. Thus S is not additively graceful. Hence $n\ne 4$. If n = 6, then H = K₄ and if n = 5, then $H=K_4-e$. If n = 3, then it follows from Theorem 2.7 that $H=K_{1,3}$ or K₃. If $H=K_{1,3}$, then the centre of the star gets the label 0 and the 3 pendent vertices receive the labels 1, 2, 3. But in this case the set of labels of the positive edges is not equal to {1, 2, 3}. Hence, if n = 3, then H = K₃. If n = 2, then it follows from Theorem 2.7 that H = P₃. If n = 1, then H = P₂. □

Fig. 4 The subgraph H of K₄ induced by 4 negative edges and the corresponding labeling

Theorem 3.9.

If a sigraph on K_p, where $p=x^2,x^2+2,x^2+4$; x odd is additively graceful then the number of negative edges is

1. even for $p=x^2$

2. even or odd for $p=x^2+2$

3. odd for $p=x^2+4.$

Proof.

Let S be an additively graceful sigraph on K_p. Then by Theorem 3.1, we have $m^2+n^2+m+n\equiv 0(\mathrm{mod} 4)$. Since $q=m+n=\frac{p(p-1)}{2}$, substituting $m=(\frac{p(p-1)}{2}-n)$; where $p={(2s-1)}^2,{(2s-1)}^2+2$ or ${(2s-1)}^2+4$; $s=1,2,3,\dots$; we get for

Case 1:

$p={(2s-1)}^2$ $$\begin{array}{c}{\left(\frac{{(2s-1)}^2({(2s-1)}^2-1)}{2}-n\right)}^2+n^2+\frac{{(2s-1)}^2({(2s-1)}^2-1)}{2}\equiv 0(\mathrm{mod} 4)\\ \frac{{(2s-1)}^4{({(2s-1)}^2-1)}^2}{4}-{(2s-1)}^2({(2s-1)}^2-1)n+n^2+n^2+\frac{{(2s-1)}^2({(2s-1)}^2-1)}{2}\equiv 0(\mathrm{mod} 4)\\ {(2s-1)}^2({(2s-1)}^2-1)\left[\frac{{(2s-1)}^2({(2s-1)}^2-1)}{4}-n+\frac{1}{2}\right]+2n^2\equiv 0(\mathrm{mod} 4)\\ {(2s-1)}^2(4s^2-4s)\left[\frac{{(2s-1)}^2(4s^2-4s)}{4}-n+\frac{1}{2}\right]+2n^2\equiv 0(\mathrm{mod} 4)\end{array}$$hence, $${(2s-1)}^{2}4s(s-1)\left[{(2s-1)}^{2}s(s-1)-n+\frac{1}{2}\right]+2n^2\equiv 0(\mathrm{mod} 4)$$ therefore,

${(2s-1)}^{2}s(s-1)+n^2$ must be even. That is, n must be even.

Case 2:

$p={(2s-1)}^2+2$ $$\begin{array}{c}{\left(\frac{({(2s-1)}^2+2)({(2s-1)}^2+1)}{2}-n\right)}^2+n^2+\frac{({(2s-1)}^2+2)({(2s-1)}^2+1)}{2}\equiv 0(\mathrm{mod} 4)\\ \frac{{({(2s-1)}^2+2)}^2{({(2s-1)}^2+1)}^2}{4}-({(2s-1)}^2+2)({(2s-1)}^2+1)n+2n^2+\frac{({(2s-1)}^2+2)({(2s-1)}^2+1)}{2}\equiv 0(\mathrm{mod} 4)\\ ({(2s-1)}^2+2)({(2s-1)}^2+1)\left[\frac{({(2s-1)}^2+2)({(2s-1)}^2+1)}{4}-n+\frac{1}{2}\right]+2n^2\equiv 0(\mathrm{mod} 4)\end{array}$$hence, $$\begin{array}{c}({(2s-1)}^2+2)(4s^2-4s+2)\left[\frac{({(2s-1)}^2+2)(2s^2-2s+1)}{2}-n+\frac{1}{2}\right]+2n^2\equiv 0(\mathrm{mod} 4)\\ ({(2s-1)}^2+2)(2s^2-2s+1)[({(2s-1)}^2+2)(2s^2-2s+1)-2n+1]+2n^2\equiv 0(\mathrm{mod} 4)\end{array}$$

The product of the first two terms is

$({(2s-1)}^2+2)(2s^2-2s+1)=2l+1$, where $l=4s^4-8s^3+9s^2-5s+1$

Therefore, we have $$\begin{array}{c}(2l+1)[2l+2-2n]+2n^2\equiv 0(\mathrm{mod} 4)\\ (2l+1)[l+1-n]+n^2\equiv 0(\mathrm{mod} 2)\end{array}$$l being odd we conclude that n can be either even or odd.

Case 3:

$p={(2s-1)}^2+4$ $$\begin{array}{c}{\left(\frac{({(2s-1)}^2+4)({(2s-1)}^2+3)}{2}-n\right)}^2+n^2+\frac{({(2s-1)}^2+4)({(2s-1)}^2+3)}{2}\equiv 0(\mathrm{mod} 4)\\ \frac{{({(2s-1)}^2+4)}^2{({(2s-1)}^2+3)}^2}{4}-({(2s-1)}^2+4)({(2s-1)}^2+3)n+2n^2+\frac{({(2s-1)}^2+4)({(2s-1)}^2+3)}{2}\equiv 0(\mathrm{mod} 4)\\ ({(2s-1)}^2+4)({(2s-1)}^2+3)\left[\frac{({(2s-1)}^2+4)({(2s-1)}^2+3)}{4}-n+\frac{1}{2}\right]+2n^2\equiv 0(\mathrm{mod} 4)\end{array}$$

hence, $$({(2s-1)}^2+4)4(s^2-s+1)\left[({(2s-1)}^2+4)(s^2-s+1)-n+\frac{1}{2}\right]+2n^2\equiv 0(\mathrm{mod} 4)$$

Therefore,

$({(2s-1)}^2+4)(s^2-s+1)+n^2$ must be even.

Hence, n must be odd. □

Example 3.10.

Figure 5 gives the additively graceful labelings for the sigraphs on K₅ for $n=$1, 3, 5, 7, 9. In fact, it can be easily verified that these are the only sigraphs on K₅ which are additively graceful.

Fig. 5 Additively graceful sigraphs on K₅ for $n=1,3,5,7,9$

Theorem 3.11.

Let G be the complete bipartite graph $K_{s,t}$ with bipartition $V_1=\{v_1,v_2,\dots ,v_s\}$ and $V_2=\{w_1,w_2,\dots ,w_t\}$. Let S be the sigraph obtained from G by assigning negative sign to all edges incident with v₁ and positive sign to all other edges. Then S is additively graceful.

Proof.

Define $f:V\to \{0,1,\dots ,t(s-1)+\lceil \frac{(t+1)}{2}\rceil \}$ by $f(v_1)=0,f(w_i)=i$ for $i=1,2,\dots ,t$ and $f(v_i)=t(i-1)+1$ for $i=2,3,\dots ,s$. This gives an additively graceful labeling of S. □

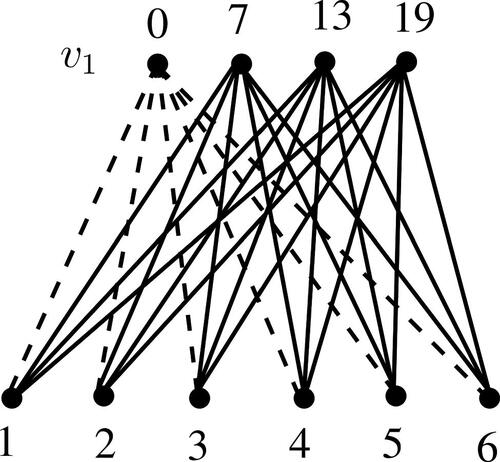
Example 3.12.

Figure 6 gives additively graceful labeling of the sigraph on $K_{4,6}$ with 6 negative edges incident on a single vertex.

Fig. 6 Additively graceful labeling of the sigraph on $K_{4,6}$

Theorem 3.13.

Let G be the complete bipartite graph $K_{2,2s+1}$ with bipartition $V_1=\{v_1,v_2\}$ and $V_2=\{w_1,w_2,\dots ,w_{2s+1}\}.$ Let S be the sigraph obtained from G by assigning positive sign to all but one edge. Then S is additively graceful.

Proof.

Let the negative edge be $v_1{w}_1$. Define $f:V\to \{0,1,\dots ,4s+2\}$ by $$\begin{array}{c}f(v_1)=0,f(v_2)=2 \text{and}\\ f(w_i)=\{\begin{array}{cc}1,\hfill & \hspace{1em}\text{for }i\text{=1};\hfill \\ 4s+9-4i,\hfill & \hspace{1em}\text{ for }2\le i\le s+1;\hfill \\ 8(s+1)-4i,\hfill & \hspace{1em}\text{ for }s+2\le i\le 2s+1.\hfill \end{array}\end{array}$$

It can be easily verified that f is an additively graceful labeling of S. □

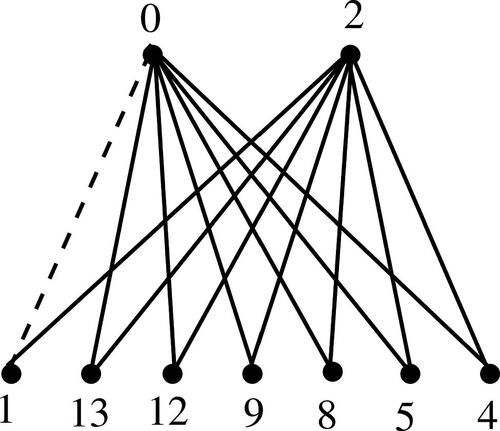
Example 3.14.

Figure 7 gives additively graceful labeling of the sigraph on $K_{2,7}$ with one negative edge.

Fig. 7 Additively graceful labeling of the sigraph on $K_{2,7}$

Theorem 3.15.

Let G be a star $K_{1,t}$ with bipartition $V_1=\left\{u\right\}$ and $V_2=\{w_1,w_2,\dots ,w_t\}$. Let S be the sigraph obtained from G by assigning positive sign to all but one edge. Then S is additively graceful.

Proof.

Let the negative edge be uw₁. Define $f:V\to \{0,1,\dots ,t\}$ by f(u) = 1, $f(w_1)=0$ and $f(w_i)=i, \text{for} 2\le i\le t.$ It can be easily verified that f is an additively graceful labeling of S. □

4 Conclusion and scope

In this paper, we have extended the concept of additively graceful graphs to the realm of sigraphs. We have obtained some necessary or sufficient conditions for additively graceful sigraphs and some results on Eulerian sigraph, complete bipartite sigraphs and complete sigraphs have also been obtained. One can investigate other classes of additively graceful sigraphs or characterize additively graceful sigraphs.

Acknowledgments

The authors are thankful to the two anonymous referees for their helpful suggestions, which resulted in improvement in the paper.