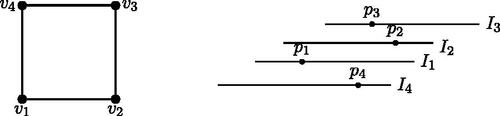On characterizing proper max-point-tolerance graphs

Abstract

Max-point-tolerance graphs (MPTG) were introduced by Catanzaro et al. in 2017 as a generalization of interval graphs. This graph class has many practical applications in the study of the human genome as well as in signal processing for networks. The same class of graphs was also studied by Soto and Caro in 2015 with a different name, p -BOX(1) graphs. In our article, we consider a natural subclass of max-point-tolerance graphs, namely, proper max-point-tolerance graphs (proper MPTG), where intervals associated with the vertices are not contained in each other properly. We present the first characterization theorem of this graph class by defining certain linear ordering on the vertex set. In the course of this study, we prove proper max-point-tolerance graphs are asteroidal triple-free, and perfect. We also find that proper max-point-tolerance graphs are equivalent to unit max-point-tolerance graphs. Further, we show that MPTG (proper MPTG) and max-tolerance graphs (proper max-tolerance graphs) are incomparable. In conclusion, we demonstrate relations between proper MPTG with other variants of MPTG and max-tolerance graphs.

KEYWORDS:

• Interval graph
• proper interval graph
• tolerance graph
• max-tolerance graph
• max-point-tolerance graph

2010 MSC:

• 05C62
• 05C75

1 Introduction

A graph $G=(V,E)$ is an interval graph if each vertex is mapped to an interval on real line in such a way so that any two of the vertices are adjacent if and only if their corresponding intervals intersect. Many people [5, 6] have done extensive research work on interval graphs for their worldwide practical applications in Computer Science and Discrete Mathematics. In 1962, Lekkerkerker and Boland [12] first characterized this graph class by proving it chordal and asteroidal triple-free. After that, many combinatorial problems, like the maximal clique problem, the independent set problem, the coloring problem, the domination problem, and most importantly, the recognition problem, have been solved in linear time for interval graphs.

Due to their significant applications in many theoretical and practical situations, interval graphs were generalized to several variations [1, 10, 14]. One of the most relevant variations of this graph class related to this article is tolerance graph which was first introduced by Golumbic and Monma [8] in 1982. A simple undirected graph $G=(V,E)$ is a min-tolerance graph (typically known as tolerance graph) if each vertex $u\in V$ corresponds to a real interval $I_u$ and a positive real number $t_u$, called tolerance, such that uv is an edge of G if and only if $|I_u\cap I_v|\ge \min \left\{t_u,t_v\right\}$. Golumbic and Trenk [9] introduced max-tolerance graphs where each vertex $u\in V$ corresponds to a real interval $I_u$ and a positive real number $t_u$ (known as tolerance) such that uv is an edge of G if and only if $|I_u\cap I_v|⩾\max \left\{t_u,t_v\right\}$. For max-tolerance graphs, we may assume $t_u\le \left|I_u\right|$ for each $u\in V$ since otherwise u becomes isolated. Max-tolerance graphs having a representation in which no interval properly contains another are called proper max-tolerance graphs. Some combinatorial problems, such as finding the maximal cliques, were obtained in polynomial time whereas the recognition problem was proved to be NP-hard [11] for max-tolerance graphs in 2006. Also, a geometrical connection of max-tolerance graphs to semi-squares was found by Kaufmann et al. [11]. The research work by Golumbic and Trenk [9] can be referred to for more information on tolerance graphs.

In 2015, Soto and Caro [15] introduced a new graph class, namely p -BOX graphs, where each vertex corresponds to a box and a point inside it in the Euclidean d-dimensional space. Any two vertices are adjacent if and only if each of the corresponding points is at the intersection of their respective boxes. When the dimension is one, this graph class is denoted by p-BOX(1). In 2017, Catanzaro et al. [3] studied these dimension one graphs independently by giving them a different name, max-point-tolerance graphs (MPTG) where each vertex $u\in V$ corresponds to a pair of an interval and a point $(I_u,p_u)$, where $I_u$ is an interval on the real line and $p_u\in I_u$, such that uv is an edge of G if and only if $\left\{p_u,p_v\right\}\subseteq I_u\cap I_v$. More precisely, each pair of intervals can “tolerate” a non-empty intersection without creating an edge as long as at least one distinguished point does not fall in the intersection. Then G is said to be represented by $\{(I_v,p_v)|v\in V\}$. They characterize MPTG by defining a special linear ordering to its vertex set. The graphs MPTG have a number of practical applications in human genome studies for DNA scheduling and in modeling telecommunication networks for sending and receiving messages [3]. Recently in [13] central-max-point-tolerance graphs (central MPTG) have been studied considering $p_u$ as the center point of $I_u$ for each $u\in V$. In the course of this research, the class of central MPTG is proven to be equivalent to unit max-tolerance graphs, where each interval possesses a unit length.

A natural and well-studied subclass of interval graphs is the class of proper interval graphs where no interval contains another properly. This graph class has various characterizations in terms of the linear ordering of its vertices, the consecutive 1’s property of its associated augmented adjacency matrix, the forbidden graph structure ($K_{1,3}$) etc [7]. It is known [2] that proper interval graphs are the same as unit interval graphs where each interval possesses the same length. So the natural question arises as to what will be the characterization of MPTG when the intervals are proper.

In this article, we introduce proper-max-point-tolerance graphs (proper MPTG). It is a MPTG having a representation where no interval is properly contained in another. We find this graph class to be asteroidal triple-free and perfect. We obtain the first characterization theorem of this graph class by introducing certain linear ordering on its vertex set, which can be an independent interest of study for the class of proper MPTG graphs. Interestingly, we note that interval graphs form a strict subclass of proper MPTG. Analogous to unit interval graphs, we define unit-max-point-tolerance graphs (unit MPTG) as a MPTG where all the intervals have equal length. Next, we show that proper MPTG graphs are the same as unit MPTG. We investigate the connection between max-tolerance graphs (proper max-tolerance graphs) and MPTG (proper MPTG) and be able to prove that these graph classes are incomparable. Incidentally, we settle a query raised in the book [9] by Golumbic and Trenk about whether unit max-tolerance graphs are the same as proper max-tolerance graphs or not. In the Conclusion section, we show the relations between the subclasses of MPTG and max-tolerance graphs related to proper MPTG.

2 Preliminaries

A matrix whose entries are only 0, 1 is a binary matrix. The augmented adjacency matrix of a simple undirected graph $G=(V,E)$ is obtained from the adjacency matrix of G by replacing 0’s by 1’s along the principal diagonal [7] and is denoted by $A^{\ast }(G)$ throughout the article.

The following characterization of MPTG is known:

Theorem 2.1.

[3, 13] Let $G=(V,E)$ be a simple undirected graph. Then the following are equivalent.

1. G is a MPTG.

2. There is an ordering of vertices such that for every quadruplet x, u, v, y the following condition holds: $$\text{If}x<u<v<y\text{ and }xv,uy\in E,\text{then}uv\in E.\mathrm{(}\text{Tex translation failed}\mathrm{)}$$ (2.1)

3. There is an ordering of vertices of G such that for any $u<v$, $u,v\in V$, (2.2) $$uv\notin E\Rightarrow uw\notin E\text{ for all }w>v\text{ or, }wv\notin E\text{ for all }w<u.$$(2.2)

4. There exists an ordering of vertices such that every 0 above the principal diagonal of the augmented adjacency matrix $A^{\ast }(G)$ has either all entries right to it are 0 (right open) or, all entries above it are 0 (up open).

If the vertices of G satisfy any of the aforementioned conditions with respect to a vertex ordering, then we call the ordering as MPTG ordering of G. One can verify that MPTG orderings need not be unique for G.

From [13] one can note that MPTG and max-tolerance graphs are not the same. In Theorem 2.4 we prove that these graph classes are incomparable. To obtain the proof, we need certain properties of proper max-tolerance graphs, as described in Corollary 2.3.

Observation 2.2.

Let $G=(V,E)$ be a proper max-tolerance graph. Then there exists a vertex ordering (${\prec }^{\ast }$) of V such that for every quadruplet $v_1,v_2,v_3,v_4$ the following holds: $$\begin{array}{c}\text{ If }{v}_1{\prec }^{\ast }{v}_2{\prec }^{\ast }{v}_3{\prec }^{\ast }{v}_4,v_1{v}_3,v_2{v}_4\in E\Rightarrow \\ v_2{v}_3\in E\text{ and }(v_1{v}_2\in E\text{ or }{v}_3{v}_4\in E\text{ or }{v}_1{v}_2,v_3{v}_4\in E).(2.3)\end{array}$$

Proof.

Let G be a proper max-tolerance graph with interval $I_i=[a_i,b_i]$ and tolerance $t_i$ for each vertex $v_i\in V$. Then arranging the intervals according to the increasing order of their left endpoints, one can show $b_2-a_3=b_2-a_4+a_4-a_3>t_2$ as $a_4>a_3$ and $v_2{v}_4\in E$. Again $b_2-a_3=b_2-b_1+b_1-a_3>t_3$ as $b_2>b_1$ and $v_1{v}_3\in E$. Therefore we get $|I_2\cap I_3|=b_2-a_3>\max \{t_2,t_3\}$ which imply $v_2{v}_3\in E$. Now if $v_1{v}_2\notin E$ then $b_1-a_2<t_1$ or $t_2$. If $b_1-a_2<t_1$ then $t_1>b_1-a_2>b_1-a_3\ge t_1$ introduces contradiction. Hence $b_1-a_2<t_2$. Thus we get $t_3\le b_1-a_3<b_1-a_2<t_2$. Again if $v_3{v}_4\notin E$ one can find $t_2<t_3$ which is again a contradiction. Hence the result follows. ▪

Corollary 2.3.

$K_{2,3}$ is not a proper max-tolerance graph.

Proof.

On the contrary, if $K_{2,3}$ is a proper max-tolerance graph, then one can find a vertex ordering (${\prec }^{\ast }$ say) from Observation 2.2 with respect to which the vertices of $K_{2,3}$ satisfies (2.3). Let $\{v_1,v_5\},\{v_2,v_3,v_4\}$ are two partite sets of it. Now if $v_1{\prec }^{\ast }{v}_5$. Then adjacency of vertices helps us to conclude that any two vertices from $\{v_2,v_3,v_4\}$ can not occur simultaneously within $v_1,v_5$ or left to $v_1$ or right to $v_5$ in ${\prec }^{\ast }$. Hence exactly one among them can occur within $v_1,v_5$ and between two other vertices, one (say $v_4$) occurs left to $v_1$ and the other (say $v_3$) occurs right to $v_5$ respectively. But again (2.3) gets contradicted for vertices $\{v_4,v_1,v_5,v_3\}$ as $v_1,v_5$ are nonadjacent. A similar contradiction will arise when $v_5{\prec }^{\ast }{v}_1$. ▪

Theorem 2.4.

Max-tolerance graphs and the class of max-point-tolerance graphs are not comparable.

Proof.

From [13] one can verify that the graph $G_2$ in Example 2.6 (see Figure 1) is a max-tolerance graph, which is not a MPTG. Now in Lemma 2.5 we prove $K_{m,n}$, $m,n\ge 13$ is not a max-tolerance graph. Next, in Lemma 2.6 we show that $K_{m,n}$ for any two positive integers m, n is a max-point-tolerance graph. Thus, $K_{m,n}$ for $m,n\ge 13$ and $G_2$ separate MPTG from max-tolerance graphs. Hence, these graph classes become incomparable. ▪

Figure 1: $G_2$ in Example 2.6 of [13].

We verify the proof of the aforementioned theorem with the help of the following lemmas:

Lemma 2.5.

Complete bipartite graph $K_{m,n}$ when $m,n\ge 13$ is not a max-tolerance graph.

Proof.

We assume on the contrary that $K_{m,n}$ for $m,n\ge 13$ is a max-tolerance graph with interval representation $\{I_v=[a_v,b_v]|v\in V\}$ and tolerance $t_v$ for each vertex $v\in V$ where the vertex set V is partitioned into two partite sets $V_1=\{x_1,\dots ,x_m\}$, $V_2=\{y_1,\dots ,y_n\}$ and E be the edge set of $K_{m,n}$.

Claim 1: No two intervals from same partite set can contain¹ an interval from other partite set.

proof:

On the contrary, we assume that $I_{x_1}$ and $I_{x_2}$ contain $I_{y_1}$. As $x_1{y}_1,x_2{y}_1\in E$, $\left|I_{y_1}\right|=|I_{x_1}\cap I_{y_1}|=|I_{x_2}\cap I_{y_1}|\ge t_{x_1},t_{x_2}$ from definition. Now if $|I_{x_1}\cap I_{x_2}|<t_{x_1}$ then $t_{x_1}\le \left|I_{y_1}\right|\le |I_{x_1}\cap I_{x_2}|<t_{x_1}$ as $I_{x_1},I_{x_2}\supseteq I_{y_1}$. Similar contradiction will arise if $|I_{x_1}\cap I_{x_2}|<t_{x_2}$. Hence, the claim is justified.

Claim 2: There always exist three vertices from each partite set whose corresponding intervals are not contained in each other. (we only need $m,n\ge 7$)

proof:

Note that $V_1,V_2$ are posets with respect to the interval containment relation. Hence, if our claim is not true, as $m,n\ge 7$ each poset must contain a totally ordered subset having cardinality at least 3. Let the totally ordered subset of $V_1$ be $\{I_{x_1},I_{x_2},I_{x_3}\}$ satisfying $I_{x_3}\subseteq I_{x_2}\subseteq I_{x_1}.$

We will show there can not be two intervals from $V_2$ that intersect $I_{x_1}$ at the same end (left or right). On the contrary, let $I_{y_1}$ and $I_{y_2}$ intersect $I_{x_1}$ in its left end and $b_{y_1}\le b_{y_2}$. Now as $I_{x_2}$ contained in $I_{x_1}$, $|I_{y_1}\cap I_{y_2}|\ge |I_{y_1}\cap I_{x_2}|\ge t_{y_1}$. Again $t_{y_2}\le |I_{y_2}\cap I_{x_2}|\le \left|I_{x_2}\right|=|I_{x_1}\cap I_{x_2}|<t_{x_1}$² $\le |I_{y_1}\cap I_{x_1}|\le |I_{y_1}\cap I_{y_2}|$. Hence it follows that $|I_{y_1}\cap I_{y_2}|\ge t_{y_1},t_{y_2}$ which is a contradiction as $y_1,y_2$ are nonadjacent.

Similarly, one can show that there can be at most one interval from $V_2$ that intersects $I_{x_2}$ at its same end. Now, as $n\ge 7$ there must exist atleast $n-2$ intervals corresponding to vertices of $V_2$ properly contained in $I_{x_2}$ which is not possible due to Claim 1. So the claim is true.

Since $\left|V_1\right|\ge 13(\ge 7)$ we can always choose three vertices $A=\{x_1,x_2,x_3\}$ from $V_1$ satisfying the conditions of Claim 2. Similarly, we choose vertices $B=\{x_4,x_5,x_6\}$ from $V_1\setminus A$ and $C=\{x_7,x_8,x_9\}$ from $(V_1\setminus A)\setminus B$ by observing $|V_1\setminus A|\ge 10$ and $|(V_1\setminus A)\setminus B|\ge 7$ respectively. Now as each $I_{x_i}$ for $1\le i\le 9$ can be contained in at most one $I_{y_j}$ from Claim 1, we can discard at most nine such $y_j$’s from $V_2$ where $1\le j\le n$. Again, as $n\ge 13$, if we discard these $y_j$’s from $V_2$ we can choose two vertices $y_{10},y_{11}$ (say) for which $I_{y_{10}}\cancel{\subset }{I}_{y_{11}}$ and $I_{y_{11}}\cancel{\subset }{I}_{y_{10}}$. Otherwise, $V_2$ becomes a totally ordered set having at least four $y_j$’s in it as $n\ge 13$. Now as $m\ge 13$, following proof of Claim 2 one can find a contradiction. Clearly $I_{x_i}\cancel{\subset }{I}_{y_{10}},I_{y_{11}}$ for $1\le i\le 9$. Again, as $I_{y_{10}}$ and $I_{y_{11}}$ can be contained in at most one interval of $V_1$ from Claim 1, between A, B, C we can always get one set C (say) for which $I_{y_{10}},I_{y_{11}}$ are not contained in any of the intervals of that set. Now it is easy to see $\{y_{10},y_{11}\}\cup C$ form $K_{2,3}$ for which no interval is contained in another. Therefore, they form an induced proper max-tolerance graph. But it can not be true from Corollary 2.3. ▪

Lemma 2.6.

$K_{m,n}$ is max-point-tolerance graph for all positive integers m, n.

Proof.

Let $V_1=\{x_1,\dots ,x_m\},V_2=\{y_1,\dots ,y_n\}$ be two partite sets of $K_{m,n}$. We assign intervals $I_{x_i}=[i,m+n+\frac{iϵ}{m}]$ and points $p_i=i$ for $1\le i\le m$ for vertices of $V_1$ and $I_{y_j}=[\frac{jϵ}{n},j+m]$ and points $p_j=j+m$ for $1\le j\le n$ for vertices of $V_2$ where $0<ϵ<1$. It is easy to check that the above assignment actually gives a max-point-tolerance representation of $K_{m,n}$. ▪

3 Proper max-point-tolerance graphs (proper MPTG)

Proposition 3.1.

If a graph G has a proper MPTG representation S, then G has a proper MPTG representation T in which all the points associated with each interval are distinct.

Proof.

Let $G=(V,E)$ be a proper MPTG and $S=\{(I_v,p_v)|v\in V\}$ be a proper MPTG representation of G where $I_v=[a_v,b_v]$ be an interval, and $p_v$ is a point within it. We arrange the intervals according to the increasing order of $p_v$’s, $p_1$ through $p_n$. We iterate the following rule at each shared point, moving from left to right until all $p_v$-values become distinct. Suppose $p_i$ is the smallest $p_v$-value shared by multiple points in S. Then $p_i=p_{i+1}=\cdots =p_m$. It is easy to see that there can be atmost two intervals having their endpoints as $p_i$ as the intervals are proper we can consider the interval endpoints to be distinct. If they are two in number, then one of them must be the left endpoint (say $a_{k_1}$), and another must be the right endpoint (say $b_{k_2}$). Take a positive value of $ϵ$ smaller than $\min \{d(p_m,p_{m+1}),d(p_m,a_k),d(p_m,b_{k^{\prime }})\}$ where $p_{m+1}$, $a_k$, $b_{k^{\prime }}$ are the associated points, left endpoint and right endpoint, respectively, occurred just after $p_m$ along the real line. To obtain a new proper MPTG representation T of G we assign $a_{k_1}=p_i$, $p_l=p_i+\frac{ϵ}{m-l+2}$ for all $i\le l\le m$, $b_{k_2}=p_i+ϵ$. It is easy to check now that the adjacencies remain intact and the intervals remain proper in T. ▪

Proposition 3.2.

Complete graphs $K_n$ for any positive integer n are proper MPTG.

Proof.

We give a proper MPTG representation of $K_n$ by assigning intervals $I_{v_k}=[a_k,b_k]$ and points $p_k$ for each vertex $v_k\in V$ where $1\le k\le n$. $I_{v_1}=[1+\frac{1}{n},n+1]$, $p_1=2$, $I_{v_2}=[1+\frac{2}{n},n+2]$, $p_2=2.5$ and $I_{v_i}=[1+\frac{i}{n},n+i]$, $p_i=i$ for $3\le i\le n$. ▪

Proposition 3.3.

Complete bipartite graphs $K_{m,n}$, for any positive integer m and n are proper MPTG.

Proof.

Follows from the same MPTG representation of $K_{m,n}$ given in Lemma 2.6. ▪

Proposition 3.4.

Caterpillars are proper MPTG.

Proof.

Let $G=(V,E)$ be a caterpillar³ with spine vertices $s_1,s_2,\dots ,s_k$ and additional vertices $a_1,a_2,\dots ,a_l$. Let $a_{k_{i-1}+1},\dots ,a_{k_i}$ be the vertices adjacent to the spine vertex $s_i$ where $1\le i\le k$, $k_0=0$ and $1\le k_i\le l$. We set intervals $I_{s_i}=[2i-3,2i+2]$ and points $p_{s_i}=2i$ for spine vertices where $1\le i\le k$ and intervals $I_{a_j}=[2i-3-\frac{n-j+1}{n+1},2i+\frac{2j}{2n+1}]$, points $p_{a_j}=2i+\frac{2j-1}{2n+1}$ for additional vertices adjacent to the spine vertex $s_i$ where $n=k_i-k_{i-1}$= number of vertices adjacent to $s_i$ and $1\le j\le n$. ▪

Let $N_G(x)$ $(N_G^{\prime }(x))$ be the set of all vertices that are adjacent (nonadjacent) to a vertex x of G. They are called neighbors (non neighbors) of x in G. The subgraph induced by neighbors of x in G is called neighborhood of x in G. An independent set of three vertices where each pair is joined by a path that avoids the neighborhood of the third is called an asteroidal triple. A graph is said to be asteroidal triple-free (AT-free) if it does not contain any asteroidal triple. For vertices u, v of a graph G, let $D(u,v)$ denote the set of vertices that intercepts (i.e., either the vertex is in the path or adjacent to some vertex of the path) all u, v paths. For vertices u, v, x of G, u and v are said to be unrelated to x if $u\notin D(v,x)$ and $v\notin D(u,x)$ [4].

Theorem 3.5.

[4] A graph G is asteroidal triple-free if and only if, for every vertex x of G, no component F of $N_G^{\prime }(x)$ contains unrelated vertices.

Lekkerkerker and Boland exhibited the importance of asteroidal triples in [12] by proving interval graphs to be chordal and AT-free. It was proved in [3] that interval graphs form a strict subclass of MPTG. But there are certain MPTG graphs that are not AT-free (see Figure 2). But interestingly, in the following lemma, we find the class of proper MPTG graphs to be asteroidal triple-free.

Figure 2: MPTG $G_1$ having asteroidal triple $\{v_1,v_2,v_3\}$.

Lemma 3.6.

If G is a proper MPTG then it is asteroidal triple-free.

Proof.

Let $G=(V,E)$ be a proper MPTG with representation $\{(I_v,p_v)|v\in V\}$ where $I_v=[a_v,b_v]$ be an interval and $p_v$ be a point within it. On contrary to Theorem 3.5 let’s assume there exists a vertex $x\in V$ and a component F of $N_G^{\prime }(x)$ containing a pair of unrelated vertices u, v (say). Let $P_1,P_2$ be two arbitrary paths of $D(x,v)$ and $D(x,u)$ respectively such that $u(v)$ is not adjacent to any vertex of $P_1(P_2)$ where $P_1=(x,v_1,\dots ,v_n=v),P_2=(x,u_1,\dots ,u_m=u)$.

Let $p_u,p_v$ occur on the same side of $p_x$ on the real line (say $p_u<p_v<p_x$). Now, if $p_{u_1}<p_v$ then $p_{u_1}<p_v<p_x$ clearly. Now as $u_1,x$ are adjacent (3.1) $$a_x\le p_{u_1}<p_v<p_x\le b_{u_1}$$(3.1)

which imply $p_v\in I_{u_1}\cap I_x$. But as v is not adjacent to $u_1,x$, $p_{u_1}<a_v<b_v<p_x$ imply $I_v⊊I_{u_1},I_x$ from (3.1), which is a contradiction as the intervals are proper. Again, if $p_{u_{m-1}}>p_v$ one can similarly find contradiction as $u_{m-1}u\in E$ and $vu,v{u}_{m-1}\notin E$. Hence $p_{u_{m-1}}(p_{u_1})$ must occur left (right) to $p_v$, i.e., $p_{u_{m-1}}<p_v<p_{u_1}$. Now, replacing u by $u_{m-1}$ and x by $u_1$ one can similarly find $p_{u_{m-2}}<p_v<p_{u_2}$. Hence, using the above technique for a finite number of times (as the length of $P_2$ is finite), one can get $p_{u_{m-k}}<p_v<p_{u_k}$ for some $1<k<m$ such that $u_k,u_{m-k}$ are adjacent in $P_2$. But this again introduces a similar contradiction.

Now consider the case when $p_u,p_v$ occur opposite to $p_x$ on the real line (say $p_u<p_x<p_v$). As F is a connected component of $N_G^{\prime }(x)$ there must exist a path $P=(u,\dots ,v)$ between u, v in F. It is easy to observe that $p_x$ must fall within an interval $I_k$ (say) for some vertex k of the path P. Again as k is not adjacent to x either $p_k<a_x$ or $p_k>b_x$. Now if $p_k<a_x$ then there must exist some vertices $k^{\prime },k^{\prime }+1$ in P such that $a_{k^{\prime }+1}\le p_{k^{\prime }}<a_x<b_x<p_{k^{\prime }+1}\le b_{k^{\prime }}$ where $k\le k^{\prime }<v$ in P, which imply $I_x⊊I_{k^{\prime }},I_{k^{\prime }+1}$, which is not true as the intervals are proper. One can find a similar contradiction when $p_k>b_x$. Hence we are done by Theorem 3.5. ▪

It is easy to observe following the above lemma that all trees are not proper MPTG although they are all MPTG [15]. Note that, it is not necessary that all AT-free graphs have to be perfect ($C_5$ is AT-free). However, in Theorem 3.10 we prove proper MPTG graphs to be perfect.

Lemma 3.7.

Let $C_n$ be a cycle of length n. Then $C_n,n\ge 5$ does not belong to the class of proper MPTG.

Proof.

Since proper MPTG graphs are AT-free following Lemma 3.6, $C_n,n\ge 6$ does not belong to the class of proper MPTG as $\{v_1,v_3,v_{n-1}\}$ form an asteroidal triple.

On the contrary, let $C_5=(V,E)$ has a proper MPTG representation $\{(I_v,p_v)|v\in V\}$ where $I_v=[a_v,b_v]$ be an interval and $p_v$ be a point within it. Let $\left\{v_i\right|1\le i\le 5\}$ be the vertices that occurred in a circularly consecutive way in clockwise (anticlockwise) order in $C_5$. Now if $p_1$ occurs between $p_2,p_5$ on the real line (say $p_2<p_1<p_5$) then as $v_2{v}_5\notin E$ either $p_2<a_5$ or $p_5>b_2$.

If $p_2<a_5$ then $a_1<a_5$ (as $v_1{v}_2\in E$) and hence $b_1<b_5$ as the intervals are proper. Thus we get $I_1\cap I_5=[a_5,b_1]$. Now as $v_4{v}_5\in E$, $p_4\in I_5$. Hence $p_2<a_5\le p_4$. If $p_4$ occurs left to $p_1$ then $p_4\in [a_5,p_1]$. But as $v_1{v}_4\notin E$, $b_4<p_1$ which imply $b_4<p_5$ which contradicts $v_4{v}_5\in E$. Hence $p_4>p_1$. Now, as $v_3$ is adjacent to both $v_2,v_4$, $[p_2,p_4]\subseteq I_3$. Therefore we get $p_1\in I_3$ as $p_2<p_1<p_4$. But as $v_1{v}_3\notin E$, either $p_3>b_1$ or $p_3<a_1$.

If $p_3>b_1$ then from the previous relations we get (3.2) $$a_3\le p_2<a_5<p_5\le b_1<p_3\le b_2.$$(3.2)

Hence $p_5\in I_3$ from (3.2). But as $v_3{v}_5\notin E$, $b_5<p_3$, which implies $I_5⊊I_3$ from (3.2), which is a contradiction as the intervals are proper. Again, if $p_3<a_1$ then $a_4\le p_3<a_1$ and therefore $b_4<b_1$. Combining, we get (3.3) $$a_4<a_1\le p_2<a_5\le p_1<p_5\le b_4<b_1.$$(3.3)

Hence $p_1\in I_4$ from (3.3). But as $v_1{v}_4\notin E$, $p_4>b_1$. Thus we get $I_1⊊I_4$ from (3.3), which is not true as the intervals are proper. One can similarly find contradiction when $p_5>b_2$.

Now if $p_2,p_5$ occurs on the same side of $p_1$ (say $p_2<p_5<p_1$) then $p_5\in [p_2,p_1]\subseteq I_1,I_2$. But as $v_2{v}_5\notin E$, $a_5>p_2$ and hence $a_5>a_1$ and therefore $b_5>b_1$ as the intervals are proper.Hence (3.4) $$I_1\cap I_5=[a_5,b_1].$$(3.4)

Now $v_4{v}_5\in E$ imply $p_4\in I_5$. Now if $p_4<b_1$ then $p_4\in I_1\cap I_5$. But as $v_1{v}_4\notin E$, $b_4<p_1<b_1$ which imply $a_4<a_1$. Hence, by combining, we get $a_4<a_1\le p_2<a_5\le p_5,p_4\le b_4<p_1\le b_2$. Thus $p_2\in I_4$ and $p_4\in I_2$, which is not true as $v_2{v}_4\notin E$.

Next, if $p_4>b_1$, then $b_4\ge p_4>b_1$ imply $a_4>a_1$. Hence, we get (3.5) $$a_1\le p_2<a_5\le p_5<p_1\le b_1<p_4\le b_4,b_5.$$(3.5)

Now, as $v_3$ is adjacent to $v_2,v_4$, $[p_2,p_4]\subseteq I_3$. This imply $p_5,p_1\in I_3$ from (3.5). But as $v_3{v}_5,v_1{v}_5\notin E$, $p_3\notin I_1,I_5$ and therefore does not belong to $I_1\cap I_5$. Hence $p_3<a_5$ or $p_3>b_1$ from (3.4).

Now if $p_3<a_5$ then $p_3<a_1$ from (3.5) as $p_3\notin I_1$. Hence, combining, we get $a_4\le p_3<a_1<b_1<p_4\le b_4$. This implies $I_1⊊I_4$ which is a contradiction. Again, if $p_3>b_1$ then $p_3>b_5$ as $p_3\notin I_5$ from (3.5). Now as $a_3\le p_2$ from (3.5) we get $I_5⊊I_3$ which is again not true as the intervals are proper. ▪

We note that the 4-wheel graph⁴ $W_4=K_4$ is a proper MPTG from Proposition 3.2. Again the 5-wheel graph $W_5$ is also a proper MPTG with representation $([30,130],80)$ for the center vertex u and $([20,120],50),([10,100],70)$, $([60,150],90)$, $([40,140],110)$ for other vertices.

Corollary 3.8.

The n-wheel graphs $W_n$ for $n\ge 6$ are not proper MPTG.

Proof.

If $W_n,n\ge 6$ be a proper MPTG then $W_n\setminus \left\{u\right\}$ would also be a proper MPTG where u is the central vertex of $W_n$. But this is not true from Lemma 3.7 as $W_n\setminus \left\{u\right\}=C_{n-1}$. ▪

Lemma 3.9.

$\overline{C_n},n\ge 7$ does not belong to the class of MPTG.

Proof.

One can note that $\{v_1,v_4,v_n,v_3\}$ form an induced 4-cycle (C say) in $\overline{C_n},n\ge 7$. From (2.1) one can find that in any MPTG ordering of vertices of C neither $\{v_1,v_n\}$ nor $\{v_4,v_3\}$ can sit together within the other.

Now if we consider $v_1\prec v_3\prec v_n\prec v_4$ in some MPTG ordering of C then it is easy to verify from (2.1) that when $n\ge 8$ neither $v_{n-3}$ nor $v_{n-2}$ can occur prior to $v_1$ or after $v_4$ as $v_{n-3},v_{n-2}$ are adjacent to $v_3,v_n$ respectively. Hence they have to sit within $v_1,v_4$. Now one can find contradiction from (2.1) applying it to the vertex set $\{v_1,v_{n-3},v_{n-2},v_4\}$ as $v_{n-3},v_{n-2}$ are nonadjacent. Similar contradictions will arise for other MPTG orderings of C. Again, for $n=7$ repeatedly applying (2.1) one can show there is no MPTG ordering of $\overline{C_7}$. ▪

From the aforementioned lemma, it is obvious that proper MPTG graphs can not contain $\overline{C_n},n\ge 7$ as an induced subgraph. Combining this fact with Lemma 3.7 one can conclude the following:

Theorem 3.10.

The class of proper MPTG graphs are perfect.

Definition 3.11.

Let $G=(V,E)$ be an undirected graph with a linear ordering (say $\mathrm{`}\mathrm{`}{<}^{″}$) on its vertex set V. We call such an ordering as proper MPTG ordering of V if it satisfies the following conditions.

1. For any $v_1,v_2,v_3\in V$, if $v_1<v_2<v_3$ and $v_1{v}_3\in E$, then $v_1{v}_2\in E$ or $v_2{v}_3\in E$. (3-point condition)

2. For any $v_1,v_2,v_3,v_4\in V$, if $v_1<v_2<v_3<v_4$ and $v_1{v}_3,v_2{v}_4\in E$, then $v_2{v}_3\in E$. (4-point   condition)

3. For any $v_1,v_2,v_3,v_4,v_5\in V$, if $v_1<v_2<v_3<v_4<v_5$ and $v_1{v}_4,v_2{v}_5\in E$, then $v_1{v}_3\in E$ or $v_3{v}_5\in E$ when $v_1{v}_2$ or $v_4{v}_5\in E$. (5-point condition-1)

4. For any $v_1,v_2,v_3,v_4,v_5\in V$, if $v_1<v_2<v_3<v_4<v_5$ and $v_1{v}_3,v_3{v}_5\in E$, then $v_1{v}_2\in E$ or $v_2{v}_4\in E$ or $v_4{v}_5\in E$. (5-point condition-2)

5. For any $v_1,v_2,v_j,v_k,v_5,v_6\in V$, if $v_1<v_2<v_j,v_k<v_5<v_6$ and $v_1{v}_j,v_j{v}_5,v_2{v}_k,v_k{v}_6\in E$ for some j, k such that $2<j,k<5$, then $v_1{v}_2\in E$ or $v_2{v}_5\in E$ or $v_5{v}_6\in E$. (6-point condition)

One can observe that any proper MPTG ordering is a MPTG ordering as it satisfies condition 2, which is the same as (2.1). Therefore, any graph satisfying a proper MPTG ordering must be a MPTG by Theorem 2.1. We now prove that proper MPTG graphs are characterized as graphs with proper MPTG orderings. In the following lemma, we present a necessary condition for proper MPTG graphs.

Lemma 3.12.

Let $G=(V,E)$ be a proper MPTG. Then G has a proper MPTG ordering of V.

Proof.

Let G be a proper MPTG with representation $\{(I_i,p_i)|i\in V\}$ where $I_i=[a_i,b_i]$ be an interval on the real line, and $p_i$ is a point within it. We arrange the vertices of V according to the increasing order of $p_i$’s. Let’s denote the ordering of V by “$<$”. We will show that with respect to this ordering all the conditions of Definition 3.11 hold true.

proof of condition $(1)$: Let $v_1<v_2<v_3$ for some $v_1,v_2,v_3\in V$ and $v_1{v}_3\in E$. Since $v_1{v}_3\in E$, $a_3\le p_1<p_2<p_3\le b_1$ which imply $p_2\in [p_1,p_3]\subseteq I_1,I_3$. Now if $v_1{v}_2,v_2{v}_3\notin E$, $p_1,p_3\notin I_2$ which imply $p_1<a_2$ and $b_2<p_3$ as $p_1<p_2<p_3$. Hence $a_3\le p_1<a_2<b_2<p_3$ which imply $[a_2,b_2]\subset [a_3,p_3]\subseteq I_3$ which contradicts that the intervals are proper. Hence the result follows. proof of condition $(2)$: Since G is a MPTG, this verification follows from the proof of Theorem 5.4 of [3]. proof of condition $(3)$: Let $v_1<v_2<v_3<v_4<v_5$ for some $v_1,v_2,v_3,v_4,v_5\in V$ and $v_1{v}_4,v_2{v}_5\in E$. Since $v_1{v}_4\in E$, $a_4\le p_1<p_2<p_3<p_4\le b_1$, which imply $p_2,p_3\in I_1,I_4$. Again as $v_2{v}_5\in E$, $a_5\le p_2<p_3<p_4<p_5<b_2$ which imply $p_3,p_4\in I_2,I_5$. Now if $v_1{v}_3,v_3{v}_5\notin E$, $p_1,p_5\notin I_3$ which imply $p_1<a_3$ and $b_3<p_5$ as $p_1<p_3<p_5$. If $v_1{v}_2\in E$ then $a_2\le p_1<a_3<b_3<p_5<b_2$ which imply $[a_3,b_3]\subset [a_2,b_2]$ which is a contradiction as the intervals are proper. Now if $v_4{v}_5\in E$ then $a_4\le p_1<a_3<b_3<p_5\le b_4$ imply $[a_3,b_3]⊊[a_4,b_4]$ which is again a contradiction as the intervals are proper. Thus, the condition holds true.

proof of condition $(4)$: Let $v_1<v_2<v_3<v_4<v_5$ for some $v_1,v_2,v_3,v_4,v_5\in V$ and $v_1{v}_3,v_3{v}_5\in E$. Since $v_1{v}_3\in E$ imply $a_3\le p_1<p_2<p_3\le b_1$. Therefore $p_2\in I_1\cap I_3$. Now if $v_1{v}_2\notin E$, then $a_2>p_1$ as $p_1<p_2$. Now as $v_3{v}_5\in E$, $a_5\le p_3<p_4<p_5\le b_3$. This imply $p_4\in I_3\cap I_5$. Now if $v_4{v}_5\notin E$, then $b_4<p_5$ as $p_4<p_5$. Now as $p_2,p_4\in I_3$ if $v_2{v}_4\notin E$ imply either $b_2<p_4$ or $p_2<a_4$ as $p_2<p_3<p_4$. If $b_2<p_4$ then $a_3\le p_1<a_2<b_2<p_4<p_5\le b_3$ which imply $[a_2,b_2]\subset [a_3,b_3]$ which is a contradiction as the intervals are proper. Again, if $p_2<a_4$ then $a_3\le p_1<p_2<a_4<b_4<p_5\le b_3$ which imply $[a_4,b_4]⊊[a_3,b_3]$ which is again a contradiction as the intervals are proper. Hence, the proof holds.

proof of condition $(5)$: Let $v_1<v_2<v_j,v_k<v_5<v_6$ for some $v_1,v_2,v_3,v_4,v_5,v_6\in V$ and $v_1{v}_j,v_j{v}_5,v_2{v}_k,v_k{v}_6\in E$ for some j, k such that $2<j,k<5$. Since $v_1{v}_j\in E$, $a_j\le p_1<p_2<p_j\le b_1$, which imply $p_2\in I_1,I_j$. Now if $v_1{v}_2\notin E$, then $a_2>p_1$ as $p_1<p_2$. Again as $v_k{v}_6\in E$, $a_6\le p_k<p_5<p_6\le b_k$, which imply $p_5\in I_k,I_6$. Now if $v_5{v}_6\notin E$, then $b_5<p_6$ as $p_5<p_6$. If $v_2{v}_5\notin E$ then either $p_2<a_5$ or $b_2<p_5$ as $p_2<p_5$. Now if $p_2<a_5$ then $a_k\le p_2<a_5\le p_j<p_5<b_5<p_6\le b_k$ as $v_2{v}_k,v_j{v}_5\in E$, which imply $[a_5,b_5]⊊[a_k,b_k]$ which is a contradiction as the intervals are proper. Again, if $b_2<p_5$ then $a_j\le p_1<a_2<b_2<p_5\le b_j$ as $v_j{v}_5\in E$, which imply $[a_2,b_2]⊊[a_j,b_j]$ which again contradicts that the intervals are proper. Hence the result follows.

Therefore, $<$ becomes a proper MPTG ordering of V. ▪

Definition 3.13.

Let $G=(V,E)$ be an undirected graph possessing a proper MPTG ordering (say $\sigma$) of V. From Theorem 2.1 it is clear that G is a MPTG with respect to $\sigma$. Let $\{(I_i,p_i)|i\in V\}$ be a MPTG representation of G. Below we define an order relation ${\prec }_{\sigma }$ among the right endpoints of each interval $I_i=[a_i,b_i]$ associated to every vertex of G when vertices are arranged in $\sigma$ order in $A^{\ast }(G)=(a_{i,j})$ along both rows and columns of it. For convenience, we shall use the symbol $\prec$ instead of ${\prec }_{\sigma }$.

Let $R_1,R_2$ be two partial order relations defined on the set $\left\{b_i\right|i\in V\}$. For $i<j$ in $A^{\ast }(G)$ we define,

$b_j{R}_1{b}_i$ if there exists some $k_2>j$ such that $a_{j,k_2}=0$⁵ and $a_{i,k_2}=1$ (3.6)

$b_j{R}_2{b}_i$ if there exists some $k_1<i$ such that $a_{k_1,i}=0$⁶ and $a_{k_1,j}=1.$ (3.7)

Now we define an order “$\prec$” between $b_i$’s in the following way. For $i<j$, (3.8) $$\begin{array}{c}{b}_j\prec b_i\text{ if }{b}_j{R}_1{b}_i\text{ or }{b}_j{R}_2{b}_i\text{ or }{b}_j{R}_1{b}_k\text{ and }{b}_k{R}_2{b}_i\text{ for some }\\ k\in V\text{ satisfying }i<k<j.\end{array}$$(3.8) (3.9) $$b_i\prec b_j\text{ otherwise}.$$(3.9)

We call the ordering “$\prec$” as proper MPTG endpoint ordering corresponding to the proper MPTG ordering $\sigma$ of V. It is important to note for $i<j$, $b_i\prec b_j$ whenever $a_{i,j}=0$. If not let $b_j\prec b_i$, then from the above definition of $\prec$, one of the following holds, $b_j{R}_1{b}_i$, $b_j{R}_2{b}_i$ or $b_j{R}_1{b}_k$ and $b_k{R}_2{b}_i$ for some $k\in V$ such that $i<k<j$. In the first two cases, condition 1 of Definition 3.11 and in the last case, condition 4 of Definition 3.11 gets contradicted.

In the following lemma, we will prove $\prec$ to be a total order⁷.

Lemma 3.14.

Let $G=(V,E)$ be an undirected graph that admits a proper MPTG ordering $\sigma$ of V, then the associated proper MPTG endpoint ordering ${\prec }_{\sigma }$ is a total order.

Proof.

Since $\sigma$ is a proper MPTG ordering of V, the associated proper MPTG end point ordering ${\prec }_{\sigma }=\prec$ is obtained by defining a certain linear order between all the $b_i$’s looking at the adjacency of the vertices in $A^{\ast }(G)=(a_{i,j})$ (see Definition 3.13) when the rows and columns of it are arranged according to $\sigma$ and $\{(I_i,p_i)|i\in V\}$ is the MPTG representation of G where $I_i=[a_i,b_i]$ and $p_i\in I_i$. Now to show $\prec$ is a total order, it is sufficient to prove “$\prec$” is transitive. Let $b_{i_1}\prec b_{i_2}$ and $b_{i_2}\prec b_{i_3}$. Below we will show $b_{i_1}\prec b_{i_3}$. Several cases may arise depending on the occurrence of $i_1,i_2,i_3$ in $\sigma$.

Case (i) ${\mathbf{i}}_{\mathbf{1}}<{\mathbf{i}}_{\mathbf{3}}<{\mathbf{i}}_{\mathbf{2}}$

We assume on contrary $b_{i_3}\prec b_{i_1}$. We use the following observations repeatedly for the rest of the proof.

Observations:

1. First we note $a_{i_3,i_2}=1$ as $i_3<i_2$.

2. Next $b_{i_3}{R}_1{b}_j$ for any $j<i_3$ imply existence of some ${\mathbf{k}}_{\mathbf{2}}^{\prime }>{\mathbf{i}}_{\mathbf{3}}$ such that $a_{i_3,k_2^{\prime }}=0,a_{j,k_2^{\prime }}=1$. Moreover, $k_2^{\prime }>i_2$ otherwise (2.1) gets contradicted for vertices $\{j,i_3,k_2^{\prime },i_2\}$.

3. Further, we see that $b_{i_2}{R}_1{b}_r$ for any $r<i_2$ imply the existence of some ${\mathbf{k}}_{\mathbf{2}}>{\mathbf{i}}_{\mathbf{2}}$ such that $a_{i_2,k_2}=0,a_{r,k_2}=1$. Note that if $b_{i_3}{R}_1{b}_j$ for any $j<i_3$ then if $k_2^{\prime }>k_2$, $a_{i_2,k_2^{\prime }}$ becomes zero as $a_{i_2,k_2}=0$ is right open, which helps us to conclude $b_{i_2}{R}_1{b}_j$ from (3.6).

4. Similarly, $b_l{R}_2{b}_{i_1}$ for any $l>i_1$ ensure the existence of some ${\mathbf{k}}_{\mathbf{1}}^{\prime }<{\mathbf{i}}_{\mathbf{1}}$ such that $a_{k_1^{\prime },i_1}=0,a_{k_1^{\prime },l}=1$.

5. Again $b_m{R}_2{b}_{i_3}$ for any $m>i_3$ ensure there is some ${\mathbf{k}}_{\mathbf{1}}<{\mathbf{i}}_{\mathbf{3}}$ satisfying $a_{k_1,i_3}=0,a_{k_1,m}=1$. We note that $k_1<i_1$ otherwise as $a_{k_1,i_3}=0$ is up open, $a_{i_1,i_3}$ becomes zero, which imply $b_{i_1}\prec b_{i_3}$ which is a contradiction. Now if $b_l{R}_2{b}_{i_1}$ holds for any $l>i_1$ then if $k_1<k_1^{\prime }<i_1$, $a_{k_1,i_1}$ becomes zero as $a_{k_1^{\prime },i_1}=0$ is up open, which implies $b_m{R}_2{b}_{i_1}$ from (3.7).

Main proof: Let $b_{i_2}{R}_1{b}_{i_3}$. Now if $b_{i_3}{R}_1{b}_j$ for any $j<i_3$ then we get $k_2^{\prime }$ must be greater than $k_2$ otherwise (2.1) gets contradicted for vertices $\{j,i_3,k_2^{\prime },k_2\}$. Hence, from observation 3 we get $b_{i_2}{R}_1{b}_j$.

Now if $b_{i_3}{R}_1{b}_{i_1}$ we get $b_{i_2}\prec b_{i_1}$ from last paragraph. Again if $b_{i_3}{R}_2{b}_{i_1}$ then $b_{i_2}\prec b_{i_1}$ follows from (3.8) as $b_{i_2}{R}_1{b}_{i_3}$ and $i_1<i_3<i_2$. Next, if $b_{i_3}{R}_1{b}_k$ and $b_k{R}_2{b}_{i_1}$ for some $k\in V$ such that $i_1<k<i_3$, we get $b_{i_2}{R}_1{b}_k$ from last paragraph. Hence from (3.8) we get $b_{i_2}{R}_1{b}_{i_1}$ as $b_k{R}_2{b}_{i_1}$ and $i_1<k<i_2$. Thus, all the above cases contradict our assumption.

Let $b_{i_2}{R}_2{b}_{i_3}$. If $b_{i_3}{R}_1{b}_{i_1}$ then $k_2^{\prime }>i_2$ from observation 2. Hence $a_{i_2,k_2^{\prime }}=1$ otherwise $b_{i_2}{R}_1{b}_{i_1}$ from (3.6) imply $b_{i_2}\prec b_{i_1}$ which is not true. Hence condition 3 of Definition 3.11 gets contradicted for vertices $\{k_1,i_1,i_3,i_2,k_2^{\prime }\}$. Again, if $b_{i_3}{R}_2{b}_{i_1}$ then from observation 5 if $k_1<k_1^{\prime }<i_1$ we get $b_{i_2}\prec b_{i_1}$ which is not true. Again, $k_1^{\prime }\ne k_1$ clearly. Hence $k_1^{\prime }<k_1$. But again (2.1) gets contradicted for vertices $\{k_1^{\prime },k_1,i_3,i_2\}$. Now if $b_{i_3}{R}_1{b}_k$ and $b_k{R}_2{b}_{i_1}$ for some $k\in V$ such that $i_1<k<i_3$. Then $a_{i_2,k_2^{\prime }}=1$ otherwise, we get $b_{i_2}{R}_1{b}_k$ which imply $b_{i_2}\prec b_{i_1}$ as $b_k{R}_2{b}_{i_1}$ and $i_1<k<i_2$. But we get a contradiction applying condition 3 of Definition 3.11 on vertices $\{k_1,k,i_3,i_2,k_2^{\prime }\}$.

Let $b_{i_2}{R}_1{b}_k$ and $b_k{R}_2{b}_{i_3}$ for some $k\in V$ such that $i_3<k<i_2$. Now if $b_{i_3}{R}_1{b}_j$ for any $j<i_3$ then if $k_2^{\prime }>k_2$, from observation 3 we get $b_{i_2}{R}_1{b}_j$.

Now if $b_{i_3}{R}_1{b}_{i_1}$ then if $k_2^{\prime }>k_2$ from last paragraph we get $b_{i_2}\prec b_{i_1}$ which is not true. Hence $i_2<k_2^{\prime }<k_2$. Again $a_{k,k_2^{\prime }}=1$ from (2.1) applying to the vertices $\{i_1,k,k_2^{\prime },k_2\}$. Hence condition 3 of Definition 3.11 gets contradicted for vertices $\{k_1,i_1,i_3,k,k_2^{\prime }\}$. Next if $b_{i_3}{R}_2{b}_{i_1}$ then if $k_1<k_1^{\prime }<i_1$ then from observation 5 we get $b_k{R}_2{b}_{i_1}$ and hence from (3.8) we find $b_{i_2}\prec b_{i_1}$ as $b_{i_2}{R}_1{b}_k$ and $i_1<k<i_2$. Again when $k_1^{\prime }<k_1$, (2.1) gets contradicted for vertices $\{k_1^{\prime },k_1,i_3,k\}$. Now let $b_{i_3}{R}_1{b}_{k^{\prime }}$ and $b_{k^{\prime }}{R}_2{b}_{i_1}$ for some $k^{\prime }\in V$ satisfying $i_1<k^{\prime }<i_3$. As $b_{i_3}{R}_1{b}_{k^{\prime }}$ then if $k_2^{\prime }>k_2$ then from the last paragraph we get $b_{i_2}{R}_1{b}_{k^{\prime }}$ which helps us to conclude from (3.8) $b_{i_2}\prec b_{i_1}$ as $b_{k^{\prime }}{R}_2{b}_{i_1}$. Hence $i_2<k_2^{\prime }<k_2$. Thus, in this case, condition 3 of Definition 3.11 gets contradicted for vertices $\{k_1,k^{\prime },i_3,k,k_2^{\prime }\}$ (note $a_{k,k_2^{\prime }}=1$ otherwise (2.1) gets contradicted for vertices $\{k^{\prime },k,k_2^{\prime },k_2\}$).

The verification of other cases is also long and rigorous. Therefore, we put them in Appendix. ▪

Definition 3.15.

Let $G=(V,E)$ be a MPTG having representation $\{([a_i,b_i],p_i)|i\in V\}$ satisfying a proper MPTG ordering $\sigma$ of V. Then from Definition 3.13 and Lemma 3.14 it follows that by observing the adjacencies of the vertices in $A^{\ast }(G)$ one can find a total order $\prec$ between all $b_i$’s in such a way that they can be put together in a single sequence $P_1$ (say). Next, we arrange $a_i$’s in a single sequence $P_2$ (say) in the same order. Let $\left|V\right|=n$. Then

$P_1:b_{{\alpha }_1}\prec b_{{\alpha }_2}\prec \cdots \prec b_{{\alpha }_n}$ and $P_2:a_{{\alpha }_1}\prec a_{{\alpha }_2}\prec \cdots \prec a_{{\alpha }_n}$ where $1\le {\alpha }_i\le n$.

We now combine $a_i,b_i,p_i$’s in a single sequence P by following the rule. Henceforth, we call P by canonical sequence corresponding to $\sigma$.

1. First, we place all $p_i$’s on the real line according to the occurrence of i’s in $\sigma$.

2. Now, using induction, starting from the last element of $P_2$ until the first element is reached, we place $a_i$’s on the real line in the following way.

We first place $a_{{\alpha }_n}$ between $p_{{({\alpha }_n)}_1-1}$ and $p_{{({\alpha }_n)}_1}$. Now for $a_{{\alpha }_k}$ if ${({\alpha }_k)}_1\ge {({\alpha }_{k+1})}_1$ then we place $a_{{\alpha }_k}$ just before $a_{{\alpha }_{k+1}}$, place $a_{{\alpha }_k}$ between $p_{{({\alpha }_k)}_1-1}$ and $p_{{({\alpha }_k)}_1}$ otherwise, where ${({\alpha }_i)}_1$ is the first column containing 1 in the ${\alpha }_i$th row in $A^{\ast }(G)$.

1. Again using induction, starting from the first element of $P_1$ until the last element is reached, we place $b_i$’s on the real line by following the rule.

First we place $b_{{\alpha }_1}$ between $p_{{({\alpha }_1)}_2}$ and $p_{{({\alpha }_1)}_2+1}$. Now for $b_{{\alpha }_k}$ if ${({\alpha }_k)}_2\le {({\alpha }_{k-1})}_2$ then we place $b_{{\alpha }_k}$ just after $b_{{\alpha }_{k-1}}$, place $b_{{\alpha }_k}$ between $p_{{({\alpha }_k)}_2}$ and $p_{{({\alpha }_k)}_2+1}$ otherwise where ${({\alpha }_i)}_2$ is the last column containing 1 in the ${\alpha }_i$th row in $A^{\ast }(G)$.

From the construction of P one can verify that if more than one $b_i(a_i)$’s occurs between two $p_i$’s then they are arranged according to their occurrence in $P_1(P_2)$ respectively. Again, it is easy to check that the order of the sequences $P_1,P_2$ get preservedin P.

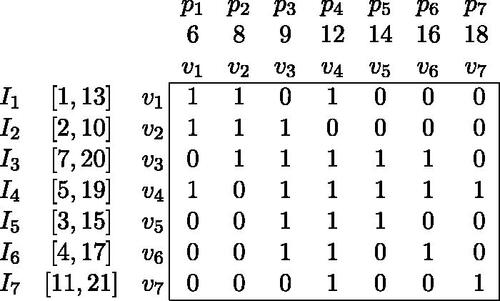
Example 3.16.

Consider the MPTG $G=(V,E)$ in Figure 3 whose augmented adjacency matrix $A^{\ast }(G)$ is arranged according to a proper MPTG ordering $\sigma =(v_1<v_2<\cdots <v_7)$ of V. One can note that all the conditions of Definition 3.11 are satisfied by $\sigma$. A MPTG representation of G is provided by assigning an interval $I_i=[a_i,b_i]$ and a point $p_i$ within $I_i$ corresponding to each vertex $v_i$ where $1\le i\le 7$. Now looking at the adjacencies of the vertices in $A^{\ast }(G)$ we construct $P_1,P_2$ sequences of endpoints $b_i,a_i$ respectively, according to the construction described in Definition 3.15.

Figure 3: Augmented adjacency matrix $A^{\ast }(G)$ of a proper MPTG G.

$P_1:b_2\prec b_1\prec b_5\prec b_6\prec b_4\prec b_3\prec b_7$.

$P_2:a_2\prec a_1\prec a_5\prec a_6\prec a_4\prec a_3\prec a_7$.

The combined sequence of $a_i,p_i,b_i$ is $P:a_2{a}_1{a}_5{a}_6{a}_4$ $p_1{a}_3{p}_2{p}_3{b}_2{a}_7{p}_4{b}_1{p}_5{b}_5{p}_6{b}_6{p}_7{b}_4{b}_3{b}_7$.

We now present the main theorem of our article, which characterizes a proper max-point-tolerance graph.

3.1 Characterization of proper MPTG

Theorem 3.17.

Let $G=(V,E)$ be an undirected graph. Then G is a proper MPTG if and only if it satisfies a proper MPTG ordering of V.

Proof.

Let $G=(V,E)$ be a proper MPTG. Then it satisfies a proper MPTG ordering of V following Lemma 3.12.

Conversely, let G possess a proper MPTG ordering (say $\sigma$) of V. Then it satisfies all the conditions of Definition 3.11 with respect to $\sigma$. Let the augmented adjacency matrix of G, i.e., $A^{\ast }(G)=(a_{ij})$ is arranged according to $\sigma$. Then, from Theorem 2.1 G becomes a MPTG with respect to $\sigma$. Let $[a_i,b_i]$ be the interval and $p_i$ be a point within it associated with each vertex $i\in V$ in its MPTG representation. Now, from the adjacencies of the vertices in $A^{\ast }(G)$ we define a proper MPTG endpoint ordering ${\prec }_{\sigma }=\prec$ among $b_i$’s as described in Definition 3.13. Moreover, in Lemma 3.14 we prove $\prec$ as a total order. Next, we construct sequences $P_1(P_2)$ consists of $b_i(a_i)$ as described in Definition 3.15. Then we construct the canonical sequence P corresponding to $\sigma$, which is basically a combined sequence containing all $a_i,b_i,p_i$’s. Now we associate the numbers 1 to 3n ($\left|V\right|=n$) to P starting from the first element of it, and define $I_i=[\overline{a_i},\overline{b_i}]$ and $p_i=\overline{p_i}$ where $\overline{a_i},\overline{b_i},\overline{p_i}$ denote the numbers associated to $a_i,b_i,p_i$ in P. Below we prove $\{(I_i,p_i)|i\in V\}$ will actually give a proper MPTG representation of G.

Step 1. First we verify that the intervals $I_i$ are proper.

First, we show $a_i<b_i$ for each i in P. From the construction of P one can easily check that each $a_i$ is placed left to $p_{{(i)}_1}$ and each $b_i$ is placed right to $p_{{(i)}_2}$ where ${(i)}_1,{(i)}_2$ denote columns containing the first and last 1 in i th row of $A^{\ast }(G)$. Now as $p_{{(i)}_1}<p_i<p_{{(i)}_2}$ in P, $a_i<b_i$.

Since $b_i,a_i$’s are arranged in $P_1,P_2$ in the same order, and they individually keep their orderings intact in P, no interval can be contained in another. Hence the intervals $\{I_i=[\overline{a_i},\overline{b_i}]|i\in V\}$ are proper with respect to our given representation.

Step 2. Note that $a_i<p_i<b_i$ in P as ${(i)}_1\le i\le {(i)}_2$ from Definition 3.15.

Step 3. Next, we verify that $([\overline{a_i},\overline{b_i}],\overline{p_i})$ is the proper MPTG representation of G.

For this, it is sufficient to show that, with respect to the above representation, $A^{\ast }(G)$ satisfies all of its adjacency relations.

Case (i): We show that $a_{i,j}=1$ imply $p_i,p_j\in I_i\cap I_j$.

Let for $i<j$, $a_{i,j}=1$. If $b_i\prec b_j$ in $P_1$ (i.e., $a_i\prec a_j$ in $P_2$) then as ${(j)}_1\le i$, $a_j<p_i$ in P. Again as ${(i)}_2>j$, $p_j<b_i$ in P. Further, if $b_j\prec b_i$ in $P_1$ (i.e., $a_j\prec a_i$ in $P_2$) then as ${(j)}_2\ge j$, $b_j>p_j$ in P. Again, ${(i)}_1\le i$ imply $a_i<p_i$. Now as the order of the elements of $P_1,P_2$ remains intact in P we get $p_i,p_j\in I_i\cap I_j$.

Case (ii): Next, we show that $a_{i,j}=0$ imply either $p_i\notin I_j$ or $p_j\notin I_i$.

The proof will follow from the following two claims.

Claim 1: For $i<j$ when $a_{i,j}=0$ is only up open⁸, $p_i<a_j$ in P .

Let for $i<j$, $a_{i,j}=0$ is only up open. Then there exists some $k>j$ such that $a_{i,k}=1$. From condition 1 of Definition 3.11 we get $a_{j,k}=1$. Again, $b_i\prec b_j$ as $i<j$ in $P_1$. Now as ${(i)}_2\ge k>j$, $b_i>p_k>p_j$. Again, we note ${(j)}_1>i$. Hence, to show $a_j>p_i$ in P it is sufficient to prove that if there exists some $l\in V$ such that $a_j\prec a_l$ in $P_2$ then ${(l)}_1>i$.

On the contrary, let’s assume $a_j\prec a_l$ for some l such that ${(l)}_1\le i$. Several cases may arise depending on the occurrence of l in $A^{\ast }(G)$. Note that l can not be equal to i as $a_l\prec a_j$ in $P_2$ then contradicts our assumption. Again $l\ne k$ otherwise $b_l{R}_2{b}_j$ from (3.7) imply $b_l\prec b_j$ in $P_1$ and hence we get $a_l\prec a_j$ in $P_2$ which introduces contradiction. Next if $l<i$ then $a_{l,j}$ becomes zero as $a_{i,j}=0$ is up open, which imply $b_l\prec b_j$ in $P_1$ and thus we get $a_l\prec a_j$ in $P_2$ which again contradicts ourassumption.

Now we consider the case when $i<l<j$. We need to use the following observations to find contradictions in this case.

Observations:

1. Since ${(l)}_1\le i$, $a_{i,l}=1$ from (2.1) applying to the vertices $\{{(l)}_1,i,l,k\}$.

2. If $b_j{R}_1{b}_r$ for any $r<j$ then there exists some ${\mathbf{k}}_{\mathbf{2}}>j$ such that $a_{j,k_2}=0,a_{r,k_2}=1$. We note that $k_2>k$ as otherwise (2.1) gets contradicted for vertices $\{r,j,k_2,k\}$.

3. If $b_m{R}_2{b}_l$ for any $m>l$ then there exists some ${\mathbf{k}}_{\mathbf{1}}<l$ such that $a_{k_1,l}=0,a_{k_1,m}=1$. If ${(l)}_1<k_1<l$ then $\{{(l)}_1,k_1,l,m\}$ contradict (2.1). Hence $k_1<{(l)}_1\le i$.

Main proof: Now if $b_j{R}_1{b}_l$ then from observation 2 we get $k_2>k$. One can verify now that condition 3 of Definition 3.11 get contradicted for vertices $\{i,l,j,k,k_2\}$ using observation 1. Again, if $b_j{R}_2{b}_l$ then $k_1<{(l)}_1\le i$ from observation 3. But in this case also (2.1) gets contradicted for vertices $\{k_1,i,j,k\}$. Now if $b_j{R}_1{b}_{k^{\prime }}$ and $b_{k^{\prime }}{R}_2{b}_l$ for some $k^{\prime }\in V$ such that $l<k^{\prime }<j$ then $k_2$ must be greater than k and $k_1<{(l)}_1\le i$ from observations 2, 3. This implies $a_{i,k^{\prime }}=1$ applying (2.1) on vertex set $\{k_1,i,k^{\prime },k\}$ But in this case condition 3 of Definition 3.11 gets contradicted for vertices $\{i,k^{\prime },j,k,k_2\}$.

Now if $l>j$ then if ${(l)}_1<i$, $a_{{(l)}_1,j}=0$ as $a_{i,j}=0$ is up open. This imply $b_l{R}_2{b}_j$ from (3.7) i.e., $b_l\prec b_j$. Thus we get $a_l\prec a_j$, which is a contradiction. Again, for ${(l)}_1=i$ we get a similar contradiction.

Hence, for any l, $a_j\prec a_l$ in $P_2$ imply ${(l)}_1>i$. Thus, from our above claim $p_i<a_j$ in P is established, and therefore $p_i\notin I_j$.

Claim 2: For $i<j$ when $a_{i,j}=0$ is right open, then either $p_i<a_j$ or $b_i<p_j$ in P.

Let for $i<j$, $a_{i,j}=0$ is right open. Then $b_i\prec b_j$ in $P_1$. As ${(i)}_2<j$ it is sufficient to prove that either for all $r\in V$ satisfying $b_r\prec b_i$ in $P_1$, ${(r)}_2<j$ which imply $b_i<p_j$ or for all $l\in V$ such that $a_j\prec a_l$ in $P_2$, ${(l)}_1>i$ which imply $p_i<a_j$.

We assume, on the contrary, the existence of some r satisfying $b_r\prec b_i$ and ${(r)}_2\ge j$. Note that r can not be greater than j as in that case $a_{i,r}$ becomes zero due to the fact $a_{i,j}=0$ is right open, which implies $b_i\prec b_r$ which contradicts our assumption. Again, when $r<i$, as ${(r)}_2\ge j$ and $a_{i,j}=0$ is right open, $a_{i,{(r)}_2}$ becomes zero, which implies $b_i{R}_1{b}_r$ from (3.6) and hence we get $b_i\prec b_r$ which contradicts our assumption. A similar contradiction will occur when $r=j$. Hence $i<r<j$.

Case (i): If $b_r{R}_1{b}_i$, then there exists $k_2>r$ such that $a_{r,k_2}=0,a_{i,k_2}=1$. Note that $k_2$ can not occur right to j in $A^{\ast }(G)$ as $a_{i,j}=0$ is right open. Hence $r<k_2<j$. Now one can find $a_{r,j}=0$ as $a_{r,k_2}=0$ is right open. Hence ${(r)}_2>j$, which again contradicts (2.1) for vertices $\{i,r,k_2,{(r)}_2\}$.

Thus, for any $r\in V$ if $b_r{R}_1{b}_i$ holds, then we get ${(r)}_2<j$. Hence, one can conclude $b_i<p_j$ as ${(i)}_2<j$ in this case.

Case (ii): If $b_r{R}_2{b}_i$ then there exist some $k_1<i$ such that $a_{k_1,i}=0,a_{k_1,r}=1$. From condition 1 of Definition 3.11, $a_{i,r}=1$. We will show in this case $p_i<a_j$. For this we assume on contrary $a_j\prec a_l$ for some $l\in V$ such that ${(l)}_1\le i$. Using Lemma 3.14 we get (3.10) $$b_r\prec b_i\prec b_j\prec b_l$$(3.10)

In the following paragraph, we list some important observations, which we vastly use in the rest of the proof.

Observations:

1. For $l<j$, $a_{l,j}=1$, for $l<r$, $a_{l,r}=1$ and for $i<r$, $a_{i,r}=1$ otherwise (3.10) gets contradicted.

2. For $i<l$, $k_1<{(l)}_1\le i$. If ${(l)}_1<k_1$ then $a_{{(l)}_1,i}$ becomes zero as $a_{k_1,i}=0$ is up open, which implies $b_l{R}_2{b}_i$ from (3.7), i.e., $b_l\prec b_i$ which is not true from (3.10). Hence $k_1<{(l)}_1\le i$.

3. Next we show $a_{r,j}=1$. We assume on contrary that $a_{r,j}=0$ then ${(r)}_2>j$.

When $l<r$ following observation 1, one can see that (2.1) gets contradicted for vertices $\{l,r,j,{(r)}_2\}$. Next, when $l>j$, $a_{{(l)}_1,j}=1$ otherwise $b_l{R}_2{b}_j$ (i.e., $b_l\prec b_j$) follows from (3.7) and the fact $k_1<{(l)}_1\le i$ (observation 2) which contradicts (3.10). Hence, applying (2.1) on vertices $\{{(l)}_1,r,j,{(r)}_2\}$ one can get a contradiction.

Again, when $r<l<j$ the following cases lead us to contradiction.

If $b_j{R}_1{b}_l$ holds then $a_{j,k_2^{\prime }}=0,a_{l,k_2^{\prime }}=1$ for some $k_2^{\prime }>j$. Now if ${(r)}_2>k_2^{\prime }$ then $a_{j,{(r)}_2}$ becomes zero as $a_{j,k_2^{\prime }}$ is right open and hence from (3.6) we get $b_j{R}_1{b}_r$, i.e., $b_j\prec b_r$ which contradicts (3.10). Again if $j<{(r)}_2<k_2^{\prime }$, then $a_{r,l}=1$ follows from (2.1) applying to the vertices $\{{(l)}_1,r,l,{(r)}_2\}$ (observation 2). Hence, from observation 6, one can see that condition 3 of Definition 3.11 gets contradicted for $\{r,l,j,{(r)}_2,k_2^{\prime }\}$.

If $b_j{R}_2{b}_l$ then there exist $k_1^{\prime }<l$ such that $a_{k_1^{\prime },l}=0,a_{k_1^{\prime },j}=1$. Hence (2.1) gets contradicted for $\{k_1^{\prime },r,j,{(r)}_2\}$.

Now if $b_j{R}_1{b}_{k^{\prime }}$ and $b_{k^{\prime }}{R}_2{b}_l$ for some $k^{\prime }\in V$ such that $l<k^{\prime }<j$. Then there exist some $k_2^{\prime }>j,k_1^{\prime }<l$ satisfying $a_{j,k_2^{\prime }}=1,a_{k^{\prime },k_2^{\prime }}=1,a_{k_1^{\prime },l}=0,a_{k_1^{\prime },k^{\prime }}=1$. Similar contradiction will arise when ${(r)}_2>k_2^{\prime }$ as described in the last paragraph. Now when $j<{(r)}_2<k_2^{\prime }$, $a_{r,k^{\prime }}=1$ applying (2.1) on vertices $\{k_1^{\prime },r,k^{\prime },{(r)}_2\}$. Hence, applying condition 3 of Definition 3.11 on vertex set $\{r,k^{\prime },j,{(r)}_2,k_2^{\prime }\}$ one can find contradiction.

1. For $i<l<j$, $a_{i,l}=1$. When $i<l<r$, using observations 1, 2 and applying (2.1) on vertices $\{{(l)}_1,i,l,r\}$ we get $a_{i,l}=1$. Next if $i<r<l$, $a_{r,l}=1$ (see proof of observation 3). Now if we assume on the contrary that $a_{i,l}=0$ then ${(l)}_1<i$. But then condition 3 of Definition 3.11 gets contradicted for the vertices $\{k_1,{(l)}_1,i,r,l\}$.

2. Again for $i<l<j$, if $b_j{R}_1{b}_m$ and $b_m{R}_2{b}_l$ hold for some m such that $l<m<j$ then $k_1<k_1^{\prime }<i$ and $a_{i,m}=1$ where $a_{k_1^{\prime },l}=0,a_{k_1^{\prime },m}=1$ for some $k_1^{\prime }<l$.

If $k_1^{\prime }<k_1$ then $a_{k_1^{\prime },i}$ becomes zero as $a_{k_1,i}=0$ is up open which implies $b_m{R}_2{b}_i$ and hence we get $b_m\prec b_j$ from Lemma 3.14 (as $b_i\prec b_j$) which is not true from above. Again, $k_1^{\prime }\ne i$ as $a_{i,l}=1$ from observation 4. Now when $i<k_1^{\prime }<l$, (2.1) gets contradicted for the vertices $\{i,k_1^{\prime },l,m\}$. Hence $k_1<k_1^{\prime }<i$.

Now if $m<r$, using observation 1 and applying (2.1) on the vertices $\{k_1^{\prime },i,m,r\}$ we get $a_{i,m}=1$. Again, when $m>r$, we obtain $a_{r,m}=1$ by applying observation 3 and (2.1) to the vertices $\{k_1^{\prime },r,m,j\}$. Further applying condition 3 of Definition 3.11 on the vertices $\{k_1,k_1^{\prime },i,r,m\}$ one can get $a_{i,m}=1$.

Main proof: If $l<k_1$, then $a_{l,i}=0$ as $a_{k_1,i}=0$ is up open, which implies $b_l\prec b_i$ as $l<i$. But this is not true from (3.10). Next if $k_1<l<i$. Now using observations 1, 3 one can verify that condition 3 of Definition 3.11 gets contradicted for vertices $\{k_1,l,i,r,j\}$. Again, when $j<l$, as $a_{i,j}=0$ is right open, $a_{i,l}$ becomes zero. Hence, from observation 2, we get $k_1<{(l)}_1<i$. One can now show that condition 3 of Definition 3.11 gets contradicted for the vertices $\{k_1,{(l)}_1,i,r,l\}$ using the fact $a_{r,l}=1$ (see proof of observation 3).

Next, we consider the case $\mathbf{i}<\mathbf{l}<\mathbf{j}$. Now if $b_j{R}_1{b}_l$ then there exists $k_2^{\prime }>j$ such that $a_{j,k_2^{\prime }}=0,a_{l,k_2^{\prime }}=1$. From observations 3, 4, we get $a_{r,j}=1$ and $a_{i,l}=1$. Now applying condition 5 of Definition 3.11 on the vertex set $\{k_1,i,l,r,j,k_2^{\prime }\}$ one can find contradiction.

If $b_j{R}_2{b}_l$ then there exists $k_1^{\prime }<l$ such that $a_{k_1^{\prime },l}=0,a_{k_1^{\prime },j}=1$. Proceeding similarly to observation 5 and replacing m by l one can prove $k_1<k_1^{\prime }<i$. Again, from observation 3, we get $a_{r,j}=1$. Hence, by applying condition 3 of Definition 3.11 to the vertices $\{k_1,k_1^{\prime },i,r,j\}$, one can find a contradiction.

Again if $b_j{R}_1{b}_{k^{\prime }}$ and $b_{k^{\prime }}{R}_2{b}_l$ for some $k^{\prime }\in V$ such that $l<k^{\prime }<j$. Then there exist $k_2^{\prime }>j,k_1^{\prime }<l$ such that $a_{j,k_2^{\prime }}=0,a_{k^{\prime },k_2^{\prime }}=1,a_{k_1^{\prime },l}=0,a_{k_1^{\prime },k^{\prime }}=1$. From observation 5 one can find $k_1<k_1^{\prime }<i$. Also note $a_{r,j}=1$ from observation 3 and $a_{i,k^{\prime }}=1$ from observation 5. Hence, applying condition 5 of Definition 3.11 on the vertex set $\{k_1,i,k^{\prime },r,j,k_2^{\prime }\}$ one can findcontradiction.

Thus, in this case, we prove that if there exists some $r\in V$ satisfying $b_r{R}_2{b}_i$ such that ${(r)}_2\ge j$ then for any $l\in V$, $a_j\prec a_l$ in $P_1$ imply ${(l)}_1>i$. Hence $p_i<a_j$ in P and therefore $p_i\notin I_j$.

Case (iii): If $b_r{R}_1{b}_{k^{\prime }}$ and $b_{k^{\prime }}{R}_2{b}_i$ for some $k^{\prime }\in V$ such that $i<k^{\prime }<r$. Then there exist $k_2>r,k_1<i$ such that $a_{r,k_2}=0,a_{k^{\prime },k_2}=1,a_{k_1,i}=0,a_{k_1,k^{\prime }}=1$. Note that $k_2>j$ otherwise (2.1) gets contradicted for vertex set $\{k^{\prime },r,k_2,{(r)}_2\}$ as ${(r)}_2\ge j$. Hence ${(k^{\prime })}_2\ge k_2>j$. Now as $b_{k^{\prime }}{R}_2{b}_i$, $i<k^{\prime }<j$ and ${(k^{\prime })}_2>j$, proceeding similarly as Case (ii), just replacing r by $k^{\prime }$ one can find the same result. ▪

Remark 3.18.

By Theorem 3.17 we are able to provide a proper MPTG representation $\{([a_v,b_v],p_v)|v\in V\}$ of a graph G (see Figure 3), which satisfies a proper MPTG ordering $\sigma =(v_1<v_2<\cdots <v_7)$. In Example 3.16 we found the canonical sequence P of the graph G from its augmented adjacency matrix $A^{\ast }(G)$, arranged according to $\sigma$ along both rows and columns.

$P:a_2{a}_1{a}_5{a}_6{a}_4{p}_1{a}_3{p}_2{p}_3{b}_2$

$a_7{p}_4{b}_1{p}_5{b}_5{p}_6{b}_6{p}_7{b}_4{b}_3{b}_7$.

Therefore we obtain the proper MPTG representation of G from the following table according to the proof of the abovetheorem. $$\begin{array}{ccccccccccc}{a}_2& a_1& a_5& a_6& a_4& p_1& a_3& p_2& p_3& b_2& \\ 1& 2& 3& 4& 5& 6& 7& 8& 9& 10& \\ a_7& p_4& b_1& p_5& b_5& p_6& b_6& p_7& b_4& b_3& b_7\\ 11& 12& 13& 14& 15& 16& 17& 18& 19& 20& 21\\ & & & & & & & & & & \end{array}$$

Catanzaro et. al [3] have shown that the interval graphs form a strict subclass of MPTG. We extend this result to the class of proper MPTG graphs.

Corollary 3.19.

Interval graphs form a strict subclass of proper MPTG.

Proof.

Let $G=(V,E)$ be an interval graph having representation $\{I_v=[a_v,b_v]|v\in V\}$. Now, arranging the intervals according to the increasing order of left endpoints ($a_v$) and ordering vertices of V with the same, it is easy to check that G satisfies all the conditions of Definition 3.11. Hence, G becomes a proper MPTG by Theorem 3.17. Also, one can easily verify that $C_4$ is a proper MPTG (see Figure 4) but it is not an interval graph. Therefore, the result follows. ▪

Figure 4: $C_4$ with its proper MPTG representation.

In [2] Bogart and West proved that proper interval graphs are the same as unit interval graphs. Here we can also conclude a similar result for the class of proper MPTG graphs.

Proposition 3.20.

Let $G=(V,E)$ be an undirected graph. Then the following are equivalent:

1. G is a proper MPTG.

2. G is a unit MPTG.

Proof.

$(1)\Rightarrow (2)$ Let $G=(V,E)$ be a proper MPTG with representation $\{(I_v,p_v)|v\in V\}$ where $I_v=[a_v,b_v]$ is an interval, and $p_v$ is a point within $I_v$. From Theorem 3.17 it follows that G must possess a proper MPTG ordering of V. Hence one can construct the sequences $P_1,P_2,P$ as described in Definition 3.15. Let $P_1:b_{k_1}\prec \cdots \prec b_{k_n}$ and $P_2:a_{k_1}\prec \cdots \prec a_{k_n}$. We assign $a_{k_1},b_{k_1}$ with real values ${\alpha }_1,{\alpha }_1+l$ in P. At i th step, we assign $a_{k_i},b_{k_i}$ with real values ${\alpha }_i,{\alpha }_i+l$ where $\max \{{\alpha }_{i-1},m_i\}<{\alpha }_i<M_i$ where $m_i=\max \{{\alpha }_j+l|1\le j\le i-1,b_{k_j}\prec a_{k_i}\text{in}P\}$ and $M_i=\min \{{\alpha }_j+l|1\le j\le i-1,a_{k_i}\prec b_{k_j}\text{in}P\}$. After the assignment is done for all $a_{k_i},b_{k_i}$ where $1\le i\le n$, assign values for $p_i$ in P in such a way so that P still remains an increasing sequence. Now it is easy to check that $([a_{k_i},b_{k_i}],p_i)$ gives us unit MPTG representation (unit length l) as the order of $a_i,b_i,p_i$ remains intact in P after assigning their values in the above way.

$(2)\Rightarrow (1)$ Converse is obvious. ▪

Remark 3.21.

The unit vs. proper question is addressed for many graph classes in reference [9]. Golumbic and Trenk wrote, “For min-tolerance graphs, the classes are different. For max-tolerance graphs, the question is still open” [9, p. 215]. We settle this query below.

Proposition 3.22.

Unit max-tolerance graphs form a strict subclass of proper max-tolerance graphs.

Proof.

An unit max-tolerance graph is a proper max-tolerance graph with the same tolerance representation. Let $\{v_1,\dots ,v_6\}$ are vertices of $\overline{C_6}$ occurred in circularly consecutive order in $C_6$. Then $I_1=[2,8],t_1=2.9,I_2=[4,10],t_2=4.5,I_3=[1,7.1],t_3=1,I_4=[5,11],t_4=3,I_5=[3,9],t_5=4.1,I_6=[5.2,12],t_6=1.5$ is a proper max-tolerance representation of $\overline{C_6}$. But from [13] one can verify that $\overline{C_6}$ is not a unit max-tolerance graph. Hence the result follows. ▪

In the following proposition, we will show that proper MPTG and proper max-tolerance graphs are not comparable, although both of them belong to the class of MPTG.

Proposition 3.23.

Proper MPTG and the class of proper max-tolerance graphs are not comparable.

Proof.

$C_5$ is a proper max-tolerance graph with representation $I_1=[1,6],t_1=0.25,I_2=[1.2,8],t_2=4.7,I_3=[3,10],t_3=4.8,I_4=[5,12],t_4=4,I_5=[5.5,13],t_5=0.35$. But $C_5\notin \text{proper MPTG}$ follows from Proposition 3.7.

Again, we note from Proposition 3.3 that $K_{2,3}$ is a proper MPTG. But it is not a proper max-tolerance graph, as follows from Corollary 2.3. ▪

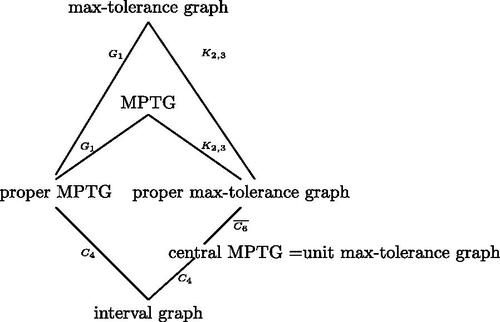
4 Conclusion

In this article, we introduce proper max-point-tolerance graphs and characterize this graph class in Theorem 3.17. We have proved in the previous section that interval graphs $\subset$ proper MPTG. Interestingly, one can note that both of these graph classes are AT-free and perfect (Section 3, [12]). Therefore, any proper MPTG that is not an interval graph must contain $C_4$ as an induced subgraph. Also interval graphs $\subset$ central MPTG $=$ unit max-tolerance graph $\subset$ max-tolerance graph according to the reference [13]. Again, Proposition 3.22 helps us to conclude that unit max-tolerance graphs $\subset$ proper max-tolerance graphs.

Next, we find that $\overline{C_6}\in$ proper MPTG $\setminus$ central MPTG. It is a proper MPTG with the representation $I_1=[20,40],p_1=39,I_2=[15,38],p_2=30,I_3=[32,46],p_3=33,I_4=[25,42],p_4=27,I_5=[28,44],p_5=37,I_6=[10,36],p_6=34$. But it is not a central MPTG, follows from Theorem 3.9 of [13]. Again, $C_n,n\ge 5\in$ central MPTG $\setminus$ proper MPTG follows from [15] and Lemma 3.7 of this article. Hence, these two classes become incomparable. Next, in Proposition 3.23 we see that proper max-tolerance graphs are not comparable to proper MPTG whereas both of these graph classes belong to the class of MPTG.

Further, we find that $G_1$ in Figure 2 is a MPTG. It is also a max-tolerance graph with representation $I_1=[10,25],t_1=5,I_2=[45,53],t_2=8,I_3=[65,75],t_3=10,I_4=[20,40],t_4=5,I_5=[30,70],t_5=10,I_6=[45,60],t_6=8,I_7=[60,80],t_7=10$. But it is not a proper MPTG. Again, $K_{2,3}$ is a max-tolerance graph with representation $I_x=[-20,0],t_x=1,I_y=[0,20],t_y=1$ for one partite set and $I_{v_1}=[-2,2],t_{v_1}=1,I_{v_2}=[-6,6],t_{v_2}=5,I_{v_3}=[-20,20],t_{v_3}=19$ for the other partite set. But it is not a proper max-tolerance graph from Corollary 2.3. Lastly, from Theorem 2.4 we establish that MPTG and max-tolerance graphs are not comparable.

Combining these we obtain relations between some subclasses of max-tolerance graphs and MPTG related to proper MPTG in Figure 5.

Figure 5: Hierarchy between subclasses of max-tolerance graph and MPTG.

Acknowledgments

The author would like to thank Prof. Shamik Ghosh of Jadavpur University, India for his valuable suggestions to build up this paper.

Disclosure statement

No conflict of interest was reported by the author.

Additional information

Funding

This research is supported by UGC (University Grants Commission) NET fellowship (21/12/2014 (ii) EU-V) of the author.

Notes

1 $I_x$ contains $I_y$ means $I_x\supseteq I_y$

2 If x, y are nonadjacent and $I_y\subseteq I_x$ then $|I_x\cap I_y|<t_x$

3 it is a tree with a path $(s_1,s_2,\dots ,s_k)$ (known as spine) such that every other vertex is of exactly one distance from the spine.

4 A n-wheel graph $W_n$ is formed by connecting a single vertex to all the vertices of a cycle of order $n-1$

5 This zero is right open from condition 4 of Theorem 2.1

6 This zero is up open from condition 4 of Theorem 2.1

7 $\prec$ is a partial order relation where any two elements are comparable

8 up open but not right open

Appendix

Here we provide a detailed verification of the other cases that occurred in Lemma 3.14.

Case (ii) $i_2<i_3<i_1$

As $b_{i_1}\prec b_{i_2}$, if $b_{i_1}{R}_1{b}_{i_2}$ then there exists some $k_2>i_1$ such that $a_{i_1,k_2}=0,a_{i_2,k_2}=1$. We note that $a_{i_3,k_2}$ must be one; otherwise, from (3.6) we get $b_{i_3}{R}_1{b}_{i_2}$, i.e., $b_{i_3}\prec b_{i_2}$ which contradicts our assumption. Hence $b_{i_1}{R}_1{b}_{i_3}$ from (3.6), i.e., $b_{i_1}\prec b_{i_3}$. Now if $b_{i_1}{R}_2{b}_{i_2}$ then there exists some $k_1<i_2$ such that $a_{k_1,i_2}=0,a_{k_1,i_1}=1$. Now if $a_{k_1,i_3}=1$ then $b_{i_3}{R}_2{b}_{i_2}$ from (3.7) imply $b_{i_3}\prec b_{i_2}$ which is again a contradiction. Hence $a_{k_1,i_3}=0$, which imply $b_{i_1}{R}_2{b}_{i_3}$ from (3.7), i.e., $b_{i_1}\prec b_{i_3}$. Now if $b_{i_1}{R}_1{b}_k$ and $b_k{R}_2{b}_{i_2}$ for some $k\in V$ such that $i_2<k<i_1$. Then there exists $k_2>i_1$ and $k_1<i_2$ such that $a_{i_1,k_2}=0,a_{k,k_2}=1,a_{k_1,i_2}=0,a_{k_1,k}=1$. Now when $i_2<k<i_3$, if $a_{i_3,k_2}=0$ then $b_{i_3}{R}_1{b}_k$ imply $b_{i_3}\prec b_{i_2}$ from (3.8) as $b_k{R}_2{b}_{i_2}$ which is a contradiction. Hence $a_{i_3,k_2}=1$ and from (3.6) it follows $b_{i_1}{R}_1{b}_{i_3}$, i.e., $b_{i_1}\prec b_{i_3}$. Now when $i_3<k<i_1$, if $a_{k_1,i_3}=1$ then $b_{i_3}{R}_2{b}_{i_2}$ from (3.7) imply $b_{i_3}\prec b_{i_2}$ which is a contradiction. Hence $a_{k_1,i_3}=0$ which imply $b_k{R}_2{b}_{i_3}$ which helps us to conclude $b_{i_1}\prec b_{i_3}$ from (3.8) as $b_{i_1}{R}_1{b}_k$.

Case (iii) $i_1<i_2<i_3$

In this case, we assume on the contrary $b_{i_3}\prec b_{i_1}$.

Let $b_{i_3}{R}_1{b}_{i_1}$. Then there exists $k_2>i_3$ such that $a_{i_3,k_2}=0,a_{i_1,k_2}=1$. Now if $a_{i_2,k_2}=1$ then $b_{i_3}{R}_1{b}_{i_2}$ from (3.6) imply $b_{i_3}\prec b_{i_2}$ which contradicts our assumption. Again, if $a_{i_2,k_2}=0$ then $b_{i_2}{R}_1{b}_{i_1}$ imply $b_{i_2}\prec b_{i_1}$ which is again a contradiction. Now if $b_{i_3}{R}_2{b}_{i_1}$ then there exists some $k_1<i_1$ such that $a_{k_1,i_1}=0,a_{k_1,i_3}=1$. Now if $a_{k_1,i_2}=0$ then $b_{i_3}{R}_2{b}_{i_2}$ from (3.7) imply $b_{i_3}\prec b_{i_2}$ which is a contradiction. Again, if $a_{k_1,i_2}=1$ then $b_{i_2}{R}_2{b}_{i_1}$ imply $b_{i_2}\prec b_{i_1}$ which is again a contradiction. Now let $b_{i_3}{R}_1{b}_k$ and $b_k{R}_2{b}_{i_1}$ for some $k\in V$ such that $i_1<k<i_3$. Then there exist $k_2>i_3$ and $k_1<i_1$ such that $a_{i_3,k_2}=0,a_{k,k_2}=1,a_{k_1,i_1}=0,a_{k_1,k}=1$. Now when $i_1<k<i_2$ then if $a_{i_2,k_2}=1$ then $b_{i_3}{R}_1{b}_{i_2}$ from (3.6) imply $b_{i_3}\prec b_{i_2}$ which is not true. Again, if $a_{i_2,k_2}=0$ then $b_{i_2}{R}_1{b}_k$ from (3.6) which helps us to conclude $b_{i_2}\prec b_{i_1}$ from (3.8) as $b_k{R}_2{b}_{i_1}$ which is a contradiction. Now when $i_2<k<i_3$ then if $a_{k_1,i_2}=1$, $b_{i_2}{R}_2{b}_{i_1}$, i.e., $b_{i_2}\prec b_{i_1}$ from (3.7) which is not true. Further, if $a_{k_1,i_2}=0$ then $b_k{R}_2{b}_{i_2}$ which helps us to conclude $b_{i_3}\prec b_{i_2}$ from (3.8) as $b_{i_3}{R}_1{b}_k$, which is again a contradiction.

Case (iv) $i_3<i_1<i_2$

Since $b_{i_2}\prec b_{i_3}$, if $b_{i_2}{R}_1{b}_{i_3}$ then there exist $k_2>i_2$ such that $a_{i_2,k_2}=0,a_{i_3,k_2}=1$. Now if $a_{i_1,k_2}=1$ then $b_{i_2}{R}_1{b}_{i_1}$ from (3.6), i.e., $b_{i_2}\prec b_{i_1}$ which is a contradiction. Hence $a_{i_1,k_2}=0$ which imply $b_{i_1}{R}_1{b}_{i_3}$. Therefore $b_{i_1}\prec b_{i_3}$. If $b_{i_2}{R}_2{b}_{i_3}$ then there exist $k_1<i_3$ such that $a_{k_1,i_3}=0,a_{k_1,i_2}=1$. If $a_{k_1,i_1}=0$ then $b_{i_2}{R}_2{b}_{i_1}$ from (3.7) imply $b_{i_2}\prec b_{i_1}$ which is a contradiction. Hence $a_{k_1,i_1}=1$ which imply $b_{i_1}{R}_2{b}_{i_3}$, i.e., $b_{i_1}\prec b_{i_3}$. If $b_{i_2}{R}_1{b}_k$ and $b_k{R}_2{b}_{i_3}$ for some $k\in V$ such that $i_3<k<i_2$. Then there exist $k_2>i_2,k_1<i_3$ such that $a_{i_2,k_2}=0,a_{k,k_2}=1,a_{k_1,i_3}=0,a_{k_1,k}=1$. Now when $i_3<k<i_1$, if $a_{i_1,k_2}=1$ then $b_{i_2}{R}_1{b}_{i_1}$ from (3.6) which imply $b_{i_2}\prec b_{i_1}$ which is a contradiction. Hence $a_{i_1,k_2}=0$ which imply $b_{i_1}{R}_1{b}_k$ which helps us to conclude $b_{i_1}\prec b_{i_3}$ from (3.8) as $b_k{R}_2{b}_{i_3}$. Again when $i_1<k<i_2$, if $a_{k_1,i_1}=0$ then $b_k{R}_2{b}_{i_1}$ imply $b_{i_2}\prec b_{i_1}$ from (3.8) (as $b_{i_2}{R}_1{b}_k$) which contradicts our assumption. Hence $a_{k_1,i_1}=1$ which imply $b_{i_1}\prec b_{i_3}$ as earlier.

Case (v) $i_3<i_2<i_1$

We need the following observations to prove this case.

Observations:

1. First note $a_{i_3,i_2}=a_{i_2,i_1}=1$ as $i_3<i_2$ and $i_2<i_1$.

2. Next, if $b_{i_1}{R}_1{b}_r$ for any $r<i_1$ then there exists some ${\mathbf{k}}_{\mathbf{2}}>i_1$ such that $a_{i_1,k_2}=0,a_{r,k_2}=1$.

3. Further $b_m{R}_2{b}_{i_2}$ for any $m>i_2$ imply existence of some ${\mathbf{k}}_{\mathbf{1}}<i_2$ such that $a_{k_1,i_2}=0,a_{k_1,m}=1$. Now if $i_3<k_1<i_2$ then $a_{i_3,i_2}$ becomes zero as $a_{k_1,i_2}=0$ is up open, which imply $b_{i_3}\prec b_{i_2}$ which contradicts our assumption. Hence $k_1<i_3$.

4. Again, $b_{i_2}{R}_1{b}_j$ for any $j<i_2$ ensure existence of some ${\mathbf{k}}_{\mathbf{2}}^{\prime }>i_2$ satisfying $a_{i_2,k_2^{\prime }}=0,a_{j,k_2^{\prime }}=1$. Clearly $k_2^{\prime }>i_1$ otherwise (2.1) gets contradicted for vertices $\{j,i_2,k_2^{\prime },i_1\}$.

5. Similarly, $b_l{R}_2{b}_{i_3}$ for any $l>i_3$ ensure existence of some ${\mathbf{k}}_{\mathbf{1}}^{\prime }<i_3$ satisfying $a_{k_1^{\prime },i_3}=0,a_{k_1^{\prime },l}=1$.

6. Let $b_{i_2}{R}_1{b}_{i_3}$. Then $k_2^{\prime }>i_1$ from observation 4. Now if $b_p{R}_2{b}_{i_2}$ for any $p>i_2$ then $k_1<i_3$ from observation 3. Next, if $a_{k_1,i_3}=1$ then condition 3 of Definition 3.11 gets contradicted for vertices $\{k_1,i_3,i_2,p,k_2^{\prime }\}$. Hence $a_{k_1,i_3}=0$, which imply $b_p{R}_2{b}_{i_3}$ from (3.7).

7. Let $b_{i_2}{R}_2{b}_{i_3}$. Then $k_1^{\prime }<i_3$ from observation 5. Now if $b_s{R}_2{b}_{i_2}$ for any $s>i_2$ then $k_1<i_3$ from observation 3. Next if $k_1^{\prime }<k_1$ then (2.1) gets contradicted for vertices $\{k_1^{\prime },k_1,i_2,s\}$. Hence $k_1<k_1^{\prime }<i_3$ which imply $a_{k_1,i_3}=0$ as $a_{k_1^{\prime },i_3}=0$ is up open. Thus we get $b_s{R}_2{b}_{i_3}$ from (3.7).

Main proof: Let $b_{i_1}{R}_1{b}_{i_2}$. Now if $b_{i_2}{R}_1{b}_j$ for any $j<i_2$ then using observations 2 and 4 we note $k_2^{\prime }>k_2$ otherwise (2.1) gets contradicted for the vertices $\{j,i_2,k_2^{\prime },k_2\}$. Now $a_{i_1,k_2^{\prime }}=0$ clearly as $a_{i_1,k_2}=0$ is right open. This imply $b_{i_1}{R}_1{b}_j$ from (3.6) which imply $b_{i_1}\prec b_j$.

If $b_{i_2}{R}_1{b}_{i_3}$, we get $b_{i_1}\prec b_{i_3}$ from last paragraph. Again, if $b_{i_2}{R}_2{b}_{i_3}$ then $b_{i_1}\prec b_{i_3}$ from (3.8) as $b_{i_1}{R}_1{b}_{i_2}$ and $i_3<i_2<i_1$. When $b_{i_2}{R}_1{b}_k$ and $b_k{R}_2{b}_{i_3}$ for some $k\in V$ such that $i_3<k<i_2$, we get $b_{i_1}{R}_1{b}_k$ from above paragraph. Hence we can conclude $b_{i_1}\prec b_{i_3}$ from (3.8) as $b_k{R}_2{b}_{i_3}$.

Now let $b_{i_1}{R}_2{b}_{i_2}$. If $b_{i_2}{R}_1{b}_{i_3}$ then using observations 3, 4, 6 one can get $b_{i_1}{R}_2{b}_{i_3}$, i.e.; $b_{i_1}\prec b_{i_3}$. Again when $b_{i_2}{R}_2{b}_{i_3}$ then $b_{i_1}{R}_2{b}_{i_3}$ follows from observation 7, i.e., $b_{i_1}\prec b_{i_3}$. Now if $b_{i_2}{R}_1{b}_k$ and $b_k{R}_2{b}_{i_3}$ for some $k\in V$ such that $i_3<k<i_2$ then if $a_{k_1,k}=1$, condition 3 of Definition 3.11 gets contradicted for vertices $\{k_1,k,i_2,i_1,k_2^{\prime }\}$ (observations 3, 4). Hence $a_{k_1,k}=0$ which imply $b_{i_1}{R}_2{b}_k$ which helps us to conclude $b_{i_1}\prec b_{i_3}$ from (3.8) as $b_k{R}_2{b}_{i_3}$.

Let $b_{i_1}{R}_1{b}_k$ and $b_k{R}_2{b}_{i_2}$ for some $k\in V$ such that $i_2<k<i_1$. If $b_{i_2}{R}_1{b}_{i_3}$ then from observations 3, 4, 6 we get $b_k{R}_2{b}_{i_3}$ which helps us to conclude $b_{i_1}\prec b_{i_3}$ from (3.8) as $b_{i_1}{R}_1{b}_k$. Again if $b_{i_2}{R}_2{b}_{i_3}$ then $b_k{R}_2{b}_{i_3}$ from observation 7 which helps us to conclude $b_{i_1}\prec b_{i_3}$ from (3.8) as $b_{i_1}{R}_1{b}_k$.

Now if $b_{i_2}{R}_1{b}_{k^{\prime }}$ and $b_{k^{\prime }}{R}_2{b}_{i_3}$ for some $k^{\prime }\in V$ such that $i_3<k^{\prime }<i_2$. Then if $k_1^{\prime }<k_1$ (observations 3, 5) then $a_{k_1,k^{\prime }}=1$ applying (2.1) on vertices $\{k_1^{\prime },k_1,k^{\prime },k\}$. Therefore, condition 3 of Definition 3.11 gets contradicted for vertices $\{k_1,k^{\prime },i_2,k,k_2^{\prime }\}$ (observations 3, 4). Hence we get $k_1<k_1^{\prime }<i_3$. Thus $a_{k_1,i_3}$ becomes zero as $a_{k_1^{\prime },i_3}=0$ is up open, which imply $b_k{R}_2{b}_{i_3}$ from (3.7). Hence from (3.8) we get $b_{i_1}\prec b_{i_3}$ as $b_{i_1}{R}_1{b}_k$ and $i_3<k<i_1$.

Case(vi) $i_2<i_1<i_3$

Let’s assume $b_{i_3}\prec b_{i_1}$ on the contrary. We make the following observations, which we will use throughout the proof.

Observations:

1. First note that $a_{i_2,i_1}=1$ as $i_2<i_1$.

2. Next, if $b_{i_1}{R}_1{b}_r$ for any $r<i_1$ then there exists ${\mathbf{k}}_{\mathbf{2}}>{\mathbf{i}}_{\mathbf{1}}$ such that $a_{i_1,k_2}=0,a_{r,k_2}=1$. Now if $i_1<k_2<i_3$ then $a_{i_1,i_3}$ becomes zero as $a_{i_1,k_2}=0$ is right open, which implies $b_{i_1}\prec b_{i_3}$. But this contradicts our assumption. Hence $k_2>i_3$.

3. Again, if $b_m{R}_2{b}_{i_2}$ for any $m>i_2$ then there exists ${\mathbf{k}}_{\mathbf{1}}<{\mathbf{i}}_{\mathbf{2}}$ satisfying $a_{k_1,i_2}=0,a_{k_1,m}=1$.

4. If $b_l{R}_2{b}_{i_1}$ for any $l>i_1$ then there exists ${\mathbf{k}}_{\mathbf{1}}^{\prime }<{\mathbf{i}}_{\mathbf{1}}$ satisfying $a_{k_1^{\prime },i_1}=0,a_{k_1^{\prime },l}=1$. Now if $i_2<k_1^{\prime }<i_1$ then (2.1) gets contradicted for vertices $\{i_2,k_1^{\prime },i_1,l\}$ using observation 1. Hence $k_1^{\prime }<i_2$.

5. Again, if $b_{i_3}{R}_1{b}_j$ for any $j<i_3$ ensure existence of some ${\mathbf{k}}_{\mathbf{2}}^{\prime }>{\mathbf{i}}_{\mathbf{3}}$ such that $a_{i_3,k_2^{\prime }}=0,a_{j,k_2^{\prime }}=1$.

6. Let $b_{i_1}{R}_1{b}_{i_2}$. Then $k_2>i_3$ from observation 2. Now if $b_j{R}_2{b}_{i_1}$ for any $i_1<j<k_2$ then from observation 4 we get $k_1^{\prime }<i_2$. Again, if $a_{k_1^{\prime },i_2}=1$ then condition 3 gets contradicted for vertices $\{k_1^{\prime },i_2,i_1,j,k_2\}$. Hence ${\mathbf{a}}_{{\mathbf{k}}_{\mathbf{1}}^{\prime },{\mathbf{i}}_{\mathbf{2}}}=\mathbf{0}$.

7. Let $b_{i_1}{R}_2{b}_{i_2}$. Then $k_1<i_2$ from observation 3. Now if $b_l{R}_2{b}_{i_1}$ holds for any $l>i_1$ then $k_1^{\prime }<i_2$ from observation 4. Moreover ${\mathbf{k}}_{\mathbf{1}}^{\prime }<{\mathbf{k}}_{\mathbf{1}}$ otherwise (2.1) gets contradicted for vertices $\{k_1,k_1^{\prime },i_1,l\}$.

Main proof:

Let $b_{i_1}{R}_1{b}_{i_2}$. Now if $b_{i_3}{R}_1{b}_{i_1}$ holds then if $k_2^{\prime }>k_2$ then (2.1) gets contradicted for the vertices $\{i_2,i_1,k_2,k_2^{\prime }\}$ (observations 2, 5). Again, if $i_3<k_2^{\prime }<k_2$ then $a_{i_3,k_2}$ becomes zero as $a_{i_3,k_2^{\prime }}=0$ is right open, which implies $b_{i_3}{R}_1{b}_{i_2}$ from (3.6), i.e., $b_{i_3}\prec b_{i_2}$ which is a contradiction. Now if $b_{i_3}{R}_2{b}_{i_1}$ then $k_1^{\prime }<i_2$ from observation 4. Again $a_{k_{1^{\prime }},i_2}=0$ from observation 6. But in this case, $b_{i_3}{R}_2{b}_{i_2}$ from (3.7) imply $b_{i_3}\prec b_{i_2}$ which is not true. Now if $b_{i_3}{R}_1{b}_k$ and $b_k{R}_2{b}_{i_1}$ for some $k\in V$ such that $i_1<k<i_3$. Note that $k_1^{\prime }<i_2$ from observation 4. Again $a_{k_1^{\prime },i_2}=0$ from observation 6. Hence we get $b_k{R}_2{b}_{i_2}$ which along with $b_{i_3}{R}_1{b}_k$ helps us to conclude $b_{i_3}\prec b_{i_2}$ from (3.8), which isnot true.

Now let $b_{i_1}{R}_2{b}_{i_2}$. Now if $b_{i_3}{R}_1{b}_{i_1}$ then $b_{i_3}\prec b_{i_2}$ from (3.8) as $b_{i_1}{R}_2{b}_{i_2}$, which is a contradiction. If $b_{i_3}{R}_2{b}_{i_1}$ then $k_1^{\prime }<k_1$ from observations 3, 4, 7. Hence $a_{k_1^{\prime },i_2}=0$ as $a_{k_1,i_2}=0$ is up open, which imply $b_{i_3}{R}_2{b}_{i_2}$ from (3.7), i.e., $b_{i_3}\prec b_{i_2}$ which is a contradiction. Again, if $b_{i_3}{R}_1{b}_k$ and $b_k{R}_2{b}_{i_1}$ for some $k\in V$ such that $i_1<k<i_3$ then $k_2^{\prime }>i_3$ and $k_1^{\prime }<i_1$ follows from observations 4, 5. Again, note $k_1^{\prime }<k_1$ from observation 7. Now $a_{k_1^{\prime },i_2}$ must be zero as $a_{k_1,i_2}=0$ is up open, which implies $b_k{R}_2{b}_{i_2}$ from (3.7) which helps us to conclude $b_{i_3}\prec b_{i_2}$ from (3.8) as $b_{i_3}{R}_1{b}_k$, which again contradicts ourassumption.

Now let $b_{i_1}{R}_1{b}_k$ and $b_k{R}_2{b}_{i_2}$ for some $k\in V$ such that $i_2<k<i_1$. Then $k_2>i_3$ from observation 2. Now if $b_{i_3}{R}_1{b}_{i_1}$ then $k_2^{\prime }$ (observation 5) can not be greater than $k_2$ as in that case (2.1) gets contradicted for vertices $\{k,i_1,k_2,k_2^{\prime }\}$. Again, if $i_3<k_2^{\prime }<k_2$ then $a_{i_3,k_2}=0$ as $a_{i_3,k_2^{\prime }}=0$ is right open, which implies $b_{i_3}{R}_1{b}_k$ from (3.6) which helps us to conclude $b_{i_3}\prec b_{i_2}$ from (3.8) as $b_k{R}_2{b}_{i_2}$, which is again a contradiction.

Now if $b_{i_3}{R}_2{b}_{i_1}$ then $k_1^{\prime }<i_2$ from observation 4. Now if $k_1<k_1^{\prime }<i_2$ (observations 3, 4) then $a_{k_1^{\prime },k}=1$ applying (2.1) on vertices $\{k_1,k_1^{\prime },k,i_3\}$. Now applying condition 3 of Definition 3.11 on vertices $\{k_1^{\prime },k,i_1,i_3,k_2\}$ one can find a contradiction. Now if $k_1^{\prime }<k_1$ then $a_{k_1^{\prime },i_2}$ becomes zero as $a_{k_1,i_2}=0$ is up open, which implies $b_{i_3}{R}_2{b}_{i_2}$ from (3.7), i.e., $b_{i_3}\prec b_{i_2}$ which is a contradiction.

Again if $b_{i_3}{R}_1{b}_k^{\prime }$ and $b_k^{\prime }{R}_2{b}_{i_1}$ for some $k^{\prime }\in V$ such that $i_1<k^{\prime }<i_3$ then $k_1^{\prime }<i_2$ from observation 4. Now if $k_1<k_1^{\prime }<i_2$ then $a_{k_1^{\prime },k}$ become one from (2.1) applying on vertices $\{k_1,k_1^{\prime },k,k^{\prime }\}$. Hence applying condition 3 of Definition 3.11 on vertices $\{k_1^{\prime },k,i_1,k^{\prime },k_2\}$ one can get a contradiction. Now if $k_1^{\prime }<k_1$ then $a_{k_1^{\prime },i_2}$ becomes zero as $a_{k_1,i_2}=0$ is up open, which imply $b_{k^{\prime }}{R}_2{b}_{i_2}$ from (3.7) which helps us to conclude $b_{i_3}\prec b_{i_2}$ from (3.8) as $b_{i_3}{R}_1{b}_{k^{\prime }}$, which is again a contradiction.