The crossing number of the generalized Petersen graph P(3k,k) in the projective plane

ABSTRACT

The crossing number of a graph G in a surface Σ, denoted by $c{r}_{\Sigma }(G)$, is the minimum number of pairwise intersections of edges in a drawing of G in Σ. Let k be an integer satisfying $k\ge 3$, the generalized Petersen graph $P(3k,k)$ is the graph with vertex set $V(P(3k,k))=\{u_i,v_i\mid i=1,2,\dots ,3k\}$ and edge set $E(P(3k,k))=\{u_i{u}_{i+1},u_i{v}_i,v_i{v}_{k+i}\mid i=1,2,\dots ,3k\},$ the subscripts are read modulo $3k.$ In this paper we investigate the crossing number of $P(3k,k)$ in the projective plane. We determine the exact value of $c{r}_{N_1}(P(3k,k))$ is k–2 when $3\le k\le 7,$ moreover, for $k\ge 8,$ we get that $k-2\le c{r}_{N_1}(P(3k,k))\le k-1.$

Keywords:

• The projective plane
• crossing number
• the generalized Petersen graph
• drawing

MR(2000) SUBJECT CLASSIFICATION:

• 05C10
• 05C62

1 Introduction

A surface Σ means a compact, connected 2-manifold. It is known that there are two kinds of closed surfaces, orientable and nonorientable [8]. Every closed connected orientable surface is homeomorphic to one of the standard surfaces S_k $(k\ge 0)$, while each closed connected nonorientable surface is homeomorphic to one of N_k $(k\ge 1)$. In particular, the projective plane, N₁, is a 2-manifold obtained by identifying every point of the 2-sphere with its antipodal point.

Let $G=(V,E)$ be a simple graph with vertex set V and edge set E. Let D be a drawing of the graph G in a surface $\Sigma ,$ we denote the number of pairwise intersections of edges in D by $v_D(G:\Sigma )$, or by v(D) when there is no ambiguity. The crossing number of G in a surface Σ, denoted by $c{r}_{\Sigma }(G)$, is the minimum number of pairwise intersections of edges in a drawing of G in Σ, i.e., $$c{r}_{\Sigma }(G)=\underset{D}{\min }{v}_D\left(G:\Sigma \right).$$

In particular, the crossing number of G in the plane S₀ is denoted by cr(G) for simplicity. It is well known that the crossing number of a graph in a surface Σ is attained only in good drawings of the graph, which are the drawings where no edge crosses itself, no adjacent edges cross each other, no two edges intersect more than once, and no three edges have a common point.

In a drawing D of $G=(V,E)$ in a surface $\Sigma ,$ if an edge is not crossed by any other edge, we say that it is clean in D, otherwise, we say it is crossed. Moreover, let $F\subseteq E$, we say F is clean in D if all of the edges in F are clean, otherwise, we say F is crossed.

Let A and B be two (not necessary disjoint) subsets of the edge set E, the number of crossings involving an edge in A and another edge in B is denoted by $v_D(A,B).$ In particular, $v_D(A,A)$ is denoted by $v_D(A).$ By counting the number of crossings in D, we have

Lemma 1.

Let A, B, C be mutually disjoint subsets of E, then $$\begin{array}{c}{v}_D(A,B\cup C)=v_D(A,B)+v_D(A,C),\\ v_D(A\cup B)=v_D(A)+v_D(A,B)+v_D(B).\end{array}$$

Computing the crossing number of a given graph is, in general, an elusive problem. Garey and Johnson have proved that the problem of determining the crossing number of an arbitrary graph in the plane is NP-complete [7]. Because of its difficulty, there are limited results concerning on this problem, see [1–4, 12–14, 16, 23] and the references therein. The Petersen graph plays the role of counterexample to many conjectures. And its generalization, the generalized Petersen graph P(n, k), is of great interest to the research community. Exoo, Harary and Kabell began to study the crossing number of P(n, k) in S₀ and they worked out the case when k = 2 [5]. For the case k = 3, Fiorini proved that $cr(P(9,3))=2$ [6], later on, Richter and Salazar [17] determined the crossing number of $P(3t+h,3)$ to be t + h if $h\in \{0,2\}$ and t + 3 if h = 1, for each $t\ge 3$, with the single exception of P(9, 3). We tried to obtain $cr(P(n,k))$ when n can be expressed as a function of k, and proved that $cr(P(3k,k))=k$ for $k\ge 4$ [22].

As for the crossing number of graphs in a surface other than the plane, it is not surprising that the results are even more limited: only the crossing number of Cartesian product graph $C_3\square C_n$ in N₁ [19], the crossing number of the complete graph K₉ in S₂ [20], the crossing number of the complete bipartite graph $K_{3,n}$ in a surface with arbitrary genus [18], the crossing number of $K_{4,n}$ either in N₁ or in S₁ [9, 10], the crossing number of the circulant graph $C(3k;\{1,k\})$ in N₁ [11], and the crossing number of the Hexagonal graph $H_{3,n}$ in a surface with arbitrary genus [21] have been determined. These facts motivate us to investigate the crossing number of $P(3k,k)$ ($k\ge 3$) in the projective plane, the main theorem of this paper is

Theorem 1.

When $3\le k\le 7,$ we have $c{r}_{N_1}(P(3k,k))=k-2$. Moreover, for $k\ge 8,$ we have $k-2\le c{r}_{N_1}(P(3k,k))\le k-1.$

Let us give an overview of the rest of this paper. Some basic notations are introduced in Section 2. Section 3 is devoted to the proof of Theorem 1 by investigating the upper and lower bound of $c{r}_{N_1}(P(3k,k))$, respectively. The lower bound of $c{r}_{N_1}(P(3k,k))$ is based on the result of Lemma 4, which will be proved finally in Section 4.

2 Preliminaries

Let $G=(V,E)$ be a graph in a surface Σ. A cycle C on Σ is called contractible if $\Sigma -C$ is disconnected and one of the components is homeomorphic to an open disc, otherwise it is named non-contractible.

For $F\subseteq E$, we denote by $G\setminus F$ the graph obtained from G by deleting all edges in F. Furthermore, we also use F to denote the subgraph induced on the edge set F if there is no ambiguity.

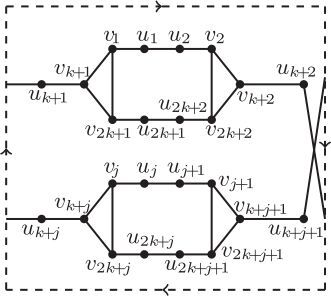
Let k be an integer greater than or equal to 3. The generalized Petersen graph $P(3k,k)$ is the graph with vertex set $$V(P(3k,k))=\{u_i,v_i\mid i=1,2,\dots ,3k\}$$and edge set $$E(P(3k,k))=\{u_i{u}_{i+1},u_i{v}_i,v_i{v}_{k+i}\mid i=1,2,\dots ,3k\},$$ the subscripts are read modulo $3k.$

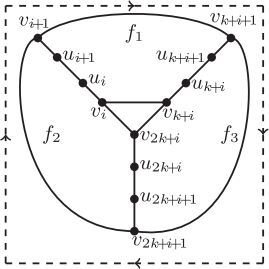
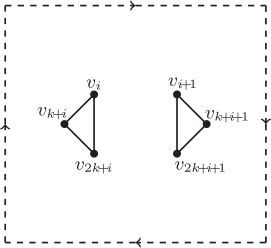
To seek the structure of $P(3k,k)$, we find it is helpful to partite the edge set $E(P(3k,k))$ into several subsets E_i and H_i as follows. For $1\le i\le k,$ let $$E_i=\{v_i{v}_{k+i},v_{k+i}{v}_{2k+i},v_{2k+i}{v}_i,u_i{v}_i,u_{k+i}{v}_{k+i},u_{2k+i}{v}_{2k+i}\}$$and let $$H_i=\{u_i{u}_{i+1},u_{k+i}{u}_{k+i+1},u_{2k+i}{u}_{2k+i+1}\},$$ the subscripts are expressed modulo $3k.$

Set $E\prime ={\cup }_{i=1}^k{E}_i.$ It is not difficult to see that (1) $$E(P(3k,k))=E\prime \cup \left(\underset{i=1}{\overset{k}{\cup }}{H}_i\right)$$(1) and that $P(3k,k)\setminus E_i$ is homeomorphic to $P(3(k-1),(k-1))$ for each $1\le i\le k$.

Note that three edges $v_i{v}_{k+i},v_{k+i}{v}_{2k+i}$ and $v_{2k+i}{v}_i$ form a 3-cycle in E_i, which is denoted by EC_i throughout the following discussions. Formally, $$E{C}_i=v_i{v}_{k+i}{v}_{2k+i}{v}_i.$$

Let D be a good drawing of $P(3k,k)$ in the projective plane. We define a function $f_D(H_i)$ ($1\le i\le k$) counting the number of crossings related to H_i in D as follows: (2) $$f_D(H_i)=v_D(H_i,H_i)+\frac{1}{2}\sum _{1\le j\le k,\mathrm{ }j\ne i}{v}_D(H_i,H_j).$$(2)

In the rest of the discussions, we find the following definition is useful.

Definition 1.

An $E\prime$-clean drawing of $P(3k,k)$ is a good drawing of $P(3k,k)$ in the projective plane such that $E\prime$ is clean.

By Eqs. (1)(1) $$E(P(3k,k))=E\prime \cup \left(\underset{i=1}{\overset{k}{\cup }}{H}_i\right)$$(1) and (2)(2) $$f_D(H_i)=v_D(H_i,H_i)+\frac{1}{2}\sum _{1\le j\le k,\mathrm{ }j\ne i}{v}_D(H_i,H_j).$$(2) and by counting the number of crossings in D, we get

Lemma 2.

Let D be an $E\prime$-clean drawing of $P(3k,k)$, then $$v(D)=\sum _{i=1}^k{f}_D(H_i).$$

3 Proof of Theorem 1

In the beginning of this section, we obtain the upper bound of $c{r}_{N_1}(P(3k,k))$ by a brief proof based on some former results.

Lemma 3.

$c{r}_{N_1}(P(9,3))\le 1$, and $c{r}_{N_1}(P(3k,k))$ $\le k-1$ for $k\ge 4.$

Proof.

Wilson’s Lemma states that the crossing number of a non-planar graph in the projective plane is strictly less than its crossing number in the plane [19]. Combining this fact with the result that $cr(P(9,3))=2$ [6] and that $cr(P(3k,k))=k$ for $k\ge 4$ [22], the lemma follows easily. □

Our main efforts are made to establish the lower bound of $c{r}_{N_1}(P(3k,k)),$ which is based on the lemma below.

Lemma 4.

For $k\ge 4,$ let D be an $E\prime$-clean drawing of $P(3k,k)$. Then $v(D)\ge k-1.$

We postpone its proof to Section 4. By assuming Lemma 4, we can prove the lower bound of $c{r}_{N_1}(P(3k,k))$ immediately.

Lemma 5.

$c{r}_{N_1}(P(3k,k))\ge k-2$ for $k\ge 3.$

Proof.

We prove the lemma by induction on k. First of all, it is seen from Figures 1 and 2 that $P(9,3)\setminus \{v_3{v}_9,v_2{v}_5,v_1{v}_7\}$ is a subdivision of $F_{13}(12,18)$, which is one of minimal forbidden subgraphs for the projective planarity (see Appendix A in [15]), therefore, the induction basis $c{r}_{N_1}(P(9,3))\ge 1$ holds. Suppose that $c{r}_{N_1}(P(3(k-1),(k-1)))\ge k-3$ when $k\ge 4,$ consider now the graph $P(3k,k).$ Let D be a good drawing of $P(3k,k)$ in $N_1.$

Fig. 1 The graph $P(9,3).$.

Fig. 2 The graph $F_{13}(12,18).$.

Case 1.

There exists an integer i $(1\le i\le k)$ such that E_i is crossed in D.

Without loss of generality, we may assume that $i=1.$ By deleting the edges of E₁ in D, we get a good drawing D₀ of $P(3(k-1),(k-1))$ in N₁ with at least k–3 crossings by the induction hypothesis, thus $$v(D)\ge v(D_0)+1\ge (k-3)+1=k-2.$$

Case 2.

E_i is clean in D for every $1\le i\le k$.

Then D is an $E\prime$-clean drawing of $P(3k,k)$. Due to Lemma 4, $v(D)\ge k-1$ holds.

Therefore, $c{r}_{N_1}(P(3k,k))\ge k-2$ when $k\ge 3.$ □

Based on the former lemmas, we can prove Theorem 1 in the following.

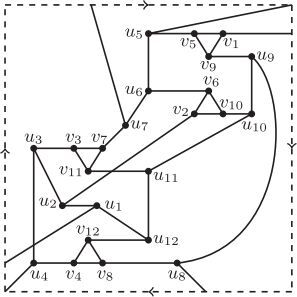
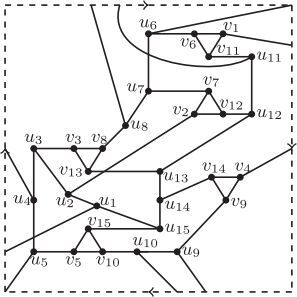
The proof of Theorem 1. Figures 3–6 demonstrate good drawings of $P(3k,k)$ in N₁ with k–2 crossings when $4\le k\le 7,$ thus $c{r}_{N_1}(P(3k,k))\le k-2.$ Together with Lemmas 3 and 5, it is confirmed that $c{r}_{N_1}(P(3k,k))=k-2$ for $3\le k\le 7.$

Fig. 3 A good drawing of P(12, 4) in N₁ with two crossings.

Fig. 4 A good drawing of P(15, 5) in N₁ with three crossings.

Fig. 5 A good drawing of P(18, 6) in N₁ with four crossings.

Fig. 6 A good drawing of P(21, 7) in N₁ with five crossings.

For $k\ge 8,$ we have $k-2\le c{r}_{N_1}(P(3k,k))\le k-1$ due to Lemmas 3 and 5. The proof is completed. □

4 The proof of Lemma 4

For $1\le i\le k,$ let (3) $$R_i=E_i\cup H_i\cup E_{i+1}.$$(3)

The following observation is obvious, but since it is appears several times in the rest of the paper, we state it formally.

Observation 1. Let D be an $E\prime$-clean drawing of $P(3k,k)$, then E_i is clean for all $1\le i\le k.$

Lemma 6.

For $k\ge 3,$ let D be an $E\prime$-clean drawing of $P(3k,k)$ such that one of the 3-cycles EC_i and $E{C}_{i+1}$ is non-contractible. Then $f_D(H_i)\ge 1.$

Proof.

Without loss of generality, assume that EC_i is non-contractible, for the other case, the proof is analogous. Then $E{C}_{i+1}$ is contractible, since otherwise, two non-contractible cycles EC_i and $E{C}_{i+1}$ will cross each other at least once in $N_1,$a contradiction to Observation 1.

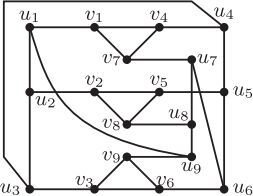
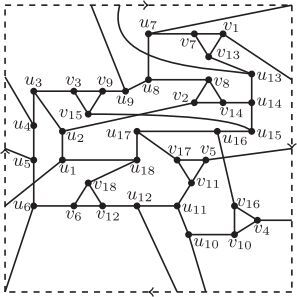
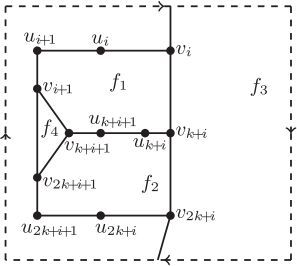
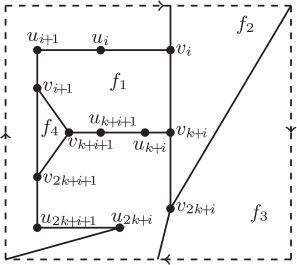
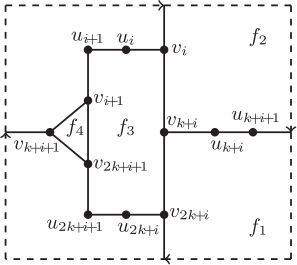
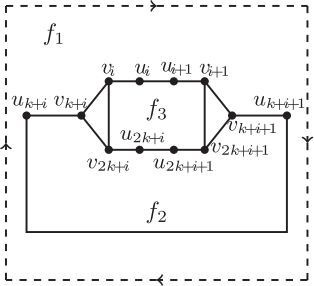
Suppose to the contrary that $f_D(H_i)<1$. Then the three edges of H_i cannot cross each other by Eq. (2)(2) $$f_D(H_i)=v_D(H_i,H_i)+\frac{1}{2}\sum _{1\le j\le k,\mathrm{ }j\ne i}{v}_D(H_i,H_j).$$(2) . By above analyses, there are three possibilities of the subdrawing of R_i, see Figures 7–9. It is seen that, in each subdrawing of $R_i,$ the projective plane has been divided into four regions.

Fig. 7 A subdrawing of $R_i.$.

Fig. 8 A subdrawing of $R_i.$.

Fig. 9 A subdrawing of $R_i.$.

Firstly, we consider the case that the subdrawing of R_i is drawn as in Figure 7. Consider now the subgraph $E_{i+2}$. It is asserted that all of the vertices of $E_{i+2}$ lie in the same region in the subdrawing of R_i by Observation 1. Furthermore, they cannot lie in the region labeled $f_4,$ otherwise the edge $u_{i+1}{u}_{i+2}$ will cross $E{C}_{i+1}$ at least once, a contradiction to Observation 1. The following three cases are investigated.

Case 1.

The vertices of $E_{i+2}$ lie in the region labeled $f_1.$

Then the edge $u_{2k+i+1}{u}_{2k+i+2}$ and the path $u_{k+i+2}{u}_{k+i+3}\cdots u_{2k+i}$ will cross H_i at least once, respectively, which implies that $f_D(H_i)\ge 1$ by Eq. (2)(2) $$f_D(H_i)=v_D(H_i,H_i)+\frac{1}{2}\sum _{1\le j\le k,\mathrm{ }j\ne i}{v}_D(H_i,H_j).$$(2) , a contradiction.

Case 2.

The vertices of $E_{i+2}$ lie in the region labeled $f_2.$

Then the edge $u_{i+1}{u}_{i+2}$ and the path $u_{2k+i+2}{u}_{2k+i+3}\cdots u_{3k}{u}_1\cdots u_i$ will cross H_i at least once, respectively, which implies that $f_D(H_i)\ge 1$, a contradiction.

Case 3.

The vertices of $E_{i+2}$ lie in the region labeled $f_3.$

Then H_i will be crossed by the edge $u_{k+i+1}{u}_{k+i+2}$ and by the path $u_{i+2}{u}_{i+3}\cdots u_{k+i}$ at least once respectively, which yields that $f_D(H_i)\ge 1$, a contradiction.

Similar contradictions occur if the subdrawing of R_i is drawn as in Figure 8 or 9. □

Lemma 7.

For $k\ge 3,$ let D be an $E\prime$-clean drawing of $P(3k,k)$. If $E{C}_i\cup E{C}_{i+1}$ is drawn as in Figure 10 or 11, then $f_D(H_i)\ge 1.$

Fig. 10 A subdrawing of $E{C}_i\cup E{C}_{i+1}.$.

Fig. 11 A subdrawing of $E{C}_i\cup E{C}_{i+1}.$.

Proof.

Suppose to the contrary that $f_D(H_i)<1.$ By Eq. (2)(2) $$f_D(H_i)=v_D(H_i,H_i)+\frac{1}{2}\sum _{1\le j\le k,\mathrm{ }j\ne i}{v}_D(H_i,H_j).$$(2) , it is claimed that

Claim 1. The edges of H_i cannot cross each other in D.

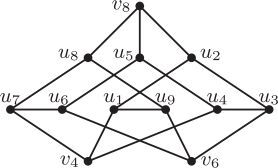
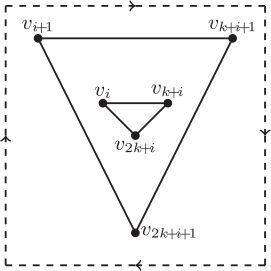
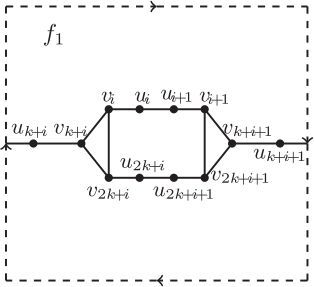
If $E{C}_i\cup E{C}_{i+1}$ is drawn as in Figure 10. Then R_i is shown as in Figure 12 by Observation 1 and Claim 1. Consider the subgraph $E_{i+2}$. It lies in one of the regions labeled $f_1,$ f₂ and f₃ by Observation 1 again. Assume that $E_{i+2}$ lies in the region labeled $f_1,$ then the edge $u_{2k+i+1}{u}_{2k+i+2}$ and the path $u_{k+i+2}{u}_{k+i+3}\cdots u_{2k+i}$ will cross H_i at least once respectively. Hence, by Eq. (2)(2) $$f_D(H_i)=v_D(H_i,H_i)+\frac{1}{2}\sum _{1\le j\le k,\mathrm{ }j\ne i}{v}_D(H_i,H_j).$$(2) , we have $f_D(H_i)\ge 1,$a contradiction. Similar contradictions occur if $E_{i+2}$ lies in the region labeled f₂ or $f_3.$

Fig. 12 A subdrawing of $R_i.$.

Using analogous arguments, we can also show that $f_D(H_i)\ge 1$ if $E{C}_i\cup E{C}_{i+1}$ is drawn as in Figure 11. $\square$

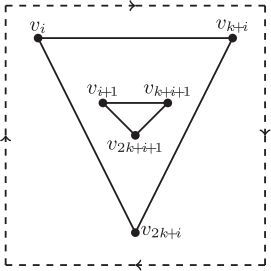
Lemma 8.

For $k\ge 3,$ let D be an $E\prime$-clean drawing of $P(3k,k)$. If $E{C}_i\cup E{C}_{i+1}$ is drawn as in Figure 13 and $f_D(H_i)<1,$ then R_i is shown as in Figure 15.

Fig. 13 A subdrawing of $E{C}_i\cup E{C}_{i+1}.$.

Proof.

First of all, we conclude that the edges of H_i cannot have internal crossings in D by the assumption that $f_D(H_i)<1$. Thus, there are two possibilities of the subdrawing of R_i in D. See Figures 14 and 15.

Fig. 14 A subdrawing of $R_i.$.

Fig. 15 A subdrawing of $R_i.$.

If R_i is drawn as in Figure 14. Observation 1 enforces that $E_{i+2}$ lies in one of the regions labeled $f_1,$ f₂ and f₃. We may assume firstly that $E_{i+2}$ lies in the region labeled $f_1,$ for the other cases the proof is similar. Under this circumstance, the edge $u_{2k+i+1}{u}_{2k+i+2}$ and the path $u_{k+i+2}{u}_{k+i+3}\cdots u_{2k+i}$ will cross H_i at least once respectively, therefore, $f_D(H_i)\ge 1$ by Eq. (2)(2) $$f_D(H_i)=v_D(H_i,H_i)+\frac{1}{2}\sum _{1\le j\le k,\mathrm{ }j\ne i}{v}_D(H_i,H_j).$$(2) , a contradiction.

Thus, R_i is shown as in Figure 15. □

Combining Lemma 7 with Lemma 8, we have

Lemma 9.

For $k\ge 3,$ let D be an $E\prime$-clean drawing of $P(3k,k)$ such that both EC_i and $E{C}_{i+1}$ are contractible cycles. If R_i is not drawn as in Figure 15, then $f_D(H_i)\ge 1.$

Proof.

Since both EC_i and $E{C}_{i+1}$ are contractible cycles, there are three possibilities of the subdrawing of $E{C}_i\cup E{C}_{i+1}$. See Figures 10, 11, and 13. Lemma 7 implies that $f_D(H_i)\ge 1$ if $E{C}_i\cup E{C}_{i+1}$ is drawn as in Figure 10 or 11. Furthermore, Lemma 8 implies that $f_D(H_i)\ge 1$ if R_i is not drawn as in Figure 15. □

Now, we are ready to prove Lemma 4.

The proof of Lemma 4. Suppose to the contrary that (4) $$v(D)<k-1.$$(4)

By Lemma 2, there exists an integer i such that $f_D(H_i)<1,$ since otherwise, $$v(D)=\sum _{i=1}^k{f}_D(H_i)\ge k,$$a contradiction to Eq. (4)(4) $$v(D)<k-1.$$(4) . The following two cases are discussed: Case 1. there exists an integer i such that $f_D(H_i)=0$ and Case 2. $f_D(H_i)>0$ for every $1\le i\le k$ and there exists an integer i such that $f_D(H_i)=\frac{1}{2}.$

Case 1.

There exists an integer i such that $f_D(H_i)=0.$

Without loss of generality, let $f_D(H_1)=0.$ Thus, we can get that

Claim 2. R₁ is clean in D.

Furthermore, there exists another integer j $(j\ne 1)$ satisfying $f_D(H_j)<1,$ otherwise, $$v(D)=\sum _{i=2}^k{f}_D(H_i)\ge k-1,$$a contradiction to Eq. (4)(4) $$v(D)<k-1.$$(4) .

Subcase 1.1.

j = 2 or j = k.

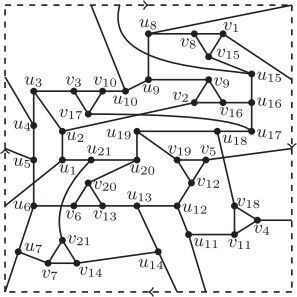
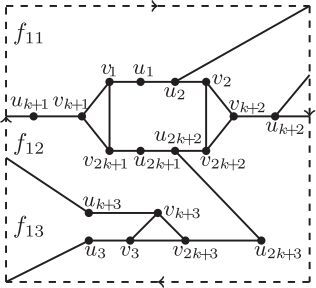
By symmetry, we only need to consider the case that j = 2. It follows from Lemma 6 that both EC₁ and EC₂ are contractible cycles since $f_D(H_1)=0.$ Moreover, Lemma 9 enforces that the subdrawing of R₁ is shown as in Figure 15 by replacing all the indices i by 1.

Now, we consider the subgraph E₃. All vertices of E₃ lie in the region labeled f₁, on whose boundary lie the vertices $u_2,u_{k+2}$ and $u_{2k+2},$ otherwise, we have $v_D(H_2,R_1)\ge 1$, contradicting Claim 2. Moreover, the edges of H₂ cannot have internal crossings by Eq. (2)(2) $$f_D(H_i)=v_D(H_i,H_i)+\frac{1}{2}\sum _{1\le j\le k,\mathrm{ }j\ne i}{v}_D(H_i,H_j).$$(2) . All these arguments confirm that the only possibility of the subdrawing of $R_1\cup H_2\cup E_3$ is shown as in Figure 16. Note that the region labeled by f₁ in Figure 15 has been separated into three regions, which are labeled by f₁₁, f₁₂ and f₁₃.

Fig. 16 A subdrawing of $R_1\cup H_2\cup E_3.$.

Next, we consider the subgraph E_k (note that $k\ge 4$ is crucial here for E_k being not equal to E₃). By Observation 1, E_k lies in one of f₁₁, f₁₂ and f₁₃. We may assume that E_k lies in f₁₁, for other cases the proof is the same. Under this circumstance, H₂ will be crossed by the edge $u_{2k}{u}_{2k+1}$ and by the path $u_{k+3}{u}_{k+4}\cdots u_{2k}$ at least once respectively. Therefore, $f_D(H_2)\ge 1$ by Eq. (2)(2) $$f_D(H_i)=v_D(H_i,H_i)+\frac{1}{2}\sum _{1\le j\le k,\mathrm{ }j\ne i}{v}_D(H_i,H_j).$$(2) , a contradiction.

Subcase 1.2.

$j\notin \{2,k\}.$

Since $f_D(H_1)=0$ and $f_D(H_j)<1,$ all of the cycles $E{C}_1,$ $E{C}_2,$ EC_j and $E{C}_{j+1}$ are contractible by Lemma 6. By Lemma 9, R₁ (respectively R_j) is drawn as in Figure 15 by replacing all the indices i by 1 (respectively j).

Note that both $u_{k+1}{v}_{k+1}{v}_1{u}_1{u}_2{v}_2{v}_{k+2}{u}_{k+2}{u}_{k+1}$ and $u_{k+j}{v}_{k+j}{v}_j{u}_j{u}_{j+1}{v}_{j+1}{v}_{k+j+1}{u}_{k+j+1}{u}_{k+j}$ are non-contractible curves. Therefore, they must cross each other in N₁, which yields that $v_D(H_1,H_j)\ge 1$ since $E\prime$ is clean in D, a contradiction to $f_D(H_1)=0$.

Case 2.

$f_D(H_i)>0$ for every $1\le i\le k$ and there exists an integer i such that $f_D(H_i)=\frac{1}{2}.$

Without loss of generality, let $f_D(H_1)=\frac{1}{2}.$ There exists an integer j ($j\notin \{2,k\}$) such that $f_D(H_j)=\frac{1}{2},$ since otherwise $$\begin{array}{c}v(D)=\sum _{i=1}^k{f}_D(H_i)\\ \ge 3\times \frac{1}{2}+\sum _{i=4}^k{f}_D(H_i)\\ \ge \frac{3}{2}+(k-3),\end{array}$$and thus $v(D)\ge k-1$ since v(D) is an integer, a contradiction to Eq. (4)(4) $$v(D)<k-1.$$(4) .

By Lemma 6, each cycle of $E{C}_1,$ $E{C}_2,$ EC_j and $E{C}_{j+1}$ is contractible. By Lemma 9, R₁ (respectively R_j) is drawn as in Figure 15 by replacing all the indices i by 1 (respectively j). Note that both $u_{k+1}{v}_{k+1}{v}_1{u}_1{u}_2{v}_2{v}_{k+2}{u}_{k+2}{u}_{k+1}$ and $u_{k+j}{v}_{k+j}{v}_j{u}_j{u}_{j+1}{v}_{j+1}{v}_{k+j+1}{u}_{k+j+1}{u}_{k+j}$ are non-contractible curves. Then $$v_D(H_1,H_j)=1$$since $f_D(H_1)=f_D(H_j)=\frac{1}{2}$. Furthermore, the crossed edge of H₁ (respectively H_j) is $u_{k+1}{u}_{k+2}$ (respectively $u_{k+j}{u}_{k+j+1}$). See Figure 17. It is seen that two vertices u₂ and u_j do not lie on the boundary of the same region, thus the path $u_2{u}_3\cdots u_j$ will cross H₁ or H_j by Observation 1, a contradiction to the assumption that $f_D(H_1)=f_D(H_j)=\frac{1}{2}$.

Fig. 17 A subdrawing of $R_1\cup R_j.$.

All of the above contradictions enforce that $v(D)\ge k-1$ if D is an $E\prime$-clean drawing of $P(3k,k)$. □

5 Conclusions

This paper studies the crossing number of the generalized Petersen graph $P(3k,k)$ in the projective plane. When $k\ge 8$, the exact value of $c{r}_{N_1}(P(3k,k))$ remains open. Does $c{r}_{N_1}(P(3k,k))=k-2$ or $c{r}_{N_1}(P(3k,k))=k-1$? From the former proofs, we know that the problem of deciding the exact value of $c{r}_{N_1}(P(3k,k))$ can be reduced to the problem of whether there exists a good drawing of $P(3k,k)$ in the projective plane with k–2 crossings. If the answer to the latter problem is” yes”, then we conclude that $c{r}_{N_1}(P(3k,k))=k-2$, otherwise, we have $c{r}_{N_1}(P(3k,k))=k-1$.

Acknowledgments

The authors would like to express their sincere thanks to the anonymous referees for their helpful comments to improve the paper.

Disclosure statement

No author associated with this paper has disclosed any potential or pertinent conflicts which may be perceived to have impending conflict with this work.

Data availability statement

No data were used to support this study.

Additional information

Funding

This work was supported by National Science Foundation of China (No. 12271157), Natural Science Foundation of Hunan Province (No. 2022JJ30028 & No. 2023JJ30072) and Hunan Education Department Foundation (No. 21C0762).