On the distinguishing chromatic number of the Kronecker products of graphs

Abstract

In this paper, we investigate the distinguishing chromatic number of Kronecker product of paths, cycles, star graphs, symmetric trees, almost symmetric trees, and bisymmetric trees.

Keywords:

• Distinguishing chromatic number
• Kronecker product

2000 MATHEMATICS SUBJECT CLASSIFICATION:

• 05C15
• 05C76

1 Introduction

Let G be a graph. A proper coloring of G is a function that assigns a color to every vertex such that two adjacent vertices receive different colors. The chromatic number of G, denoted by $\chi (G)$, is the minimum number of colors needed for a proper coloring. In this paper, we use the term coloring to mean proper coloring. The distinguishing number of a graph, which was introduced in 1996 by Albertson and Colline [1], has been studied in several papers (see, e.g., [2] and [4]). The concept of distinguishing coloring and distinguishing chromatic number was introduced by Colline and Trank [5]. The distinguishing coloring is a coloring of a graph G with the property that no nontrivial automorphism preserves coloring, and the minimum number of colors required for distinguishing coloring is called the distinguishing chromatic number, which is denoted by ${\chi }_D(G)$. For recent results on the distinguishing coloring and distinguishing chromatic number of graphs and different products see [3, 7, 9, 10].

The Kronecker product of two graphs G and H, which is denoted by G × H, is a graph with vertex set $V(G)\times V(H)$, and two distinct vertices (a, b) and (x, y) are adjacent in G × H if and only if a is adjacent to x in G and b is adjacent to y in H. The Kronecker product is one of the most important graph products and seems to have been first introduced by Čulik, who called it the cardinal product [12]. The adjacency matrix of the Kronecker graph product is given by the Kronecker matrix product of the adjacency matrices of the factor graphs; see [13] for details. Note that the Kronecker product is commutative and associative. We recall the following theorem.

Theorem 1.1.

[8, Weichsel’s Theorem] Suppose that G and H are connected nontrivial graphs. If at least one of G or H has an odd cycle, then G × H is connected. If both G and H are bipartite, then G × H has exactly two components.

Recently, in 2017, Alikhani and Soltani [2] studied the distinguishing number of Kronecker product of two graphs, such as complete graph and a complete multipartite graph.

In Section 2 of this paper, we present some results for the distinguishing chromatic number of the Kronecker product of paths, cycles, and star graphs. In Section 3, we investigate the distinguishing chromatic number of the Kronecker product of almost symmetric trees, symmetric trees, and bisymmetric trees.

We use the standard graph notation in [8]. We denote the path and the cycle of length n by P_n and C_n, respectively. Also S_n stands for the star graph with n + 1 vertices. An almost symmetric tree, denoted by $T_{d,h}^{\prime }$, is a tree with a central vertex x of degree d – 1, all leaves have the same distance h from x, and all the vertices that are not leaves have degree d. Recall that ${\chi }_D(P_{2k})=3,{\chi }_D(P_{2k-1})=2$, that ${\chi }_D(C_4)={\chi }_D(C_6)=4$, that ${\chi }_D(C_n)=3$, that ${\chi }_D(K_{p,q})=p+q$, and that ${\chi }_D(T_{d,h}^{\prime })=d$, where $k,m,n,p,q\in \mathbb{N}$; see [5].

In drawing the graph G × H, we index the rows by the vertices of G and index the columns by the vertices of H. We set the vertices of an almost symmetric tree by using the Breadth-first search algorithm; see [6]. A cycle consisting of vertices of two consecutive columns i and i + 1 is called $(i,i+1)$-column cycle. Similarly $(i,i+1)$-row cycle is a cycle that consists of the vertices of two rows of i and i + 1.

2 The results for paths, cycles, and star graphs

In this section, we study the distinguishing chromatic number of Kronecker product of paths, cycles, and star graphs. We begin this section with the following theorem.

Theorem 2.1.

Let P_n be a path of length n. Then ${\chi }_D(P_2\times P_2)=5$ and ${\chi }_D(P_2\times P_{2k})=4$, otherwise ${\chi }_D(P_n\times P_m)=3$, where $k,n,m\in \mathbb{N}$.

Proof.

Let P_n be a path of length n. First consider the graph $P_n\times P_m$ that is not isomorphic to $P_2\times P_2$ and $P_2\times P_{2k}$, where $k,n,m\in \mathbb{N}$. In order to determine the distinguishing chromatic number of $P_n\times P_m$, we consider the following three cases:

Case 1:

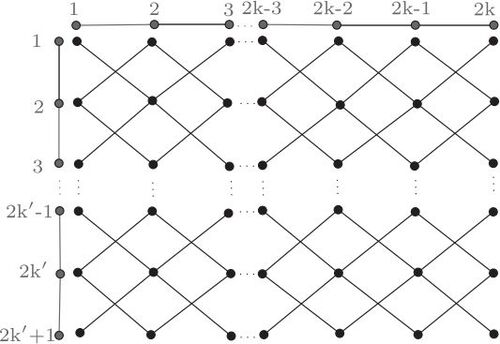
Let $n=2k\prime$ and let $m=2k-1$, where $k,k\prime \in \mathbb{N}$. It follows from Theorem 1.1 that Pn × Pm has two components and is shown in Figure 1.

Fig. 1 $P_{2k\prime }\times P_{2k-1}$.

We know that for every $n,m\in \mathbb{N},\chi (P_n\times P_m)=2$, while ${\chi }_D(P_n\times P_m)\ne 2$ because $P_n\times P_m$ is a symmetric graph. Thus we need at least three colors for distinguishing coloring. Consider one of the components of $P_n\times P_m$, say component 1, and color it with two colors 1 and 2 properly. Now we change the color of the vertices $(2k\prime +1,2i)$ with color 3, where $i\in \{1,\dots ,k\}$. We color the other connected component similar to the first component by replacing the class of colors 1 and 2 with each other. We claim that this coloring is distinguishing. Since the neighbors of the vertices of color 3 in the two connected components have different colors, we cannot map a vertex of color 3 to any of vertices of color 3 in the other connected component. Note that every component has only one pendant vertex x with color 3, so it is fixed. Let a and b be two vertices of color 3 in one component. Then clearly $d(a,x)\ne d(b,x)$. Therefore we can deduce that all vertices with color 3, are fixed vertices. All vertices in row $2k\prime$ have two fixed neighbors except one of them is of degree 2. Thus all of them are fixed vertices. One can easily see that, all vertices in the other rows are fixed. Therefore we have ${\chi }_D(P_{2k\prime }\times P_{2k-1})=3$ for $k,k\prime \in \mathbb{N}$.

Case 2:

Let $n=2k\prime -1$ and let $m=2k-1$, where $k,k\prime \in \mathbb{N}$. Without loss of generality, we may assume that $n\le m$. Similar to the previous case, $P_n\times P_m$ has two isomorphic connected components and it is clear that ${\chi }_D(P_n\times P_m)\ne 2$. Thus we need at least three colors for distinguishing coloring. For $k=k\prime =1$, it is clear that ${\chi }_D(P_1\times P_1)=3$. So we have $k\ne 1$. Now, we color the vertices of this graph with colors 1 and 2 properly except the vertices $(2k\prime ,2k-2),(2k\prime ,2k-1)$, and $(2k\prime ,2k)$, which are colored with color 3. Note that the two components cannot be mapped to each other, because they have different number of vertices of color 3. Also, since the vertices of color 3 in the same component have different degrees, they are fixed. In each component, there are two pendant vertices with different colors, and so these vertices are fixed. Since non of the vertices in the first and the last columns, receive color 3, and also the vertices in the last row, have different distances from the vertices of color 3, we get that all the vertices in the last row are fixed. In each row, similar to Case 1, one can easily see that all vertices in the other rows are fixed. Thus this coloring is distinguishing. Therefore we have ${\chi }_D(P_{2k\prime -1}\times P_{2k-1})=3$ for $k,k\prime \in \mathbb{N}$.

Case 3:

Let $n=2k\prime$ and Let $m=2k$, where $k,k\prime \in \mathbb{N}$. Without loss of generality, we may assume that $n\le m$. Similar to Case 1, $P_n\times P_m$ has two connected components and it is clear that ${\chi }_D(P_n\times P_m)\ne 2$. Thus we need at least three colors for distinguishing coloring. We change the color of the vertices $(2k\prime +1,2k-1),(2k\prime +1,2k)$, and $(2k\prime +1,2k+1)$ with color 3, after coloring all vertices with colors 1 and 2 properly. By a similar argument, which is used in Case 2, we can see that this coloring is distinguishing. Therefore we have ${\chi }_D(P_{2k\prime }\times P_{2k})=3$ for $k,k\prime \in \mathbb{N}$.

Now we prove that ${\chi }_D(P_2\times P_{2k})=4$, where $k\in \mathbb{N}$. Clearly we need at least three colors. For distinguishing coloring with three colors, we must color all the vertices in the row 2, with the same color, say color 3; otherwise, we color two distinct vertices in row 2 of distance 2 with different colors. Then there will be two vertices with the same color that can be mapped to each other, which implies that this coloring is not distinguishing. Now, for distinguishing coloring, we color the remaining vertices that have the same neighbor with different colors. Since each component has a nontrivial automorphism that preserves coloring, its coloring with three colors is not a distinguishing coloring. Hence we need at least four colors. In the above coloring, we change the color of the vertices $(2,2k+1)$ and $(3,2k+1)$ with color 4. One can easily see that this coloring is distinguishing.

Since $P_2\times P_2$ consists of two components isomorphic to S₄ and Q₂, ${\chi }_D(S_4)=5$ and ${\chi }_D(Q_2)=4$, we have that ${\chi }_D(P_2\times P_2)=5$. □

Theorem 2.2.

Let P_n and S_n denote respectively a path of length n and a star on n + 1 vertices where $n\ge 3$. Then ${\chi }_D(S_n\times P_m)$ equals to n + 1 if m is an odd number and equals to n + 2, if m is an even number with $m\ne 2$, and ${\chi }_D(S_n\times P_2)=2n+1$.

Proof.

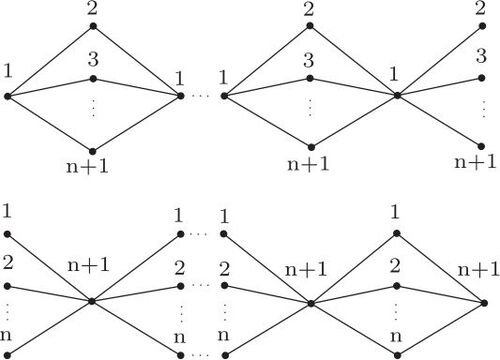
Note that if $n\in \{1,2\}$, then ${\chi }_D(S_n\times P_m)$ is determined in Theorem 2.1. Now, $S_n\times P_{2k-1}$ consists of two connected components that are pictured in Figure 2.

Fig. 2 Components of $S_2\times P_{2k-1}$.

Since each of the components has a vertex with n pendant neighbors, we need at least n + 1 colors for distinguishing coloring. It is enough to color one of the components. Because, the other component can be colored similar to the first one by replacing the class of colors of two vertices of degree 2 and 2n with each other. All vertices with degree greater than two, should be colored with the same color. Otherwise, there exist two vertices that are colored with the same color and can be mapped to each other, which implies that the coloring is not distinguishing. Also, we color the vertices of degree 2 with the remaining n colors.

Now, consider the graph $S_n\times P_{2k}$. Since each component is symmetric, for distinguishing coloring, we need at least n + 2 colors, and it is enough to color one vertex of degree n and one pendant vertex with color n + 2 in the similar coloring of the previous situation. Therefore, this coloring will be distinguishing, and so ${\chi }_D(S_n\times P_m)=n+2$.

In the case that m = 2, $S_n\times P_2$ consists of two components isomorphic to $S_{2n}$ and $K_{2,n}$. Hence ${\chi }_D(S_n\times P_2)=2n+1$. □

Theorem 2.3.

Let C_m be a cycle of length m and let S_n be a star graph with n + 1 vertices, where $n\ge 3$. Then ${\chi }_D(S_n\times C_m)=n+2$ and ${\chi }_D(S_n\times C_4)=2n+2$.

Proof.

First consider the graph $S_n\times C_m$, where m is an odd number. By the fact that $S_n\times C_{2(2k+1)}=2(S_n\times C_{2k+1})$, it is enough to color the graph similar to the coloring of one of the components of the corresponding even cycle. Now, assume that in $S_n\times C_m$, where $m\ne 4$ is an even number, and so $S_n\times C_m$ have two connected components. It is enough to color one of the components, because in the other component, we change the class of colors of one vertex of degree 2 with the class of colors of one vertex of degree 2n. As a similar method, which is used in the proof of Theorem 2.2, we have ${\chi }_D(S_n\times C_m)>n+1$. Now, consider all vertices of degree 2n as the vertices of a cycle, and we use 3 or 4 colors for distinguishing coloring of this cycle. Now, for distinguish coloring of vertices of degree 2, we color the vertices that have the same neighbors, with different colors. Since the vertices of degree 2n are colored distinguishingly, they are fixed. This implies that all vertices of degree 2 are also fixed vertices. Therefore ${\chi }_D(S_n\times C_m)=n+2$. Now, we consider the graph $S_n\times C_4$. Clearly $S_n\times C_4\cong 2K_{2,2n}$. Since ${\chi }_D(K_{2,2n})=2n+2$, we have ${\chi }_D(S_n\times C_4)=2n+2$. □

Proposition 2.4.

Let S_n be a star graph with n + 1 vertices. Then ${\chi }_D(S_n\times S_m)={\chi }_D(S_n){\chi }_D(S_m)-{\chi }_D(S_n)-{\chi }_D(S_m)+1=mn+1$.

Proof.

We have that $S_n\times S_m$ is a disconnected graph with two components S_mn and $K_{m,n}$. Since ${\chi }_D(S_{mn})=mn+1,{\chi }_D(K_{m,n})=m+n$, and ${\chi }_D(S_n\times S_m)=\max \{{\chi }_D(S_{mn}),{\chi }_D(K_{m,n})\}$, we conclude that ${\chi }_D(S_n\times S_m)=mn+1={\chi }_D(S_n){\chi }_D(S_m)-{\chi }_D(S_n)-{\chi }_D(S_m)+1$. □

In the following theorem, we determine the distinguishing chromatic number of the Kronecker product of paths and cycles of even length.

Theorem 2.5.

Let P_m be a path of length m and let C_n be a cycle of length n, where $n=2k$ is an even number. Then $${\chi }_D(P_m\times C_{2k})=\{\begin{array}{cc}3& m\ge 3,k\ne 2\mathrm{or}m=1,k\notin \{2,3\},\\ 4& m=2,k\ne 2orm=1,k\in \{2,3\}\\ & \mathrm{or k}=2,m\in \{4,6,\dots \},\\ 5& k=2,m\in \{3,5,\dots \},\\ 6& m=2,k=2.\end{array}$$

Proof.

Note that $P_1\times C_{2k}$, where $k\notin \{2,3\}$, consists of two components that are isomorphic to $C_{2k}$. Since ${\chi }_D(C_{2k})=3$ for $k\notin \{2,3\},{\chi }_D(P_1\times C_{2k})=3$. Also, $P_1\times C_4$ and $P_1\times C_6$ are isomorphic to two cycles of length 4 and two cycles of length 6, respectively. So ${\chi }_D(P_1\times C_{2k})=4$ for $k=\{2,3\}$.

Consider $P_2\times C_{2k}$, where $k\ne 2$. This graph consists of two connected components. By Figure 2 and similar to the proof of Theorem 2.3, one can see that we need at least 4 colors. Now, consider all vertices of degree 4, as the vertices of a cycle. For distinguishing coloring of these vertices, 3 or 4 colors are needed, depends on the length of the cycle. The remaining vertices have degree 2. Also any two vertices of degree 2 with the same neighbors, should receive remaining different colors. The other component can be colored by changing the class of two suitable colors with each other. By the process of coloring, it can be seen that this coloring is distinguishing. Therefore we have ${\chi }_D(P_2\times C_{2k})=4$, where $k\ne 2$.

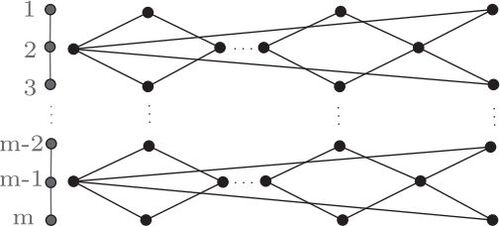
For m = 2 and k = 2, $P_2\times C_4$ consists of two connected components that are isomorphic to $K_{2,4}$. So ${\chi }_D(P_2\times C_4)=6$. Now, suppose that $m\ge 3$ and $k\notin \{2,3\}$. Then $P_m\times C_{2k}$ consists of two connected components, which are pictured in Figure 3.

Fig. 3 One component of $P_m\times C_{2k}$.

Clearly we need at least 3 colors for distinguishing coloring. In one of the components, we color all vertices with colors 1 and 2 properly, and then we replace the colors of one vertex in row 1 and one vertex in row 2 with distance 3 from each other, with color 3. The colors of neighbors of the vertices with color 3 are different, and so the vertices of color 3 are fixed. The vertices of rows 1 and 2 that form a cycle, are colored distinguishingly and so they are fixed. For $i\ge 3$, each vertex in row i has two distinct fixed neighbors, thus it is fixed. Hence the coloring is distinguishing and ${\chi }_D(P_m\times C_{2k})=3$ for $m\ge 3$ and $k\notin \{2,3\}$.

Now, assume that $m\ge 3$ and that k = 3. Then proper coloring of two components of $P_m\times C_{2k}$ with two colors is not distinguishing. We color one of the components with 3 colors as follows and the other component will be colored similarly by changing the class of colors 1 and 3 with each other. First we color the vertices with colors 1 and 2 properly and then we choose an arbitrary vertex, say a, in row 1 and two vertices of distance 2 from a, say b and c, where b is in row 1 and c is in the same column as a is in. Change the colors of the vertices a, b, and c with color 3. Since there are only one row and one column with two vertices of color 3, and also there are only one row and one column with only one vertex of color 3, the vertices a, b, and c are fixed, which implies that all other vertices are also fixed. Hence ${\chi }_D(P_m\times C_6)=3$ for $m\ge 3$.

Now let k = 2 and let m be an even number. Then $P_m\times C_4$ consists of two isomorphic connected components. If the vertices in the same row with distance 2 from each other, have the same color, then since they have the same neighbors, they can be mapped to each other. So for distinguishing coloring, we need at least 4 colors. We first color the vertices in the first component. We color every vertices in column i, where $i\in \{1,2,3,4\}$, with color i. Since the vertices of degree 2 have different colors, these vertices are fixed. Now, for distinguishing coloring of the vertices in the other component, we change the class of colors 1 and 4 with each other. One can easily see that every vertex has two fixed neighbors. So all vertices are fixed. Thus ${\chi }_D(P_m\times C_4)=4$, where m is an even number.

For k = 2 and the odd number m, $P_m\times C_4$ need at least 4 colors, and we color its components similar to the previous situation and note that this coloring is unique. Since m is an odd number, each of the components is symmetric. So, for distinguishing coloring of each component, a new color, say color 5, is needed. We replace the color of a vertex of degree 2 with color 5, in each of the components. Therefore ${\chi }_D(P_m\times C_4)=5$, when m is an odd number. The components of $P_2\times C_4$ are isomorphic to $K_{2,4}$. Thus ${\chi }_D(P_2\times C_4)=6$. □

In Theorem 2.5, we determine the distinguishing number of $P_m\times C_n$, whenever n is an even number. Also, as it is seen in the proof of Theorem 2.5, for distinguishing coloring of components, we only change the class of some colors. Therefore since $P_m\times C_{2(2k+1)}=2(P_m\times C_{2k+1})$, we have ${\chi }_D(P_m\times C_{2(2k+1)})={\chi }_D(P_m\times C_{2k+1})$. Hence we have the following corollary.

Corollary 2.6. Let P_m be a path of length m and let C_n be a cycle of length n. Then $${\chi }_D(P_m\times C_{2k+1})=\{\begin{array}{cc}3& m=2\mathit{\text{\hspace{1em}or\hspace{1em}m}}=1,k=1,\\ 4& m\notin \{1,2\}\mathit{\text{\hspace{1em}or\hspace{1em}m}}=1,k\ne 1.\end{array}$$

Theorem 2.7.

Let C_n be a cycle of length n. Then $${\chi }_D(C_m\times C_n)=\{\begin{array}{cc}8& m=n=4,\\ 5& m=n=3\mathit{\text{\hspace{1em}or\hspace{1em}m}}=4,n\ne 4,\\ 4& m=3,n=5,\\ 3& o.w.\end{array}$$

Proof.

First suppose that $n=m=4$. So we have $C_4\times C_4\cong 2K_{4,4}$. Hence we need at least 8 colors. After coloring one of the components with 8 colors, we color the second component similar to the first one by changing the colors of two adjacent vertices, say a and b, with each other. Now, if f is a nontrivial homomorphism that preserves coloring, then there exists a vertex x in the first component such that f(x) = a is in the second component. Now, the neighbors of x receive different colors from the neighbors of f(x) = a, which is impossible. Thus ${\chi }_D(C_4\times C_4)=8$.

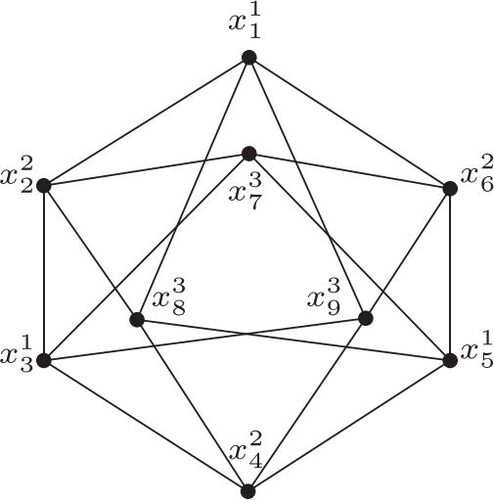
Now assume that $m=n=3$. By the notation $x_i^j$, we mean that the vertex x_i has color j. The graph $C_3\times C_3$, which is pictured in the Figure 4, is a connected graph that needs 3 colors for a proper coloring.

Fig. 4 $C_3\times C_3$.

Note that this coloring with 3 colors is unique, and as it is seen in Figure 4, it is not distinguishing. Now, we choose an arbitrary vertex, say x₁, and we recolor it with the new color 4. Then at most two of the vertices $x_3,x_4,x_5$, and x₇ can receive color 4. But in each of the situations, the coloring is symmetric, and so we need the new color 5. Now, it is enough to recolor two adjacent vertices in Figure 4, with colors 4 and 5, to obtain a distinguishing coloring. Therefore $\chi (C_3\times C_3)=5$.

In the graph $C_4\times C_m$, where $m\notin \{3,4,6\}$, if two vertices in the same column of one component have the same color, then they can be mapped to each other, because they have the same set of neighbors. Thus we need at least 4 colors and all coloring with 4 colors are isomorphic and these colorings are not distinguishing, because the vertices in the first column can be mapped to the vertices of the last column. So we need a new color. Now in the coloring with 4 colors, consider the (1, 2)-row cycle and color two vertices of this cycle that have distance 3 from each other with color 5. Clearly, these vertices are fixed and because of this cycle the columns cannot be mapped to each other. The second component, if there exists, will be colored similar to the first one by changing the class of colors 1 and 5 with each other. One can easily check that all vertices are fixed. Therefore ${\chi }_D(C_4\times C_m)=5$, where $m\notin \{3,4,6\}$. Now, let m = 2 and let $n\in \{3,6\}$. Then since $C_4\times C_6\cong 2(C_4\times C_3)$, we color the graph $C_4\times C_3$. By using a similar argument, we need 5 colors. In coloring with 4 colors, we change the color of two vertices (2, 2) and (3, 1) by color 5. Since the vertices of color 5 cannot be mapped to each other, all of the vertices are fixed. Therefore ${\chi }_D(C_4\times C_3)=5$.

For coloring of the graph $C_3\times C_5$, we need at least 3 colors. But in the coloring with 3 colors, the vertices of one row or one column must be colored with color 3. If the vertices of a row receive color 3, the coloring is symmetric, then it is not distinguishing. If the vertices of a column receive color 3 and other vertices are colored with 1 and 2, then there are 6 vertices that can receive color 3. At least 2 vertices of these 6 vertices must get color 3. But the coloring is symmetric and is not distinguishing. Hence we need a new color. Consider the coloring in which the vertices of one column receive color 3, and the other vertices are colored with colors 1 and 2. Now, we choose two vertices of distance 3 from each other on the row cycle, and we color them with color 4. Thus ${\chi }_D(C_3\times C_5)=4$. We prove that for the other situations, the distinguishing chromatic number of $C_m\times C_n$ is equal to 3 by considering the following cases.

Case 1.

Let $m=2k$ and let $n=2k\prime$, where $k,k\prime \in \mathbb{N}$. We may assume that $m\le n$. We have two following subcases.

Subcase 1.1.

Let $k\ge 3$ and let $C_m\times C_n\ncong C_6\times C_6$. We color one of the components with colors 1 and 2. But, since the coloring is not distinguishing, we color two vertices of the $(i,i+1)$-column cycle with color 3 that have distance 3 from each other. The second component will be colored similar to the first one by changing the color of two suitable classes of colors. By the similar argument as we used in the proof of Theorem 2.2, one can see that all vertices are fixed. Therefore, in this subcase, the distinguishing chromatic number is 3.

Subcase 1.2.

Let $k=k\prime =3$. We color 3 vertices in the same column with the same color 3, say a, b, and c, and also we recolor the vertex of distance 2 from a in the row of a, say d, by color 3. Since d is the only vertex in its column with color 3, hence a, b and c cannot be mapped to each other. Now, if c is mapped to d, then the common neighbor d and c that is adjacent to a must be fixed. So a and b are fixed. Thus the common neighbor of a and b that is adjacent to d, cannot be mapped to the neighbors of c. Hence c and d cannot be mapped to each other. By applying a similar argument, a or b cannot be mapped to d. All vertices are fixed, because the vertices a, b, c, and d are fixed. The second component will be colored distinguishingly similar to the first one by changing two suitable classes of colors. Thus ${\chi }_D(C_6\times C_6)=3$.

Case 2.

Let $m=2k+1$ and let $n=2k\prime +1$, where $k\ne 1$ or $k\prime \ne 1$ and also $C_m\times C_n\ncong C_3\times C_5$. Suppose that $m\le n$. Then we have the following subcases.

Subcase 2.1.

Let $k\ne 1$ and let $k\prime \ne 1$. We may assume that $m\le n$. We need at least 3 colors, and we color the vertices on the same row with the same color. we color the rows by colors $1,3,2,1,2,1,2,\dots$, respectively. Then consider the (4, 5)-row cycle, and change the color of two vertices of this cycle of distance 3 from each other with color 3. The vertices of this cycle cannot be mapped to each other and also cannot be mapped to the vertices of other rows, so they are fixed. Hence the other vertices have two fixed neighbors and they are fixed. Therefore, in this subcase, the distinguishing chromatic number is 3.

Subcase 2.2.

Let k = 1 and let $k\prime \ge 3$. Similar to the previous subcase, we need 3 colors. We color the columns by $1,3,2,1,2,1,2,\dots$. In the (1, 2)-row cycle, let w be a vertex of color 3 and let x and y be two vertices on this cycle such that $d(w,x)=2,d(w,y)=5$, and $d(x,y)=3$. We change the color of x and y with color 3. Thus the vertices of this cycle must be fixed and so all vertices are fixed. Therefore ${\chi }_D(C_3\times C_{(2k\prime +1)})=3$, where $k\prime \ge 3$.

Case 3.

Let $m=2k$ and let $n=2k\prime +1$, where $k\ge 3$. We have two following subcases.

Subcase 3.1.

Let $k\prime =1$. If k = 3, then ${\chi }_D(C_6\times C_3)=3$ since $C_6\times C_6\cong 2(C_6\times C_3)$. Now, If $k\ne 3$, then we color the columns by colors $1,2,1,\dots$. Also, we replace the colors of two vertices of distance 3 from each other that are in a row cycle, by color 3. Since the neighbors of the vertices with color 3 have different colors, these vertices are fixed. Hence, all of the vertices are fixed. Therefore, the distinguishing chromatic number is 3 in this subcase.

Subcase 3.2.

Let $k\prime \ne 1$. We color the rows with colors 1 and 2. Now we recolor two vertices of distance 3 with each other in a row cycle, with color 3. Thus the distinguishing chromatic number of this graph is 3. □

Lemma 2.8.

[11] If $G=(V_0\cup V_1,E)$ and $H=(W_0\cup W_1,F)$ are bipartite graphs, then $(V_0\times W_0)\cup (V_1\times W_1)$ and $(V_0\times W_1)\cup (V_1\times W_0)$ are vertex sets of the two components of G × H.

Proposition 2.9.

If $K_{m,n}$ and $K_{p,q}$ are complete bipartite graphs such that $p\ge q$ and $m\ge n$, then ${\chi }_D(K_{m,n}\times K_{p,q})=mp+nq$.

Proof.

The Kronecker product of two graphs $K_{m,n}$ and $K_{p,q}$ is the disjoint union of the graphs $K_{mp,nq}$ and $K_{mq,np}$, by Lemma 2.8. Since $p\ge q$ and $m\ge n$, so $|V(K_{mp,nq})|\ge |V(K_{mq,np})|$. Hence we have $${\chi }_D(K_{m,n}\times K_{p,q})=\max \{K_{mp,nq},K_{mq,np}\}=mp+nq.$$

3 The results for almost symmetric trees, symmetric trees, and bisymmetric trees

In the following, we discuss the distinguishing chromatic number of the Kronecker product of almost symmetric trees.

Lemma 3.1.

Let P_m be a path of length m and let $T_{d,h}^{\prime }$ be an almost symmetric tree with $d\ge 3$. Assume that $P_m\times T_{d,h}^{\prime }$ is colored with d colors. If there are at least two vertices in the same column of $P_m\times T_{d,h}^{\prime }$ with different colors, then the coloring is not distinguishing.

Proof.

Assume that there are at least two vertices in column l with different colors. Without loss of the generality, we may assume that there are vertices a and b of distance 2 from each other on the column l, with different colors, say colors 1 and 2. The vertices a and b have two neighbors with the same color i, where $i\in \{3,4,\dots ,d\}$ on the next two columns, say columns j and k. If the columns j and k are corresponding to the pendant vertices of $T_{d,h}^{\prime }$, then they can be mapped to each other, which implies that this coloring is not distinguishing. Otherwise, at least one of the columns j or k has two vertices with different colors, say column j. Now, by continuing this method, we find two vertices with the same color corresponding to the children of a vertex of $T_{d,h}^{\prime }$ that can be mapped to each other. Hence this coloring is not distinguishing. □

Corollary 3.2.

Let P_m be a path and let $T_{d,h}^{\prime }$ be an almost symmetric tree with $d\ge 3$. Assume that $P_m\times T_{d,h}^{\prime }$ is colored distinguishing with d colors. Then the vertices on each of the columns have the same colors.

Theorem 3.3.

Let P_m be a path and let $T_{d,h}^{\prime }$ be an almost symmetric tree, where $d\ge 3$. Then ${\chi }_D(P_1\times T_{d,h}^{\prime })=d,{\chi }_D(P_2\times T_{d,h}^{\prime })=2(d-1)+1,{\chi }_D(P_{2k+1}\times T_{d,h}^{\prime })=d$, and ${\chi }_D(P_{2k}\times T_{d,h}^{\prime })=d+1$, where $k\in \mathbb{N}$.

Proof.

First, consider $P_1\times T_{d,h}^{\prime }$, which is isomorphic to $2T_{d,h}^{\prime }$. Since ${\chi }_D(T_{d,h}^{\prime })=d$, we have ${\chi }_D(P_1\times T_{d,h}^{\prime })=d$.

Now, let m = 2. Then one of the components $P_2\times T_{d,h}^{\prime }$ has at least a vertex with $2(d-1)$ neighbors of degree one. Thus we need at least $2(d-1)+1$ colors for distinguishing coloring. The vertices with the same neighbors in the previous columns receive different colors from each other. Since there are at most $2(d-1)$ vertices with the same neighbor in the previous column and we have $2(d-1)+1$ colors, it is possible to color the graph and the coloring is distinguishing. Hence ${\chi }_D(P_2\times T_{d,h}^{\prime })=2(d-1)+1$.

Now, suppose that $m=2k+1$. So the components of the Kronecker product $P_{2k+1}\times T_{d,h}^{\prime }$ are isomorphic to each other. Note that the vertices of a column in each component cannot be mapped to each other, because it is not symmetric. Also there are d – 1 vertices, corresponding to the d – 1 children of a parent in $T_{d,h}^{\prime }$, with the same neighbors in the previous column. So we need at least d colors. The vertices of each column of each component must have the same color, by Lemma 3.1. We consider the distinguishing coloring of $T_{d,h}^{\prime }$, and we color the vertices of a column of one of the components of $P_m\times T_{d,h}^{\prime }$ with color of the corresponding vertex of tree $T_{d,h}^{\prime }$. So the columns cannot be mapped to each other. The other component can be colored similar to the first one by changing the suitable class of colors with each other. Thus ${\chi }_D(P_{2k+1}\times T_{d,h}^{\prime })=d$.

Finally, assume that $m=2k$. Then two components of $P_{2k}\times T_{d,h}^{\prime }$ are isomorphic to each other and symmetric. So the coloring with d colors is not distinguishing and we need d + 1 colors. First we color the graph $P_{2k}\times T_{d,h}^{\prime }$ similar to the distinguishing coloring of $P_{2k+1}\times T_{d,h}^{\prime }$. Now, we recolor a vertex of degree 2 on the first column of each of the components with color d + 1. Thus the vertices of each column cannot be mapped to each other. Hence ${\chi }_D(P_{2k}\times T_{d,h}^{\prime })=d+1$. □

The proof of the following lemma is similar to the proof of Lemma 3.1.

Lemma 3.4.

Let C_m be a cycle of length m and let $T_{d,h}^{\prime }$ be an almost symmetric tree, where $d\ge 3$. Assume that $C_m\times T_{d,h}^{\prime }$ is colored with d colors. If there are at least two vertices in the same column of $C_m\times T_{d,h}^{\prime }$ with different colors, then the coloring is not distinguishing.

Theorem 3.5.

Let C_m be a cycle of length m and let $T_{d,h}^{\prime }$ be an almost symmetric tree, where $d\ge 3$. Then ${\chi }_D(C_4\times T_{d,h}^{\prime })=2(d-1)+2$ and otherwise ${\chi }_D(C_m\times T_{d,h}^{\prime })=d+1$.

Proof.

First, note that if h = 1, the theorem coincide to Theorem 2.3. Now, consider $h\ge 2$. Note that there are d – 1 vertices, corresponding to the d – 1 leaves of a parent in $T_{d,h}^{\prime }$, with the same neighbors in the previous column. So we need at least d colors. The vertices in the same column have the same color, by Lemma 3.4. The vertices of every column have the color of corresponding vertex of $T_{d,h}^{\prime }$. Since the graph is symmetric, this coloring is not distinguishing. So we need at least d + 1 colors. Now, if $m\notin \{3,4,6\}$, then we consider the (1, 2)-column cycle in the coloring with d colors and we recolor 2 vertices of distance 3 from each other with color d + 1. Since this cycle is fixed, the vertices of a column cannot be mapped to each other. Hence ${\chi }_D(C_m\times T_{d,h}^{\prime })=d+1$, where $m\notin \{3,4,6\}$. Note that if m is an even number, then the other component of the graph $C_m\times T_{d,h}^{\prime }$ is colored similar to the first one by changing the color of two suitable classes of coloring.

Consider the graph $C_3\times T_n$. We color the graph with d colors. Now consider the column 1 and a column of corresponding to the vertex of row 2 of $T_{d,h}^{\prime }$, say column 4, which have different color from the central vertex of $T_{d,h}^{\prime }$. We recolor a vertex, say a, in column 1 of $C_3\times T_{d,h}^{\prime }$ with color d + 1, and also we recolor a vertex in column 4 with color d + 1 whose neighbors in the column 2 are different from the neighbors of the vertex a in column 2. It is clear that the columns cannot be mapped to each other. Since the vertices of color d + 1 have different degrees, they are fixed. The vertices of every column are fixed, because the vertices of columns 1, 2, and 4 are fixed. Thus ${\chi }_D(C_3\times T_{d,h}^{\prime })=d+1$. Similarly ${\chi }_D(C_6\times T_{d,h}^{\prime })=d+1$.

Now, consider the graph $C_4\times T_{d,h}^{\prime }$, which has two isomorphic connected components. Assume that columns $l_1,\dots ,l_{d-1}$ are the columns of corresponding to the d – 1 leaves of a vertex of $T_{d,h}^{\prime }$. Since there are $2(d-1)$ vertices in columns $l_1,\dots ,l_{d-1}$ that have two neighbors in the previous column and must receive different colors, we need $2(d-1)+2$ colors. In one of the components, we color the vertices with the same neighbors in the previous columns with different colors and the other component is colored similar to the first one by changing two suitable classes of colors with each other. Therefore ${\chi }_D(C_4\times T_{d,h}^{\prime })=2(d-1)+2$. □

In the following, we discuss the Kronecker product of almost symmetric trees $T_{d,h}^{\prime }$ and $T_{d\prime ,h\prime }^{\prime }$, where $d\ge d\prime \ge 3$.

Remark 3.6.

Let $T_{d,h}^{\prime }$ and $T_{d\prime ,h\prime }^{\prime }$ be two almost symmetric trees with $d\ge d\prime \ge 3$. Then the graph $T_{d,h}^{\prime }\times T_{d\prime ,h\prime }^{\prime }$ consists of two nonisomorphic connected component. Assume that the component 1 is the component that consists of the vertex (x, y), where x and y are the central vertices of $T_{d,h}^{\prime }$ and $T_{d\prime ,h\prime }^{\prime }$, respectively. Now, since both of $T_{d,h}^{\prime }$ and $T_{d\prime ,h\prime }^{\prime }$ consist of vertices with d – 1 and $d\prime -1$ leaves associated to a vertex, $T_{d,h}^{\prime }\times T_{d\prime ,h\prime }^{\prime }$ has a vertex that is adjacent to $(d-1)(d\prime -1)$ pendant vertices. So for distinguishing coloring, we need at least $(d-1)(d\prime -1)+1$ colors. Note that if both of the integer d – 1 and $d\prime -1$ are even or odd, then the pendant vertices of $T_{d,h}^{\prime }\times T_{d\prime ,h\prime }^{\prime }$ are in component 1. Otherwise the pendant vertices of $T_{d,h}^{\prime }\times T_{d\prime ,h\prime }^{\prime }$ are in component 2. Now we want to sort the vertices of $T_n\times T_m$ by blocks. For this purpose, we put the vertices of the product of the arbitrary level of $T_{d,h}^{\prime }$ and an arbitrary level of $T_{d\prime ,h\prime }^{\prime }$ in the same block. 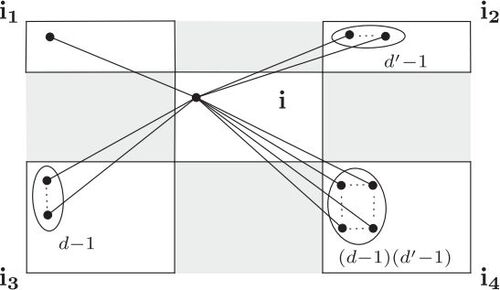The vertices of a block, whose degrees belong to the set $\{1,d,d-1,d\prime ,dd\prime ,(d-1)d\prime ,d\prime -1,d(d\prime -1),(d-1)(d\prime -1)\}$ are adjacent to the vertices in the at most 4 neighbor diagonal blocks, as it is pictured in Figure 5. The blocks of the graph belong to the components 1 and 2, alternatively, as it is seen in Figure 6 in which the white blocks belong to component 1 and other blocks belong to component 2. Note that, in Figure 5, all adjacent vertices to an arbitrary vertex in the center block are shown.

Fig. 5 Adjacent vertices to a vertex in $T_{d,h}^{\prime }\times T{\prime }_{d\prime ,h\prime }$.

Fig. 6 $T_{3,4}^{\prime }\times T_{3,4}^{\prime }$.

Theorem 3.7.

For almost symmetric trees $T_{d,h}^{\prime }$ and $T_{d\prime ,h\prime }^{\prime }$, it follows that ${\chi }_D(T_{d,h}^{\prime }\times T_{d\prime ,h\prime }^{\prime })=(d-1)(d\prime -1)+1$, where $d\ge d\prime \ge 3$.

Proof.

First, we color the component 1 with $(d-1)(d\prime -1)+1$ colors as follows. We color the vertices in the blocks (i, i), where $i\in \{1,2,\dots ,\min \{h,h\prime \left\}\right\}$, with $(d-1)(d\prime -1)+1$ colors such that $(d-1)(d\prime -1)$ vertices in same block that have the same neighbor in the block $(i-1,i-1)$ receive different colors from each other. Note that we color these $(d-1)(d\prime +1)$ vertices in the same block clockwise by using the colors $1,2,\dots ,(d-1)(d\prime +1)+1$, respectively. So the vertices in the block (i, i) are fixed. Now, we color the above blocks of the diagonal blocks (i, i). Consider the block (j, k), where k > j, and also consider the vertices $(r,c_1),\dots ,(r,c_{d\prime -1})$ in this block, where $c_1,\dots ,c_{d\prime -1}$ are the children of a parent of $T_{d\prime ,h\prime }^{\prime }$, say $r\prime$. By Figure 5, we color them with different colors from each other and from their neighbors in the blocks ${(j,k)}_1$ and ${(j,k)}_3$. Note that the sets of neighbors of vertices $(r,c_1),\dots ,(r,c_{d\prime -1})$ in the blocks ${(j,k)}_1$ and ${(j,k)}_3$ are equal, and the neighbors of these vertices in block ${(j,k)}_3$ are $(c_1^{\prime },r\prime ),\dots ,(c_{d-1}^{\prime },r\prime )$, where $c_1^{\prime },\dots ,c_{d-1}^{\prime }$ are the children of the vertex r in $T_{d,h}^{\prime }$, and also the neighbor of the vertices $(r,c_1),\dots ,(r,c_{d\prime -1})$ in the block ${(j,k)}_1$ is $(x,r\prime )$, where x is the parent of r in $T_{d\prime ,h\prime }^{\prime }$. Now, we color the blocks that are under the diagonal blocks (i, i). Consider the block (j, k), where j > k, and also consider the vertices $(l_1,r),\dots ,(l_{d-1},r)$ in this block, where $l_1,\dots ,l_{d-1}$ are the children of a parent of $T_{d,h}^{\prime }$, say $r\prime$. By Figure 5, we color them with different colors from each other and from their neighbors in the blocks ${(j,k)}_1$ and ${(j,k)}_2$. Note that the sets of neighbors of vertices $(l_1,r),\dots ,(l_{d-1},r)$ in the blocks ${(j,k)}_1$ and ${(j,k)}_2$ are equal, and the neighbors of these vertices in the block ${(j,k)}_2$ are $(r\prime ,l_1^{\prime }),\dots ,(r\prime ,l_{d\prime -1}^{\prime })$, where $l_1^{\prime },\dots ,l_{d\prime -1}^{\prime }$ are the children of the vertex r of $T_{d\prime ,h\prime }^{\prime }$, and also the neighbor of the vertices $(l_1,r),\dots ,(l_{d-1},r)$ in the block ${(j,k)}_1$ is $(r\prime ,x)$, where x is the parent r in $T_{d,h}^{\prime }$. With this coloring, both of two vertices of corresponding to the children of a parent in $T_{d,h}^{\prime }$ or $T_{d\prime ,h\prime }^{\prime }$ have different colors and so they cannot be mapped to each other. Also if two vertices with the same colors in the same block are mapped to each other, then the neighbors in the previous block neighbor must be mapped to each other, but they have different colors. Hence this coloring associated to the component 1 is distinguishing. Finally, we color the component 2 as follows. Consider the blocks $(i,i+1)$, where $i\in \{1,2,\dots ,\min \{h,h\prime \left\}\right\}$ and color the vertices in this block by a similar method of coloring of diagonal blocks (i, i) in the component 1. We color the remaining vertices by using a similar method of coloring of component 1, distinguishingly. Note that if $h\ne h\prime$, then the pendant vertices belong to nondiagonal block and the pendant vertices with the same neighbor must be colored with different colors. Therefore ${\chi }_D(T_{d,h}^{\prime }\times T_{d\prime ,h\prime }^{\prime })=(d-1)(d\prime -1)+1$, where $d\ge d\prime \ge 3$. □

Example 3.8.

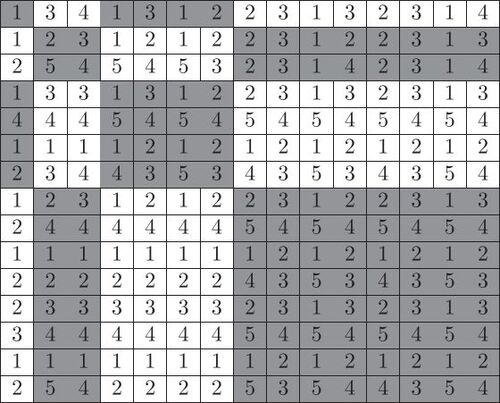
We color the graph of the Kronecker product $T_{3,4}^{\prime }$ and $T_{3,4}^{\prime }$ by using the method of Theorem 3.7 (see Figure 6).

A bisymmetric tree, which is denoted by $T_{d,h}^{″}$, is a tree that is constructed by joining the central vertices of two almost symmetric trees $T_{d,h}^{\prime }$. Also, a symmetric tree $T_{d,h}$ is a tree with a central vertex x, all leaves have the same distance h from x, and all the vertices that are not leaves have degree d. In fact, $T_{d,h}$ is obtained by joining the central vertices of two almost symmetric trees $T_{d,h}^{\prime }$ and $T_{d,h-1}^{\prime }$. We set the vertices of a symmetric tree or a bisymmetric tree in rows or columns by using the following method.

Let $T_{d,h}$ be obtained by joining the central vertices of $T_{d,h}^{\prime }$ and $T_{d,h-1}^{\prime }$. Also, let $T_{d,h}^{″}$ be obtained by joining the two almost symmetric trees $T_{d,h}^{\prime }$. For $T_{d,h}$, we put the vertices of $T_{d,h}^{\prime }$ as the reverse order in the Breadth-first search algorithm, and then we put the vertices of $T_{d,h-1}^{\prime }$ as the order of the Breadth-first search algorithm in columns or rows. Similarly, for the bisymmetric tree $T_{d,h}^{\prime }$, we put the vertices of one of the almost symmetric trees $T_{d,h}^{\prime }$ as the reverse order in the Breadth-first search algorithm. Then we put the vertices of the other $T_{d,h}^{\prime }$ as the order of the Breadth-first search algorithm in columns or rows. As a similar method, which is used in Remark 3.6, we can set the vertices of the Kronecker product of these trees to each other or an almost symmetric tree in blocks. So we have 4 partitions associating to the Kronecker product of the almost symmetric trees and index these partitions clockwise. Now for distinguishing coloring, first we color the partitions 1 and 3 by the method used in the proof of Theorem 3.7, such that the blocks (1, 1), (1, 2), and (2, 1) in partition 1 have different colors from these blocks in partition 3, and then we color partitions 2 and 4 as follows. Consider one of the partitions 2 and 4, say partition 2. We color all of the blocks by the method used in the proof of Theorem 3.7, by considering the colored blocks of neighbor partitions. Since all of the partitions are colored distinguishingly and the blocks of the partitions have different colors from each other, this coloring is distinguishing. Therefore we have the following theorem.

Theorem 3.9.

Let $T_{d,h}^{″}$ be a bisymmetric tree and let $T_{d,h}$ be a symmetric tree. Then ${\chi }_D(A\times T_{d,h}^{″})={\chi }_D(A\times T_{d,h})={\chi }_D(A\times T_{d,h}^{\prime })$, where A is a path, a cycle, an Almost symmetric tree, a bisymmetric tree, or a symmetric tree.

Acknowledgments

The authors are deeply grateful to the referees for careful reading of the manuscript and helpful suggestions.

Correction Statement

This article has been republished with minor changes. These changes do not impact the academic content of the article.