Integrity monitoring of fixed ambiguity Precise Point Positioning (PPP) solutions

Abstract

Traditional positioning methods, such as conventional Real Time Kinematic (cRTK) rely upon local reference networks to enable users to achieve high-accuracy positioning. The need for such relatively dense networks has significant cost implications. Precise Point Positioning (PPP) on the other hand is a positioning method capable of centimeter-level positioning without the need for such local networks, hence providing significant cost benefits especially in remote areas. This paper presents the state-of-the-art PPP method using both GPS and GLONASS measurements to estimate the float position solution before attempting to resolve GPS integer ambiguities. Integrity monitoring is carried out using the Imperial College Carrier-phase Receiver Autonomous Integrity Monitoring method. A new method to detect and exclude GPS base-satellite failures is developed. A base-satellite is a satellite whose measurements are differenced from other satellite’s measurements when using between-satellite-differenced measurements to estimate position. The failure detection and exclusion methods are tested using static GNSS data recorded by International GNSS Service stations both in static and dynamic processing modes. The results show that failure detection can be achieved in all cases tested and failure exclusion can be achieved for static cases. In the kinematic processing cases, failure exclusion is more difficult because the higher noise in the measurement residuals increases the difficulty to distinguish between failures associated with the base-satellite and other satellites.

Keywords:

• Precise Point Positioning (PPP)
• integrity
• ambiguity resolution
• failure exclusion

1. Introduction

There are many applications which require high accuracy (centimeter-level) positioning, such as land surveying, precision farming, and marine applications. Traditionally,high positioning accuracy is achieved using the conventional Real-Time Kinematic (cRTK) method. The principle of cRTK is to cancel or mitigate errors which are common to two or more GNSS receivers by differencing measurements across receivers (1). However, in order to achieve a high accuracy, the distance from the reference receiver (baseline) must typically be shorter than 50 km when using dual-frequency GNSS receivers (1). The density of the required network makes cRTK costly and unviable, particularly in remote areas.

To overcome the issue of high cost associated with cRTK positioning, PPP can be used. The principle of PPP is to correct or mitigate errors using error correction products, for example, precise satellite orbit and clock corrections and advanced error modeling, which in the cRTK mode are canceled or mitigated by differencing measurements across receivers. The PPP error correction products can be generated using a sparse global reference network with, for example, 50 stations strategically placed around the Earth, generating corrections for users anywhere on the Earth (2).

A key aspect of reliable positioning is integrity monitoring, particularly relevant for mission (e.g. safety) critical applications. Integrity anomalies or failures can be caused, for example, by problems in a GNSS satellite (e.g. satellite clock jump), the control segment (e.g. human error), or on the user side (e.g. receiver failure or multipath) (1).

The concept of using redundant GNSS measurements to monitor integrity is originally presented in Ref. (3). It requires at least five code-phase measurements. Monitoring can be carried out in the range and position domains. In the range domain, predicted code-phase measurements based on the position solutions calculated by different four satellite groups are compared to the measured code-phase measurements. An integrity alert is generated if the difference between the predicted and measured code-phase measurements exceeds a certain threshold. In the position domain, positions calculated from different groups of four satellites are compared to the position calculated using measurements from all five satellites. An integrity alert is generated if the difference between the position estimates exceeds a given threshold (3).

Integrity monitoring at user level is range domain based and is referred to as Receiver Autonomous Integrity Monitoring (RAIM). In the case of the code-phase least squares approach, at least five measurements are required. The test statistic for RAIM is calculated based on the magnitude of the measurement residual vector and compared to the detection threshold, defined on the basis of the allowed rate of false alarm, the degrees of freedom, and the assumed measurement standard deviations (4).

The integrity monitoring method equivalent to RAIM for carrier-phase observables is the Carrier-phase Receiver Autonomous Integrity Monitoring (CRAIM) method. The version presented in Ref. (5) is used to detect and exclude failures for the least-squares method based on single-differenced measurements. The carrier-phase integer ambiguities are assumed to be known.

The Imperial College Carrier-phase Receiver Autonomous Integrity Monitoring (ICRAIM), presented in Ref. (6), was originally applied to cRTK solutions estimated using an Extended Kalman Filter (EKF). Failure detection is achieved using a measurement type specific test statistic.

ICRAIM is applied to PPP in Ref. (7), where it is tested with a small set of simulated data. Issues with calculating protection levels are identified in Ref. (8), when ICRAIM is applied to static EKF-based PPP. ICRAIM is used to monitor the integrity of fixed-ambiguity PPP solutions and a failure exclusion method is presented in Ref. (9). This is extended in Ref. (10), for the case of combined GPS and GLONASS measurements to calculate a float position solution, but fixing GPS ambiguities only.

In this paper, selected code-phase and carrier-phase failure cases are tested. This includes both static and dynamic processing cases, where the EKF position process noise is set to 0 and 0.1 m/s, respectively. The paper further develops and tests an improved method for the base-satellite failure detection.

2 PPP method

2.1 Receiver clock errors and fractional cycle bias

In this paper, the PPP method uses a combination of both GPS and GLONASS measurements. The Between-Satellite-Difference (BSD) operation shown in Equation (1) for code-phase measurements and Equation (2) for carrier-phase measurements (in meters) is applied to GPS measurements to remove the receiver clock error and Fractional Cycle Bias (FCB) (11).(1) (2) where i is the index of the satellite, j is the base-satellite, F is the frequency band (1 = L1 and 2 = L2), P is the code-phase measurement, and L is the carrier-phase measurement in meters. The BSD operation is generated such that the GPS satellite at the highest elevation is selected as the base-satellite. The measurements associated with this base-satellite are then subtracted from the remaining satellites’ measurements. GLONASS measurements are used un-differenced.

2.2 Ionosphere errors

The ionosphere-free combination in Equation (3) for code-phase and Equation (4) for carrier-phase measurements (in cycles) is used to eliminate first-order ionospheric errors (12). The magnitude of the ionospheric delay can reach tens of meters, if the first-order ionospheric error is not eliminated (12).(3) (4)

In the above equations, f is the frequency with subscripts ‘1’ and ‘2’ to designate the L1 and L2 bands, respectively; φ is the carrier-phase measurement.

2.3 Troposphere errors

A further potentially important error source is the troposphere. Depending on the satellite elevation and tropospheric conditions, the tropospheric delay can cause approximately between 2.4 and 25 m error in the range measurements (1). Thus, tropospheric delay needs to be addressed in PPP. The UNB3 m tropospheric model is employed to estimate the tropospheric dry delay and initial wet delay components (13) using the Global Mapping Function (GMF) (14) to map delays to the receiver to the satellite range domain. The tropospheric wet delay is estimated as an EKF state, because it cannot be modeled with sufficient accuracy from the tropospheric model. The tropospheric gradient to the East and North directions are also estimated as EKF states and the Chen function in Ref. (15) is used to map the gradients to the measurement domain.

2.4 Differential code bias

When employing both the C and P code type of code-phase measurements, the C1/P1 and C2/P2 Differential Code Biases (DCB) also need to be corrected, because the biases can cause up to meter level errors in the code-phase measurements (12). DCB correction products from the Center of Orbit Determination in Europe (CODE) are used in Ref. (16).

2.5 Satellite orbit and clock

The French Space Agency’s (CNES) real-time satellite orbit and clock corrections are used to correct the satellite orbit and clock errors both from GPS and GLONASS measurements (17). The standard deviation of the CNES GPS satellite clock corrections is 0.12 ns, equivalent to 3.6 cm, and the 3-D accuracy of CNES GPS orbit corrections is better than 5 cm on average (18). Satellite orbit errors in the radial direction are significantly smaller than the 3-D orbit error (19) and thus negligible.

Separate GPS carrier and code-phase satellite clock corrections are provided. This method is referred to as Integer Recoverable Clock (IRC), as used for example in Refs. (18, 20). The narrow-lane FCB errors in the carrier-phase measurements are removed after applying the satellite clock corrections (18), enabling narrow-lane GPS ambiguity resolution.

2.6 Phase center offsets

To obtain centimeter-level positioning accuracy, a correction of the satellite and receiver phase center offsets and variations is required (2). Corrections in the ANTEX 1.4 format are applied in this paper (21). Moreover, the satellite phase wind-up effect must be corrected, because it can cause errors up to one cycle (22). In this paper, the model presented in (23) is used.

2.7 Displacement effects

In addition, site-displacement effects including solid earth tides, pole tides, and ocean loading can cause decimeter-level position errors (22). The site-displacement correction models presented in Ref. (22) are employed to correct for these effects.

2.8 Noise and multipath

GPS carrier-phase measurement standard deviation is calculated as(5) where the values of a and b are set to 0.003 m, and el is the elevation of the satellite. The formula is similar to that used in the RTKLIB software (24). It is assumed that the standard deviation of GPS code-phase measurements is 100 times larger of GLONASS carrier-phase measurements, three times larger of GLONASS code-phase measurements, and 2000 times larger than the standard deviation of GPS carrier-phase measurements.

The effect of multipath errors as in Ref. (1) is mitigated by elevation-based measurement weighting and antenna and receiver design. However, there are no methods to fully eliminate multipath errors.

2.9 Other sources of error

There are also other smaller error sources with typical error magnitudes between one and two centimeters or less, such as higher order ionospheric delays (25) and atmospheric pressure loading (26). These error sources are not corrected in this paper.

2.10 Ambiguity resolution and validation

Ambiguity resolution is attempted for GPS ambiguities only; GLONASS ambiguities being kept as float. The ionosphere-free ambiguity term is given by:(6) where N₁and N₂ are the ambiguities on the L1 and L2 frequency bands, respectively. Due to the non-integer nature of the ionosphere-free ambiguity term, it is not possible to solve the ambiguities directly (11). Therefore, ambiguity resolution is carried out in two stages: wide-lane and narrow-lane ambiguity resolution.

Float wide-lane ambiguity values are estimated using a geometry-free approach based on the Melbourne-Wubbena combination according to (27):(7)

FCB from the estimates are corrected employing CNES wide-lane FCB corrections as in Ref. (17). The wide-lane estimates are fed to the EKF, and wide-lane ambiguities are estimated as EKF states. Wide-lane ambiguity resolution is achieved using the probabilistic test described in Ref. (28). After fixing the wide-lane ambiguity for a satellite pair, the narrow-lane ambiguity can be estimated based on the ionosphere-free ( and fixed wide-lane ambiguities (:(8)

At least five wide-lane ambiguities are required before narrow-lane ambiguity resolution is attempted. Narrow-lane ambiguity resolution is attempted for the different combinations of ambiguities by employing the Minimum Constellation Method (MCM), presented in Ref. (29). Integer ambiguity candidate vector search is carried out for each combination using the LAMBDA method (30).

Narrow-lane ambiguity validation is carried out using the ratio test (31). The ratio between the squared residuals of the second best (R₂) and best ambiguity (R₁) candidates (31) is tested against a given threshold calculated from the required confidence level and degrees of freedom (32):(9)

If the ratio test statistic is over the threshold, the ambiguity candidate vector is accepted. More than one accepted ambiguity candidate vector may be obtained with the MCM. In that case, the best candidate vector is selected based on the largest number of resolved ambiguities in the candidate vector and the largest ratio test confidence level (10). The ratio test is unable to determine the absolute correctness of the ambiguity candidate vector; it only determines how close the fixed ambiguity candidate vector is to the float solution (31). Therefore, a requirement in this paper is that the best ambiguity candidate vector and fixed ambiguity values in the vector remain the same for more than 30 consecutive epochs (150 s with 5 s data rate) (10).

Finally, when both the wide-lane and narrow-lane ambiguities are fixed to integers, the fixed ionosphere-free ambiguity is calculated as Ref. (11):(10)

2.11 Data processing

The iNsight project (http://www.insight-gnss.org/) POINT software is used in this paper to process the data on the basis of an Extended Kalman Filter (EKF). The estimated EKF states are: position (latitude, longitude, and height), GLONASS receiver clock error, GPS and GLONASS ionosphere-free ambiguities, GPS wide-lane ambiguities, tropospheric wet delay, and tropospheric gradients. In this paper, post-processing is carried out, however the results may be computed in real-time, because the correction products are generated in real-time.

3 Integrity monitoring

The ICRAIM method presented in Ref. (6) is used in this paper to monitor the integrity. Three different test statistics are employed: total (all measurements as weighted in the EKF), code-phase only, and carrier-phase only (6). The aim of using separate test statistics for different measurement types is to improve error detection associated with different measurement types (6). Measurements residuals (r_k) are obtained from the EKF:(11) where k is the epoch, z_k is the measurement vector, H_k is the EKF design matrix, and is the EKF state vector after the EKF update step. The total test statistic is calculated as:(12) where W is the EKF weight matrix. The code-phase only test statistic is calculated as:(13) where is the measurement variance matrix. The carrier-phase only test statistic is calculated as:(14) where is the measurement standard deviation matrix. It is assumed that the test statistics follow the Chi distribution. An error is detected if a test statistic is over the detection threshold.

Protection levels are estimated to obtain an upper bound of the position error for a given probability of missed detection (6). Integrity monitoring of an EKF-based solution requires a concept different from the slope concept used with the least-squares approach (4). A nominal bias, caused by non-Gaussian errors, such as satellite orbit, site-displacement, and tropospheric delays is added to the protection level estimates (8). In this paper, an empirically chosen nominal bias value of 5 cm is used. Horizontal and vertical protection levels are calculated as:(15)

and(16) where P_local is the Kalman filter, P matrix converted to the local (East, North, Up) coordinates; k_H and k_V are factors calculated based on the allowed rate of missed detection, nominalBias is the chosen nominal bias value, ah is calculated as:(17) where G = (H^TR⁻¹H)⁻¹H^TR⁻¹, and av as:(18)

where G = (H^TR⁻¹H)⁻¹H^TR⁻¹, in which H and R are the EKF design and measurement variance matrices, respectively.

3.1 Failure exclusion

Failure exclusion is attempted, if any of the test statistics is exceeding its threshold. The BSD approach used for GPS measurements requires failure exclusion to be applied separately for failures associated with the base-satellite and other satellites. For GLONASS measurements, there is no need for separate handling, because GLONASS measurements are un-differenced.

In the case of the base-satellite failure, the magnitude of measurement residuals increases typically for each satellite pair. In the case of failures associated with other satellites, the magnitude of the residuals increases typically only for the measurements associated with the failed satellite. Thus, the base-satellite failure can be detected based on the contribution of residuals from different satellite pairs. The test used to detect the base-satellite failure is:(19) where re is a measurement residual, n is the number of measurements used to calculate the test statistic. This test is carried out separately for each test statistic and measurement residuals are calculated using the same approach as for the test statistics. Both the largest and second largest residuals are used in the test, because of the potential of multiple failures. The test decision threshold in Equation (19) is chosen empirically.

If a failure is detected with the base-satellite, the base-satellite is excluded for 30 s. Otherwise, the satellite with the largest residual is excluded for 30 s. The same approach is used for failure exclusion of GLONASS measurements.

4 Test data and results

Data recorded on 23 October 2012 at four International GNSS Service (IGS) stations (BRST, MATE, LAMA, and ZIM2) was used to test the integrity monitoring algorithms. Five error cases were tested by adding simulated errors to these data. Errors were simulated to occur between 14:34:40 and 14:51:20 (GPS time) for cases 1, 2, 4, and 5 and between 15:08:00 and 15:24:40 for case 3. The GPS satellites PRN 3 (G3) and PRN 19 (G19) and GLONASS satellite PRN 7 (R7) are simulated to incur simultaneous errors for cases 1, 2, 3, and 4. For case 5, G19 and R7 are simulated to incur simultaneous errors.

4.1 Case 1

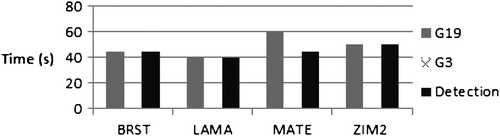
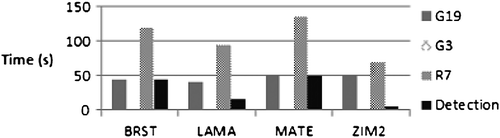
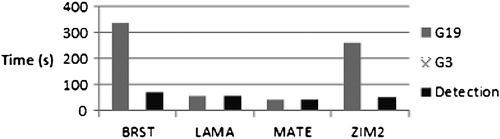
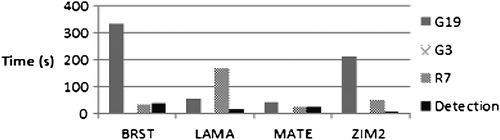
A 0.001 m/s ramp error in the L2 carrier-phase measurements was injected for the previously mentioned satellites. G19 is used as a base-satellite. The EKF position process noise was set to 0 (static processing). Figure 1 shows the time needed to detect the failure and to exclude the errors for the GPS-only processing case. Figure 2 shows the corresponding information when using both GPS and GLONASS.

Figure 1 Time required to detect and exclude errors (Case 1, GPS only).

Figure 2 Time required to detect and exclude errors (Case 1, GPS/GLONASS).

The failure was detected within 50 s in both cases. In the GPS/GLONASS case, failure detection occurs even earlier, because of failures in the real GNSS data which cause the test statistic to exceed the threshold. It takes up to 60 s, depending on the case, to exclude G19, the base-satellite. G3 is not excluded, because ambiguities are reset each time when the base-satellite is excluded, resulting in an error associated with G3 that is not sufficiently large. R7 is excluded between 70 s and 135 s.

4.2 Case 2

A 0.001 m/s ramp error in the L2 carrier-phase measurements was injected for the previously mentioned satellites. GPS satellite PRN 11 (G11) is used as the base-satellite. The EKF position process noise was set to 0 (static processing). Figure 3 (GPS only) and Figure 4 (GPS/GLONASS) show the error detection and exclusion results. All errors were excluded, with a maximum delay of 120 s for G3.

Figure 3 Time required to detect and exclude errors (Case 2, GPS only).

Figure 4 Time required to detect and exclude errors (Case 2, GPS/GLONASS).

4.3 Case 3

A 5 m step type of L1 code-phase error was injected for the previously mentioned satellites and G19 was used as the base-satellite. The EKF position process noise was set to 0 (static processing). The code-phase error associated with G19 is so significant that the satellite is excluded immediately after the error has occurred. This is also the case with G3, which is excluded when it becomes a base-satellite after excluding G19. R7 is not excluded, because GLONASS code-phase measurements have significantly lower weight than GPS code-phase measurements.

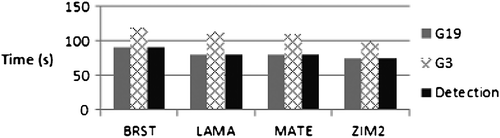
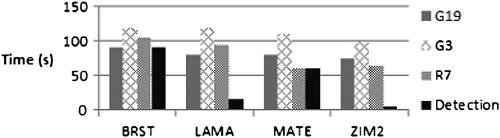
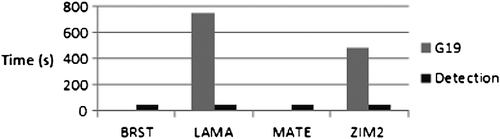
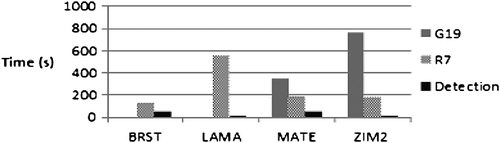
4.4 Case 4

A 0.001 m/s ramp error in the L1 carrier-phase measurements was injected for the previously mentioned satellites. G19 was used as the base-satellite. The EKF position process noise was set to 0.1 m (dynamic processing). Results are shown in Figures 5 (GPS only) and 6 (GPS/GLONASS). Failure detection for this scenario took approximately the same amount of time as for test case 1. However, failure exclusion took more time than in the static processing case 1. G3 was not excluded, because the error with the base-satellite was dominating the residual errors. The error associated with R7 was excluded in all cases.

Figure 5 Time required to detect and exclude errors (Case 4, GPS only).

Figure 6 Time required to detect and exclude errors (Case 4, GPS/GLONASS).

4.5 Case 5

A 0.001 m/s ramp error in the L1 carrier-phase measurements was injected for the previously mentioned satellites. G11 was used as the base-satellite. The EKF position process noise was set to 0.1 m (dynamic processing). Figures 7 (GPS) and 8 (GPS/GLONASS) show the results. Failure detection was achieved approximately as quickly as in case 1. However, failure exclusion was more complicated due to higher noise levels in the residuals, because kinematic process settings were used. Failed GLONASS satellites were successfully excluded, but the time required was longer than in case 1.

Figure 7 Time required to detect and exclude errors (Case 5, GPS only).

Figure 8 Time required to detect and exclude errors (Case 5, GPS/GLONASS).

5 Conclusions

State-of-the-art fixed ambiguity PPP is presented in this paper. Both GPS and GLONASS measurements are used in the computation of the float position solution, followed by GPS ambiguity resolution. Integrity monitoring is carried out using the ICRAIM method. A new method was developed to detect GPS base-satellite failures.

The results show that failure detection can be achieved for all test cases. Failure exclusion was successful for the static processing test cases. However, failure exclusion was found to be more difficult for the dynamic processing cases, due to the difficulty in distinguishing between failures associated with the base-satellite and other satellites. Future work will include testing failure detection and exclusion for real kinematic data.

Notes on contributors

Mr Altti Jokinen is a PhD student at the Centre for Transport Studies (CTS) within the Department of Civil and Environmental Engineering at Imperial College London. His research focus is on Precise Point Positioning (PPP). Before starting his PhD studies in September 2010, he carried out research and development work on cellular phone GNSS positioning at the Nokia Corporation.

Dr Shaojun Feng is a research fellow at the CTS within the Department of Civil and Environmental Engineering at Imperial College London. He leads the navigation research team within the Imperial College Engineering Geomatic Group (ICEGG). He is a fellow of Royal Institute of Navigation (RIN) and member of the US Institute of Navigation.

Dr Wolfgang Schuster is an assistant professor (research fellow) in Positioning and Navigation Systems (PNS) and Air Traffic Management, at the CTS in the Department of Civil and Environmental Engineering at Imperial College London. He is the director of the Intelligent Transport Systems Group and of the Air Traffic Management Group at Imperial. His work focuses on the development of methodologies and technologies to improve the efficiency and safety of air transport and to minimize aviation’s impacts on the environment. In regard to PNS, his main contributions are in the domain of intelligent integrity monitoring.

Professor Washington Ochieng is the head of the CTS and holds the chair in PNS in the Department of Civil and Environmental Engineering at Imperial College London. He is also the director of the ICEGG. He is a chartered engineer, fellow of the Royal Institute of Navigation and the Institution of Civil Engineers, and member of the US Institute of Navigation.

Dr Chris Hide is a senior research fellow at the Nottingham Geospatial Institute (NGI). He has a BSc degree in Mathematics and Topographic Science from the University of Wales and a PhD in Engineering Surveying from the University of Nottingham. He has carried out research on integrated GPS and INS systems for more than 10 years.

Professor Terry Moore is the director of the NGI at the University of Nottingham; where he is the professor of Satellite Navigation and also currently associate dean within the Faculty of Engineering. He has 30 years of research experience in surveying, positioning, and navigation technologies. He is a member of Council and a fellow of the Royal Institute of Navigation.

Dr Chris Hill is a principal research officer at the NGI. He has a PhD from the University of Nottingham on the subject of Satellite Laser Ranging, and has worked on a variety of GPS and GNSS research projects over the last 20 years. He is a fellow of the RIN.

Acknowledgments

This research was carried out as a part of the iNsight (www.insight-gnss.org) project. iNsight is a collaborative research project funded by the UK’s Engineering and Physical Sciences Research Council (EPSRC) to extend the applications and improve the efficiency of positioning through the exploitation of new global navigation satellite systems signals. It is being undertaken by a consortium of 12 UK university and industrial groups: Imperial College London, University College London, the University of Nottingham, the University of Westminster, EADS Astrium, Nottingham Scientific Ltd, Leica Geosystems, Ordnance Survey of Great Britain, QinetiQ, STMicroelectronics, Thales Research and Technology UK Limited, and the UK Civil Aviation Authority.