Tessellations in GIS: Part I—putting it all together

Abstract

This article attempts to describe the role of tessellated models of space within the discipline of geographic information systems (GIS)—a speciality coming largely out of geography and land surveying, where there was a strong need to represent information about the land’s surface within a computer system rather than on the original paper maps. We look at some of the basic operations in GIS, including dynamic and kinetic applications. We examine issues of topology and data structures and produce a tessellation model that may be widely applied both to traditional “object” and “field” data types. Based on this framework, it can be argued that tessellation models are fundamental to our understanding and processing of geographical space, and provide a coherent framework for understanding the “space” in which we exist. This first article examines static structures, and a subsequent article looks at “change”—what happens when things move.

Keywords:

• GIS
• tessellation model
• static structure
• topology
• data structure
• object and field
• Voronoi diagram

1. Introduction

We attempt to describe the role of tessellated models of space within the discipline of geographic information systems (GIS)—a speciality coming largely out of geography and land surveying, where there was a strong need to represent information about the land’s surface within a computer system rather than on the original paper maps.

We will therefore start with a very short “History of GIS”—what they were expected to do, and how they were expected to do it, together with a few samples of the types of geographic problems to be addressed. These are often surprisingly diverse, and the appropriate methodologies are not always obvious.

We then ask what “Geographic Data” is. A key concept is the difference between “field”-type data such as temperature, and “object”-type data, such as houses on a map. It should be noted that “geographic data” do not consist merely of coordinates—usually referred to as “geometry”—but also some kind of connectedness information—usually referred to as “topology”—and a variety of attributes, semantics, etc. These issues apply both to the normal two dimensions (2D) map information as well as to some recent advances using three dimensions (3D) data.

The more one looks at these issues, and how they can be represented, the more one realizes that there are many different “Models of Space,” often mental models that may differ between one user and another. These may not be easy to classify, but they form our understanding of what manipulations are feasible for the space we are working in. A simple example is a terrain model: we may think of it as a grid made of square cells; a grid formed from a regular lattice of points; a triangulation connecting arbitrary data locations to give an adjacency network; a triangulation formed of flat plates; a cellular structure representing the proximal region for each data point; and probably several more. We will focus again on what appears to be the key issue: the distinction between “fields” and “objects.”

Even here some care should be taken, as we often make assumptions about the dimensionality of the field (perhaps a 2D surface) and its “meaning”: its “Embedding” in a space of the same or higher dimension—an example is a 2D surface representing ground elevation in 3D space, which may be a field on that surface, but probably is not in the 3D space as a whole. As we become more concerned with data of various spatial dimensions, we need to discuss its meaning in terms of the embedding and embedded dimensions—in particular insofar as it concerns fields and their continuity.

This leads us directly to a key question—If fields allow us to express spatial relationships, how can we handle “discrete objects”? We propose the concept of “Spatial Extension” to handle this issue, and thus introduce the Voronoi diagram (VD) as a fundamental idea in GIS.

Our field model thus covers the relevant space, but not necessarily representing the value of a continuous function. Indeed, it is formed of discrete tiles having their own particular attributes and, as they are connected, some representation of adjacency. This leads us directly to discussing “Graphs and Data Structures,” which not only are particularly useful for the analysis of a variety of spatial questions, but lend themselves very well to computer representations. We will give some basic properties and emphasize the importance of the dual of a planar graph. On this basis, we will examine some of the common spatial data structures for computer representations, emphasizing the quad-edge structure as it handles both primal and dual graphs simultaneously. This can manage traditional polygon maps (e.g. political boundaries) as well as our tessellations of spatially extended objects—the VD.

This probably suffices for modest quantities of data, but at a geographical scale, this is often insufficient: we need some understanding of “Spatial Indexing and Hierarchies” for rapid identification of objects from coordinates. Unfortunately, it is well known that the VD of irregular point data cannot be nested in a higher level VD so that the boundaries match. We propose a solution to this problem by relaxing the rules a little: a higher level VD cell contains all the generating points of the lower level VD, even though boundary matching is not exact. With a suitable data structure, this gives us a useful hierarchical structure for large data sets in 2D and 3D, and this may also serve as a disk paging structure that preserves nearby data points in the same or nearby pages.

This completes our exploration of static tessellations for GIS. However, few things remain unchanged, whether due to editing or real-world changes. In a subsequent article, we discuss various types of “Change” in a map, and look at a variety of algorithms and applications: incremental methods, where items are added one at a time; dynamic algorithms, where deletion is possible without having to rebuild the whole graph data structure; and kinetic algorithms, intended to handle topological changes induced by point movement in the real or simulated exterior world. Some of the most interesting applications here involve collision detection problems, e.g. for shipping, and map-drawing algorithms, where the moving point represents the pen that is drawing cartographic objects such as roads and buildings. Here, the lower dimensional entities (points or lines) are embedded in the higher (2D) map space—but their spatial extensions provide a tessellated model with many useful properties based on their adjacency structure.

Based on this framework, it can be argued that tessellation models are fundamental to our understanding and processing of geographical space, and provide a coherent framework for understanding the “space” in which we exist.

2. History of GIS

GISs were developed in a variety of disciplines, but all started with the assumption that the data being managed was spatial (in 2D or 3D Euclidean space as a rule) and was “geographic” in its spatial scale—that is, neither atomic or cosmic (Gold 2006).

At geographic scales, many of the types of information being processed can come from the discipline of geography, although similar claims can be made for cartography, surveying and others. This results in a wide variety of data types and queries, and it may be useful to give a taste of these before continuing with tessellations and their applications in GIS.

Originally, GIS was developed as a computer automation of traditional manual mapping. The main operations were related to the types of queries that were feasible using paper, pens, and transparent overlays (Figure 1). Starting with paper maps of the particular information required (e.g. roads, soil types, cadastre, zoning) combined maps were produced that could respond to regional queries, such as the area of prime agricultural land within a proposed urban zone, or the number of houses within a fixed distance of a river. Elementary operations involved combining polygon layers (overlay), reclassification of polygons with varying combinations of attributes, buffer zones of varying distances from map features—and of course scale change and generalization of map detail. With the development of large digital databases, considerable emphasis was placed on the storage, management, and integration of different data sets.

Figure 1. Polygon map of Mexico (from Manifold.net).

It was clear that (two-dimensional) geographic data could be made up of zero-, one-, and two-dimensional map features—where map features were the graphical representation of entities on the ground. Examples are points, road centerlines, and administrative districts. However, even this needed to be refined, as some geographic information, such as elevation, or temperature, was continuous or “field” data in 2D. The same was true of some other polygon data, where the map was completely tessellated with soil types, vegetation types or urban zoning. “Fields” were clearly different from “Objects”—discrete, unconnected and non-tessellating objects of 2D or lower. These concepts held true in a wide variety of disciplines, such as geology, forestry, agriculture, sociology, and many others.

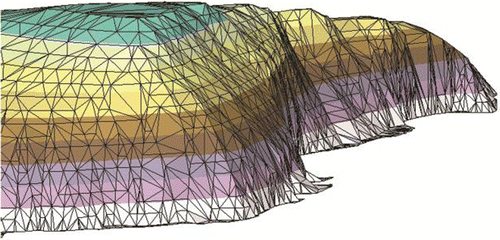
Where we have real-world field data, with attributes measurable at any location, the problem immediately becomes as follows: How to store this information in the computer, as well as how to collect it in the first place. Where the attribute is described by real numbers, it makes sense to take point observations, store them in the computer and interpolate as required—although for recent, high-density remote sensing data, sampled on some form of grid, the whole raster image (being a tessellation of pixels) is preserved and manipulated as desired later. A related structure, a (usually relatively coarse) grid, was used in the early days of computing, when resources were expensive, with grid values estimated from some set of nearby points. More recently, a triangulation triangulated irregular network (TIN) of the original data points is the preferred model, as the original data are preserved in the interpolated surface (Figure 2). In the case of TINs, the Delaunay triangulation is used for its mathematical properties, and for further interpolation, the dual Voronoi cells may be generated—in this case, the triangulation becomes merely the topological connectivity of these cells.

Figure 2. Perspective view of a triangulated surface.

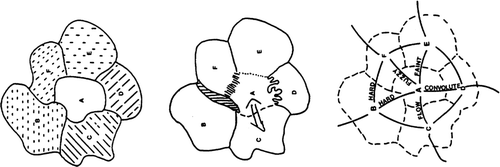
Where the attribute is some nominal label, such as urban zones, an arbitrary tessellation needs to be stored as a polygonal object—but with some indicator of its adjacency relationships with neighboring polygons (a form of topology). Where the attribute is countable—such as population—it is common to use the same type of arbitrary tessellation. Thus, fields may always be represented as tessellations composed of contiguous cells plus a “topological” model representing their connectivity. In fact, in quite a few cases, the dual is as important as the polygon itself: a forest stand may clearly exist, but its boundary with adjacent stands may be unclear; the boundary type itself may change; or the key issue may be movement between cells (Figure 3).

Figure 3. Polygons and duals.

In most traditional GISs, “objects” are composed of “vectors”—straight-line segments between points. Thus, a set of houses, for example, would consist of these sketches with no interconnecting topology. Where the vectors were used to draw arbitrary polygon maps, a connectivity evidently existed. This was difficult to create due to the linear spatial model of the data and due to the problem, with finite precision arithmetic, of defining the intersections of the boundaries at “nodes,” and the order of these boundaries around the nodes—the primary requirement of a topological model.

Thus, the primary technical problem for early polygon-based GISs was to move from the coordinates of the original input data points to a topologically valid graph showing the connectivity of the desired polygons (regions), arcs (edges), and nodes. At the same time, the problem of managing point-based field data was moving toward a TIN-based structure, while unconnected “vector” data had no topological structure beyond the order of the input points.

A few examples will give the flavor of a variety of “geographic” perspectives of spatial data that must be mapped onto the available sets of tools.

Martin (1999), for example, discusses spatial representation from the point of view of a social scientist. He gives examples of point (P), line (L), area (A), and surface (S) types for the primary real-world entity, the digital object in the computer, the types of manipulation or analysis desired, and the forms of visualization. Thus, real-world entities include individual disease cases (P), journeys to work (L), property ownership (A), and population density (S). For digital objects, he mentions postcode coordinates (P), street segments (L), land parcels (A), and elevation models (S). For possible manipulation techniques, he cites nearest-neighbor analysis (P), network analysis (L), centroid generation (A), and slope analysis (S). Visualization includes point plotting (P), line drawing (L), choropleth mapping (A), and contour mapping (S). Note that he distinguishes between area objects (which may not be connected) and surfaces (which in principle are continuous).

Laurini and Thompson (1992) classified “spatial units” into points (e.g. historic sites), lines (e.g. rivers), areas (e.g. countries), and 3D blocks (e.g. aquifers). Basic queries are of the form “What do we have at/in this point/line/area/zone?” where “zone” may be a circular region, a buffer zone or some arbitrary region. They also pointed out that these queries may be compound—e.g. whether a railway passes through a region, crosses a river, or touches a town. They mention issues that we will touch on later: Those entities may be connected to form networks, and the possibility of dual substitution: centroids for polygons; proximal areas for points; points plus polygons for graphs. Both they and Burrough and McDonnell (1998) discuss Goodchild’s (1987) emphasis on the field versus entity (or object) view of space, as well as the “vector” versus “raster” concept and technology, and the use of “layers” to separate various types of entities.

Given these various concerns, the history of GIS has been the development of increasingly large computer systems to manage ever larger quantities of spatial information—that is, information whose whole value is dependent on having a spatial location.

Initially there was point- and line-drawing computer cartography; then simple polygon mapping; then choropleth (polygon) mapping with “topology,” and then grid and—later—TIN representations of surfaces, and network analysis functions. This spatial information has a variety of attributes—but it also is associated with a variety of spatial entities: point locations (x, y, and possibly z); one-dimensional lines or curves; two-dimensional discrete structures; or two-dimensional continuous entities which are usually broken into contiguous tiles for convenience of analysis, storage, and representation. This contiguity will usually need to be preserved (or recalculated) for analyses which involve interaction between tiles. Contiguity, or adjacency, will also need to be estimated for some analyses involving discrete entities.

As GIS usually implies large data sets, there is in addition frequently a need to provide rapid access to entities at specific locations. At the simplest level, this involves an index to main memory; for larger data sets, this involves spatial clustering of nearby entities so that a portion of the map may be stored or retrieved from the same portion of the computer’s hard disc. Tessellations may be used as co-ordinate indexing schemes—sometimes hierarchical, sometimes not. The spatial partitions are used as pigeon-holes to store pointers to objects having 2D or 3D coordinates.

3. Geographic data

In GIS, data are often classified as of either “field” or “object” types. Field data imply spatial continuity, whereas objects are unconnected entities, such as houses. Field data again may be classified as having discrete or continuous attributes—for example land use classification vs. temperature. Traditionally, tessellations are used for discrete attribute fields, and not for objects. Point observations of fields may be interpolated over the whole space and either be classified and treated as discrete, or else modeled as surfaces—as in triangulated terrain models. While usually considered in 2D geographic space, the same principles apply in 3D.

However, recent re-examination of tessellations suggests that they are valuable for object-type data as well—if they are based on an adaptive tessellation such as the VD, rather than a spatial partitioning like the quad tree. Following from this is the idea that cell adjacency relationships describe the relative positions of the generator objects (a local coordinate system). Thus, the static, dynamic, or kinetic VD may be used for navigation, map construction, and updating, as well as simulating fluid flow, etc. It should be remembered that one of the original, and ongoing, concerns of GIS is the valid construction of connected graphs (polygons, rivers, etc.) from approximate co-ordinate data.

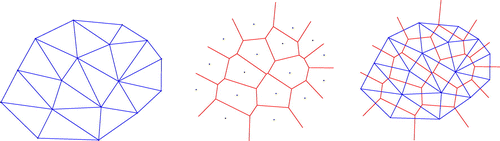
Finally, while the Voronoi and Delaunay duality is well known (Figure 4), there are many applications where both of these structures are needed simultaneously—for example in crust and skeleton construction and catchment area modeling (Gold and Dakowicz 2005). Data structures in 2D or 3D that preserve these relationships, and associated attributes, are becoming more interesting.

Figure 4. Delaunay triangulation and Voronoi diagram.

In a 2007 workshop (Gold 2007), discussion of 2D and 3D GIS attempted to give some definition of spatial data. They concluded that a 3D (or even 2D) model may include a variety of types of information:

(1)	Geometry (absolute or relative coordinates in 2D or 3D);
(2)	Topology (some form of connectedness between elements, sufficient to permit navigation);
(3)	Attributes (properties attached to the elements, relevant to a specific application);
(4)	Semantics (some specification of meaning of the element, perhaps geometric or thematic);
(5)	Functions (the types of operations appropriate to the element);
(6)	Time and scale (at what time, and at what scale, the element is relevant).

They also noted that it was difficult to give a final definition, as a 3D (or 2D) data set may be used for different purposes:

(1)	visualization alone;
(2)	analysis and computation, e.g. calculation of volumes—not usually involving time;
(3)	simulation and decision support (“what-if” modeling, including parameter change) that usually implies development over time;
(4)	management, acquisition and storage of data, including data structure updating over time.

3.1. Geometry

It is traditional in GIS to talk about geometry (coordinate information) and topology (connectivity information) separately when talking about vector data consisting of points, lines, and polygons. More complex objects (e.g. building outlines) are composed of these elements, with attributes attached. The same approach may be used for space-covering polygon tessellations, where boundaries are shared by adjacent polygons, etc. Thus, a building outline consists of a set of data points (with at least x − y information about its location) that identify its “geometry.”

3.2. Topology

However, these data points (vertices) are useless without some connectivity information—at a minimum, an ordering of vertices around the building to “connect the dots.” If we have a connected set of polygons, such as administrative districts forming a tessellation, we must not only connect the dots along the boundaries, but also connect the boundaries around each polygon. There is a variety of ways to construct this “topology,” and this is still a subject of research interest. Nevertheless, we have geometry “objects” or “entities” as well as topological ones, and we may need to specify “node” objects where boundaries meet, as well as compound “map objects,” such as polygons or buildings.

3.3. Properties and attributes

While topological entities do not usually need additional information beyond connectivity, the remaining “cartographic objects” are attempts to represent aspects of the real world. Each entity type may have specific properties, such as semantics, function, time, and scale as mentioned above, in addition to various attributes such as color, population, area, etc.

4. Models of space

Perhaps the simplest model of space “in the head” is a set of points on the plane, with no specified relationships between them. Nevertheless, some sorts of relationships are often imagined by the viewer, based on relative proximity. Many relationships that are “obvious” to the viewer, such as clusters, are not at all obvious to a computer, and this causes a good deal of confusion. This gave rise, at the same workshop, to the remark: “Topology exists, whether you want it or not. The question really is – do you want it to be explicit or implicit?” The same holds true for other disconnected objects in the map—for example building polygons or linear features.

Alternatively we may imagine some continuous model of space—a field. One example is a terrain model: we may think of it as a grid made of square cells; a grid formed from a regular lattice of (either unconnected or connected) points; a triangulation connecting arbitrary data locations to give an adjacency network; a space-filling triangulation formed of flat plates; or a cellular structure representing the proximal region for each data point. In addition, we may want to imagine movement between cells: possibly water runoff. Here, we need to have both a container for the current water in some cell and some adjacency statement to permit movement. If we think of a grid of square cells, these form the “buckets,” and their four neighbors give the adjacency. However, if we need to estimate slopes, in order to simulate flow rates, we immediately switch to the dual, with a node at the center of each cell, connected to its neighbors, each with a slope based on the elevation difference of the nodes. We already are working with two spatial models at once. The same is true for irregular distributions: proximal (Voronoi) cells form the buckets in our “Block World” and the dual triangulation of their generating nodes gives the slopes (and perhaps planar TIN model) in our “Slope World.” Similarly, any polygon map has a dual based on the adjacency given by shared boundaries. Duality is hidden everywhere—even in the apparently distinct problem of identifying road centerlines or river watersheds: A subset of the dual of the boundary or river simplifies the job greatly.

The oldest argument in GIS was therefore between a “raster” (grid) view of the world—a field model, partitioning space on the basis of coordinates, and a “vector” view—consisting initially of disconnected one dimension (1D) line segments, each associated with some cartographic object. Transfer between one and the other inevitably produced loss of precision. Constructing cartographic objects from rasters meant attempting to glue squares of similar “colour” together, while from vectors the topological problem of connecting 1D elements (spaghetti) with imprecise coordinates was also difficult when based solely on metric distance. Interpolation problems—often based on weighted averages of a metrically defined set of neighbors—also ran into problems. Other disciplines, such as computer-aided design (CAD) had similar problems when trying to construct bounding surfaces—but alternatively mechanical parts could be designed from solid primitive objects using constructive solid geometry, which again had problems when attempting to construct the boundary of the composite object.

We will focus next on what appears to be the biggest issue: the distinction between “fields” and “objects.”

4.1. Objects and fields

GIS has traditionally separated the mapping of objects, and of fields, and has used separate data structures for each. In addition, as shown in the previous discussion, it is not always clear when we are talking about objects, and when about fields. Perhaps the simplest distinction is based on what may be the most fundamental GIS query: “What is here?” when pointing at some map location. For fields, there is always an answer (perhaps temperature or population density) within the boundary of the map. For objects, the answer may be “nothing”—e.g. for a map of houses the answer will be “House” or “Not House.” Thus for fields, with complete map coverage, usually by pixels, polygons, or triangles, there is some implicit or explicit definition of adjacency where two cells meet at a common boundary.

This is not present for discrete unconnected objects, creating difficulties when the mapping of moving objects is desired. While no interaction between a moving object and its neighbors may be needed for simple applications, any attempt at real-world simulation needs to maintain proximity relationships between them in order to prevent collision. It should be noted that this applies for dynamic (insertion and deletion) situations as well as kinetic ones involving point movement. Another fundamental GIS operation—interpolation—is of this type: A query point is considered to have been inserted at the desired location; its set of neighbors obtained; and an attribute (e.g. elevation) estimate calculated from this set. In all these dynamic or kinetic cases, a set of neighboring objects is required, based on spatial proximity.

Many techniques have been developed to obtain this set, often based on metric distance (Gold 1992). However, many inconsistencies have been noted where pure distance has been used (Jones et al. 1995). A more consistent approach has been developed more recently (Jones and Ware 1998) based on a field spatial model—an object set is converted to a field model by calculating a proximal map: Each object has an associated polygon representing the portion of the map closer to that object than to any other. This partitions the map into polygons, and thus, adjacency relationships can be defined based on the common boundaries. Thus, the “What is here?” query is transformed to “What is closest to here?” As a query of a map-covering field, an answer is always obtainable—and the adjacency data structure is identical to that for other field models. (Rasters are a special case where the N–E–S–W relationships between adjacent cells need not be preserved explicitly.) These proximal maps—called Thiessen polygons, Dirichlet cells, or VDs—give a spatial model providing a unifying concept between objects and fields as well as adjacency information—or connectivity information, or topology as it is frequently called in GIS. The closest topological notion from adjacency is connectedness. We will call this adjacency information topology in these papers.

Some care must be taken, however, in the use of the word “field,” especially as we move toward more 3D GIS methods. If by “field” we mean that we expect a non-null answer to the question “What is here?” then this applies to more than the 2D plane discussed above, and it applies whatever space dimensionality the field is embedded in. Thus, a curve or “polyline” in a map is a 1D entity in 2D space, and it may be queried anywhere along the curve—but not elsewhere in the 2D map. A 2D topographic surface—e.g. a TIN—may be thought of as embedded in the 2D plane, or alternatively a landscape in 3D. It may be queried in 3D only if we may assume the irrelevance of the elevation dimension, i.e. the surface is monotonic in x and y. If there are bridges and tunnels, then the 2D surface must be treated as embedded in 3D space.

In summary, fields may have continuous or discrete attributes. In the first case, they are represented as grids or TINs; in the second case, they are more commonly represented as arbitrary contiguous polygons or rasters. Where map entities are discrete objects, they may typically be represented as points, edges, or polygons having no intrinsic topological connectivity to nearby entities.

Thus, the idea of fields in GIS gives us a concept of connectedness. However, we need to go beyond this to consider two other aspects: How many dimensions are we actually working in (as well as the dimensionality of the structures we are considering); and are these static, or dynamic—allowing local change in the boundaries and their connectivity? We give a few simple examples.

One dimension (1D) is usually ignored, but is relevant for transport and network analysis. The term “dynamic segmentation” serves as a reminder that we may have attribute information associated with a partition of one-dimensional space.

2D is a simple map in that location is specified based on two independent coordinates. All else is attribute—including elevation models with z attributes attached to a two-dimensional structure (grid or TIN). A “primitive” 2D map consists of independent unconnected “objects”; a “boundary” 2D map consists of a set of connected elements, as either a set of adjacent polygons or a network (possible with attributes); a “solid” 2D map consists of attribute-filled boundaries, such that any location has a value (thus producing a “field”).

3D location requires three independent coordinates. We may have a primitive map with unconnected data points or objects; we may have a boundary map defining closed 3D cells; we may have a solid map with attributes associated with each cell.

In all of these dimensions, we may have independent objects, boundaries, discrete attribute fill (such as polygon classes), or continuous fill (such as smooth topography).

5. Embedding

Examination of the multidimensional development of GIS depends on the concept of “embedding”—entities of a specific dimension are incorporated in a space of (the same or) higher dimension. Table 1 (Gold 2005) shows the embedded/embedding relationships and how this relates to the choice of dimensions, spatial data structures, and operations (the symbols are defined below: Clearly the table could be expressed simply, but perhaps less intuitively, in algebraic form).

Table 1. Relationships between the object dimensions and space dimensions.

Embedded dimension	Space dimension				Data type
	0	1	2	3
0	F	B	BB	BBB	Nodes
1		F	B	BB	Curves
2			F	B	Surfaces
3				F	Volumes

Notes: Field (F); boundary (B); boundaries of boundaries (BB); boundaries of boundaries of boundaries (BBB).

The columns indicate the number of spatial dimensions we are working in: traditional maps are 2D, and more recent GIS work attempts to build 3D models. More trivially, 0D space is a single point, and 1D space is a curve—but this curve may have some topological relations: It may be composed of several curve segments, separated by nodes. Hence, in 1D space, the curve segment is a “field” (F) with boundary nodes (B).

The rows indicate the dimensionality of the entities being worked with. 0D entities are nodes, which form boundaries of curves that are embedded in 1D and higher space. 1D curves are space-filling fields in 1D space, and boundaries of space-filling surfaces (fields) in 2D space—but they themselves are bounded by 0D nodes: “boundaries of boundaries” or (BB). Similarly, volume entities are fields in 3D space, bounded by 2D surfaces, etc.

All of these are trivial mathematics—perhaps first discussed in a GIS context by Corbett (1975). The utility of the table here is to visualize how it applies to multidimensional data structures. What is often not remembered is that a lower dimension structure may be embedded in a higher dimension space: Even if it is not space-filling, it may still be a field in its own right. A curve in 1D space is a field with connectivity information: It may exist in 2D space either as a boundary of a 2D field or as a discrete curve. Thus, the same topological structure may have different interpretations. Similarly, a 2D field (with bounding curves and their bounding nodes) may be placed in 3D either independently or as the boundary of a volume, and the interpretation is not always clear. In GIS, a terrain model is often referred to as “3D” when in fact it is a 2D surface in 3D space. (Most people forget that it is really the boundary of a 3D volume, the “Polyhedral Earth.”) The terrain model may be a triangulation—composed of triangular faces bounded by curves—but for some applications, it is more appropriate to ignore the faces and just consider the graph of edges and nodes.

Another point that can be made is that the triangulation structure of cell (2, 2) is simply an interpretation (or application) of cell (1, 2) which is a set of edges and nodes, without any regions defined for any closed loops (think of a road network), with only two coordinates defined for its nodes (cell (0, 2)). Cell (2, 2), by defining 2D elements, has forced this graph to be planar. Similarly, cell (1, 3) is a graph with edges and (3D) nodes. If closed loops are surfaces (faces: cell (2, 3)), we force some order on the original graph, as we may choose to say that faces may not be penetrated or intersect. If we insist that faces are boundaries of closed volumes (cell (3, 3)), we have a 3D cellular complex defined, in the end, by a graph structure.

Most 2D GIS applications are traditionally concerned with field maps F (cell (2, 2), polyhedral mapping). Boundary maps B (cell (1, 2)) are not so much used directly, but if the cell (2, 2) constraints are lifted, then the resulting “D-1” maps are often used for transportation networks. The other common situation, terrain modeling, involves 3D space with 2D embedded structures (cell (2, 3)) as previously described for TINs. Confusion between the embedding space dimension and the embedded entity dimension often causes a TIN to be labeled 3D or even 2.5D.

In conclusion, any entity or structure may be embedded in the same or a higher dimensional space, but its meaning will usually change: The number of coordinates associated with its nodes will change but its data structure will not.

Table 1 makes clear that at all levels we need to operate on a set of nodes that contain the appropriate coordinates for the dimensionality (row 0). Thus, movement necessarily involves changing these coordinates. If we want “topology” in our models of the world, we need to add the basic connectedness by adding edges (row 1) to our nodes. The resulting graphs are readily manageable by computer. 2D and 3D networks can be created in this way, with or without 2D or 3D “field” entities.

If we move to row 2 of Table 1, we find that we need to constrain the appropriate graph from row 1 in order to generate and preserve faces at cycles, based on the node coordinates. In 2D, we need to work with Euler’s formula, and other properties of planar graphs, as is well known (e.g. Buckley and Lewinter 2003). In GIS, we have the additional questions of generating appropriate nodes to link our digitized boundaries. The result gives us our polygon map. In 3D, we need the Euler–Poincaré formula, as bridges and tunnels are possible—see Tse and Gold (2002). In addition, the construction of bounded volumes is more complex, and 3D visualization and selection is still difficult.

6. Discrete objects

The concept of embedding a data structure within a space of the same or higher dimension allows us to see the common features between various approaches to multidimensional GIS. Examination of the requirements of those data structures indicates the need for local maintenance, based on clear geometric conditions. This in turn shows how the structures may be made dynamic and kinetic, leading to practical implementations of dynamic and kinetic GIS applications.

6.1. Fields

Space is continuous—so are fields, which, in GIS, attempt to represent space by tessellations, as we need to break down spatial continuity into discrete elements for computer storage and processing. Then, of course, in order to simulate our original space, we need to sew the tiles back together with an appropriate topological structure. In effect, we first classify our space into tiles, and then classify the attributes in each tile. As any cartographer would admit, classification inevitably distorts the truth—but we have little choice. Note, however, that Table 1 indicates that this applies to the dimensionality of the structure rather than the embedding space: The continuity properties of a 2D field such as skin pattern on a giraffe are largely independent of the form of the animal. Nevertheless, fields are preserved with continuity, represented by their topological properties.

6.2. Objects: spatial extension

The fundamental GIS problem (which is the same as the CAD problem in 3D) is how to produce a connected structure (a field of some type, with some kind of topology) from imprecise coordinate data (elementary objects). It is well known that detecting adjacency/connectivity from metric proximity alone is invalid. A valid approach is to generate the VD of our point objects in the embedding space: This gives sufficient information to determine the connectivity of our desired structure. This is perhaps consistent with Einstein’s (1961) comment:

I wished to show that space-time is not necessarily something to which one can ascribe a separate existence, independently of the actual objects of physical reality. Physical objects are not in space, but these objects are spatially extended. In this way the concept of ‘empty space’ loses its meaning.

Thus, if we expand our individual cartographic objects (points, houses, etc.) on a regular basis until their “bubbles” meet, we can produce a “field” model from our independent objects, with its associated topological structure. In Euclidean space, with point generators and a fixed expansion rate, this produces the ordinary VD. If we connect each pair of generators whose cells touch, we get the Delaunay triangulation—if necessary by arbitrarily triangulating degenerate cases where cells only just touch because more than three generators are co-circular. This forms the “dual” graph of the Voronoi representation, and vice versa. Similarly, primal and dual structures may be preserved for traditional polygon (choropleth) maps.

7. Graphs and data structures

7.1. Graph-theoretic methods for fields and duals

The connectivity model or “topology” for tessellations consists of nodes and edges—it is a graph. In the 2D plane, closed regions are possible (Table 1) and we have a planar graph. There are many books describing elementary graph theory. A good introduction is Buckley and Lewinter (2003).

There are also many computer algorithms that perform various types of searches on graphs, and they are basic to very many applications. Graphs may be un-weighted or weighted (with values on edges or nodes), they may be undirected or directed (allowing traversal in only one direction) and they may be unconnected or connected. Simple algorithms on these graphs include depth-first search, breadth-first search, shortest paths, minimum-spanning trees, and network flow. They may also be non-planar or planar, and in planar graphs, any minimally closed paths form regions that may be entities in their own right, for example as map polygons. A simple way to identify map polygons, given a set of edges and nodes, is to perform a breadth-first search of the graph (which will produce a tree structure) and note when the algorithm attempts to close a loop. A breadth-first search will produce a minimal loop, but for this to work correctly, the “child” edge must be the next one (anticlockwise or clockwise around the node) from the “parent” edge. This requires knowledge of the ordering of edges around nodes, which can only be determined for planar graphs. This, incidentally, is traditionally the primary problem for GIS (the “topology” problem), where edges were digitized by hand and would not necessarily all meet at the node without any crossings, and thus with no obvious rotational order.

For a planar map such as this, a dual graph exists, where the region entity is treated as a node, and nodes in adjacent regions are connected. The node in the original graph is now surrounded by a loop of edges, becoming a region in the dual graph. Except where more than three regions meet at a node, the result is a triangulation. If we spatially extend a set of points, as described previously, we generate a set of regions, the simple VD, which has a dual, the Delaunay triangulation (DT). Because the VD is unique, the DT is unique—which is not the case for other triangulations.

The difficulty of finding the order of edges around a node in traditional GIS is because the 1D edges have relationships that are not fully described in 2D space. The ideal solution is to spatially extend these edges so they generate a space-filling tiling where all topological relations are fully described. This will be discussed further on.

Because the VD is now not just a graph, but has specific geometric properties, we need geometric predicates that will give “correct” answers using computer finite precision arithmetic. Only two are needed: “CCW” to determine the anticlockwise or clockwise ordering of three points in 2D (Guibas and Stolfi 1985; and also Gold et al. 1977), and “Incircle” (Guibas and Stolfi 1985) to find if a fourth point falls inside the circle defined by the first three. Shewchuk (1997) has given algorithms that are correct to any level of precision, and also for the 3D equivalents.

In 3D (cell (3, 3) in Table 1), volumes become entities as well—the 3D equivalent of a planar graph. Thus, these become nodes in the dual graph. Faces bound adjacent volumes, so the dual of a face is an edge. (Likewise, the dual of an edge is a face, and the dual of a node is a volume.) We will discuss this briefly later on, where we point out that the combination of the primal and dual graphs describes all the 3D entities and relationships—so all of our spatial relationships can be treated as graphs.

7.2. Implementation and data structures for graphs

7.2.1. Two dimensions

The boundary model (B) of cell (2, 3) is often implemented in CAD systems (Lee 1999). Here, the solid is defined by its boundary, which is defined by the vertices, edges, faces, and the relationships between them. “Euler operators” are used to modify the boundary. The following data structures are used to implement B-Reps for solid objects:

•	half-edge of (Mäntylä 1988)
•	winged-edge of (Weiler 1988)
•	quad-edge, an edge algebra (Guibas and Stolfi 1985)
•	DCEL—doubly connected edge list of (Muller and Preparata 1978)
•	GIS topological models (e.g. Egenhofer and Franzosa 1991; Molenaar 1992; and Zlatanova et al. 2004).

7.2.2. Three dimensions

The solid spatial model (F) of cell (3, 3) may be implemented entirely of solid atomic elements by either constructive solid geometry (CSG—the Boolean combinations of simple solids often used in CAD systems), or by regular 3D (volume) decomposition, using either voxels or octrees. (Here, the adjacency relations are implicit and do not require the maintenance of the graph structures of row 1 of Table 1).

Alternatively, we may use irregular 3D (volume) decomposition—often a Voronoi spatial decomposition—which combines the properties of an object-based adjacency model with a spatial decomposition model, where the spatial decomposition is defined as all the 2D or 3D locations that are closer to a particular geometric object (often, but not necessarily, a vertex) than to any other. This fully defines the model and its adjacency relationships. It requires a data structure for implementation. This may be any of the following:

•	dual Delaunay tetrahedra—four vertices and adjacent tetrahedra: It is not an algebra and requires local searching (Boissonnat et al. 2002)
•	facet-edge of (Dobkin and Laszlo 1989) and its extension to any dimensions (Brisson 1989)
•	G-maps of (Lienhardt 1994) and (Bertrand et al. 1993)
•	augmented quad-edge (an edge algebra, like the quad-edge). See (Gold et al. 2005; Boguslawski and Gold 2007; Ledoux and Gold 2007).
•	dual half-edge (Boguslawski and Gold 2011)

The tetrahedral model is the most frequently used, because of its simplicity, but it is not an algebra and reconstruction of the dual is tedious. Non-manifold systems allow a mixture of wireframes, surfaces, and solids, so the space may not be just a simple partition. See (Weiler 1988) and (De Floriani and Hui 2003).

All of these data structures operate on graphs: nodes plus connecting edges. They may operate on the primal graph (e.g. a triangulation) or the dual graph (e.g. the VD) in the 2D case. In the primal case, the nodes are data points (geometry), and in the dual case, the calculated vertices of the VD. The quad-edge has the advantage of combining the two graphs, so the Voronoi vertices may be interpreted as the “faces” of the cells. In all these cases, loops of the edge-to-edge pointers navigate around the potential face. As will be seen, for spatial data, there are often advantages in either primal or dual space or both together, so we want the same data structure and set of operations to be valid for both the primal and the dual graphs: It is not necessary to know which space one is navigating in at any particular moment. The quad-edge has this property.

In 3D, the dual of a volume is a node, and vice versa, and the dual of a face is a penetrating edge. Thus, the Augmented quad-edge has representations of volumes as well as faces, edges and nodes—both for the primal and dual graphs of a 3D cell complex such as a VD.

7.2.3. CAD data structures

It is fairly clear that GIS is still firmly two-dimensional in its implementation, despite various attempts to extend it, and despite frequent complaints about the inability to model non-planar networks, bridges, caves, etc. within the traditional TIN surface model. In order to alleviate this, the first step is to recognize that a terrain surface modeled by a TIN is not a two-dimensional entity—it is an air– (or water–) earth interface, the boundary between the “Polyhedral Earth” and the exterior. Simply put: every TIN has an “underneath”—it is a portion of a model of a complete solid. This causes few difficulties in practice.

Once this polyhedral model is accepted, attention naturally turns to other disciplines’ experience in polyhedral modeling. Computational geometry has developed a variety of tools for managing surface models (de Berg et al. 1997). In particular, the field of CAD has been developing tools for solid model representation for many years, for example (Baumgart 1972; Mäntylä and Sulonen 1982; Mäntylä 1988). CAD systems often use a boundary (or b-rep) approach to describe individual polyhedra or shells, using some of the edge structures mentioned above. These are manipulated by “Euler operators”—actions that guarantee that the surface remains closed during, for example, extrusion. Tse and Gold (2002) showed the simple relationships between these operators and the quad-edge structure.

The examination of CAD modeling techniques does not seem attractive at first sight. The intersection of cubes and tubes, as in CSG modeling, hardly applies to terrain models. Modern non-manifold models of surfaces can have astoundingly complex data structures (Lee 1999) and would be massive overkill for TIN enhancement. However, the simpler manifold-based “b-rep” CAD models appear to be reasonable for our purposes. In particular, the careful specification of “Euler operators” that guarantee to preserve the topological validity of the bounding surface seems particularly appropriate. Euler operators ensure the integrity of boundary models. As stated by Mäntylä in 1988, “In a ‘b-rep’ model, an object is represented indirectly by a description of its boundary. The boundary is divided into a finite set of faces, which in turn are represented by their bounding edges and vertices.” According to his definition, b-reps are best suited for objects bounded by a compact (i.e. bounded and closed) manifold. However, if the main concern were building a non-manifold object, it would be better to use other models.

Within GIS, city modeling has become quite frequent: the most popular format being CityGML (Gröger and Plümer 2012). This defines several levels of detail for the description of buildings—only the highest level giving interior features. Wagner et al. (2012) describe the problems of consistency validation—checking that the coordinates of the parts of the building match each other. Ellul (2012) examined the improvement in rendering speed of exterior city models when taking into account the topology of the individual faces. Kraft and Huhnt (2014) examined geometrical completeness in building models.

7.2.4. Quad-Edge

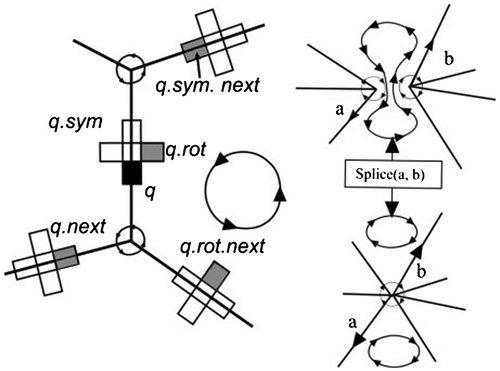
We have examined the basis for various sets of Euler operators mentioned in the CAD literature and their data structures. This is usually the “winged-edge” data structure (Baumgart 1972), which has a variety of supporting pointer structures, some of which, upon closer examination, are not necessary in order to maintain a TIN or triangulation-based b-rep surface model. In particular, if all faces are triangles, then no holes may be created in the interior of individual faces, and thus, some elements of both the winged-edge structure and the classical Euler operators may be removed. We have used the quad-edge structure of (Guibas and Stolfi 1985). More particularly, the quad-edge structure has been used to implement a set of Euler operators that have been shown to suffice for the maintenance of surface triangulations. According to (Weiler 1985, 1986), if a topological representation contains enough information to recreate nine adjacency relationships without error or ambiguity, it can be considered a sufficient adjacency topology representation. These Euler operators form the basis of the standard (two-dimensional) incremental triangulation algorithm. In addition, Euler operators can serve to generate holes within our surfaces, thus permitting the modeling of bridges, overpasses, etc. that are so conspicuously lacking in the traditional GIS TIN model. The individual quad-edge and Euler operators take only a few lines of code each. “Make-Edge” and “Splice” are the two simple operations on the quad-edge structure, which is formed from four connected “Quad” objects, using the simple implementation of (Gold 1998). Every Quad has three pointers:

N—link to next Quad (Next) anticlockwise around a face or vertex

R—link to next 1/4 Edge (Rot) anticlockwise around the four Quads (“Sym” is two Rots)

V—link to vertex (or face)

The Make-Edge operator creates a new independent edge. The Splice operation, which is its own inverse, either splits a face loop and merges two vertex loops (upper to lower parts of Figure 5) or else splits a vertex loop and merges two face loops (lower to upper). This operation suffices to maintain any connected graph on an orientable manifold, as is the case for CAD b-rep models, and TINs. However, in TINs, there are no loops (holes in individual faces), so these will not be considered.

Figure 5. Quad-Edge structure and Splice operation.

We can thus summarize some useful properties of our VDs and data structures:

•	Discrete objects propagate to fields
•	These fields provide a topological structure for adjacency
•	We have a space-filling, not a line-intersection, spatial model
•	Valid topology is produced, even with low-precision co-ordinates
•	Attributes may be attached to both primal and dual entities
•	Operations may be performed in both primal and dual space simultaneously.

8. Spatial indexing and hierarchies

8.1. Indexing

van Oosterom (1999) summarized spatial access (indexing) methods in GIS. He states:

Two characteristics of spatial datasets are that they are frequently large and that the data are quite often distributed in an irregular manner … Therefore spatial indexing is required, in order to find the required objects efficiently without looking at every object … Clustering is needed to group those objects which are often requested together.

He describes a variety of possible methods: tree structures, space-filling curves, and regular or irregular cells. Tree structures he mentions include KD-trees, BSP-trees, quad trees of various types, R-trees, and several multiscale access methods (reactive-trees and GAP-trees). Possible space-filling curves include Peano and Hilbert varieties. Regular cell methods include grid-based methods (grid-files, field-trees) and global grids such as the QTM structure. Irregular cell methods include the Thiessen or Voronoi, as used by Christaller, and the Hipparchus system of Lukatela (2000). Equivalent indexing methods can usually be used in 3D without any major problems. Different techniques have different advantages and disadvantages—the main conclusion being that any indexing system is better than none. For very large data sets, a hierarchical system is desirable. It is mathematically direct to model space in terms of graphs—then standard graph traversals can search for attributes—in database terms, this implies that spatial localization is performed before attribute queries. A hierarchy model may serve to place large graphs on disk storage—one of the major reasons for a database in the first place.

8.2. The hierarchy problem

The techniques described so far are graph-theoretical methods, which are simple to store in computer main memory, but which may be difficult to preserve when their size exceeds the available space. In this case graph-partitioning, methods are needed to save spatially adjacent portions of the network on particular disk pages. Gold and Angel (2006) described a hierarchical method for Delaunay triangulations that appears to handle that problem. Firstly, a simple walk through a triangulation provides a reasonable point-location algorithm—e.g. Gold et al. (1977). Secondly, for very large maps, this may be speeded up by having one or more levels of a Delaunay hierarchy, where higher levels may consist of subsets of the points in the lower levels. Having located the nearest point in a higher level, a downward link leads to the equivalent point in the lower level, and the process continues (Devillers 2002). Thirdly, the Voronoi equivalent view of this method gives higher level cells that contain the point generators of lower level cells, generating a spatial geographic hierarchy following (Christaller 1966). Fourthly, some level may be designated as a disk “page,” and duplicate elements of an edge data structure (e.g. the quad-edge of Guibas and Stolfi 1985) may be used to permit navigation across page faults (Gold and Angel 2006). The graph structure can be maintained dynamically. This approach may reduce the need for special spatial database structures to manage large graphs.

Gold and Angel (2006) described a method, based on Christaller’s (1966) work, for creating hierarchical structures for the indexing of point data sets and TINs stored as edge data structures—in particular the quad-edge structure of Guibas and Stolfi (1985). Based on the dual Voronoi/Delaunay relationship, clusters of points are associated with a Voronoi cell at a higher level, and its generating point may be associated with a higher level yet. This provides a rapid indexing system allowing the fast location of the nearest point to some specified location. The method permitted any desired technique for the specification of the index points at the higher level, e.g. random selection. It was designed to accommodate index cell adaptation to the insertion or deletion of points at the lower level. Disk paging of large data sets is briefly discussed using the same techniques.

Gold and Dakowicz (2007) described an integrated method for handling object and field data in a GIS. This is based on the generation of proximal fields (VDs) around compound objects composed of points and line segments, e.g. house outlines. The dual of these fields gives a triangulation, identical in structure to the simple TIN for data points. The line segments are constructed by the movement of an active point (the “pen”) and the concomitant preservation of the Voronoi/Delaunay relationships. The overall result is a field model (Voronoi cells) for all types of data, stored along with the dual Delaunay triangulation.

The main property of the VD that is of interest here is that it partitions space into proximal regions such that any location is associated with its nearest Voronoi generator. This allows the automated tessellation of space, and provides an adjacency structure that is valuable for generating topology (Gold 2000). The VD also provides a “geometric walk” facility (Gold et al. 1977; Guibas and Stolfi 1985) that permits the navigation of the VD—or the dual DT. It also provides a simple indexing system, where the Voronoi cell may be a container for a collection of data points—e.g. Lukatela (2000).

The VD and the dual DT are basic tools in spatial analysis. The VD is used for topology generation, for volumetric calculations (e.g. as Thiessen polygons for rainfall, or for runoff calculation) and the DT is the basis of the TIN terrain model. (While any triangulation is possible, only the DT, because of its basis in the VD, is guaranteed to be locally modifiable.) They are also well studied in computational geometry, and form the basis of many spatial algorithms. For key surveys, see Aurenhammer (1991) and Okabe et al. (2000).

What is often missing from the VD is a useable hierarchical model. This would permit proper hierarchical indexing, generalization, and paging of spatial data. The problem is simple to state: A hierarchical structure of Voronoi cells (VCs) within Voronoi cells means that the boundaries of the secondary cells are cut off by the boundaries of the (larger) primary cells. Examples of this approach are given in Swets and Weng (1999) for image retrieval and in Pulo (2001) for graph drawing algorithms. This means that VCs are not fully hierarchical to each other, unlike a quad tree where each region is a subdivision of a higher region.

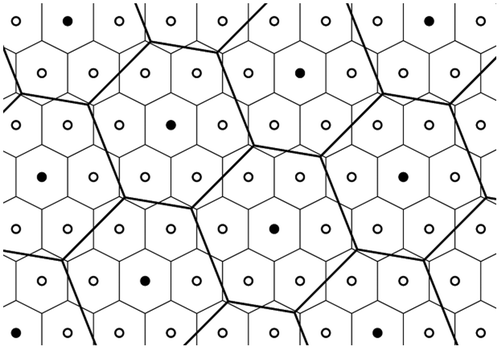
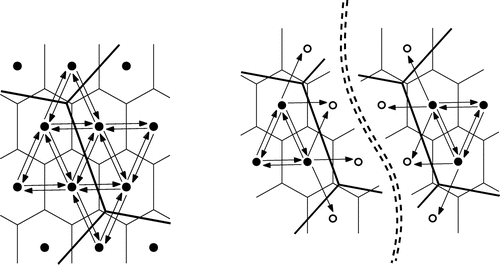
Spatial partitions may be based on the coordinates alone, as in the grid or quad tree; on manual boundaries, as in the choropleth map; or formed automatically from previously defined generators, as in the VD. An interesting case is the work of Christaller (1966). Here, for the administration-optimizing model in particular, a regular pattern of generators is produced so that lower level administrative district centers fall within higher order districts. The tributary area of a higher order central place includes the whole of the tributary areas of the neighboring lower order central places, even though the boundaries of the lower order central places do not necessarily conform to the higher order boundaries if they were taken alone—see Figure 6, and Haggett (1979, 363).

Figure 6. Christaller hierarchy.

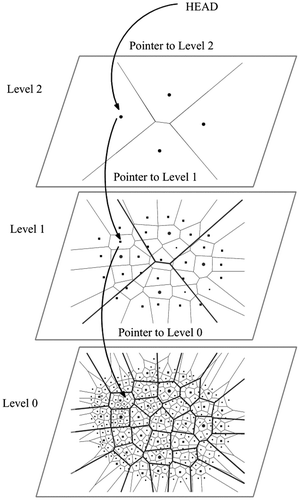
This forms the basis for our Voronoi hierarchy: A VC of the (higher) level i contains all Voronoi generators of the (lower) level (i − 1) that are closer to that level-i generator than to any other. (We will refer to the base level of actual data as level 0.) Thus, a level-1 index cell will contain several (or many) level-0 points, and a level-2 index cell will contain several level-1 generators. Thus, a form of hierarchical VD may be envisaged, where the index VC contains a set of generators of the underlying VD, without necessarily containing all of their generated VCs. This system is fully hierarchical, with as many levels as desired, with each higher level forming a generalization of the level below.

Straightforward algorithms may be devised to implement this structure, given the standard VD, stored as a quad-edge structure where edges of both the Voronoi and Delaunay subdivisions are stored explicitly (Guibas and Stolfi 1985): Each index cell generator has a pointer to a generator in the next lower level. Figure 7 illustrates the structure. Note that a reference to a level-0 generator consists of a chain of pointers from the head pointer of the whole structure. Thus, a reference to the parent of a generator is always preserved by the indexing system. Figure 8 shows three levels superimposed. The index cells may be distributed in a variety of ways, depending on the application requirements. The intention is to have a dynamic system—permitting deletion as well as insertion of points, and hence allowing updating. The only implementation difficulties occur if an index cell is allowed to be empty of child generators—here, decisions must be made as to how to handle the down pointer. Nevertheless, in the ordinary case, a variety of strategies and applications appear to be interesting.

Figure 7. Hierarchical indexing.

Figure 8. Three hierarchical levels.

The most-studied aspect of the hierarchical model is for spatial indexing, but this has focused exclusively on the DT, not the VD. The most obvious application is to generate a fast and flexible point-location strategy—using a simple “walk” algorithm, start at some initial index cell generator, and search until the closest one to the desired location is found. Then, follow the down pointer to the next level, and continue the walk as before. After following all the levels, the closest base-level data point is found. Details of the method (only using data points as index cell generators, and working only with the DT) are given in Devillers (2002) but other similar papers, such as Mücke et al. (1996) and DeFloriani (1989) may be found. Amenta et al. (2003) used a “biased randomized insertion order” to improve the disk behavior of very large data sets, but this is not intended for user-specified insertion and deletion. The simple walk algorithm of Gold et al. (1977) and Guibas and Stolfi (1985) consists of starting at some arbitrary location in the DT structure and testing the desired destination location p against each edge of the initial triangle using a simple determinant test (called CCW in Guibas and Stolfi 1985). If p is outside any edge, then the alternate triangle for that edge is selected and the process repeated until p is inside all three triangle edges. It is important to note that this is a “geometric” test, using the coordinates of p to find the containing triangle or closest data point.

Devillers’ (2002) method consists of starting at the top of the index structure, walking to the closest generator, following a pointer down to some generator in the next lower level, and continuing until the closest point in the base level is found. In his method, index generators are obtained as a subset of those of the next level down using a specific form of random selection in order to achieve an analysis of efficiency and are entirely focused on a rapid search in the DT. Nevertheless, the VD is implicit in his use of the DT. Gold and Angel’s (2006) approach focuses on the VD and guarantees that the generator pointed to in level i is inside the VC of the generator in level (i + 1), thus achieving the Christaller model mentioned previously.

The generators in our approach may be obtained in any fashion desired for the application: a subset of the generators below; a regular square or hexagonal pattern; by a random process—perhaps with some rejection radius to prevent too great a proximity; or any other method. Nevertheless, all indexing methods are significantly faster than a simple walk without any indexing. The number of levels desired is dependent on the size of the data set and the application.

The index structure and data set properties are particularly intimately linked when data deletion is permitted. In Devillers’ method, if a generator is deleted when it is the object of the index cell’s down pointer, then that index cell generator is deleted—and so on as far up the hierarchy as necessary. In our more general approach, the down pointer may be associated with any generator within the index generator’s VC, so deletion of the lower point means that its parent’s down pointer must be examined, and modified, before deletion occurs. This is straightforward as all point-location queries start at the top and preserve all down pointers to the base point. Again depending on the desired application, the index generator may have its down pointer adjusted to point to any other child generator—either a neighbor to the deleted generator or the closest point to the index generator. The only complications occur when the number of an index generator’s children approaches zero—here, the generator’s pointer may be set to null or else the generator may be deleted, allowing adjacent cells to occupy the space. Details of the algorithms are given in Gold and Angel (2006). Mohamed, Khokhar, and Trajcevski (2013) used Voronoi trees for hierarchical wireless sensor networks, and Akdogan et al. (2014) used a ‘throwaway’ spatial index for dynamic location data.

8.3. Paging

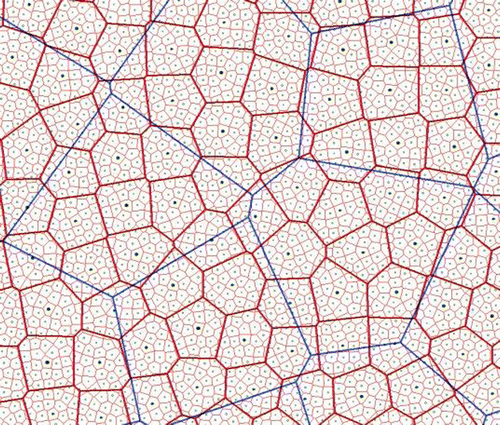
An interesting extension of this concept is when the data set is too large for machine memory, and the data structure must be broken up—invalidating pointers across page (or index cell) boundaries. Here, the quad-edge structure is convenient. Figure 9 shows the pointer structure for a simple TIN—the pointers associated with the dual VD have been left out for simplicity. Edges that cross page boundaries, so that one node is on each page, are duplicated on each page, along with both end nodes. Upon walking through the structure as usual, when a page-crossing edge is detected (because the node at the other end of the edge is outside the page’s index cell), the walk algorithm reverts to the index cell level (the next pointer back in the pointer chain) in order to find the index cell containing the “to” node that fell off the previous page. Following the down pointer into this cell/page, the new structure is traversed to find the node that was previously off-page. All neighboring edges to this node are then tested to find the duplicated edge (based on the coordinates of the “from” node on the previous page). Regular processing may then resume.

Figure 9. Original pointer structure (left) and duplication at page boundaries (right).

Page recovery from disk of all spatially adjacent nodes and edges within the page index cell may be invoked as needed. Thus, duplication of the boundary edges and associated nodes, together with the geometric walk of the page-level index VD, permits direct navigation between pages, and thus allows storage of spatially local data on each disk page, greatly speeding up the processing of large data sets. This has been a significant concern in the handling of large graph-based maps. The paging structure is identical to the index structure except for the duplication of page-crossing edges at the page level. This paging structure is also useful when computing tasks are to be shared between processors, and may be used for the parallel processing of large maps.

9. Conclusions

This first article has examined some of the basic operations in GIS and the object and field models of space. The Voronoi extension of objects and the graphs that express the resulting adjacencies are defined. The required data structures are briefly described, along with 2D and 3D structures and hierarchical indexing. The importance of graph duality is emphasized. Based on this framework, it can be argued that tessellation models are fundamental to our understanding and processing of geographical space, and provide a coherent framework for understanding the “space” in which we exist. A companion paper discusses the handling of change in these structures.

Notes on contributor

Christopher Gold is an Emeritus Professor at the University of South Wales, a Visiting Professor at Southwest Jiaotong University, and a Visiting Professor at LIESMARS, Wuhan University. He has held research chairs at Laval University, Quebec, Canada, and at the University of South Wales. He received the Wang Zhizhuo Award from the Chinese Society of Geodesy, Photogrammetry and Cartography in 2008. His research has been devoted to the development of appropriate spatial models for various aspects of GIS and the promotion of Voronoi diagrams as a fundamental tool for spatial analysis.