The precise multimode GNSS positioning for UAV and its application in large scale photogrammetry

Abstract

In this paper, we use multimode GNSS instead of single GPS constellation to resolve the three exterior line elements of each image. The principles of differential GNSS positioning and GNSS-supported aerial triangulation (AT) are presented and an implementation case is demonstrated. With multi-constellation system, the number of visible satellites is significantly increased and the geometry distribution of the satellites is well improved. The positioning accuracy and robustness are therefore getting better compared to GPS positioning. Experimental results show that differential GNSS has remarkable increment on the integer rate of ambiguity solution when GPS has few number and low elevation angle of satellites. The combined AT adjustment of GNSS resolution and 10 ground control points (GCPs) achieve the horizontal accuracy of ±18 cm and vertical accuracy of ±23 cm for the check points, which are comparable with traditional bundle adjustment with dense GCPs and better than GPS-supported AT. The achieved accuracy also satisfies the requirement for 1:500 topographic maps with the bonus of 84% GCPs eliminated. In conclusion, GNSS-supported AT is of feasibility and superiority for large scale Unmanned Aerial Vehicle-based photogrammetry.

Keywords:

• Multi-constellation
• differential GNSS
• UAV photogrammetry
• GNSS-supported aerial triangulation

1. Introduction

Aerial triangulation (AT) is used to establish precise and accurate relationships between the individual image coordinate systems and a defined datum and projection (ground). Traditional aerial photogrammetry has difficulty in collecting large scale and quickly updating geographic data. In recent years, Unmanned Aerial Vehicles (UAV) are making remarkable improvements for commercial and some professional applications. UAV-based low altitude photogrammetry is flexible for deployment and less costly. Therefore, UAV is very suitable for surveying applications like smart city, disaster emergency, and land supervision. It is an important supplement for traditional photogrammetry methods (Tsai et al. 2010).

Nevertheless, UAV-based photogrammetry has some disadvantages, mostly caused by the small space and loading capability. UAV is easily deviated from the designed route by airflow, thus the rotation angle of image is comparably much larger than traditional airborne method and the neighbor images have irregular overlaps (Gonçalves and Henriques 2015). UAV cannot carry a Position and Orientation System (POS) with tactical-level Inertial Measurement Unit (IMU) for dense ground control points (GCPs)-free AT, while low-level IMU like MEMS sensor is not very helpful for the adjustment (Li 1991). The UAV platform usually carries a consumer camera, which has a small coverage area and considerable lens distortion. It leads to several times of the image number and the tie point number. If the traditional bundle adjustment with dense GCPs is used, the workload for GCPs will be very considerable (Gonçalves and Henriques 2015).

In the six exterior elements measured by POS, the line elements are more important than the orientation elements. In some applications, if the orientation elements are difficult or costly for directly measuring, only exterior line elements are used for photogrammetry. Researchers started to use GPS to obtain the exterior line elements at the end of 1980s (Friess 1991; Gruen, Cocard, and Kahle 1993; Ackermann 1994; Li, Yuan, and Wu 1997; Lichti 2002). At present, both theory and application on GPS-supported AT are well developed, and several AT software applications with GPS supporting function are available on the market. GPS-supported AT reduces the number of GCPs to four and all the four GCPs are located at the corners of the adjusted block, thus the field workload and mapping cycle are both reduced (Guo et al. 2006; Yuan et al. 2009). It is widely applied in aerial photogrammetry, including the low altitude mapping like light airplane (Yuan, Gao, and Zhou 2012), unmanned airship (Liu et al. 2014), and UAV platforms (Li et al. 2012).

Unlike the stable movement of an airship, a UAV has more vigorous maneuver, vibration, and substantial amplitude rolling when it makes a turn. It leads to the frequent satellite loss of lock and degraded accuracy of pass points. A multi-constellations GNSS receiver, collecting GPS, BDS, and GLONASS signal, does not require added space and weight in a UAV. Moreover, the redundancy and reliability of the positioning solution can be enhanced significantly with the benefits of triple the satellite number and better geometric distribution. This work researches the GNSS-supported AT based on a UAV platform and consumer camera. The post-differential processing technology is applied to the double-frequency GNSS phase data to deduce the precise coordinates of the exposure station, which are consequently involved in the bundle adjustment as weighted observations. In this study, our aim is to achieve UAV-based large-scale photogrammetry with few GCPs.

2. Algorithm of multimode GNSS positioning method

2.1. Spatial-temporal unification of multimode GNSS

Satellite navigation is actually an application of spatial resection principle to calculate the coordinate of the station with known satellites’ positions, which means that the coordinate frame of station is determined by the satellites. Therefore, the spatial-temporal unification of multimode GNSS is to obtain the coordinates of satellites in a uniform frame at the time of signal receiving (Li et al. 2013). The observation data of multimode GNSS is recorded in one file with GPS time as the time tag. However, the ephemeris of GPS, GLONASS, and BDS are saved in separated files, also with different time system. The ephemeris of BDS and GPS are recorded in their own time system and the ephemeris of GLONASS uses Coordinated Universal Time. Therefore, the time of BDS and GLONASS in observation data should be firstly converted to their respective time systems to resolve satellite positions in corresponding coordinate frames. Then, PZ90 coordinates of GLONASS can be converted to WGS84, while CGCS2000 coordinates of BDS can be regarded as WGS84 (Li 2011).

2.2. Multimode-GNSS-integrated differential solution

Carrier phase observation is used in multimode GNSS differential positioning (Sun 2004; Wang et al. 2010) and the observation equation is shown as follows:(1)

where the subscript i denotes the ith receiver and superscript m denotes the mth satellite; t_i and t^m are clock errors of receiver and satellite, respectively; c is the speed of light; is the carrier phase observation; is the initial integer ambiguity; γ_i and γ^m are the initial phase offsets of receiver and satellite, respectively; is the wavelength of the mth satellite; and are the ionospheric and tropospheric delay, respectively; is the real distance between satellite and receiver.

For one satellite m, we can derive a single differential equation between a rover station i and a base station j. It eliminates the ionospheric delay and tropospheric delay considering the base and rover have similar atmospheric delay at a short baseline (e.g. 30 km or less). Meanwhile, the satellite clock error t^m and initial phase offset γ^m are independent of the station, which can be directly eliminated by the single difference. Therefore, the single differential equation can be derived as:(2)

where Δ denotes the single difference between stations.

Applying the second difference between satellites for Equation (2(2) ) leads to the double-differential equation:(3)

where denotes the double-difference, and superscript 0 stands for the reference satellite. The receiver clock error is eliminated by the satellite difference. Revise Equation (3(3) ) and we have:(4)

where is the double-differential integer ambiguity. and equal to 0 for GPS and BDS satellites since these two constellations both use code division multiple access (CDMA). However, the carrier phase wavelengths are different for GLONASS satellites in which frequency division multiple access (FDMA) is used. Therefore, the third and fourth terms in Equation (4(4) ) are not 0 and can be initialized with pseudo-range observations. The single differential equation for pseudo-range observations is:

(5)

where is the single difference for pseudo-range observations. Substituting Equation (5(5) ) into Equation (3(3) ) leads to the single differential integer ambiguity:(6)

The error of single differential integer ambiguity in Equation (6(6) ) is mainly determined by the accuracy of pseudo-range. Generally, the empirical error of pseudo-range is 5 m and the initial single differential phase offset does not exceed two cycles. As a consequence, the estimation error of is about 27 cycles. On the other hand, the maximum value of is 0.000723 m according to the frequency distribution of the GLONASS system, which is approximately 0.0038 times of the wavelength. The impact on the double-differential ambiguity is only 0.1 cycles and thus little effect on fixed solution of Equation (4(4) ). If the satellite with middle wavelength is selected as the reference, the error of caused by wavelength difference does not exceed 0.0076 cycles, which can be neglected in calculation.

Based on the above analysis, if the double-differential integer ambiguity is regarded as an augmented parameter, unified differential positioning equation of multimode GNSS can be written as:(7)

For the differential solution in airborne applications, satellites with low elevation angle are usually excluded for their weak signal-to-noise ration and intense multipath effect. If the residual of a satellite is larger than the threshold in resolving Equation (7(7) ) by least square adjustment, it will be eliminated and the adjustment needs to be performed again until all the satellites meet the residual requirement. However, it leads to the problem of float ambiguity for those epochs with less visible satellites. In single GPS differential positioning, the number of visible satellites and the observation quality, influenced by flying instability and the distribution of GPS constellation, are not good enough to get precise and robust solution. When multimode GNSS system is applied, the increased satellite number and optimized distribution will definitely reduce the influence of UAV maneuver. Consequently, the precision and robustness of positioning solution can be guaranteed.

3. Principle of GNSS-supported AT

Taking account of the traditional self-calibration bundle adjustment, coordinates drift of exposure station and other system errors, the model of GNSS-supported AT can be written as Equation (8(8) ) (Yuan 2001):(8)

where V_X, , , and V_G are the image points coordinates, GCPs coordinates, virtual self-calibration parameters, and the correction for coordinates of exposure station, respectively. x, t, c, r, and d are the corrections for pass points, exterior orientation elements of image, self-calibration parameters, level arm, and coordinates drift, respectively. The meaning of other denotations can be referred in the reference (Yuan 2001). It should be noted that the V_G equation is newly augmented after introducing the GNSS solutions into the bundle adjustment as the airborne control points. The accuracy of exterior orientatioelements is directly affected by the quality of exposure station’s coordinates, which mainly depend on the GNSS solution of nearby epochs (Yuan, Fu, and Lou 2007; Yuan, Gao, and Zhou 2012). The coordinates of exposure station can be interpolated by fixed, float, or single point positioning (SPP) solution, if the integer ambiguity is successfully resolved. Insufficiency of the fixed GPS solution rate leads to considerable accuracy difference between exposure stations and sparse distribution of airborne control points like GCPs. If these low accuracy exposure stations locate at the edge of surveying area, every air strip has independent level arm correction r and drift correction d which need to be resolved (Yuan 2009). The augmented unknown parameters require comparative number of GCPs as traditional bundle adjustment, and the superiority of GPS-supported AT is lost therewith.

4. GNSS-supported UAV AT experiment

A UAV-based surveying system was designed to verify the performance of GNSS-supported AT. A Canon 5D Mark III was used as the surveying camera with a 36 mm × 24 mm CCD size, 5760 × 3840 pixel resolution and 6.25 μm pixel length. The GNSS receiver in airborne and the base station are AGS200 and R1, respectively, by Geosun Navigation Technology Co., Ltd. They can both collect double-frequency GPS/BDS/GLONASS signal and they work at the sampling rate of 20 and 5 Hz in this test, respectively. It is noted that the airborne-carried receiver, AGS200, only weighs 380 g, and it is very suitable for a UAV platform. The antenna of the AGS200 was mounted on the UAV shell right up to the camera. The horizontal level arm between the camera and antenna can be approximately considered as 0 and the vertical was measured as 12 cm by a band tape because the precision of level arm is not highly required by the bundle adjustment. The camera is electrically connected to the GNSS receiver to trigger the latter recording of the exposure time, which could reach 30 ns accuracy considering the signal transmission and receiver response time. By taking interpolation between epochs’ coordinates before and after the exposure time, the coordinates of exposure station can be worked out. Figure 1 shows the UAV and the configuration of the sensors.

Figure 1. Configuration of GNSS-supported AT system.

4.1. Differential GNSS processing

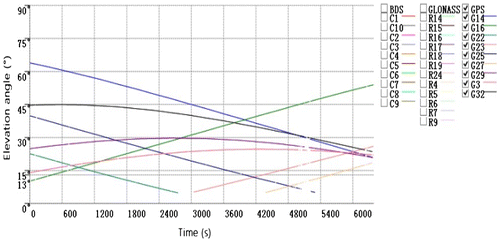
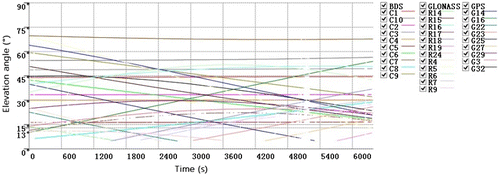
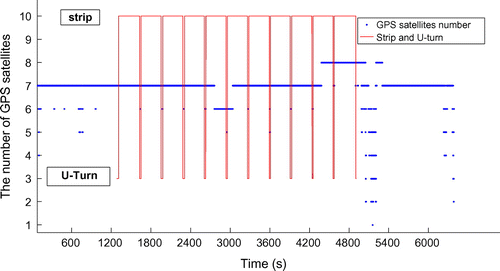
The GNSS-supported AT was tested in a real surveying task in April 2015, in Shandong Province, China. The surveying area is approximately 20 km² and 2401 images were collected. The post-processing software, GGPOS, was used for the differential positioning. Two processing modes were carried out to check out the promotion of multi-constellations, which are single GPS positioning and GPS/BDS/GLONASS combination positioning. The UAV trajectory of GPS and GNSS solution are showed in Figures 2 and 3, respectively. The green and red line represent fixed and float solution, respectively, and the missing trajectory means it is SPP solution, which is not displayed in these figures. Table 1 presents the proportion of SPP, float, and fixed solution by GPS and GNSS. It can be noticed that multi-constellation has a 26.9% improvement for the fixed solution rate. Most SPP and float solution happened in the area from the 7th air strip to the 11th one, which corresponded with the time from 3109 to 4505 s. Figures 4 and 5 show the elevation angles of GPS and GNSS satellites, respectively. Figure 6 shows the number of GPS satellites. There are only five GPS satellites above the elevation angle of 13° in the unfixed area, and one or two satellites disappeared when the UAV made a U-turn maneuver. Low elevation angle causes the decreased signal-to-noise ration and enhanced multi-path effect; therefore, positioning solutions were getting worse. In contrast, multi-constellation provides more observable satellites and higher elevation angle, as shown in Figure 5. There are 22 satellites above 13° in most areas and 18 satellites from the 7th air strip to the 11th one. Moreover, the satellites are well distributed in geometric, which helps the improvement in redundancy and reliability of the post-processing.

Figure 2. Trajectory of the GPS system solution.

Figure 3. Trajectory of the multimode GNSS system solution.

Table 1. Ratio of differential positioning between GPS and multimode GNSS system.

Constellation	SPP solution %	Float solution %	Fixed solution %
GPS	5.7	22.9	71.3
GNSS	1.0	0.8	98.2

Figure 4. Elevation angle of GPS satellites.

Figure 5. Elevation angle of GPS/BDS/GLONASS satellites.

Figure 6. Number of GPS satellites.

4.2. GNSS-supported bundle adjustment

The coordinates of antenna phase center can be obtained by interpolating the solution of differential GNSS, where the EVENTMARK time will be used. The AT software, GodWork, developed by Wuhan University, was used for image matching and free net adjustment. The coordinates of tie points and GCPs in image plane from GodWork, and the coordinates of antenna phase center from GGPOS, were taken as the observations of the bundle adjustment to eliminate the level arm from the camera to antenna. The traditional bundle adjustment with dense GCPs was used as the reference to evaluate the performance of the GNSS-supported AT. The testing started with 4 corner GCPs, followed by 10, 19, and 40 GCPs at the short sides of the surveying area. Also, GPS-supported AT was tested in the same condition to make a comparison. The statistical results of pass points are listed in Table 2 (all the numbers of the check points in horizontal and vertical are equal to 65) and the discussions are presented as follows.

Table 2. Bundle adjustment accuracy comparison of different methods.

Experiment no	Adjustment method	Number of OPs		Max residuals of OPs (m)		RMS of OPs (m)		Max error of CPs (m)		RMS of CPs (m)
		XY	Z	XY	Z	XY	Z	XY	Z	XY	Z
1	Traditional method	65	65	0.313	0.348	0.157	0.081	0.342	0.819	0.171	0.179
2	Without GNSS	4	4	0.056	0.016	0.041	0.011	0.604	−18.093	0.242	11.630
	GPS	4	4	0.089	−0.079	0.069	0.054	0.687	1.749	0.260	0.437
	GNSS	4	4	0.116	0.035	0.104	0.025	0.360	−0.862	0.190	0.387
3	Without GNSS	10	10	0.257	−0.065	0.121	0.038	0.411	−2.792	0.187	1.442
	GPS	10	10	0.364	0.148	0.168	0.069	0.564	1.469	0.234	0.390
	GNSS	10	10	0.286	−0.138	0.156	0.060	0.406	−0.787	0.183	0.229
4	Without GNSS	19	19	0.311	−0.077	0.140	0.042	0.426	−0.913	0.181	0.229
	GPS	19	19	0.383	0.361	0.157	0.105	0.519	0.897	0.213	0.268
	GNSS	19	19	0.164	0.288	0.150	0.064	0.413	−0.690	0.183	0.196
5	Without GNSS	40	40	0.310	0.207	0.149	0.059	0.363	0.534	0.173	0.153
	GPS	40	40	0.353	0.329	0.160	0.099	0.432	0.819	0.193	0.237
	GNSS	40	40	0.306	0.259	0.159	0.073	0.355	0.586	0.177	0.149

Notes: OP and CP denote the orientation point and the check point, respectively. XY and Z denote the horizontal and vertical coordinates, respectively.

(1) In GNSS-supported AT with 4 corner GCPs, the horizontal and the vertical mean square errors of orientation points are 0.104–0.025 m, respectively. The horizontal and the vertical mean square errors of check points are 0.190–0.397 m, respectively. The horizontal accuracy of check points is very close to traditional bundle adjustment with dense GCPs, while the elevation accuracy is relatively poor. It basically satisfies the accuracy requirement of Chinese national standards (CH/Z 3003–2010) for 1:500 DLG and DOM mapping in flat area. The over ranging error of elevation is partly caused by control strip which was not performed in the flight. When 10 GCPs are used in the adjustment, all statics are good for the above standards. There is about 84% GCPs reduction in this situation.

(2) When there are 19 GCPs used in the adjustment, GPS-supported AT can basically satisfy the accuracy requirement of 1:500 DLG and DOM mapping in flat area. However, the GNSS-supported AT still prevail in 20% horizontal improvement and 30% elevation improvement compared to GPS-supported AT.

5. Conclusions

In UAV-based photogrammetry, positioning performance of single GPS constellation is easily affected by platform vibration and satellites’ geometric distribution. The pass points’ coordinates and bundle adjustment are accordingly deteriorated. Differential GNSS can improve the accuracy and reliability of UAV positioning solution. The aerial test indicates that the differential GNSS has 37.7% improvement of the fixed solution rate compared to the differential GPS. The accuracy of GNSS-supported bundle adjustment with 10 GCPs is very close to that of the traditional bundle adjustment with dense GCPs, which leads to 84% reduction in field survey. And accuracy of the check points is better than ±18 cm in horizontal and ±23 cm in vertical, which are, respectively improved by 20–30% compared to GPS-supported bundle adjustment. This result also meets Chinese standards of topographic mapping at 1:500 scales in flat area. The research verified the applicability and economic benefit of GNSS-supported bundle adjustment in large-scale UAV photogrammetry.

Funding

This work was supported by the Chongqing Research Program of Basic Research and Frontier Technology [grant number cstc2016jcyjA0300] and the National Special Fund for Surveying and Mapping Geographic Information Scientific Research in the Public Welfare of China [grant number 201412015].

Notes on contributors

Hongxing Sun is an associate professor of the State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University. His research interests include Differential GNSS positioning, GNSS/INS integration, and Mobile Mapping System.

Leilei Li is a lecturer of College of Aerospace Engineering, Chongqing University. His research is focused on GNSS/INS integration, non-linear filtering, and Inertial Sensors.

Xuewen Ding is a postgraduate student of the State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University. His current research interests include GNSS/INS integration and UAV-based photogrammetry.

Bingxuan Guo is a professor of the State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University. His current interesting research field is UAV image processing and GNSS-supported aerial triangulation.