Where Do the Maximum Absolute q-Series Coefficients of (1 − q)(1 − q²)(1 − q³)…(1 − q^n − 1)(1 − qⁿ) Occur?

Abstract

We used the MACH2 supercomputer to study coefficients in the q-series expansion of $(1-q)(1-q^2)\dots (1-q^n)$, for all $n\le 75000$. As a result, we were able to conjecture some periodic properties associated with the before unknown location of the maximum coefficient of these polynomials with odd n. Remarkably, the observed period is 62,624.

Key Words:

• Euler Pentagonal Number Theorem
• q-Pochhammer symbol
• Experimental Mathematics
• Approximation
• Maximum
• MACH2
• High-Performance Computing

2010 Mathematics Subject Classification:

• 05A15
• 05A30
• 11Y55
• 11Y60
• 90C10

1. Introduction

Let the q-Pochhammer symbol be (1.1) $${(q;q)}_n:=\prod _{i=1}^n(1-q^i)=\sum _{i=0}^{n(n+1)/2}{a}_{n,i} q^i,$$(1.1) for any $n\in {\mathbb{Z}}_{\ge 0}\cup \left\{\infty \right\}.$ Euler’s famous pentagonal number theorem [1] states that infinite product can be written as a sparse power series with all of its coefficients from the set $\{-1,0,1\}.$ More precisely:

Theorem 1.1.

(Euler’s Pentagonal Number Theorem, 1750). (1.2) $${(q;q)}_{\infty }=\sum _{n=-\infty }^{\infty }{(-1)}^n{q}^{n(3n-1)/2}=1-q-q^2+q^5+q^7-q^{12}-q^{15}+q^{22}+\dots .$$(1.2)

In contrast, it is easy to check that the coefficients of the finite products ${(q;q)}_n,$ for $n\in {\mathbb{Z}}_{\ge 0},$ do not share this property and attain values larger than 1 in size. The authors [2] recently proved that the only ${(q;q)}_n$'s where the series coefficients stay in the set $\{-1,0,1\}$ are when $n=0,1,2,3,$ and 5. The first maximums of the absolute value of the coefficients are (1.3) $$1,1,1,1,2,1,2,2,2,2,3,2,4,3,3,4,6,5,6,7,8,8,10,11,16,16,19,21,28,29,34,\dots .$$(1.3) From now on we will use maximum absolute coefficient in place of the wordy “the maximum of the absolute value of the coefficients” to simplify our language.

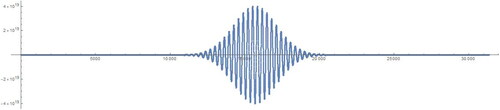
In general, when the coefficients $a_{n,i}$ of ${(q;q)}_n$ are studied, we see tame coefficients at both ends of the polynomial ${(q;q)}_n$ and a bubble of oscillation involving enormous integers in the middle. We plot the ordered pairs $(i,a_{250,i})$ in Figure 1, to show the shape of ${(q;q)}_{250}.$ This is to give an idea of the nature of the coefficients of ${(q;q)}_n.$ Note that “tame” coefficients are small only relative to the coefficients that appear at the oscillation. For example, in Figure 1, the 5000th coefficient of ${(q;q)}_{250}$ seems to be close to the x-axis, but its value $a_{250,5000}$ is –7,983,490.

Figure 1. Coefficients $a_{250,i}$ plotted on a number line.

Moreover, Sudler [3,4] showed that the maximum absolute coefficients’ size grows exponentially with n: (1.4) $$\text{log}\hspace{0.17em}{\mathcal{M}}_n=Kn+\mathcal{O}(\hspace{0.17em}\text{log}\hspace{0.17em}n),$$(1.4) where, $${\mathcal{M}}_n:=\underset{{}_{0\le i\le n(n+1)/2}}{\max }\left|a_{n,i}\right|.$$

Sudler and Mr. A. Hurwitz from University of California, Los Angeles calculated $K\simeq 0.19861.$ On top of that, Wright [5] proved that $$e^K=\underset{n\to \infty }{\lim }\frac{{\mathcal{M}}_n}{{\mathcal{M}}_{n-1}}.$$

Although research on the size of these coefficients existed [3,4, 6], there has not been an extensive study of the location of the maximum absolute coefficients of ${(q;q)}_n$ in the literature. When one checks the sequence (1.3)(1.3) $$1,1,1,1,2,1,2,2,2,2,3,2,4,3,3,4,6,5,6,7,8,8,10,11,16,16,19,21,28,29,34,\dots .$$(1.3) in the Online Encyclopedia of Integer Sequences they are greeted with the open problem [7] (paraphrased):

If n is even, then ${\mathcal{M}}_n$ is the absolute value of the coefficients of $q^{\lfloor n(n+1)/4)\rfloor }$ and $q^{\lceil n(n+1)/4)\rceil }.$ If n is odd, it is an open question as for which i, $\left|a_{n,i}\right|={\mathcal{M}}_n,$where $\lfloor ·\rfloor$ and $\lceil ·\rceil$ are the classical floor and ceiling functions.

In this work we present an experimental answer to the question regarding the location of the maximum absolute coefficients of ${(q;q)}_n$ for odd n. Let L(n) denote the lowest exponent i of q in the ${(q;q)}_n$ polynomial, where the coefficient $a_{n,i}$ of qⁱ is the maximum absolute coefficient ${\mathcal{M}}_n.$ Then, for example, we claim the following.

Conjecture 1.2.

For any $k\ge 0$, we have $$\begin{array}{c}L(391+62624k)=980441344k^2+12238861k+38194,\\ L(5909+68324k)=980441344k^2+185018477k+8728680.\end{array}$$

The locations of the largest absolute value of the coefficients for all n as well as the maximum absolute coefficients for all $n\le 75000$ are carefully calculated and verified. This task required painstaking attention to detail, a lot of patience, and a grand computing power for today’s standards. The supercomputer MACH2 was used for this task, which is the largest European installation of its kind. Even with this computing power, the computation was challenging due to the number and the size of the objects that needed to be stored and manipulated at full precision. For perspective, the degree of the polynomial ${(q;q)}_{75000}$ is 2,812,537,500 and the absolute maximum coefficient ${\mathcal{M}}_{75000}$ has 6,465 digits.

In Section 2, we briefly mention how the calculations are carried out. All the main results and our conjectures are presented in Section 3. In Section 4 we shortly discuss some possible future research directions and some related conjectures that appeared in the literature.

2. A brief note on the calculations

To save memory in calculations, one needs to observe that $a_{n,i},$ as defined in (1.1)(1.1) $${(q;q)}_n:=\prod _{i=1}^n(1-q^i)=\sum _{i=0}^{n(n+1)/2}{a}_{n,i} q^i,$$(1.1) , satisfies the relation (2.1) $$a_{n,i}={(-1)}^n{a}_{n,n(n+1)/2-i}.$$(2.1) Using (2.1)(2.1) $$a_{n,i}={(-1)}^n{a}_{n,n(n+1)/2-i}.$$(2.1) , one can reduce the storage to only half of the coefficients of ${(q;q)}_n.$ Another point is that the multiplication $(1-q^n){(q;q)}_{n-1}$ to get ${(q;q)}_n$ from ${(q;q)}_{n-1}$ is the same as the addition (2.2) $$a_{n,i}=a_{n-1,i}-a_{n-1,i-n},$$(2.2) for all $i\ge n,$ on the coefficient level. Finally, we note that the first n – 1 coefficients of ${(q;q)}_{n-1}$ do not change when multiplied with $(1-q^n).$ Moreover, they coincide with the first n – 1 coefficients of (1.2)(1.2) $${(q;q)}_{\infty }=\sum _{n=-\infty }^{\infty }{(-1)}^n{q}^{n(3n-1)/2}=1-q-q^2+q^5+q^7-q^{12}-q^{15}+q^{22}+\dots .$$(1.2) . Since the maximum absolute coefficients grow (1.4)(1.4) $$\text{log}\hspace{0.17em}{\mathcal{M}}_n=Kn+\mathcal{O}(\hspace{0.17em}\text{log}\hspace{0.17em}n),$$(1.4) , they would not appear in the first n – 1 coefficients that are ±1 or 0.

The task of openly multiplying ${(q;q)}_n$ and locating the maximum of the absolute values of the coefficients started on a reasonably sized RISC server using Maple. One can compute up to a commendable n = 10000 by multiplying these objects using a modern desktop computer. In our experience, the Maple gives up around this point. With Mathematica, we were able to take our calculations to around 15000. This is more or less the upper limit of what computer algebra systems can handle on a today’s consumer level computer. Once this natural boundary was reached we moved on to programing our own versions of the coefficient level multiplication algorithm; first this was done with Python, later with C++. Python does arbitrary precision arithmetics automatically, and Gnu MultiPrecision Library [8] was used for handling large integers in C++. The calculations were carried on the MACH2 supercomputer¹.

3. The location of the maximum absolute coefficients

Let L(n) denote the lowest exponent i of q in the ${(q;q)}_n$ polynomial, where the coefficient of qⁱ is the maximum absolute coefficient ${\mathcal{M}}_n.$ When explicitly expanding the polynomials ${(q;q)}_n,$ the maximum of the absolute value of the coefficients starts to appear in one or two places consistently for $n\ge 34.$ We would like to start by acknowledging that, for all $n\ge 17,L(2n)=\lfloor n(n+1)/4)\rfloor$ or, in other words, the maximum absolute coefficients of ${(q;q)}_{2n}$ appear as the coefficient(s) of $q^{\lfloor n(n+1)/4)\rfloor }$ and $q^{\lceil n(n+1)/4)\rceil }.$ Now with our explicit computations, this claim (which appears in the Online Encyclopedia of Integer Sequences A160089) extends to all even $n\le 75000.$

For 0 modulo 4 cases the maximum absolute coefficients are the absolute maximum, and for 2 modulo 4 cases the maximum absolute coefficients are the negative of the absolute minimum of ${(q;q)}_n.$ For the odd n, both the maximum of the absolute value of the coefficients and its negative appear in ${(q;q)}_n$ due to (2.1)(2.1) $$a_{n,i}={(-1)}^n{a}_{n,n(n+1)/2-i}.$$(2.1) . Furthermore, we make the claim:

Conjecture 3.1.

For $n\ge 35$, if $n\equiv 1\mathrm{ }\mathrm{(}\text{mod}\mathrm{ }4\mathrm{)}$, absolute maximum occurs only once as the coefficient of some qⁱ, where $i<n(n+1)/4$ and if $n\equiv 3\mathrm{ }\mathrm{(}\text{mod}\mathrm{ }4\mathrm{)}$ the absolute maximum occurs only once as the coefficient of some qⁱ, where $i>n(n+1)/4.$

There are some initial cases where the maximum absolute coefficient appears as the polynomial coefficients of ${(q;q)}_n$ more than twice. For example, in the n = 33 case the absolute maximum coefficient 56 appears as the coefficients of q²⁷⁰ and q²⁷² and the absolute minimum coefficient –56 appears as the coefficients of q²⁸⁹ and q²⁹¹, so the maximum absolute coefficient appears a total of 4 times as a coefficient of the polynomial ${(q;q)}_{33}.$ We see that for $n\ge 35,$ the maximum absolute coefficient appears as coefficients of only two terms in the q-series expansion of the rising factorial.

We will split the cases for the odd values of n in two groups modulo 4. Before doing so, we define the D_n as the half difference between the two locations of the maximum absolute coefficients for a given odd $n\ge 35.$ This is the same as saying how far off the maximum absolute coefficient is from the half degree $n(n+1)/4$ of the polynomial ${(q;q)}_n.$ Hence, knowing this value and n is enough to recover the location of the maximum absolute coefficients. Also we define the canonical difference $$E_n:=D_n-D_{n-4},$$ for all odd $n\ge 35.$

Let $n\ge 35$ be an odd integer, and assume that all necessary E_i and a D_m value for some $m\le n,$ with $n\equiv m$ modulo 4 are given. Then, one can recover the location of the maximum absolute coefficients for ${(q;q)}_n$ as (3.1) $$L(n)=\frac{n(n+1)}{4}-\left(D_m+\sum _{i=1}^{(n-m)/4}{E}_{m+4i}\right),$$(3.1) where $a_{n,i}$ is defined as in (1.1)(1.1) $${(q;q)}_n:=\prod _{i=1}^n(1-q^i)=\sum _{i=0}^{n(n+1)/2}{a}_{n,i} q^i,$$(1.1) .

The first observation we have made and confirmed for $n\le 75000$ is:

Conjecture 3.2.

For all odd $n\ge 35,E_n\in \{0,1,2\}$. Furthermore, $E_n>0$ for all odd $n\ge 61.$

By looking at the values $n\ge 57$ and $\ge 87$ for 1 and 3 modulo 4, we list E_n’s. The patterns starting from these beginning points look highly periodic with period 19, although this is sadly not the case. The 19 length patterns of 1’s and 2’s that E_n’s change slightly as the calculations are carried. We match the 19 length patterns that the calculations yield with letters and form an alphabet with 20 letters. The letters that we see in the calculations and their 19 consecutive E_n value equivalents are given in Table 1.

Table 1. The selected alphabet associated with the E_m values.

Note that each letter represents 19 consecutive E_n values (1 or 2) written together without commas to keep the notation simple. The calculation of any letter requires the expansion of 19 × 4 = 76 consecutive ${(q;q)}_n$ polynomials and finding the location of the maximum absolute coefficient and its location of each odd index n. This alphabet makes it possible to find the individual E_n values. Furthermore, together with (3.1)(3.1) $$L(n)=\frac{n(n+1)}{4}-\left(D_m+\sum _{i=1}^{(n-m)/4}{E}_{m+4i}\right),$$(3.1) , this makes it possible to find the locations of the maximum absolute coefficients. Also note that a and k are symmetric with respect to their centers and a is also special that it is the only letter with six 2 values, whereas all the other words come with five 2 values. It is easy to see that the letters $b,c,d,e,f,g,h,i,$ and j read from right to left are the letters $t,s,r,q,p,o,n,m,$ and l, respectively.

These letters are observed to be generating almost periodic words starting from $n\ge 209$ and $\ge 391$ for 1 and 3 modulo 4 values, respectively. We will write exponents of the letters defined in Table 1 to indicate the number of times a letter has occurred consecutively. From the said starting point we see that the 1 modulo 4 differences give rise to the string $$\underset{\text{word}\mathrm{ }1}{\underbrace{a^1{b}^4{c}^4{d}^4{e}^4{f}^3{g}^4{h}^5{i}^4{j}^4{k}^3{l}^4{m}^4{n}^4{o}^5{p}^3{q}^4{r}^4{s}^4{t}^3}}\underset{\text{word}2,\text{etc}.}{\underbrace{a^1{b}^4{c}^4{d}^4{e}^4{f}^3{g}^4{h}^4{i}^5{j}^4{k}^3\dots }}.$$

We see that the letter a appears a single time in each word. This phenomenon is the same for the 3 modulo 4 case. We break this string into words for 1 and 3 mod 4 to start every line with an a and write the words in Table 2; 1 and 3 mod 4 cases on the left side and the right side, respectively. In Table 2, we also include a line to break period blocks of the size 11 × 20 box both odd residue classes mod 4.

Table 2. The words for $n\equiv 1$ and 3 mod 4 cases associated with the alphabet of Table 1.

What one can observe from the encoding of Table 2 is that there is the base word (3.2) $$a^1{b}^3{c}^4{d}^4{e}^4{f}^3{g}^4{h}^4{i}^4{j}^4{k}^3{l}^4{m}^4{n}^4{o}^4{p}^3{q}^4{r}^4{s}^4{t}^3$$(3.2) in each line and an overlying, moving perturbation. It is observed that the first line of the 1 modulo 4 case does not fit any period block and stays as an outlier. We interpret this as the asymptotic behavior of the perturbation kicking in action a little later than the 3 modulo 4 case. More importantly, this perturbation is observably periodic. To express the observed structure better, we represent the base word (3.2) as a vector, where we write the frequencies of the letters as a vector of 20 entries (3.3) $$\mathbf{B}=(1,3,4,4,4,3,4,4,4,4,3,4,4,4,4,3,4,4,4,3).$$(3.3) Then Table 2 can be expressed as adding some perturbation vectors to B. We define the perturbation vectors for the 1 and 3 modulo 4 classes side-by-side in Table 3.

Table 3. The perturbation vectors of a full observed period for 1 and 3 modulo 4 cases side-by-side.

Notice that ${\mathbf{u}}_{11}$ and ${\mathbf{v}}_7$ are the only two vectors that have two 1’s and all the rest include three 1’s. The first component is always 0. There is a clear pattern in the perturbations and how the motion of the perturbation is from one vector to the following. We have indicated the observed pattern of 1 or 2 repetitions of the perturbations using red and blue (resp.) in Table 3. Both in the 1 and 3 mod 4 cases, there are 6 red 1’s which correspond to a letter’s extra appearance as perturbance only a single time in the period. The blue 1’s in the components indicate that the corresponding letter occurs as a part of the perturbation twice. After these observations, the periodicity of this perturbation becomes clearer in vector form.

We claim the following:

Conjecture 3.3.

For any $i>j\ge 1$, the i-th and j-th row that appears in Table 2 and beyond can be associated with the vectors $\mathbf{B}+{\mathbf{u}}_{(i-1\mathrm{ }\mathrm{(}\text{mod}\mathrm{ }11\mathrm{)})}$ and $\mathbf{B}+{\mathbf{v}}_{(j\mathrm{ }\mathrm{(}\text{mod}\mathrm{ }11\mathrm{)})}$ for 1 and 3 modulo 4 words, respectively.

Moreover, we claim, with these two essential periods for the perturbation, that we can locate the maximum absolute coefficients’ locations for any ${(q;q)}_n$ with odd n.

The base word associated with B has 72 letters, each letter representing 19 consecutive E_n values, where each of these values are an additional 4 index n shifts of ${(q;q)}_n.$ There are 11 base words corresponding to both odd residue classes mod 4. This translates to shifts of the n of ${(q;q)}_n$ by $72\times 19\times 4\times 11=60,192.$ On top of that, the total amount of perturbation is 32 letters, reflecting another 2,432 to the shifts of the subindex of ${(q;q)}_n,$ respectively. All together, the period of E_n’s is conjectured to be 62,624. Lastly, the sum of E_n’s is 19,787. Now we can start stating our conjectures for the maximum absolute coefficients’ location, using (3.1)(3.1) $$L(n)=\frac{n(n+1)}{4}-\left(D_m+\sum _{i=1}^{(n-m)/4}{E}_{m+4i}\right),$$(3.1) . Our first example is Conjecture 1.2 that is represented in a simplified fachion in the introduction.

Conjecture 1.2.

We have, $$\begin{array}{c}L(5909+68324k)=\frac{(5909+62624k)(5910+62624k)}{4}-\frac{3735}{2}-19787k,\\ L(391+62624k)=\frac{(391+62624k)(392+62624k)}{4}-124-19787k,\end{array}$$ for any $k\ge 0.$

Note that $D_{5909}=3735/2$ and $D_{391}=124.$ Although these formulas might seem limited, one can easily use these explicit values with E_n’s as represented in Table 2 to find the location of the maximum coefficient of any odd value greater than 5909. The location calculations for the $n\le 5000$ already exist in the Online Encyclopedia of Integer Sequences, under the sequence number A160089 [7], and one can easily recover the gap between 5000 and 5909, by our above mentioned calculations.

We list similar conjectures that correspond to the start of each word of the periods of 1 and 3 modulo 4 cases:

Conjecture 3.4.

For any $k\ge 0,r=0,1,2,\dots 10$, let $$A(k,r)=5700r+62624k-76 {\delta }_{r,11},\mathrm{ }\mathit{\text{and}}\mathrm{ }B(k,r)=5700r+62624k-76 {\delta }_{r\ge 7},$$ where ${\delta }_{i,j}$ is the Kronecker delta and ${\delta }_{i\ge j}$ yields 1 if $i\ge j$, and 0, otherwise. Then, $$\begin{array}{c}L(5909+A(k,r))=\frac{(5909+A(k,r))(5910+A(k,r))}{4}-D_{5909+A(0,r)}-19787k,\\ L(391+B(k,r))=\frac{(391+B(k,r))(392+B(k,r))}{4}-D_{391+B(0,s)}-19787k,\end{array}$$ where the full list of needed seed values of D_n’s are $$\begin{array}{cc}{D}_{5909}=1867.5& D_{391}=124,\\ D_{17309}=5469.5,& D_{11791}=3726,\\ D_{28709}=9071.5,& D_{23191}=7328,\\ D_{40109}=12673.5,& D_{34591}=10930,\\ D_{51509}=16275.5,& D_{45915}=14508,\\ D_{62833}=19853.5& D_{57315}=18110.\\ D_{11609}=3668.5,& D_{6091}=1925,\\ D_{23009}=7270.5,& D_{17491}=5527,\\ D_{34409}=9675.5,& D_{28891}=9129,\\ D_{45809}=14474.5,& D_{40215}=12707,\\ D_{57209}=18076.5,& D_{51615}=16309,\end{array}$$

In Conjecture 3.4, A(k, r) and B(k, r) are used to move to the start of any word. The variable r is used to move within the periods, and k is used for going over full periods. Conjecture 3.4 reduces to Conjecture 1.2 for r = 0. One important note we need to make is the use of the correctional δ functions. The number 76, as explained after the introduction of the chosen alphabet, corresponds to the number of consecutive n’s needed to expand ${(q;q)}_n$ for forming a single letter. We have already observed that two words in Table 2 (one for each case) in the period have one less letter than the others. The δ functions are introduced only to address this issue.

4. Future directions

We have handled the odd cases in two groups corresponding to residue classes modulo 4. We can also start with a uniform approach. For all odd $n\ge 35,$ let $${\tilde{E}}_n=2(D_n-D_{n-2}).$$

It is clear that one can define a formula for L(N), which would be an analog of (3.1(3.1) $$L(n)=\frac{n(n+1)}{4}-\left(D_m+\sum _{i=1}^{(n-m)/4}{E}_{m+4i}\right),$$(3.1) ), using these ${\tilde{E}}_n$ values and the D_n’s. The period in this unified approach seems to be much larger than 11. Nevertheless, one intriguing claim analogous to Conjecture 3.2 is:

Conjecture 4.1.

Let n be an odd number $\ge 61$, then ${\tilde{E}}_n=1$ or 3.

Using the last maximum absolute coefficients we can note that $${\mathcal{M}}_{75000}/{\mathcal{M}}_{74999}=1.2197054247521000707\dots .$$

Moreover, $${\left({\mathcal{M}}_{75000}\right)}^{1/75000}=1.2195493261856946041\dots ,$$ which is a closer estimate than Finch’s [6] approximation for this value, but it neither supports nor disproves Kotesovec’s [7] conjecture: (4.1) $$\underset{n\to \infty }{\lim }\sqrt{{\mathcal{M}}_{n}n}=\underset{n\to \infty }{\lim }{\left({\int }_0^1\prod _{j=1}^{n}4{\hspace{0.17em}\text{sin}\hspace{0.17em}}^2(\pi jz)dz\right)}^{\frac{1}{2n}}=1.21971547612163368901359933\dots .$$(4.1)

We also checked the possible fitting functions and their limits using our data to understand these constants better. We assume that these sequences look like $$a_0+\frac{a_1}{n}+\dots ,$$ for large n where the major contribution comes from the first two coefficients. Starting from n = 50000, we fitted the function ${\mathcal{M}}_n/{\mathcal{M}}_{n-1}$ to understand their asymptotic behavior better. We use the Aitken’s delta-squared series acceleration method [9] that eliminates the a₁ term in the asymptotics in estimating this limit. Then the approximation for the limiting constant a₀ is $$\underset{n\to \infty }{\lim }{\mathcal{M}}_n/{\mathcal{M}}_{n-1}\approx 1.2197154761199955231\dots .$$

This estimated limit matches Kotesovec’s conjecture (4.1)(4.1) $$\underset{n\to \infty }{\lim }\sqrt{{\mathcal{M}}_{n}n}=\underset{n\to \infty }{\lim }{\left({\int }_0^1\prod _{j=1}^{n}4{\hspace{0.17em}\text{sin}\hspace{0.17em}}^2(\pi jz)dz\right)}^{\frac{1}{2n}}=1.21971547612163368901359933\dots .$$(4.1) in 10 decimal digits.

Acknowledgment

The authors would like to sincerely thank the interest and encouragement of Jakob Ablinger, Stefano Capparelli, Steven Finch, Ralf Hemmecke, Veronika Pillwein, Carsten Schneider, Zafeirakis Zafeirakopoulos, and Wadim Zudilin. We are particularly grateful to Christoph Koutschan and Elaine Wong and the anonymous referee for their interest, careful reading, and helpful comments on the manuscript.

The authors would like to acknowledge Johannes Blümlein and Carsten Schneider for allowing us to use their servers for the initial calculations at the Research Institute for Symbolic Computation (RISC), Ralf Wahner and Werner Danielczyk-Landerl for their help in the storage of the early calculations at RISC, and Johann Messner from the MACH2 team for his help in carrying out the calculations.

Declaration of Interest

No potential conflict of interest was reported by the author(s).

Additional information

Funding

Research of the first author is partly supported by the Simons foundation, Award ID: 308929. Research of the second author is supported by the Austrian Science Fund FWF, SFB F50-07, SFB F50-09 and SFB F50-11 Projects.

Notes

1 See https://www.risc.jku.at/projects/mach2.