Local Inhomogeneous Weighted Summary Statistics for Marked Point Processes

Abstract

We introduce a family of local inhomogeneous mark-weighted summary statistics, of order two and higher, for general marked point processes. Depending on how the involved weight function is specified, these summary statistics capture different kinds of local dependence structures. We first derive some basic properties and show how these new statistical tools can be used to construct most existing summary statistics for (marked) point processes. We then propose a local test of random labeling. This procedure allows us to identify points, and consequently regions, where the random labeling assumption does not hold, for example, when the (functional) marks are spatially dependent. Through a simulation study we show that the test is able to detect local deviations from random labeling. We also provide an application to an earthquake point pattern with functional marks given by seismic waveforms.

KEYWORDS:

• Earthquakes
• Functional marked point process
• Local envelope test
• Mark correlation function
• Marked K-function
• Random labeling

1 Introduction

The analysis of a point pattern, given as a collection of points in a region, typically begins with computing an estimate of some summary statistic which may be used to find specific structures in the data and suggest suitable models (Van Lieshout 2000; Daley and Vere-Jones 2008; Illian et al. 2008; Gelfand et al. 2010; Chiu et al. 2013).

The choice of summary statistic depends both on the pattern at hand and on the feature or hypothesis of interest.

A widely used summary statistic for descriptive analyses and diagnostics, which is obtained as an instance of the so-called reduced second moment measure (Cressie and Collins 2001; Møller 2003; Chiu et al. 2013), is Ripley’s K-function (Ripley 1976), which is based on the assumption of a non-marked stationary and isotropic point process. In the marked case, assuming discrete marks and stationarity, cross versions of the K- or nearest neighbor distance distribution functions have been proposed (Diggle 2013). For real-valued marks, the mark correlation type-functions in Penttinen and Stoyan (1989) and Illian et al. (2008) are widely used and such second order statistics have been studied in more detail and reformulated by Schlather (2001), in order to obtain a more rigorous formulation. However, although the assumption of stationarity is mathematically appealing, it can rarely be justified in practice since the intensity tends to change over the study region. This is to say that the underlying point process is inhomogeneous and, in the unmarked case, Baddeley, Møller, and Waagepetersen (2000) proposed an inhomogeneous extension of the K-function for a class of point processes, which are referred to as second order intensity-reweighted stationary. Their ideas were extended to spatio-temporal point processes in Gabriel and Diggle (2009) and Møller and Ghorbani (2012). Further, Møller and Waagepetersen (2003) proposed an extension of this K-function to second order intensity-reweighted stationary multivariate point processes. As indicated in Cronie and van Lieshout (2016) and Iftimi, Cronie, and Montes (2019), this structure may be extended to K-functions for general marked point processes. To analyze higher order interactions in general stationary marked point processes, Van Lieshout (2006) proposed marked versions of the nearest neighbor distance distribution functions, the empty space function and the J-function. These summary statistics, which allow us to study spatial interactions between different mark groupings of the points, were later extended to the inhomogeneous setting by Cronie and van Lieshout (2016) and Iftimi, Cronie, and Montes (2019). In particular, to test for random labeling, Cronie and van Lieshout (2016) proposed inhomogeneous Lotwick-Silverman-type Monte Carlo tests based on their new summary statistics, while Iftimi, Cronie, and Montes (2019) proposed second order Monte Carlo tests based on permuting the attached marks. Further details on the random shift-type testing considered in Lotwick-Silverman-type tests can be found in Mrkvička et al. (2021).

Despite the relatively long history of point process theory (see e.g., Stoyan and Stoyan 1994; Daley and Vere-Jones 2008; Diggle 2013), few approaches have been proposed to analyze spatial point patterns where the features of interest are functions/curves instead of qualitative or quantitative variables. Examples of point patterns with associated functional data include forest patterns where for each tree we have a growth function, curves representing the incidence of an epidemic over a period of time, and the evolution of distinct economic parameters such as unemployment and price rates, all for distinct spatial locations. The study of such configurations allows analyzing the effects of the spatial structure on individual functions. Illian et al. (2006) consider for each point a transformed Ripley’s (1976) K-function to characterize spatial point patterns of ecological plant communities, while Mateu, Lorenzo, and Porcu (2007) build new marked point processes formed by spatial locations and curves defined in terms of Local Indicators of Spatial Association (LISA) functions, which describe local characteristics of the points. They use this approach to classify and discriminate between points belonging to a clutter and those belonging to a feature. Finally, the idea of analyzing point patterns with attached functions has been presented coherently by Comas, Delicado, and Mateu (2011) and Ghorbani et al. (2021).

Ghorbani et al. (2021) introduced a very broad framework for the analysis of Functional Marked Point Processes (FMPPs), indicating how they connect the point process framework with both Functional Data Analysis (FDA; Ramsay and Silverman (2002)) and geostatistics. In particular, they defined a new family of summary statistics, so-called weighted nth order marked inhomogeneous K-functions, together with their nonparametric estimators, which they exploited to analyze Spanish population structures, such as demographic evolution and sex ratio over time. This summary statistic family can be used to run a Monte Carlo test of random labeling, for example, by means of global envelopes test (GET; Myllymäki et al. 2017), to assess whether the functional marks of the analyzed pattern are spatially dependent. However, this procedure is essentially global, since it does not provide information on the points which mostly contributed to the rejection of the random labeling hypothesis. Therefore, motivated by the need of detecting such points, and thus the regions in which they are located, where the functional marks really do depend on the surrounding structure, in this article we introduce a new class of summary statistics, local t-weighted marked nth order inhomogeneous K-functions. These are used to propose a local test of random labeling. Here t refers to a function which governs how much weight we put on different aspects of the marked point process/pattern.

Further, we use the developed tools to analyze seismic data. Note that while the spatial (and temporal) locations of the epicenters of earthquakes are typically analyzed within the framework of point processes, the associated seismic waveforms are commonly investigated in separate analyses through FDA. Applying the local test allows us to identify where one would expect waveforms (i.e., functional marks) to be similar to those of nearby points.

All the performed analyses are carried out through the R Core Team (2022) software, and the codes are available from the first author. Preliminary data manipulation is performed through the software Python (Van Rossum and Drake Jr 1995).

The structure of the article is as follows. In Section 2, the motivation of this article is presented, showing the dataset and problem that will be further analyzed along the article. Section 3 contains some preliminaries on functional marked point processes. In Section 4, we present our proposed local t-weighted nth order inhomogeneous K-functions and their main properties, also relating them to their global counterparts. Section 5 outlines the main steps to run a local test of random labeling. In Section 6, we present a motivating example to show the further advantages of a local test, compared to a global one. To have a comprehensive understanding of the performance of the proposed local test, we show simulation results under different scenarios. Section 7 provides an application to seismic data. Finally, conclusions are drawn in Section 8.

2 Data and Motivation

Earthquakes’ detection provides a whole set of data which are usually studied separately, that is, spatial (and temporal) occurrence of points through point process theory (Siino et al. 2017; Iftimi, Cronie, and Montes 2019; D’Angelo et al. 2022, to cite just a few recent works), and the analysis of waveforms through FDA (Adelfio et al. 2011, 2012; Chiodi et al. 2013).

A recently released set of data on Italian seismic activity encompasses both of these data types. The Italian seismic dataset for machine learning (INSTANCE) is a dataset of seismic waveforms data and associated metadata (Michelini et al. 2021), which includes 54,008 earthquakes for a total of 115,9249 three-channel waveforms. It also contains 132,330 three-channel noise waveforms. For each of these waveforms, 115 metadata (i.e., statistical variables) are available, providing information on station, trace, source, path and quality. Overall, the data are collected by 19 networks which consist of 620 seismic stations. The dataset is available on http://www.pi.ingv.it/instance/.

The earthquake list in the dataset is based on the Italian seismic bulletin (http://terremoti.ingv.it/bsi) of the “Istituto Nazionale di Geofisica e Vulcanologia,” includes events which occurred between January 2005 and January 2020, and in the magnitude range between 0.0 and 6.5. The waveform data have been recorded primarily by the Italian National Seismic Network. Figure 1 (a)–(b) depict the earthquake locations and the seismic stations which recorded the events.

Fig. 1 The Italian seismic dataset for machine learning (INSTANCE). (a) Earthquake locations; (b) Seismic stations used for waveforms extraction. The symbol sizes are proportional to earthquake magnitude and number of arrival phases recorded by stations, respectively; (c) Seismic waveforms of some events with magnitude in the range $[2,4]$. Vertical lines indicate the seismic waves’ arrival times. Source: Michelini et al. (2021).

In Figure 1(c), some waveforms contained in the dataset are represented. All the waveform traces have a length of 120 sec, are sampled at 100 Hz, and are provided both in counts and ground motion physical units after deconvolution of the instrument transfer functions. The waveform dataset is accompanied by metadata consisting of more than 100 variables providing comprehensive information on the earthquake source, the recording stations, the trace features, and other derived quantities.

3 Preliminaries on Marked Point Processes

Throughout the article, we consider a marked point process $Y={\{(x_i,m_i)\}}_{i=1}^N$ (Daley and Vere-Jones 2008, Definition 6.4.1), with ground points x_i in the d-dimensional Euclidean space ${\mathbb{R}}^d,d\ge 1$, which is equipped with the Lebesgue measure $\left|A\right|={\int }_A\mathrm{d}z$ for Borel sets $A\in \mathcal{B}({\mathbb{R}}^d)$; a closed Euclidean r-ball around $x\in {\mathbb{R}}^d$ will be denoted by $b[x,r]$. By definition, the ground process $Y_g={\left\{x_i\right\}}_{i=1}^N$, obtained from Y by ignoring the marks, is a well-defined point process on ${\mathbb{R}}^d$ in its own right. Note that, formally, Y is a random element in the measurable space $(N_{lf},\mathcal{N})$ of locally finite point configurations/patterns $\mathbf{x}=\{((x_1,m_1),\dots ,(x_n,m_n))\},n\ge 0$ (Van Lieshout 2000; Daley and Vere-Jones 2008). We assume that the mark space $\mathcal{M}$ is Polish and equipped with a finite reference measure ν on the Borel σ-algebra $\mathcal{B}(\mathcal{M})$. The Borel σ-algebra $\mathcal{B}({\mathbb{R}}^d\times \mathcal{M})=\mathcal{B}({\mathbb{R}}^d)\otimes \mathcal{B}(\mathcal{M})$ is endowed with the product measure $A\times E\mapsto \left|A\right|\nu (E),A\times E\in \mathcal{B}({\mathbb{R}}^d\times \mathcal{M})$. We will let $Y(A\times E)=\sum _{(x,m)\in Y}\mathbf{1}\{(x,m)\in A\times E\}$, where $\mathbf{1}$ is the indicator function, denote the cardinality of the random set $Y\cap (A\times E)$. We assume that Y is simple, that is, it almost surely (a.s.) does not contain multiple points in the sense that $P(Y(\{(x,m)\})=0\text{ or }1)=1$ for all $(x,m)\in {\mathbb{R}}^d\times \mathcal{M}$.

Given this general setup, one may obtain various forms of marked point processes, most notably multivariate/multitype point processes with $\mathcal{M}=\{1,\dots ,k\}$ (Diggle 2013) and functional marked point processes with $\mathcal{M}$ given by a suitable function space (Ghorbani et al. 2021).

3.1 Functional Marked Point Processes

In this section, we provide the definition of functional marked point processes following Ghorbani et al. (2021).

In classical FDA, one analyses a collection of functions $\{f_1(t),\dots ,f_n(t)\},t\in \mathcal{T}\subset [0,\infty ),n\ge 1$, which take values in some Euclidean space ${\mathbb{R}}^k,k\ge 1$, and belong to some suitable function space, typically an L₂-space. Although t usually represents time, it could also represent some other quantity, for example, spatial distance. Classically, one would assume that such collections of functions constitute realizations or samples of some collection of iid random functions or stochastic processes $\{F_1(t),\dots ,F_n(t)\},t\in \mathcal{T}$. Such an assumption may, however, be questioned in certain settings. For example, two functions f_i and f_j, which are spatially close to each other in ${\mathbb{R}}^k$, could gain (or lose) from being close to each other. Accordingly, it seems natural to relax the iid assumption for $F_1,\dots ,F_N$. A natural way to handle such a scenario is to generate $F_1,\dots ,F_N$ conditionally on some collection of (dependent) random spatial locations. Note that the conditional distribution of $F_1,\dots ,F_N$ could render them either independent or dependent.

To facilitate such a setting, we consider a functional marked point process (Ghorbani et al. 2021), which is defined as a marked point process where the marks are random elements in some (Polish) function space, $\mathcal{M}$, most notably the space of L₂-functions $f:\mathcal{T}\to {\mathbb{R}}^k$. Realizations of FMPPs are called functional marked point patterns. It is noteworthy that the original formal construction of functional marked point processes by Ghorbani et al. (2021) also included an additional nonfunctional mark, so that each ground process point would be marked by a pair which consists of a function and a nonfunctional variable. We here do not consider such auxiliary nonfunctional marks.

3.2 Product Densities

Provided that it exists, the nth order intensity/product density function ${\rho }^{(n)},n\ge 1$, which is the density of the nth order factorial moment measure ${\alpha }^{(n)}$, may be specified through the nth order Campbell formula. It states that, for any nonnegative measurable function h on ${({\mathbb{R}}^d\times \mathcal{M})}^n$, the expectation of the random sum of h satisfies (1) $$\begin{array}{cc}& \mathbb{E}\left[\sum _{(x_1,m_1),\dots ,(x_n,m_n)\in Y}^{\ne }h((x_1,m_1),\dots ,(x_n,m_n))\right]\\ & =\mathrm{}\int \mathrm{}\cdots \int \mathrm{}h((x_1,m_1),\dots ,(x_n,m_n)){\rho }^{(n)}((x_1,m_1),\dots ,(x_n,m_n))\\ & \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\prod _{i=1}^n\mathrm{d}{x}_i\nu (d{m}_i),\end{array}$$(1) where $\ne$ indicates that the sum is over n-tuples of distinct points of Y. Heuristically, ${\rho }^{(n)}((x_1,m_1),\dots ,(x_n,m_n))\mathrm{d}{x}_1\nu (d{m}_1)\dots$ $\mathrm{d}{x}_n\nu (d{m}_n)$ gives the probability that Y has points in infinitesimal neighborhoods $d(x_i,m_i)\ni (x_i,m_i)\in {\mathbb{R}}^d\times \mathcal{M}$ with measures $\mathrm{d}{x}_i\nu (d{m}_i),i=1,\dots ,n$. Moreover, we retrieve ${\alpha }^{(n)}((A_1\times E_1)\times \cdots \times (A_n\times E_n)),(A_i\times E_i)\in \mathcal{B}({\mathbb{R}}^d\times \mathcal{M})$, $i=1,\dots ,n$, by letting h be given by the indicator function $\mathbf{1}\{(x_1,m_1)\in (A_1\times E_1),\dots ,(x_n,m_n)\in (A_n\times E_n)\}$. It further follows that $${\rho }^{(n)}((x_1,m_1),\dots ,(x_n,m_n))$$ $$\hspace{1em}=f_{x_1,\dots ,x_n}(m_1,\dots ,m_n){\rho }_g^{(n)}(x_1,\dots ,x_n),$$ where ${\rho }_g^{(n)}$ is the nth order product density of Y_g and $f_{x_1,\dots ,x_n}(·)$ is a conditional density function on ${\mathcal{M}}^n$ which governs the joint distribution of n marks, given that their associated ground process points are given by $x_1,\dots ,x_n\in {\mathbb{R}}^d$. These, in turn, yield the corresponding mark distributions $$M^{x_1,\dots ,x_n}(E_1,\dots ,E_n)$$ $$\hspace{1em}={\int }_{E_1}\cdots {\int }_{E_n}{f}_{x_1,\dots ,x_n}(m_1,\dots ,m_n)\prod _{i=1}^n\nu (d{m}_i),$$ which govern the joint distribution on n marks, given the associated ground process locations.

The intensity measure of Y, which coincides with the first order factorial moment measure, here satisfies (2) $$\begin{array}{c}\alpha (A\times E)=\mathbb{E}[Y(A\times E)]\\ ={\int }_A{\int }_E\rho (x,m)\mathrm{d}x\nu (dm)\\ ={\int }_A{\int }_E{f}_x(m){\rho }_g(x)\mathrm{d}x\nu (dm)\\ ={\int }_A{M}^x(E){\rho }_g(x)\mathrm{d}x,\end{array}$$(2) where the first-order intensity functions $\rho ={\rho }^{(1)}$ and ${\rho }_g={\rho }_g^{(1)}$ are typically referred to as the intensity functions of Y and Y_g. Note that ρ may be viewed as a “heat map” which reflects the infinitesimal chance of having a point of Y at/around an arbitrary location in ${\mathbb{R}}^d\times \mathcal{M}$. When the intensity function (of the ground process) is constant, we say that the (ground) process is homogeneous, otherwise it is called inhomogeneous.

When, conditional on the ground process, all marks have the same marginal univariate distribution, so that $M^z(E)={\int }_E{f}_z(m)\mathrm{d}\nu (dm)={\int }_{E}f(m)\mathrm{d}\nu (m)=M(E)$, we say that X has a common (marginal) mark distribution. This holds for example, when Y is stationary, that is, when its distribution is invariant under translations of the ground points; here $\alpha (A\times E)={\rho }_{g}M(E)\left|A\right|$ and ${\rho }_g>0$ is the constant intensity of the ground process. We will see that, at times, it is particularly convenient to have here that the reference measure ν coincides with the common mark distribution M, which implies that the common mark density f is set to 1 and $\rho (x,m)={\rho }_g(x)$.

When Y is independently marked, that is, when the marks are independent conditional on the ground process, $f_{x_1,\dots ,x_n}(m_1,\dots ,m_n)=f_{x_1}(m_1)\cdots f_{x_n}(m_n)$ for any $n\ge 1$ and if, in addition, there is a common mark distribution, whereby the marks are iid conditional on the ground process, we say that Y is randomly labeled and note that $f_{x_1,\dots ,x_n}(m_1,\dots ,m_n)=f(m_1)\cdots f(m_n)$.

3.2.1 Intensity Reweighted Stationarity

We next turn to the notion of a kth order marked intensity reweighted stationary (k-MIRS) marked point process Y (Ghorbani et al. 2021). We say that Y is k-MIRS, $k\in \{1,2,\dots \}$, if ρ is bounded away from 0 and the correlation functions $$g^{(n)}((x_1,m_1),\dots ,(x_n,m_n))$$ $$\hspace{1em}=\frac{{\rho }^{(n)}((x_1,m_1),\dots ,(x_n,m_n))}{\rho (x_1,m_1)\dots \rho (x_n,m_n)}$$ $$\hspace{1em}=\frac{f_{x_1,\dots ,x_n}(m_1,\dots ,m_n)}{f_{x_1}(m_1)\dots f_{x_n}(m_n)}\frac{{\rho }_g^{(n)}(x_1,\dots ,x_n)}{{\rho }_g(x_1)\dots {\rho }_g(x_n)},\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}n\ge 1,$$satisfy $g^{(n)}((x_1,m_1),\dots ,(x_n,m_n))=g^{(n)}((z+x_1,m_1),\dots ,(z+x_n,m_n))$ for any $z\in {\mathbb{R}}^d$ and any $n\le k$. Note that $g^{(1)}(·)\equiv 1$ and that the second ratio on the right-hand side is the nth order correlation function, $g_g^{(n)}$, of the ground process. Provided that the product densities of all orders exist, stationarity implies k-MIRS for all orders $k\ge 1$. Note further that $g^{(n)}(·)\equiv 1,n\ge 1$, for a Poisson process and when $g^{(n)}((x_1,m_1),\dots ,(x_n,m_n))>1$ points of Y_g in infinitesimal neighborhoods of $x_1,\dots ,x_n$ with marks in infinitesimal neighborhoods of $m_1,\dots ,m_n$ tend to cluster/aggregate. Similarly, $g^{(n)}((x_1,m_1),\dots ,(x_n,m_n))<1$ indicates inhibition/regularity.

3.3 Palm Distributions

Let Y be a simple marked point process whose intensity function exists. Many of the summary statistics we will consider can be expressed in terms of reduced Palm distributions. These satisfy the reduced Campbell–Mecke formula which states that, for any nonnegative measurable function h on the product space $({\mathbb{R}}^d\times \mathcal{M})\times N_{lf}$, (3) $$\begin{array}{c}\mathbb{E}\left[\sum _{(z,m)\in Y}h((z,m),Y\backslash \{(z,m)\})\right]\\ \hspace{1em}=\int \mathbb{E}[h((x,m),Y^{!(x,m)})]\rho (x,m)\mathrm{d}x\nu (dm)\\ \hspace{1em}=\int {\mathbb{E}}^{!(x,m)}[h((x,m),Y)]\rho (x,m)\mathrm{d}x\nu (dm).\end{array}$$(3)

Here $Y^{!(x,m)}$ is the reduced Palm process at $(x,m)\in {\mathbb{R}}^d\times \mathcal{M}$, which we interpret as Y conditioned on the null event that there is a point in (x, m), which is removed upon realization. The probability distribution $P^{!(x,m)}(·)={\mathbb{P}}^{!(x,m)}(Y\in ·)=\mathbb{P}(Y^{!(x,m)}\in ·)$ on $(N_{lf},\mathcal{N})$, which corresponds to ${\mathbb{E}}^{!(x,m)}$, is called the reduced Palm distribution at (x, m).

4 Local Weighted Marked Summary Statistics

Global summary statistics have had a prominent role in the statistical analysis of point processes. More precisely, their nonparametric estimators are typically used to characterize the degree of spatial interaction present in the underlying data-generating point process. In Section 1, we have reviewed a few such examples, for instance K-functions.

The individual contributions to a global statistic, which are commonly called Local Indicators of Spatial Association (LISA) functions, can be used to identify outlying components measuring the influence of each contribution to the global statistic (Anselin 1995). This is the case of the scatterplot based on the local Moran index (Anselin 1996). On the other hand, the individual contributions can be used to test for specific local structures, such as spatial association and hot spot detection in areal data (Getis and Ord 1992). Basically, the local statistics mentioned so far are often used to analyze areal data but Getis and Franklin (1987) introduced a local version of the K-function for spatial point processes to show that trees exhibit different kinds of heterogeneity when examined at different scales of analysis. The notion of individual functions for certain statistics has also been studied in Stoyan and Stoyan (1994) and Mateu, Lorenzo, and Porcu (2010) showed that the local product density function (Cressie and Collins 2001) is more sensitive to identifying different local structures and unusual points than the local K-function. Applications of LISA functions range from detection of features in images with noise (Mateu, Lorenzo, and Porcu 2007) to detection of disease clusters (Moraga and Montes 2011). In Siino et al. (2018) the authors extend local indicators of spatial association to the spatio-temporal context (LISTA functions) based on the second order product density, and these local functions have been used to define a proper statistical test for clustering detection. Recently, LISTA functions have been used both for diagnostic (Adelfio et al. 2020) and fitting purposes (D’Angelo, Adelfio, and Mateu 2023). Finally, D’Angelo, Adelfio, and Mateu (2021) extended LISTA functions to spatio-temporal point processes living on linear networks.

As we have clearly indicated, an alternative to studying the aforementioned global summary statistics for marked point processes is considering local summary statistics which describe the spatial interaction in the vicinity of a given marked point. In order to do so here in the marked context, we introduce the function (4) $$\begin{array}{c}L((x,m),\mathbf{x})=L_n((x,m),\mathbf{x};\tilde{t},\tilde{\rho })\\ =\sum _{(x_1,m_1),\dots ,(x_{n-1},m_{n-1})\in \mathbf{x}}^{\ne }\frac{\tilde{t}((x,m),(x_1,m_1),\dots ,(x_{n-1},m_{n-1}))}{\tilde{\rho }(x,m)\tilde{\rho }(x_1,m_1)\dots \tilde{\rho }(x_{n-1},m_{n-1})},\end{array}$$(4) for $(x,m)\in {\mathbb{R}}^d\times \mathcal{M}$, point pattern $\mathbf{x}\in N_{lf}$, and measurable $\tilde{t}:{({\mathbb{R}}^d\times \mathcal{M})}^n\to \mathbb{R}$, $n\ge 2$. Note that, formally, the argument $\tilde{\rho }$ does not need to be the true intensity function ρ of Y, it could for example, be a plug-in estimator. We will exploit Definition 1, and thereby (4), to define proper notions of (mark-weighted nth order inhomogeneous) local summary statistics.

Definition 1.

Given a marked point process Y, we refer to $L((x,m),Y\setminus \{(x,m)\};\tilde{t},\tilde{\rho }),(x,m)\in Y$, as the family of nth order local marked cumulative summary statistics of Y associated with $\tilde{t}$ and $\tilde{\rho }$.

The construction of a specific local statistic is obtained by identifying when, for some function family $\left\{{\tilde{t}}_r\right\}$, (5) $$G(r,Y)=\sum _{(x,m)\in Y}{L}_n((x,m),Y\setminus \{(x,m)\};{\tilde{t}}_r,\tilde{\rho })$$(5) forms an estimator of an existing global summary statistic.

Using nth order local marked cumulative summary statistics to quantify local spatial interactions for a point pattern x entails inserting an estimate $\widehat{\rho }(x,m)={\widehat{f}}_z(m){\widehat{\rho }}_g(x)$ for the unknown intensity $\rho (x,m)=f_z(m){\rho }_g(x)$, that is, setting $\tilde{\rho }=\widehat{\rho }$. When we assume that there is a common mark distribution which coincides with the mark reference measure ν, we obtain that $\widehat{\rho }(x,m)={\widehat{\rho }}_g(x)$, that is, the intensity estimate does not depend on the mark values. Imposing this assumption is particularly convenient when dealing with functional marks since estimation of the mark density, which here is a density on a function space, is rather challenging and beyond the scope of this article. Note that when Y is randomly labeled, it has a common mark distribution and in this setting the assumption $\widehat{\rho }(x,m)={\widehat{\rho }}_g(x)$ thus makes sense.

Turning to the distributional properties of the nth order local marked cumulative summary statistics, we next derive their expectations under the assumption of k-MIRS. Note, in particular, that the choice of $\tilde{t}$ plays a significant role here.

Theorem 1.

When Y is k-MIRS and $\tilde{\rho }=\rho$, for any $W\in \mathcal{B}({\mathbb{R}}^d)$ the expectation of $L((x,m),Y\setminus \{(x,m)\}\cap W\times \mathcal{M};\tilde{t},\rho ),(x,m)\in Y\cap W\times \mathcal{M}$, is almost everywhere given by $${\int }_{W-x}\cdots {\int }_{W-x}({\int }_{\mathcal{M}}\cdots {\int }_{\mathcal{M}}\tilde{t}((x,m),(x_1+x,m_1),\dots ,$$ $$(x_{n-1}+x,m_{n-1}))\frac{f_{0,x_1,\dots ,x_{n-1}}(m,m_1,\dots ,m_{n-1})}{f_0(m)f_{x_1}(m_1)\dots f_{x_{n-1}}(m_{n-1})}$$ $$\hspace{1em}\nu (d{m}_1)\dots \nu (d{m}_{n-1}))g_g^{(n)}(0,x_1,\dots ,x_{n-1})\mathrm{d}{x}_1\dots \mathrm{d}{x}_{n-1},$$when $2\le n\le k$. Moreover, the expectation of $G(r,Y\cap W\times \mathcal{M})$ is obtained by replacing $\tilde{t}$ by ${\tilde{t}}_r$ in the expression above and integrating it over $W\times \mathcal{M}$ with respect to the reference measure on ${\mathbb{R}}^d\times \mathcal{M}$.

Proof.

Note first that the expectation coincides with $$\begin{array}{c}{\mathbb{E}}^{!(x,m)}[L_n((x,m),Y\cap W\times \mathcal{M};\tilde{t},\rho )]\\ ={\mathbb{E}}^{!(x,m)}[\underset{(x_1,m_1),\dots ,(x_{n-1},m_{n-1})\in Y\cap W\times \mathcal{M}}{\sum ^{\ne }}\\ \frac{\tilde{t}((x,m),(x_1,m_1),\dots ,(x_{n-1},m_{n-1}))}{\rho (x,m)\rho (x_1,m_1)\dots \rho (x_{n-1},m_{n-1})}].\end{array}$$

Hence, our starting point will be the reduced Campbell-Mecke formula. Consider an arbitrary bounded $A\times E\in \mathcal{B}({\mathbb{R}}^d\times \mathcal{M})$. It follows that $$\begin{array}{c}\mathbb{E}[\sum _{(x,m)\in Y\cap A\times E}^{}\sum _{(x_1,m_1),\dots ,(x_{n-1},m_{n-1})\in Y\setminus \{(x,m)\}\cap W\times \mathcal{M}}^{\ne }\\ \hspace{1em}\frac{\tilde{t}((x,m),(x_1,m_1),\dots ,(x_{n-1},m_{n-1}))}{\rho (x,m)\rho (x_1,m_1)\dots \rho (x_{n-1},m_{n-1})}]\\ ={\int }_{A\times E}{\mathbb{E}}^{!(x,m)}[\sum _{\ne }^{(x_1,m_1),\dots ,(x_{n-1},m_{n-1})\in Y\cap W\times \mathcal{M}}\\ \hspace{1em}\frac{\tilde{t}((x,m),(x_1,m_1),\dots ,(x_{n-1},m_{n-1}))}{\rho (x_1,m_1)\dots \rho (x_{n-1},m_{n-1})}]\mathrm{d}x\nu (dm).\end{array}$$

On the other hand, by the Campbell formula we have that $$\begin{array}{c}\mathbb{E}[\sum _{(x,m)\in Y\cap A\times E}^{}\sum _{(x_1,m_1),\dots ,(x_{n-1},m_{n-1})\in Y\setminus \{(x,m)\}\cap W\times \mathcal{M}}^{\ne }\\ \hspace{1em}\frac{\tilde{t}((x,m),(x_1,m_1),\dots ,(x_{n-1},m_{n-1}))}{\rho (x,m)\rho (x_1,m_1)\dots \rho (x_{n-1},m_{n-1})}]\\ ={\int }_{A\times E}{\int }_{{\mathbb{R}}^d\times \mathcal{M}}\cdots {\int }_{{\mathbb{R}}^d\times \mathcal{M}}\mathbf{1}\{x_1,\dots ,x_{n-1}\in W\}\tilde{t}((x,m),\\ (x_1,m_1),\dots ,(x_{n-1},m_{n-1}))g^{(n)}((x,m),(x_1,m_1),\dots ,\\ \hspace{1em}(x_{n-1},m_{n-1}))\mathrm{d}{x}_1\nu (d{m}_1)\dots \mathrm{d}{x}_{n-1}\nu (d{m}_{n-1})\mathrm{d}x\nu (dm)\\ ={\int }_{A\times E}{\int }_{{\mathbb{R}}^d\times \mathcal{M}}\cdots {\int }_{{\mathbb{R}}^d\times \mathcal{M}}\prod _{i=1}^{n-1}\mathbf{1}\{u_i\in W-x\}\tilde{t}((x,m),\\ \times (u_1+x,m_1),\dots ,(u_{n-1}+x,m_{n-1}))g^{(n)}((0,m),(u_1,m_1),\dots ,\\ \hspace{1em}(u_{n-1},m_{n-1}))\mathrm{d}{u}_1\nu (d{m}_1)\dots \mathrm{d}{u}_{n-1}\nu (d{m}_{n-1})\mathrm{d}x\nu (dm)\end{array}$$by the imposed k-MIRS and a change of variables, $u_i+x=x_i$. Hence, since $A\times E\in \mathcal{B}({\mathbb{R}}^d\times \mathcal{M})$ was arbitrary, for almost every (x, m) we have that $${\mathbb{E}}^{!(x,m)}[L_n((x,m),Y;\tilde{t},\rho )]$$ $$={\int }_{(W-x)\times \mathcal{M}}\cdots {\int }_{(W-x)\times \mathcal{M}}\tilde{t}((x,m),(u_1+x,m_1),\dots ,$$ $$(u_{n-1}+x,m_{n-1}))g^{(n)}((0,m),(u_1,m_1),\dots ,$$ $$\hspace{1em}(u_{n-1},m_{n-1}))\mathrm{d}{u}_1\nu (d{m}_1)\cdots \mathrm{d}{u}_{n-1}\nu (d{m}_{n-1})$$ $$={\int }_{W-x}\cdots {\int }_{W-x}({\int }_{\mathcal{M}}\cdots {\int }_{\mathcal{M}}\tilde{t}((x,m),(u_1+x,m_1),\dots ,$$ $$(u_{n-1}+x,m_{n-1}))\frac{f_{0,u_1,\dots ,u_{n-1}}(m,m_1,\dots ,m_{n-1})}{f_0(m)f_{u_1}(m_1)\cdots f_{u_{n-1}}(m_{n-1})}$$ $$\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\nu (d{m}_1)\cdots \nu (d{m}_{n-1}))g_g^{(n)}(0,u_1,\dots ,u_{n-1})\mathrm{d}{u}_1\cdots \mathrm{d}{u}_{n-1},$$ by Fubini’s theorem. □

The first thing we note is that when Y is independently marked then the density ratio in the expression for the expectation vanishes. In addition, if Y is a Poisson process on ${\mathbb{R}}^d\times \mathcal{M}$ which satisfies being a marked point process with mark space $\mathcal{M}$, then the expectation reduces to an integral with $\tilde{t}$ as integrand. These observations may be used as benchmarks for when Y exhibits mark (in)dependence and spatial interaction locally.

4.1 Special Cases

We next illustrate how (5), through Definition 1 and (4), reduces to several existing summary statistic estimators by varying $\tilde{t}$ and $\tilde{\rho }$.

4.1.1 Ground K-functions

First, set n = 2 and $\tilde{t}$ to ${\tilde{t}}_r((x,m),(x_1,m_1))=w(x,x_1)\mathbf{1}\{x_1\in x+C\}/\left|W\right|,r\ge 0$, where $W\subseteq {\mathbb{R}}^d,\left|W\right|>0$, and $w(·)$ is an edge correction term. If the ground process is stationary with intensity ${\rho }_g>0$ and $\tilde{\rho }(x,m)\equiv {\rho }_g$, then (5) with Y set to $Y\cap W\times \mathcal{M}$ reduces to an estimator of Ripley’s K-function when $x+C=x+b[0,r]=b[x,r]$ whereas if the ground process is inhomogeneous and we set $\tilde{\rho }(x,m)={\rho }_g(x)$, it follows that (5) reduces to an estimator of the inhomogeneous K-function (Baddeley, Møller, and Waagepetersen 2000) for Y_g. The extension to space-time is straightforward; replace the Euclidean ball $b[0,r]$ by $C=\{(x,s):\Vert x\Vert \le r,|s|\le t\}\in \mathcal{B}({\mathbb{R}}^{d+1})$, where $\Vert ·\Vert$ denotes the Euclidean norm (Gabriel and Diggle 2009; Cronie and Van Lieshout 2015; Iftimi, Cronie, and Montes 2019).

4.1.2 Marked K-Functions

When n = 2, by instead letting ${\tilde{t}}_r((x,m),(x_1,m_1))=w(x,x_1)\mathbf{1}\{x_1\in x+C\}\mathbf{1}\{m\in E,m_1\in E_1\}/(|W|\nu (E)\nu (E_1))$ and $\tilde{\rho }=\rho$ in (4), using a suitable edge correction function $w(·)$, then $G(r,Y\cap W\times \mathcal{M})$ in (5) reduces to an estimator of the marked second-order reduced moment measure ${\mathcal{K}}^{E{E}_1}(C)$ of Iftimi, Cronie, and Montes (2019), which measures the intensity reweighted interactions between points with marks in E and points with marks in E₁, when their separation vectors belong to $C\in \mathcal{B}({\mathbb{R}}^d)$. We note that measures of this kind are in general not symmetric, that is, ${\mathcal{K}}^{E{E}_1}(·)\ne {\mathcal{K}}^{E_{1}E}(·)$ (Iftimi, Cronie, and Montes 2019). Furthermore, choosing C to be the closed origin-centered ball $b[0,r]$ of radius $r\ge 0$, we consider the marked inhomogeneous K-function $K_{\text{inhom}}^{E{E}_1}(r)$ of Cronie and van Lieshout (2016), which measures pairwise intensity reweighted spatial dependence within distance r between points with marks in E and points with marks in E₁.

By additionally letting n > 2, we obtain a definition of a marked nth order reduced moment measure, ${\mathcal{K}}^{E{\times }_{i=1}^{n-1}{E}_i}(C_1\times \cdots \times C_{n-1})$, which measures the intensity reweighted spatial interaction between an arbitrary point with mark in E and distinct $(n-1)$-tuples of other points, where the separation vectors between the E-marked point and these n – 1 points, which have marks in $E_1,\dots ,E_{n-1}$, belong to $C_1,\dots ,C_{n-1}$. We note that $C_i=b[0,r],i=1,\dots ,n-1,r\ge 0$, yields an n-point version of the marked inhomogeneous K-function $K_{\text{inhom}}^{E{\times }_{i=1}^{n-1}{E}_i}(r)$ of Cronie and van Lieshout (2016), which may be used to analyze intensity reweighted interactions between a point with mark in E and n – 1 of its r-close neighbors, which have marks belonging to the respective sets $E_1,\dots ,E_{n-1}$.

4.1.3 Weighted Marked Reduced Moment Measures and K-functions

Finally, by letting $\tilde{\rho }=\rho$ and $\tilde{t}((x,m),(x_1,m_1),\dots ,$ $(x_{n-1},m_{n-1}))$ be given by the product of (6) $$\begin{array}{c}\tilde{t}(m,m_1,\dots ,m_{n-1})\\ \hspace{1em}=t(m,m_1,\dots ,m_{n-1})\frac{\mathbf{1}\{m\in E\}}{\nu (E)}\prod _{i=1}^{n-1}\frac{\mathbf{1}\{m_i\in E_i\}}{\nu (E_i)},\\ \tilde{w}(x,x_1,\dots ,x_{n-1})\\ \hspace{1em}=w(x,x_1,\dots ,x_{n-1})\prod _{i=1}^{n-1}\mathbf{1}\{x_i\in (x+C_i)\},\end{array}$$(6) for $E\in \mathcal{B}(\mathcal{M}),\nu (E)>0$, and $C_i\times E_i\in \mathcal{B}({\mathbb{R}}^d)\times \mathcal{B}(\mathcal{M})=\mathcal{B}({\mathbb{R}}^d\times \mathcal{M}),\nu (E_i)>0,i=1,\dots ,n-1$, we obtain an unbiased estimator ${\widehat{\mathcal{K}}}_t^{E{\times }_{i=1}^{n-1}{E}_i}(C_1\times \cdots \times C_{n-1})=G(r,Y\cap W\times \mathcal{M})$ of the t-weighted marked nth order reduced moment measure of Ghorbani et al. (2021), (7) $$\begin{array}{c}{\mathcal{K}}_t^{E{\times }_{i=1}^{n-1}{E}_i}(C_1\times \cdots \times C_{n-1})=\frac{1}{\left|W\right|\nu (E)\prod _{i=1}^{n-1}\nu (E_i)}\\ \mathbb{E}[\sum _{(x,m)\in Y\cap W\times E}\sum _{(x_1,m_1),\dots ,(x_{n-1},m_{n-1})\in Y\setminus \{(x,m)\}}^{\ne }\frac{t(m,m_1,\dots ,m_{n-1})}{\rho (x,m)}\\ \hspace{1em}\prod _{i=1}^{n-1}\frac{\mathbf{1}\{x_i-x\in C_i\}\mathbf{1}\{m_i\in E_i\}}{\rho (x_i,m_i)}]\end{array}$$(7) assuming that the edge correction function w is such that unbiasedness holds. Examples of such w include the minus sampling edge correction and the translational edge correction (Ghorbani et al. 2021). Note here that one just as well could have merged the scaled indicators in the expression for $\tilde{t}$ with t so that $\tilde{t}=t$; Ghorbani et al. (2021) included this mark set filtering to highlight that their summary statistic generalizes previously proposed ones.

4.2 Local t-Weighted Marked nth Order Inhomogeneous K-Function

In this section, we provide the estimator corresponding to the local contributions of (7) and discuss its properties.

Definition 2.

Let $\tilde{t}$ be (up to indicator-scaling) as in (6) and consider (8) $$\begin{array}{cc}& {\widehat{\mathcal{K}}}_t^{(x,m){\times }_{i=1}^{n-1}{E}_i}(C_1\times \cdots \times C_{n-1})\\ & =L_n((x,m),Y\setminus \{(x,m)\}\cap W\times \mathcal{M};\tilde{t},\tilde{\rho })\\ & =\frac{1}{\tilde{\rho }(x,m)\nu (E)\prod _{i=1}^{n-1}\nu (E_i)}\\ & \hspace{1em}\sum _{(x_1,m_1),\dots ,(x_{n-1},m_{n-1})\in Y\setminus \{(x,m)\}\cap W\times \mathcal{M}}^{\ne }w(x,x_1,\dots ,x_{n-1})\\ & \hspace{1em}t(m,m_1,\dots ,m_{n-1})\prod _{i=1}^{n-1}\frac{\mathbf{1}\{x_i-x\in C_i\}\mathbf{1}\{m_i\in E_i\}}{\tilde{\rho }(x_i,m_i)},\\ & \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}(x,m)\in Y\cap W\times \mathcal{M},\end{array}$$(8) for some suitable edge correction w in (6), $W\in \mathcal{B}({\mathbb{R}}^d),E\in \mathcal{B}(\mathcal{M}),\nu (E)>0$, and $C_i\times E_i\in \mathcal{B}({\mathbb{R}}^d\times \mathcal{M}),\nu (E_i)>0,i=1,\dots ,n-1$. We refer to ${\widehat{\mathcal{K}}}_t^{(x,m){\times }_{i=1}^{n-1}{E}_i}(r)={\widehat{\mathcal{K}}}_t^{(x,m){\times }_{i=1}^{n-1}{E}_i}(b{[0,r]}^{n-1}),r\ge 0$, as a local t-weighted marked nth order inhomogeneous K-function. In particular, ${\widehat{\mathcal{K}}}_{t,n}^{(x,m)}(r)={\widehat{\mathcal{K}}}_t^{(x,m)\times {\mathcal{M}}^{n-1}}(r)$ does not perform any explicit mark set filtering.

Note first that when there is a common mark distribution which coincides with the reference measure on $\mathcal{M}$, setting $\tilde{\rho }=\rho$ we, for instance, obtain $${\widehat{\mathcal{K}}}_{t,n}^{(x,m)}(r)=\sum _{(x_1,m_1),\dots ,(x_{n-1},m_{n-1})\in Y\setminus \{(x,m)\}\cap (b[x,r]\cap W)\times \mathcal{M}}^{\ne }$$ $$\hspace{1em}\frac{t(m,m_1,\dots ,m_{n-1})w(x,x_1,\dots ,x_{n-1})}{{\rho }_g(x){\rho }_g(x_1)\dots {\rho }_g(x_{n-1})}$$since ν must be a probability measure here.

Regarding the distributional properties of (8), when Y is k-MIRS, Theorem 1 tells us that the expectation is given by $$\frac{1}{\nu (E)}\prod _{i=1}^{n-1}\frac{1}{\nu (E_i)}{\int }_{{\mathbb{R}}^d}\cdots {\int }_{{\mathbb{R}}^d}w(x,x_1+x,\dots ,x_{n-1}+x)$$ $$\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\prod _{i=1}^{n-1}\mathbf{1}\{x_i\in (x+C_i)\cap (W-x)\}$$ $$\hspace{1em}({\int }_{E_1}\cdots {\int }_{E_{n-1}}t(m,m_1,\dots ,m_{n-1})$$ $$\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\frac{f_{0,x_1,\dots ,x_{n-1}}(m,m_1,\dots ,m_{n-1})}{f_0(m)f_{x_1}(m_1)\cdots f_{x_{n-1}}(m_{n-1})}\nu (d{m}_1)\cdots \nu (d{m}_{n-1}))$$ $$\hspace{1em}{g}_g^{(n)}(0,x_1,\dots ,x_{n-1})\mathrm{d}{x}_1\cdots \mathrm{d}{x}_{n-1}.$$

In particular, under independent marking the mark related integral within brackets reduces to ${\int }_{E_1}\cdots {\int }_{E_{n-1}}t(m,m_1,\dots ,m_{n-1})\nu (d{m}_1)\dots \nu (d{m}_{n-1})$, whereby (8) is given by the product of this term and a term measuring intensity reweighted spatial interaction.

4.2.1 Test Functions for FMPPs

Turning to the FMPP case, by choosing different test functions $t(·)$ for the functional marks, we may extract different features. We here focus on pairwise interactions, that is, n = 2.

The test function t is intended to reflect similarities between functions. Hence, a natural starting point would be a metric $t(f_1,f_2)=d(f_1,f_2)$ on the function space $\mathcal{M}$, which does not necessarily need to be the underlying assumed metric on $\mathcal{M}$. The first candidate that comes to mind is an L_p-distance: (9) $$t(f_1,f_2)={\left({\int }_a^b|f_1(t)-f_2(t){|}^p\mathrm{d}t\right)}^{1/p},\hspace{1em}1\le p\le \infty ,$$(9) where $p=\infty$ represents the supremum metric. For any choice of p in (9), similarity between functions implies a small value of the test function. Other tentative functions are semi-metrics based on the L_p distance between the sth derivatives of the functions, for different combinations of p and s, with the L₁ and L₂ distances being particular cases, and semi-metrics based on functional principal component analysis.

A further alternative is the functional marked counterpart of the test function for the classical variogram, given by (10) $$t(f_1,f_2)={\int }_a^b(f_1(t)-\stackrel{¯¯}{F}(t))(f_2(t)-\stackrel{¯¯}{F}(t))\mathrm{d}t,$$(10) with $\stackrel{¯¯}{F}(t)=(1/n){\sum }_{i=1}^n{f}_i(t)$ being the average functional mark at time t for the observed functional part of the point pattern; such averaging is motivated by the assumption of a common mark distribution.

5 Local Test for Random labeling

Simple hypotheses for spatial point patterns, such as Complete Spatial Randomness, are commonly tested using an estimator of a global summary statistic, for example, Ripley’s K-function. In this context, one typically resorts to Monte Carlo testing. The first step is then to generate Q simulations under the null hypothesis, and to estimate the chosen summary statistic for both the observed pattern and the simulations. In order to study whether there is random labeling in a (functional) marked point process, the simulations are obtained by permuting the (functional) marks, that is, randomly assigning them to the spatial points of the ground pattern, which are kept fixed. Then, the chosen summary statistic is estimated for each of these permutations and global envelopes at a given nominal level are generated based on them. The result of the test can be assessed graphically: if the summary statistic estimate for the observed pattern exits the envelopes, we proceed with the assumption that the underlying FMPP is not randomly labeled. Furthermore, it is possible to calculate a p-value based on the position of the observed summary statistic within the qth envelopes, following Myllymäki et al. (2017). We know, however, that the conclusion drawn from the application of the above-mentioned global test pertains to the whole analyzed process, indicating whether all the functional marks are randomly labeled or not. Motivated by the will to further detect the specific points, and regions, where the functional marks really do depend on the other marked points, we propose a local test for random labeling. The main idea is to run a global envelope test on each point of the analyzed pattern by means of the previously proposed local t-weighted marked inhomogeneous K-functions, to draw different conclusions about the individual points, based on the obtained p-values. In Algorithm 1 we outline the proposed local test. Note that we alternatively may use sampling without replacement in step 5 of Algorithm 1. Moreover, if convinced that multiple testing issues are present here, one may adjust the Type I error probability α by using for example, the Holm-Bonferroni method.

Algorithm 1

Local test of random labeling

1: Set a fixed nominal value α for Type I error;

2: Consider a (functional) marked point pattern $\mathbf{x}={\{(x_j,m_j)\}}_{j=1}^k,k\ge 1$;

3: Set a number of simulations, $Q\ge 1$;

4: for each $q=1,\dots ,Q$: do

5: Randomly sample k (functional) marks, with replacement, from the original k ones;

6: Denote the resulting point pattern by ${\mathbf{x}}_q={\{(x_j,m_j^q)\}}_{j=1}^k$;

7: end for

8: for each $j=1,\dots ,k$, do

9: Compute $L_n^{(j,q)}={\{{\widehat{\mathcal{K}}}_t^{(x_j,m_j^q){\times }_{i=1}^{n-1}{E}_i}(r;{\mathbf{x}}_q)\}}_{r\in [0,r_{\max }]}$ for all $q=1,\dots ,Q$;

10: Apply global envelope testing, using the functions $L_n^{(j,q)},q=1,\dots ,Q$, to generate the envelopes;

11: Obtain a p-value p_j from the test;

12: Reject the null hypothesis for the j ${}^{th}$ point if $p_j\le \alpha$.

13: end for

6 Motivating Example and Simulation Study

This section is dedicated to simulation studies to assess the performance of our proposed local test. First, Section 6.1 provides a motivating example of the use of such a test, by means of simulated data resembling seismic events, which in turn have motivated this work. In particular, this means simulating the functional marks as seismic waveforms, following the typical abrupt change in variance of the signal in correspondence with the arrivals of the first P- and S-waves. Then, Section 6.2 presents an extensive simulation study, showing diverse and more general settings. Specifically, we assess the performance of the test by summarizing the results in terms of classification rates.

6.1 The Need for a Local Test

We simulate a homogeneous spatial point pattern with 250 points on the unit square, $W=[0,1]\times [0,1]$, which represents the ground pattern. 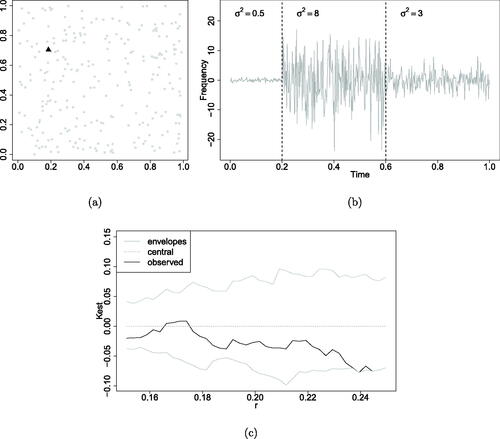For each ground point x_i, we simulate a functional mark of the from $$f_i(t)=y(t)=\mu (t)+ϵ(t),\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}t\in \mathcal{T}=[0,1],$$ $$ϵ(t)\sim N(0,\sigma {(t)}^2),$$ $$\sigma {(t)}^2=0.2+7.5\mathbf{1}\{t>0.4\}-51\{t>0.6\},$$where the mean signal $\mu (t)$ is taken to be zero. The spatial ground point pattern and the corresponding waveform for a given point are shown in Figure 2(a) and (b). Since the marks/waveforms are simulated from the same model, and independently of each other and the spatial locations of the points, we see that such a process is indeed randomly labeled.

Fig. 2 (a) Simulated earthquake locations. (b) Simulated waveform marking the highlighted point on panel (a). (c) Result of the global test.

Having generated the data, we first run a global envelope test for random labeling, by randomly permuting the simulated waveforms, that is, the functional marks, keeping the location of the points fixed. We run the test by means of the t-weighted marked nth order inhomogeneous K-function of Ghorbani et al. (2021), with n = 2, making it a second order summary statistic, and t given by the test function (10), that is, the functional marked counterpart of the test function for the classical variogram. As previously mentioned, we assume that there is a common mark distribution which coincides with the reference measure on the mark space so that the intensity function is estimated by the ground process intensity estimate. To be as objective as possible, we do not use the homogeneous intensity estimator ${\widehat{\rho }}_g(·)=Y_g(W)/\left|W\right|$ here but instead we use a kernel intensity estimator, as in practice it would be unknown to us whether the actual ground process is (in)homogeneous. We use a Gaussian kernel intensity estimator ${\widehat{\rho }}_g(·)$, where we select the bandwidth, h, according to Cronie and Van Lieshout (2018). More specifically, we minimize the discrepancy between the area of the observation window and the sum of reciprocal estimated intensity values at the points of the point pattern, that is, we minimize $\mathit{CvL}(h)={(|W|-\sum _{i}1/{\widehat{\rho }}_g(x_i;h))}^2$, where the sum is taken over all the data points x_i and ${\widehat{\rho }}_g(x_i;h)$ is the kernel intensity estimate with bandwidth h, evaluated in x_i. Then, once the bandwidth has been selected, the intensity estimate is corrected for edge effects through global edge correction (the option diggle = FALSE in the spatstat function density.ppp), that is, dividing the estimate by the convolution of the Gaussian kernel with the window of observation (Diggle 1985). Finally, for w we use Ripley’s isotropic edge correction in the summary statistic to correct for edge effects. We repeated the procedure 39 times, obtaining the result depicted in Figure 2(c). We stress that our approach seems to be robust with respect to the bandwidth specification in this particular scenario setting, that is, the choice of bandwidth selection approach plays a minor role in the final result.

As evident from Figure 2(c), the observed summary statistic completely lies within the envelopes, and this confirms the expected result of lack of spatial dependence/structure of the functional marks. This result is further corroborated by the nonsignificant p-value, equal to 0.25.

6.1.1 Simulating Spatially Dependent Functional Marks

To make the functional marks spatially dependent, we then superimpose a homogeneous spatial point pattern with 50 points, generated in the $[0,0.5]\times [0,0.5]$ square, that is, the bottom left region of the entire study region W. For these additional points, we generate different functional marks than before, namely with the underlying trend $\mu (t)=10+6\hspace{0.17em}\sin \hspace{0.17em}(3\pi z_t)$. Consequently, we have simulated a FMPP with spatially varying functional marks, that is, not randomly labeled. We therefore expect a global test of random labeling to confirm this.

We first run the same global test of random labeling as before. Here, the K-function is based on a kernel intensity estimate whose bandwidth is selected by Diggle’s (2013) rule. It represents a good alternative to Cronie and Van Lieshout’s (2018) one, being slightly faster to compute. We use Q = 39 and obtain a global p-value of 0.025. This, together with the observed K-function lying outside the envelopes (Figure 3(a)), indicates the ability of the global test to correctly detect the spatial dependence of the functional marks.

Fig. 3 (a) Result of global test for the spatially dependent simulated data. (b) Output of the local test: the black triangles are the significant points for which the hypothesis of random labeling is rejected.

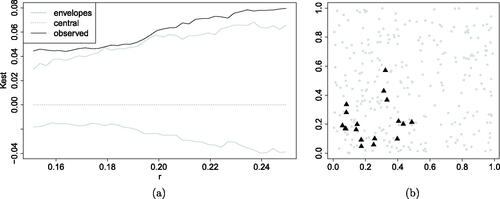
We know, however, that this conclusion should not be drawn for each point of the pattern, if we consider local restrictions of it, but specifically for those in the vicinity of the $[0,0.5]\times [0,0.5]$ square. We therefore proceed by running our proposed local test, based on the proposed second order local K-function ${\widehat{\mathcal{K}}}_{t,2}^{(x,m)}(r),r\in [0,r_{\max }]$, in Definition (2), with the same choice of test function $t(·)$ and the same intensity estimation scheme as for the global one. Figure 3(b) depicts the points of the simulated point pattern, and it displays as black triangles those points for which the local test came out significant. Hence, this illustrates that the proposed local test is able to correctly identify some of the points, and consequently some parts of the region, where the hypothesis of random labeling does not hold locally. Note that a universally preferable option for $r_{\max }$ does not exist. In this article, it is set to $\min (x_W,y_W)/4$, where x_W and y_W represent the maximum width and height of the observation region W, respectively; note that this rule of thumb is supported by Diggle (2013). Indeed, changing the value of $r_{\max }$ has an impact on the final results, and we found that our choice provided the best compromise among the options.

6.2 Extended Simulation Study

This section aims to study the proposed method’s performance in terms of classification rates considering different scenarios, concerning both the ground processes and the functional marks’ structures. To this end, we simulate under different such scenarios, to obtain a comprehensive understanding of the results of the local test in different settings.

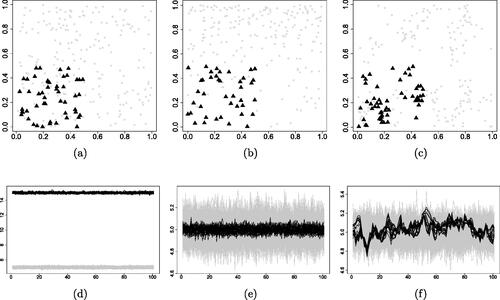
In detail, we consider three types of ground process structures, all with an expected point count of 200: (a) a homogeneous Poisson process; (b) an inhomogeneous Poisson process with intensity function ${\rho }_g(x)={\rho }_g(x_1,x_2)=\hspace{0.17em}\exp \hspace{0.17em}(3.5+3x_2),x\in W$; (3) a Thomas process, with intensity of the Poisson process of cluster centeres equal to 25, standard deviation of random displacement of a point from its cluster center equal to 0.05, and mean number of points per cluster equal to 7. They are all generated in W, that is, the unit square, and will be referred to as the base patterns. Then, we superimpose additional simulated patterns in the $[0,0.5]\times [0,0.5]$ square, coming from the same generating processes, but with an expected number of points of 50; hereby the expected total number of points on $[0,0.5]\times [0,0.5]$ is $50+200/4=100$ and on its complement it is 150. These additional patterns will be referred to as feature patterns. A graphical representation of these three ground patterns comes in Figure 4 (a)–(c).

Fig. 4 Simulation scenarios. (a)–(c) Spatial ground patterns; (d)–(f) Functional marks of model (11) (in gray) and of the marking models in item 1, 2, and 3, respectively (in black).

As for the functional marks, we consider the time domain $\mathcal{T}=[0,10]$ and, practically, we sample each simulated mark function in 100 equally spaced time points in $\mathcal{T}$. We assume that each functional mark satisfies $f_i(t)=Z(x_i,t)$, where x_i is the ith ground point and (11) $$Z(x,t)=\mu +\xi (x,t),\hspace{1em}(x,t)\in W\times \mathcal{T},$$(11) for a zero-mean stationary Gaussian random field ξ with covariance function C(h, u); here h and u denote the spatial and the temporal lags, respectively. For the base patterns, we consider μ = 5 and a pure nugget effect model with covariance function $C(h,u)={\sigma }^2\mathbf{1}\{h=0\},{\sigma }^2=0.01$. In other words, each f_i is random noise with mean 5 and variance 0.01 and all f_i’s are iid; see the grey curves in Figure 4(d)–(f). For the feature patterns, we consider three different marking models:

1. Shifted base model: We here let ξ have the same form as in the base model but let $\mu =5.5$.

2. Decreased variance base model: We here let ξ have the same form as in the base model but let ${\sigma }^2=0.001$.

3. Nonseparable space-time model: We here let μ = 5 and consider a space isotropic covariance function given by $C(h,u)={(\psi (u)+1)}^{-\delta /2}\varphi (h/\sqrt{\psi (u)+1})$. Here, $\varphi$ is a normal mixture and the corresponding covariance function only depends on the distance between two points, while ψ is a variogram model, which we choose according to a fractal Brownian motion with fractal dimension α = 1; this is an intrinsically stationary isotropic variogram model.

We note that the first two of these scenarios represent independent but not identically distributed marks, whereas in the third scenario we additionally have that the marks are also dependent. In Figure 4 (d)–(f), the functional marks corresponding to the marking models in item 1, 2, and 3 are depicted.

We show the results of the local test in terms of true-positive rate (TPR), false-positive rate (FPR), and accuracy (ACC), averaging over 100 simulated point patterns in Table 1. The rates are defined as $$\text{TPR}=\frac{\text{true positives}}{\text{positives}},$$ $$\text{FPR}=\frac{\text{false negatives}}{\text{negatives}},$$ $$\text{ACC}=\frac{\text{true positives and negatives}}{\text{positives and negatives}}.$$

Table 1 Results of the local test averaged over 100 simulated point patterns with an expected point count of 250 each.

Ground process	Marking model	TPR	FPR	ACC
Homogeneous Poisson	(1)	0.112	0.346	0.583
Homogeneous Poisson	(2)	0.583	0.066	0.820
Homogeneous Poisson	(3)	0.870	0.024	0.896
Inhomogeneous Poisson	(1)	0.032	0.585	0.449
Inhomogeneous Poisson	(2)	0.648	0.084	0.856
Inhomogeneous Poisson	(3)	0.895	0.023	0.932
Thomas	(1)	0.109	0.394	0.571
Thomas	(2)	0.637	0.088	0.846
Thomas	(3)	0.865	0.025	0.925

We of course wish to have TPR and ACC close to 1 and FPR close to 0.

As shown in Table 1, the performance of the local test in terms of classification rates strongly depends on the difference in the functional marks. Specifically, changing only the mean of the underlying random field is not enough for properly identifying the points of the feature patterns. This sufficiently improves when changing the variance only, but the best result is obtained when the whole model is changed, that is, changing the correlation structure. The effect of the type of ground pattern is less evident but still present. The inhomogeneous Poisson scenario reports the best classification rates, followed by the Thomas and homogeneous Poisson ones.

Finally, we found that the test function $t(·)$ based on the L₂ distance in (9) gave the better results overall. To further explore how the choice of test function influences the test, we also compared to a test function incorporating a derivative function accounting for the shape of the functional marks. This yielded similar results but turned out to be more computationally demanding.

7 Real Seismic Data Analysis

We analyze data coming from the ISTANCE dataset, presented in Section 2. More specifically, we analyze a sample dataset provided at http://www.pi.ingv.it/instance/. The observed point pattern consists of 300 seismic events which occurred in a period ranging from 21st July 2012 to the 9th December 2016. As shown in Figure 5, the observation area is $[6.729,18.002]\times [36.64,46.46]$, including also seismic events occurring around Italy. They tend to gather into two main clusters. The northernmost originated in May 2012, when two major earthquakes struck Northern Italy, causing 27 deaths and widespread damage. The events are known in Italy as the 2012 Emilia earthquakes, because they mainly affected the Emilia region. Then, the Central Italy seismic sequence began in August 2016, and it is now defined by the INGV as the Amatrice-Norcia-Visso seismic sequence. The analyzed events’ magnitudes vary between 0.5 to 4.8.

Fig. 5 Earthquake locations.

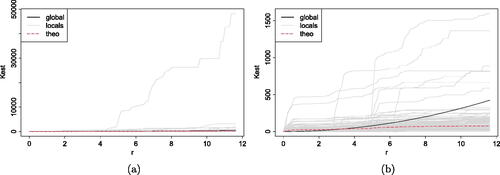
We first compute the proposed local K-function. Figure 6 depicts the estimated local summary statistics. In particular, the steady black lines represent the global statistics, while the grey ones represent the individual contributions. In dashed lines we also represent the theoretical value. In panel (a), the K-function is based on a kernel intensity estimate whose bandwidth is selected by Diggle’s (2013) rule, while in panel (b) the bandwidth is chosen as in Cronie and Van Lieshout (2018). We observe some relevant differences: while with Cronie and Van Lieshout’s (2018) rule we depict different local K-functions deviating from the global one, following Diggle (2013), we find a unique outlying local K-function. This may be explained by the fact that Cronie and Van Lieshout’s (2018) approach tends to yield a bit too large bandwidths when large parts of the study region contain no points, while Diggle’s (2013) approach tends to yield too small bandwidths in general; see Cronie and Van Lieshout (2018) for details. Note that by increasing the bandwidth we decrease the intensity estimate and, as a consequence, the summand denominators in (8) are decreased. Therefore, we run the proposed local test of random labeling with both options for the bandwidth selection and, as expected, the differences observed in the computation of the local K-functions are reflected in the results of the test.

Fig. 6 Local K-functions. (a) The K-function is based on a kernel intensity estimate whose bandwidth is selected by Diggle’s (2013) rule. (b) The bandwidth is chosen as in Cronie and Van Lieshout (2018).

Figure 7 displays the significant points (black triangles) and the nonsignificant ones (grey points). Panel (a) shows the results with Diggle’s (2013) bandwidth while the ones in panel (b) are obtained with Cronie and Van Lieshout’s (2018) bandwidth. For both choices, we selected a significance level of 0.1. We observe that the significant points tend to be similar in both cases, therefore, the choice of bandwidth (selection method) does not seem to be crucial. We note that such bandwidth-induced differences were missing in the previously run simulation study. We attribute this sensitivity of the procedure to the shapes of the functional marks, that are obviously more variable, if compared to the simulated ones.

Fig. 7 Results of the local test at $\alpha =0.1$. Nonsignificant events are displayed as gray points and significant events are the black triangles. (a) The K-function is based on a kernel intensity estimate whose bandwidth is selected by Diggle’s (2013) rule. (b) The bandwidth is chosen as in Cronie and Van Lieshout (2018).

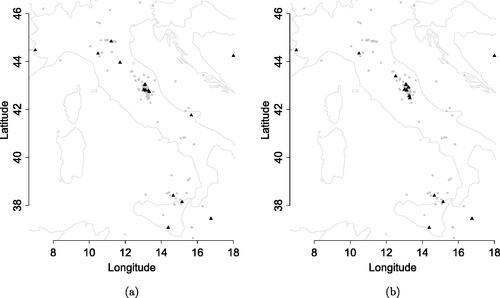
Nevertheless, both bandwidths lead to significant events belonging to important well known Italian seismic sequences. Of course, these sequences are likely generated by different underlying processes, giving rise to long-term and highly correlated aftershocks. The implication of this result is twofold. On one hand, we have been able to correctly identify seismic events belonging to important well-known Italian seismic sequences. On the other hand, we have found that the shocks related to these sequences exhibit different local dependence structure and therefore, these events are likely generated by different underlying processes, corresponding to different seismic sources.

8 Conclusions

In this work, we have proposed a general form for local summary statistics for marked point processes, which has been exploited to define the family of local inhomogeneous mark-weighted summary statistics for spatial point processes with functional marks, that is, Functional Marked Point Processes (FMPP). We have employed such local summary statistics to construct a local test for random labeling, that is, to identify points, as well as regions, where this hypothesis does not hold.

More specifically, we first introduce a general local function for marked point patterns. With this specification, we are able to show that this function may be exploited to generate most summary statistics established in the literature. With particular reference to the functional marked context, we define the family of local t-weighted marked nth order inhomogeneous summary statistics based on the K-function, which is a local contribution to a global summary statistic estimator. We obtain a result for the expectation of the general local summary statistic and exploit it to derive an expression for the expectation of our t-weighted local statistics.

Having access to these tools, we have proposed a local test of random labeling, resorting to the second order version of our proposed local estimator, obtaining a local test useful for identifying specific regions where a global test would not detect atypical behavior of the points.

To study the performance of the test in terms of classification rates, we have conducted a simulation study, considering a number of scenarios with different ground processes and structures for the functional marks. Such simulations have shown that in many settings, the local test performs well in identifying points of a pattern where the hypothesis of random labeling is not verified.

We can draw a number of future work paths. Nevertheless, the local functions proposed in this article can be considered as a very informative synthesis of the local second-order behavior, useful for characterizing the study area by an extended marked model, based on the FMPP theory. Incorporating local characteristics as functional marks would become part of the so called Constructed Functional Marks (CFMs), which are marks reflecting the geometries of point configurations in neighborhoods of the individual points.

Concerning the application to seismic data, we aim at including also auxiliary (nonfunctional) marks into the analysis. These could contain synthetic information about the waveforms, such as the arrival times of the seismic event, or the inter-time between the two. The achievement of the unification of earthquake data and the FMPP theory would result in building a framework where it would be possible to exploit the available information of the seismic point process altogether.

A final comment concerns the possible extension of this article’s tools to spatio-temporal ground processes, which of course are of importance for processes which typically exhibit spatio-temporal interactions, such as the seismic one. Undoubtedly, such extensions would be crucial for accounting for the temporal dimension of the seismic events, whose realization depends on their past history, as proved by the existence of aftershocks. This would mean to consider a spatio-temporal marked point process $Y={\{(x_i,m_i)\}}_{i=1}^N$, with ground points x_i in the three-dimensional space ${\mathbb{R}}^2\times {\mathbb{R}}^{+}$ and exploit the methodological framework introduced in this article. Moreover, local summary statistics in space and time are well established, both theoretically (Siino et al. 2018; Adelfio et al. 2020) and computationally (Gabriel et al. 2021). Although such an extension could be straightforwardly achieved by essentially having our summary statistic functions incorporate an additional argument, t, which controls the temporal lags (see Iftimi, Cronie, and Montes 2019), this adds another level of complexity which we believe is out of the scopes of this article, but it surely represents an interesting path to cover in future.

Supplementary Materials

Supplementary material contains the source codes to reproduce experimental results.

Open Access

The authors would like publish open access, making use of the Bibsam deal which Swedish universities have with Taylor & Francis.

Disclosure Statement

The authors have no potential conflict of interest to report.

Additional information

Funding

This work was supported by “FFR 2023 - Giada Adelfio,” “FFR 2023 - Nicoletta D’Angelo.” We acknowledge financial support from the Italy’s National Recovery and Resilience Plan (PNRR), grant agreement No PE0000018 - GRINS - Growing Resilient, INclusive and Sustainable.