Construction of modular function bases for Γ₀(121) related to p(11n+6)

Abstract

Motivated by arithmetic properties of partition numbers $p\left(n\right)$, our goal is to find algorithmically a Ramanujan type identity of the form $\sum _{n=0}^{\mathrm{\infty }}p(11n+6)q^n=R$, where $R$ is a polynomial in products of the form $e_{\alpha }:=\prod _{n=1}^{\mathrm{\infty }}(1-q^{{11}^{\alpha }n})$ with $\alpha =0,1,2$. To this end we multiply the left side by an appropriate factor such the result is a modular function for ${\mathrm{\Gamma }}_0\left(121\right)$ having only poles at infinity. It turns out that polynomials in the $e_{\alpha }$ do not generate the full space of such functions, so we were led to modify our goal. More concretely, we give three different ways to construct the space of modular functions for ${\mathrm{\Gamma }}_0\left(121\right)$ having only poles at infinity. This in turn leads to three different representations of $R$ not solely in terms of the $e_{\alpha }$ but, for example, by using as generators also other functions like the modular invariant $j$.

Keywords:

• Ramanujan identities
• bases for modular functions
• integral bases

2010 Mathematics Subject Classifications:

• 14H55
• 11F03
• 11P83

1. Introduction

This note, despite its algebraic nature, has been inspired by classical additive number theory having partition numbers $p\left(n\right)$ as one of its primary objects. For a fixed integer $n\ge 0$, $p\left(n\right)$ is defined as the number of additive decompositions of n; e.g. $p\left(4\right)=5$: 4, 3 + 1, 2 + 2, 2 + 1 + 1, 1 + 1 + 1 + 1. Notice that the order in which the parts occur is considered irrelevant. From numerical tables, Ramanujan [1] observed congruences satisfied by subsequences of $p\left(n\right)$; for example, $5\mid p(5n+4)$, $7\mid p(7n+5)$, or $11\mid p(11n+6)$. For the cases 5 and 7, Ramanujan established identities as a witness for the corresponding divisibility property, (1.1) $\prod _{k=1}^{\mathrm{\infty }}\frac{(1-q^k{)}^6}{(1-q^{5k}{)}^5}\sum _{n=0}^{\mathrm{\infty }}p(5n+4)q^n=5$(1.1) and (1.2) $\frac{1}{q}\prod _{k=1}^{\mathrm{\infty }}\frac{(1-q^k{)}^8}{(1-q^{7k}{)}^7}\sum _{n=0}^{\mathrm{\infty }}p(7n+5)q^n=49+7\frac{1}{q}\prod _{k=1}^{\mathrm{\infty }}\frac{(1-q^k{)}^4}{(1-q^{7k}{)}^4}.$(1.2) For the 11 case Ramanujan did not present any such identity. Only recently, with the help of his Ramanujan-Kolberg algorithm, Radu was able to derive such kind of a witness identity of Ramanujan type; see [2, (58)]. Radu's work triggered further algorithmic developments on this theme. We mention a few examples.

First, another witness identity was derived by Hemmecke in a generalized algebraic setting [3, (9)]; this identity reveals the 11 divisibility in explicit manner.

Another kind of witness identity is presented in [4, Thm. 1.1]: Suppose (1.3) $t:=\frac{1}{q^5}\prod _{k=1}^{\mathrm{\infty }}{\left(\frac{1-q^k}{1-q^{11k}}\right)}^{12},$(1.3) and (1.4) $f:=qt\prod _{k=1}^{\mathrm{\infty }}(1-q^{11k})\sum _{n=0}^{\mathrm{\infty }}p(11n+6)q^n.$(1.4) Then (1.5) $\begin{array}{rl}{f}^5& =5\cdot {11}^4{f}^4+{11}^4(-2\cdot 5\cdot {11}^4+251t)f^3\\ & +{11}^3(2\cdot 5\cdot {11}^9+2\cdot 3\cdot 5\cdot {11}^5\cdot 31t+4093t^2)f^2\\ & +{11}^4(-5\cdot {11}^{12}+2\cdot 5\cdot {11}^8\cdot 17t-2^2\cdot 3\cdot {11}^3\cdot 1289t^2+3\cdot 41t^3)f\\ & +{11}^5({11}^4+t)({11}^{11}-3\cdot 7\cdot {11}^{7}t+{11}^2\cdot 1321t^2+t^3).\end{array}$(1.5) The divisibility $11\mid p(11n+6)$ follows immediately from the fact that all coefficients of powers of q on the right-hand side of (1.5(1.5) $\begin{array}{rl}{f}^5& =5\cdot {11}^4{f}^4+{11}^4(-2\cdot 5\cdot {11}^4+251t)f^3\\ & +{11}^3(2\cdot 5\cdot {11}^9+2\cdot 3\cdot 5\cdot {11}^5\cdot 31t+4093t^2)f^2\\ & +{11}^4(-5\cdot {11}^{12}+2\cdot 5\cdot {11}^8\cdot 17t-2^2\cdot 3\cdot {11}^3\cdot 1289t^2+3\cdot 41t^3)f\\ & +{11}^5({11}^4+t)({11}^{11}-3\cdot 7\cdot {11}^{7}t+{11}^2\cdot 1321t^2+t^3).\end{array}$(1.5) ) are integers containing 11 as a factor. This property clearly carries over to $f$ since $f^5$ is an element of an integral domain – regardless whether the $q$-series/products involved are considered as formal Laurent series or as analytic functions.

Analytically, when taking $q=q\left(\tau \right):=\exp \left(2\pi \mathrm{i}\tau \right)\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\tau \in \mathbb{H}:=\left\{\tau \in \mathbb{C}\left|\phantom{\tau \in \mathbb{C}}\mathrm{I}\mathrm{m}\left(\tau \right)>0\right.\right\},$ the witness identities (1.1(1.1) $\prod _{k=1}^{\mathrm{\infty }}\frac{(1-q^k{)}^6}{(1-q^{5k}{)}^5}\sum _{n=0}^{\mathrm{\infty }}p(5n+4)q^n=5$(1.1) ), (1.2(1.2) $\frac{1}{q}\prod _{k=1}^{\mathrm{\infty }}\frac{(1-q^k{)}^8}{(1-q^{7k}{)}^7}\sum _{n=0}^{\mathrm{\infty }}p(7n+5)q^n=49+7\frac{1}{q}\prod _{k=1}^{\mathrm{\infty }}\frac{(1-q^k{)}^4}{(1-q^{7k}{)}^4}.$(1.2) ), and (1.5(1.5) $\begin{array}{rl}{f}^5& =5\cdot {11}^4{f}^4+{11}^4(-2\cdot 5\cdot {11}^4+251t)f^3\\ & +{11}^3(2\cdot 5\cdot {11}^9+2\cdot 3\cdot 5\cdot {11}^5\cdot 31t+4093t^2)f^2\\ & +{11}^4(-5\cdot {11}^{12}+2\cdot 5\cdot {11}^8\cdot 17t-2^2\cdot 3\cdot {11}^3\cdot 1289t^2+3\cdot 41t^3)f\\ & +{11}^5({11}^4+t)({11}^{11}-3\cdot 7\cdot {11}^{7}t+{11}^2\cdot 1321t^2+t^3).\end{array}$(1.5) ) can be explained in the world of modular functions. Let $M^{\mathrm{\infty }}\left(N\right)$ denote the $\mathbb{C}$-algebra of modular functions for ${\mathrm{\Gamma }}_0\left(N\right)$ having a pole (of some order) at most at infinity; definitions of these notions are given in Section 2. Then (1.1(1.1) $\prod _{k=1}^{\mathrm{\infty }}\frac{(1-q^k{)}^6}{(1-q^{5k}{)}^5}\sum _{n=0}^{\mathrm{\infty }}p(5n+4)q^n=5$(1.1) ) means that its left side is a modular function in $M^{\mathrm{\infty }}\left(5\right)$ which turns out to be the constant function 5. Similarly, (1.2(1.2) $\frac{1}{q}\prod _{k=1}^{\mathrm{\infty }}\frac{(1-q^k{)}^8}{(1-q^{7k}{)}^7}\sum _{n=0}^{\mathrm{\infty }}p(7n+5)q^n=49+7\frac{1}{q}\prod _{k=1}^{\mathrm{\infty }}\frac{(1-q^k{)}^4}{(1-q^{7k}{)}^4}.$(1.2) ) means that its left side is a modular function in $M^{\mathrm{\infty }}\left(7\right)$ which can be written in the form as on its right side as a linear combination of 49 times the constant modular function 1, plus 7 times a modular function in $M^{\mathrm{\infty }}\left(7\right)$ representable as a $q$-product.

Despite that fact that f and t being again modular functions, in $M^{\mathrm{\infty }}\left(11\right)$, from an algebraic point of view the structure of (1.5(1.5) $\begin{array}{rl}{f}^5& =5\cdot {11}^4{f}^4+{11}^4(-2\cdot 5\cdot {11}^4+251t)f^3\\ & +{11}^3(2\cdot 5\cdot {11}^9+2\cdot 3\cdot 5\cdot {11}^5\cdot 31t+4093t^2)f^2\\ & +{11}^4(-5\cdot {11}^{12}+2\cdot 5\cdot {11}^8\cdot 17t-2^2\cdot 3\cdot {11}^3\cdot 1289t^2+3\cdot 41t^3)f\\ & +{11}^5({11}^4+t)({11}^{11}-3\cdot 7\cdot {11}^{7}t+{11}^2\cdot 1321t^2+t^3).\end{array}$(1.5) ) is more involved – and also more interesting. Namely, it expresses the algebraic fact that (1.6) $\mathbb{C}[f,t]={⟨1,f,f^2,f^3,f^4⟩}_{\mathbb{C}\left[t\right]}.$(1.6) This means that the $\mathbb{C}$-algebra of polynomials in $f$ and $t$ with complex coefficients can be represented as a module freely generated by $1,f,\dots ,f^4$ over the ring $\mathbb{C}\left[t\right]$ of polynomials in $t$ with complex coefficients. The free generation is obvious, as in all cases we will consider, owing to the fact that the pole order of the generators $f^j$ are pairwise different.

In general, for non-constant modular functions $t,b_1,\dots ,b_{n-1}$ in $M^{\mathrm{\infty }}\left(N\right)$, our notation for such modules is: ${⟨1,b_1,\dots ,b_{n-1}⟩}_{\mathbb{C}\left[t\right]}:=\left\{p_0\left(t\right)+p_1\left(t\right)b_1+\cdots +p_{n-1}\left(t\right)b_{n-1}\left|\phantom{p_0\left(t\right)+p_1\left(t\right)b_1+\cdots +p_{n-1}\left(t\right)b_{n-1}}{p}_j\left(X\right)\in \mathbb{C}\left[X\right]\right.\right\}.$ In various applications one needs a $\mathbb{C}\left[t\right]$-module representation of the whole space $M^{\mathrm{\infty }}\left(N\right)$. For example, when using modular functions to prove Ramanujan's congruences for powers of 11 (i.e. ${11}^2\mid p({11}^{2}n+116)$, ${11}^3\mid p({11}^{3}n+721)$, etc.) one needs to work with a $\mathbb{C}\left[t\right]$-module representation of $M^{\mathrm{\infty }}\left(11\right)$. According to the Weierstraß gap theorem, see [5, Thm. 12.2] for a version in the context of modular functions, there is a representation (1.7) $M^{\mathrm{\infty }}\left(11\right)={⟨1,F_2,F_3,F_4,F_6⟩}_{\mathbb{C}\left[t\right]},$(1.7) with $t=\frac{1}{q^5}+O\left(q^{-4}\right)\in M^{\mathrm{\infty }}\left(11\right)$ as in (1.3(1.3) $t:=\frac{1}{q^5}\prod _{k=1}^{\mathrm{\infty }}{\left(\frac{1-q^k}{1-q^{11k}}\right)}^{12},$(1.3) ) and with $F_j\in M^{\mathrm{\infty }}\left(11\right)$ of the form $F_j=\frac{1}{q^j}+O\left(q^{-j+1}\right)$. Atkin [6] was the first to construct such $F_j$ explicitly. In [7] Atkin's construction was revisited and a simpler representation of the $F_j$ was found by using a trace operator; more precisely, a special instance of [8, (1)]. An explicit discussion of the representation (1.7(1.7) $M^{\mathrm{\infty }}\left(11\right)={⟨1,F_2,F_3,F_4,F_6⟩}_{\mathbb{C}\left[t\right]},$(1.7) ) can also be found in [5].

Summarizing, despite the usefulness of the module representation (1.6(1.6) $\mathbb{C}[f,t]={⟨1,f,f^2,f^3,f^4⟩}_{\mathbb{C}\left[t\right]}.$(1.6) ), it does not give the full space, for instance, $F_2\notin \mathbb{C}[t,f]$ in view of the pole orders 4 and 5 of $f$ and $t$, respectively. It is the main objective of this note to show how a basis of the full space $M^{\mathrm{\infty }}\left(N\right)$ can be obtained algorithmically. To be as concrete as possible, we will do this in the form of a case study where we fix $N:=121$. Despite being a special case, we feel this specialization will allow to illustrate general features and, on the other hand, will be sufficiently general to lead also to interesting non-trivial number theoretic applications.

To construct module bases for the full space such that $M^{\mathrm{\infty }}\left(N\right)={⟨1,b_1,\dots ,b_{n-1}⟩}_{\mathbb{C}\left[t\right]},$ two concepts turn out to be fundamental: order-completeness and the notion of an integral basis; see Definition 4.1. The connection to the classical notion of integral elements is made by

Lemma 1.1

[5, Lemma 4.2]

Let $f=\frac{1}{q^m}+O\left(q^{-m+1}\right)$ be a modular function for ${\mathrm{\Gamma }}_0\left(N\right)$ as defined in Section 2. Let $t\in M^{\mathrm{\infty }}\left(N\right)$ with q-expansion $t=\frac{1}{q^{\ell }}+O\left(q^{-\ell +1}\right)$. Suppose $gcd(\ell ,m)=1$. Then f satisfies an algebraic relation $f^n+p_1\left(t\right)f^{n-1}+\cdots +p_n\left(t\right)=0$ with polynomials $p_j\left(X\right)\in \mathbb{C}\left[X\right]$ (i.e. $f$ is integral over $\mathbb{C}\left[t\right]$) if and only if $f\in M^{\mathrm{\infty }}\left(N\right).$ Moreover, if $f\in M^{\mathrm{\infty }}\left(N\right)$, then there exists an algebraic relation with $n=\ell$.

The main reason to aim at the computation of an integral basis is the following. Many of the modular functions arising in q-series identities can be modified in a straight-forward manner to turn them into members of $M^{\mathrm{\infty }}\left(N\right)$, for example, by multiplying with eta quotients. In such cases the $q$-expansions at the pole ∞ often are available in a ‘natural fashion’. The knowledge of an integral basis $B$ for $M^{\mathrm{\infty }}\left(N\right)$ that is computed from known functions such as eta-quotients or the Klein $j$ function then allows to algorithmically express $f$ as a $\mathbb{C}\left[t\right]$-linear combination of the elements of $B$.

The content of our note is structured as follows. Section 2 recalls the most important modular function notions needed. Section 3 gives a brief summary of the main problem of this note which is solved by three different methods in Sections 6–8. To describe these solutions we need some preparations. Section 4 discusses the problem of using eta-quotients for module representations. Section 5 returns to the theme of representing the generating function $\sum _{n\ge 1}p(11n+6)q^n$ and prepares the ground for the computation of integral bases. Section 6 solves the problem of computing an integral basis for $M^{\mathrm{\infty }}\left(121\right)$ by using the modular invariant; i.e. Klein's $j$ function. Section 7 solves the integral basis problem using the trace operator already mentioned in connection with (1.7(1.7) $M^{\mathrm{\infty }}\left(11\right)={⟨1,F_2,F_3,F_4,F_6⟩}_{\mathbb{C}\left[t\right]},$(1.7) ). Finally, Section 8 explains how the Maple package algcurves can be invoked to derive the desired integral basis.

2. Notation

Let $\mathbb{H}=\left\{\tau \in \mathbb{C}\left|\phantom{\tau \in \mathbb{C}}\mathrm{I}\mathrm{m}\left(\tau \right)>0\right.\right\}$ denote the complex upper half-plane. In the following N denotes a positive integer. We define the groups $\begin{array}{rl}{\mathrm{S}\mathrm{L}}_2\left(\mathbb{Z}\right)& =\left\{\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\left|\phantom{\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)}a,b,c,d\in \mathbb{Z}\mathrm{a}\mathrm{n}\mathrm{d}ad-bc=1\right.\right\},\\ {\mathrm{\Gamma }}_0\left(N\right)& =\left\{\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\in {\mathrm{S}\mathrm{L}}_2\left(\mathbb{Z}\right)\left|\phantom{\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\in {\mathrm{S}\mathrm{L}}_2\left(\mathbb{Z}\right)}c\equiv 0\left(\mathrm{mod}N\right)\right.\right\};\end{array}$${\mathrm{S}\mathrm{L}}_2\left(\mathbb{Z}\right)={\mathrm{\Gamma }}_0\left(1\right)$ acts on $\mathbb{H}$ by $\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\tau =\frac{a\tau +b}{c\tau +d}$. This action induces an action on meromorphic functions $f:\mathbb{H}\to \hat{\mathbb{C}}:=\mathbb{C}\cup \left\{\mathrm{\infty }\right\}$, namely $\left(f|\gamma \right)\left(\tau \right):=f\left(\gamma \tau \right).$ A modular function for ${\mathrm{\Gamma }}_0\left(N\right)$ is a meromorphic function $f:\mathbb{H}\to \hat{\mathbb{C}}$ such that

1. for all $\gamma \in {\mathrm{\Gamma }}_0\left(N\right)$: $f|\gamma =f$; and

2. if $\gamma =\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\in {\mathrm{S}\mathrm{L}}_2\left(\mathbb{Z}\right)$ then $f\left(\frac{a\tau +b}{c\tau +d}\right)$ admits a Laurent series expansion in powers of $q^{1/w_N\left(c\right)}$, where $w_N\left(c\right):=N/gcd(c^2,N)$, of the form (2.1) $f\left(\gamma \tau \right)=\sum _{n=m}^{\mathrm{\infty }}{f}_n{q}^{n/w_N\left(c\right)},\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}q=\exp \left(2\pi \mathrm{i}\tau \right),m\in \mathbb{Z}.$(2.1)

Because of $\gamma \mathrm{\infty }:=\underset{\mathrm{I}\mathrm{m}\left(\tau \right)\to \mathrm{\infty }}{lim}\gamma \tau =a/c$, we say that (2.1(2.1) $f\left(\gamma \tau \right)=\sum _{n=m}^{\mathrm{\infty }}{f}_n{q}^{n/w_N\left(c\right)},\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}q=\exp \left(2\pi \mathrm{i}\tau \right),m\in \mathbb{Z}.$(2.1) ) is a q-expansion of f at a/c. Understanding $a/0=\mathrm{\infty }$, this extends to defining q-expansions at ∞. Note that if ${\gamma }^{\prime }\mathrm{\infty }=\gamma \mathrm{\infty }=a/c$ then ${\gamma }^{\prime }=\gamma \left(\begin{array}{cc}\pm 1& h\\ 0& \pm 1\end{array}\right)$ for some $h\in \mathbb{Z}$ and, thus, (2.2) $f\left({\gamma }^{\prime }\tau \right)=\sum _{n=m}^{\mathrm{\infty }}{f}_n\exp (\pm 2\pi \mathrm{i}h/w_n(c){)}^n{q}^{n/w_N\left(c\right)};$(2.2) i.e. we can (uniquely) extend the definition of f to points on $\hat{\mathbb{H}}:=\mathbb{H}\cup \mathbb{Q}\cup \left\{\mathrm{\infty }\right\}$ as $f\left(a/c\right)=\left\{\begin{array}{ll}{f}_0& \mathrm{i}\mathrm{f}m=0,\\ 0& \mathrm{i}\mathrm{f}m>0,\\ \mathrm{\infty }& \mathrm{i}\mathrm{f}m<0.\end{array}\right.$ Let $M^{\mathrm{\infty }}\left(N\right)$ be the set of modular functions for ${\mathrm{\Gamma }}_0\left(N\right)$ that only have a pole (if any) at infinity. An element $f\in M^{\mathrm{\infty }}\left(N\right)$ has a representation as a Laurent series in q.

We denote by $\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{d}\left(f\right)=-{\mathrm{o}\mathrm{r}\mathrm{d}}_{q}f$ the pole order (at infinity) of f; here ${\mathrm{o}\mathrm{r}\mathrm{d}}_{q}f$ is defined as the index of the least non-zero coefficient in the expansion (2.1(2.1) $f\left(\gamma \tau \right)=\sum _{n=m}^{\mathrm{\infty }}{f}_n{q}^{n/w_N\left(c\right)},\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}q=\exp \left(2\pi \mathrm{i}\tau \right),m\in \mathbb{Z}.$(2.1) ) of f in powers of q. In view of (2.2(2.2) $f\left({\gamma }^{\prime }\tau \right)=\sum _{n=m}^{\mathrm{\infty }}{f}_n\exp (\pm 2\pi \mathrm{i}h/w_n(c){)}^n{q}^{n/w_N\left(c\right)};$(2.2) ) with c = 0 and thus $w_N\left(c\right)=1$, we note that q-expansions at infinity are unique in integer powers of q.

Denote by $M_{\mathbb{Q}}^{\mathrm{\infty }}\left(N\right)$ the elements of $M^{\mathrm{\infty }}\left(N\right)$ whose q-series expansion have rational coefficients. From Theorem 3.52 of [9] it follows that $M^{\mathrm{\infty }}\left(N\right)$ is generated as a $\mathbb{C}$-vectorspace by elements of $M_{\mathbb{Q}}^{\mathrm{\infty }}\left(N\right)$.

The action of ${\mathrm{S}\mathrm{L}}_2\left(\mathbb{Z}\right)$ on $\mathbb{H}$ extends in an obvious way to an action on $\hat{\mathbb{H}}$. The orbits of the action of the subgroup ${\mathrm{\Gamma }}_0\left(N\right)\subset {\mathrm{S}\mathrm{L}}_2\left(\mathbb{Z}\right)$ are denoted by $[\tau {]}_N:=\left\{\gamma \tau \left|\phantom{\gamma \tau }\gamma \in {\mathrm{\Gamma }}_0\left(N\right)\right.\right\},\tau \in \hat{\mathbb{H}}.$ The set of all such orbits is denoted by $X_0\left(N\right):=\left\{[\tau {]}_N\left|\phantom{[\tau {]}_N}\tau \in \hat{\mathbb{H}}\right.\right\}.$ There are only finitely many cosets with respect to ${\mathrm{\Gamma }}_0\left(N\right)$; more precisely, for $N\ge 2$, $\left[{\mathrm{S}\mathrm{L}}_2\right(\mathbb{Z}):{\mathrm{\Gamma }}_0(N\left)\right]=N\prod _{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{m}\mathrm{e}p\mid N}\left(1+\frac{1}{p}\right).$  Owing to this fact together with the observation $\mathbb{Q}\cup \left\{\mathrm{\infty }\right\}=\left\{\gamma \mathrm{\infty }\left|\phantom{\gamma \mathrm{\infty }}\gamma \in {\mathrm{S}\mathrm{L}}_2\left(\mathbb{Z}\right)\right.\right\}$, there are only finitely many orbits $[\tau {]}_N$ with $\tau \in \mathbb{Q}\cup \left\{\mathrm{\infty }\right\}$. These orbits are called cusps of $X_0\left(N\right)$.

As usual, $\eta :\mathbb{H}\to \mathbb{C},\tau \mapsto \exp \left(\frac{\pi \mathrm{i}\tau }{12}\right)\prod _{n=1}^{\mathrm{\infty }}(1-\exp (2\pi \mathrm{i}\tau {)}^n)$ denotes the Dedekind eta function.

Let $1={\delta }_1<{\delta }_2<\cdots <{\delta }_n=N$ be the positive divisors of N. For convenience, we allow to index n-dimensional vectors by the divisors of N, instead of the usual index set $\left\{1,\dots ,n\right\}$.

We define $R\left(N\right)$ to be the set of integer tuples $r=(r_{{\delta }_1},\dots ,r_{{\delta }_n})\in {\mathbb{Z}}^n$. With $R^{\ast }\left(N\right)$ we denote the subset of all tuples $r=(r_{\delta }{)}_{\delta \mid N}$ of $R\left(N\right)$ that fulfill the following conditions: (2.3) $\begin{array}{rl}\sum _{\delta \mid N}{r}_{\delta }& =0,\end{array}$(2.3) (2.4) $\begin{array}{rl}\sum _{\delta \mid N}\delta r_{\delta }& \equiv 0\left(\mathrm{mod}24\right),\end{array}$(2.4) (2.5) $\begin{array}{rl}\sum _{\delta \mid N}\frac{N}{\delta }{r}_{\delta }& \equiv 0\left(\mathrm{mod}24\right),\mathrm{a}\mathrm{n}\mathrm{d}\end{array}$(2.5) (2.6) $\begin{array}{rl}\sqrt{\prod _{\delta \mid N}{\delta }^{r_{\delta }}}& \in \mathbb{Q}.\end{array}$(2.6) Note that $R^{\ast }\left(N\right)$ is an additive monoid.

To elements $r=(r_{\delta }{)}_{\delta \mid N}\in R^{\ast }(N)$ we associate eta-quotients $g_r\left(\tau \right):=\prod _{\delta \mid N}\eta (\delta \tau {)}^{r_{\delta }}.$ By [10, Theorem 1], the elements of $E\left(N\right):=\left\{g_r\left(\tau \right)\left|\phantom{g_r\left(\tau \right)}r\in R^{\ast }\left(N\right)\right.\right\}$ are modular functions for ${\mathrm{\Gamma }}_0\left(N\right)$. Moreover, we define $E^{\mathrm{\infty }}\left(N\right):=E\left(N\right)\cap M^{\mathrm{\infty }}\left(N\right).$ If L is a ring and S is a subset of an L-module, we denote by ${⟨S⟩}_L$ the set of L-linear combinations of elements of S. If L is a field, then ${⟨S⟩}_L$ is a vector space. If $S\subset L$, then $⟨S{⟩}_L$ is an ideal of L.

3. The problem

As pointed out in the introduction, this case study was inspired by recent algorithmic progress made in connection with classical number theoretic observations made by Ramanujan. For N = 121, the problem is to find an integral basis of the space $M^{\mathrm{\infty }}\left(121\right)$ of modular functions having a pole (if any) only at infinity.

We present a solution to this problem by following three different approaches, namely, by using Klein's j-invariant, by using series that are obtained by the trace operator, applied to some eta-quotients living in $M^{\mathrm{\infty }}\left(242\right)$, and by employing the integral_basis command from Maple.

Essentially, in each of the three approaches we construct a basis for $M^{\mathrm{\infty }}\left(121\right)$. These bases cannot be shown explicitly in this paper because of size. For this reason we have put the explicit expressions of the bases at https://risc.jku.at/people/hemmecke/papers/integralbasis/. Each basis at the above URL has been computed in the computer algebra system FriCAS¹ by the package QEta.²

In this article, we explicitly mark the references to these bases by giving the name of the file that contains the respective expression(s). This filename has to be appended to the above URL in order to retrieve the data from the internet.

4. A basis for the eta-quotients in $M_{\mathbb{Q}}^{\mathrm{\infty }}\left(121\right)$

In [2], Radu shows that $E^{\mathrm{\infty }}\left(N\right)$ is a finitely generated (multiplicative) monoid; i.e. there exist $m_1,\dots ,m_k\in E^{\mathrm{\infty }}\left(N\right)$ such that any element of $f\in E^{\mathrm{\infty }}\left(N\right)$ can be written as $f=\prod _{i=1}^k{m}_i^{e_i}$. Radu also describes an algorithm to compute such monoid generators. Furthermore, Radu gives an algorithm to compute elements $t,z_0,\dots ,z_{\ell -1}\in \mathbb{Q}[m_1,\dots ,m_k]=\mathbb{Q}\left[E^{\mathrm{\infty }}\right(N\left)\right]={⟨E^{\mathrm{\infty }}\left(N\right)⟩}_{\mathbb{Q}}$ such that $\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{d}\left(t\right)=\ell$, $\mathbb{Q}[m_1,\dots ,m_k]={⟨z_0,\dots ,z_{\ell -1}⟩}_{\mathbb{Q}\left[t\right]}$, and $\left\{z_0,\dots ,z_{\ell -1}\right\}$ is order-complete. This latter notion is defined in

Definition 4.1

[5]

An n element subset $B=\left\{b_0,\dots ,b_{n-1}\right\}\subseteq M^{\mathrm{\infty }}\left(N\right)$ is called order-complete if $1\in B$ and for each $i\in \left\{1,\dots ,n-1\right\}$ there exists $b\in B$ such that $\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{d}\left(b\right)\equiv i\left(\mathrm{mod}n\right)$. Let $t\in M^{\mathrm{\infty }}\left(N\right)$ and let $M\subseteq M^{\mathrm{\infty }}\left(N\right)$ be a $\mathbb{C}\left[t\right]$-module. Then B is called an order-complete basis for M, if $n=\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{d}\left(t\right)$ and $M={⟨B⟩}_{\mathbb{C}\left[t\right]}$.Such an order-complete basis B is called integral basis for $M^{\mathrm{\infty }}\left(N\right)$ if $M=M^{\mathrm{\infty }}\left(N\right)$; i.e. ${⟨B⟩}_{\mathbb{C}\left[t\right]}=M^{\mathrm{\infty }}\left(N\right)$.

One can use the reduction process from [3] (see, in particular, Theorem 3.2) to algorithmically determine polynomials $c_0,\dots ,c_{\ell -1}\in \mathbb{Q}\left[T\right]$ T an indeterminate, and a remainder series $r\in M_{\mathbb{Q}}^{\mathrm{\infty }}\left(N\right)$ such that for a given element $f\in M_{\mathbb{Q}}^{\mathrm{\infty }}\left(N\right)$, (4.1) $f=\sum _{i=0}^{\ell -1}{c}_i\left(t\right)z_i+r$(4.1) with r = 0 or $r\ne 0$ and $\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{d}\left(r\right)<max\left\{\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{d}\left(z_i\right)\left|\phantom{\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{d}\left(z_i\right)}i\in \left\{0,\dots ,\ell -1\right\}\right.\right\}$. Then r = 0 if and only if $f\in \mathbb{Q}[m_1,\dots ,m_k]$.

For this article, we use an implementation of the algorithm samba from [3] in our QEta package. Given modular functions $m_1=t,m_2\dots ,m_k\in M_{\mathbb{Q}}^{\mathrm{\infty }}\left(N\right)$ with $\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{d}\left(t\right)>0$, the algorithm samba computes a basis $B=\left\{z_0,\dots ,z_{\ell -1}\right\}$ such that $1\in B$ and $\mathbb{Q}[m_1,\dots ,m_k]={⟨z_0,\dots ,z_{\ell -1}⟩}_{\mathbb{Q}\left[t\right]}={⟨B⟩}_{\mathbb{Q}[t}$. In this paper the input $m_1,\dots ,m_k$ is always such that $z_0,\dots ,z_{\ell -1}$ is order-complete.

For N = 121, Radu's algorithm [2] delivers two monoid generators in $E^{\mathrm{\infty }}\left(121\right)$, namely (4.2) $t=\frac{\eta \left(\tau \right)}{\eta \left(121\tau \right)}=q^{-5}-q^{-4}-q^{-3}+O\left(q^{-2}\right),$(4.2) and (4.3) $u=\frac{\eta (11\tau {)}^{12}}{\eta \left(\tau \right)\eta (121\tau {)}^{11}}=q^{-50}+q^{-49}+2q^{-48}+O\left(q^{-47}\right).$(4.3) Next, by application of the algorithm samba to t and u one obtains the element (4.4) $z=\frac{1}{11}(u-t^{10})=q^{-49}-3q^{-48}+3q^{-47}+O\left(q^{-46}\right)$(4.4) such that (4.5) $\mathbb{Q}[t,u]={⟨1,z,z^2,z^3,z^4⟩}_{\mathbb{Q}\left[t\right]};$(4.5) i.e. $B=\left\{1,z,z^2,z^3,z^4\right\}$ forms an order-complete basis of $\mathbb{Q}[t,u]={⟨E^{\mathrm{\infty }}\left(121\right)⟩}_{\mathbb{Q}}$.

We remark that in this simple example the reduction expressed by the left equality in (4.4(4.4) $z=\frac{1}{11}(u-t^{10})=q^{-49}-3q^{-48}+3q^{-47}+O\left(q^{-46}\right)$(4.4) ) can be ‘seen’ immediately. Also note that, by using $(1-x{)}^{11}\equiv 1-x^{11}(\mathrm{mod}11)$, one can easily show that the q-series of z has integer coefficients.

Definition 4.2

[5, Definition 12.1]

Let M be a subalgebra of $M^{\mathrm{\infty }}\left(N\right)$. A positive integer n is called a gap in M, if there is no $f\in M$ with $\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{d}\left(f\right)=n$. We also define the gap number $g_M$ as the total number of gaps in M; i.e. $g_M:=\mathrm{\#}\left\{n\in {\mathbb{Z}}_{>0}\left|\phantom{n\in {\mathbb{Z}}_{>0}}n\mathrm{i}\mathrm{s}\mathrm{a}\mathrm{g}\mathrm{a}\mathrm{p}\mathrm{i}\mathrm{n}M\right.\right\}$.

The gap number $g_M$ for $M=\mathbb{Q}[t,u]$ can be determined by an application of relation (4.5(4.5) $\mathbb{Q}[t,u]={⟨1,z,z^2,z^3,z^4⟩}_{\mathbb{Q}\left[t\right]};$(4.5) ) as $g_M=\frac{1}{5}\left(\right(49-4)+(98-3)+(147-2)+(196-1\left)\right)=96.$ The Riemann surface $X_0\left(121\right)$ is a curve of genus 6, see https://oeis.org/A001617. The genus can be computed in FriCAS with our QEta package by calling

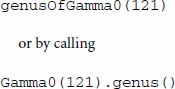
in the computer algebra system Sage.³

By the Weierstraß gap theorem (see [11, Thm. III.5.3], respectively [5, Thm. 12.2] for the given context), one has $g_{M^{\mathrm{\infty }}\left(121\right)}=6.$ Consequently, $M⊊M^{\mathrm{\infty }}\left(121\right)$ is a proper submodule; i.e. $M^{\mathrm{\infty }}\left(121\right)$ is not generated as a $\mathbb{C}$-vectorspace by using only eta-quotients from $M^{\mathrm{\infty }}\left(121\right)$.

5. The generating function for $p(11n+6)$

In this section, we use a method described in the proof of Proposition 4.3 in [5] to find a new relation for the generating function of $p(11n+6)$ that shows $11\mid p(11n+6)$ for all $n\in \mathbb{N}$. We aim at computing the cofactor d and the coefficients $c_i$ as described in the following Lemma.

Lemma 5.1

[5, Proposition 4.3]

Let $f,t,z\in M^{\mathrm{\infty }}\left(N\right)$, with $\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{d}\left(t\right)\ge 1$ and $gcd\left(\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{d}\right(t),\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{d}(z\left)\right)=1$. Then $d\left(t\right)f=c_0\left(t\right)+c_1\left(t\right)z+\cdots +c_{n-1}\left(t\right)z^{n-1}$ for some polynomials $d\left(x\right),c_i\left(x\right)\in \mathbb{C}\left[x\right]$, $i=0,\dots ,n-1$.

Using the method described in [2, Section 4.1] and implemented in the package QEta,⁴ one can find (and prove!) that (5.1) $\begin{array}{rl}f& :=\frac{\eta \left(\tau {)}^{11}\eta \right(11\tau )}{\eta (121\tau {)}^{11}}{q}^{\frac{13}{24}}\sum _{n=1}^{\mathrm{\infty }}p(11n+6)q^n\\ & \phantom{:}=11q^{-54}+176q^{-53}+935q^{-52}+O\left(q^{-51}\right),\end{array}$(5.1) where $q=q\left(\tau \right)=\exp \left(2\pi \mathrm{i}\tau \right)$, is a modular function for ${\mathrm{\Gamma }}_0\left(121\right)$ with a pole (of order 54) only at infinity.

However, by reducing f by the basis B above we obtain $r=f-11tz=220q^{-53}+880q^{-52}+2640q^{-51}+O\left(q^{-50}\right)\in M^{\mathrm{\infty }}\left(121\right)$ and, therefore, $f\notin M=\mathbb{Q}[t,u]$.

Since the maximal pole order of an element of the basis from (4.5(4.5) $\mathbb{Q}[t,u]={⟨1,z,z^2,z^3,z^4⟩}_{\mathbb{Q}\left[t\right]};$(4.5) ) is $\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{d}\left(z^4\right)=196$, it is possible by (4.1(4.1) $f=\sum _{i=0}^{\ell -1}{c}_i\left(t\right)z_i+r$(4.1) ) to (algorithmically) reduce any element $f\in M^{\mathrm{\infty }}\left(121\right)$ to an element r of pole order $\le 191$.

Let us consider the 192 coefficients of the principal part of the (reduced) elements for $t^{i}f$, for $i=0,\dots ,192$ and put them into a matrix (one row for any element), i.e. the $(i,j)$th entry of the matrix is $\left[q^{-j}\right]\left(t^{i}f\right)$ (i.e. the coefficient of $q^{-j}$ in the q-series expansion of $t^{i}f$). Since there are more rows than columns, it is clear that there must be a $\mathbb{Q}$-linear relation among the rows of this matrix. We can thus find a polynomial $d\in \mathbb{Q}\left[T\right]$ with the property that $d\left(t\right)f$ can be reduced to a modular function with vanishing principal part, i.e. $d\left(t\right)f\in M=\mathbb{Q}[t,u]$.

It turns out that the polynomial d that we have computed can be factored as $d=d_1{d}_2^2{d}_3^2{d}_4{d}_5$ where $\begin{array}{rl}{d}_1& =T^2-11,\\ d_2& =T^2-2T+11,\\ d_3& =T^2-3T+11,\\ d_4& =T^{25}+430T^{24}-31200T^{23}+578905T^{22}-6007240T^{21}+42281581T^{20}\\ & -218350660T^{19}+851271410T^{18}-2472691265T^{17}+4848984855T^{16}\\ & -3205367440T^{15}-18988485230T^{14}+93248895025T^{13}-243431953930T^{12}\\ & +416601090015T^{11}-403942642466T^{10}-112485265695T^9\\ & +1267233014520T^8-2655224484605T^7+3433152350925T^6\\ & -3075192506826T^5+1978532471630T^4-978548291765T^3\\ & +412640845925T^2-129687123005T+25937424601,\\ d_5& =T^{30}-920T^{29}-19225T^{28}+1258030T^{27}-19448535T^{26}+75396538T^{25}\\ & +2157132615T^{24}-50735009930T^{23}+643909614260T^{22}-5980486211480T^{21}\\ & +44473273280260T^{20}-276140775186430T^{19}+1465665176339650T^{18}\\ & -6744922810982730T^{17}+27144546684208910T^{16}-95977332323506700T^{15}\\ & +298590013526298010T^{14}-816135660128910330T^{13}\\ & +1950800349708074150T^{12}-4042977089504521630T^{11}\\ & +7162465135059153260T^{10}-10594796133295720280T^9\\ & +12547976761628658460T^8-10875499956118688330T^7\\ & +5086405868720041965T^6+1955592019551431338T^5\\ & -5548894011786504885T^4+3948237050766319630T^3\\ & -663699140967073475T^2-349369846896581720T+4177248169415651.\end{array}$ Keeping track of the reduction steps of $d\left(t\right)f$ with respect to the basis B from (4.5(4.5) $\mathbb{Q}[t,u]={⟨1,z,z^2,z^3,z^4⟩}_{\mathbb{Q}\left[t\right]};$(4.5) ) then leads to a polynomial of $c(T,Z):=\sum _{k=0}^4{c}_k\left(T\right)Z^k\in \mathbb{Q}[T,Z]$ such that $d\left(t\right)f=c(t,z)$, in other words, we have found another identity for the generating function for $p(11n+6)$ in term of eta-quotients. The polynomial c can be factored to reveal a factor of 11 and the degrees of the $c_k$ are 75, 66, 56, 46, and 36, respectively, see dc.input.

As mentioned above the q-series expansion of z has integer coefficients. Thus the identity reveals and proves divisibility by 11 of $p(11n+6)$ for all $n\in \mathbb{N}$.

With (4.5(4.5) $\mathbb{Q}[t,u]={⟨1,z,z^2,z^3,z^4⟩}_{\mathbb{Q}\left[t\right]};$(4.5) ) we have found an order-complete basis of $M=\mathbb{Q}[t,u]$ with $g_M=96$. The computations described above not only gave us an identity for f, but they also showed that $f\in M^{\mathrm{\infty }}\left(121\right)\setminus \mathbb{Q}[t,u]$.

Adding f to the generators, we can determine an order-complete basis $B^{\left(f\right)}=\left\{b_0^{\left(f\right)},b_1^{\left(f\right)},\dots ,b_4^{\left(f\right)}\right\}$ of $\mathbb{Q}[t,u,f]$, i.e. $\mathbb{Q}[t,u,f]={⟨B^{\left(f\right)}⟩}_{\mathbb{Q}\left[t\right]}$, with respective pole orders 0, 66, 42, 33, 24; see bf.input. Thus, $\mathbb{Q}[t,u,f]$ has gap number 31 and $B^{\left(f\right)}$ is not an integral basis for $M^{\mathrm{\infty }}\left(121\right)$.

Remark

Inspired by the Ramanujan congruence ${11}^2\mid p({11}^{2}n+116)$ one could, for instance, add to the generators the element $\begin{array}{rl}{f}_2& :=\frac{\eta (\tau {)}^{122}}{\eta (121\tau {)}^{121}}{q}^{23/24}\sum _{n=1}^{\mathrm{\infty }}p(121n+116)q^n\in M^{\mathrm{\infty }}\left(121\right)\\ & \phantom{:}=1188908248q^{-604}+83416057119615q^{-603}+O\left(q^{-601}\right).\end{array}$ But this does not lead to a better basis, because $f_2\in \mathbb{Q}[t,u,f]$ which is seen by the relation displayed at f2.input.

6. An integral basis by using the Klein j function

Let us come back to the basis $B^{\left(f\right)}$ computed in Section 5, see bf.input. This basis is not an integral basis, so we must consider to include other elements of $M^{\mathrm{\infty }}\left(121\right)$.

Klein's j-invariant (also called modular invariant or absolute invariant) is a modular function for ${\mathrm{\Gamma }}_0\left(1\right)={\mathrm{S}\mathrm{L}}_2\left(\mathbb{Z}\right)$, $j\left(\tau \right)=q^{-1}+744+196884q+21493760q^2+864299970q^3+O\left(q^{10}\right).$ In the theory of modular functions the j-invariant is fundamental because every modular function can be expressed as a rational function in j. For a definition and further properties of j see, for example, Chapter VII of [12].

We attempt to add more modular functions for ${\mathrm{\Gamma }}_0\left(N\right)$ and call samba in the hope to get an integral basis. We know, for example, that $j\left(\tau \right)$ is a modular function for ${\mathrm{S}\mathrm{L}}_2\left(\mathbb{Z}\right)$ and consequently also for ${\mathrm{\Gamma }}_0\left(N\right)$. Since for $\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\in {\mathrm{\Gamma }}_0\left(N\right)$ we have $j\left(N\frac{a\tau +b}{c\tau +d}\right)=j\left(\frac{a\left(N\tau \right)+Nb}{\left(c/N\right)\left(N\tau \right)+d}\right)=j\left(N\tau \right)$, also $j\left(N\tau \right)$ is a modular function for ${\mathrm{\Gamma }}_0\left(N\right)$.

We multiply $j_0\left(\tau \right):=j\left(\tau \right)$ and $j_2\left(\tau \right):=j\left({11}^2\tau \right)$ by suitable eta-quotients with the goal to arrive at elements in $M^{\mathrm{\infty }}\left(121\right)$. Let us define $j_0^{\mathrm{\infty }}:=t^{25}uj,j_2^{\mathrm{\infty }}:=tu{j}_2,$ where t and u are the eta-quotients defined in (4.2(4.2) $t=\frac{\eta \left(\tau \right)}{\eta \left(121\tau \right)}=q^{-5}-q^{-4}-q^{-3}+O\left(q^{-2}\right),$(4.2) ) and (4.3(4.3) $u=\frac{\eta (11\tau {)}^{12}}{\eta \left(\tau \right)\eta (121\tau {)}^{11}}=q^{-50}+q^{-49}+2q^{-48}+O\left(q^{-47}\right).$(4.3) ), then $j_0^{\mathrm{\infty }},j_2^{\mathrm{\infty }}\in M^{\mathrm{\infty }}\left(121\right)$.

Calling samba from our QEta package with input t, u, $j_0^{\mathrm{\infty }}$, $j_2^{\mathrm{\infty }}$ leads to an order-complete basis $B^{\left(j\right)}=\left\{b_0^{\left(j\right)},\dots ,b_4^{\left(j\right)}\right\}$, with $\mathbb{Q}[t,u,j_0^{\mathrm{\infty }},j_2^{\mathrm{\infty }}]={⟨B^{\left(j\right)}⟩}_{\mathbb{Q}\left[t\right]}$ where $\begin{array}{rl}{b}_0^{\left(j\right)}& =1,\\ b_1^{\left(j\right)}& =q^{-16}+2q^{-4}+q^{-3}+q^{-1}+O\left(q^2\right),\\ b_2^{\left(j\right)}& =q^{-7}+q^{-6}-q+q^3+q^4-q^9+O\left(q^{11}\right),\\ b_3^{\left(j\right)}& =q^{-8}+q^{-6}+q^{-2}-q+q^3+q^5+O\left(q^{10}\right),\\ b_4^{\left(j\right)}& =q^{-9}-q^{-3}+q^{-1}+q^2-q^6-q^7+O\left(q^9\right);\end{array}$ i.e. $\mathbb{Q}[t,u,j_0^{\mathrm{\infty }},j_2^{\mathrm{\infty }}]$ has gap number 6. In other words, $B^{\left(j\right)}$ is an integral basis for $M^{\mathrm{\infty }}\left(121\right)=\mathbb{Q}[t,u,j_0^{\mathrm{\infty }},j_2^{\mathrm{\infty }}]$.

We were also able to compute the representation of the elements of $B^{\left(j\right)}$ in terms of the original functions t, u, $j_0$ and $j_2$, but these polynomials are too big to be presented in this article; see bj.input on our website.

Since $B^{\left(j\right)}$ is an integral basis for $M^{\mathrm{\infty }}\left(121\right)$, we can construct a polynomial $p^{\left(j\right)}\in \mathbb{Q}[T,U,J_0,J_2]$ such that $f=p^{\left(j\right)}(t,u,j_0,j_2)$ by reducing f with respect to $B^{\left(j\right)}$ and keeping track of the cofactors of this reduction, see fj.input. Unfortunately, this relation cannot be used to demonstrate $11\mid p(11n+6)$.

7. An integral basis obtained with the trace map

We can generate a new modular function by applying the trace operator to a modular function from $M^{\mathrm{\infty }}\left(242\right)$.

The trace ${\mathrm{t}\mathrm{r}}_{121}^{242}:M^{\mathrm{\infty }}\left(242\right)\to M^{\mathrm{\infty }}\left(121\right)$ is given through the Atkin-Lehner involution, see, for example, Equation (1) in [8].

In our case we have $f|{\mathrm{t}\mathrm{r}}_{121}^{242}=f+2f|W_2^{242}|U_2$ where $W_2^{242}=\left(\begin{array}{cc}2& -1\\ 242& -120\end{array}\right)$ is the matrix corresponding to the Atkin-Lehner involution, and $U_2$ is the operator on functions $\phi :\mathbb{H}\to \mathbb{C}$ so that $\left(\phi |U_2\right)\left(\tau \right):=\frac{\phi \left(\frac{\tau }{2}\right)+\phi \left(\frac{\tau +1}{2}\right)}{2}.$ For concrete computations with such trace maps the reader is referred to [7]. Here we only remark that if $\phi \left(\tau \right)=\sum _{n\ge m}c\left(n\right)q^n$, $q=\exp \left(2\pi \mathrm{i}\tau \right)$, is the q-series expansion of φ, then the effect of the action of $U_2$ is $\left(\phi |U_2\right)\left(\tau \right)=\sum _{n\ge \lceil m/2\rceil }c\left(2n\right)q^n.$ Also, notice that the action of $W_2^{242}$ is defined via the slightly more general action of the general linear group ${\mathrm{G}\mathrm{L}}_2\left(\mathbb{Z}\right)$: for all $\gamma =\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\in {\mathrm{G}\mathrm{L}}_2\left(\mathbb{Z}\right)$, $\left(f|\gamma \right)\left(\tau \right):=f\left(\gamma \tau \right)=f\left(\frac{a\tau +b}{c\tau +d}\right).$ Similar to the computation of (4.2(4.2) $t=\frac{\eta \left(\tau \right)}{\eta \left(121\tau \right)}=q^{-5}-q^{-4}-q^{-3}+O\left(q^{-2}\right),$(4.2) ) and (4.3(4.3) $u=\frac{\eta (11\tau {)}^{12}}{\eta \left(\tau \right)\eta (121\tau {)}^{11}}=q^{-50}+q^{-49}+2q^{-48}+O\left(q^{-47}\right).$(4.3) ), Radu's algorithm [2] yields 94 eta-quotients ${\overline{m}}_1,\dots ,{\overline{m}}_{94}$ as a complete set of monoid generators of $E^{\mathrm{\infty }}\left(242\right)$; i.e. $\mathbb{Q}\left[E^{\mathrm{\infty }}\right(242\left)\right]=\mathbb{Q}[{\overline{m}}_1,\dots ,{\overline{m}}_{94}]$.

There are $g_2,h_2\in \left\{{\overline{m}}_1,\dots ,{\overline{m}}_{94}\right\}$ such that $\begin{array}{rl}{g}_2\left(\tau \right)& =\frac{\eta \left(2\tau {)}^2\eta \right(121\tau )}{\eta \left(\tau \right)\eta \left(242\tau \right)}=q^{-15}+q^{-14}+O\left(q^{-12}\right),\\ h_2\left(\tau \right)& =\frac{\eta \left(\tau {)}^6\eta \right(22\tau \left)\eta \right(121\tau {)}^5}{\eta \left(2\tau {)}^3\eta \right(11\tau \left)\eta \right(242\tau {)}^8}=q^{-55}-6q^{-54}+12q^{-53}+O\left(q^{-52}\right).\end{array}$ By exploiting the modular transformation properties it is straight-forward to compute the q-expansions $\begin{array}{rl}g\left(\tau \right)& :=\left(g_2|{\mathrm{t}\mathrm{r}}_{121}^{242}\right)\left(\tau \right)=q^{-15}+q^{-14}+O\left(q^{-12}\right),\\ h\left(\tau \right)& :=\left(h_2|{\mathrm{t}\mathrm{r}}_{121}^{242}\right)\left(\tau \right)=q^{-55}-6q^{-54}+O\left(q^{-53}\right).\end{array}$ We first apply samba to the input t, u, and g, where t and u are defined in (4.2(4.2) $t=\frac{\eta \left(\tau \right)}{\eta \left(121\tau \right)}=q^{-5}-q^{-4}-q^{-3}+O\left(q^{-2}\right),$(4.2) ) and (4.3(4.3) $u=\frac{\eta (11\tau {)}^{12}}{\eta \left(\tau \right)\eta (121\tau {)}^{11}}=q^{-50}+q^{-49}+2q^{-48}+O\left(q^{-47}\right).$(4.3) ). That leads to an order-complete basis $B^{\left(g\right)}$ with gap number 8 for the module $\mathbb{Q}[t,u,g]$; i.e. we still did not succeed to obtain an integral basis for $M^{\mathrm{\infty }}\left(121\right)$; see bg.input.

However, since the reduction of f with respect to that basis yields non-zero, in fact, a series of pole order 8, we call samba with input t, u, f, and g and arrive at an integral basis $B^{\left(fg\right)}$ for $M^{\mathrm{\infty }}\left(121\right)$; see bfg.input

Alternatively, we also arrive at an integral basis $B^{\left(h\right)}$ for $M^{\mathrm{\infty }}\left(121\right)$, if we call samba with input t, u, and h; see bh.input. Similar to the computation of the polynomial d in Section 5, we can compute a polynomial $d^{\ast }\in \mathbb{Q}\left[T\right]$ with $d^{\ast }\left(t\right)h\in M=\mathbb{Q}[t,u]$. In addition to the factors of d in Section 5, $d^{\ast }$ has one more factor, $d_6$; i.e. we have $d^{\ast }=d_1{d}_2^2{d}_3^2{d}_4{d}_5{d}_6$ where $\begin{array}{rl}{d}_6& =T^{25}-55T^{24}+1925T^{23}-50215T^{22}+1116830T^{21}-19094526T^{20}\\ & +234488925T^{19}-1994909455T^{18}+10473000120T^{17}-10225933245T^{16}\\ & -403942642466T^{15}+4582611990165T^{14}-29455266425530T^{13}\\ & +124114279278275T^{12}-278010412252430T^{11}-516227631579440T^{10}\\ & +8590272458708655T^9-48185757511261315T^8+182477586874892210T^7\\ & -514859434575326060T^6+1096675319198574181T^5\\ & -1713935680161223640T^4+1816851879425670505T^3\\ & -1077108618890647200T^2+163292428440793630T+4177248169415651.\end{array}$ See ds.input on our website.

That the additional polynomial $d_6$ appears is, in fact, not a surprise, but can be explained by the following Theorem 7.1. It is a factor of the discriminant (wrt. y) of a polynomial $p(x,y)$ such that $p(t,z)=0$, see dz.input.

Theorem 7.1 is an extension of Lemma 5.1 in the sense that we do not just claim the existence of a polynomial $d\left(x\right)$, but rather state that choosing the discriminant (see exact formulation in the theorem) will work for any $f\in M^{\mathrm{\infty }}\left(N\right)$.

Theorem 7.1

Let $f,t,z\in M^{\mathrm{\infty }}\left(N\right)$, with $\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{d}\left(t\right)\ge 1$ and $gcd\left(\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{d}\right(t),\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{d}(z\left)\right)=1$. Let $p(x,y)=y^n+p_{n-1}\left(x\right)y^{n-1}+\cdots +p_1\left(x\right)y+p_0\left(x\right)\in \mathbb{C}[x,y]$ be the minimal polynomial between t and z, that is $p(t,z)=0$. Let $D\left(x\right)={\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{c}}_y\left(p\right(x,y\left)\right)$ be the usual discriminant of $p(x,y)$ with respect to y. Then $D\left(t\right)f=c_0\left(t\right)+c_1\left(t\right)z+\cdots +c_{n-1}\left(t\right)z^{n-1}$ for some polynomials $c_i\left(x\right)\in \mathbb{C}\left[x\right]$, $i=0,\dots ,n-1$.

Proof.

Note that the existence of such a monic polynomial $p(x,y)$ is given by Lemma 1.1. Definition 7.1 of [5] defines the discriminant polynomial $D_t\left(z\right)\left(x\right)$ for an order-complete basis $\left\{1,z,\dots ,z^{n-1}\right\}$ of the $\mathbb{C}\left[t\right]$-module $\mathbb{C}[t,z]$. In that definition we see that the discriminant is the square of the determinant of a certain Vandermonde matrix: $\mid V(z_1^{\ast },\dots ,z_n^{\ast }){\mid }^2$. By comparing the definition of the entries $z_i^{\ast }$ in [5] with the definition of $F\circ (G|U_i{)}^{-1}$ in the proof of Theorem 7.1 of [7], we observe that they coincide. However, in that paper G corresponds to $t^{\ast }$ and F to $z^{\ast }$ where $t^{\ast }$ and $z^{\ast }$ denote the functions $X_0\left(N\right)\to \hat{\mathbb{C}}$ corresponding to t and z, see Remark 5.1 in [5]. Furthermore, in the proof of Theorem 7.1 of [7] it is also shown that the symmetric functions are exactly the coefficients of the polynomial $p(t^{\ast },y)$, i.e. $p_{n-i}\left(t^{\ast }\right)=(-1{)}^i{e}_i(z_1^{\ast },\dots ,z_n^{\ast })$, $i=1,\dots ,n-1$. By considering modular functions instead of functions $X_0\left(N\right)\to \hat{\mathbb{C}}$, we can remove the star and, therefore, $p(t,y)=(y-z_1)(y-z_2)\cdots (y-z_n)$. We see that by definition ${\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{c}}_y\left(p\right(t,y\left)\right)=\prod _{i<j}(z_i-z_j{)}^2$ which coincides with $\mid V(z_1,..,z_n){\mid }^2$ and also with $D\left(t\right)$.

As described in Section 4 of [5], we can by successive pole-order-reduction steps transform the initial order-complete basis $B_0=\left\{1,z,\dots ,z^{n-1}\right\}$ into an integral basis $B_r=\left\{1,{\text{β}}_1,\dots ,{\text{β}}_{n-1}\right\}$ for $M^{\mathrm{\infty }}\left(N\right)$, see in particular [5, Proposition 4.6].

In the $k$th step of this process one replaces the order-complete basis $B_{k-1}=\left\{1,b_1,\dots ,b_{n-1}\right\}$ with another order-complete basis $B_k=\left\{1,b_1,b_2\dots ,b_{s-1},h_{\alpha },b_{s+1},\dots ,b_{n-1}\right\}$ where $h_{\alpha }=({\alpha }_0+{\alpha }_1{b}_1+{\alpha }_2{b}_2+\cdots +{\alpha }_n{b}_{n-1})/(t-\alpha )$ for some $\alpha ,{\alpha }_i\in \mathbb{C}$, i.e. $\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{d}\left(h_{\alpha }\right)<\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{d}\left(b_s\right)$.

The discriminant polynomials $D_t\left(z\right)\left(x\right)=D_t(z,z^2,\dots ,z^{n-1})\left(x\right)$ is a special case of the concept of an order-reduction polynomial $D_t(b_1,\dots ,b_{n-1})\left(x\right)\in \mathbb{C}\left[x\right]$, see [5, Definition 5.3]. By [5, Proposition 8.1] we have the following relation $D_t(b_1,b_2\dots ,b_{s-1},h_{\alpha },b_{s+1},\dots ,b_{n-1})\left(x\right)=\frac{c_s^2}{(x-\alpha {)}^2}{D}_t(b_1,\dots ,b_{n-1})\left(x\right)$ for some $c_s\in \mathbb{C}\setminus \left\{0\right\}$, i.e. $(x-\alpha {)}^2$ divides the discriminant $D\left(x\right)$. Collecting all the $(x-\alpha )$ factors accordingly, we can express the elements ${\text{β}}_i$ of the final integral basis as follows: (7.1) ${\text{β}}_i=\left(p_{i0}\right(t)+p_{i1}(t)z+p_{i2}(t)z^2+\cdots +p_{i,n-1}(t\left)z^{n-1}\right)/q_i\left(t\right)$(7.1) for some $p_{ij}\left(x\right),q_i\left(x\right)\in \mathbb{C}\left[x\right]$ with $gcd\left(p_{i0}\right(x),\dots ,p_{i,n-1}(t),q_i(t\left)\right)=1$. By construction, $q_i\left(x\right)$ divides the discriminant $D\left(x\right)$.

Since $f\in M^{\mathrm{\infty }}\left(N\right)$ and $B_r=\left\{1,{\text{β}}_1,\dots ,{\text{β}}_{n-1}\right\}$ is an integral basis for $M^{\mathrm{\infty }}\left(N\right)$, we can write $f=h_0\left(t\right)+h_1\left(t\right){\text{β}}_1+\cdots +h_{n-1}\left(t\right){\text{β}}_{n-1}$ for some polynomials $h_i\left(x\right)\in \mathbb{C}\left[x\right]$. Replacing the ${\text{β}}_i$ by their respective representation given by (7.1(7.1) ${\text{β}}_i=\left(p_{i0}\right(t)+p_{i1}(t)z+p_{i2}(t)z^2+\cdots +p_{i,n-1}(t\left)z^{n-1}\right)/q_i\left(t\right)$(7.1) ) and multiplying by the discriminant $D\left(x\right)$, we see that $D\left(t\right)f=c_0\left(t\right)+c_1\left(t\right)z+\cdots +c_{n-1}\left(t\right)z^{n-1}$ as claimed by the theorem.

8. An integral basis by using Maple's algcurves

In this section we explain a third method to obtain an integral basis for $M^{\mathrm{\infty }}\left(121\right)$; namely, by using the Maple package algcurves. By using (4.5(4.5) $\mathbb{Q}[t,u]={⟨1,z,z^2,z^3,z^4⟩}_{\mathbb{Q}\left[t\right]};$(4.5) ) and Lemma 1.1, together with Prop. 3.5 and Prop. 4.3 in [5] one can prove in a fairly straightforward fashion that $M^{\mathrm{\infty }}\left(121\right)=\left\{\phi \in \mathbb{C}(t,z)\left|\phantom{\phi \in \mathbb{C}(t,z)}\phi \mathrm{i}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}\mathbb{C}\left[t\right]\right.\right\}$ where $z:=\frac{1}{11}(u-t^{10})$. Note that $gcd\left(\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{d}\right(z),\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{d}(t\left)\right)=gcd(49,5)=1$, so Prop. 3.5 applies. However $\mathbb{C}(t,z)=\mathbb{C}(t,u)$. Hence $M^{\mathrm{\infty }}\left(121\right)=\left\{\phi \in \mathbb{C}(t,u)\left|\phantom{\phi \in \mathbb{C}(t,u)}\phi \mathrm{i}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}\mathbb{C}\left[t\right]\right.\right\}.$ Next note that $\mathbb{C}(t,u)$ is isomorphic to $\mathbb{C}(T,U)/\left(p\right(T,U\left)\right)$, were $p(T,U)$ is the minimal polynomial such that $p(t,u)=0$. This polynomial can be found at p.maple. To compute the set of all integral elements $g\in \mathbb{C}(T,U)/\left(p\right(T,U\left)\right)$ we can use Mark van Hoeij's Maple package algcurves via

This returns the basis $\left\{1,U,U^2,U^3,v(T,U)\right\}$ where v is a rational function in T and U that is rather huge; see v.input. The q-series expansion of $v(t,u)$ has pole order 1670.

By specification of Maple's integral_basis function (see [13]) we know that all $\phi \in \mathbb{C}(t,u)$ that are integral over $\mathbb{C}\left[t\right]$, i.e. all elements $\phi \in M^{\mathrm{\infty }}\left(121\right)$, can be expressed in the form $\phi =p_0\left(t\right)+p_1\left(t\right)u+p_2\left(t\right)u^2+p_3\left(t\right)u^3+p_4\left(t\right)v(t,u)$ where $p_i\left(T\right)\in \mathbb{C}\left[T\right]$, $i=0,\dots ,4$. However, the basis $\left\{1,u,u^2,u^3,v(t,u)\right\}$ is not order-complete. In order to make this basis order-complete, we apply the samba algorithm to t, u, $u^2$, $u^3$, $v(t,u)$. This computation takes about 30 minutes and yields a basis $B^{\left(v\right)}=\left\{1,b_1^{\left(v\right)},\dots ,b_4^{\left(v\right)}\right\}$. Note that if also the non-leading terms of the q-expansion of the basis elements are reduced by the other basis elements, then $B^{\left(v\right)}$ agrees with the basis $B^{\left(j\right)}$ computed in Section 6.

Since $b_i^{\left(v\right)}\in M^{\mathrm{\infty }}\left(121\right)$, we have $b_i^{\left(v\right)}=p_{i,0}\left(t\right)+p_{i,1}\left(t\right)u+p_{i,2}\left(t\right)u^2+p_{i,3}\left(t\right)u^3+p_{i,4}\left(t\right)v(t,u).$ Unfortunately, we cannot give the explicit form of the $p_{i,j}\left(T\right)\in \mathbb{Q}\left[T\right]$, because they are too big and therefore only listed on our website in the file bv.input. However, we give their degree for the reader to get an idea. We define the matrix $A=(a_{i,j}{)}_{i\in \{1,\dots ,4\},j\in \{0,\dots ,4\}}$, where $a_{i,j}:={\mathrm{deg}}_T\left(p_{i,j}\right(T\left)\right)$ and $A=\left(\begin{array}{ccccc}358& 358& 358& 358& 54\\ 356& 356& 356& 356& 52\\ 356& 356& 356& 356& 52\\ 356& 356& 356& 356& 52\end{array}\right).$

9. Conclusion

There exist already several identities for expressing $\sum p(11n+6)q^n$ in terms of eta-quotients. In [3] we gave a relation in terms of eta-quotients for ${\mathrm{\Gamma }}_0(2\cdot 11)$. Initially, our goal was to get rid of the factor 2, which in this context seems unnatural, and try to work with eta-quotients for ${\mathrm{\Gamma }}_0(11\cdot 11)$. As shown in Section 5, f cannot be expressed in that way. However, it is possible to find a polynomial d such that $d\left(t\right)f$ indeed is a sum of eta-quotients from $M^{\mathrm{\infty }}\left(121\right)$.

The wish to avoid such a polynomial prefactor d in turn led us to attempts to express f by other functions, like the Klein j invariant, an eta-quotient from $M^{\mathrm{\infty }}\left(242\right)$, and a modular function $v(t,u)$ coming from the output of van Hoeij's Maple package. Any of these additions not only gave us a way to express f, but, more generally, a way way to compute an integral basis B such that any function of $\phi \in M^{\mathrm{\infty }}\left(121\right)$ can be expressed as a $\mathbb{C}\left[t\right]$-linear combination of elements of B. Moreover, in contrast to the basis returned by van Hoeij's Maple package, our basis can be used to algorithmically find polynomials $p_b\in \mathbb{Q}\left[t\right]$ with $\phi =\sum _{b\in B}{p}_p\left(t\right)b$.

Acknowledgments

Paule and Radu were supported by grant SFB F50-06 of the Austrian Science Fund (FWF). We thank the anonymous referees for their comments and careful reading of our manuscript.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

Paule and Radu were supported by grant SFB F50-06 of the Austrian Science Fund (FWF).

Notes

1 FriCAS 1.3.2 [14].

2 QEta 2.1 [15].

3 Sage 8.0 [16].

4 The Mathematica package RaduRK by Nicolas A. Smoot (see [17]) also implements this method.