Design of radiant enclosures using inverse and non-linear programming techniques

Abstract

Traditionally, radiant enclosures have been designed using a forward “trial-and-error” methodology. Recently, however, inverse and optimization methodologies have been applied to design radiant enclosures. Both of these methodologies solve the design problem faster, and the quality of the solutions is usually better than those obtained through the forward design methodology. This article presents forward, inverse, and optimization formulations of the infinitesimal-area method that can be used to solve design problems involving radiant enclosures. The inverse and optimization methodologies are then demonstrated and compared by using them to design a 2-D radiant enclosure containing a transparent medium.

Keywords:

• Thermal radiation
• Enclosure
• Inverse
• Optimization
• Design

1. Introduction

The design of radiant enclosures is a very common and difficult problem encountered in thermal engineering. Most often, the objective is to irradiate a design surface with heater surfaces located elsewhere in the enclosure. For example, the design surface may consist of semiconductor wafers that need to be processed, food products that need to be baked, or a coated surface that needs to be dried or cured. The heater settings, which control the heat flux distribution over the heater surface, must be chosen to achieve the desired temperature and heat flux distributions over the design surface. The main difficulty in this analysis is that, for the problem to be mathematically well-posed, only one thermal boundary condition can be specified over each surface. In this sense, the problem (like most design problems) is an inverse problem.

Until recently, a forward design methodology has been exclusively used to treat radiant enclosures. In this methodology, the designer first specifies the temperature distribution over the design surface and then guesses heater settings that might produce the desired heat flux distribution, as shown in Fig. 1(a). The resulting mathematical problem is well-posed, and the unknown boundary conditions are easily found by solving the corresponding well-conditioned set of linear equations using standard linear algebra techniques. Unfortunately, the heat flux distribution realized over the design surface rarely matches the desired distribution, so the designer must adjust the heater settings and repeat the analysis; this process continues until an acceptable solution is found. This usually requires many iterations, and although the final solution might be satisfactory, it is rarely optimal.

FIGURE 1 Boundary conditions for different design methodologies: (a) forward; (b) inverse; (c) optimization.

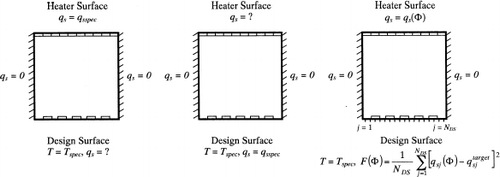
Two alternative methods have been developed that overcome the shortcomings of the forward design technique. In the inverse design technique, the designer specifies both the temperature and the heat flux distributions over the design surface, while the heater settings remain unspecified, as shown in Fig. 1(b). (This is the explicit formulation of the inverse problem, since both boundary conditions over the design surface are explicitly enforced.) The resulting problem is mathematically ill-posed, and special numerical techniques must be employed to solve the corresponding set of ill-conditioned linear equations. These methods only require a single iteration to find a solution, although it is sometimes a non-physical one. Harutunian et al. [1] first used inverse methods to design a 2-D radiant enclosure consisting of diffuse-grey walls and containing a transparent medium. This technique has since been applied to design enclosures containing participating media [2], specularly reflecting surfaces [3], and multimode heat transfer effects [4].

Recently, optimization methods have also been adopted to design radiant enclosures. These methods work by minimizing an objective function, F(Φ), that is defined in such a way that the minimum of the objective function corresponds to the ideal design configuration. The minimization is accomplished by iteratively varying a set of design parameters, Φ, that control the system configuration; in this application, the design parameters control the heat flux distribution over the heater surface. In the optimization design technique, the inverse design problem is solved in its implicit form, since only one of the two known boundary conditions is enforced over the design surface. As shown in Fig. 1(c), the designer first specifies the temperature distribution over the design surface, while the objective function is defined as the variance between the desired heat flux distribution and the heat flux distribution produced by a particular set of heater settings, evaluated at N _DS discrete points over the design surface. The objective function is then minimized using specialized numerical algorithms, which make intelligent perturbations to the heater settings at each iteration based on the local topography of F(Φ). In this way, the heater settings that produce the desired heat flux and temperature distribution are quickly identified. Optimization has only recently been applied to design radiant enclosures; Fedorov et al. [5] and Daun et al. [6] used optimization methods to determine the heater settings that produce the desired heat flux and temperature distribution over the design surface of a radiant enclosure. Daun et al. [7] also used these methods to solve for the geometry of a diffuse-walled enclosure that results in a desired radiosity distribution over the design surface.

The purpose of this article is to demonstrate how inverse and optimization methods are used to design radiant enclosures. Both techniques presented here are based on the infinitesimal-area method developed by Daun and Hollands [8], and are in a format appropriate for the analysis of 2-D radiant enclosures. The inverse design problem is solved by truncated singular value decomposition (TSVD), while the optimization is carried out using Newton minimization. The forward design methodology is first presented followed by the inverse and optimization methodologies, respectively. Finally, the inverse and optimization design methodologies are demonstrated and compared by applying them to design a 2-D radiant enclosure.

2. Forward Design Methodology

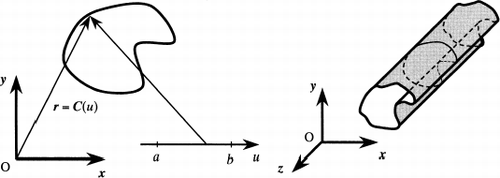
The forward design methodology is based on the infinitesimal-area technique of Daun and Hollands [8]. The first step in the analysis is to identify a suitable parametric representation for the enclosure geometry. In particular, the enclosure geometry is defined by

where r is the position vector and C (u) = {P(u), Q(u)} ^T is a vector function of parameter u with components P(u) and Q(u) in the x- and y-directions, respectively. By allowing u to range over its entire domain, a ≤ u ≤ b, the position vector carves out the shape and extent of the enclosure surface, as shown in Fig. 2. The boundary conditions are also expressed parametrically; the emissivity distribution, ε(u), is specified, and either the heat flux, q _s (u), or the temperature, T(u), is known at every location on the enclosure surface. Here, it is assumed that T(u) is specified over the design surface and q _s (u) is known over the heater surface.

FIGURE 2 Parametric representation of the enclosure geometry.

Once the enclosure is represented parametrically, the equation governing the radiosity distribution can be formed. The radiosity distribution is governed by a Fredholm integral equation of the second kind,

where, if T(u) is known,

with E _b (u) = σT ⁴(u), or if q _s (u) is known,

The kernel of Eq. (2), k(u, u ′), represents the differential view factor from a point on the enclosure surface corresponding to u to an infinitesimal strip element centred at u ′, divided by du ′.

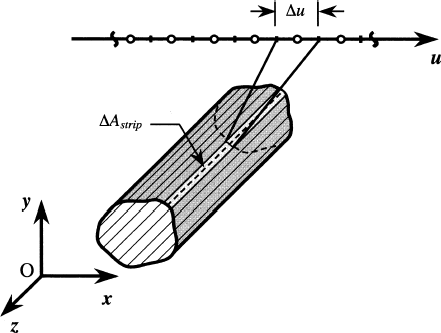
Analytical solutions to integral equations are usually not tractable, so Eq. (2) must be solved numerically. The first step is to discretize the parametric domain into N elements, with the ith element centered at u _i with a width Δu _i . Each of these discrete elements corresponds to an infinitely long strip of finite width on the enclosure surface, as shown in Fig. 3. If the radiosity is assumed to be uniform over these strips, Eq. (2) can be rewritten in discrete form,

where q _oi = q _o (u _i ), b _i = b(u _i ), g _i = g(u _i  ), and dF _{i − strip  j} represents the view factor from a point on the enclosure surface at u _i to the strip element centred at u _j . The blockage factor, β _ij , is a binary term equal to zero if the path between u _i and u _j is obstructed by an intervening surface, and is otherwise equal to unity. It is found either through analytical geometry or by ray-tracing. Writing Eq. (5) for all the elements results in a system of N equations containing N unknowns, which can be rewritten as a matrix equation

where x = {q _o1, q _o2,…, q _{o N} } ^T , b = {b ₁, b ₂, …, b _N } ^T , and

The radiosity distribution is found by solving Eq. (6) using standard numerical linear algebra techniques. Once this has been done, the heat flux distribution over the design surface is calculated by post-processing the radiosity solution

where q _si = q _s (u _i ). If the resulting heat flux distribution differs from the desired distribution, the heater settings are adjusted and the analysis is repeated. This process continues until the heat flux distribution over the design surface matches within an acceptable tolerance, which usually requires many manual iterations to accomplish.

FIGURE 3 Discretization of the enclosure surface.

3. Inverse Design Methodology

In contrast to the forward design methodology where only one thermal boundary condition is specified over each surface, the inverse design method enforces both the temperature and heat flux distributions over the design surface, while the boundary conditions over the heater surface remain unspecified.

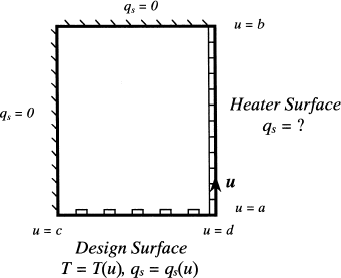
Suppose that the enclosure surface is parameterized so that a ≤ u<b corresponds to the heater surface, b ≤ u<c corresponds to surfaces where either q _s (u) or E _b (u) is known, and c ≤ u<d corresponds to the design surface. Such an enclosure is shown in Fig. 4. First, the radiosity distribution over the design surface is found immediately from

As in the forward methodology, the radiosity distribution over the remaining surfaces is governed by Eq. (2). In this case, however, the integral is rewritten as two integrals; over the heater surface, the radiosity distribution is governed by

while for the remaining enclosure surfaces,

where b(u) and g(u) are again defined by Eqs. (3) or (4) depending on whether u lies on a surface where T(u) or q _s (u) is known, respectively. In both cases, the integral on the right hand side can be solved since q _o (u) is known over the design surface, for c ≤ u<d.

FIGURE 4 Example of an inverse radiant enclosure problem.

Analytical solutions to Eqs. (10) and (11) are usually not tractable, so a numerical technique must be used to solve the radiosity distribution. As before, the parametric region is discretized to form N elements. Let elements i = 1, … , k correspond to the heater surface, elements i = k + 1, … , m correspond to the surfaces where either q _s (u _i ) or T(u _i ) is known, and elements i = m + 1, … , N correspond to the design surface, where q _o (u _i ) is known. By assuming a uniform radiosity distribution over each element, Eqs. (10) and (11) can be rewritten in discrete form:

for elements over the heater surface, and

for all other elements.

Writing Eqs. (12) and (13) for the elements with unknown radiosities, i = 1, …, m, results in a system of m linear equations containing m + k unknowns, the extra k unknowns due to the unknown heat flux terms in Eq. (12). As before, these equations can be rewritten as a matrix equation,

where A is a rectangular matrix consisting of m rows and m + k columns and x contains all the unknown radiosity terms, q _oi for i = 1, …,m, as well as the unknown heat flux terms from the heater surface, q _si for i = 1, …, k. Vector b is formed from the known radiosity terms from the design surface, q _oi for i = m + 1, …, N, and the specified boundary conditions (either q _si or ε _i E _bi ) from the other surfaces.

Since there are more unknowns than equations, matrix A admits an infinite number of solutions so traditional linear algebra techniques cannot be used to solve Eq. (14). Instead, special regularization techniques are employed to select solutions with desirable properties from this infinite set, in general by minimizing the norm of x . These include Tikhonov regularization, conjugate gradient regularization, and truncated singular value decomposition (TSVD); Hansen [9] describes these techniques in detail. Although each of these methods can be used in the present application, TSVD offers the most insight into the nature of the problem and is thus demonstrated here.

The TSVD method is based on the singular value decomposition of the A matrix,

where U is an orthogonal matrix with m rows and m + k columns, W is a diagonal matrix with m + k rows and columns, and V is the transpose of an (m + k) × (m + k) orthogonal matrix. The diagonal elements of W, w _i , are the singular values of matrix A and are either positive or zero. If A were well-conditioned, then Eq. (14) could be solved by

Since A contains k more columns than rows, however, at least k singular values will be equal to zero and Eq. (16) cannot be used. (This is, in fact, why traditional linear algebra techniques cannot be used to invert a singular matrix.) In TSVD, singular values that are smaller than a user-defined criterion are negated (or truncated) by setting the corresponding 1/w _i terms equal to zero. If few singular values are truncated, the radiosity and heat flux distributions usually have very irregular distributions; moreover, the solution is quite often non-physical because the radiosity and emissive power assume local values less than zero. As more singular values are truncated, the radiosity and heat flux distributions become more regular and a feasible solution to the design problem is usually found. Truncating singular values is done at the expense of introducing a residual error into the solution, δ = A x − b , but if few singular values are truncated the magnitude of δ is usually small compared to that of x . This is demonstrated later in the article.

4. Optimization Methodology

Unlike the methods discussed in the previous section, optimization methods solve a well-posed “forward” design problem using sophisticated techniques that limit the number of times the radiosity distribution must be calculated in order to find a viable solution to the design problem. The goal of design optimization is to minimize an objective function, F(Φ), by varying a set of design parameters contained in vector Φ that specify the design configuration. The objective function is defined so that the optimum design configuration corresponds to the set of design parameters, Φ^*, that minimizes F(Φ), F(Φ^*) = Min[F(Φ)]. In this application, the objective function is set equal to the variance between the desired heat flux distribution and the heat flux distribution realized with particular heater settings, evaluated at N _DS discrete points over the design surface:

The design parameters contained in Φ are the heater settings that control the heat flux distribution over the heater surface. The heater settings that produce the heat flux distribution that best matches the desired distribution over the design surface are contained in Φ^*, which is found by minimizing F(Φ).

Many different techniques have been developed to minimize objective functions. Gradient-based methods are most often used when the objective function is continuously differentiable. These methods find Φ^* iteratively; at the kth iteration, a search direction p _k is first chosen based on the local curvature of F(Φ _k ). Next, a step size α _k isre the heater settings that control the heat flux distribution over the heater surface. The heater settings that produce the heat flux distribution that best matches the desired distribution over the design surface are contained in Φ^*, which is found by minimizing F(Φ).

Many different techniques have been developed to minimize objective functions. Gradient-based methods are most often used when the objective function is continuously differentiable. These methods find Φ^* iteratively; at the kth iteration, a search direction p _k is first chosen based on the local curvature of F(Φ _k ). Next, a step size α _k is iteratively; at the kth iteration, a search direction p _k is first chosen based on the local curvature of F(Φ _k ). Next, a step size α _k is calculated, usually by performing a univariate (line) minimization on F(Φ _k + α _k p _k ) using Newton–Raphson, bisection, or golden section techniques. The new set of design parameters are then found by taking a “step” in the p _k direction:

Gradient-based methods differ on how p _k is chosen. Almost all methods use the first-order sensitivities contained in the gradient vector, g (Φ), where and some methods also use the second-order sensitivities contained in the Hessian matrix, H(Φ), where Gill et al. [10] provide an excellent summary of gradient-based optimization methods.

In this application Newton's method is used to minimize the objective function. The search direction is found by solving the equation

Compared to other gradient-based minimization methods, Newton's method usually requires the fewest iterations to find Φ^*, since both first- and second-order curvature information is used to find p _k . This does not mean, however, that Newton's method is always the most efficient, since extra computational effort is required at each iteration to find the Hessian matrix and to solve Eq. (19) for p _k . Newton's method should only be used if the second-order objective function sensitivities can be calculated in an efficient way.

The first step in calculating g (Φ) and H(Φ) is to rewrite the objective function so that it is dependent on the design parameters as well as an intermediate “system response” variable, which in turn is a function of the design parameters. In this application, the objective function is rewritten as

where the system response, q _s (Φ), is a vector that contains the heat flux evaluated at discrete locations over the enclosure surface. The first- and second-order design sensitivities are found by differentiating Eq. (20) with respect to a particular design parameter. Using the objective function defined in Eq. (17), the terms in the gradient vector are given by

and the terms in the Hessian matrix are given by

Clearly, the most difficult part of finding g (Φ) and H(Φ) lies in calculating the heat flux sensitivities. In this application, the most efficient way to do this is by differentiating the governing equations to find the radiosity sensitivities, which are then used to find the heat flux sensitivities. The governing equation is rewritten here to demonstrate the functional dependence of the radiosity distribution on the design parameters; assuming that the surface emissivity and geometry are independent of Φ, the radiosity distribution is governed by

Differentiating Eq. (23) with respect to the design parameters results in two other Fredholm integral equations of the second kind,

and

By following steps analogous to those used to solve Eq. (2), it can be shown that the first- and second-order radiosity sensitivities are found by solving

and

respectively, where A is defined by Eq. (7), and If A has already been decomposed to solve the radiosity distribution, the radiosity sensitivities are easily found by post-processing.

Once the radiosity sensitivities are calculated, the heat flux sensitivities are solved by substituting the radiosity sensitivities into the partial derivatives of Eq. (8),

and

Finally, g (Φ) and H(Φ) are formed by substituting the heat flux sensitivities into Eqs. (21) and (22).

5. Demonstration of Design Methodologies

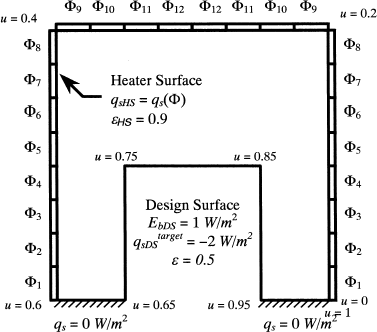
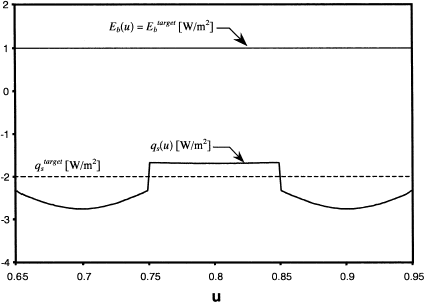
The inverse and optimization design methodologies are used to solve the design problem shown in Fig. 5. The goal of the analysis is to produce a uniform emissive power of E _b = 1 W/m² and a uniform heat flux of over the design surface, using 24 heaters located on three heater surfaces. Since the heat flux is uniform over each heater, and because the problem is symmetric, only twelve variables are required to fully characterize the heat flux distribution over the heater surface. These variables are denoted Φ _k , for k = 1, … , 12, where Φ _k is equal to the heat flux over the kth heater in units of W/m².

FIGURE 5 Radiant enclosure design problem.

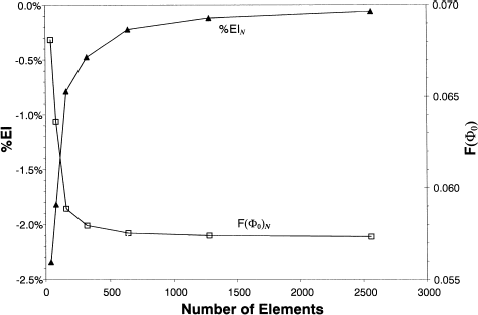
A total of 640 surface elements were used in both analyses, chosen based on the grid refinement study shown in Fig. 6; 384 of those elements lie on the heater surface, 192 are on the design surface, and the remaining 64 elements are located on the two adiabatic surfaces. The grid refinement study was performed with Φ _k = 1, k = 1, … , 12, which corresponds with the initial enclosure configuration of the optimization method, Φ₀. It is based on the objective function defined in Eq. (17), as well as the degree of energy conservation, defined as

which should be equal to zero for an exact solution. Since the heat flux is assumed to be uniform over each surface element, however, energy conservation is not exactly satisfied. As N becomes very large, however, %EI tends to zero and F(Φ) approaches its grid-independent solution. Similar grid refinement studies were performed on the solutions obtained from the inverse and optimization methodologies, in order to ensure the grid independence of the results.

FIGURE 6 Grid refinement study.

5.1. Inverse Design Method

In order to enforce a uniform heat flux distribution over each heater, the unknown heat flux terms corresponding to each element on the heater surfaces, q _si , were replaced by the heater settings, Φ _i . This both reduced the degree of rank deficiency (the number of unknowns exceeds the number of equations by 12, rather than 384) and prevents the occurrence of highly oscillatory heat flux distributions that are often produced by this solution technique, and are undesirable from a design perspective.

Also, although the system of linear equations used in the forward design methodology enforces energy conservation, this is not true for the inverse formulation because the boundary conditions over the heater surfaces are unspecified. Accordingly, it is necessary to add an energy conservation equation to the A matrix,

where A _heater is the surface area of each heater and A _DS is the total area of the design surface [11]. Once the A matrix is formed, it is decomposed into the three matrices of Eq. (15) using the TSVD algorithm. The 460 singular values are reordered and shown in Fig. 7; eleven of them are equal to zero due to the rank-deficiency of the A matrix, while the remaining small singular values are associated with the ill-posed nature of the problem. The next step is to truncate the smallest singular values, and then calculate the heat flux distribution over the design surface and the heater surface using Eq. (16).

FIGURE 7 Singular values found by decomposing the A matrix.

The heat flux and emissive power distribution over the heater surface obtained using all the singular values ( p = 460), all the non-zero singular values ( p = 449), and the case for p = 448 are shown in Figs. 8–10, respectively. The corresponding design parameters are included in Table I and the values of || x || ₂ and || δ || ₂ for each solution are in Table II. In each case, the required temperature and heat flux distributions over the design surface are enforced, so and for 0.65 ≤ u<0.95. The solution calculated using all of the singular values, shown in Fig. 8, has a very non-regular heat flux distribution over the heater surface, which is reflected in the large value of || x || ₂ for this case in Table II. Truncating the eleven null singular values and keeping p = 449 singular values produces a more regularized solution and a very small residual, as shown in Fig. 9. As more singular values are truncated, however, the solution becomes smoother but also non-physical because E _b (u) assumes negative values over some surfaces, as shown in Fig. 10. At this point, too many singular values have been nullified and the original governing equations are no longer enforced, as demonstrated by the large value of || δ || ₂.

FIGURE 8 Distribution of q _s (u) and E _b (u) over the heater surface, found using p = 460 singular values.

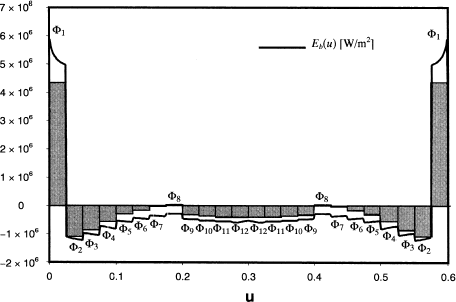
FIGURE 9 Distribution of q _s (u) and E _b (u) over the heater surface, found using p = 449 singular values.

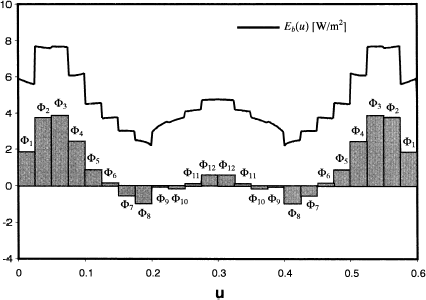
FIGURE 10 Distribution of q _s (u) and E _b (u) over the heater surface, found using p = 448 singular values.

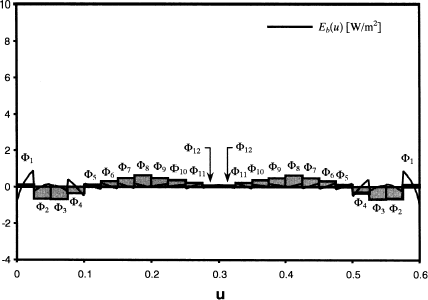
TABLE I Heater settings corresponding to Figs. 8–10 [W/m²]

p	Φ 1	Φ 2	Φ 3	Φ 4
460	4.37 × 10^6	−1.69 × 10^6	−8.49 × 10^5	−5.50 × 10^5
449	1.87	3.78	3.87	2.44
448	0.11	−0.63	−0.67	−0.29
Φ5	Φ6	Φ7	Φ8
460	−2.57 × 10^5	−1.52 × 10^5	−3.97 × 10^4	4.83 × 10^4
449	0.90	0.13	−0.54	−0.98
448	0.11	0.31	0.48	0.65
Φ9	Φ10	Φ11	Φ12
460	−3.14 × 10^5	−3.58 × 10^5	−3.85 × 10^5	−4.00 × 10^5
449	−0.06	−0.14	0.14	0.59
448	0.49	0.37	0.23	0.05

TABLE II Values of || x ||₂ and || δ ||₂ corresponding to Figs. 8–10

Number of singular values	|| x ||2	|| δ || 2
p = 460	9.31 × 10^14	1.20 × 10^−14
p = 449	1.02 × 10^4	1.18 × 10^−25
p = 448	2.85 × 10^1	1.29 × 10^3

Although the solution found with p = 449 singular values is physically obtainable, it is impractical to implement in an industrial setting because some of the heaters act as heat sinks. The designer is more likely to insulate these heaters and incur the resulting error in the heat flux distribution over the design surface. In this application, Φ₇, Φ₈, Φ₉, and Φ₁₀ are set equal to zero while the remaining heater settings are unaltered. The heat flux distribution over the design surface is then recalculated using the forward design method. It is compared with the desired design surface conditions in Fig. 11.

FIGURE 11 Distribution of q _s (u) over the design surface, found by nullifying the negative heater settings of the p = 449 solution.

5.2. Optimization Design Methodology

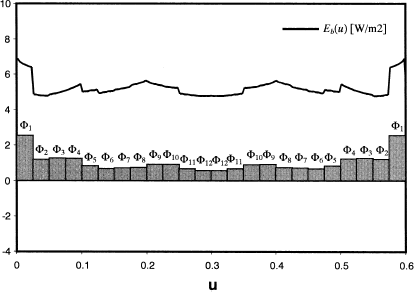
The design problem was also solved by minimizing the objective function defined in Eq. (17), using Newton's method. Initially, all of the design parameters (heater settings) were set equal to unity, . Three iterations were required to identify a local minimum of the objective function, F(Φ^*) = 2.92 × 10⁻⁸, corresponding to the solution illustrated in Fig. 12 and the design parameters shown in Table III. The heat flux distribution over the design surface closely matches the desired distribution, as shown in Fig. 14. Nevertheless, the solution is non-physical because E _b (u) is negative over some regions of the enclosure surface. It is important to note, however, that this solution is mathematically feasible and satisfies Eq. (6).

FIGURE 12 Heater settings found by minimizing the non-regularized objective function, Eq. (17).

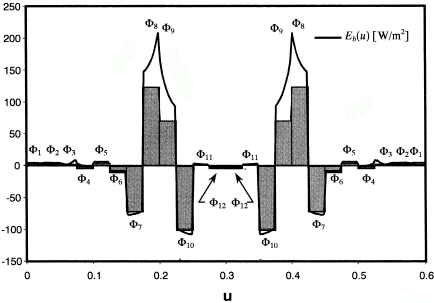
FIGURE 14 Distribution of q _s (u) over the design surface, found by minimizing non-regularized and regularized objective functions.

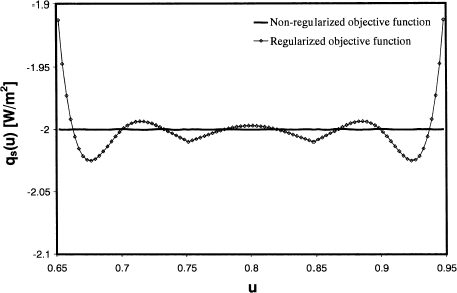
TABLE III Optimal heater settings for the regularized and non-regularized objective functions [W/m²]

Φ 1	Φ 2	Φ 3	Φ 4
Φ^*	1.33	2.11	2.29	−3.56
	2.54	1.17	1.25	1.24
Φ5	Φ6	Φ7	Φ8
Φ^*	2.50	−10.18	−71.25	122.8
	0.82	0.62	0.66	0.74
Φ9	Φ10	Φ11	Φ12
Φ^*	69.94	−100.0	0.10	−3.89
	0.91	0.88	0.55	0.56

A more useful solution is found by adding an additional term to the objective function equal to the L ₂ norm of the design parameters, defining a new objective function:

This new objective function was derived based on the observation that non-physical solutions usually arise from large heat flux variations over the heater surfaces, and in this way the function “regularizes” the solution in a way similar to singular value truncation. (This approach has been employed elsewhere in the literature, for example Dorai and Tortorelli [12]). The value of γ was set equal to 0.9999, and Newton's method was again employed to minimize the objective function starting with the same initial design parameters. Three iterations were required to identify a new local minimum, , which corresponds to The heat flux and emissive power distributions over the heater surface corresponding to this solution are illustrated in Fig. 13, and the design parameters are shown in Table III. The heat flux distribution over the design surface is shown in Fig. 14; the maximum deviation between the desired and realised heat flux distributions is 5.13% on the edges of the design surface, which is within the tolerances demanded by most engineering applications.

FIGURE 13 Heater settings found by minimizing the regularized objective function, Eq. (32).

In general, optimization problems with constraints are solved using constrained minimization algorithms. While very powerful, these algorithms are also more complex than unconstrained optimization and require more computational effort to implement. In this application, adding the regularization term to the original objective function enabled us to avoid using these more complicated minimization techniques.

5.3. Comparison of Inverse and Optimization Design Methods

The inverse and optimization design methodologies can be compared based on the ease of problem formulation, computational effort, and solution quality.

The inverse design methodology is somewhat more difficult to implement, since the equations governing radiosity distribution must be rewritten and rearranged. Also, the TSVD method requires the designer to have some specialized mathematical knowledge to interpret the results of the singular value decomposition. In contrast, optimization methods are based on the same set of equations used by the forward design method. Their complexity depends largely on how the sensitivities are calculated; in this application, they are easily found by direct differentiation.

Both methods require approximately the same computational effort and memory storage to solve the design problem. The TSVD method performs one singular value decomposition on the A matrix, which requires approximately the same CPU time as the single matrix inversion carried out during the optimization process. In this problem, the inverse and optimization methodologies solved the design problem in a matter of seconds.

The main difference between the two methodologies lies in the quality of the final solutions, shown in Figs. 11 and 14. The optimization solution is far better than the solution obtained using the inverse design methodology because the optimization methodology can accommodate design constraints, while the inverse methodology cannot. In this application, the heat flux over the heater surface had to be non-negative, Φ _k  ≥ 0 for k = 1, … , 2. In the optimization methodology, this was enforced by adding a “regularization” term to the original objective function. In contrast, the inverse methodology can only be used to find the best “mathematical” solution to the problem, which is then modified to allow for practical design considerations. The ability of optimization methods to accommodate practical design constraints is one of the main assets of these techniques.

6. Conclusions

Both optimization and inverse design methods have been used to solve industrial design problems involving radiant enclosures. These methods require far less time than the forward “trial and error” method that is traditionally used to design radiant enclosures, and the quality of the solutions is usually much better.

While both methods were successfully implemented, the optimization method provided a solution that better satisfied the design requirements. This is because optimization methods can accommodate practical design constraints, while in most instances the solutions obtained using the inverse methodology can only be altered to satisfy these constraints after the primary analysis.

Nomenclature

Table

A	=	coefficient matrix for radiosity equation
b(u)	=	see Eqs. (3) and (4)
b i	=	b(u i )
b	=	right-hand vector for radiosity equation
b ′	=	right-hand vector for 1st-order radiosity sensitivity
b ″	=	right-hand vector for 2nd-order radiosity sensitivity
C (u)	=	parametric vector defining enclosure geometry
	=	view factor from u i to an infinitely long strip centred at u j
E b (u)	=	emissive power at u, W/m^2
	=	desired emissive power distribution over the design surface, W/m^2
%EI	=	energy imbalance
F(Φ)	=	objective function
F r (Φ)	=	modified objective function, Eq. (32)
F [Φ, q s (Φ)]	=	objective function with expanded dependencies
g (Φ)	=	gradient vector
g p	=	element of the gradient vector
g(u)	=	see Eqs. (3) and (4)
g i	=	g(u i )
H(Φ)	=	Hessian matrix
H pq	=	element of Hessian matrix
k(u i , u j )	=	Kernel of Eq. (2)
N	=	number of discrete surface elements
N DS	=	number of discrete surface elements on design surface
P(u)	=	x-component of C (u)
p	=	number of singular values used to solve Eq. (16)
p k	=	search direction
Q(u)	=	y-component of C (u)
q o (u)	=	radiosity at u, W/m^2
q s (u)	=	heat flux at u, W/m^2
	=	desired heat flux distribution over the design surface, W/m^2
q s (Φ)	=	system response vector
r	=	position vector
T(u)	=	temperature at u, K
U	=	matrix obtained by singular value decompositon, Eq. (15)
u	=	parameter for enclosure representation
V	=	matrix obtained by singular value decompositon, Eq. (15)
W	=	singular value matrix
w i	=	singular value corresponding to ith diagonal element of W
x	=	solution vector for radiosity
x ′	=	1st-order radiosity sensitivity vector
x ″	=	2nd-order radiosity sensitivity vector

Greek Symbols

Table

α k	=	step size
β ij	=	blockage factor
δ	=	residual vector
ΔA	=	area of discrete surface element
ε(u)	=	surface emissivity at u
σ	=	Stephan–Boltzmann constant, 5.67 × 10^−8 W/m^2K^4
Φ p	=	pth design parameter
Φ	=	vector of design parameters (heater settings)

Acknowledgements

This work was supported by National Science Foundation Grants CTS 70545 and DMI 9702217, the Natural Sciences and Engineering Research Council of Canada, and the State of Texas.

Additional information

Notes on contributors

K.J. Daun*

*E-mail: [email protected]

Notes

*E-mail: [email protected]