On the Exploratory Road to Unraveling Factor Loading Non-invariance: A New Multigroup Rotation Approach

Abstract

Multigroup exploratory factor analysis (EFA) has gained popularity to address measurement invariance for two reasons. Firstly, repeatedly respecifying confirmatory factor analysis (CFA) models strongly capitalizes on chance and using EFA as a precursor works better. Secondly, the fixed zero loadings of CFA are often too restrictive. In multigroup EFA, factor loading invariance is rejected if the fit decreases significantly when fixing the loadings to be equal across groups. To locate the precise factor loading non-invariances by means of hypothesis testing, the factors’ rotational freedom needs to be resolved per group. In the literature, a solution exists for identifying optimal rotations for one group or invariant loadings across groups. Building on this, we present multigroup factor rotation (MGFR) for identifying loading non-invariances. Specifically, MGFR rotates group-specific loadings both to simple structure and between-group agreement, while disentangling loading differences from differences in the structural model (i.e., factor (co)variances).

Keywords:

• Measurement invariance
• factor loading invariance
• multigroup exploratory factor analysis
• rotation identification

Introduction

In behavioral sciences, latent constructs, e.g., emotions or personality traits, are ubiquitously measured by questionnaire items. The measurement model (MM) indicates which item is (assumed to be) measuring which construct and the leading method to evaluate whether this MM holds is confirmatory factor analysis (CFA; Lawley & Maxwell, 1962). The extent to which an item relates to a construct or ‘factor’ is quantified by a ‘factor loading’. CFA evaluates whether each item has a non-zero loading on the targeted construct only. Many research questions pertain to comparing constructs across groups, e.g., comparing the Big Five personality traits across countries (Schmitt, Allik, McCrae, & Benet-Martínez, 2007). For such comparisons, invariance of the MM or ‘measurement invariance’ (MI) across the groups is an essential prerequisite (Meredith, 1993). MI can be tested by multigroup factor analysis (Jöreskog, 1971; Sörbom, 1974). Despite the predominance of CFA-based methods, multigroup exploratory factor analysis (EFA) has gained popularity to address MI (Dolan, Oort, Stoel, & Wicherts, 2009; Marsh, Morin, Parker, & Kaur, 2014). The reason for this is twofold. Firstly, respecifying CFA models in an exploratory way capitalizes on chance (Browne, 2001; MacCallum, Roznowski, & Necowitz, 1992) and using EFA as a precursor has proven to be a better strategy (Gerbing & Hamilton, 1996). Secondly, fixed zero loadings are often too restrictive and may cause bias (McCrae, Zonderman, Costa, Bond, & Paunonen, 1996; Muthén & Asparouhov, 2012).

MI testing with multigroup EFA starts by evaluating whether the fit significantly decreases when fixing the factor loadings to be equal (i.e., invariant) across groups, indicating that factor loading (or ‘weak’) invariance does not hold. Because EFA is used within the groups, the factors have rotational freedom, i.e., ‘rotating’ them yields an alternative set of factors which fit equally well to the data but may be easier to interpret (Browne, 2001; Osborne, 2015). When merely testing invariance for all loadings, the factor rotation is irrelevant. The rotation becomes of interest, however, when one wants to determine what the invariant MM is (Asparouhov & Muthén, 2009; Dolan et al., 2009). To this end, simple structure rotation (i.e., striving for one non-zero loading per item; Thurstone, 1947) or target rotation towards an assumed MM can be applied. To enable hypothesis testing for rotated loadings, Jennrich (1973) showed how to obtain a fully identified model with optimally rotated maximum likelihood (ML) estimates.

Jennrich’s approach does the trick for single-group factor models and multigroup factor models with invariant loadings, but leaves much to be desired when loadings are non-invariant across groups. In that case, pinpointing the precise loading differences would allow to find sources of non-invariance and interesting differences in the functioning of items (differential item functioning or DIF; Holland & Wainer, 1993). To this end, an optimal rotation needs to be obtained for each group. Using Jennrich’s approach per group precludes pursuing optimal between-group agreement of the loadings and thus impedes a correct evaluation of differences and similarities. Therefore, we present a multigroup extension to accommodate the search for loading differences. Specifically, each group is rotated both to simple structure per group and agreement across groups. At the same time, loading differences are disentangled from differences irrelevant to the MI question (i.e., factor (co)variances). The novel multigroup factor rotation (MGFR) can be applied with several rotation criteria and with a user-specified focus on agreement or simple structure.

The remainder of this paper is organized as follows: Section 2 recaps MI testing by multigroup EFA, followed by a discussion of optimal rotation identification including the novel MGFR. Section 3 covers an extensive simulation study to evaluate the performance of MGFR with regard to the identification of loading differences and group-specific MMs and derives recommendations for empirical practice. Section 4 illustrates the added value of MGFR for an empirical data set. Section 5 includes points of discussion and directions for future research.

Method

Multigroup exploratory factor analysis

We denote the groups by g = 1, …, G and the subjects within the groups by n_g = 1, …, N_g. The J-dimensional random vector of observed item scores for subject $n_g$ is denoted by ${\mathbf{y}}_{n_g}$. The EFA model for the scores of subject $n_g$ can be written as (Lawley & Maxwell, 1962):

(1) ${\mathbf{y}}_{n_g}={\tau }_g+{\mathbf{\Lambda }}_g{\eta }_{n_g}+{\epsilon }_{n_g}$(1)

where ${\tau }_g$ indicates a J-dimensional group-specific intercept vector, ${\mathbf{\Lambda }}_g$ denotes a J × Q matrix of group-specific factor loadings, ${\eta }_{n_g}$ is a Q-dimensional vector of scores on the Q factors and ${\epsilon }_{n_g}$ is a J-dimensional vector of residuals. The factor scores are assumed to be identically and independently distributed (i.i.d.) as $MVN\left({\alpha }_g,{\mathbf{\Psi }}_g\right)$, independently of ${\epsilon }_{n_g}$, which are i.i.d. as $MVN\left(\mathbf{0},{\mathbf{D}}_g\right)$. The factor means of group g are denoted by ${\alpha }_g$, whereas ${\mathbf{\Psi }}_g$ pertains to the group-specific factor covariance matrix and ${\mathbf{D}}_g$ to a diagonal matrix containing the group-specific unique variances of the items. The model-implied covariance matrix per group is ${\mathrm{\Sigma }}_g={\mathbf{\Lambda }}_g{\mathbf{\Psi }}_g{{\mathbf{\Lambda }}_g}^{\mathrm{\prime }}+{\mathbf{D}}_g$.

Estimating Equation 1 for each group corresponds to the baseline model for MI testing. To partially identify the model, the factor means ${\alpha }_g$ are fixed to zero and the factor covariance matrix ${\mathbf{\Psi }}_g$ to identity (i.e., orthonormal factors) per group g. Note that, unlike multigroup EFA, multigroup CFA imposes zero loadings on ${\mathbf{\Lambda }}_g$ according to an assumed MM and it assumes this pattern of zero loadings to be invariant across groups (configural invariance; Meredith, 1993).

To test for MI, a series of progressively more restricted models is fitted. Factor loading invariance is evaluated by comparing the fit of the baseline model and the model with invariant loadings, i.e., ${\mathbf{\Lambda }}_g=\mathbf{\Lambda }$ for g = 1, …, G. For the latter model, orthonormality of the factors is no longer imposed per group but, e.g., for the mean factor (co)variances across groups. In the literature, several criteria and guidelines are discussed to evaluate whether a drop in fit is statistically significant (Hu & Bentler, 1999). When it is not significant, factor loading (or weak) invariance is established and the next level of MI – which is beyond the scope of this paper – can be tested by restricting the intercepts ${\tau }_g$ to be invariant across groups, while freely estimating factor means ${\alpha }_g$ per group (Dolan et al., 2009; Meredith, 1993). When the fit is significantly worse with invariant factor loadings – i.e., factor loading invariance is rejected – one can scrutinize the baseline model to locate factor loading non-invariances.

Note that, in case of multigroup CFA, the baseline model is already very restrictive due to the assumption of configural invariance. Therefore, multigroup CFA extensions for dealing with loading non-invariances – such as multigroup Bayesian structural equation modeling (multigroup BSEM; Muthén & Asparouhov, 2013) and multigroup factor alignment (Asparouhov & Muthén, 2014) – only capture differences in the size of primary loadings, whereas differences in crossloadings and the position of primary loadings are disregarded.

Thus, multigroup EFA has the important advantage that it leaves room to evaluate (the lack of) MI without having to predefine the MM and to find all types and combinations of loading differences. In the baseline model (Equation 1), the rotational freedom of the factors per group is beneficial to this aim. Specifically, striving for simple structure per group (e.g., Clarkson & Jennrich, 1988) as well as between-group agreement (e.g., Ten Berge, 1977) allows for the group-specific MMs to be determined and loading differences to be pinpointed. Thus, sources of configural and weak non-invariance can be traced simultaneously.

Multigroup EFA can be estimated by open-source software such as lavaan (Rosseel, 2012) and Mx (Neale, Boker, Xie, & Maes, 2003) as well as commercial software such as Latent Gold (LG; Vermunt & Magidson, 2013) and Mplus (Muthén & Muthén, 2005). LG-syntax for multigroup EFA with (optimally rotated) group-specific loadings is given in Appendix A.

Optimal rotation in multigroup EFA

In this section, we first discuss the case where loading invariance holds and one loading matrix needs to be rotated. Then, we build on this to propose MGFR for the case where loading invariance fails and G loading matrices need to be rotated.

In case of factor loading invariance

To partially identify a single EFA solution, up to rotation, $Q\left(Q+1\right)/2$ restrictions are needed. Usually, the factor covariance matrix $\mathbf{\Psi }$ is restricted to be an identity matrix, implying factor variances of one and covariances of zero. In case of multigroup EFA with invariant loadings $\mathbf{\Lambda }$, the restrictions on $\mathbf{\Psi }$ are not imposed per group but, e.g., for the mean factor (co)variances across groups, or for one ‘reference’ group (Hessen, Dolan, & Wicherts, 2006). To obtain a fully identified model, i.e., with an identified rotation, a total of Q² restrictions are necessary, yet not always sufficient (Jöreskog, 1979). Jennrich (1973) derived the necessary restrictions for obtaining the optimal rotation according to a criterion of choice. This solution can be readily applied to rotate invariant loadings in multigroup EFA. In this paper, we focus on oblique rotation, which implies that factor covariances are no longer fixed to zero and thus that only Q restrictions are imposed directly on $\mathbf{\Psi }$. Therefore, $Q\left(Q-1\right)$ additional restrictions are needed to identify the rotation. Specifically, to obtain an optimal oblique rotation according to rotation criterion R, the following matrix F is restricted to be diagonal:

(2) $\mathbf{F}\mathbf{=}{\mathbf{\Lambda }}^{\prime }\frac{\mathit{d}\mathbf{R}}{d\mathbf{\Lambda }}{\mathbf{\Psi }}^{\mathbf{-}\mathbf{1}}$(2)

Imposing these restrictions is done by means of constrained ML estimation (Asparouhov & Muthén, 2009) or the gradient projection algorithm (Jennrich, 2001, 2002). Upon identifying the rotation, and thus obtaining a fully identified model, standard errors for the model parameters and hypothesis testing to determine significant factor loadings, and thus the invariant MM, are available (Jennrich, 1973).

Simple Structure Rotation Criteria

For the choice of rotation criterion R in Equation 2, several simple structure rotation criteria exist that minimize either the variable complexity (i.e., the number of non-zero loadings per variable), factor complexity (i.e., the number of non-zero loadings per factor), or a combination of both (Schmitt & Sass, 2011). We focus on oblique simple structure rotation to minimize the variable complexity since this matches the concept of a MM, i.e., items as pure measurements of one factor. Geomin (Yates, 1987) is a popular criterion (e.g., it is default in Mplus; Asparouhov & Muthén, 2009) but is sensitive to local minima (Asparouhov & Muthén, 2009; Browne, 2001). (Direct) oblimin¹ (Clarkson & Jennrich, 1988) is a widely-used rotation offered in the statistical packages SPSS (Nie, Bent, & Hull, 1970) and STATA (Hamilton, 2012). Stepwise rotation procedures such as promax (Hendrickson & White, 1964) and promin (Lorenzo-Seva, 1999) cannot be readily applied as the rotation criterion in Equation 2. Simple structure rotation criteria often perform suboptimal when the variable complexity is higher than one for some items (Ferrando & Lorenzo-Seva, 2000, 1999; Schmitt & Sass, 2011). To avoid this deficiency, weighted oblimin (Lorenzo-Seva, 2000) was presented, but the weighting procedure is known to fail in some cases (Kiers, 1994). Target rotation (Browne, 2001) towards a zero loading pattern is a better alternative to achieve simple structure, since crossloadings can be tolerated by leaving the corresponding element of the target unspecified. Simplimax (Kiers, 1994) can be used to determine the optimal target for a given loading matrix. When one has prior beliefs about the MM, a target corresponding to this MM can be applied. In this paper, the oblimin criterion is applied for simple structure rotation R^SS, where ${\lambda }_{jq}$ is the loading of item j on factor q:

(3) $R^{SS}=\sum _{q=1}^Q\sum _{q^{\prime }=q+1}^Q\sum _{j=1}^J{\lambda }_{jq}^2{\lambda }_{j{q}^{\prime }}^2.$(3)

In case of factor loading non-invariance

If invariant factor loadings are untenable, the group-specific loadings are scrutinized to identify sources of non-invariance. To this end, the optimal rotation needs to be identified for each group and one may choose to apply the restrictions in Equation 2 to each group separately, implying $G\times Q\left(Q-1\right)$ restrictions, while the factor variances remain fixed to one per group. This approach entails two pitfalls. Firstly, the rotation for each group separately disregards the resulting (dis)agreement of loadings across groups, resulting in overestimated loading differences. Secondly, when keeping the factor variances fixed to one per group during rotation, differences in factor scale show up in the loadings, while these differences are irrelevant to the MI question. Specifically, factor variances (as well as factor covariances) are part of the structural model rather than the MM (Dolan et al., 2009; Meredith, 1993).

To strive for agreement and simple structure, MGFR minimizes multigroup criterion R^MG:

(4) $R^{MG}\left({\mathbf{\Lambda }}_1,...,{\mathbf{\Lambda }}_g,...,{\mathbf{\Lambda }}_G\right)=w{R}^A+(1-w)\sum _{g=1}^G{R}_g^{SS}$(4)

where R^A refers to the agreement criterion across all groups and $R_g^{SS}$ refers to a simple structure criterion within group g. For R^A, we consider two criteria discussed below. For $R_g^{SS}$, oblimin, geomin and target rotation are currently supported (see Appendix A). The relative influence of the agreement and simple structures on R^MG is determined by the user-specified weighting parameter w. Thus, the novelty of this criterion lies not only in combining R^A and $R_g^{SS}$(g = 1, …, G) but also in the weighting of this combination,² resulting in a flexible framework of rotations that includes every degree of focus on either agreement or simple structure.

To partially identify the scales of the group-specific factors, we restrict the across-group mean factor variances to one: $\frac{1}{G}\sum _{g=1}^{G}diag\left({\mathbf{\Psi }}_g\right)={\left[\mathbf{1}\right]}_Q$. As such, we allow for factor variances to differ between groups and avoid the arbitrariness of choosing a reference group with fixed variances. The group-specific factor variances will be further identified by the R^A part (i.e., optimizing between-group agreement), whereas the factor covariances are identified by both parts of the rotation (i.e., maximizing simple structure per group as well as between-group agreement).

Given the Q scaling restrictions, $\left(G-1\right)Q^2+Q\left(Q-1\right)$ additional restrictions are needed to identify the optimal multigroup rotation. To find the restrictions that minimize R^MG, we use its differential in the point corresponding to the optimally rotated loadings ${\mathbf{\Lambda }}_g$ for g = 1, …, G:

(5) $d{R}^{MG}\left({\mathbf{\Lambda }}_1,...,{\mathbf{\Lambda }}_g,...,{\mathbf{\Lambda }}_G\right)=\sum _{g=1}^{G}d{R}^{MG}\left({\mathbf{\Lambda }}_g\right)$(5)

The differential is derived in Appendix B and results in the following restrictions for each group:

(6) $\begin{array}{rl}& {\mathbf{F}}_g^{MG}={{\mathbf{\Lambda }}^{\prime }}_g\frac{d{R}^{MG}}{d{\mathbf{\Lambda }}_g}{\mathbf{\Psi }}_g^{-1}-diag\left(\frac{1}{G}\sum _{g^{\prime }=1}^G{{\mathbf{\Lambda }}^{\prime }}_{g^{\prime }}\frac{d{R}^{MG}}{d{\mathbf{\Lambda }}_{g^{\prime }}}{\mathbf{\Psi }}_{g^{\prime }}^{-1}\right)\\ & ={\left[\mathbf{0}\right]}_{Q\times Q}\end{array}$(6)

Again, standard errors can be obtained for the optimally rotated loadings (Jennrich, 1973) and hypothesis testing can be performed. To look for factor loading non-invariances, one can test per loading whether it is significantly different across the groups using a Wald test. To evaluate group-specific MMs (or causes of configural non-invariance), one can also test which loadings are significantly different from zero per group and evaluate how these results differ across groups.

Agreement Rotation Criteria

A widely used criterion for agreement rotation of multiple loading matrices is generalized procrustes (GP; Ten Berge, 1977), which optimizes agreement in the least squares sense:

(7) $R^A=\sum _{g=1}^G\sum _{g^{\prime }=g+1}^G\sum _{j=1}^J\sum _{q=1}^Q{\left({\lambda }_{gjq}-{\lambda }_{g^{\prime }jq}\right)}^2$(7)

Due to the square, the loss due to a loading difference smaller than one is attenuated, and more so for smaller differences. The loss due to a difference larger than one is amplified. Thus, GP aims to minimize large loading differences and tolerate small differences. This implies that, in the attempt to minimize (true) large differences, (false) small differences may be created. Note that GP is originally an orthogonal rotation, but since it is combined with oblique simple structure rotations, MGFR does not impose orthogonality on GP and thus disentangles loading differences from differences in factor variances as well as correlations.

As an alternative, some aspects of the (confirmatory) multigroup factor alignment (Asparouhov & Muthén, 2014) can be included in MGFR. Specifically, in multigroup factor alignment, the factors are ‘aligned’ (i.e., rescaled and shifted in terms of their factor means) to minimize the following function of loading and intercept differences, separately per factor q:

(8) $\begin{array}{rl}& \sum _{g=1}^G\sum _{g^{\prime }=g+1}^G\sum _{j=1}^J\sqrt{N_g{N}_{g^{\prime }}}\\ & \left(\sqrt{\sqrt{{\left({\lambda }_{gjq}-{\lambda }_{g^{\prime }jq}\right)}^2+\epsilon }}+\sqrt{\sqrt{{\left({\tau }_{gj}-{\tau }_{g^{\prime }j}\right)}^2+\epsilon }}\right)\end{array}$(8)

where $\epsilon$ is a small number included to facilitate the minimization and $\sqrt{N_g{N}_{g^{\prime }}}$ is a weight depending on the group sizes. On the one hand, intercept (and factor mean) differences are beyond the scope of this paper and are thus omitted from the criterion (i.e., they are fixed during rotation) for MGFR. On the other hand, we are dealing with (the rotation of) EFA rather than CFA and thus apply the criterion across all factors simultaneously. Therefore, it becomes:

(9) $R^A=\sum _{g=1}^G\sum _{g^{\prime }=g+1}^G\sum _{j=1}^J\sum _{q=1}^Q\sqrt{\sqrt{{\left({\lambda }_{gjq}-{\lambda }_{g^{\prime }jq}\right)}^2+\epsilon }}$(9)

where $\sqrt{N_g{N}_{g^{\prime }}}$ is omitted since $R_g^{SS}$ does not include such a weight. We will refer to this adjusted alignment criterion as the ‘loading alignment’ (LA) criterion. The square root attenuates the loss for loading differences larger than one, whereas the loss is amplified for differences smaller than one, and more so for small differences. Therefore, minimizing the LA criterion eliminates small loading differences while large differences are tolerated. Thus, it strives for loading differences to be either zero or large (Asparouhov & Muthén, 2014), which fits our aim of distinguishing invariant from non-invariant loadings irrespective of the size of the non-invariance.

Implementation of optimal rotation

MGFR is implemented in LG 6.0 and applied by syntax (Appendix A). In the future, it can be readily implemented in other software (e.g., implementation in lavaan is under development). The performed steps are:

1. ML estimation: The model is estimated without the optimal rotation restrictions, i.e., maximizing the log-likelihood (LL), with factor variances fixed to one per group.

2. Gradient projection per group: Using the estimates from Step 1 as initial values and keeping the factor variances fixed, the gradient project algorithm (Jennrich, 2001, 2002) is applied for each group g = 1, …, G to minimize $R_g^{SS}$ by imposing diagonality on Equation 2.

3. Reflection and permutation: The factors of group 1 are ordered according to their explained variance and reflected such that (most) strong loadings have a positive sign. Then, the factors of groups g = 2, …, G are permuted and reflected to minimize the applied agreement criterion with the factor loadings of group 1 (i.e., $R_{g{g}^{\prime }}^A$ with g’ = 1).

4. Constrained ML estimation: The factor loadings and (co)variances are updated by maximizing the objective function LL + l × vec(F^MG), where l is a vector of Lagrange multipliers and F^MG contains all group-specific restrictions ${\mathbf{F}}_g^{MG}$ (Equation 6) and is transformed into a vector by the ‘vec’ operator. Fisher scoring (Lee & Jennrich, 1979) is used, with possible step size adjustments to prevent inadmissible factor covariance matrices, until the updates converge to a solution with both l and F^MG equal to zero, i.e., the (optimally rotated) ML solution.

Note that, apart from the occasional non-convergence in the standard multigroup EFA estimation (Step 1), convergence of the multigroup rotation (Step 4) is not guaranteed and may fail when initial values are far from the optimal rotation. The initial values correspond to the unrotated factor loadings resulting from Step 1, which are partially optimized by rotation to simple structure per group (Step 2) and reflection and permutation to between-group agreement (Step 3), in order to facilitate the convergence of Step 4. If Step 4 fails to converge, repeating the procedure from Step 1 and onwards yields a new set of initial values and may solve the non-convergence. Note that especially the loading alignment criterion is a difficult one to optimize.

Simulation study

Problem

The goal of the simulation study is to evaluate the performance of MGFR with respect to: (1) the convergence of the optimal rotation, (2) the recovery of the factor loadings by the optimal rotation, and (3) the false positives (FP) and false negatives (FN) of hypothesis testing – based on the optimal rotation – for loading differences and non-zero loadings. For the rotation, we use generalized procrustes (GP; Equation 7) and loading alignment (LA; Equation 9) as R^A and oblimin (O; Equation 3) as $R_g^{SS}$ for g = 1, …, G, with a variety of weights w. For the hypothesis testing, we focus on Wald tests because they are part of the default output of LG. We manipulated six factors that were expected to affect MGFR and/or the hypothesis testing: (1) the number of groups, (2) the group sizes, (3) the number of factors, (4) the type and size of the loading differences, and (5) the number of loading differences.

In terms of their effect on the performance of MGFR, we hypothesize the following: It will be more difficult to recover the optimal multigroup rotation when the rotation pertains to more groups and thus more loading matrices (1), when the sampling fluctuations of the group-specific factor loadings and factor covariance matrices are higher due to smaller groups (2), when the rotation pertains to more factors (3), and when the degree of the simple structure violations and disagreement between the groups is higher (4, 5). Non-convergence of MGFR becomes more likely as one or more of these aspects adds to the complexity of the rotation. The Wald tests for loading differences and non-zero loadings depend on the MGFR and their performance is thus indirectly affected by the above-mentioned aspects. On top of those indirect effects, we hypothesize (Hogarty, Hines, Kromrey, Ferron, & Mumford, 2005; Pennell, 1968) that the power of the Wald tests will be lower when the sample size is lower (1, 2), the sampling fluctuations of factor loadings are higher (2), the number of factors is higher for the same number of variables (3), the loading differences are larger (4) and the simple structure violations are more severe (4) and/or more numerous (5).

Design and procedure

These factors were systematically varied in a complete factorial design:

1. the number of groups G at 3 levels: 2, 4, 6;

2. the group sizes N_g (i.e., number of observations per group) at 3 levels: 200, 600, 1000;

3. the number of factors Q at 2 levels: 2, 4;

4. the type and size of loading differences at 5 levels: primary loading shift, crossloading of .40, crossloading of .20, primary loading decrease of .40, primary loading decrease of .20;

5. the number of loading differences at 2 levels: 4, 16;

The group-specific factor loadings are all based on the same simple structure. In this ‘base loading matrix’, the fixed number of variables (i.e., 20) are equally distributed over the factors, i.e., each factor gets 10 non-zero loadings when Q = 2 (Table 1) and five non-zero loadings when Q = 4 (Table 2). Given that the unique variances vary around .40 (see below), the non-zero loadings are equal to $\sqrt{.60}$ to obtain total variances of around one. From the common base, two different group-specific loading matrices are derived, each of which will pertain to half of the groups. Specifically, depending on the type and number of loading differences, for each of these two loading matrices, loadings were altered for a different set of variables (Table 1, 2), referred to as ‘DIF items’. In case of a primary loading shift, two differences are induced per DIF item and thus one DIF item is selected per group-specific loading matrix to obtain a total of four loading differences across groups, or four DIF items (equally distributed across factors) are selected per loading matrix to obtain a total of 16 loading differences.³ In particular, when Q = 2, the loadings $\left[\begin{array}{c}\sqrt{.6}0\end{array}\right]$ of the base matrix are replaced by $\left[\begin{array}{cc}0& \sqrt{.6}\end{array}\right]$ (Table 1). When Q = 4, primary loadings are shifted similarly between factors 1 and 2 on the one hand, and between factors 3 and 4 on the other hand; e.g., $\left[\begin{array}{cccc}\sqrt{.6}& 0& 0& 0\end{array}\right]$ becomes $\left[\begin{array}{cccc}0& \sqrt{.6}& 0& 0\end{array}\right]$. For the crossloading differences and primary loading decreases, one loading was altered per DIF item and thus two DIF items are selected per loading matrix to obtain four differences across groups, or 8 to obtain 16 differences (Table 2). In case of crossloadings, the loadings $\left[\begin{array}{cc}\sqrt{.6}& 0\left(0\right)\left(0\right)\end{array}\right]$ become $\left[\begin{array}{c}\sqrt{.6}.4\left(0\right)\left(0\right)\end{array}\right]$ or $\left[\begin{array}{cccc}\sqrt{.6}& .2& \left(0\right)& \left(0\right)\end{array}\right]$ depending on the size of the crossloadings. Note that a crossloading of .20 may be considered ‘ignorable’, whereas one of .40 is not (Stevens, 1992). To manipulate a primary loading decrease, the loadings $\left[\begin{array}{cccc}\sqrt{.6}& 0& \left(0\right)& \left(0\right)\end{array}\right]$ are replaced by $\left[\begin{array}{cccc}\sqrt{.6}-.4& 0& \left(0\right)& \left(0\right)\end{array}\right]$ or $\left[\begin{array}{cccc}\sqrt{.6}-.2& 0& \left(0\right)& \left(0\right)\end{array}\right]$ depending on the size of the decrease (see online supplements). Note that a primary loading decrease of .40 is considered a large non-invariance (Stark, Chernyshenko, & Drasgow, 2006) that can lead to incorrect statistical inference and biased parameter estimates (Hancock, Lawrence, & Nevitt, 2000). When G > 2, each of the two generated loading matrices was assigned to a random half of the groups. A number of remarks are in order: Firstly, in the case of four loading differences, only factors 1 and 2 are affected, even when Q = 4. Secondly, a primary loading shift maintains the item’s communality whereas a crossloading increases it and a primary loading decrease lowers it. Thirdly, and most importantly, primary loading shifts and crossloadings are violations of configural invariance and thus differences that are very hard to trace by CFA-based methods such as multigroup BSEM or multigroup factor alignment.

Table 1 Base Loading Matrix and the Derived Group-Specific Loading Matrices, in case of Two Factors and Primary Loading Shifts. Differences are Indicated in Bold Face and Differences between Brackets are Only Induced in the Case of 16 Loading Differences

	Base loading matrix		Group-specific loading matrix 1		Group-specific loading matrix 2
	F1	F2	F1	F2	F1	F2
V1	$\sqrt{.6}$	0	0	$\sqrt{.6}$	$\sqrt{.6}$	0
V2	$\sqrt{.6}$	0	(0)	($\sqrt{.6}$)	$\sqrt{.6}$	0
V3	$\sqrt{.6}$	0	$\sqrt{.6}$	0	0	$\sqrt{.6}$
V4	$\sqrt{.6}$	0	$\sqrt{.6}$	0	(0)	($\sqrt{.6}$)
V5	$\sqrt{.6}$	0	$\sqrt{.6}$	0	$\sqrt{.6}$	0
V6	$\sqrt{.6}$	0	$\sqrt{.6}$	0	$\sqrt{.6}$	0
V7	$\sqrt{.6}$	0	$\sqrt{.6}$	0	$\sqrt{.6}$	0
V8	$\sqrt{.6}$	0	$\sqrt{.6}$	0	$\sqrt{.6}$	0
V9	$\sqrt{.6}$	0	$\sqrt{.6}$	0	$\sqrt{.6}$	0
V10	$\sqrt{.6}$	0	$\sqrt{.6}$	0	$\sqrt{.6}$	0
V11	0	$\sqrt{.6}$	($\sqrt{.6}$)	(0)	0	$\sqrt{.6}$
V12	0	$\sqrt{.6}$	($\sqrt{.6}$)	(0)	0	$\sqrt{.6}$
V13	0	$\sqrt{.6}$	0	$\sqrt{.6}$	($\sqrt{.6}$)	(0)
V14	0	$\sqrt{.6}$	0	$\sqrt{.6}$	($\sqrt{.6}$)	(0)
V15	0	$\sqrt{.6}$	0	$\sqrt{.6}$	0	$\sqrt{.6}$
V16	0	$\sqrt{.6}$	0	$\sqrt{.6}$	0	$\sqrt{.6}$
V17	0	$\sqrt{.6}$	0	$\sqrt{.6}$	0	$\sqrt{.6}$
V18	0	$\sqrt{.6}$	0	$\sqrt{.6}$	0	$\sqrt{.6}$
V19	0	$\sqrt{.6}$	0	$\sqrt{.6}$	0	$\sqrt{.6}$
V20	0	$\sqrt{.6}$	0	$\sqrt{.6}$	0	$\sqrt{.6}$

Table 2 Base Loading Matrix and the Derived Group-Specific Loading Matrices, in case of Four Factors and Crossloading Differences. The Crossloadings (CL) are either Equal to .40 Or .20. Differences are Indicated in Bold Face and Differences between Brackets are Only Induced in the Case of 16 Loading Differences

	Base loading matrix				Group-specific loading matrix 1				Group-specific loading matrix 2
	F1	F2	F3	F4	F1	F2	F3	F4	F1	F2	F3	F4
V1	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$	CL	0	0	$\sqrt{.6}$	0	0	0
V2	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$	(CL)	0	0	$\sqrt{.6}$	0	0	0
V3	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$	CL	0	0
V4	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$	(CL)	0	0
V5	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$	0	0	0
V6	0	$\sqrt{.6}$	0	0	CL	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$	0	0
V7	0	$\sqrt{.6}$	0	0	(CL)	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$	0	0
V8	0	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$	0	0	CL	$\sqrt{.6}$	0	0
V9	0	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$	0	0	(CL)	$\sqrt{.6}$	0	0
V10	0	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$	0	0
V11	0	0	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$	(CL)	0	0	$\sqrt{.6}$	0
V12	0	0	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$	(CL)	0	0	$\sqrt{.6}$	0
V13	0	0	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$	(CL)
V14	0	0	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$	(CL)
V15	0	0	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$	0
V16	0	0	0	$\sqrt{.6}$	0	0	(CL)	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$
V17	0	0	0	$\sqrt{.6}$	0	0	(CL)	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$
V18	0	0	0	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$	0	0	(CL)	$\sqrt{.6}$
V19	0	0	0	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$	0	0	(CL)	$\sqrt{.6}$
V20	0	0	0	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$	0	0	0	$\sqrt{.6}$

The group-specific factor correlations are randomly sampled from a uniform distribution between −.50 and .50, i.e., $U\left(-.50,.50\right)$, and factor variances from $U\left(.50,1.50\right)$. Whenever a resulting ${\mathbf{\Psi }}_g$ is not positive definite, the sampling is repeated. Group-specific unique variances (i.e., diagonal of ${\mathbf{D}}_g$) are sampled from $U\left(.20,.60\right)$. Factor scores are sampled from $MVN\left(\mathbf{0},{\mathbf{\Psi }}_g\right)$ and residuals from $MVN\left(\mathbf{0},{\mathbf{D}}_g\right)$, according to the specified group sizes. The group size of 200 corresponds to the recommended minimal sample size for obtaining accurate factor loading estimates when item communalities are moderate (Fabrigar, Wegener, MacCallum, & Strahan, 1999; MacCallum, Widaman, Zhang, & Hong, 1999), whereas 1000 delimits a range of group sizes that largely corresponds to previous MI studies (Asparouhov & Muthén, 2014; Meade & Lautenschlager, 2004). Finally, the simulated data are created according to Equation 1. Note that the intercepts ${\tau }_g$ are zero, since the focus is on loading differences.

According to this procedure, 50 data sets were generated per cell of the design, using Matlab R2017a. Thus, 3 (number of groups) × 3 (group sizes) × 2 (number of factors) × 5 (type/size of loading differences) × 2 (number of loading differences) × 50 (replications) = 9 000 data sets were generated. The data were analyzed by LG 6.0, using syntaxes (Appendix A). Since MGFR was applied with several R^MG criteria, one set of unrotated ML estimates (Step 1) was obtained and used as starting values for the optimal rotation (Steps 2–4) per criterion. The average CPU time for multigroup EFA without rotation was 12s on an i7 processor with 8GB RAM. For three data sets, this estimation was repeated because it failed to converge the first time. Then, the following rotation criteria were applied – where ‘GP’ refers to generalized procrustes, ‘LA’ to loading alignment and ‘O’ to oblimin: .01GP + .99O, .10GP + .90O, .30GP + .70O, .50GP + .50O, .70GP + .30O, .01LA + .99O. For the latter, LA was applied with an $\epsilon$-value of 1 × 10⁻¹². The average CPU time of the rotation was 12s per criterion. Note that rotations with a higher weight of the LA criterion are omitted from the reported results, because they had markedly lower convergence rates, i.e., between 77% and 40% (increasing the $\epsilon$-value did not help). Also, since LA is based on square roots rather than squares of loading differences, it has a larger impact on R^MG than GP. Therefore, a small weight is sufficient to properly identify the group-specific factor (co)variances while maintaining simple structure per group. Note that the goal of the simulation study was to prove that MGFR makes it possible to correctly identify a wide range of factor loading non-invariances in multigroup EFA and not so much to determine the best rotation criterion.

Results

In this section, we first discuss the convergence of the optimal rotation per criterion. Next, the recovery of the rotated loadings and corresponding factor (co)variances is discussed. Then, we present Wald test results based on the rotated loadings: for significant loading differences and non-zero loadings. We end with conclusions and recommendations for empirical practice.

Convergence of optimal rotation identification

Initially, the percentage of data sets for which the rotation converged, %_conv, was 92.4%, 96.6%, 96.1%, 91.9%, and 82.4% when R^A = GP and w = .01, .10, .30, .50 and .70, respectively. When R^A = LA with a weight w of .01, the %_conv-value was 90.9%. After re-running the non-converged rotations once, starting from a different random rotation of the loadings, the %_conv-values increased between 2 and 5%. In Table 3, these %_conv are given for the six rotations, in function of the simulated conditions. Clearly, %_conv is affected most by Q, with %_conv equal to or near 100% when Q = 2. The ‘.70GP + .30O’ rotation has a markedly lower %_conv for Q = 4 than the other criteria. Thus, for comparability reasons, this criterion is also omitted from the results discussed below. The following results are based on the converged rotations only.

Table 3 Convergence Frequencies (%) of the Optimal Rotation Procedure for Six Rotation Criteria, in Function of the Simulated Conditions. ‘GP’ = Generalized Procrustes, ‘LA’ = Loading Alignment, ‘O’ = Oblimin, ‘PLS’ = Primary Loading Shifts, ‘CL’ = Crossloadings, and ‘PLD’ = Primary Loading Decreases

	.01GP + .99O	.10GP + .90O	.30GP + .70O	.50GP + .50O	.70GP + .30O	.01LA + .99O
G = 2	96.0	98.4	98.7	98.4	96.7	96.8
G = 4	94.3	97.2	96.8	94.6	87.7	92.7
G = 6	94.3	96.1	95.7	90.5	76.8	87.3
Ng = 200	96.7	97.4	97.3	96.1	91.9	96.4
Ng = 600	95.4	97.4	97.5	94.9	86.0	92.7
Ng = 1000	92.6	96.9	96.5	92.4	83.4	87.7
Q = 2	100	100	100	100	99.9	94.7
Q = 4	89.8	94.5	94.2	89.0	74.2	89.8
PLS	95.1	97.8	97.5	95.5	83.4	89.8
CL .40	95.7	96.8	97.0	93.4	86.1	94.9
CL .20	95.9	97.5	96.9	94.8	89.1	96.1
PLD .40	94.1	96.9	97.1	95.6	90.1	89.4
PLD .20	93.8	97.2	96.9	93.2	86.7	91.1
4 diff.	94.4	96.9	96.9	94.2	84.9	89.9
16 diff.	95.4	97.6	97.2	94.7	89.3	94.6
Total	94.9	97.2	97.1	94.5	87.1	92.3

Goodness-of-recovery of optimally rotated loadings

The recovery of the optimally rotated loadings is quantified by a goodness-of-loading-recovery statistic (GOLR), i.e., by computing congruence coefficients $\phi$ (Tucker, 1951) between the true (${\lambda }_{gq}$) and estimated (${\stackrel{\mathbf{ˆ}}{\lambda }}_{gq}$) loadings per factor and averaging across factors q and groups g:

(10) $GOLR=\frac{\sum _{g=1}^G\sum _{q=1}^Q\phi \left({\lambda }_{gq},{\stackrel{\mathbf{ˆ}}{\lambda }}_{gq}\right)}{GQ}.$(10)

The GOLR evaluates the proportional equivalence of loadings (i.e., insensitive to factor rescaling) and varies between 0 (no agreement) and 1 (perfect agreement). Per criterion, the average GOLR is .99 (SD = .01). This excellent recovery is hardly affected by the conditions.

Goodness-of-recovery of factor variances and covariances

To quantify the recovery of the factor (co)variances, the mean absolute difference (MAD) between the true (${\psi }_{gq{q}^{\prime }}$) and estimated (${\stackrel{\mathit{ˆ}}{\psi }}_{gq{q}^{\prime }}$) factor (co)variances is calculated as follows:

(11) $MA{D}_{\mathrm{\Psi }}=\frac{\sum _{g=1}^G\sum _{q=1}^Q\sum _{q^{\prime }=q}^Q\left|{\psi }_{gq{q}^{\prime }}-{\stackrel{\mathit{ˆ}}{\psi }}_{gq{q}^{\prime }}\right|}{GQ\left(Q+1\right)/2}.$(11)

The average $MA{D}_{\mathrm{\Psi }}$ -values in function of the criteria and conditions are given in Table 4. They vary around .07 or .08, indicating an overall good recovery of the ${\mathbf{\Psi }}_g$-matrices by each criterion. For primary loading shifts, which cause severe disagreement between groups, a stronger enforcement of agreement by (a higher weight of) generalized procrustes leads to a worse recovery of the group-specific factor (co)variances. For the crossloading differences of .40, using a higher weight for oblimin to impose simple structure degrades the recovery of the factor (co)variances.

Table 4 Mean Absolute Difference between True and Estimated Factor Variances and Covariances, in Function of Five Rotation Criteria and the Simulated Conditions. See Table 3 Caption for Abbreviations

	.01GP + .99O	.10GP + .90O	.30GP + .70O	.50GP + .50O	.01LA + .99O
G = 2	.08	.06	.07	.07	.07
G = 4	.08	.07	.07	.08	.07
G = 6	.08	.07	.08	.09	.07
Ng = 200	.10	.08	.09	.10	.09
Ng = 600	.08	.06	.07	.07	.06
Ng = 1000	.07	.06	.06	.07	.06
Q = 2	.08	.07	.08	.08	.07
Q = 4	.08	.07	.07	.08	.07
PLS	.06	.07	.11	.15	.05
CL .40	.13	.10	.08	.08	.11
CL .20	.09	.07	.07	.07	.08
PLD .40	.06	.05	.05	.06	.06
PLD .20	.06	.05	.05	.05	.06
4 diff.	.07	.05	.06	.07	.06
16 diff.	.09	.08	.09	.09	.08
Total	.08	.07	.07	.08	.07

Wald tests for significant factor loading differences

To be conservative, we use .01 as the significance level⁴ α and the Bonferroni correction for multiple testing (Bonferroni, 1936), i.e., we divided α by J × Q and consider a loading to differ significantly when, for the corresponding Wald test, p < .00025 for Q = 2 and p < .000125 for Q = 4. Table 5 presents percentages of data sets for which the Wald tests were perfectly correct (% correct; i.e., no false positives or false negatives), without false positives (0 FP) and without false negatives (0 FN). For the % correct, we conclude that: (1) Overall, the ‘.50GP + .50O’ rotation gives the best results. (2) As an exception, for primary loading shifts, ‘.01LA + .99O’ performs better. (3) For primary loading decreases of .40 and .20, ‘.10GP + .90O’ and ‘.30GP + .70O’ perform very similar to ‘.50GP + .50O’. (4) The lowest % correct are, not surprisingly, observed for small differences, i.e., crossloadings and primary loading decreases of .20. (5) The performance is better in case of more groups, more observations per group, less factors and less differences.

Table 5 Percentages (%) of Data Sets for Which the Wald Test Results (α = .01, Bonferroni Corrected) for Between-Group Loading Differences are Perfectly Correct (i.e., No False Positives and No False Negatives; % Correct), without False Positives (0 FP) and without False Negatives (0 FN). For Each Simulated Condition, the Best % Correct Is Indicated in Bold Face. See Table 3 Caption for Other Abbreviations

	.01GP + .99O	.10GP + .90O	.30GP + .70O	.50GP + .50O	.01LA + .99O	.01GP + .99O		.10GP + .90O		.30GP + .70O		.50GP + .50O		.01LA + .99O
	% correct	% correct	% correct	% correct	% correct	0 FP	0 FN	0 FP	0 FN	0 FP	0 FN	0 FP	0 FN	0 FP	0 FN
G = 2	43	56	60	61	49	80	57	89	65	92	66	93	67	90	56
G = 4	45	68	71	74	61	64	75	84	82	87	83	89	83	85	73
G = 6	44	67	71	73	64	56	82	77	88	82	88	84	88	81	80
Ng = 200	36	48	50	50	41	77	48	90	54	92	55	92	55	90	46
Ng = 600	48	70	74	77	64	65	79	83	86	87	86	89	87	85	77
Ng = 1000	48	73	78	81	70	58	87	78	95	82	95	86	96	81	87
Q = 2	56	72	76	79	69	73	81	88	84	92	84	94	84	90	78
Q = 4	30	55	58	59	46	60	60	79	72	82	74	82	73	80	60
PLS	72	79	76	74	93	73	98	79	100	76	100	74	100	94	99
CL .40	25	57	73	81	50	31	91	63	93	78	94	86	94	57	90
CL .20	25	51	52	54	49	57	56	91	56	94	56	96	56	91	53
PLD .40	67	84	86	86	70	86	76	92	91	93	92	92	93	93	74
PLD .20	31	47	50	50	29	88	33	93	51	94	53	95	52	93	30
4 diff.	53	74	76	76	68	72	75	90	82	93	82	92	82	90	76
16 diff.	36	53	58	62	48	62	66	77	74	81	75	85	76	81	63
Total	44	64	67	69	58	67	71	83	78	87	79	89	79	85	69

When inspecting the ‘0 FP’ and ‘0 FN’ percentages, it is clear that: (1) For crossloadings and primary loading decreases of .20, the lower % correct is mainly due to false negatives. (2) With an increasing G and N_g, we observe the well-known trade-off between false positives and false negatives in function of sample size. (3) In case of more factors and more loading differences, the ‘0 FN’ and ‘0 FP’ percentages both decrease, which is due to the rotation being more intricate in these cases. Specifically, when Q = 4 more factor variances and covariances need to be optimized and 16 differences make it challenging to pursue agreement and/or simple structure per group – the latter is true for 16 crossloading differences in particular. (4) Focusing on the best criterion per type/size of loading differences, the occurrence of false positives is notably higher for crossloadings of .40. This confirms the suboptimal performance of oblimin – and most simple structure criteria – in case of item complexities larger than one (Lorenzo-Seva, 1999).

Earlier, we pointed out that using generalized procrustes as R^A could result in (false) small differences in an attempt to minimize (true) large differences, whereas loading alignment eliminates small differences while tolerating large ones. This explains why ‘.01LA + .99O’ performs best in case of primary loading shifts (i.e., the largest differences, of size $\sqrt{.6}$) and why ‘.50GP + .50O’ performs better for the other differences (of size .40 or .20). This is supported by the fact that ‘.50GP + .50O’ often results in false positives for primary loading shifts (Table 5).

Focusing on the best performing rotation for each type/size of loading differences (specified above), we inspected how many false positives (FP) and false negatives (FN) occurred for each affected data set. Out of the 614 data sets with FP, only one FP was found for 401 (65%) and two FP for 97 data sets (16%). Out of the 1799 data sets with FN, only one FN was found for 465 (26%) and two FN for 308 data sets (17%). FN are mainly found for differences of .20.

To evaluate how MGFR performs in case of no differences, we performed an additional simulation study according to the procedure described above, without manipulating loading differences (i.e., retaining manipulated factors 1–3). Out of these 900 data sets, 97% of the converged ‘.50GP + .50O’ rotations resulted in zero FP, whereas for 89 data sets this rotation did not converge. Note that ‘.01LA + .99O’ failed to converge for 99% of these data sets.

Wald tests for significant factor loadings

For evaluating the MM(s) of the groups, we look at Wald tests for significance of factor loadings across groups.⁵ Again, we focus on α = .01 and the Bonferroni correction divides α by J × Q. The percentage of data sets without false negatives (FN) does not differ across rotation criteria and is affected most by the type of loading differences. For ‘.50GP + .50O’ and ‘.01LA + .99O’, no FN occurred for 99 to 100% of the data sets with primary loading shifts or primary loading decreases. For crossloadings of .40, 92 to 93% of the data sets are without FN and, for crossloadings of .20, 60 to 61%. The results for the false positives (FP) are more intricate and are detailed in Table 6. The most important conclusion is that both the percentage of data sets without FP and the best performing rotation in this respect depend strongly on the type of loading differences. In case of primary loading shifts, generalized procrustes with a higher weight appears to create more small crossloadings that are detected as FP, whereas the loading alignment criterion ‘.01LA + .99O’ – also the preferred criterion for detecting differences in case of primary loading shifts – performs very well with 96% of the data sets being free from FP. In case of crossloadings of .40 and .20, the best criterion for detecting the differences – i.e., ‘.50GP + .50O’ – is also the best one for avoiding FP in terms of non-zero loadings. The percentage of data sets without FP is still quite low – i.e., 42% and 56% for the crossloadings of .40 and .20, respectively – again confirming that achieving simple structure is challenged by the crossloadings. In case of PL decreases of .40 and .20, ‘.50GP + .50O’ is clearly suboptimal for detecting significant non-zero loadings whereas it is the best one for detecting the differences. Luckily, in Section 3.3.4., we found that ‘.10GP + .90O’ performed nearly the same in terms of revealing differences while it is the best one to avoid false positive loadings in case of PL decreases. Selecting the mentioned best criterion for each type of loading differences, out of the 2085 data sets with FP, one FP was found for 751 (36%) and two for 384 (18%) data sets.

Table 6 Percentages (%) of Data Sets for Which the Wald Test Results (α = .01, Bonferroni Corrected) for Significant Loadings across Groups are without False Positives (0 FP). See Table 3 Caption for Other Abbreviations

	.01GP + .99O	.10GP + .90O	.30GP + .70O	.50GP + .50O	.01LA + .99O
G = 2	76	71	64	62	76
G = 4	68	56	50	49	69
G = 6	63	47	41	40	63
Ng = 200	78	73	67	64	80
Ng = 600	67	54	48	48	67
Ng = 1000	63	47	40	39	61
Q = 2	74	63	59	62	73
Q = 4	64	54	45	38	67
PLS	95	38	09	03	96
CL .40	17	19	30	42	18
CL .20	48	50	52	56	50
PLD .40	94	92	84	73	94
PLD .20	93	92	85	79	95
4 diff.	78	70	61	57	78
16 diff.	61	46	43	44	61
Total	69	58	52	51	70

Conclusions and recommendations for empirical practice

MGFR showed a good performance, especially given that the simulation study included small loading differences of .20. By means of the best rotation criterion for each configuration of loading differences, the loadings were recovered and rotated very well. Wald tests for detecting the differences were flawless for roughly 70% of the data sets (i.e., for 70% of the data sets, no false positives or false negatives were found). When false positives (FP) or false negatives (FN) did occur (i.e., for 30% of the data sets), they often pertained to just one or two loadings. The simulation confirmed how the number of groups and group sizes make out the FN-FP trade-off. Furthermore, the performance drops somewhat in case of more factors and more differences, which make the rotation more challenging. It proved to be possible to evaluate the MM(s) at the same time, but, in case of crossloadings, one should be aware of FP and, in case of primary loading decreases, a lower weight for generalized procrustes is advised.

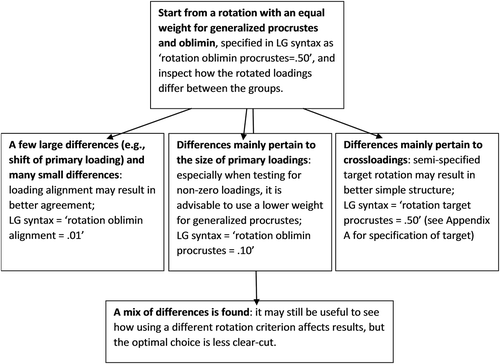
Since the best rotation criterion for detecting loading differences, as well as non-zero loadings, depends on the type and size of loading differences for a given data set, the following recommendations are in order (Figure 1): Because the type and size of loading differences are unknown beforehand and empirical data often contain a mix of differences, it is wise to first use the overall best criterion for distinguishing factor loading non-invariances; i.e., ‘.50GP + .50O’. Interestingly, this is equivalent to an unweighted combination of the generalized procrustes (GP) and oblimin (O) criterion. Then, one could scrutinize the between-group differences of the obtained loadings and adjust the criterion as follows: (1) When the rotated solution reveals a few larger differences and many very small differences, it is advisable to see whether the loading alignment (LA) criterion ‘.01LA + .99O’ eliminates the small ones. (2) When differences pertain to primary loading decreases and one also wants to identify non-zero loadings, lowering w to .10 improves results for the latter while hardly affecting the detection of differences. (3) When differences pertain to crossloadings, using LA or lowering w is not advisable. In this case, one may try whether an informed semi-specified target rotation (see Appendix A) improves the simple structure. (4) When a mix of differences occurs, the optimal choice is less clear-cut. Then, the advice is to resort to ‘.50GP + .50O’, but comparing to other criteria may still be informative.

Figure 1 Decision tree on how to decide on the rotation criterion for an empirical data set.

Application

To illustrate the empirical value of MGFR, we applied it to data on the Open Sex Role Inventory (OSRI) downloaded from https://openpsychometrics.org/_rawdata/. The OSRI is a modernized measure of masculinity and femininity based on the Bem Sex Role Inventory (BSRI; Bem, 1974). Bem postulated that masculinity and femininity are two separate dimensions, allowing to characterize someone as masculine, feminine, androgynous or undifferentiated. The assumed MM of the BSRI has been widely contested, however (Choi & Fuqua, 2003). The OSRI contains 22 items (supposedly) measuring masculine characteristics alternated by 22 items measuring femininity (Appendix C). To the best of our knowledge, no studies on the MM of the OSRI have been published. Therefore, an EFA-based approach is preferred over CFA.

Note that the data is collected through the website and is thus not a random sample. For the purpose of our illustration, this is not a problem. Information is available on education, race, religion, gender and sexual orientation, as well as the country respondents are located in and whether English is their native language. We excluded non-native English speaking respondents to avoid differences due to misunderstanding items. Mainly respondents in the USA (2240), Great-Britain (357), Canada (180) and Australia (118) were left. Multigroup EFA confirmed factor loading invariance across gender, but revealed differences across sexual orientations and these results are reported below. Respondents with missing data on the items or grouping variable were excluded. For the reported analyses, 2767 respondents were included: 1539 hetero-, 568 bi-, 230 homo-, and 172 asexuals, and 258 who specified their sexuality as ‘other’.

The inadequacy of the masculine-feminine MM is confirmed by the fit of the corresponding baseline multigroup CFA model: CFI = .82 and RMSEA = .064. The CFI of multigroup EFA with two factors is .90 (RMSEA = .049) and dropped to .87 (RMSEA = .054) when imposing loading non-invariance. To identify the loading differences, MGFR was first applied with the generalized procrusted (GP) based criterion ‘.50GP + .50O’ as recommended in Figure 1. A mix of differences is found, corresponding to crossloadings appearing and primary loadings increasing or decreasing in one or more groups, but differences are never as sizeable as the primary loading shifts in the simulation study (i.e., loading alignment is not recommended). ‘.50GP + .50O’ rotation resulted in 14 loading differences and 71 non-zero loadings (out of 88), whereas ‘.10GP + .90O’ rotation resulted in 16 differences and 68 non-zero loadings, even though the rotated loadings look very similar. ‘.30GP + .70O’ rotation seemed to be a good middle ground with 14 differences and 69 non-zero loadings and these rotated loadings are given in Table 7, with Wald test p-values. Using simplimax-based group-specific targets did not improve the rotation.

Table 7 Rotated Loadings per Sexual Orientation for the OSRI Data and Wald Test P-Values. ‘M’ Refers to Masculinity, ‘F’ to Femininity, ‘Wald(=)’ to Tests for Loading Differences and ‘Wald(0)’ to Tests for Non-Zero Loadings. P-Values that are Significant at a Bonferroni-Corrected 1% Significance Level (i.e., P < .00014) are in Bold Face, as Well as Loadings that Differ Significantly across Groups

	Hetero-sexual		Bisexual		Homo-sexual		Asexual		Other		Wald(=) p-values		Wald(0) p-values
	M	F	M	F	M	F	M	F	M	F	M	F	M	F
Q1	.17	.03	.14	.10	−.06	.15	.07	.11	−.16	.18	.0007	.3100	.0000	.0020
Q2	−.44	.38	−.23	.54	.00	.56	−.13	.53	.00	.50	.0000	.1100	.0000	.0000
Q3	.66	−.19	.76	.00	.52	−.09	.48	−.05	.37	−.02	.0000	.0850	.0000	.0094
Q4	−.42	.60	−.04	.94	−.09	1.09	−.08	1.06	−.04	1.06	.0000	.0000	.0000	.0000
Q5	.47	−.01	.61	.22	.48	.17	.64	.15	.58	.03	.1000	.0130	.0000	.0001
Q6	−.14	.52	.02	.65	.05	.83	.12	.61	.03	.73	.0160	.0011	.0320	.0000
Q7	.21	.06	.07	.06	.11	.08	.12	−.03	.20	.15	.4100	.3200	.0000	.0620
Q8	−.27	.36	−.18	.50	−.16	.49	−.16	.47	−.14	.56	.4900	.1500	.0000	.0000
Q9	.43	−.21	.32	−.26	.61	−.24	.50	−.27	.44	−.34	.0150	.5400	.0000	.0000
Q10	−.34	.56	−.37	.77	−.13	.72	−.16	.81	−.18	.72	.0057	.0110	.0000	.0000
Q11	.32	−.01	.11	.05	−.08	.03	.19	.00	.15	.10	.0000	.6200	.0000	.5500
Q12	−.16	.19	−.22	.29	−.26	.35	−.29	.17	−.13	.37	.4300	.0810	.0000	.0000
Q13	.55	−.27	.61	−.20	.67	−.28	.72	−.25	.74	−.26	.0950	.9100	.0000	.0000
Q14	−.51	.11	−.31	.13	−.40	.17	−.42	.20	−.15	.17	.0019	.8800	.0000	.0000
Q15	.63	−.09	.79	.14	.80	.04	.78	.06	.72	.13	.0970	.0092	.0000	.0042
Q16	−.06	.69	.10	.83	.10	.87	.13	.90	.00	.87	.0420	.0360	.0270	.0000
Q17	.64	−.17	.70	−.02	.79	−.10	.74	−.06	.72	−.13	.3900	.4200	.0000	.0020
Q18	−.27	.59	−.12	.70	−.04	.81	−.03	.82	.04	.75	.0025	.0340	.0000	.0000
Q19	.27	.05	.32	.18	.17	.08	.23	.08	.25	.24	.5700	.1200	.0000	.0001
Q20	−.35	.44	−.33	.50	−.37	.45	−.39	.32	−.39	.44	.9600	.4400	.0000	.0000
Q21	.74	−.21	.58	−.20	.49	−.27	.49	−.18	.52	−.05	.0003	.0290	.0000	.0000
Q22	−.31	.28	−.24	.29	−.52	.38	−.42	.36	−.33	.51	.0065	.0210	.0000	.0000
Q23	.49	−.24	.47	−.05	.61	−.09	.42	−.07	.54	−.06	.1600	.0410	.0000	.0000
Q24	−.08	.34	.06	.29	.03	.30	.01	.23	−.08	.38	.2400	.3800	.3000	.0000
Q25	.40	−.22	.33	−.26	.14	−.16	.32	−.11	.36	−.05	.0270	.0970	.0000	.0000
Q26	−.29	.40	−.25	.51	−.12	.45	−.24	.33	−.02	.34	.0041	.1100	.0000	.0000
Q27	.45	−.02	.63	.06	.63	−.03	.72	.12	.64	.04	.0051	.3000	.0000	.2900
Q28	.20	1.45	.09	.87	−.17	.76	.02	1.05	−.18	.86	.0000	.0000	.0000	.0000
Q29	.41	−.05	.47	−.06	.38	.13	.54	.03	.57	.21	.1900	.0033	.0000	.0021
Q30	−.22	.51	−.11	.98	−.05	.83	−.11	.80	−.09	.83	.2700	.0000	.0001	.0000
Q31	.50	−.06	.58	−.05	.51	−.03	.57	−.06	.34	−.07	.1300	.9900	.0000	.4700
Q32	−.34	.35	−.27	.27	−.49	.41	−.30	.27	−.49	.54	.0330	.0065	.0000	.0000
Q33	.57	−.02	.62	−.11	.39	−.09	.34	−.07	.44	−.12	.0280	.8000	.0000	.2600
Q34	−.34	.38	−.27	.27	−.32	.29	−.44	.20	−.49	.33	.0750	.2000	.0000	.0000
Q35	.51	−.14	.58	−.13	.63	−.13	.47	−.11	.68	.00	.1500	.3500	.0000	.0055
Q36	−.38	.52	−.18	.82	−.10	.83	−.21	.80	−.08	.89	.0004	.0000	.0000	.0000
Q37	.23	−.11	.46	−.05	.50	.03	.57	−.02	.64	−.19	.0000	.0910	.0000	.0058
Q38	−.44	.31	−.48	.53	−.24	.52	−.25	.47	−.26	.43	.0086	.0360	.0000	.0000
Q39	.51	−.19	.68	.00	.69	.10	.72	−.10	.69	−.07	.0110	.0008	.0000	.0001
Q40	−.36	.70	−.04	1.13	−.03	1.04	−.30	1.03	−.01	.99	.0000	.0000	.0000	.0000
Q41	.55	−.15	.80	−.06	.79	−.06	.73	−.13	.80	.03	.0012	.1100	.0000	.0074
Q42	−.28	.34	−.22	.48	−.09	.54	−.06	.41	−.08	.60	.0200	.0087	.0000	.0000
Q43	.47	−.06	.49	.05	.61	.20	.66	−.03	.59	.05	.1100	.0270	.0000	.0330
Q44	.19	1.51	.08	.92	−.20	.79	.00	1.10	−.16	.86	.0000	.0000	.0000	.0000

Even though the factors can more or less be labelled ‘M’ (masculinity) and ‘F’ (femininity), hardly any of the items are pure measures of either M or F, which is supported by the p-values for the non-zero loadings (Table 7). Most of the significant loading differences seem to exist between heterosexuals on the one hand and (some of) the other groups on the other hand. This is confirmed by pairwise Wald tests that are obtained by the ‘knownclass’ option in LG (i.e., clustering the groups into five latent classes and enforcing a perfect prediction of class by group; Vermunt & Magidson, 2013). For example, for heterosexuals, Q4 (‘I give people handmade gifts’) has a negative crossloading on M and a decreased primary loading for F. The factor covariance is non-significant for all groups: −.05 for heterosexuals, .05 for bisexuals, −.03 for homosexuals, −.08 for asexuals and −.04 for ‘other’. The factor variances differ quite a bit across groups: the variances of M are 1.33, .98, .90, .89, .90, and the variances of F are .99, .89, 1.00, .88, 1.25 for that same order of groups, respectively. Therefore, oblimin rotation per group with fixed factor variances, using the Jennrich (1973) restrictions, overestimates the loading differences, i.e., 26 differences are found to be significant. In any case, before using the OSRI for comparing masculinity and femininity across sexual orientations, it needs to be revised to a large extent.

Discussion

Testing for MI is essential before comparing latent constructs across groups. When factor loading invariance fails, further MI tests are ruled out and one can either ignore the non-invariance and risk invalid conclusions, refrain from further analyses, or take action by scrutinizing loading differences. The latter may give clues on how non-invariances can be avoided in future research (e.g., excluding or rephrasing items). When looking for all kinds of differences (i.e., including primary loading shifts and crossloadings), multigroup EFA is the way to go. To properly identify these non-invariances, MGFR pursues both agreement and simple structure, disentangles loading differences from differences in the structural model, and enables hypothesis tests for the loadings.

When using the loading alignment criterion for agreement, MGFR may be conceived as an EFA extension of multigroup factor alignment (MGFA; Asparouhov & Muthén, 2014) in that it both aligns and rotates, albeit that – for now – it focuses on factor loadings only. Unlike MGFA, MGFR deals with all factors at once and allows for group-specific MMs to be investigated rather than assumed. Of course, before making latent construct comparisons, intercept invariance should be addressed as well, but like in MI testing, we prefer to tackle the levels of MI in a stepwise manner. While MGFA only assesses primary loadings and assumes differences to be small and pertaining to a minority of the loadings or groups (i.e., partial and/or approximate MI), we are not even assuming an invariant zero loading pattern. Therefore, it makes no sense to align the intercepts for enabling factor mean comparisons while rotating the factors toward one another to assess whether they are somewhat comparable in the first place. In future research, it would be interesting to study how MGFR can be combined with intercept alignment and whether it indeed needs to be a stepwise approach. To this end, the principles of MGFA need to be extended to the multi-factor EFA case, whereas currently it cannot even align CFA models with a crossloading. Clearly, the latter warrants a separate study in itself.

Since MGFR proved to be very promising, it would be worthwhile to devote more research to refining and extending it in a number of respects. Firstly, it would be interesting to determine invariant sets (Asparouhov & Muthén, 2014) of groups per factor loading, building on the pairwise Wald tests mentioned in the Application section. Secondly, the unrotated solution that is fed to the rotation procedure corresponds to a single set of random ‘starting values’ for the rotation and the latter may fail to converge or end up in a local optimum depending on these values. Future research will include an evaluation of the sensitivity to local optima and the possibility of a multistart MGFR procedure or a multigroup extension of the gradient projection algorithm, compatible with free factor variances. For now, the user is advised to repeat the analysis a few times to see whether this affects results. Thirdly, the rotation depends on the weight of the agreement versus the simple structure criterion. The best weight to use depends on the loading differences. It would be interesting to evaluate whether it can be automatically optimized for the loadings of a given data set. For now, the user is advised to compare a few rotations (Figure 1).

Finally, an interesting question is to what extent MGFR can serve as a precursor to multigroup EFA or CFA with partial loading invariance according to the identified loading differences and MM(s). Needless to say, this requires a crossvalidation approach (Gerbing & Hamilton, 1996), e.g., where each group is split in random halves, and thus larger sample sizes. When group sizes are too small or the number of groups is large, MGFR can team up with a mixture approach such as proposed by De Roover, Vermunt, Timmerman, and Ceulemans (2017), where groups are clustered according to the similarity of their loadings and the rotation would be applied per cluster.

Supplemental material

Supplemental data for this article can be accessed here.

Additional information

Funding

The first author was supported by the Netherlands Organization for Scientific Research (NWO) [Veni grant 451-16-004].

Notes

¹ Oblimin performs best when the parameter $\gamma$ is equal to zero (Jennrich, 1979) and then it is in fact direct quartimin rotation (Jennrich & Sampson, 1966), but we will refer to it as ‘oblimin’ throughout the rest of the paper.

² Note that Lorenzo‐Seva, Kiers, and Berge (2002) already presented a set of oblique rotations of multiple loading matrices to a compromise of simple structure and optimal agreement. These rotations are performed in a stepwise manner, however, making them hard to implement as a single rotation criterion in MGFR. Also, they either do not allow for differences in factor correlations between the groups or do not maintain between-group agreement in the final step, resulting in a suboptimal between-group agreement of the rotated loadings.

³ Note that when inducing >16 loading differences, the differences could be partially cancelled out by permuting factors (in case of primary loading shifts), increasing factor correlations (in case of crossloadings) or rescaling factors (in case of primary loading decreases).

⁴ The results for a (Bonferroni-corrected) significance level of .05 may be requested from the first author.

⁵ The output of LG 6.0 also contains z tests per group. In this case, the Bonferroni correction divides α by J × Q × G, which implies a loss in power. For these tests, the results on FP are highly similar as described in the text. The percentage of data sets without FN is lower, however, and this is especially the case for crossloadings of .40 and .20 and primary loading decreases of .40. Specifically, with ‘.50GP +.50O’ rotation, it is 80% for crossloadings of .40, 26% for crossloadings of .20, and 80% for primary loading decreases of .40. In practice, the results of the Wald tests for significant loadings across groups can be used to selectively test for significant loadings per group (i.e., to determine for which groups they apply), thus warranting a less rigorous correction for multiple testing.

⁶ The total differential is the sum of the partial derivatives multiplied by the corresponding differential/infinitisemal change.

Appendix A

An example syntax for a twenty-item four-factor multigroup EFA with optimal rotation is:

options

algorithm

tolerance = 1e-008 emtolerance = 0.01 emiterations = 2500 nriterations = 500;

startvalues

seed = 0 sets = 5 tolerance = 1e-005 iterations = 100 PCA;

missing includeall;

rotation oblimin procrustes = .50;

output

iterationdetail classification parameters = effect standarderrors rotation writeparameters = ’results_parameters.csv’ write = ’results.csv’ writeloadings = ’results_loadings.txt’;

variables

dependent V1 continuous, V2 continuous, V3 continuous, V4 continuous, V5 continuous, V6 continuous, V7 continuous, V8 continuous, V9 continuous, V10 continuous, V11 continuous, V12 continuous, V13 continuous, V14 continuous, V15 continuous, V16 continuous, V17 continuous, V18 continuous, V19 continuous, V20 continuous;

independent G nominal;

latent

F1 continuous,

F2 continuous,

F3 continuous,

F4 continuous;

equations

//factor variances and covariances

F1 | G;

F2 | G;

F3 | G;

F4 | G;

F1 <-> F2 | G;

F1 <-> F3 | G;

F1 <-> F4 | G;

F2 <-> F3 | G;

F2 <-> F4 | G;

F3 <-> F4 | G;

//regression models for items

V1 - V20 <- 1 | G + F1 | G + F2 | G + F3 | G + F4 | G;

//unique variances

V1 - V20 | G;

The categorical variable ‘G’ indicates the group memberships of the observations and ‘V1ʹ to ‘V20ʹ refer to the twenty items – they are to be replaced by the variable labels in the data set at hand. Details about the technical settings can be found in the Latent Gold manual (Vermunt & Magidson, 2013). ‘PCA’ refers to randomized PCA-based starting values that are described in De Roover, Vermunt, Timmerman, and Ceulemans (2017). Note that both the factor variances and covariances are free to vary across groups and that the optimal rotation is requested by ‘rotation oblimin procrustes = .50ʹ. In general, the latter has the following structure:

rotation <simple structure criterion> <agreement criterion><w>

The simple structure criterion can be ‘oblimin’, ‘geomin’ or ‘varimax’ – where the latter is orthogonal and should be used with factor covariances equal to zero (i.e., deleting the ‘Fx <-> Fx | G’ lines in the syntax). The agreement criterion can be either ‘procrustes’ for generalized procrustes or ‘alignment’ for loading alignment. When one wants to use alignment with a user-specified value for $\epsilon$ (the default is 1 × 10⁻¹²), the command becomes, e.g., ‘rotation oblimin alignment = .01 epsilon = 1e−6ʹ.

As an alternative simple structure criterion, target rotation can be applied by using ‘target = ’filename.txt’’, where the file should contain group-specific targets (i.e., one for each group) or one target to be used for all groups. Note that ‘−99ʹ or ‘.’ is used to indicate non-specified parts of the targets. For instance, two semi-specified group-specific targets for eight items and two factors would be communicated as follows:

‘0 −99

0 −99

0 −99

0 −99

−99 0

−99 0

−99 0

−99 −99

−99 −99

0 −99

0 −99

0 −99

0 −99

−99 0

−99 0

−99 0ʹ

To start from user-specified parameter values and only perform the rotation (e.g., to try different rotation criteria without repeating the model estimation), the ‘algorithm’ and ‘startvalues’ options can be modified as follows:

algorithm

tolerance = 1e-008 emtolerance = 0.01 emiterations = 0 nriterations = 0;

startvalues

seed = 0 sets = 1 tolerance = 1e-005 iterations = 0;

The user-specified parameter values are communicated through a text file containing the parameter values in the internal order of the parameters (Vermunt & Magidson, 2013), which is specified at the end of the syntax as ‘startingvalues.txt’.

Appendix B

When the unrotated factors of group g are orthonormal, the true (i.e., population-level) optimally rotated factor loadings ${\mathbf{\Lambda }}_g$ and factor covariance matrix ${\mathbf{\Psi }}_g$ can be expressed as functions of the unrotated orthonormal true loadings A_g as follows:

(12) $\begin{array}{c}{\mathbf{\Lambda }}_g={\mathbf{A}}_g{\mathbf{T}}_g\\ {\mathbf{\Psi }}_g={\left({{\mathbf{T}}^{\prime }}_g{\mathbf{T}}_g\right)}^{-1}\end{array}$(12)

where T_g indicates the group-specific Q × Q rotation matrix. As opposed to Jennrich (1973), no restrictions are imposed on the diagonal of (any of) the group-specific factor covariance matrices ${\mathbf{\Psi }}_g$. Instead, the following restriction is imposed across all groups, where the ‘diag’ operator extracts the diagonal elements of  Ψ_g:

(13) $\begin{array}{r}\frac{1}{G}\sum _{g=1}^{G}diag\left({\mathbf{\Psi }}_g\right)={\left[\mathbf{1}\right]}_{Q}or\sum _{g=1}^{G}diag\left({\mathbf{\Psi }}_g\right)=G{\left[\mathbf{1}\right]}_Q\end{array}$(13)

The differentials of the relations in Equations 12 and 13 are as follows:

(14) $d{\mathbf{\Lambda }}_g=d{\mathbf{A}}_g{\mathbf{T}}_g+{\mathbf{A}}_{g}d{\mathbf{T}}_g$(14)

(15) $d{\mathbf{\Psi }}_g=-{\mathbf{\Psi }}_g({{\mathbf{T}}^{\prime }}_{g}d{\mathbf{T}}_g+d{{\mathbf{T}}^{\prime }}_g{\mathbf{T}}_g){\mathbf{\Psi }}_g$(15)

(16) $\sum _{g=1}^{G}diag\left(d{\mathbf{\Psi }}_g\right)={\left[\mathbf{0}\right]}_Q$(16)

Let K_g be defined as:

(17) ${\mathbf{K}}_g={\mathbf{T}}_g^{-1}d{\mathbf{T}}_g{\mathbf{\Psi }}_{g}sod{\mathbf{T}}_g={\mathbf{T}}_g{\mathbf{K}}_g{\mathbf{\Psi }}_g^{-1}$(17)

Equations 14 through 16 then become:

(18) $d{\mathbf{\Lambda }}_g=d{\mathbf{A}}_g{\mathbf{T}}_g+{\mathbf{\Lambda }}_g{\mathbf{K}}_g{\mathbf{\Psi }}_g^{-1}$(18)

(19) $d{\mathbf{\Psi }}_g=-({\mathbf{K}}_g+{{\mathbf{K}}^{\prime }}_g)$(19)

(20) $\sum _{g=1}^{G}diag\left(d{\mathbf{\Psi }}_g\right)=-\sum _{g=1}^{G}diag({\mathbf{K}}_g+{{\mathbf{K}}^{\prime }}_g)=-\sum _{g=1}^{G}diag(2{\mathbf{K}}_g)={\left[\mathbf{0}\right]}_Q$(20)

It follows that ${\sum }_{g=1}^{G}diag({\mathbf{K}}_g)={\left[\mathbf{0}\right]}_Q$. Due to these restrictions, the diagonal elements of ${\mathbf{K}}_g$ may be decomposed as follows:

(21) $diag\left(K_g\right)=diag\left({\tilde{K}}_g\right)-\frac{1}{G}{\displaystyle \sum _{g^{\prime }=1}^{G}diag\left({\tilde{K}}_{g^{\prime }}\right)}=diag\left({\tilde{K}}_g\right)-diag\left(\overline{K}\right)$(21)

When ${\mathbf{\Lambda }}_g$ are the optimally rotated loadings for groups g = 1, …, G, the differential in Equation 5 is equal to zero, thus⁶:

(22) $\sum _{g=1}^{G}d{R}^{MG}\left({\mathbf{\Lambda }}_g\right)=\sum _{g=1}^G\sum _{j=1}^J\sum _{q=1}^Q\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{gjq}}d{\lambda }_{gjq}=\sum _{g=1}^G\sum _{j=1}^J\sum _{q=1}^Q\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{gjq}}{\left(d{\mathbf{\Lambda }}_g\right)}_{jq}=0$(22)

where ${\left(d{\mathbf{\Lambda }}_g\right)}_{jq}$ refers to the element in row j and column q of the differential in Equation 18. Since the optimal rotation restrictions affect the rotated loadings through the rotation matrix T_g only, the differential becomes:

(23) $\sum _{g=1}^G\sum _{j=1}^J\sum _{q=1}^Q\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{gjq}}{\left({\mathbf{\Lambda }}_g{\mathbf{K}}_g{\mathbf{\Psi }}_g^{-1}\right)}_{jq}=0$(23)

Since restrictions are imposed (across groups) on the diagonal elements of ${\mathbf{K}}_g$, but not on the offdiagonal elements, we will elaborate Equation 23 for its diagonal and offdiagonal elements separately. To this end, we introduce the matrix ${\mathbf{K}}_g^{\ast }\left(u,u\right)$ which consists of zeros except for the element in row u and column u, which is equal to the corresponding element of ${\mathbf{K}}_g$, i.e., $k_{guu}$. Similarly, ${\bar{k}}_{uu}$ refers to the element in row u and column u of the matrix $\overline{K}$ introduced in Equation 21. Then Equation 23 is equivalent to requiring:

(24) $\begin{array}{rl}& \sum _{g=1}^G\sum _{j=1}^J\sum _{q=1}^Q\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{gjq}}{\left({\mathbf{\Lambda }}_g{\mathbf{K}}_g^{\ast }\left(u,u\right){\mathbf{\Psi }}_g^{-1}\right)}_{jq}\\ & =\sum _{g=1}^G\sum _{j=1}^J\sum _{q=1}^Q\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{gjq}}{\lambda }_{gju}{k}_{guu}{\psi }_{guq}^{-1}\\ & =\sum _{g=1}^G\sum _{j=1}^J\sum _{q=1}^Q\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{gjq}}{\lambda }_{gju}\left({\tilde{k}}_{guu}-{\bar{k}}_{uu}\right){\psi }_{guq}^{-1}\\ & =\sum _{g=1}^G\sum _{j=1}^J\sum _{q=1}^Q\left[\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{gjq}}{\lambda }_{gju}{\tilde{k}}_{guu}{\psi }_{guq}^{-1}-\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{gjq}}{\lambda }_{gju}{\bar{k}}_{uu}{\psi }_{guq}^{-1}\right]\\ & =\sum _{g=1}^G\sum _{j=1}^J\sum _{q=1}^Q\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{gjq}}{\lambda }_{gju}{\tilde{k}}_{guu}{\psi }_{guq}^{-1}\\ & -\sum _{g=1}^G\sum _{j=1}^J\sum _{q=1}^Q\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{gjq}}{\lambda }_{gju}{\bar{k}}_{uu}{\psi }_{guq}^{-1}\\ & =\sum _{g=1}^G\sum _{j=1}^J\sum _{q=1}^Q\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{gjq}}{\lambda }_{gju}{\tilde{k}}_{guu}{\psi }_{guq}^{-1}\\ & -\sum _{g=1}^G\sum _{j=1}^J\sum _{q=1}^Q\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{gjq}}{\lambda }_{gju}\left(\frac{1}{G}\sum _{g^{\prime }=1}^G{\tilde{k}}_{g^{\prime }uu}\right){\psi }_{guq}^{-1}\\ & =\sum _{g=1}^G\sum _{j=1}^J\sum _{q=1}^Q\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{gjq}}{\lambda }_{gju}{\tilde{k}}_{guu}{\psi }_{guq}^{-1}\\ & -\frac{1}{G}\sum _{g=1}^G\sum _{j=1}^J\sum _{q=1}^Q\sum _{g^{\prime }=1}^G\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{gjq}}{\lambda }_{gju}{\tilde{k}}_{g^{\prime }uu}{\psi }_{guq}^{-1}\\ & =\sum _{g=1}^G\sum _{j=1}^J\sum _{q=1}^Q\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{gjq}}{\lambda }_{gju}{\tilde{k}}_{guu}{\psi }_{guq}^{-1}\\ & -\frac{1}{G}\sum _{g=1}^G\sum _{g^{\prime }=1}^G\sum _{j=1}^J\sum _{q=1}^Q\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{g^{\prime }jq}}{\lambda }_{g^{\prime }ju}{\tilde{k}}_{guu}{\psi }_{g^{\prime }uq}^{-1}\\ & =\sum _{g=1}^G\hspace{0.17em}\left(\sum _{j=1}^J\sum _{q=1}^Q\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{gjq}}{\lambda }_{gju}{\tilde{k}}_{guu}{\psi }_{guq}^{-1}\right.\\ & \left.-\frac{1}{G}\sum _{g^{\prime }=1}^G\sum _{j=1}^J\sum _{q=1}^Q\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{g^{\prime }jq}}{\lambda }_{g^{\prime }ju}{\tilde{k}}_{guu}{\psi }_{g^{\prime }uq}^{-1}\right)=0\end{array}$(24)

Without loss of generality, assume that ${\tilde{k}}_{guu}=1$, so that Equation 24 is equivalent to:

(25) $\begin{array}{rl}& \sum _{g=1}^G\left(\sum _{j=1}^J\sum _{q=1}^Q\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{gjq}}{\lambda }_{gju}{\psi }_{guq}^{-1}-\frac{1}{G}\sum _{g^{\prime }=1}^G\sum _{j=1}^J\sum _{q=1}^Q\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{g^{\prime }jq}}{\lambda }_{g^{\prime }ju}{\psi }_{g^{\prime }uq}^{-1}\right)\\ & =\sum _{g=1}^G\left(\sum _{j=1}^J\sum _{q=1}^Q{\lambda }_{gju}\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{gjq}}{\psi }_{gqu}^{-1}-\frac{1}{G}\sum _{g^{\prime }=1}^G\sum _{j=1}^J\sum _{q=1}^Q{\lambda }_{g^{\prime }ju}\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{g^{\prime }jq}}{\psi }_{g^{\prime }qu}^{-1}\right)=0\end{array}$(25)

Similarly, by using the matrix ${\mathbf{K}}_g^{\ast }\left(u,v\right)$ where $u\ne v$ and assuming that $k_{guv}=1$, we derive the following for the offdiagonal elements:

(26) $\begin{array}{rl}& \sum _{g=1}^G\sum _{j=1}^J\sum _{q=1}^Q\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{gjq}}{\left({\mathbf{\Lambda }}_g{\mathbf{K}}_g^{\ast }\left(u,v\right){\mathbf{\Psi }}_g^{-1}\right)}_{jq}\\ & =\sum _{g=1}^G\sum _{j=1}^J\sum _{q=1}^Q\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{gjq}}{\lambda }_{gju}{k}_{guv}{\psi }_{gvq}^{-1}\\ & =\sum _{g=1}^G\sum _{j=1}^J\sum _{q=1}^Q\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{gjq}}{\lambda }_{gju}{\psi }_{gvq}^{-1}\\ & =\sum _{g=1}^G\sum _{j=1}^J\sum _{q=1}^Q{\lambda }_{gju}\frac{\mathrm{\partial }{R}^{MG}}{\mathrm{\partial }{\lambda }_{gjq}}{\psi }_{gqv}^{-1}=0\end{array}$(26)

Therefore, the optimal rotation restrictions for each group can be expressed in matrix form as follows:

(27) $\begin{array}{rl}& {\mathbf{F}}^{MG}={{\mathbf{\Lambda }}^{\prime }}_g\frac{d{R}^{MG}}{d{\mathbf{\Lambda }}_g}{\mathbf{\Psi }}_g^{-1}-diag\left(\frac{1}{G}\sum _{g^{\prime }=1}^G{{\mathbf{\Lambda }}^{\prime }}_{g^{\prime }}\frac{d{R}^{MG}}{d{\mathbf{\Lambda }}_{g^{\prime }}}{\mathbf{\Psi }}_{g^{\prime }}^{-1}\right)\\ & ={\left[\mathbf{0}\right]}_{Q\times Q}\end{array}$(27)

where – in this case – the ‘diag’ operator indicates that the offdiagonal elements are set to zero. Note that, when one prefers to use a reference group with factor variances fixed to one instead of restricting the across-group mean of the factor variances, one can use the restrictions ${{\mathbf{\Lambda }}^{\prime }}_g\frac{d{R}^{MG}}{d{\mathbf{\Lambda }}_g}{\mathbf{\Psi }}_g^{-1}={\left[\mathbf{0}\right]}_{Q\times Q}$ for the non-reference groups and the restrictions in Equation 2 (Jennrich, 1973) for the reference group. In that case, the agreement part of the criterion R^MG is essential to prevent the factor variances of the non-reference groups to become very large in order to minimize the oblimin criterion.

Appendix C

List of items for the Open Sex Role Inventory and what they intend to measure between brackets; ‘M’ refers to masculinity and ‘F’ to femininity:

Q1. I have studied how to win at gambling (M).

Q2. I have thought about dying my hair (F).

Q3. I have thrown knives, axes or other sharp things (M).

Q4. I give people handmade gifts (F).

Q5. I have day dreamed about saving someone from a burning building (M).

Q6. I get embarrassed when people read things I have written (F).

Q7. I have been very interested in historical wars (M).

Q8. I know the birthdays of my friends (F).

Q9. I like guns (M).

Q10. I am happiest when I am in my bed (F).

Q11. I did not work very hard in school (M).

Q12. I use lotion on my hands (F).

Q13. I would prefer a class in mathematics to a class in pottery (M).

Q14. I dance when I am alone (F).

Q15. I have thought it would be exciting to be an outlaw (M).

Q16. When I was a child, I put on fake concerts and plays with my friends (F).

Q17. I have considered joining the military (M).

Q18. I get dizzy when I stand up sharply (F).

Q19. I do not think it is normal to get emotionally upset upon hearing about the deaths of people you did not know (M).

Q20. I sometimes feel like crying when I get angry (F).

Q21. I do not remember birthdays (M).

Q22. I save the letters I get (F).

Q23. I playfully insult my friends (M).

Q24. I oppose medical experimentation with animals (F).

Q25. I could do an impressive amount of push ups (M).

Q26. I jump up and down in excitement sometimes (F).

Q27. I think a natural disaster would be kind of exciting (M).

Q28. I wear a blanket around the house (F).

Q29. I have burned things up with a magnifying glass (M).

Q30. I think horoscopes are fun (F).

Q31. I don’t pack much luggage when I travel (M).

Q32. I have thought about becoming a vegetarian (F).

Q33. I hate shopping (M).

Q34. I have kept a personal journal (F).

Q35. I have taken apart machines just to see how they work (M).

Q36. I take lots of pictures of my activities (F).

Q37. I have played a lot of video games (M).

Q38. I leave nice notes for people now and then (F).

Q39. I have set fuels, aerosols or other chemicals on fire, just for fun (M).

Q40. I really like dancing (F).

Q41. I take stairs two at a time (M).

Q42. I bake sweets just for myself sometimes (F).

Q43. I think a natural disaster would be kind of exciting (M).

Q44. I decorate my things (e.g. stickers on laptop) (F).