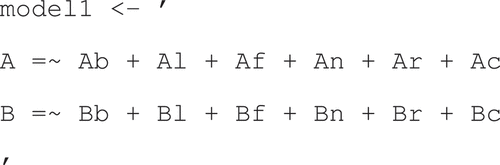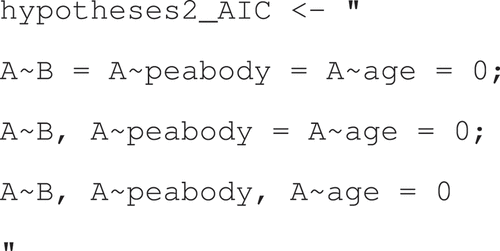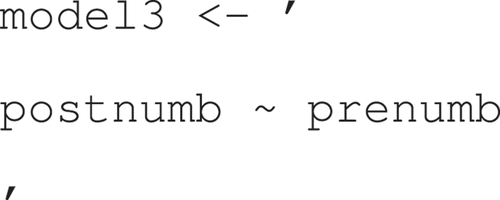AIC-type Theory-Based Model Selection for Structural Equation Models

ABSTRACT

Structural equation modeling (SEM) software commonly report information criteria, like the AIC, for the model under investigation and for the unconstrained/saturated model. With these criteria, (non-)nested models can be compared. This comes down to evaluating equalities (e.g., setting some paths equal or to 0). These criteria cannot evaluate inequality restrictions on the parameters, while the AIC-type criterion called GORICA can. For example, GORICA can evaluate the hypothesis stating that one predictor has more (standardized) strength than some other predictors. This paper illustrates inequality-constrained hypothesis-evaluation in SEM models using the GORICA (in R). Examples will be presented for confirmatory factor analysis, latent regression, and multigroup latent regression.

KEYWORDS:

• GORICA
• model selection
• theory-based hypotheses
• lavaan

Introduction

Common practice in structural equation modeling (SEM; Bollen, 1989) is to compare nested and non-nested models. The fit of nested models can be compared with a ${\chi }^2$-difference test or with information criteria like Akaike’s information criterion (AIC; Akaike, 1973) and Bayesian information criterion (BIC; Schwarz, 1978). The AIC and BIC can also compare non-nested models. They can be used to select the best model out of a set of two or more models (as opposed to two nested models with the ${\chi }^2$-difference test). These criteria evaluate models/hypotheses with equalities; for instance, setting the strength of some paths equal to each other, setting one or more paths to zero, or setting some (co)variances to zero. With the AIC and BIC (but also the ${\chi }^2$-difference test), it is impossible to evaluate theory-based hypotheses containing inequality/order restrictions on the parameters, while researchers often have such hypotheses. For example, a researcher may on forehand expect that one predictor has more strength than other predictors or that the variances of random effects are positive. These hypotheses can be expressed in order restrictions on the parameters: e.g., $H_{1a}:{\beta }_1>{\beta }_2>{\beta }_3$ and $H_{1b}:\kappa >0,\omega >0$, respectively. Such hypotheses are often referred to as informative hypotheses (Hoijtink, 2012), inequality-constrained hypotheses, order-restricted hypotheses, or theory-based hypotheses. These hypotheses cannot be evaluated with the AIC and BIC, but can be evaluated with Bayesian model selection (cf. Van Lissa et al., 2020) and with AIC-type order-restricted information criteria: the generalized order-restricted information criteria (GORIC; Kuiper et al., 2012, 2011 and its approximate version GORICA (2021).

An advantage of GORICA over GORIC is that its software is suitable for broad range of statistical models (e.g., SEM models). Notably, the software for the GORIC is currently only applicable to multivariate normal linear models, like the multivariate regression model. Another advantage of the GORICA is that it is sufficient to have the parameter estimates of the parameters addressed in the hypotheses of interest, and their covariance matrix. For SEM models, these can easily be obtained with the R package lavaan (Beaujean, 2014; Gana & Broc, 2019; http://lavaan.org; Rosseel, 2012) or the R package tidySEM (Van Lissa, 2019) which then uses lavaan or Mplus. I will devote this tutorial paper to theory-based model selection using the GORICA together with the lavaan package.

Preliminaries: GORICA

An information criterion (IC) balances fit and complexity, where fit denotes the compatibility of the hypothesis with the data, expressed by the maximum log likelihood part, and complexity the size of the hypothesis in terms of number of parameters, expressed by the penalty part:

$IC=-2\{\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{u}\mathrm{m}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{l}\mathrm{i}\mathrm{k}\mathrm{e}\mathrm{l}\mathrm{i}\mathrm{h}\mathrm{o}\mathrm{o}\mathrm{d}-\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{a}\mathrm{l}\mathrm{t}\mathrm{y}\}.$

Stated otherwise, an IC selects the hypothesis that describes the data best with the least number of parameters, out of a set of candidate hypotheses. An often used information criterion is the Akaike information criterion (AIC; Akaike, 1973), where the penalty equals the number of distinct model parameters: e.g., the number of distinct regression parameters, including the intercept, and the distinct error (co)variance(s). The AIC is an estimate of the Kullback–Leibler (KL) discrepancy (Kullback & Leibler, 1951), the distance between a candidate hypothesis and the true unknown hypothesis. Therefore, the hypothesis with the smallest AIC value is the preferred one in the set of candidate hypotheses. The AIC can evaluate hypotheses with equality constraints (“=”) and/or no constraints (“,”), that is, hypotheses where (some) parameters are set equal to zero or equal to each other; e.g., ${\beta }_1={\beta }_2,{\beta }_3={\beta }_4$.

By using the generalized order-restricted information criterion (GORIC; Kuiper et al., 2012, 2011) or its approximation (GORICA; 2021), researchers’ theories which often include order restrictions on the population parameters can directly be examined by evaluating theory-based hypotheses, like ${\beta }_1>{\beta }_2>{\beta }_3>{\beta }_4$. Thus, the GORIC and GORICA can evaluate theory-based hypotheses containing order restrictions on the parameters (“$<$” and/or “$>$”) besides equality restrictions (“=”) and no constraints (“,”). The GORIC is, like the AIC, an estimate of the KL discrepancy. In comparison with the AIC, its expression is based on the order-restricted maximum likelihood (i.e., the maximum likelihood under the order restrictions in the hypothesis) and has a corrected penalty (using so-called chi-bar-square weights) such that the order restrictions are properly accounted for. The latter comes loosely speaking down to deriving the expected number of distinct parameters. For example, ${\beta }_1>{\beta }_2$ represents 1.5 distinct regression parameters and not 2, as would be the case in the AIC. If there are no order restrictions (i.e., only equality constraints (“=”) and/or no constraints (“,”)), the GORIC reduces to the AIC. To ease the calculation of the GORIC for a broad range of models, the GORICA was derived using the fact that maximum likelihood estimates (mle’s) are asymptotically normally distributed. The fit part of the GORICA is based on the mle’s, which are a summary for the data, instead of the data themselves, which is used in the GORIC and AIC. Furthermore, the fit part of the GORICA is always based on the normal distribution even if the data do not follow one (like in a logistic regression). The fit values of the GORIC and GORICA differ in absolute sense but asymptotically not in relative sense when comparing candidate hypotheses. The penalty of the GORICA equates that of the GORIC.

In general, information criterion values themselves are not interpretable and only the differences between the values can be inspected. To improve the interpretation of the AIC, Akaike-weights (e.g., Akaike, 1978; Burnham & Anderson, 2002) can be computed. These weights represent the relative likelihood of a hypothesis given the data and the set of hypotheses (Burnham & Anderson, 2002; Wagenmakers & Farrell, 2004). Similarly, there exist GORICA weights (Kuiper et al., 2012):

$w_i=\frac{exp\left(-\frac{1}{2}GORIC{A}_i\right)}{{\sum }_{m=1}^{M}exp\left(-\frac{1}{2}GORIC{A}_m\right)}$

for $i=1,\dots ,M$, with $M$ the total number of hypotheses in the set. For instance, GORICA weights for Hypothesis $H_1$ and a competing hypothesis $H_2$ of $w_1=0.875$ and $w_2=0.125$ mean that $H_1$ has $w_1/w_2=7$ times more support than the competing hypothesis $H_2$.

The set of hypotheses of interest should consist of at least two hypotheses. One can include one or more competing hypotheses, for example, when there are multiple theories regarding the same set of parameters in the literature. It is possible to include the null hypothesis, but when it is not of interest, I advise against it. More specifically, since equality restrictions will never be exactly true (cf. Example 2), I advise to only include equalities in a hypothesis when they reflect an a priori theory or in case of exploration, like in case of ‘predictor selection’. Furthermore, be careful with hypotheses of interest that overlap, since their support will share (or better, divide) the support for the overlapping part (cf. Example 2). In general, only include the hypotheses that are a priori of interest and carefully inspect the results of these hypotheses.

Let us assume that the literature states two competing hypotheses: ${\beta }_1>{\beta }_2,{\beta }_1>{\beta }_3$ and ${\beta }_1<{\beta }_2,{\beta }_1<{\beta }_3$. Note that these hypotheses do not cover the whole parameter space, that is, do not cover all possible theories (e.g., ${\beta }_1>{\beta }_2,{\beta }_1<{\beta }_3$ is not included). Consequently, when both hypotheses of interest are weak hypotheses, GORICA selects the best out of a set of weak hypotheses. To refrain from this, one should include a safeguard hypothesis (Kuiper et al., 2012). A common choice is the unconstrained hypothesis $H_u$, where none of the parameters are restricted; in the SEM literature, often referred to as the saturated model. $H_u$ covers the whole space and represents all possible theories, thus, including the one(s) of interest. The unconstrained hypothesis should be used to investigate whether the hypotheses of interest are weak or not. When at least one is not (i.e., $w_m>w_u$, that is, $w_m/w_u>1$), the relative support for the hypotheses of interest (e.g., $w_1/w_2$) can be inspected. A more powerful choice for the fail-safe hypothesis is the complement (Vanbrabant et al., 2020), currently in software only available for one theory-based hypothesis. In case of one theory-based hypothesis $H_1$, its complement represents all theories except the one expressed in $H_1$, that is, the full parameter space without $H_1$ (i.e., $H_c:$ not $H_1$). In contrast to the unconstrained hypothesis, the complement acts like another hypothesis of interest and, therefore, $w_1/w_c$ is of interest. If, in the weights-example above, $H_2$ is the complement of $H_1$, $H_1$ is $w_1/w_c=0.875/0.125=7$ times more supported than its complement. Furthermore, $w_c=0.125$ can be interpreted as a 12.5% error probability associated with a decision in favor of $H_1$.¹

It is important to note that comparing parameters (e.g., ${\beta }_1>{\beta }_2$) is only meaningful if these parameters are measured on the same scale, for instance, in case of standardized parameters. In case of grouping variables, comparison of parameters should be done on the unstandardized parameters (because of interpretation: what does a parameter for the standardized version of gender mean?). In case (some of) the parameters are compared with a value (e.g., ${\beta }_1>0.6,{\beta }_2>0.6$), standardized parameters may be needed such that the value(s) can be specified meaningfully. Notably, in the sem function in lavaan, the ‘std.lv = TRUE’ command renders standardized parameter estimates.

In the GORICA, two kinds of parameters are distinguished: target parameters² and nuisance parameters. The first are the ones addressed in the theory-based hypotheses and the latter are the ones not involved in the hypotheses of interest. Target parameters are usually (some of the) regression coefficients, intercepts, and factor loadings. Nuisance parameters are usually (residual) variances. The GORICA uses the (standardized) target parameter estimates and their covariance matrix. Notably, including the nuisance parameters does not effect the GORICA weights.

GORICA in R

There are two R functions that can calculate GORICA values and weights: the gorica function in the gorica package (Kuiper et al., 2020) and goric function (Vanbrabant & Kuiper, 2020) in the restriktor package (Vanbrabant & Rosseel, 2020). Both can take a fit object as input (e.g., an lm object or a lavaan object) but also the target parameter estimates and their covariance matrix (which can also be extracted from fit objects). Both functions, goric and gorica, render of course the same results. There are, however, some differences between the functions in functionality.

One difference is that the goric function has more options regarding the calculation of the penalty. The goric function uses by default a way to calculate the penalty which is faster than using bootstrap (the only way to calculate the penalty in the gorica function). This method often also renders more stable penalty values than the bootstrap method does. The precision of the penalty value obtained with the bootstrap method can be increased by increasing the number of iterations but this increases the computation time even more. When using the bootstrap method in the goric function, it is possible to state the number of available cores which then decreases the computation time somewhat. In some cases, the goric function detects that the default method does not work (fast enough) and it will automatically use the bootstrap method instead (and give a message that it did). It will not detect all cases, thus, when the goric function takes too much time, it may be better to specify yourself that it should do bootstrap by using the command: mix.weights = “boot”. More details can be found in the R scripts in the supplementary material on my github page (https://github.com/rebeccakuiper/GORICA_in_SEM).

Another difference is that the gorica function more easily handles lavaan objects. For instance, the gorica function can use the default names in the lavaan object, while the goric function requires you to specify the names of the target parameters in the models (consisting of only characters and numbers) such that it can use these. Notably, in a multi-group analysis (cf. Example 3), one cannot specify all the parameter names. Thus, in that case, the goric function cannot handle a lavaan object but needs the user to extract the target parameter estimates and their covariance matrix from the lavaan object. More details can be found in the R scripts in the supplementary material on my github page (https://github.com/rebeccakuiper/GORICA_in_SEM).

In the following sections, I will demonstrate how the GORICA can be applied to SEM models using the lavaan package. I will illustrate the evaluation of theory-based hypotheses by the GORICA in confirmatory factor analysis, latent regression, and multiple-group regression. The paper concludes with a discussion.

Theory-based SEM using GORICA

In this section, I discuss three examples which are based on the ones used in Van Lissa et al. (2020). I start with the general, running example and then apply this to three types of statistical models: confirmatory factor analysis, latent regression, and multiple-group regression. For each of the examples, a three-step procedure for the GORICA is used:

1. First, the model of interest and one or more theory-based hypotheses are formulated.

2. Second, the sem function in lavaan is used to estimate the (standardized) parameters of the SEM model under investigation, and their covariance matrix.

3. Third, the hypotheses and the results of the lavaan analysis are used as input for the gorica function in the gorica package (or the goric function in the restriktor package), returning GORICA values and weights.

In the example section below, I will start with formulating the model of interest and one or more theory-based hypotheses, both in words and R code. Then, I will discuss the results based on the estimates and their confidence intervals and based on the AIC, which cannot address hypothesis/-es of interest containing order restrictions. Subsequently, I will show the required R code to evaluate the hypothesis/-es of interest using GORICA and discuss its results. To save space, only the code for the gorica function is displayed in the examples below. Annotated R scripts, for both the gorica and goric functions, can be found in the supplementary material on my github page(https://github.com/rebeccakuiper/GORICA_in_SEM). This also includes code to make the path diagrams for the examples, using the lavaanPlot package (Lishinski, 2018).

Running example: Sesame Street data

The examples below will all be applied to the same data set: a simulated data set based on the Sesame Street data (Stevens, 1996), which is included as the dataset “sesamsim” in the gorica package. The example concerns the effect of watching one year of the tv-series “Sesame Street” on the knowledge of numbers of $N=240$ children aged between 34 to 69 months. Several variables have been measured before and after watching Sesame Street for one year: Knowledge of numbers before ($Bn$) and after ($An$) watching, and analogously, knowledge of body parts ($Bb$ and $Ab$), letters ($Bl$ and $Al$), forms ($Bf$ and $Af$), relationships ($Br$ and $Ar$), and classifications ($Bc$ and $Ac$). The score ranges on these variables ranges from “1 to 20” to ’1 to 70‘. In the examples, I will use these variables as well as the following ones: biological age in months ($age$; score range: 34 to 69), the Peabody test measuring the mental age of children ($peabody$; score range: 15 to 89), and gender ($sex$; 1 = boy, 2 = girl).

Example 1: Confirmatory factor analysis

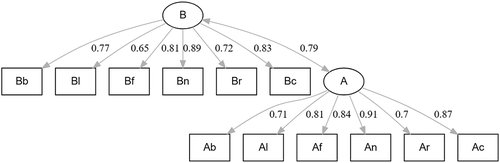
In this example, I will illustrate the evaluation of theory-based hypotheses in a two-factor confirmatory factor analysis, in which the $A$(fter) measurements load on the factor $A$, and the $B$(efore) measurements load on the factor $B$; as depicted in Figure 1. For the lavaan package, this is represented as follows:

Figure 1. The two-factor confirmatory factor model of Example 1; with standardized model estimates.

It is reasonable to expect that indicators are strongly related to the factors to which they are assigned. This is reflected by the following hypothesis (in R code) which states that each factor loading is larger than .6:

In this example, the target parameters are the factor loadings. These should be standardized such that the comparison of factor loadings to a reference value of .6 makes sense. In the sem function, the “std.lv = TRUE” command implies that the model is identified using standardized latent variables $B$ and $A$:

The standardized estimates are displayed in Figure 1 and these are all significant. When inspecting the 95% confidence intervals of the standardized estimates in Table 1 (obtained using “standardizedSolution(fit1)”), one concludes for each parameter that it is significantly different from .6 except for the first loading for factor $B$ (“$B$ =~ $Bl$”). Note that, by inspecting the confidence intervals, the restrictions in the hypothesis are not tested simultaneously. Therefore, it is unclear what to conclude now with respect to the hypothesis of interest. One might say that it is not fully supported. Independent of the conclusion, the support for the hypothesis of interest is not quantified by inspecting confidence intervals. To quantify the support of a hypothesis, one needs model selection methods like the AIC or GORICA.

Table 1. Standardized estimates (Std. est.) and 95% confidence intervals bounds in the confirmatory factor analysis example

Relationship	Std. est.	Lower bound	Upper bound
$A$ =~$Ab$	0.710	0.643	0.778
$A$ =~$Al$	0.811	0.763	0.860
$A$ =~$Af$	0.837	0.794	0.880
$A$ =~$An$	0.906	0.877	0.935
$A$ =~$Ar$	0.698	0.629	0.767
$A$ =~$Ac$	0.873	0.837	0.909
$B$ =~$Bb$	0.766	0.708	0.824
$B$ =~$Bl$	0.648	0.569	0.727
$B$ =~$Bf$	0.810	0.760	0.860
$B$ =~$Bn$	0.888	0.853	0.923
$B$ =~$Br$	0.721	0.654	0.787
$B$ =~$Bc$	0.828	0.782	0.874

AIC

When using the AIC, one cannot evaluate “hypothesis1” directly. One can, for example, evaluate whether all the factor loadings equal .6. That hypothesis can be compared to the hypothesis with no restrictions, $H_u$. When specifying the equality restrictions in the lavaan model, it renders an error (“The covariance matrix of the latent variables $A$ and $B$ is not positive definite”), because the correlation between $A$ and $B$ is due to restrictions estimated as $4.14>1$. Hence, we do not obtain an AIC value. This might imply that the restrictions do not hold. Since the GORICA weights asymptotically equate the Akaike weights in case of equalities, I will determine these as well and denote them as AIC weights.

In this example, the AIC weights are 0 and 1, implying full support for $H_u$. Now, one knows that at least one loading does not equal .6 and that there is overwhelming support for this. By inspecting the standardized factor loading estimates (which are all over .6), one might conclude that at least one loading is higher than 0.6, but still the others may equate .6.

Alternatively, one could have inspected many orderings to inspect all combinations of equalities. Then, some of these might obtain some support and $H_u$ will obtain support. If, for example, the ordering “$B$ =~ $Bl$ = .6” obtains the most support, one concludes that this loading equals .6 and the others do not. This does not provide information regarding the hypothesis of interest, except perhaps that it is not supported (but not how much). If $H_u$ obtains the most support, one concludes (if all possible orderings were included) that none of the loadings equal 0.6. By inspecting the standardized factor loading estimates, one might state that the hypothesis is supported, but still one cannot quantify the support for the hypothesis of interest.

By evaluating the hypothesis of interest directly, one can quantify its support. This can be done by applying the GORICA, as will be done next.

GORICA

The GORICA will evaluate “hypothesis1” ($H_1$) directly. Since there is only one hypothesis of interest, it will be evaluated against its complement (i.e., not $H_1$). The complement consist of all theories except $H_1$, meaning that at least one constraint is incorrect. Hence, here, the complement means that at least one factor loading is smaller than $.6$.

The hypothesis stated in “hypothesis1” and the lavaan output object “fit1” are input to the gorica function, as done below in the presented R code. In the first line, a seed is set. This is necessary for the computational replicability, because the computation of the penalty term in the GORICA requires sampling. If a different seed is used, a different random sample will be drawn, and there might be differences in the resulting penalty values. These differences are usually negligible, which can easily be examined with a sensitivity analysis by changing the seed and comparing the results (as demonstrated in the accompanying R scripts). If there is much sensitivity, the number of iterations to calculate the penalty should be increased. The second line in the R code below calls the gorica function. The “standardize = TRUE” command will ensure that the hypotheses are evaluated in terms of standardized parameters. The command “comparison = ‘complement’” enables the comparison of hypothesis1 ($H_1$) against its complement.

The main results are presented in Table 2. The table shows that the hypothesis of interest ($H_1$) has the largest fit and the smallest complexity and, thus, the smallest GORICA value and highest GORICA weight. The GORICA weight for $H_1$ (against it complement $H_{c1}$) is 0.99, that is, the support in the data in favor of $H_1$ is overwhelming: $H_1$ is $0.99/0.01\approx =82.3$ times more supported than its complement, with an error probability of $1-w_1=w_{c1}=.01$.

Table 2. Hypothesis evaluation in the confirmatory factor analysis example

Hypothesis	fit	complexity	GORICA	GORICA weights
$H_1$	33.581	8.147	−50.867	0.988
complement of $H_1$	32.879	11.883	−41.993	0.012

Conclusion: There is overwhelming support for the hypothesis that each factor loading is larger than .6.

Example 2: Latent regression

In this example, I will illustrate the evaluation of theory-based hypotheses in a latent regression model. The factors $B$ and $A$ have the same indicators as in Example 1. The difference is the addition of a latent regression in which $A$ is regressed on $B$, $age$, and $peabody$, to investigate whether children’s knowledge after watching Sesame Street for a year is predicted by their knowledge one year before, as well as by their biological and mental age (which have a correlation of .24); as graphically displayed in Figure 2. For the lavaan package, this is represented as follows:

Figure 2. The latent regression model of Example 2; with standardized model estimates.

On forehand, I expect that the children’s pre-knowledge is the most important predictor for the post-knowledge and that the relationship is positive. Furthermore, I am unsure whether the other two predictors add to the prediction; but, if they do, I expect a non-negative relation and that mental age is a better predictor than biological age. This can be represented by the following three (overlapping) hypotheses ($H_1$-$H_3$):

where the first hypothesis, $H_1$, specifies that a larger score on $B$ corresponds to a larger score on $A$ (i.e., a positive relation between $B$ and $A$) and that $age$ and $peabody$ do not predict $A$; the second hypothesis, $H_2$, specifies that the positive relation between $B$ and $A$ is stronger than the positive relation between $peabody$ and $A$ and that $age$ cannot be used to predict $A$; and the third hypothesis, $H_3$, specifies that the predictive power of $B$ is larger than that of $peabody$, which, in turn, is larger than that of $age$ which in turn is positive. Bear in mind that, only in case all these hypotheses are of interest, these should all be included in the set; especially if there is overlap like here (as will become clear later on).

The statistical model in “model2” is estimated as follows with the sem function:

The standardized estimates are displayed in Figure 2. When inspecting the 95% confidence intervals of the standardized regression estimates in Table 3 (obtained using “standardizedSolution(fit2)”), one concludes that only $B$ is a significant predictor and that this has a positive effect. Note that the restrictions in each of the three hypotheses of interest were not tested simultaneously. Therefore, it is unclear what to conclude now with respect to the hypothesis of interest. One might say that the first hypothesis in hypotheses2 (“$A$~$B>A$~$peabody=A$~$age=0$”) is supported. However, the (relative) support for this hypothesis of interest was not quantified. To quantify the support of a hypothesis, one needs model selection methods like the AIC or GORICA.

Table 3. Standardized estimates (Std. est.) and 95% confidence intervals bounds in the latent regression example

Relationship	Std. est.	Lower bound	Upper bound
$A$~$B$	0.789	0.730	0.848
$A$~$age$	0.000	−0.093	0.092
$A$~$peabody$	−0.016	−0.108	0.077

AIC

When using the AIC, one cannot evaluate “hypotheses2” directly. One can, for example, evaluate

together with the unconstrained hypothesis, $H_u$, as safeguard. Since the lavaan function gave errors for each hypothesis, I used the approximate AIC weights again. This results in AIC weights of .00, .65, .25, and .10. Thus, the hypothesis “$A$~$B,A$~$peabody=A$~$age=0$” is the preferred hypothesis, stating that children’s pre-knowledge (B) is a relevant predictor and the other two are not. It is not a weak hypothesis (.65 > .10) and it is 2.6 times more supported than “$A$~$B,A$~$peabody,A$~$age=0$” stating that mental age (peapody) is a relevant predictor as well. By inspecting the sign of the standardized regression parameter estimates, one might be able to state that the hypothesis of interest is supported, but one cannot quantify its support. By evaluating the hypothesis of interest directly, one can quantify its support. This can be done by applying the GORICA, as will be done next.

GORICA

The GORICA will evaluate the hypotheses in “hypotheses2” directly. Since these hypotheses do not cover the whole space, a fail-safe hypothesis is needed. Because the software can currently only compare one hypothesis of interest (at a time) against its complement and not for a set of hypotheses simultaneously, the complement cannot be used as the safeguard hypothesis. Therefore, the unconstrained hypothesis ($H_u$) will be included in the set (which is the default in the gorica function).

The following code is used to evaluate the three hypotheses of interest specified for the latent regression example together with the unconstrained hypothesis as safeguard:

The results are displayed in Table 4. Since all hypotheses have more support than the safeguard hypothesis $H_u$, all three hypotheses are not weak. With a support of .38, $H_1$ is the best hypothesis. However, the weights for $H_2$ and $H_3$ are close to that of $H_1$. In direct comparison, one can see that $H_1$ is only $.38/.31\approx 1.2$ and $.38/.28\approx 1.4$ more supported than $H_2$ and $H_3$, respectively. Consequently, $H_2$ and $H_3$ are also good hypotheses. If the hypotheses of interest do not overlap, there is just no compelling support for one of them and future research is needed to find support in favor or against these hypotheses (which is always a good research strategy of course). However, in this example, the three hypotheses of interest are nested ($H_1$ is a subset of $H_2$ which in turn is a subset of $H_3$). Then, more inspection is needed. Here, all have the same log likelihood value. This means that the distinction between these three hypotheses is solely based on the penalty values. Thus, the most restricted hypothesis (i.e., the one with the smallest penalty) is the preferred one. Moreover, the direct comparisons are not that meaningful now, since the relative weights all attained their maximum (cf. Vanbrabant et al., 2020). Because of the overlap, some of the support for the other hypotheses (here, $H_2$ and $H_3$) and also some support for $H_u$ reflects support for the preferred one (here, $H_1$) as well. Therefore, I will also examine $H_1$ against its complement $H_{c1}$ (i.e., $A$~$B<0$ in this case); reported in Table 5. This table shows that $H_1$ is $.87/.13\approx 6.9$ times more supported than its complement, with an error probability of $1-w_1=w_{c1}=.13$.

Table 4. Hypothesis evaluation in the latent regression example

Hypothesis	fit	complexity	GORICA	GORICA weights
$H_1$	6.836	0.500	−12.672	0.379
$H_2$	6.836	0.687	−12.297	0.314
$H_3$	6.836	0.822	−12.028	0.274
unconstrained ($H_u$)	6.894	3.000	−7.789	0.033

Table 5. Hypothesis evaluation in the latent regression example – vs complement

Hypothesis	fit	complexity	GORICA	GORICA weights
$H_1$	6.836	0.500	−12.672	0.988
complement of $H_1$	6.894	2.500	−8.789	0.126

Intermezzo: This example shows that one should carefully inspect the results of overlapping hypotheses: the relative support (i.e., ratio of GORICA weights) for the preferred hypothesis is often not compelling since it will share support with the overlapping ones. This example also gives some insight in equality restrictions never being exactly true: The log likelihood of $H_1$ (i.e., 6.84) is lower but close to the maximum value (i.e., 6.89), that is, the log likelihood of $H_u$. Because of sampling variation, this will always be the case for equalities that are true in the population, also for higher sample sizes. Therefore, its support (i.e., its GORICA weight) will never be exactly equal to 1. Notably, this is only a problem for true equalities, the asymptotic support for true inequalities is 1 (and that of incorrect equalities and incorrect inequalities is 0). Thus, be careful with specifying equality restrictions in hypotheses and with overlapping hypotheses. From my reasoning for the hypotheses, it is clear that I did not have clear a priori expectations, but if you do then make sure to evaluate only those (e.g., $H_1$ vs its complement).

Conclusion: Since the hypotheses overlap and the most restricted one ($H_1$) receives the most support (and is not weak), $H_1$ is the preferred hypothesis. Because the support for the other hypotheses also contain support for $H_1$, I compared $H_1$ to its complement and found convincing support for $H_1$. Thus, there is support for the hypothesis that a larger score on $B$ corresponds to a larger score on $A$ (i.e., a positive effect) and that $age$ and $peabody$ do not predict $A$. It is approximately 7 times more likely than its complement containing competing hypotheses.

Example 3: Multiple-group regression

In this example, I will illustrate the evaluation of theory-based hypotheses in a multi-group regression model, by including the grouping variable gender ($sex$) in the model. This means that there is one regression model for girls and one for boys, where the standardized model parameter estimates may differ between girls and boys. In the regression, $postnumb$ is regressed on $prenumb$, to investigate whether children’s knowledge of numbers after watching Sesame Street for a year is predicted by their knowledge of numbers one year before. For the lavaan package, this is represented as follows:

In the code, I use this model and add a grouping variable $sex$ (with two levels: “boy” and “girl”) to the sem function by including the following command: group = “sex”, as depicted below after specifying the hypothesis.

One hypothesis ($H_1$) is evaluated in which the difference in contribution of $prenumb$ to the prediction of $postnumb$ between boys and girls is examined. Hence, there are two groups and the default labeling is “$postnumb$~$prenumb$” and “$postnumb$~$prenumb.g2$”. Because of our own labeling (“boy” and “girl”), we can now use the following labels instead: “$postnumb$~$prenumb.boy$” and “$postnumb$~$prenumb.girl$”.

Using the latter, the hypothesis of interest is given by

where $H_1$ specifies that the relationship between postnumb and prenumb is higher for girls than for boys.

The statistical model in “model3” is estimated as follows with the sem function:

The standardized group-specific regression parameter estimates and their 95% confidence intervals (obtained with “standardizedSolution(fit3)”) are displayed in Table 6. Since the intervals overlap, it is unclear whether the parameters are significantly different or not. Since they overlap a lot, one can conclude that this is support for equal parameters. Notably, a better approach would be to inspect the confidence interval of the difference in estimates between boys and girls. Nevertheless, such a confidence interval (or a p-value) is not a quantification of the support for the hypothesis of interest. To quantify the support of a hypothesis, one needs model selection methods like the AIC or GORICA.

Table 6. Standardized estimates (Std. est.) and 95% confidence intervals bounds in the multiple-group regression example

Relationship	Group	Std. est.	Lower bound	Upper bound
$postnumb$~$prenumb$	boy	0.680	0.593	0.766
$postnumb$~$peabody$	girl	0.672	0.587	0.757

AIC

When using the AIC, one cannot evaluate “hypothesis3” directly. One can evaluate “$postnumb$~$prenumb.boy=postnumb$ ~ $prenumb.girl$”. This hypothesis is then compared to the hypothesis with no restrictions $H_u$. Since lavaan can only equate the unstandardized parameters (unless the data is scaled properly), I will use the approximate AIC again. The resulting AIC weights are .73 and .27, which means that the equality restriction is 2.7 times more supported than not restricting them. Hence, there is support for equal relationships. Even though this may have lead to the correct conclusion, it does not quantify the support for the a priori hypothesis of interest stating a positive effect. By evaluating the hypothesis of interest directly, one can quantify its support. This can be done by applying the GORICA, as will be done next.

GORICA

The GORICA will evaluate “hypothesis3” ($H_1$) directly. Since there is only one hypothesis of interest, I will use the compliment as safeguard (comparison = “complement”), which in this case equals $H_{c1}:postnumb$~$prenumb.boy>postnumb$~$prenumb.girl$.

The following code is used to evaluate the hypothesis of interest specified for the multiple- group regression example against its compliment:

The results are depicted in Table 7. This table shows that the hypothesis of interest and its compliment are equally likely, since both have a weight of approximately .50. Since the hypotheses do not overlap and are equally complex (i.e., have the same penalty value), this implies that their boundary is the preferred hypothesis, that is, $H_0:postnumb$~$prenumb.boy>postnumb$~$prenumb.girl$.

Table 7. Hypothesis evaluation in the multiple-group regression example

Hypothesis	fit	complexity	GORICA	GORICA weights
$H_1$	4.420	1.497	−5.846	0.499
complement of $H_1$	4.428	1.503	−5.851	0.501

Conclusion: There is support for the boundary of the hypothesis of interest and its complement, indicating that the relationship between postnumb and prenumb is equally high for girls and boys.

Discussion

This paper introduced theory-based hypotheses evaluation in SEM using the GORICA. The combination of the R packages gorica (or restriktor) and lavaan enables a free, open, and user friendly evaluation of theory-based hypotheses for SEM models. The approach elaborated in this paper has the following distinguishing features:

More than two hypotheses can simultaneously be evaluated, as was illustrated in Example 2. Additionally, one hypothesis of interest can be evaluated against it compliment (i.e., all possible theories excluding the one of interest); as was illustrated in all three examples. The GORICA weights are measures of support for each hypothesis in the set and the ratio of two GORICA weights is a measure of relative support for two hypotheses. As was illustrated by the relative support (i.e., ratio of two GORICA weights) in Examples 1 and 2, the support in the data for the hypothesis of interest can be convincingly stronger than the support for its compliment. The relative support can also be indecisive, as was illustrated in Examples 2 and 3. In Example 2, this was due to nested models and one should then investigate the support further (by examining the preferred hypothesis against its compliment). In Example 3, both hypotheses were equally likely and not overlapping (and of the same size), which indicates support for their boundary.

The challenge which should be overcome is the performance of the GORICA (and GORIC) in case of true equalities, which is work in progress. In case of true inequalities, the performance of the GORIC and GORICA is good, as shown by simulations Kuiper et al. (2011) and 2021, respectively. They show that the GORIC and GORICA will asymptotically choose the correct/best inequality-constrained hypothesis 100% of the times. They further show that, in case there is no overlap in hypotheses, the weight for the correct hypothesis will asymptotically go to one.

Correction Statement

This article has been republished with minor changes. These changes do not impact the academic content of the article.

Additional information

Funding

This work was supported by the the Netherlands Organization for Scientific Research (NWO) [VENI Grant 451-16-019].

Notes

¹ Since the weights depends on the hypotheses in the set, one should be careful when hypotheses overlap (because the support for the overlap is then divided among those). I advise to only use this error probability interpretation when the set of hypotheses covers all possible hypotheses (i.e., the whole parameter space) but without any overlap. For example, use this interpretation when one hypothesis is compared with its complement.

² (2021) refer to these as structural parameters, which may be confusing in a SEM context because of the parameters in the structural model. Therefore, I use the term target parameters.