Effect of diffusion limitation and substrate inhibition on steady states of a biofilm reactor treating a single pollutant

ABSTRACT

The occurrence of multiple steady states in a toluene biodegrading, diffusion-limited biofilm under aerobic conditions was investigated by computer models: one steady-state, and one nonsteady-state. Two stable and one unstable intermediate steady-state were identified in a narrow set of combinations of parameters values. The nonsteady-state model predicts conditions that evolve to a steady state that is within 0.02–1% of the solution of the steady-state model, depending on the number of grid points used, confirming the algorithms are valid. Multiple steady states occur if, (1) a biofilm is exposed to a constant gas-phase pollution concentration, which exceeds or undershoots a certain threshold, (2) in a narrow range of parameter values and (3) provided that the pollutant degradation follows Haldane kinetics. Such a biofilm displays half-saturation (i.e., Michaelis-Menten)-like apparent (“falsified”) kinetics from a concentration range starting at zero up to the occurrence of a second steady state. Multiple steady states and falsified kinetics can negatively affect a biofilter and the experimental determination of kinetic parameters, respectively.

Implications: The occurrence of multiple steady states in a VOC treating biofilm, shows the significant impact of degradation kinetics and diffusion limitation on the biofilm behavior. Moreover, the implied possible sudden drop of removal efficiency of a biofilter, based on the occurrence of multiple steady states lead to possible bottle-necks in biofilter application and operation.

Introduction

With growing awareness of hazards related to gaseous emissions released into the environment and their magnitude, the demand for pollution control technologies and regulations is increasing. One of the concerning compounds released by industries such as oil and gas, chemicals, pulp and paper, etc. are Volatile Organic Compounds (VOCs). Benzene, toluene, ethylbenzene and xylenes (BTEX) are among these VOCs and have major adverse effects. Biofiltration is a useful waste gas treatment technique that does not produce unwanted by-products. In a biofilter, microorganisms adhere to a synthetic, inorganic or organic surface of the filter media and act as a biocatalyst. The treatment of a single compound VOC (Álvarez-Hornos et al. 2008; Fu et al. 2011; Khan et al. 2016; Roy et al. 2003; Singh et al. 2010; Vergara-Fernández et al. 2007) and mixtures (Lee, Ryu, and Cho 2009; Mohammad et al. 2016; Namkoong, Park, and VanderGheynst 2003; Rene et al. 2012) have been evaluated in lab-scale or pilot-scale. Many experimental studies show rapid, often erratic changes in the elimination capacity, even when the biofilter is run in constant conditions. No clear mechanistic cause of this type of inconsistent performance has been put forward to date.

Computer simulation models have been developed to aid biofilter design and predict the behavior of a system. Ottengraf and Van Den Oever (Ottengraf and Van Den Oever 1983) were among the first who developed a biofilter model. Assumptions made in their model were e.g. (1) the resistance at the interface between the biolayer and the gas phase is negligible; hence, Henry’s law is applicable, (2) nutrient transport in the biolayer occurs by diffusion, (3) compared to the diameter of the packing particles, the thickness of the biofilm is negligible, (4) substrate degradation kinetics follows zero-order kinetics, and (5) the gas flow can be considered as plug flow. This basic biofilter model does not account for substrate inhibition effects or biomass growth. Shareefdeen et al. (Shareefdeen et al. 1993) developed the first steady-state biofilter model to describe methanol vapor degradation and one assumption was that oxygen and substrate were reaction rate limiting components. The dynamic model developed by Deshusses and Dunn (Deshusses and Dunn 1995; Deshusses, Hamer, and Dunn 1995) includes pollutant interaction and considered biodegradation of methyl ethyl ketone and methyl isobutyl ketone in a downward flow biofilter. One of the advantages is that it incorporates substrate inhibition and substrate interaction and it accounts for diffusion limitation. Li and De Visscher (Li and De Visscher 2008) developed a toluene biofilter model that combines Haldane kinetics with the Verhulst equation for microbial growth. The main advantage is that it describes changes in activity as a result of changing concentration or flow rate. De Visscher et al. (De Visscher, Sen, and Süß 2015) replaced the Verhulst portion of the model of Li and De Visscher (Li and De Visscher 2008) with a nitrogen dynamics and limitation model. This model includes toluene limitation but not oxygen limitation. Because of the assumption of a variable biofilm thickness, the model has the flexibility of deciding whether or not diffusion limitation should be considered on the calculated toluene degradation.

As shown in the literature, the development of simulation models that describe the behavior and performance of an actual biofilter has been given much effort (Datta, Philip, and Bhallamudi 2014; Kraakman and Rocha-rios 2011; Kumar, Bala, and Majumder 2012; Mathur and Majumder 2010). In other industrially utilized biological processes such as biofilm reactors, much effort has been spent on process simulation as well (Kiranmai, Jyothirmai, and Murty 2005; Melo and Vieira 1999). For example, in a biofilm reactor, multiple steady states were mathematically investigated (Olivieri et al. 2011; Russo et al. 2008; Volcke et al. 2007). In Volcke et al., it was shown that nitrification in a continuous stirred-tank reactor (CSTR) can lead to multiple steady states within a defined inlet concentration range. In Russo et al., (Russo et al. 2008) a three-phase internal loop airlift biofilm reactor is represented in terms of conversion of phenol by immobilized cells of Pseudomonas sp. OX1. The model incorporates adhesion of cells, growth of attached cells, and biofilm detachment. Adhesion of suspended cells was described by first-order kinetics and the linear relationship between biofilm detachment rate and biofilm loading was assumed in order to describe the effect of abrasion due to particle collisions. Multiple steady states were confirmed based on co-operative and competitive effects between immobilized and free cells. This proposed model was further developed by Olivieri et al. (Olivieri et al. 2011) and comprises double-substrate kinetics for cell and biofilm growth, description of substrate conversion in the biofilm as a parameter for the reactor performance and, as in the previous model, cell adhesion and biofilm detachment. Two different conversion regimes were identified, one controlled by the free cells and one controlled by the immobilized cells. For both regimes, multiple steady states were indicated. The regime controlled by immobilized cells was more complex in terms of multiplicity and stability of individual steady states.

The reason for multiple steady states could be explained by different considerations, such as mixing of the contaminant through the liquid media, diffusion into the biofilm and the effects of free cells and immobilized cells. Multiple steady states are known to occur in some chemostat-type processes (Zhang and Henson 2001). However, the possibility of multiple steady states when only substrate degradation in a diffusion-limited biofilm is considered has not been investigated to date. This system does not include mechanical mixing or a homogeneous pollutant concentration. Instead, molecular diffusion driven by a concentration gradient is the only transport mechanism.

Based on simulation results, it is known that the concentration of signaling molecules in quorum sensing displays two steady states. This occurs through an autocatalytic process regulated by the diffusion of the signaling molecules through the cell wall. The two steady states are hypothesized to be responsible for the switching mechanism between two metabolic states (e.g., virulent or non-virulent) (Klapper and Dockery 2010). The term kinetic bifurcation is sometimes used to indicate multiple steady states. However, because the term bifurcation more commonly refers to oscillating or chaotic reaction dynamics, a phenomenon unrelated to the multiple steady states studied here, the term will not be used in this work.

For this study it is hypothesized that molecular diffusion in a biofilm as the sole mass transfer mechanism, combined with biodegradation following Haldane kinetics, can trigger multiple steady states. Consequently, a biofilm can undergo a drastic alteration in removal efficiency in response to small gas-phase concentration changes as the system jumps from one steady state to the other. This would explain the sometimes erratic biofilter performance observed in experimental studies. The objective of this study is to test the hypotheses, and to establish the parameter space (i.e., set of parameter combinations) that lead to multiple steady states.

Model description

The occurrence of two or more steady states has been studied in biofilm reactors, as aforementioned, and has been well established. However, the presence of more than one steady state in an aerobic biofilm treating a gaseous VOC has not been studied yet. This case is solely based on the diffusion of contaminant in the biofilm and degrading a pollutant with Haldane kinetics. A steady-state and a nonsteady-state model were developed to determine the steady states. By developing two independent models it is possible to compare the outputs and hence validate the numerical aspects of the algorithms used. The steady-state model allows to rapidly screen for sets of conditions where multiple steady states can occur, and is more convenient in that respect. The nonsteady-state model determines which steady state will be reached given a prior history of the concentration in the system. Both models can calculate the overall reaction rates, effectiveness factors and concentration profiles in the biofilm. The following assumptions were made:

1. Since the gas phase concentration is in a low range, the gas-biofilm equilibrium is described by Henry’s law.

2. A planar (slab) geometry of the biofilm is assumed.

3. Substrate biodegradation and substrate inhibition was assumed to follow Haldane kinetics.

4. Two Models: a non-steady state and steady state

5. In the biodegradation kinetics, it is assumed that only one pollutant is limiting. Oxygen is assumed to be available in excess and not considered as a limiting factor.

Model development

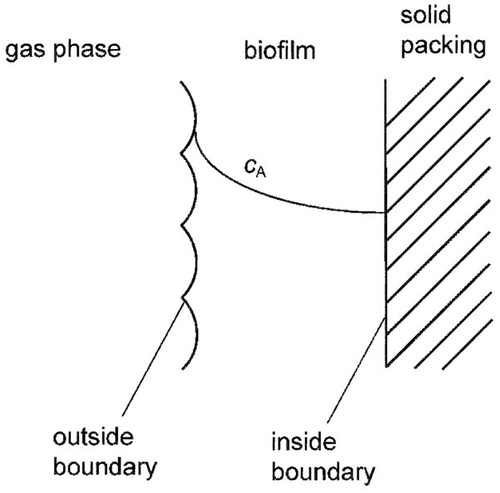
Figure 1 shows a schematic overview of a biofilm and its properties.

Figure 1. Schematics of a biofilm.

For the steady-state and nonsteady-state models molecular diffusion in the biofilm is governed by Fick’s law were A is the component to be degraded:

(1) $\mathrm{J}=\text{-}{\mathrm{D}}_{\mathrm{A}}\ast \frac{\mathrm{d}{\mathrm{c}}_{\mathrm{A}}}{\mathrm{d}\mathrm{x}}$(1)

were J is the flux of component A. D_A represents the diffusion coefficient of component A [g_substrate m⁻² h⁻¹], c_A is the concentration of the compound A [g_substrate m⁻³] in the biofilm, and x represents the length coordinate [m] in the direction of the biofilm thickness.

For both models, the biodegradation rate of toluene was assumed to follow Haldane kinetics, which considers substrate inhibition. It calculates the reaction rate as follows(Haldane 1930):

(2) $\mathrm{r}=\text{-}\frac{{\mathrm{V}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\ast {\mathrm{c}}_{\mathrm{A}}\ast {\rho }_{\mathrm{b}\mathrm{i}\mathrm{o}}}{{\mathrm{K}}_{\mathrm{s}}+{\mathrm{c}}_{\mathrm{A}}+\frac{{\mathrm{c}}_{{\mathrm{A}}^2}}{\mathrm{K}\mathrm{I}}}$(2)

V_max, K_s, K_I and ρ_bio express the maximum toluene degradation rate per unit weight of biomass per hour [g_substrate g_{dw substrate degrading biomass}⁻¹ h⁻¹], the half-saturation constant [g_substrate m⁻³], the inhibition constant [g_substrate m⁻³] and the biomass density in the biofilm [g_biomass m⁻³], respectively.

For the non-steady state model, a material balance of compound A in the biofilm, leads to the following equation (Shareefdeen et al. 1993):

(3) $\frac{\mathrm{\partial }{\mathrm{c}}_{\mathrm{A}}}{\mathrm{\partial }\mathrm{t}}={\mathrm{D}}_{\mathrm{A}}\frac{\mathrm{\partial }2{\mathrm{c}}_{\mathrm{A}}}{\mathrm{\partial }{\mathrm{x}}^2}\text{-}\frac{{\mathrm{V}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\cdot {\mathrm{c}}_{\mathrm{A}}}{{\mathrm{K}}_{\mathrm{s}}+{\mathrm{c}}_{\mathrm{A}}+\frac{{\mathrm{c}}_{\mathrm{A}}^2}{{\mathrm{K}}_{\mathrm{I}}}}\cdot {\rho }_{\mathrm{b}\mathrm{i}\mathrm{o}}$(3)

Next, define:

(4) $\mathrm{x}={\mathrm{x}}^{\mathrm{\prime }}\cdot \mathrm{L}$(4)

where L is the biofilm thickness [m], x represents the distance coordinate in the biofilm [m], and x’ is a dimensionless distance coordinate in the biofilm (i.e., the distance to the inner biofilm boundary, relative to the biofilm depth). The substitution of eq (4) into equation (4) lead to the following term:

(5) $\frac{\mathrm{\partial }{\mathrm{c}}_{\mathrm{A}}}{\mathrm{\partial }\mathrm{t}}=\frac{{\mathrm{D}}_{\mathrm{A}}}{{\mathrm{L}}^2}\cdot \frac{\mathrm{\partial }{ }^2{\mathrm{c}}_{\mathrm{A}}}{\mathrm{\partial }{\mathrm{x}}^{\mathrm{\prime }2}}\text{-}\frac{{\mathrm{V}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\cdot {\mathrm{c}}_{\mathrm{A}}}{{\mathrm{K}}_{\mathrm{s}}+{\mathrm{c}}_{\mathrm{A}}+\frac{{\mathrm{S}}^2}{{\mathrm{K}}_{\mathrm{I}}}}\cdot \rho \mathrm{b}\mathrm{i}\mathrm{o}$(5)

The concentration profile in the biofilm can be calculated with eq (5) by solving the partial differential equation as indicated below. The boundary conditions are as follows:

(6) ${\mathrm{c}}_{\mathrm{A}}\left|{ }_{{\mathrm{X}}^{\mathrm{\prime }}=1}=\right.\frac{{\mathrm{c}}_{\mathrm{A}\mathrm{g}\mathrm{a}\mathrm{s}}}{\mathrm{H}}$(6)

(7) ${\left.\frac{\mathrm{\partial }{\mathrm{c}}_{\mathrm{A}}}{{\mathrm{\partial }}_{{\mathrm{X}}^{\mathrm{\prime }}}}\right|}_{{\mathrm{X}}^{\mathrm{\prime }}=0}=0$(7)

x = 0 represents the inside boundary of the biofilm, away from the gas phase (Figure 1) and H represents the dimensionless Henry constant. In other words, the concentration at the surface of the biofilm which is exposed to the gas phase, will be calculated by dividing the gas phase pollutant concentration by the Henry constant (eq 6). The boundary condition at the inner boundary of the biofilm represents zero pollutant flux, i.e., the solid biofilter material is assumed to form a barrier impenetrable to compound A (eq 7).

In order to solve the second order partial differential equation, Orthogonal Collocation was used to approximate the concentration profile in the biofilm for the non-steady state model, following the approach by Villadsen and Stewart (1967). This algorithm uses an optimized grid space similar to quadrature, and uses the entire concentration profile to calculate concentration derivatives in the grid points with a high order of accuracy. This converts the partial differential equation into a set of ordinary differential equations in time, which are solved with an implicit algorithm as implemented in the Matlab function ode15s (Shampine and Reichelt 1997) . This approach might need more time to develop but saves computational time significantly in comparison with a finite difference scheme. The resulting ordinary differential equations are solved with Gear’s algorithm as implemented in Matlab.

The nonsteady-state model was run twice for every set of variables, once with zero initial concentration in the biofilm, and once with equilibrium concentration in the biofilm.

The steady-state method is based on eq (5) with the time derivative set equal to zero:

(8) $\frac{{\mathrm{D}}_{\mathrm{A}}}{{\mathrm{L}}^2}\ast \frac{{\mathrm{\partial }}^2{\mathrm{c}}_{\mathrm{A}}}{\mathrm{\partial }{\mathrm{x}}^{\mathrm{\prime }2}}\text{-}\frac{{\mathrm{V}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\ast {\mathrm{c}}_{\mathrm{A}}}{{\mathrm{K}}_{\mathrm{s}}+{\mathrm{c}}_{\mathrm{A}}+\frac{{\mathrm{S}}^2}{{\mathrm{K}}_{\mathrm{I}}}}\ast {\rho }_{\mathrm{b}\mathrm{i}\mathrm{o}}=0$(8)

which is solved with the 4–5th order Runge-Kutta-Fehlberg method with adaptive step size as implemented in the Matlab function ode45 (Shampine and Reichelt 1997), with the boundary condition of eq (6). As a second boundary condition the concentration gradient at the inside boundary of the biofilm was used (i.e., concentrations at the inside of the biofilm which is adjoined to the biofilm carrier). To convert this problem with two boundary conditions to an initial-value problem, the equations are solved with a set of concentrations at the inside boundary of the biofilm, where the concentration gradient is set to zero. For each initial concentration, the concentration at the outside biofilm boundary (i.e., at the gas side) is calculated. Next, the outside boundary pollutant concentration (, i.e., the boundary exposed to the gas-phase) is plotted versus inside boundary pollutant concentration (biofilm boundary adjoined to the biofilm carrier). If multiple inside concentrations lead to the same outside concentration, this is indicative of multiple steady states. These steady states are confirmed with calculations with the non-steady state model as described above. The two models predict the same steady states within 1% when 7 collocation points are used in the nonsteady-state model, and within 0.02% when 12 collocation points are used, confirming that the algorithms used are valid. In Table 1 a summary of used parameters and their units is listed.

Table 1. Summary of used parameters.

Parameter	Abbreviation	Unit
Flux of degredading compount	J	g m^−2 h^−1
Diffusion coefficient of degrading compount	DA	gsubstrate m^−2 h^−1
Concentration of degrading compount	cA	gsubstrate m^−3
Length coordinate	x	m
Reaction rate	r	g m^−3 h^−1
Maximum toluene degradation rate	Vmax	gsubstrate gdw substrate degrading biomass^−1 h^−1
Half-saturtion constant	Ks	gsubstrate m^−3
Inhibition constant	KI	gsubstrate m^−3
Biomass density	ρβιο	gbiomass m^−3
Biofilm thickness	L	m
Distance coordinate in the biofilm	x	m
Dimensionless distance coordinate in the biofilm	x’	–
Henry constant	H	–
Collocation points	N	–

Dimension analysis – Buckingham π theorem

In this study, the establishment of the parameter space where different steady states occur is arduous because of the large number of variables and dimensions. Dimension analysis is a way to reduce the complexity of a physical problem, based on similarity. The Buckingham π theorem (Buckingham 1914) is the basis of dimension analysis and states that a system described by n variables entailing k dimensions contains n – k independent dimensionless numbers that completely describe the system. Hence, defining p as the number of independent dimensionless numbers:

(9) $\mathrm{p}=\mathrm{n}-\mathrm{k}$(9)

In this model, there are nine relevant variables: r_average (the overall degradation rate in the biofilm, g_substrate m⁻² s⁻¹), r_external (the degradation rate assuming external conditions throughout the biofilm, g_substrate m⁻² s⁻¹), ρ_bio, V_max, D_A, K_s, K_I, c_Agas H⁻¹, and L. These include four dimensions (g_substrate, g_biomass, m, s) and based on eq (9), leading to five dimensionless numbers (π₁, π₂, π₃, π₄, π₅). Dimensionless numbers were chosen by defining ratios that have physical meaning. The following numbers were chosen:

(10) ${\pi }_1=\frac{{\mathrm{r}}_{\mathrm{a}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{g}\mathrm{e}}}{{\mathrm{r}}_{\mathrm{e}\mathrm{x}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{n}\mathrm{a}\mathrm{l}}}$(10)

(11) ${\pi }_2=\frac{{\rho }_{\mathrm{b}\mathrm{i}\mathrm{o}}\ast {\mathrm{V}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{\frac{D_A}{{\mathrm{L}}^2}\ast {\mathrm{c}}_{\mathrm{A}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}}}=\frac{{\rho }_{\mathrm{b}\mathrm{i}\mathrm{o}}{\mathrm{V}}_{\mathrm{m}\mathrm{a}\mathrm{x}}{\mathrm{L}}^2\mathrm{H}}{D_{\mathrm{A}}{c}_{\mathrm{g}\mathrm{a}\mathrm{s}}}$(11)

(12) $\pi 3=\frac{{\mathrm{K}}_{\mathrm{m}}}{{\mathrm{K}}_{\mathrm{I}}}$(12)

(13) $\pi 4=\frac{{\mathrm{c}}_{\mathrm{A}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}}}{{\mathrm{K}}_{\mathrm{m}}}=\frac{{\mathrm{c}}_{\mathrm{A}\mathrm{g}\mathrm{a}\mathrm{s}}}{{\mathrm{H}\mathrm{K}}_{\mathrm{m}}}$(13)

(14) ${\pi }_5=\frac{r_{external}}{L{V}_{max}\rho bio}$(14)

π₁ is known as the effectiveness factor in catalysis. The average reaction rate is calculated by integrating the local reaction rate across the biofilm, or (in steady state) by calculating the flux of A at the external biofilm boundary using Fick’s law. π₂ is the ratio of the biofilm’s ability to react A to the biofilm’s ability to diffuse A. π₃ is the ratio of half-saturation to substrate inhibition. Low π₃ means strong inhibition. π₄ is the ratio of external boundary concentration to half-saturation concentration. π₅ is the ratio of the reaction rate at the external biofilm boundary to the maximum reaction rate in the absence of inhibition.

Of these five dimensionless numbers, one dimensionless number (π₅) can be written explicitly in terms of two of the other dimensionless numbers, and represents the intrinsic reaction kinetics, so there is no need to explore it with computer simulations. This is shown in eq (15):

(15) ${\pi }_5=\frac{{\pi }_4}{1+{\pi }_4+{\pi }_3{\pi }_4^2}$(15)

Hence, it can be left out of the analysis and, four dimensionless numbers remain.

Results and discussion

Sample result

Figure 2 shows an example of the output generated by the steady-state model. The data in Table 2 were used for this model. The parameters are chosen so the resulting behavior is typical of toluene biofiltration. The concentrations in the figure are liquid-phase concentrations. Hence, for toluene (H = 0.276), the gas-phase concentration is 0.276 times the values in the y axis.

Table 2. Model parameters for falsified kinetics (Li and De Visscher (2008) and this study).

Apparent kinetics
Parameter	Value	Unit
Biomass density ρbio	1 x 10^5	gbiomass m^−3
Maximum toluene degradation rate (Vmax)	0.28	gSubstrate gdw Substrate degrading biomass^−1 h^−1
Michaelis-Menten constant (Ks)	1.5	gSubstrate m^−3
Inhibition constant (KI)	0.893	gSubstrate m^−3
Collocation points (N)	7	–
Diffusion coefficient (DA)	5.4x10^−10	m^−2 s^−1
Biofilm thickness	100x10^−6	m

Figure 2. Concentration at the pollutant at the outside surface of the biofilm as a function of the inside surface concentration of the particle. Two stable steady states are predicted as indicated by the dashed lines (i.e., 13.7–15.4 g m⁻³). Parameters used in the calculations are shown in Table 2.

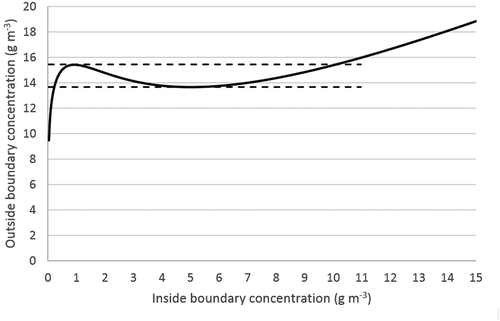
An area of two steady states can be seen in Figure 2, which shows the concentration of the pollutant at the outside surface (interface between biofilm and the gas-phase) of the biofilm as a function of the concentration at the inside surface (interface between biofilm and filterbed material). In a certain range of outside surface concentration, two possible steady states occur. In this case, the range of two possible steady states is approximately 14–15 g m⁻³ at the biofilm surface exposed to the gas-phase (i.e., around 4 g m⁻³ in the gas phase). Strictly speaking, there are three steady states in this range. However, the middle steady state is unstable. In this range, a slight increase of the pollutant concentration on the outside of the biofilm leads to a pronounced decrease of the reaction rate and hence of the concentration gradient (diffusion limitation), leading to a further increase of the pollutant concentration on the inside of the biofilm. Starting from the same steady state, a slight decrease of the concentration will lead to a pronounced increase of the reaction rate and hence of the concentration gradient (diffusion limitation), further decreasing the concentration. It follows that the steady state is unstable, and will never establish spontaneously.

Parameter space analysis

In this section, the set of dimensionless number combinations that leads to multiple steady states is determined. This section is not limited to any specific compound, and is valid for any biofilm system consistent with the assumptions made including biofilms in wastewater treatment, particularly nitrifying biofilms, where Haldane kinetics is expected to occur (e.g.,(Volcke et al. 2007)).

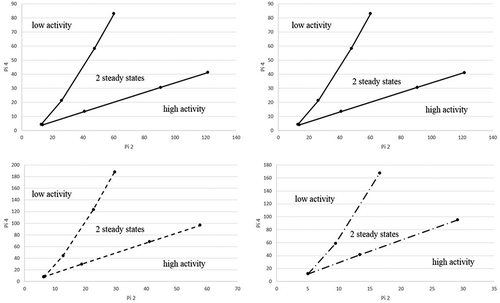
The boundaries of the two steady state area are depicted in Figure 3. In order to display the area of two steady states the dimensionless parameters π₂, π₃ and π₄ (eq 2.0, 2.1, 2.2) were used to generate the figure.

The left upper chart, right upper chart, left lower chart and right lower chart in Figure 3, correspond with π₃ values of 5, 2, 1, and 0.5, respectively. For each value of π₃, π₄ was adjusted to determine the lower and the upper threshold for the occurrence of two steady states. The area between the two solid lines describes the area where two steady states can exist, whereas the solid lines are the boundaries of the single steady state area. The intersection of the two solid lines (henceforth called the origin) is the point where the two steady states converge to a single steady state. Larger values of π₂ (i.e., more active or thicker biofilm or lower diffusivity) and π₄ (higher concentrations) lead to larger differences between the reaction rates of the two steady states. However, identical results in terms of the effectiveness factor (π₁) are obtained when π₂, π₃, and π₄ are kept constant while changing the individual variables. This was tested with model runs, confirming that the Buckingham π theorem was applied correctly. With change in reaction rate the removal efficiency (RE) of the biofilter will be affected as well. In particular, if the reaction rate drops, RE decreases as well. In case a biofilter is operating at a high removal efficiency (RE) and consequently with high activity, it is possible to jump to the low activity steady state, by a slight increase of surface concentration of the biofilm. On the contrary, if a biofilter is operating at low RE and consequently with low activity, a jump to a high activity steady state is possible by reducing the gas-phase concentration. The biofilm thickness is another parameter that can trigger a jump.

Apparent half-saturation kinetics

Substrate biodegradation and inhibition in this model follow Haldane kinetics. The apparent kinetics used here refers to the distortion of the prevailing Haldane kinetics caused by diffusion limitation. This will be illustrated using the model parameters listed in Table 2. These parameters are chosen so that the apparent kinetics is representative of toluene biofiltration (De Visscher, Sen, and Süß 2015; Li and De Visscher 2008).

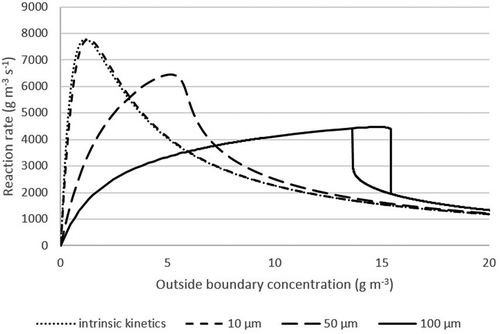
In Figure 4, the overall (or average) reaction rate of the pollutant in the biofilm is shown as a function of the inlet concentration and is depicted for different biofilm thicknesses. Overall reaction rates were calculated by integrating the local reaction rate across the biofilm. It can be seen that with increasing biofilm thickness the predicted kinetic behavior is changing. For the intrinsic kinetics (0 μm biofilm thickness), the model describes Haldane kinetics, as was used in the model, which means that there is no diffusion limitation. A very similar prediction is made at a biofilm thickness of 10 µm. In this case, even though a small biofilm exists, diffusion limitation is negligible. With increasing biofilm thickness, diffusion limitation has more influence on reaction kinetics, as can be seen for a biofilm thickness of 50 µm and 100 µm. At 100 µm the overall kinetics is more similar to the half-saturation kinetics as opposed to Haldane kinetics, which can be explained by diffusion limitation. If an experimental determination of kinetic parameters is conducted under these conditions, the apparent kinetics looks like half-saturation kinetics but actually is Haldane kinetics with diffusion limitation. The apparent (falsified) kinetic parameters best fitting the diffusion-limited kinetics up to 15 g m⁻³ in the presence of a 100 µm biofilm are V_max = 0.0516 g_substrate g_dw⁻¹ h⁻¹, and K_m = 2.62 g m⁻³. The fit between the falsified kinetics and the diffusion-limited simulation results in this concentration range is 1.1% (standard deviation).

Furthermore, the model predicts a sudden drop in reaction rate at a biofilm thickness of 100 µm and increasing the toluene concentration at the outside boundary above 15 g m⁻³, as shown in Figure 4. This corresponds with a gas-phase concentration of about 4 g m⁻³. When the outside concentration is decreased, starting from a high outside concentration, the reaction rate as a function of concentration deviates from the initial one. This confirms the area of two different steady states during biofilter operation, as aforementioned. To relate this data back to the parameter space analysis, with a concentration of 15 g m⁻³ on the outside biofilm boundary, the biofilm state corresponds with π₂ = 9.6, π₃ = 1.7, and π₄ = 10. Interpolating between the top right chart and the bottom left chart in Figure 1, we see that the conditions are in the two-steady-state region, close to the tip where the steady states coincide.

Note that the curves in Figure 4 express activity per volume of biomass, not per volume of biofilter, to avoid that the results would have different orders of magnitude. As a result, the thin biofilm seems more active.

Implications

The reason for the different steady states in this study can be explained based on the diffusion behavior of the pollutant into the biofilm in combination with the characteristics of Haldane kinetics. Haldane kinetics is characterized by a maximum reaction rate at intermediate concentrations and low reaction rates at both low and high concentrations. If the outside surface concentration of a biofilm exceeds a certain threshold, the concentration is high enough to lead to low reaction rates near the biofilm surface. If a high concentration is present throughout the biofilm, the reactivity is low throughout the biofilm. Due to the low reactivity, diffusion limitation is not pronounced and the high concentration throughout the biofilm will be maintained over time. As long as a second concentration threshold is not exceeded, it is also possible to maintain an intermediate concentration inside the biofilm, leading to high reactivity and a pronounced diffusion limitation, which in turn maintains a strong concentration gradient, which in turn maintains the intermediate concentration on the inside of the biofilm.

The occurrence of two operational stages with different reaction rates, as shown in Figure 3, led to two steady-state concentration profiles along the biofilm, as a result of diffusion limitation. In general, a diminishingly small change of the concentration at the biofilm surface exposed to the gas phase results in the development of two significantly differing diffusion profiles in the biofilm, computed with the steady state model and shown in Figure 5. One profile reaches a higher concentration at the inside of the biofilm (solid line) than the other and consequently displays lower activity. In turn, with a higher activity (dashed line), a lower concentration is present in the biofilm. When a biofilm initially empty of toluene is exposed to an outside boundary concentration of 15 g m⁻³ (i.e., about 4 g m⁻³ in the gas phase), the high-activity steady state develops. If an initially toluene-saturated biofilm is exposed to the same boundary condition, the low-activity steady state develops. A high-activity steady state can be pushed to a low-activity steady state by exposing the biofilm to a toluene concentration spike. Conversely, a low-activity steady state can be pushed to a high-activity steady state by temporarily purging the system of toluene.

Figure 5. Diffusion profile in a biofilm as a function of biofilm depth showing two different steady states: dashed line – high active steady state; solid line – low activity steady state. Parameters used in the calculations are shown in Table 2. Outside boundary condition: 15 g m^−3.

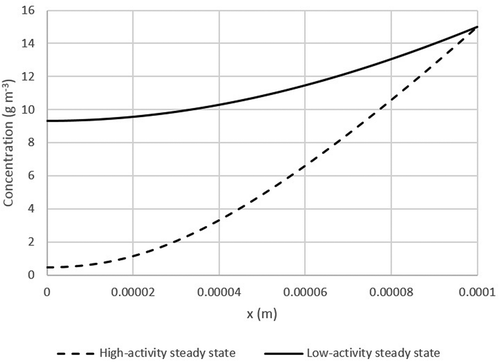
Figure 3. Parameter space where two steady states can occur (between the lines). Top left: π₃ = 5; top right: π ₃ = 2; bottom left: π₃ = 1; bottom right: π₃ = 0.5 Definitions of π variables: see eqs. (11, 12, 13).

The two steady states demonstrated here result from a different mechanism than observed in past studies. In well-mixed liquid systems the dilution of fresh influent by a dilute solution prevents the substrate concentration from reaching inhibitively high values. In this study, diffusion limitation is what maintains the low substrate concentration needed to avoid inhibition. In quorum sensing simulations, no inhibition mechanism is assumed. Instead, the diffusion through the bacterial membrane cell dilutes the signal molecule, preventing it from reaching concentrations that initiate a runaway autocatalytic process. Close proximity of bacteria lowers the flux of signal molecules through the membrane, triggering the quorum-sensing switch.

Figure 4 (see Table 2 for model parameters) explains several aspects of biofiltration, such as the need to start up a biofilter at low concentration, as the activity is highest at low concentration when the biofilm is thin. As the biofilms grow, the biofilter grows more robust to high pollutant concentrations, (i.e., the optimal concentration increases). However, mature biofilters tend to show highly variable pollutant elimination capacities, which could be the result of alternating steady states. The parameter boundaries for multiple steady states tends to be confined, e.g., existing only in a narrow range of biofilm thicknesses. However, sloughing of a biofilm can cause a range of biofilm thicknesses, and a thickness that is variable in time at any given location. Hence, it is likely that, at sufficiently high pollutant concentrations, parts of a biofilter are at a state of changing steady states at any given time, triggering jumps in the elimination capacity as a result of pollutant concentration fluctuations and/or sloughing.As a practical implication of this study, biofilters displaying rapid changes in the elimination capacity that cannot be explained by growth kinetics, or changing inlet conditions, are indicative of multiple steady states, meaning that the pollutant concentration is too high to ensure stable operation of the biofilter. Such biofilters can be stabilized by reducing the inlet concentration.

Figure 4. Falsified kinetics – Simulation of various biofilms thicknesses with Haldane kinetics. Parameters used in the calculations are shown in Table 2.

Conclusion

The presented numerical results predict that within a limited range of parameter values (biofilm thickness, kinetic parameters, etc.) and in a limited pollutant concentration range, two steady states occur in the biofilm of a biofilter. Consequently, as the pollutant concentration increases, a drastic jump from a high active to low active steady state is observed in the biofilm as the concentration exceeds the stability region of the high active steady state. The emergence of two stable steady states occurs: (1) within a limited envelope of parameter values, (2) within a limited range of pollutant concentrations at the outside surface of the biofilm, and (3) provided that biodegradation rates follows Haldane kinetics.

In addition, when the intrinsic kinetics follows the Haldane equation, the kinetics is distorted by diffusion limitations, and the kinetics takes on the appearance of half-saturation kinetics.

The practical implication is that a sudden drop in reaction rate and hence a decrease of the removal efficiency of the operating biofilter can be expected when the inlet pollutant concentration exceeds the stability region of the system. Furthermore, distortion of apparent kinetics can potentially interfere with the determination of kinetic parameters.

Additional information

Notes on contributors

Michael Süß

Michael Süß, was a Ph.D. candidate at the University of Calgary, Calgary—Canada, at the time this research was conducted.

Alex De Visscher

Alex De Visscher is a Professor and Chair, Chemical and Materials Engineering, Concordia University, Montreal, Quebec, Canada.