Hazardous waste management system for Thailand’s local administrative organization via route and location selection

ABSTRACT

This study proposed a decision support system (DSS) for optimizing transportation routing and disposal hub location for Thailand’s local administrative organizations’ hazardous waste management. The first step is to choose the origin and destination, as well as to collect data for each route. Each route’s decision criteria were based on traffic quality and risk measures from the perspective of users. An analytic hierarchy process (AHP) was used to compute effective weights for decision criteria. To achieve optimal routing, AHP weights were combined with a zero-one goal programming technique. The DSS operates systematically and successfully, taking into account both transportation risk and socioeconomic factors, and provides appropriate routes. Overall, this waste management system may provide useful information to decision-makers for prioritizing disposal site alternatives and implementing feasible waste management actions. The zero-one location design was then used to determine the best hub location. Based on two scenarios of six and fifteen CoG hubs, the results revealed that the best model for managing a case company’s hazardous waste was to establish 15 hubs scattered throughout the country for collecting points and then transporting them to the waste disposal plant in Phitsanulok province. Locating the hub near sink points would reduce transportation costs and backhaul issues, reducing the environmental impact of GHG emissions and increasing system efficiency.

Implications: The problem of waste pollution has become increasingly serious all over the world, particularly in developing countries that face significant pollution control challenges. End-of-life wastes cause economic, health, and environmental problems if they are not properly managed. As the world’s population and living standards rise, so does the amount of waste produced. The environmental impact is significant, with massive amounts of waste generated each year with only basic or minimal treatment to mitigate its impact. As a result, there is an urgent need for a method that can precisely optimize transportation routing and disposal hub location for Thailand’s local administrative organizations’ hazardous waste management (LAOs). The proposed decision support system (DSS) may provide useful information to decision-makers in prioritizing disposal site alternatives and implementing feasible waste management actions.

Introduction

Except for waste from factories and hospitals, community hazardous waste includes waste that has been contaminated with or contains peroxide and other toxic, flammable, oxidizing, irritating, corrosive, and explosive substances. Hazardous waste generated by homes, businesses, or communities is currently not properly managed, according to academic principles. The community’s hazardous waste operators and employees are in grave danger. The consequences of these hazardous wastes, which, if not properly managed, may have long-term effects on public health and the environment. The current authority of a LAO to manage hazardous waste in the community was granted by the local government.

The majority of LAOs lack the waste management tools they require. According to academic principles, the community may be at risk because no law specifies how hazardous waste should be transported from the community to the disposal site. The goal of community hazardous waste management is to create a safe environment and to reduce the impact of community hazardous waste contamination on human health and the environment.

A decision support system for LAO’s hazardous waste management is urgently needed. Hazardous waste management for a large region should be centralized so that hazardous waste in various subregions will be safely and efficiently disposed of. Strengthen the capacity of the LAO and private companies in the management of resources, capital, personnel, and technology so that they can serve as the area’s local authoritative organizer in charge of hazardous waste disposal.

According to our preliminary survey, LAO’s hazardous waste management policy has been in place for some time, but a waste disposal plant provider (WDP) in Phitsanulok Province lacks a decision support system (DSS) for assessing suitable routes and locations within their budget and time constraints. The WDP is already in place, offering suggested routes, costs, and delivery times to waste-collection hubs. The risk of unexpected transportation failure is high: during rainy seasons, hazardous waste may be delayed due to poor road conditions. Furthermore, the local government must have a depot to store a small collection of hazardous waste from the community up to the required quantity for transporting to a remote disposal location of the chosen logistic service provider.

Therefore, the goal of this research is to develop a decision support system (DSS) that can independently suggest proper routes from the local government depot and the remote disposal site of WDP for LAO based on a variety of qualitative decision factors. The DSS should provide appropriate routes based on transportation risk and socioeconomic factors. The best locations for hubs would also be determined using a Facility Location Problem (FLP) technique. Locations for business establishments would be chosen to keep service and penalty costs as low as possible. This means that DSS users will be able to make more reliable decisions using both qualitative and quantitative criteria.

This paper is organized as follows. Section 2 describes the background of the conceptual model in this study and some other relevant studies. The following section describes the decision support mechanism, Zero-One Programming Model (DSS-ZOPM). Section 4 reports the evaluation results. Finally, Section 5 concludes the paper and gives some recommendations for the local Thai government and future research direction (Figure 1).

Figure 1. Conceptual diagram of waste management optimization by DSS.

Literature reviews

According to Ghiani et al. (2014), a waste management system can be divided into two main sub-systems, (1) a regional waste management system involving strategic decision level in network design, such as investments for facilities, and (2) a municipal collection system involving tactical and operational decision levels, such as transport routes and waste flow allocation. Waste is defined as any material or substance, which is no longer suited for its intended use and needed to be eliminated (Laurent et al. 2014). Based on the level of risk, or how dangerous it is, waste can be classified into two major categories: non-hazardous or solid waste, and hazardous waste. The definition of “hazardous waste” is different in different countries.

Waste is hazardous if it affects human health, welfare, or the environment (EPA 2009). Fazzo et al. (2017) defined hazardous waste as non-household waste, including hazardous chemical waste. The hazardous waste in this study refers to waste generated from households and communities, including ignitable, toxic, poisonous, corrosive, flammable, combustible otherwise poses a threat to human health or the environment, which can be liquids, solids, gases, or sludge. The amount of those hazardous wastes increasing rapidly and seriously due to an expansion of population in Thailand, as well as the outbreak of an epidemic crisis that has changed people’s way of life (World Health Organization 2020).

Keeping people stay at home for stopping the spread of infection, refraining from traveling, and not going out to buy products in department stores or flea markets has resulted in an increasing amount of plastic waste (due to lockdowns, suspension of reusable items in stores, etc.), and other intensification waste of single-use products (such as surgical masks and gloves, etc.) from COVID 19 protection.

During the last decade, some scholars have developed several applications for hazardous waste management with different types of decisions such as facility location, routing or allocation and integrated network design problems. Those problems were complex involving multiple objectives and decision variables. Two solution approaches i.e. exact and approximation methods were applied to solve those optimization problems for effective management.

Samanlioglu (2013) formulated a location-allocation model to minimize simultaneously the total cost, transportation risk and location risk using a lexicographic weighted Tchebycheff for hazardous waste, in order to generate the Pareto-optimal solutions. Berglund and Kwon (2014) proposed a robust facility location problem for hazmat transportation by considering routing decisions of carriers using an exact full enumeration method for small or medium-size problems. This study aimed to find the locations of incinerators by minimizing fixed facility cost, transportation cost and exposure risk under a deterministic environment using numerical experiments. Jiang et al. (2014) constructed a mathematical model based on locating hazardous material treatment facilities and routing with different transportation modes and applied it in a real local multimodal network case study in Northeast China. Later Li et al. (2015) employed an integer linear program method to select the optimal location for collecting and handling industrial hazardous waste. The model was also applied in a case study in Hebei Province, China. Ghezavati and Morakabatchian (2015) developed a multi-objective location-routing model by considering fuzzy customer satisfaction. They implemented the proposed model with a real case in Petrochemical Special Economic Zone in Iran, which was solved by Lingo software. Zhao et al. (2016) suggested a multi-objective mixed-integer programming model by jointly the total cost and total risk to solve facility location and routing problems. The model was solved by an extended weighted Tchebycheff approximation and extended ε-constraint approximations. Yılmaz, Kara and Yetiş (2017) proposed a multi-objective mixed-integer location/routing model to minimize transportation costs and risks for large-scale hazardous waste management systems in Turkey. Homayouni and Pishvaee (2020) developed a multi-objective robust optimization model to design a collection and disposal network of hazardous waste under uncertain conditions. It aimed to optimize the trade-off between cost and risk of transportation and operations through the network decisions. The augmented ε-constraint method was then employed to solve the model with a real case study.

Several highly efficient approximation methods have been implemented for hazardous waste network design problems for improving computational performance. For instance, Berglund and Kwon (2014) used genetic algorithm to solve a robust facility location problem for hazmat transportation for large-scale problems. Ma et al. (2018) developed a multi-objective robust optimization model and used a fuzzy C-means clustering particle swarm optimization algorithm to group the demand points. An adaptive archives grid was then applied to solve robust routes of transportation. Rabbani, Heidari, and Yazdanparast (2019) introduced a multi-objective stochastic industrial hazardous waste location and routing model by considering a multi-period planning horizon and incorporating the inventory decisions into the model. Meta-heuristic algorithm such as non-dominated sorting genetic algorithm (NSGA II) and monte carlo simulation were applied to solve the model using a numerical problem. Araee and Aghamohammadi (2020) established a multi-objective model for solving vehicle routing problems for hazardous waste collection by taking travel time, travel risks, and economic aspects into consideration.Two meta-heuristic algorithms i.e. multi-objective particle swarm optimization algorithm (MOPSO) and the non-dominated sorting genetic algorithm (NSGA II) were employed to solve the model. Yu et al. (2020) proposed a novel stochastic bi-objective mixed-integer linear programming (MILP) to determine the number of locations and sizes of treatment, recycling and disposal facilities, as well as organize the transportation of hazardous waste among different facilities. A sample average approximation-based goal programming (SAA-GP) approach was adopted to solve the proposed model. Recently, Pourhejazy et al. (2021) introduced an original capacitated general routing model with time-window (CGRPTW) to identify a routing for hazardous waste electrical and electronic equipment (WEEE) collection practices. The proposed model was tested using various operational situations. Raeisi and Ghoushchi (2022) presented a multi-objective location-routing problem for hazardous wastes to reduce the risk of COVID-19 infection. Several meta-heuristic algorithms i.e. non-dominated sorting genetic algorithm-II, multi-objective particle swarm optimization, multi-objective invasive weed optimization, pareto envelope-based selection algorithm, multi-objective evolutionary algorithm based on decomposition and multi-objective gray wolf optimizer algorithms were used to solve numerical experiment problems and compared the results. The findings suggested that the multi-objective invasive weed optimization algorithm was the most efficient among those algorithms in solving large-scale sample problems. Table 1 summarizes those relevant literature.

Table 1. The relevant literature on hazardous waste management system.

References	Objective	Solution Method	Decision Problem	Validation Methodology
Samanlioglu (2013)	Minimize simultaneously total cost, transportation risk and location risk	A lexicographic weighted Tchebycheff approach (CPLEX)	Location-routing problem	Case study
Berglund and Kwon (2014)	Minimize total cost (fixed facility cost, transportation cost and exposure risk)	An exact full enumeration method, Genetic algorithm	Location-routing problem	Numerical experiment
Jiang et al. (2014)	Multi-objective and multimodal model	Exact method (LINGO)	Location-routing problem	Case study
Li et al. (2015)	Optimal locating approach	Integer linear programming method	Location	Case study
Ghezavati and Morakabatchian (2015)	Multi-objective location-routing model	Exact method (LINGO)	Case study	Case study
Zhao et al. (2016)	Multi-objective continuous network flow model by minimizing jointly total cost and total risk	Scalarization-based multi-objective integer programming approaches i.e. weighted-sum approach, Tchebycheff approach and e-constraint approach	Location-routing problem	Numerical experiment and case study
Yılmaz, Kara, and Yetiş (2017)	Mixed-integer location/routing model by minimizing transportation cost and risks	Exact methos	Location-routing problem	Case study
Ma et al. (2018)	Multi-objective robust optimization model	A fuzzy C-means clustering particle swarm optimization algorithm	Vehicle Routing Problems (VRPs)	Case study
Rabbani, Heidari, and Yazdanparast (2019)	A stochastic mixed-integer nonlinear programming model	Non-dominated sorting genetic Algorithm (NSGA-II) and monte carlo simulation	Location-routing problem, and inventory	Numerical experiment
Araee and Aghamohammadi (2020)	Multi-objective model by minimizing travel time, travel risks, and economic aspects	Two meta-heuristic algorithms: multi-objective particle swarm optimization algorithm (MOPSO) and the non-dominated sorting genetic algorithm (NSGA II)	Vehicle Routing Problems (VRPs)	Numerical experiment
Homayouni and Pishvaee (2020)	A multi-objective robust optimization model by minimizing the total cost including transportation and operations costs, and total risk of transportation and operations	Augmented ε-constraint method	Location- allocation problem	Numerical experiment and case study
Yu et al. (2020)	Two single-objective optimization problems for cost and risk minimization	A sample average approximation based goal programming algorithm (SAA-GP)	Location	Numerical experiment and case study
Pourhejazy et al. (2021)	Mixed-integer Linear Programming MILP (Capacitated General Routing Problem with Time-Window, CGRPTW)	Two metaheuristic algorithms i.e. neighborhood search procedures and tabu search	Vehicle Routing Problems (VRPs)	Case study
Raeisi and Ghoushchi (2022)	Robust-fuzzy optimization model	Several meta-heuristic algorithms such as non-dominated sorting genetic algorithm-II, multi-objective particle swarm optimization, multi-objective invasive weed optimization, pareto envelope-based selection algorithm, multi-objective evolutionary algorithm based on decomposition and multi-objective gray wolf optimizer algorithms	Location-routing problem	Numerical experiment

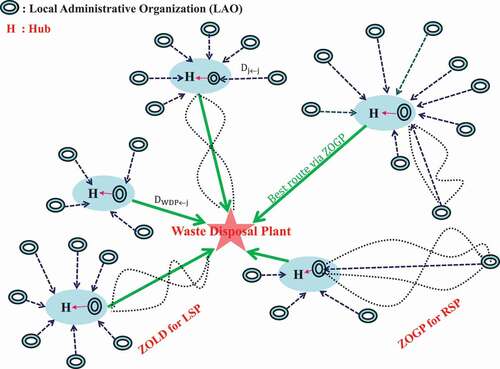
In Thailand, hubs with proper handling, transportation, storage, and disposal to protect the environment and reduce risk to human health is of importance. A decision support system to manage community waste hazards properly and safely is proposed for optimizing transportation routing from local administrative organizations (LAOs) to hubs and from hubs to waste disposal plants. A route selection tool can assist logistics service providers in selecting transport routes based on a variety of qualitative criteria. Furthermore, the best routes in terms of socioeconomic factors and transportation risks will be used to identify the best hub locations for connecting all local administration organizations with the exception of the southern region.

Route Selection Problem (RSP)

Transportation is currently one of the most important activities. All types of business include not only the transportation of raw materials to the factory or the transportation of goods from the manufacturer’s factory to the consumer or desired location, but also the transportation of waste from users to waste disposal plants. Specifically, the transportation of hazardous waste from LAOs to waste disposal plants, which is a critical process that affects public health and harms the future environment. To avoid accidents during transportation, transportation delays, and hazardous waste damage from transportation, operations planning is required. The following techniques are required to help optimize logistics processes, reduce logistics costs, and create a competitive advantage and customer satisfaction.

The risk of transportation

The following are methods for assessing the risk of route cost data and the period of transportation of dangerous goods. Hazardous waste risk refers to waste damage or loss, whether during transportation, changing modes of transportation, or within the storage area or warehouse, and the number of traffic crossings. There is a time difference in shipping. The convenience of the transportation route is one of the infrastructure and facility risks. They include the route’s slope, road width, the loading capacity of bridges, and cars, the rainy season, unexpected expenses, the accident rate, route flexibility, the availability of various handling equipment along the route, and the ability to adjust the route if the unexpected occurs.

It begins by gathering data for each route and selecting the origin and destination. The amount of hazardous waste transported on the route, as well as the radius of the area affected by accidents caused by hazardous waste transported, are factors in the risk of an accident of hazardous waste transport. The density of the population or household or places susceptible to accidents, or areas or elements in sensitive or vulnerable areas, is defined as the impact risk. Ancient monuments, educational institutions, and religious sites, for example, are likely to be negatively impacted if they are directly or indirectly affected by such transportation routes.

The integrated Analytic Hierarchy Process and Zero One Goal Programming (AHP-ZOGP)

Saaty created the analytic hierarchy process (AHP) technique in the 1970s, which builds a multi-criteria decision-making problem in various hierarchies as a goal, criteria, sub-criteria, and decision alternatives (Saaty 1980). The AHP technique uses pairwise comparisons to determine the relative importance of elements at each level of the hierarchy. It then evaluates alternatives at the bottom of the hierarchy to make the best decision among multiple alternatives. To generate priorities and make a decision in an organized manner, the decision must be decomposed into the following steps. The first step is to create a graphical representation of the problem in terms of the overall goal, the criteria, and the decision alternatives or problem hierarchy.

The second step is to specify experts’ opinions on the relative importance of each criterion in terms of its contribution to the overall goal’s achievement. The third step is to assign a preference or priority to each decision alternative based on how it contributes to each criterion. Finally, to provide information on relative importance and preferences, a mathematical process is used to synthesize the information and check for consistency, providing a priority ranking of all alternatives in terms of their overall preference.

In some cases, the decision criteria may be made up of disparate and contradictory goals. Zero One Goal Programming (ZOGP) is a Multiple Criteria Decision Making (MCDM) technique used when a decision-maker wants to satisfy several goals to achieve the best result. This technique proposed by Charnes, Cooper, and Rhodes (1978) has a single goal: maximize profit at the lowest possible cost or risk. The explanation for one objective may affect the others. For limited resources, this technique attempts to minimize deviation from several objectives.

Facility Location Problem (FLP)

In terms of cost-effectiveness and environmental concerns, the location of hazardous waste collection facilities from various sources, prior to transport to a waste disposal plant provider (WDP), an incineration plant is critical for effective integrated hazardous waste management. (Adeleke and Olukanni 2020). Plastria (1997) defined those facilities as “undesirable” facilities, as they have an undesirable effect on the environment and human health. According to Owen and Daskin (1998), regarding a large amount of investment to establish such a facility, selecting a location should be efficient and accessible in the time horizon. Over several decades, several studies have been carried out to find suitable waste disposal plants in several streams of the literature using various models and methods (e.g., Merkhofer and Keeney 1987; Stowers and Palekar 1993; Olusina and Shyllon 2014).

One of the main streams in domains of hazardous waste has focused on facility location problems (FLP) regarding locating waste collection facilities describing practical problems using mathematical modeling. An early mathematical model for selecting hazardous waste disposal facilities was proposed by Koo, Shin, and Yoo (1991). Later, similar attempts can be found in many studies, for example, Badran and El-Hagar (2006), Alumur and Kara (2007), Ghiani, Lagan, Manni, and Triki (2012), Eiselt and Marianov (2014), Rathore, Sarmah, and Singh (2019), Asefi et al. (2019), Adeleke, Olukanni, and Olusanya (2019), Homayouni and Pishvaee (2020), Yu et al. (2020), and Raeisi and Ghoushchi (2022).

The FLP problems involved the determination of the number and the best location of facilities subject to constraints (e.g., cost, time, and efficiency), which demands at each point must be served by the established facilities (Farahani, SteadieSeifi, and Asgari 2010; Francis, McGinnis, and White 1992). The branches of locating facilities are extensive and long-lasting, relating to various operational and logistical decisions. The theory of FLP has been investigated for more than ten decades, which was originated by Weber in 1909. In his study, a single warehouse was determined by minimizing the total distance between the warehouse and several customers.

Afterward, FLP has been of interest to many scholars, and the first explicit formulation of FLP was by Balinski in 1965 (Alenezy and Khalaf 2013). Traditional FLP in the early 60s is a single objective problem, which considering how to locate a single facility (e.g. depot, warehouse, collecting point, the siting of landfills, etc.) to incur the minimum total distance or lowest total cost between the facility and several end-users in an optimal manner (Farahani and Hekmatfar 2009). Multi-FLP is a general case, in which more than one facility is allocated simultaneously. As mentioned by Sule (2001), the assignment of one or more locations and the allocation of demand points at minimum cost would increase the flow of resources and services obtained by the facilities to end-users and utilize those facilities in a globally optimized solution, which can avoid the use of redundant locations.

Over the years, the literature on FLP the problem has been very widespread. A survey on robust optimization approaches in location problems was provided by Baron, Milner, and Naseraldin (2011). Normally, FLP problems can be distinguished into two main categories, i.e.static/dynamic models, and deterministic/stochastic models. The first category involves the time horizon of the model, by which static models entail analyzing the model in a unique time frame, by contrasting dynamic models entail with the problem parameters can change during the planning horizon.

The latter category involves the input data in deterministic models, by which all presume that parameters are known, while all of the system parameters (e.g. demand, transport cost, and construction cost, etc.) in the stochastic models are considered uncertain or unpredictable during the time horizon, thus they have some sort of probability associated with those inputs. According to Current, Ratick, and ReVelle (1997), models of dynamic location problems can be classified into two categories- explicitly and implicitly dynamics. In implicitly dynamic problems, all the facilities open at the same time during the course of time, while in explicitly dynamic problems, facilities can be opened or closed several times for a defined time frame. Nevertheless, Current, Daskin, and Schilling (2002) claimed that the deterministic approach is more commonly applied, along with the static approach.

Relating to solid waste management, Morrissey and Browne (2004) stated that most of the literature in operations research has addressed the problem from the view of a cost-benefit analysis, by considering all of the positive and negative effects of each decision in a common measurement, such as the monetary scale. Those analyses usually aim to find the best locations for landfill disposal sites, while minimizing cost. Normally, the cost objective consists of transportation cost and fixed cost such as facilities cost. Selecting sites for hazardous material waste disposal, especially for infectious waste disposal plants are very important and complex decisions, due to costly and difficult to reverse.

Badran and El-Haggar (2006) and Ghiani et al. (2012) developed a mathematical model for selecting collection site locations. Additionally, Eiselt (2007), Erkut et al. (2008), and Galante et al. (2010) developed facility location model for transfer station locations. Besides, Fiorucci et al. (2003) and Noche et al. (2010) examined waste processing facility locations. Later, Yu and Solvang (2017) purposed a generic multi-objective location-allocation model for optimal network design of waste management systems by the trading-off system operating costs, greenhouse gas emissions, and environmental impact. This study also reviewed several previous pieces of literature relating to waste management. In addition, Adeleke and Olukanni (2020) summarized a state-of-the-art of existing articles in the field of FLP in waste management.

The latest extension of existing articles, between January 1990 to September 2020, in the field of reverse logistics of municipal hazardous waste (RLMHW), can be seen in the study of Xin et al. (2021). Both studies suggested some room for further investigation, for instance, it would be interesting to emphasize special waste types such as waste electrical and electronic equipment (WEEE) and medical waste. Other aspects that would be interesting to develop are the application of network problems of hazardous waste and the optimization of collection routes that should be adopted in different regions of the world, as well as the development of heuristic and hyper-heuristic algorithms for solving those problems.

A Decision Support System via Zero-One Programming Models (DSS-ZOPM)

To organize a waste management system for community hazards, the impact of transportation of hazardous waste from the community must be analyzed and taken into account on multiple levels: economically, socially, and environmentally. When there is a sufficient quantity, the local government must establish a collection point or collection site, as well as a location to store hazardous waste from the community, which must be sent for treatment or disposed of by the authorized company. As a result, the local government is required for the transportation of hazardous waste from the community, which must be carried out in accordance with the rules and methods outlined in relevant legislation, such as the Public Health Act and its amendments, as well as the Ministry of Interior’s announcement of the Documentation System Transportation of Hazardous Wastes. The procedures for transporting hazardous waste from the community in the area of the local administrative organization are discussed in this paper.

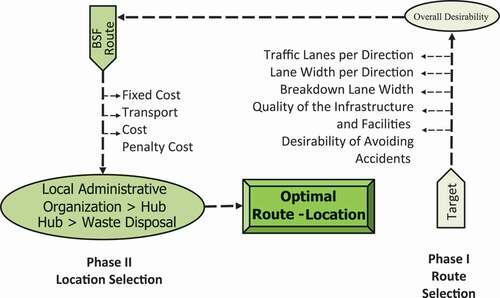
The goal is for the local government to manage the collection site and transportation of hazardous waste from the community to the disposal site. It can be used as a guideline in the community for the transportation and disposal of hazardous waste. The local government can use zero-one programming models to implement a decision support system for hazardous waste management. In academic terms, this system entails the planning of small and large hazardous waste collection sites or hubs, as well as the development of optimal transportation routes to transport hazardous waste from the community for treatment or disposal (Figure 2). It provides route selection-based decision support via zero-one goal programming, as well as location selection-based decision support via zero-one location design. The ZOGP finds the best so far (BSF) route from each LAO to the hub, and the ZOLD model finds the best allocation of LAOs to each hub.

Figure 2. Diagram of a decision support system via zero-one programming models (DSS-ZOPM).

Route selection problem based decision support via zero-one goal programming

Goal programming (GP) is the most widely used multi-objective decision-making technique, with the unique feature of considering the environmental, organizational, and managerial situation through all T goal levels and priorities. The optimal transportation route can be determined and delivered using Zero-One Goal Programming (ZOGP). By specifying various risk or qualitative measures, the objective function integrates AHP weights to achieve optimal transportation routing based on user constraints (Gkoulias, Palantzas, and Nalmpantis 2021; Réquia, Roig, and Koutrakis 2015). The ZOGP principle for calculating the optimal route is the lowest level of transportation risk and socioeconomic factors, which is expressed as a coefficient of $x_r$ zero-one decision variables in the constraints equations of each target under user need. The ZOGP parameters and decision variables (Table 2) of all R routes are shown below.

(1) $\mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}z={\sum }_{g=1}^T{w}_g{d}_g^{+}$(1)

Table 2. Parameters and decision variables including their definitions for route selection.

Parameter and Decision Variable	Definition
$a_{gr}$	Constant decision variable’s coefficient of the goal g the decision variable r
$d_g^{-}$	Underachievement deviation of the goal g
$d_g^{+}$	Overachievement deviation of the goal g
$G_g$	Value of the goal g
$w_g$	AHP weight of the goal g
$x_r$	Decision variable r with a value of 0 indicating no selection and 1 indicating selection

subject to:

(2) $\sum _{r=1}^R{a}_{gr}{x}_r\le G_g;g=1,2,3,\dots ,\mathrm{T}$(2)

(3) $\sum _{r=1}^R{x}_r=1$(3)

(4) $x_r\in 0,1;r=1,2,3,\dots ,\mathrm{R}$(4)

Location selection problem-based decision support via zero-one location design

This section describes a mathematical model for determining the best hub locations (He and Xie 2022). Table 3 lists all of the indices, parameters, and decision variables used in the Zero-One Location Design model (ZOLD). Our ZOLD model selects locations with the lowest transport costs. To create a mathematical model for selecting hub locations, accurate transport activity costs and freight cost data are required (Feng 2021). The variable and return costs are the transport costs from all LAOs to the hubs and all hubs to the waste disposal plant (WDP). The model’s limitation in terms of facilitating different load-bearing capacities is the use of standard size capacity shipment. These results in the penalty cost associated with the use of a half truckload or partial load.

Table 3. Indices, parameters, and decision variables including their definitions for ZOLD.

Parameters and Decision Variables	Definitions
i	Local administration organization (LAO); i ∈ {1, 2, 3, …, 62}
j	Hub index; j ∈ {1, 2, 3, …, H}; H = 6 or 15
$C_j^F$	Fixed cost for hub j
$C_{j\leftarrow i}^T$	Six-wheel vehicle transport cost: LAO i → hub j
$C_{WDP\leftarrow j}^T$	Ten-wheel vehicle transport cost: hub j → WDP
$P_{j\leftarrow i}$	Penalty for not using full six-wheel vehicle capacity: LAO i → hub j
$P_{WDP\leftarrow j}$	Penalty for not using full ten-wheel vehicle capacity: hub j → WDP
$D_{j\leftarrow i}$	BSF distance: LAO i → hub j
$D_{WDP\leftarrow j}$	BSF distance: hub j → WDP
$R_{j\leftarrow i}$	The actual number of six-wheel vehicles used: LAO i → hub j $or{Q}_i/C{A}_{SWT}$
$R_{WDP\leftarrow j}$	The actual number of ten-wheel vehicles used: hub j → WDP $or\left({\sum }_{i=1}^{62-H}{Q}_i{X}_{ij}\right)/C{A}_{TWT}$
$N_{j\leftarrow i}$	Number of six-wheel vehicles used: LAO i → hub j
$N_{WDP\leftarrow j}$	Number of ten-wheel vehicles used: hub j → WDP
$Q_k$	Hazardous waste quantities in each province, k
$C{A}_{SWT}$	Six-wheel vehicles capacity
$C{A}_{TWT}$	Ten-wheel vehicles capacity
$Y_iϵ\left\{0,1\right\}$	$Y_i$: 1 if hub j is selected; 0 otherwise
$X_{ij}ϵ\left\{0,1\right\}$	$X_{ij}$: 1 if there is the transport: LAO i → hub j; 0 otherwise

The objective function (5) is to find the hub locations that result in the lowest overall cost including fixed and transport costs. Transport cost also contains penalty costs for not using the full capacity of a vehicle on any trip, i.e. from the hub, j, to WDP, from LAO, i, to hub, j. There are two kinds of vehicles that can transport hazardous waste from the community. A six-wheel truck can transport no more than 7 tons per trip from LAO, i, to hub, j. A ten-wheel roll-off truck will be able to carry a load of no more than 10 tons per trip from the hub, j, to WDP. It will be possible to lift and place containers on the floor. In the main container, there are sub-containers for transporting hazardous waste from classified communities.

Constraint (6) confirms that at least one hub must be considered. Constraint (7) requires that LAOs in all provinces will be able to dispose of hazardous wastes. Constraint (8) requires that hazardous wastes be delivered from LAO, i, to one hub. Constraints (9) and (10) are used to calculate the number of vehicle trips needed from the hubs to the storage area, as well as from the hub to the WDP in Phitsanulok Province. The decision variables are numerically constrained by constraints (11) to (12). Our ZOLD reduces total fixed costs and transport costs for all vehicles.

(5) $\begin{array}{rl}& \mathrm{M}\mathrm{I}\mathrm{N}\mathrm{Z}=\sum _{\mathrm{j}=1}^{\mathrm{H}}{\mathrm{C}}_{\mathrm{j}}^{\mathrm{F}}{\mathrm{Y}}_{\mathrm{j}}\\ & +\sum _{\mathrm{j}=1}^{\mathrm{H}}\sum _{\mathrm{i}=1}^{62-\mathrm{H}}{\mathrm{C}}_{\mathrm{j}\leftarrow \mathrm{i}}^{\mathrm{T}}{\mathrm{D}}_{\mathrm{j}\leftarrow \mathrm{i}}{\mathrm{N}}_{\mathrm{j}\leftarrow \mathrm{i}}{\mathrm{X}}_{\mathrm{i}\mathrm{j}}\\ & +\sum _{\mathrm{j}=1}^{\mathrm{H}}{\mathrm{C}}_{\mathrm{W}\mathrm{D}\mathrm{P}\leftarrow \mathrm{j}}^{\mathrm{T}}{\mathrm{D}}_{\mathrm{W}\mathrm{D}\mathrm{P}\leftarrow \mathrm{j}}{\mathrm{N}}_{\mathrm{W}\mathrm{D}\mathrm{P}\leftarrow \mathrm{j}}\\ & +\sum _{\mathrm{j}=1}^{\mathrm{H}}\sum _{\mathrm{i}=1}^{62-\mathrm{H}}{\mathrm{P}}_{\mathrm{j}\leftarrow \mathrm{i}}{\mathrm{D}}_{\mathrm{j}\leftarrow \mathrm{i}}\mathrm{C}{\mathrm{A}}_{\mathrm{S}\mathrm{W}\mathrm{T}}({\mathrm{R}}_{\mathrm{j}\leftarrow \mathrm{i}}-{\mathrm{N}}_{\mathrm{j}\leftarrow \mathrm{i}})\\ & +\sum _{\mathrm{j}=1}^{\mathrm{H}}{\mathrm{P}}_{\mathrm{W}\mathrm{D}\mathrm{P}\leftarrow \mathrm{j}}{\mathrm{D}}_{\mathrm{W}\mathrm{D}\mathrm{P}\leftarrow \mathrm{j}}\mathrm{C}{\mathrm{A}}_{\mathrm{T}\mathrm{W}\mathrm{T}}\\ & \left({\mathrm{R}}_{\mathrm{W}\mathrm{D}\mathrm{P}\leftarrow \mathrm{j}}-{\mathrm{N}}_{\mathrm{W}\mathrm{D}\mathrm{P}\leftarrow \mathrm{j}}\right)\end{array}$(5)

subject to:

(6) $\sum _{\mathrm{j}=1}^{\mathrm{H}}{\mathrm{Y}}_{\mathrm{j}}\ge 1$(6)

(7) $\sum _{\mathrm{i}=1}^{62-\mathrm{H}}{\mathrm{X}}_{\mathrm{i}\mathrm{j}}=1;{\mathrm{\forall }}_{\mathrm{j}}$(7)

(8) ${\mathrm{X}}_{\mathrm{i}\mathrm{j}}\le {\mathrm{Y}}_{\mathrm{j}};{\mathrm{\forall }}_{\mathrm{i}}{\mathrm{\forall }}_{\mathrm{j}}$(8)

(9) ${\mathrm{N}}_{\mathrm{j}\leftarrow \mathrm{i}}\ge {\mathrm{R}}_{\mathrm{j}\leftarrow \mathrm{i}};{\mathrm{\forall }}_{\mathrm{i}}{\mathrm{\forall }}_{\mathrm{j}}$(9)

(10) ${\mathrm{N}}_{\mathrm{W}\mathrm{D}\mathrm{P}\leftarrow \mathrm{j}}\ge {\mathrm{R}}_{\mathrm{W}\mathrm{D}\mathrm{P}\leftarrow \mathrm{j}};{\mathrm{\forall }}_{\mathrm{j}}$(10)

(11) ${\mathrm{Y}}_{\mathrm{j}}ϵ\left\{0,1\right\};{\mathrm{\forall }}_{\mathrm{j}}$(11)

(12) ${\mathrm{X}}_{\mathrm{i}\mathrm{j}}ϵ\left\{0,1\right\};{\mathrm{\forall }}_{\mathrm{i}}{\mathrm{\forall }}_{\mathrm{j}}$(12)

In general, the center of gravity (CoG) is used to determine the best location hubs (H) by minimizing the weighted distance between the facility and its supply and demand points, where the distance is weighted by the mass supplied or consumed (Krajewski, Ritzman, and Malhotra 2007). This method is a mathematical technique that employs formulae to compute the coordinates of the center point by locating the system’s center of gravity, which meets distance and volume criteria. A geographical CoG can be calculated using (X, Y) pairs formed by latitudes and longitudes or any suitable grid that minimizes transport costs. According to Giles and Galvin (1996), this method is widely used when determining warehouse locations. In this case, multi-point CoG-based scenarios were created to identify potential storage area and hub locations in each region and province group. Each LAO was in charge of transporting hazardous waste to a single hub.

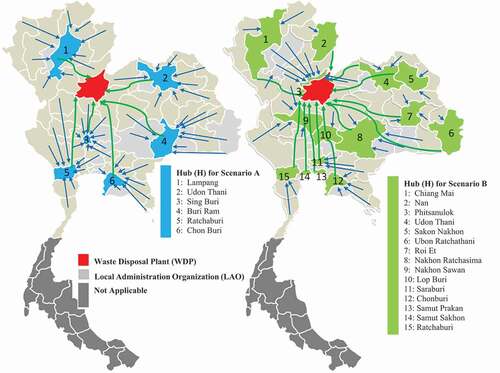
In this study, two scenarios were proposed as alternatives for hub locations, with the exception of Bangkok and the southern part of the country. Six hub locations were chosen from six regions in scenario A, while 15 hub locations were chosen from groups of provinces used by the Royal Thai Government Gazette in scenario B. They were all selected using the CoG method, which weighted the distance by the mass of the supplied or hazardous waste. Table 4 depicts the facility alternatives for hubs that were further investigated in order to find a suitable location set in our case study.

Table 4. Alternative locations for the hubs using CoG.

Scenario	Alternative locations for hubs
A	Lampang, Sing Buri, Ratchaburi, Chonburi, Udon Thani, Buri Ram
B	Chiang Mai, Nan, Phitsanulok, Nakhon Sawan, Lop Buri, Saraburi, Ratchaburi, Samut Sakhon, Samut Prakan, Chonburi, Roi Et, Udon Thani, Sakon Nakhon, Nakhon Ratchasima, Ubon Ratchathani

Computational results and analyzes

The local government should establish an agency responsible for the management of hazardous waste from the community by defining roles and responsibilities. The local government is responsible for preparing materials, equipment, and structures required for public relations collection, containment, and facilitation in the transportation, treatment, and disposal of hazardous waste from the community. To assess the community’s readiness to manage hazardous waste, the local government should collect hazardous waste management-related information from the community. It will be used in management formulation and facility preparation, including appropriate budgeting, and the information gathered should include the size of each source.

The prevalence of hazardous waste from various sources varies depending on the area conditions and economic growth. If there is a difference in economic prosperity, this should be taken into account. As a result, a waste survey is required. By multiplying the hazardous waste birth rate by the size of the various sources, the amount of hazardous waste in each LAO was calculated. The volume of community hazard waste collected in each area should be expected to be proportional to the proportion of community cooperation. Determination of the type of exclusion that the local government can consider using a form of segregation or a combination method based on the appropriateness of each area. The hazardous waste that needs to be disposed of will be evaluated for further action by the decision support system.

Route selection problem based decision support via the ZOGP

The number of traffic lanes per direction (C1), lane width per direction (C2), and breakdown lane width (C3) on urban expressways and intercity highways were measured. The risk level of infrastructure and transportation route facilities (C4) can be calculated by multiplying the accident rate probability by the percentage of increased transit time. The level of risk associated with the impact of hazardous waste transport accidents (C5) can be calculated by multiplying the accident probability by the household density rate per square kilometer.

To determine the relative importance of the quantitative and qualitative decision criteria, an analytical hierarchy process (AHP) was also used. The weight of the decision criterion was determined by conducting interviews and administering questionnaires to three target groups: hazardous waste disposal and transportation providers, as well as Local Administrative Organizations. Transportation providers and hazardous waste disposal companies are familiar with route selection and have conducted research on transportation route assessments. Local administrative organizations are made up of representatives from relevant government agencies who have surveyed or traveled on routes.

There are seven possible routes to Phitsanulok Province when considering the best so far (BSF) route from the hubs in Lampang Province or (WDP← H1, Rt) to the waste disposal plant. The importance of decision criteria employs the AHP approach to assist in the determination of significance weights for comparison via the Expert Choice program. On the first phase, the third group of weights from the Local Administrative Organizations (LAO) deviates significantly from the first two from the weights calculated by three groups of experts. In order to obtain the pairwise comparison matrix, an additional survey from the LAO was conducted in this study (Table 5). Under the acceptable C.R. level of [0.076, 0.083, 0.078], the criterion weights of [C1, C2, C3, C4, C5] obtained from the hazardous waste disposal provider, transportation provider, and Local Administrative Organizations were [0.124, 0.108, 0.371, 0.132, 0.265], [0.121, 0.129, 0.353, 0.151, 0.246], and [0.109, 0.108, 0.375, 0.152, 0.256], respectively. Following the determination of the significance weighting of the decision criterion by the three groups of experts, representatives of the three groups were determined using the arithmetic mean, allowing the significance weights to be summed up as follows. [C1, C2, C3, C4, C5] criterion weights were [0.118, 0.115, 0.366, 0.145, 0.256].

Table 5. Pairwise comparison matrix for the route selection.

	C1	C2	C3	C4	C5
C1	1.000	2.000	3.000	3.000	3.000
C2	0.500	1.000	4.000	2.000	2.000
C3	0.333	0.250	1.000	2.000	0.333
C4	0.333	0.500	0.500	1.000	1.000
C5	0.333	0.500	3.000	1.000	1.000

In our ZOGP model, all system limitations or constraints for route selection are either ordinary linear programming constraints or strict constraints that cannot be violated. The route will be chosen if all resource constraints are met. The selection of the most suitable route for hazardous waste transportation with the least deviation from the goal, provided that no route with a higher level of risk and socioeconomic factors than the route decision-maker is considered. The indexes, parameters, and variables of the ZOGP model are written as Eq. (1)(1) $\mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}z={\sum }_{g=1}^T{w}_g{d}_g^{+}$(1) through (4(4) $x_r\in 0,1;r=1,2,3,\dots ,\mathrm{R}$(4) ). The parameters and decision variables of the AHP-ZOGP model are shown in Table 5.

Because the units of the number of traffic lanes per direction, lane width per direction, breakdown lane width, and risk vary greatly in size due to the nature of the given data, the coefficients for each route must adjust values measured on different scales to a notionally common scale. All units are then converted to percentages via the Weitendorf’s criteria normalization method (Gardziejczyk and Zabicki 2017). In our integrated AHP and ZOGP, the selection of routes in the previous section was determined by the sum of all goal deviation percentages. The best so far (BSF) paths of all routes from the LAOs to the WDP in Phitsanulok Province via hubs based on the quantity of hazardous waste, to be disposed of, are shown in Table 6.

Table 6. The objective function value (Z), individual deviation percentage from the goal, and BSF routes (Rt) from the 6 hubs to the waste disposal plant (WDP←H, Rt) for the first scenario.

H	R(WDP←H, Rt)	Z	Deviation Percentage for the goal, g
			1	2	3	4	5
Lampang	R(WDP←H1, 1)	0.247	0.316	0.174	0.308	0.064	0.266
Udon Thani	R(WDP←H1, 2)	0.130	0.120	0.177	0.048	0.309	0.131
Sing Buri	R(WDP←H2, 3)	0.122	0.100	0.298	0.018	0.180	0.168
Buri Ram	R(WDP←H6, 5)	0.089	0.114	0.033	0.027	0.015	0.235
Ratchaburi	R(WDP←H3, 1)	0.247	0.302	0.152	0.219	0.236	0.312
Chonburi	R(WDP←H4, 2)	0.278	0.297	0.224	0.265	0.294	0.305

This section explains how to use our new conceptual framework for route selection, which incorporates the Integrated Analytic Hierarchy Process and Zero-One Goal Programming (AHP-ZOGP). The case study employed a realistic hazardous waste management transport service for the Local Administrative Organization, with the destination of Phitsanulok Province originating in all provinces of Thailand except the south. The database was compiled through interviews with both the freight company and customers. Our AHP-ZOGP mathematical model was evaluated using a spreadsheet. The optimization model included the concept of normalized deviation to account for decreasing marginal utility. Earlier attempts to evaluate deviation trade-offs focused on calculating the substitution increment between competing objectives (Luangpaiboon 2015). It is critical to investigate the implications of combining these functions into a single objective function.

The options for minimizing the associated objectives were heavily reliant on potential routes. More importantly, the analysis aided in the identification of factors that need to be improved in order to achieve the BSF solution. The first phase of the AHP-ZOGP has the advantage of allowing the user to choose the best route for further optimizing locations for LAOs and hubs, as well as a waste disposal plant and hubs. Furthermore, because the new conceptual framework used historical data to create probability assessment scales and severity impact assessment scales, the framework has a risk calculation advantage because the decision-maker can reduce the bias of risk assessment on each route. When selecting transport routes based on traffic lanes per direction, lane width per direction, the need for hazardous waste management, hazardous waste risk, infrastructure and facility risk, and the risk of a hazardous waste transport accident, this new decision support approach is adaptable and useful for logistics service providers. The results of our study differed slightly from those of the Zero-One Desirability Programming Model (Koohathongsumrit and Luangpaiboon 2020), which considered all decision criteria. The quantitative decision criteria that were removed from the ZOGP but retained in the ZOLD due to the LAO policy for other applications, on the other hand. The first phase’s contribution is the implementation of a supervision program that connects all local administration organizations for other applications other than hazardous waste.

Location selection problem-based decision support via the ZOLD

A Zero-One Location Design model (ZOLD) is developed and applied here for evaluating two scenarios. The objective of both scenarios was to determine the optimal set of facility locations for each proposed hub generated from COG analysis. The BSF routes based on the qualitative data were then collected to develop a decision support system (DSS), which can accommodate evaluation models to determine the appropriate locations of hubs in our Zero-One Location Design (ZOLD) model. Scenario A represents six hubs which were representatives of each location in every six regions of the country. Whereas scenario B represents fifteen hubs which were representatives of each location in each province group of the country locations. Via the OpenSolver Excel, the model selected locations with the lowest transport and penalty costs. Two scenarios were created and solved by the ZOLD model based on the volume of hazardous waste generation ranging between 33,264 and 663,932 kilograms per year, distance from the collection area to each hub, and relevant costs using LINGO software (Roe and Winston 1997). The parameters of ${\mathrm{C}}_{\mathrm{j}}^{\mathrm{F}}$, ${\mathrm{C}}_{\mathrm{j}\leftarrow \mathrm{i}}^{\mathrm{T}}$,${\mathrm{C}}_{\mathrm{W}\mathrm{D}\mathrm{P}\leftarrow \mathrm{j}}^{\mathrm{T}}$,${\mathrm{P}}_{\mathrm{j}\leftarrow \mathrm{i}}$,and ${\mathrm{P}}_{\mathrm{W}\mathrm{D}\mathrm{P}\leftarrow \mathrm{j}}$ were set at 34285.71, 4.29, 4.29, 2.14, and 2.14, respectively.

The objective aimed to find the optimal hubs that minimized the fixed cost of locating facilities, transport costs, and penalty costs from demand and supply points in order to establish facilities for two options as shown in Tables 7 and 8. Figure 3 depicts the map elements in both scenarios based on the waste disposal plant, local administration organizations, and hubs. Table 9 demonstrates the results of both scenarios. The total cost of scenario A equals USD 1,936,845.00 per year, whereas the total cost of scenario B is equal to USD 1,596,766.57 per year. The findings reveal that scenario B outperformed scenario A. The accuracy of overfitting of this study was slightly different from the previous ZOLD model developed by Atthirawong and Luangpaiboon (2022). This may due to the model attempting too hard to capture the random chance in the dataset. One of the most important aspects of avoiding overfitting may be the additional tuning terms that determine how much to penalize the flexibility of the previous model.

Table 7. Local administrative organizations in each hub in charging hazardous waste transportation for scenario A.

Hub	Range of services (Set of LAOs)
Lampang	Chiang Mai, Lamphun, Uttaradit, Phrae, Nan, Phayao, Chiang Rai, Mae Hong Son, Tak, Sukhothai
Udon Thani	Bueng Kan, Nong Bua Lam Phu, Loei, Nong Khai, Kalasin, Sakon Nakhon, Nakhon Panom, Mukdahan
Sing Buri	Ang Thong, Lopburi, Chai Nat, Phichit, Phetchabun, Suphan Buri, Nakhon Sawan
Buri Ram	Nakhon Ratchasima, Surin, Si Sa Ket, Ubon Ratchathani, Yasothon, Chaiyaphum, Amnat Charoen, Khon Kaen, Maha Sarakham, Roi Et
Ratchaburi	Nonthaburi, Pathum Thani, Phra Nakhon Si Ayutthaya, Uthai Thani, Kamphaeng Phet, Nakhon Pathom, Samut Sakhon, Samut Songkhram, Phetchaburi, Prachuap Khiri Khan, Kanchanaburi
Chon Buri	Samut Prakan, Saraburi, Rayong, Chanthaburi,Trat, Chachoengsao, Prachin Buri, Nakhon Nayok, Sa Kaeo

Table 8. Local administrative organizations in each hub in charging hazardous waste transportation for scenario B.

Hub	Range of services (Set of LAOs)
Chiang Mai	Chiang Rai, Mae Hong Son
Nan	Phayao
Phitsanulok	Lamphun, Lampang, Uttaradit, Phrae, Tak, Sukhothai, Phichit, Nong Bua Lam Phu, Khon Kaen, Loei
Udon Thani	Bueng Kan, Nong Khai
Sakon Nakhon	Nakhon Panom, Mukdahan
Ubon Ratchathani	Amnat Charoen
Roi Et	Yasothon, Maha Sarakham, Kalasin
Nakhon Ratchasima	Buri Ram, Surin, Si Sa Ket, Chaiyaphum
Nakhon Sawan	Chai Nat, Kanchanaburi, Suphan Buri, Uthai Thani, Kamphaeng Phet
Lop Buri	Phetchabun
Saraburi	Prachin Buri, Nakhon Nayok, Sa Kaeo
Chonburi	Rayong, Chanthaburi, Trat, Chachoengsao
Samut Prakan	Nonthaburi, Pathum Thani, Phra Nakhon Si Ayutthaya, Sing Buri, Ang Thong
Samut Sakhon	Nakhon Pathom, Samut Songkhram
Ratchaburi	Phetchaburi, Prachuap Khiri Khan

Table 9. Comparative cost (USD) from ZOLD model based on both scenarios.

Scenario	Fixed cost	Transport cost		Penalty cost		Total cost
		LAO to Hub	Hub to WDP	LAO to Hub	Hub to WDP
A	205,714.29	841,204.29	435,935.00	383,657.86	70,333.57	1,936,845.00
B	514,285.71	171,840.00	259,253.00	512,300.71	139,087.14	1,596,766.57

Figure 3. Scatter diagram of the hazardous waste management solution set.

Conclusion and discussion

Thailand has experienced a steady increase in community hazardous waste, only a portion of which has been managed through proper disposal techniques and management. Similarly, several Thai LAOs in each province have encountered difficulties in establishing waste management services, such as a lack of available locations to construct waste disposal sites to cover the waste generated in their areas. Furthermore, some local residents oppose the establishment of waste disposal sites due to a variety of risks associated with dirt and air pollution from these sites.

To address this issue, the Thai government has implemented public policies that encourage collaboration between each Local Administrative Organization (LAO) and other sectors in hazardous waste management. As such, this paper presented a decision support system (DSS) in which can accommodate evaluation models to optimize transportation routing and hub location for a service provider company, a partner of Local Administrative Organizations (LAOs), and the waste disposal plant (WDP), in establishing waste disposal sites for waste collection and waste transportation to a waste disposal plant provider (WDP), locating in Phitsanulok Province, for disposal hazardous waste effectively.

The DSS was developed based upon the hybridization of advanced decision technology models for the protection of human health and the environment in waste management for a local community network of the local administrative organization to the disposal plant. The Analytic Hierarchy Process (AHP) can assist in bringing consistency weight to decision criteria, which are expressed in subjective measures based on user perspectives. To achieve optimal transportation routing, AHP weights can be integrated into a zero-one goal programming model.

The Zero-One Location Design model (ZOLD) was created to find the optimal facility location of hubs by minimizing the overall total cost, which includes transportation costs, penalties for less than a truckload or not using the full capacity of a vehicle on any trip, and hub facility costs. The LINGO software was used to solve the model’s exact solution. The department of LAO of Thailand provided data from the previous three years, from January 2018 to December 2020, to validate the model’s effectiveness. The findings revealed that the best model for managing a case company’s hazardous waste was to establish 15 hubs scattered across the country for collecting points and then transporting them to WDP in Phitsanulok province.

The COG method, which was used to identify a suitable geographic location within an area that minimized the cost of transporting waste from LAOs and to hubs, was used to calculate those 15 hubs. The ZOLD model assigned a set of LAOs to each hub. The computation results revealed that establishing 15 hubs was less expensive than establishing six hubs because hazardous waste could be gathered over a shorter distance. Even though more location facilities were required, the overall cost was lower than establishing only six hubs in each region. Furthermore, locating the hub near sink points would help to reduce transportation costs and backhaul issues. Reducing the number of necessary trips and backhaul would also help to reduce the environmental impact of GHG emissions while increasing system efficiency.

Appropriate community hazardous waste management planning and strategies could significantly reduce the environmental and economic costs imposed on both management authorities and local communities. In terms of transportation and overall costs, the findings of this study suggest that establishing hub locations in a smaller group of provinces is preferable to establishing only one hub for one region. To effectively manage this issue, relevant agencies, including local governments, should develop a sub-region zoning hazardous waste management system. It should be noted, however, that the overall cost of managing those hazardous wastes was still quite high. As a result, waste minimization programs based on source reduction, reuse, and recycling must be effectively employed and implemented by all parties in order to reduce the amount of hazardous waste generated and disposed of at the source. By avoiding waste collection and disposal costs, as well as lowering emissions prevention and regulatory compliance costs, waste reduction would benefit all stakeholders, including regulators, decision-makers, waste processors, and local governments, among others. Citizens should be encouraged to raise awareness and engage in environmentally conscious behavior in order to achieve this goal.

There is still some room for future investigation. To begin, the amount of hazardous waste produced varies over time, depending on the number of industries and population centers. As a result, it may be worthwhile to investigate developing a model under uncertainty hazardous waste generation by including some other aspects such as maintenance, repair, and operational costs related to treatment, transportation, and disposal. Another study could look into a multi-objective model for solving the location-routing problem of waste treatment and disposal sites, as well as routing different types of waste to treatment centers all at once. The future work can also be extended by using other multi-criteria decision-making techniques such as DEMATEL, Fuzzy AHP, and Fuzzy ANP, to prioritize and compare risk factors from the transportation of hazardous waste. Finally, developing a meta-heuristics approach for solving the mentioned problem may provide more efficient and effective solutions in a reasonable time.

Acknowledgments

WA thanks to the School of Science, King Mongkut’s Institute of Technology Ladkrabang for the research work conducted. PL was supported by the research funding from the Faculty of Engineering, Thammasat School of Engineering and Thammasat University Research Unit in Industrial Statistics and Operational Research, Thammasat University, Pathumthani, 12120, THAILAND.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data availability statement

Data available on request from the authors: The data that support the findings of this study are available from the corresponding author, PL, upon reasonable request.

Additional information

Notes on contributors

Walailak Atthirawong

Walailak Atthirawong is an associate professor of Operations Research at Faculty of Science, King Mongkut’s Institute of Technology Ladkrabang (KMITL) in Thailand. She had received doctoral degree from the University of Nottingham in Manufacturing Engineering and Operations Management, England. She is actively engaged research in logistics and supply chain management, multi-criteria decision making, applied statistics and optimization.

Pongchanun Luangpaiboon

Pongchanun Luangpaiboon is a professor of Thammasat University Research Unit in Industrial Statistics and Operational Research, the department of Industrial Engineering, Faculty of Engineering, School of Engineering at Thammasat University (Rangsit Campus). He graduated his Bachelor (1989-1993) and Master Degrees (1993-1995) in Industrial Engineering from Kasetsart University, Thailand and Ph.D. in the Department of Engineering Mathematics from Newcastle upon Tyne, England. His research interests consist of industrial statistics, operational research, artificial intelligence and response surface methods.