Estimation of market prices of risks in the G.A.R.C.H. diffusion model

Abstract

In this paper we propose an estimation procedure which uses joint data on the underlying asset and option prices to extract market prices of return and volatility risks in the context of the G.A.R.C.H. diffusion model. The procedure is flexible and simple to implement. Firstly, a quasi-closed form pricing formula for European options in the G.A.R.C.H. diffusion model is derived. This result greatly eases the computational burden for computing option prices, and well suited for our model estimation. Then, based upon the joint data, we develop an efficient importance sampling-based maximum likelihood (E.I.S.-M.L.) estimation method for the objective and risk-neutral parameters of the G.A.R.C.H. diffusion model and a particle filter algorithm for latent state variable. Hence, this allows us to infer the market prices of risks that link the objective measure and the risk-neutral measure. Finally, we illustrate our approach using actual data on the Hang Seng Index (H.S.I.) and index warrant prices. The results show that both the return and volatility risks are priced by the market. Moreover, an option pricing study demonstrates that the market price of the volatility risk plays an important role in fitting option prices.

Keywords:

• Market prices of risks
• G.A.R.C.H. diffusion model
• option pricing
• efficient importance sampling
• maximum likelihood
• particle filter

JEL classifications:

• C13
• C32
• C58
• G13

1. Introduction

According to modern asset pricing theory, the value of any contingent claim can be computed as the conditional expectation under the risk-neutral measure of the discounted future cash flows. Thus, the valuation of any contingent claim, like a European option, involves a change of the measure, from the objective or real-world measure to the risk-neutral measure. However, the characterisation of the risk-neutral measure is intimately related to the market prices of risks or risk premiums for return and volatility risks, which in turn are determined by the model one adopts to describe the dynamics of the underlying asset returns.

In continuous-time modelling in finance, stochastic volatility (S.V.) models, such as the models of Hull and White (1987), Scott (1987), Stein and Stein (1991), Heston (1993), and many others, have attracted a great deal of attention, as they have captured successfully many of the stylised facts of financial asset returns, such as time-varying volatility, volatility clustering, and leverage effect. Among these models, the square-root S.V. model of Heston (1993) which belongs to the general class of affine models seems to be the most popular model. The main reason for this is because the affine S.V. model of Heston (1993) provides computational tractability that leads to closed-form solutions for option pricing. Unfortunately, there is a growing literature that provides empirical evidence against affine S.V. models. In particular, a number of studies show that Heston’s (1993) square-root model is mis-specified and cannot capture stylised facts of volatility dynamics (see e.g., Aït-Sahalia & Kimmel, 2007; Andersen, Benzoni, & Lund, 2002; Chacko & Viceira, 2003; Chernov, Gallant, Ghysels, & Tauchen, 2003; Jones, 2003, among many others).

Recently, non-affine S.V. models, such as generalised autoregressive conditional heteroskedasticity (G.A.R.C.H.) or general constant elasticity of variance (C.E.V.)-type diffusion models, have been found to capture the dynamics of the underlying asset prices much better than the affine S.V. model of Heston (1993) (Aït-Sahalia & Kimmel, 2007; Jones, 2003). In particular, the G.A.R.C.H. diffusion model of non-affine specification of Nelson (1990) has attracted a great deal of attention in recent years in the finance literature. The model is closely related to the discrete-time G.A.R.C.H. model. In fact, Nelson (1990) proved that the discrete-time G.A.R.C.H. model converges in distribution to the G.A.R.C.H. diffusion model as the sampling interval tends to zero. In recent years, a number of papers have provided strong evidence for the G.A.R.C.H. diffusion model not only for underlying asset but also for option data (e.g., Chourdakis & Dotsis, 2011; Christoffersen, Jacobs, & Mimouni, 2006, 2010; Kaeck & Alexander, 2012, 2013; Wu, Ma, & Wang, 2012). Many studies argue that the mis-specification of the affine S.V. model of Heston (1993) may be due to the omission of jumps in price and/or volatility (e.g., Bates, 1996; Broadie, Chernov, & Johannes, 2007; Eraker, 2004; Eraker, Johannes, & Polson, 2003; Pan, 2002). However, recent studies, such as Kaeck and Alexander (2012, 2013), show that the simple G.A.R.C.H. diffusion model without jumps outperforms even jump extensions of affine specifications, and can provide realistic volatility dynamics and good option pricing performance.

In this paper, we describe and implement an estimation procedure for estimating the G.A.R.C.H. diffusion model using joint data on the underlying asset and option prices.¹ The fundamental advantage of this approach is that it is able to estimate jointly the objective and risk-neutral parameters of the model, as well as the market prices of return and volatility risks that govern the change of measure in a way that maintains the internal consistency of the objective and risk-neutral measures.² There is a large and growing literature on the use of joint data on the underlying asset and option prices for the joint estimation of the model in recent years (e.g., Bollerslev, Gibson, & Zhou, 2011; Cheng, Gallant, Ji, & Lee, 2008; Chernov & Ghysels, 2000; Eraker, 2004; Ferriani & Pastorello, 2012; Garcia, Lewis, Pastorello, & Renault, 2011; Johannes, Polson, & Stroud, 2009; Jones, 2003; Pan, 2002; Polson & Stroud, 2003).

However, most of these papers employ affine S.V. models. The direct calibration of non-affine S.V. models to joint data on the underlying asset and option prices is very difficult to handle because closed-form expressions for option prices are unavailable, and all of the calculations would have to resort to simulation methods or numerical methods on integral differential equations. These procedures are computationally intensive and, when large trading books have to be quickly and frequently evaluated, are not practically feasible. As a consequence, to date, there is much less work on the non-affine specifications, including the G.A.R.C.H. diffusion model in the option pricing literature, let alone calibration of the models to joint data. In order to circumvent this problem, we derive in this paper a quasi-closed form solution for option prices in the G.A.R.C.H. diffusion model. A study closely related to this is Barone-Adesi, Rasmussen, and Ravanelli (2005), who derive an analytical approximate solution for European option prices in the G.A.R.C.H. diffusion model. However, their approximate solution is available only when the price and volatility processes are uncorrelated, while we have extended our solution to the case where the correlation between price and volatility is different from zero. In fact, the inclusion of a non-zero correlation between price and volatility is important. It captures the so-called ‘leverage effect’, a well-known empirical fact that exists in many financial time series (Black, 1976; Christie, 1982). Monte Carlo simulations demonstrate that our solution is quite accurate. This greatly reduces the computational time for the pricing of options in the G.A.R.C.H. diffusion model, and is well suited for our model estimation.

The lack of a closed-form expression of the likelihood function makes the estimation of S.V. models a challenging topic in the empirical finance literature. The main difficulty lies in that the volatility is latent and needs to be integrated out from the joint density function of observations and latent state variable to evaluate the likelihood function. In the last decade, many estimation methods have been proposed for estimating S.V. models, including quasi maximum likelihood (Harvey, Ruiz, & Shephard, 1994), empirical characteristic function (Singleton, 2001), generalised method of moments (G.M.M.) (Chacko & Viceira, 2003), Markov chain Monte Carlo (M.C.M.C.) (Eraker, 2001) and simulated maximum likelihood (Durham, 2006, 2007; Jungbacker & Koopman, 2007; Liesenfeld & Richard, 2003, 2006), etc. Adding option data for estimating S.V. models creates further a significant computational challenge. Several procedures which use joint data on the underlying asset and option prices for estimating the parameters of S.V. models under both objective and risk-neutral measures have been proposed, such as the efficient method of moments (E.M.M.) (Chernov & Ghysels, 2000), G.M.M. (Bollerslev et al., 2011; Garcia et al., 2011; Pan, 2002) and M.C.M.C. (Cheng et al., 2008; Eraker, 2004; Jones, 2003). The estimation procedure we adopt in this paper is based on the maximum likelihood (M.L.) method where the likelihood function is evaluated using the efficient importance sampling (E.I.S.) technique of Richard and Zhang (2007). The E.I.S.-based M.L. (E.I.S.-M.L.) method is easy to implement and enables us to estimate the parameters of the G.A.R.C.H. diffusion model precisely. Since knowledge of the estimated model parameters is not sufficient to compute an option price or market price of risk, we also have to know the latent spot volatility. We develop in this paper a particle filter algorithm for extracting latent volatility using joint data.

Recently, Ferriani and Pastorello (2012) adopted a very similar approach to ours, but considered the log volatility and C.E.V. models of non-affine specifications. However, the models they considered are rejected by the actual data on the S&P 500 index and index option prices. In addition, the likelihood function in Ferriani and Pastorello (2012) is evaluated using a Laplace importance sampling (L.I.S.) method combined with a modified Brownian bridge strategy. The L.I.S. is a local Gaussian approximation scheme to the likelihood function. Also, the method requires complicated computation and is time-consuming. In contrast, the method of this paper relies on the E.I.S. technique, which is a global approximation scheme to evaluate the likelihood function. As such, the method is efficient and simple to implement.

Our paper is also closely related to the research of Wu, Yang, Ma, and Zhao (2014), who consider the problem of option pricing under the G.A.R.C.H. diffusion model. They estimated the model parameters using the E.I.S.-M.L. method, relying exclusively on the underlying asset prices. Our strategy differs from their approach as we take advantage of the additional information provided by the option prices. With the single underlying asset prices data, only objective parameters can be obtained, hence the market prices of risks that link the objective and risk-neutral measures cannot be identified. Our paper contributes to the literature by using joint data on the underlying asset and option prices within the E.I.S.-M.L. estimation framework of the popular G.A.R.C.H. diffusion model. The proposed approach is a more sophisticated updating procedure, which is able to estimate jointly the objective and risk-neutral parameters of the model, as well as the market prices of risks. Moreover, many studies have provided evidence that the use of option prices can lead to more accurate estimates of model parameters and volatility (see, e.g., Cheng et al., 2008; Chernov & Ghysels, 2000; Eraker, 2004; Johannes et al., 2009; Polson & Stroud, 2003). Thus, it is also advantageous to estimate the model parameters and volatility using additional option price information so that more precise parameter and volatility estimates can be obtained.

In order to illustrate our estimation procedure empirically, we apply the method to estimate the market prices of return and volatility risks using actual data on the Hang Seng Index (H.S.I.) and index warrant prices. We find that both the return and volatility risks are priced by the market. Moreover, an option pricing study demonstrates that the market price of the volatility risk plays a very important role in fitting option prices.

The rest of the paper is organised as follows. In Section 2, we propose under the objective probability measure the G.A.R.C.H. diffusion model, and proceed to derive the corresponding system under the risk-neutral measure as well as the market prices of risks. Also, a quasi-closed form pricing formula for European options in the G.A.R.C.H. diffusion model is derived. In Section 3, we detail the E.I.S.-M.L. and particle filter methods for the parameter and latent state variable estimation of the G.A.R.C.H. diffusion model. Section 4 illustrates an application of our approach to actual data on the H.S.I. index and index warrant prices, and we conclude in Section 5. Technical details are provided in appendices to the paper.

2. Model and pricing

We adopt the G.A.R.C.H. diffusion model of non-affine specification of Nelson (1990) to characterise the dynamics of the underlying asset prices, and form the basis for the option pricing analysis. We describe the model under the objective measure in Section 2.1, and derive the corresponding system under the risk-neutral measure as well as the market prices of risks in Section 2.2. A description of option pricing under this dynamic setting is presented in Section 2.3. The explicit expressions for the characteristic functions of the G.A.R.C.H. diffusion model are given in Appendix A.

2.1. The G.A.R.C.H. diffusion model

In the G.A.R.C.H. diffusion model, the dynamics under the objective measure of the underlying asset price, S_t, and the associated volatility, V_t, are assumed to be given by

(1) $$d{S}_t=\mu S_{t}dt+\sqrt{V_t}{S}_{t}d{W}_{1t}$$(1)

(2) $$d{V}_t=(\alpha -\beta V_t)dt+\sigma V_t[\rho d{W}_{1t}+\sqrt{1-{\rho }^2}d{W}_{2t}]$$(2)

where μ is the mean of the underlying asset returns, α/β is the long-run mean of volatility, β is the mean reversion rate of volatility, σ is the volatility of volatility, and W_t = [W_1t, W_2t]^T is a standard Brownian motion.

Equations (1(1) $$d{S}_t=\mu S_{t}dt+\sqrt{V_t}{S}_{t}d{W}_{1t}$$(1) ) and (2(2) $$d{V}_t=(\alpha -\beta V_t)dt+\sigma V_t[\rho d{W}_{1t}+\sqrt{1-{\rho }^2}d{W}_{2t}]$$(2) ) imply that ${\text{Corr}}_t(d{S}_t/S_t,d{V}_t)=\rho$. The correlation parameter, ρ, is typically found to be negative, which captures the well known ‘leverage effect’ originated by Black (1976) and Christie (1982).

2.2. Risk-neutral measure and market prices of risks

In order to derive the dynamics of the underlying asset returns under the risk-neutral measure, we need to specify the market prices of risks. Following Heston (1993) and Chernov and Ghysels (2000), we assign the market prices of risks so that the dynamics of the underlying asset returns have the same form under the risk-neutral measures as under the objective measure, and the dynamics of (S_t, V_t) under the risk-neutral measure are of the form

(3) $$d{S}_t=r{S}_{t}dt+\sqrt{V_t}{S}_{t}d{W}_{1t}^{\ast }$$(3)

(4) $$d{V}_t=({\alpha }^{\ast }-{\beta }^{\ast }{V}_t)dt+\sigma V_t[\rho d{W}_{1t}^{\ast }+\sqrt{1-{\rho }^2}d{W}_{2t}^{\ast }]$$(4)

where r is the risk-free interest rate, $W_t^{\ast }={[W_{1t}^{\ast },W_{2t}^{\ast }]}^T$ is a standard Brownian motion under the risk-neutral measure.

To change the objective measure to the risk-neutral one, we need to use Girsanov’s theorem. Specifically, let us consider the Radon–Nikodym derivative of the objective measure with respect to the risk-neutral one, which is

(5) $${\xi }_t=exp\left\{-\frac{1}{2}{\int }_0^t({\lambda }_{1u}^2+{\lambda }_{2u}^2)du-{\int }_0^t{\lambda }_{1u}d{W}_{1u}-{\int }_0^t{\lambda }_{2u}d{W}_{2u}\right\}$$(5)

where ${\lambda }_t={({\lambda }_{1t},{\lambda }_{2t})}^{\prime }$ is the vector of the market prices of risks, return and volatility risks, respectively. When we know the parameter values under both the objective and risk-neutral measures, we can obtain the market prices of risks, ${\lambda }_t$. In fact, by Girsanov’s theorem we have

(6) $$\mu S_t=r{S}_t+{\lambda }_{1t}\sqrt{V_t}{S}_t$$(6)

(7) $$\alpha -\beta V_t={\alpha }^{\ast }-{\beta }^{\ast }{V}_t+\sigma V_t(\rho {\lambda }_{1t}+\sqrt{1-{\rho }^2}{\lambda }_{2t})$$(7)

Therefore,

(8) $${\lambda }_{1t}=\frac{\mu -r}{\sqrt{V_t}}$$(8)

(9) $${\lambda }_{2t}=\frac{c_1}{V_t}-\frac{c_2}{\sqrt{V_t}}-c_3$$(9)

where$$c_1=\frac{\alpha -{\alpha }^{\ast }}{\sigma \sqrt{1-{\rho }^2}},c_2=\frac{\rho (\mu -r)}{\sqrt{1-{\rho }^2}},c_3=\frac{\beta -{\beta }^{\ast }}{\sigma \sqrt{1-{\rho }^2}}$$

2.3. Option pricing

Using the well-established theory of arbitrage pricing, the price of a call option at time t, with time to maturity τ and strike K can be computed as

(10) $$C(t,\tau ,K,S_t,V_t)=e^{-r\tau }{E}^{\ast }[max(S_T-K,0)|{\mathcal{F}}_t]$$(10)

where T = t + τ, $E^{\ast }[·|{\mathcal{F}}_t]$ is the conditional expectation with respect to the risk-neutral measure conditional to the information set ${\mathcal{F}}_t$.

According to Heston (1993), there exists a pair of probabilities Π_j, j = 1, 2, such that the call option price C(t, τ, K, S_t, V_t) is given by

(11) $$C(t,\tau ,K,S_t,V_t)=S_t{\mathrm{\Pi }}_1(t,\tau ,S_t,V_t)-K{e}^{-r\tau }{\mathrm{\Pi }}_2(t,\tau ,S_t,V_t)$$(11)

Specifically, ${\Pi }_j(t,\tau ,S_t,V_t)={Pr}_j(ln{S}_T\ge lnK|S_t,V_t),j=1,2$, where these probabilities can be determined by inverting the characteristic functions f_j, j = 1, 2, that is

(12) $${\mathrm{\Pi }}_j(t,\tau ,S_t,V_t)=\frac{1}{2}+\frac{1}{\pi }{\int }_0^{\infty }\text{Re}\left[\frac{e^{-i\varphi lnK}{f}_j(t,\tau ,S_t,V_t;\varphi )}{i\varphi }\right]d\varphi ,j=1,2$$(12)

where $\text{Re}[·]$ denotes the real component of a complex number.

However, the G.A.R.C.H. diffusion model belongs to the class of non-affine models, and the characteristic functions f_j, j = 1, 2 are unavailable in closed form. In fact, we compute some approximations of f_j, j = 1, 2. Indeed, we utilise a perturbation method to derive approximate solutions, like Chacko and Viceira (2003) and Wu et al. (2012) have done in another setting. The explicit expressions of the approximate characteristic functions f_j, j = 1, 2 are given in Appendix A.

3. Estimation

In this section, we focus on how to estimate the objective and risk-neutral parameters and unobservable state variables of the G.A.R.C.H. diffusion model using the joint data on the underlying asset and option prices. First, we describe how to estimate jointly the objective and risk-neutral parameters using E.I.S.-M.L. method. Then we illustrate how to estimate the unobservable state variables using a particle filter algorithm.

3.1. M.L. estimation

First, we take the stabilising transformation s_t = ln S_t, h_t = ln V_t. By Itô’s lemma, we have

(13) $$d{s}_t=(\mu -\frac{1}{2}{e}^{h_t})dt+e^{h_t/2}d{W}_{1t}$$(13)

(14) $$d{h}_t=(\alpha e^{-h_t}-\beta -\frac{1}{2}{\sigma }^2)dt+\sigma [\rho d{W}_{1t}+\sqrt{1-{\rho }^2}d{W}_{2t}]$$(14)

In the empirical literature, the above continuous-time model must be discretised to facilitate the parameter estimation. A simple Euler discretisation leads to the following discrete-time stochastic processes:

(15) $$x_t=(\mu -\frac{1}{2}{e}^{h_{t-1}})\mathrm{\Delta }+e^{h_{t-1}/2}\sqrt{\mathrm{\Delta }}{\epsilon }_t$$(15)

(16) $$h_t=h_{t-1}+(\alpha e^{-h_{t-1}}-\beta -\frac{1}{2}{\sigma }^2)\mathrm{\Delta }+\sigma \sqrt{\mathrm{\Delta }}[\rho {\epsilon }_t+\sqrt{(1-{\rho }^2)}{\eta }_t]$$(16)

where x_t = s_t − s_t-1 is the continuously compounded return of the underlying asset, Δ is the time interval,³ ${\epsilon }_t=(W_{1t}-W_{1t-1})/\sqrt{\Delta }$, ${\eta }_t=(W_{2t}-W_{2t-1})/\sqrt{\Delta }$. It can be shown that ɛ_t and η_t are independent and identically distributed (i.i.d.) standard normal random variables and uncorrelated.

In order to perform the joint estimation of objective and risk-neutral parameters, we consider the additional information provided by the option prices. As is common in derivative pricing applications, the distribution of option prices is determined by both an option pricing formula, which is (11) in our case, and an assumption of pricing errors (Cheng et al., 2008; Eraker, 2004; Jacquier & Jarrow, 2000; Polson & Stroud, 2003). The pricing errors are not only required to permit application of likelihood-based methods but are also plausible reflections of market microstructure effects (e.g., price discreteness, infrequent trading, bid-ask bounce). We assume an error structure for the pricing error to express the observed option price as follows:

(17) $$ln{C}_t=lnC(t,\tau ,K,S_t,V_t)+\delta {\nu }_t$$(17)

where ν_t is a standard normal random variable and is independent of ɛ_t and η_t, and the nonlinear pricing function C(t, τ, K, S_t, V_t) has been given earlier.

It is clear that Equations (15(15) $$x_t=(\mu -\frac{1}{2}{e}^{h_{t-1}})\mathrm{\Delta }+e^{h_{t-1}/2}\sqrt{\mathrm{\Delta }}{\epsilon }_t$$(15) )–(17(17) $$ln{C}_t=lnC(t,\tau ,K,S_t,V_t)+\delta {\nu }_t$$(17) ) constitute a nonlinear and non-Gaussian state-space model with volatility as the unobservable state variable. To estimate this model using the M.L. method, we need to integrate out the unobservable state variables from the joint density of the observations and unobservable state variables and derive an explicit expression for the marginal likelihood of observations.

Let X = {x₁, …, x_T} be a vector of the observed underlying asset returns, let Y = { ln C₁, …, ln C_T} be a vector of the observed option prices and let H = {h₁, …, h_T} be a vector of the unobservable state variables which are the log volatilities in our case. The likelihood function of the observed samples of option prices and the underlying asset returns can in principle be expressed as

(18) $$\mathcal{L}(Y,X;\mathrm{\Theta },h_0)=\int p(Y,X,H;\mathrm{\Theta },h_0)dH$$(18)

where Θ = (μ, α, β, σ, ρ, α^*, β^*, δ)^′ is the parameter vector, which consists of the objective and risk-neutral parameters (μ, α, β, σ, ρ, α^*, β^*)^′ of the G.A.R.C.H. diffusion model and the parameter δ in measurement Equation (17(17) $$ln{C}_t=lnC(t,\tau ,K,S_t,V_t)+\delta {\nu }_t$$(17) ), h₀ is the initial log volatility which we will estimate along with parameter vector Θ, and p(Y, X, H; Θ, h₀) is the joint density of Y, X and H, which can be written as

(19) $$p(Y,X,H;\mathrm{\Theta },h_0)=p(Y|X,H,\mathrm{\Theta })p(X,H;\mathrm{\Theta },h_0)$$(19)

and

(20) $$p(Y|X,H,\mathrm{\Theta })=\prod _{t=1}^{T}p(ln{C}_t|x_t,h_t,\mathrm{\Theta })$$(20)

(21) $$p(X,H;\mathrm{\Theta },h_0)=\prod _{t=1}^{T}p(x_t|h_{t-1},\mathrm{\Theta })p(h_t|x_t,h_{t-1},\mathrm{\Theta })$$(21)

where p( ln C_t|x_t, h_t, Θ) is the normal density of ln C_t with the conditional mean ln C(t, τ, K, S_t, V_t) and the conditional variance δ², p(x_t|h_t-1, Θ) is the normal density of x_t with the conditional mean $(\mu -\frac{1}{2}{e}^{h_{t-1}})\Delta$ and the conditional variance $e^{h_{t-1}}\Delta$ and p(h_t|x_t, h_t-1, Θ) is the normal density of h_t with the conditional mean μ_t and the conditional variance ${\sigma }_t^2$ which is given by

(22) $${\mu }_t=h_{t-1}+(\alpha e^{-h_{t-1}}-\beta -\frac{1}{2}{\sigma }^2)\mathrm{\Delta }+\sigma \rho \frac{x_t-(\mu -\frac{1}{2}{e}^{h_{t-1}})\mathrm{\Delta }}{e^{h_{t-1}/2}}$$(22)

(23) $${\sigma }_t^2={\sigma }^2(1-{\rho }^2)\mathrm{\Delta }$$(23)

Given the likelihood function in Equation (18(18) $$\mathcal{L}(Y,X;\mathrm{\Theta },h_0)=\int p(Y,X,H;\mathrm{\Theta },h_0)dH$$(18) ), the M.L. estimates of the model parameters can be obtained by$$(\widehat{\mathrm{\Theta }},{\widehat{h}}_0)=\text{arg}\underset{(\mathrm{\Theta },h_0)}{max}ln\mathcal{L}(Y,X;\mathrm{\Theta },h_0)$$

Under suitable regularity conditions, the M.L. estimator $(\widehat{\Theta },{\widehat{h}}_0)$ is consistent and asymptotically normal.

3.2. E.I.S. to likelihood approximation

Since a typical financial time series has at least several hundreds of observations, the high-dimensional integral in the right hand of Equation (18) rarely has analytical expression. Meanwhile, using traditional numerical integration methods to approximate the integral is also infeasible. In order to overcome this problem, a plausible solution is to use Monte Carlo simulation methods.

From Equations (19)–(21), the likelihood function in Equation (18(18) $$\mathcal{L}(Y,X;\mathrm{\Theta },h_0)=\int p(Y,X,H;\mathrm{\Theta },h_0)dH$$(18) ) can be rewritten as

(24) $$\mathcal{L}(Y,X;\mathrm{\Theta },h_0)=\int \prod _{t=1}^{T}p(ln{C}_t|x_t,h_t,\mathrm{\Theta })p(x_t|h_{t-1},\mathrm{\Theta })p(h_t|x_t,h_{t-1},\mathrm{\Theta })dH$$(24)

Let $h_t^{(s)}$ be drawn independently from the so-called natural importance sampling (N.I.S.) density $p(h_t|x_t,h_{t-1}^{(s)},\mathrm{\Theta })$, then the corresponding N.I.S.-Monte Carlo estimate is given by

(25) $$\tilde{\mathcal{L}}(Y,X;\mathrm{\Theta },h_0)=\frac{1}{S}\sum _{s=1}^S\left[\prod _{t=1}^{T}p(ln{C}_t|x_t,h_t^{(s)},\mathrm{\Theta })p(x_t|h_{t-1}^{(s)},\mathrm{\Theta })\right]$$(25)

A primary advantage of the N.I.S. is that it is intuitive and simple to implement. However, it turns out that the N.I.S. estimate is highly inefficient since its sampling variance rapidly increases with the sample size T. Thus this estimate cannot be relied on practically. To overcome this drawback of the N.I.S., we adopt the E.I.S. proposed by Richard and Zhang (2007). Based upon this Monte Carlo integration technique, high-dimensional integral can be evaluated quickly with high numerical accuracy.

The E.I.S. requires an auxiliary parametric importance sampler from which samples can be obtained efficiently. Let ${\{m_t(h_t|x_t,h_{t-1},a_t)\}}_{t=1}^T$ be an auxiliary sampler (i.e., E.I.S. sampler) indexed by the auxiliary parameter ${\{a_t\}}_{t=1}^T$. The likelihood function in Equation (24(24) $$\mathcal{L}(Y,X;\mathrm{\Theta },h_0)=\int \prod _{t=1}^{T}p(ln{C}_t|x_t,h_t,\mathrm{\Theta })p(x_t|h_{t-1},\mathrm{\Theta })p(h_t|x_t,h_{t-1},\mathrm{\Theta })dH$$(24) ) is rewritten as(26) $$\mathcal{L}(Y,X;\mathrm{\Theta },h_0)=\int \prod _{t=1}^T\frac{p(ln{C}_t|x_t,h_t,\mathrm{\Theta })p(x_t|h_{t-1},\mathrm{\Theta })p(h_t|x_t,h_{t-1},\mathrm{\Theta })}{m_t(h_t|x_t,h_{t-1},a_t)}\times \prod _{t=1}^T{m}_t(h_t|x_t,h_{t-1},a_t)dH$$(26)

The corresponding E.I.S.-Monte Carlo estimate is then given by

(27) $$\widehat{\mathcal{L}}(Y,X;\mathrm{\Theta },h_0)=\frac{1}{S}\sum _{s=1}^S\left[\prod _{t=1}^T\frac{p(ln{C}_t|x_t,h_t^{(s)},\mathrm{\Theta })p(x_t|h_{t-1}^{(s)},\mathrm{\Theta })p(h_t^{(s)}|x_t,h_{t-1}^{(s)},\mathrm{\Theta })}{m_t(h_t^{(s)}|x_t,h_{t-1}^{(s)},a_t)}\right]$$(27)

where $h_t^{(s)}$ is drawn independently from the E.I.S. density $m_t(h_t|x_t,h_{t-1}^{(s)},a_t)$.

Following Richard and Zhang (2007), we write E.I.S. density m_t as

(28) $$m_t(h_t|x_t,h_{t-1},a_t)=\frac{k_t(h_t|x_t,h_{t-1},a_t)}{{\chi }_t(x_t,h_{t-1},a_t)}$$(28)

(29) $${\chi }_t(x_t,h_{t-1},a_t)=\int k_t(h_t|x_t,h_{t-1},a_t)d{h}_t$$(29)

where k_t(h_t|x_t, h_t-1, a_t) is the density kernel. For the state-space model in Equations (15(15) $$x_t=(\mu -\frac{1}{2}{e}^{h_{t-1}})\mathrm{\Delta }+e^{h_{t-1}/2}\sqrt{\mathrm{\Delta }}{\epsilon }_t$$(15) )–(17(17) $$ln{C}_t=lnC(t,\tau ,K,S_t,V_t)+\delta {\nu }_t$$(17) ), we set

(30) $$k_t(h_t|x_t,h_{t-1},a_t)=p(h_t|x_t,h_{t-1},\mathrm{\Theta })exp\{a_{1,t}{h}_t+a_{2,t}{h}_t^2\}$$(30)

where a_t = (a_1,t, a_2,t), and the E.I.S. distribution and the explicit expression for ln χ_t are given in Appendix B.

From (28) and (30), we have(31) $$\begin{array}{c}\prod _{t=1}^T\frac{p(ln{C}_t|x_t,h_t,\mathrm{\Theta })p(x_t|h_{t-1},\mathrm{\Theta })p(h_t|x_t,h_{t-1},\mathrm{\Theta })}{m_t(h_t|x_t,h_{t-1},a_t)}\\ =\prod _{t=1}^T\frac{p(ln{C}_t|x_t,h_t,\mathrm{\Theta })p(x_t|h_{t-1},\mathrm{\Theta })p(h_t|x_t,h_{t-1},\mathrm{\Theta })}{k_t(h_t|x_t,h_{t-1},a_t)/{\chi }_t(x_t,h_{t-1},a_t)}\\ =\prod _{t=1}^T\frac{p(ln{C}_t|x_t,h_t,\mathrm{\Theta })p(x_t|h_{t-1},\mathrm{\Theta }){\chi }_t(x_t,h_{t-1},a_t)}{exp\{a_{1,t}{h}_t+a_{2,t}{h}_t^2\}}\\ =p(x_1|h_0,\mathrm{\Theta }){\chi }_1(x_1,h_0,a_1)\times \prod _{t=1}^T\frac{p(ln{C}_t|x_t,h_t,\mathrm{\Theta })p(x_{t+1}|h_t,\mathrm{\Theta }){\chi }_{t+1}(x_{t+1},h_t,a_{t+1})}{exp\{a_{1,t}{h}_t+a_{2,t}{h}_t^2\}}\\ \end{array}$$(31)

where p(x_T+1|h_T, Θ) ≡ χ_T+1(x_T+1, h_T, a_T+1) ≡ 1. In order to minimise the E.I.S.-Monte Carlo variance of Equation (27(27) $$\widehat{\mathcal{L}}(Y,X;\mathrm{\Theta },h_0)=\frac{1}{S}\sum _{s=1}^S\left[\prod _{t=1}^T\frac{p(ln{C}_t|x_t,h_t^{(s)},\mathrm{\Theta })p(x_t|h_{t-1}^{(s)},\mathrm{\Theta })p(h_t^{(s)}|x_t,h_{t-1}^{(s)},\mathrm{\Theta })}{m_t(h_t^{(s)}|x_t,h_{t-1}^{(s)},a_t)}\right]$$(27) ), we set up the following minimisation problem:(32) $$\begin{array}{c}({\widehat{a}}_t(\mathrm{\Theta }),{\widehat{c}}_t(\mathrm{\Theta }))=arg\underset{(a_t,c_t)}{min}\sum _{s=1}^S\{ln\left[p(ln{C}_t|x_t,h_t^{(s)},\mathrm{\Theta })p(x_{t+1}|h_t^{(s)},\mathrm{\Theta }){\chi }_{t+1}(x_{t+1},h_t^{(s)},{\widehat{a}}_{t+1})\right]\\ -c_t-a_{1,t}{h}_t^{(s)}+a_{2,t}{(h_t^{(s)})}^2{\}}^2\\ \end{array}$$(32)

where c_t is estimated along with the auxiliary parameter a_t.

It is clear that the minimisation problem described in Equation (32(32) $$\begin{array}{c}({\widehat{a}}_t(\mathrm{\Theta }),{\widehat{c}}_t(\mathrm{\Theta }))=arg\underset{(a_t,c_t)}{min}\sum _{s=1}^S\{ln\left[p(ln{C}_t|x_t,h_t^{(s)},\mathrm{\Theta })p(x_{t+1}|h_t^{(s)},\mathrm{\Theta }){\chi }_{t+1}(x_{t+1},h_t^{(s)},{\widehat{a}}_{t+1})\right]\\ -c_t-a_{1,t}{h}_t^{(s)}+a_{2,t}{(h_t^{(s)})}^2{\}}^2\\ \end{array}$$(32) ) is equivalent to the following auxiliary linear regression:(33) $$\begin{array}{c}lnp(ln{C}_t|x_t,h_t^{(s)},\mathrm{\Theta })+lnp(x_{t+1}|h_t^{(s)},\mathrm{\Theta })+ln{\chi }_{t+1}(x_{t+1},h_t^{(s)},{\widehat{a}}_{t+1})\\ =c_t+a_{1,t}{h}_t^{(s)}+a_{2,t}{(h_t^{(s)})}^2+u_t^{(s)},s=1,\dots ,S\\ \end{array}$$(33)

where $u_t^{(s)}$ is the error term. Since χ_t+1 depends on a_t+1, the coefficients are calculated recursively, proceeding from t = T, T − 1, ..., 1.

In summary, it is possible to compute the likelihood function of the state-space model in Equations (15(15) $$x_t=(\mu -\frac{1}{2}{e}^{h_{t-1}})\mathrm{\Delta }+e^{h_{t-1}/2}\sqrt{\mathrm{\Delta }}{\epsilon }_t$$(15) )–(17(17) $$ln{C}_t=lnC(t,\tau ,K,S_t,V_t)+\delta {\nu }_t$$(17) ) for given the parameter vector (Θ, h₀), based upon the following E.I.S. algorithm:

Step 1: Draw initial samples ${\{h_1^{(s)},\dots ,h_T^{(s)}\}}_{s=1}^S$ from the N.I.S. sampler ${\{p(h_t|x_t,h_{t-1},\Theta )\}}_{t=1}^T$.

Step 2: Calculate ${\widehat{a}}_t$ by estimating the regression model (33), working backwards from t = T to t = 1.

Step 3: Draw new samples ${\{h_1^{(s)},\dots ,h_T^{(s)}\}}_{s=1}^S$ from the E.I.S. sampler ${\{m_t(h_t|x_t,h_{t-1},{\widehat{a}}_t)\}}_{t=1}^T$.

Step 4: Repeat Step 2 and Step 3, until a reasonable convergence of the parameters ${\widehat{a}}_t$ is obtained.

Step 5: Calculate the likelihood approximation using $\widehat{\mathcal{L}}(Y,X;\mathrm{\Theta },h_0)=\frac{1}{S}\sum _{s=1}^S\left[\prod _{t=1}^T\frac{p(ln{C}_t|x_t,h_t^{(s)},\mathrm{\Theta })p(x_t|h_{t-1}^{(s)},\mathrm{\Theta })p(h_t^{(s)}|x_t,h_{t-1}^{(s)},\mathrm{\Theta })}{m_t(h_t^{(s)}|x_t,h_{t-1}^{(s)},{\widehat{a}}_t)}\right]$

Following Richard and Zhang (2007), a same set of Common Random Numbers (C.R.N.s) is used to obtain the draws from the E.I.S. sampler in order to ensure the likelihood approximation $\widehat{L}$ be a smooth function of the parameter vector (Θ, h₀). The convergence of the E.I.S. algorithm is discussed in Koopman, Shephard, and Creal (2009). Typically, a reasonable convergence can be obtained after 3–5 iterations.

3.3. Particle filter

Given the parameter vector (Θ, h₀), we adopt the particle filter method of Gordon, Salmond, and Smith (1993) to obtain the filtered estimates of the latent state variable. The particle filter is a sequential Monte Carlo technique using simulated samples to generate prediction and filtering distributions for general nonlinear and non-Gaussian state-space models. It is flexible and easy to implement.

For our practical filtering problem, we are interested in the filtered log volatility, $E[h_t|{\mathcal{F}}_t]$, where ${\mathcal{F}}_t$ denotes the information set generated by the joint observations {(C₁, x₁), …, (C_t, x_t)}. Suppose that $p(h_{t-1}|{\mathcal{F}}_{t-1})$ is known and we want to obtain $p(h_t|{\mathcal{F}}_t)$. First, notice that

(34) $$p(h_t|{\mathcal{F}}_t)=\int p(h_t,h_{t-1}|{\mathcal{F}}_t)d{h}_{t-1}=\int \frac{p(h_t,h_{t-1}|{\mathcal{F}}_t)}{p(h_{t-1}|{\mathcal{F}}_{t-1})}dP(h_{t-1}|{\mathcal{F}}_{t-1})$$(34)

Also, from $p(ln{C}_t,x_t,h_t,h_{t-1}|{\mathcal{F}}_{t-1})=p(h_t,h_{t-1}|{\mathcal{F}}_t)p(ln{C}_t,x_t|{\mathcal{F}}_{t-1})$, we get(35) $$\begin{array}{c}p(h_t,h_{t-1}|{\mathcal{F}}_t)=\frac{p(ln{C}_t,x_t,h_t,h_{t-1}|{\mathcal{F}}_{t-1})}{p(ln{C}_t,x_t|{\mathcal{F}}_{t-1})}=\frac{p(ln{C}_t,x_t|h_t,h_{t-1},\mathrm{\Theta })p(h_t,h_{t-1}|{\mathcal{F}}_{t-1})}{p(ln{C}_t,x_t|{\mathcal{F}}_{t-1})}\\ =\frac{p(ln{C}_t|x_t,h_t,\mathrm{\Theta })p(x_t|h_t,h_{t-1},\mathrm{\Theta })p(h_t|h_{t-1},\mathrm{\Theta })p(h_{t-1}|{\mathcal{F}}_{t-1})}{p(ln{C}_t,x_t|{\mathcal{F}}_{t-1})}\\ \end{array}$$(35)

where$p(ln{C}_t,x_t|{\mathcal{F}}_{t-1})=\int \int p(ln{C}_t|x_t,h_t,\Theta )p(x_t|h_t,h_{t-1},\Theta )p(h_t|h_{t-1},\Theta )p(h_{t-1}|{\mathcal{F}}_{t-1})d{h}_{t-1}d{h}_t$

and p(x_t|h_t, h_t-1, Θ) is the normal density of x_t with the conditional mean $(\mu -\frac{1}{2}{e}^{h_{t-1}})\Delta +\rho e^{h_{t-1}/2}[h_t-h_{t-1}-(\alpha e^{-h_{t-1}}-\beta -\frac{1}{2}{\sigma }^2)\Delta ]/\sigma$ and the conditional variance $e^{h_{t-1}}(1-{\rho }^2)\Delta$ and p(h_t|h_t-1, Θ) is the normal density of h_t with the conditional mean $h_{t-1}+(\alpha e^{-h_{t-1}}-\beta -\frac{1}{2}{\sigma }^2)\Delta$ and the conditional variance σ²Δ.

Plugging (35) into (34), we get

(36) $$p(h_t|{\mathcal{F}}_t)=\int \frac{p(ln{C}_t|x_t,h_t,\mathrm{\Theta })p(x_t|h_t,h_{t-1},\mathrm{\Theta })p(h_t|h_{t-1},\mathrm{\Theta })}{p(ln{C}_t,x_t|{\mathcal{F}}_{t-1})}dP(h_{t-1}|{\mathcal{F}}_{t-1})$$(36)

In summary, the particle filter algorithm for estimating the latent log volatility is as follows:

Step 1: Given a set of random samples $\{h_{t-1}^{(1)},\dots ,h_{t-1}^{(N)}\}$ from the probability density function (PDF) $p(h_{t-1}|{\mathcal{F}}_{t-1})$.

Step 2: Draw samples $\{h_t^{(1\ast )},\dots ,h_t^{(N\ast )}\}$ from the P.D.F. p(h_t|h_t-1, Θ).

Step 3: Compute the normalised weight for each sample $q_j=\frac{p(ln{C}_t|x_t,h_t^{(j\ast )},\mathrm{\Theta })p(x_t|h_t^{(j\ast )},h_{t-1}^{(j)},\mathrm{\Theta })}{\sum _{i=1}^{N}p(ln{C}_t|x_t,h_t^{(i\ast )},\mathrm{\Theta })p(x_t|h_t^{(i\ast )},h_{t-1}^{(i)},\mathrm{\Theta })},j=1,\dots ,N$

Thus define a discrete distribution over $\{h_t^{(1\ast )},\dots ,h_t^{(N\ast )}\}$, with probability mass {q₁, …, q_N}.

Step 4: Resample N times from the discrete distribution defined above to generate samples $\{h_t^{(1)},\dots ,h_t^{(N)}\}$.

4. Empirical application

Unlike many previous studies that have focused mainly on the S&P500 index and index option, in this section we apply the approach developed to the H.S.I. index and index warrant data on the Hong Kong Stock Exchange.⁴ The H.S.I. index warrant was chosen over the H.S.I. index option because the index warrant was more actively traded than the index option in the Hong Kong stock market.

4.1. The data

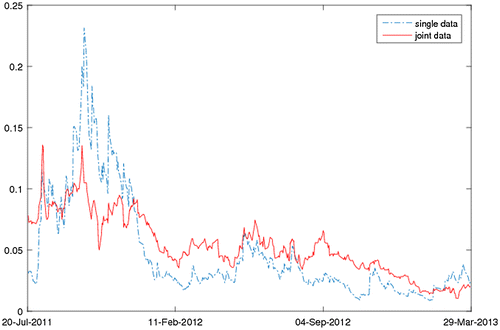
In the empirical analysis we use daily data on the H.S.I. returns and index warrant prices from 21 July 2011 to 28 March 2013. The H.S.I. returns are calculated as x_t = log p_t − log p_t-1, where p_t is the closing price of the H.S.I. index. On the Hong Kong Stock Exchange, a number of warrants were traded on the H.S.I. index, corresponding to different exercise prices, maturity dates and exercise ratios. We selected the HS-HSI.@EC1309, which is one of the most actively traded H.S.I. index warrants.⁵ The selected warrant is European-style call warrant which is similar to a European-style call option. Its maturity date is 27 September 2013, exercise price is 25,000 and exercise ratio is 12,000. The sample size is 836 for joint H.S.I. index and index warrant data. The joint time-series is plotted in Figure 1. Finally, we use the 1-year Hong Kong Interbank Offer Rate (H.I.B.O.R.) as a proxy for the risk-free interest rate. All of the data are obtained from the Wind Database of China.

Figure 1. Joint time series of H.S.I. returns and HS-HSI@EC1309 prices for the sample period from 21 July 2011 to 28 March 2013. Source: Author calculation.

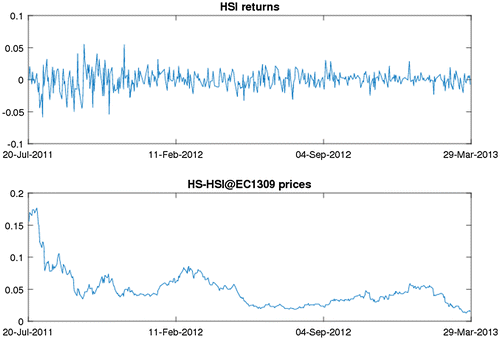
Summary statistics for the H.S.I. returns and HS-HSI@EC1309 prices are shown in Table 1. As can be seen from the table, the H.S.I. returns are skewed and leptokurtic. Jarque–Bera statistics suggests that the assumption of normality is rejected for the H.S.I. return series. Furthermore, from Figure 1 we can observe that the H.S.I. returns exhibit time-varying volatility and volatility clustering during the sample period. These results suggest that the S.V. model, e.g., the G.A.R.C.H. diffusion model, may be appropriate for modelling the H.S.I. index.

Table 1. Summary statistics of H.S.I. returns and HS-HSI@EC1309 prices.

Data	Mean	Max	Min	Std.	Skew	Kurt	Jarque–Bera
H.S.I. returns	0.0000	0.0552	−0.0583	0.0140	−0.2706	5.6206	124.714 (0.000)
HS-HSI@ EC1309 prices	0.0489	0.1770	0.0130	0.0284	2.0931	9.0129	934.910 (0.000)

Notes: The number in parenthesis is the P-values of Jarque–Bera tests.

Source: Author calculation.

4.2. Estimation results

Based upon the joint data, the objective and risk-neutral parameters of the G.A.R.C.H. diffusion model are estimated by applying the E.I.S.-M.L. method described in Section 3. Table 2 reports the estimation results. Traditionally, this model is estimated using single returns data, so we also report this configuration for comparison. While the use of option prices can lead to very accurate estimates, even in short samples in our case, estimation of the model from the single returns data requires relatively long samples to properly identify all parameters. We use daily data on the H.S.I. index over the period from 3 January 2005 to 28 March 2013, a sample size of 2044 observations, to estimate the model.

Table 2. Estimation results.

	Single data	Joint data
μ	0.1210 (0.0605) [0.0000]	0.1869(0.0672) [0.0001]
α	0.1095 (0.0339) [0.0001]	0.1444(0.0461) [0.0001]
β	1.6063 (1.2040) [0.0031]	3.8642(2.5730) [0.0021]
σ	2.2768 (0.2884) [0.0006]	1.2707(0.0412) [0.0004]
ρ	−0.5149 (0.0807) [0.0003]	−0.5276(0.0156) [0.0002]
α^*		0.0353(0.0081) [0.0000]
β^*		0.7603(0.0219) [0.0003]
δ		0.0176(0.0017) [0.0000]
Log-lik	5979.28 [0.0045]	1881.83 [0.0021]

Notes: The E.I.S.-M.L. method is implemented by using S = 32 Monte Carlo draws and 5 E.I.S. iterations. The number in parenthesis is the asymptotic (statistical) standard error which is obtained from a numerical approximation to the Hessian. The number in bracket is the Monte Carlo (numerical) standard error based upon 20 Monte Carlo replications under different sets of C.R.N.s.

Source: Author calculation.

Our results show that there are large discrepancies in the estimates with single data and joint data. The mean of the H.S.I. returns with the single data is μ = 0.1210, which is lower than the value 0.1869 with the joint data. The long-run mean of the volatility with the single data is α/β = 0.0682, which is obviously higher than the value of 0.0374 with the joint data. The estimate of the long-run mean of the volatility with joint data is closer to the unconditional sample variance of 0.0490 (= 0.0140² × 250) (see Table 1).

The estimates of the mean reversion rate of the volatility β differ considerably, implying that the estimated spot volatility process is much more persistent when estimated from the joint data than when estimated from the single data. This result is consistent with previous findings (see e.g., Cheng et al., 2008). The estimate of the volatility of volatility σ is noticeably smaller with the joint data than using the single data. Notice that the ‘leverage effect’ parameter ρ is significantly negative with both single data and joint data, indicating that the return and the volatility processes are negatively correlated during the sample period. But the estimate with the joint data is slightly more negative than with the single data ($\rho =-0.5276$ versus –0.5149, respectively).

With the joint data, the estimated objective and risk-neutral parameters (α, β) and (α^*, β^*) are quite different. Under the risk-neutral measure, the long-run mean of the volatility is α^*/β^* = 0.0464 and the mean reversion rate of the volatility is β^* = 0.7603. The volatility dynamic under the risk-neutral measure is different from that under the objective probability measure. In other words, the volatility risk has mostly likely been priced by the market.

The estimate for δ, which is the standard error of the pricing error, is small, implying that the pricing results based on the G.A.R.C.H. diffusion are fairly stable.

The use of additional derivative data provides noticeably more precise parameter estimates, in some cases by a factor of about 5–7. In fact, the most significant reduction for the asymptotic (statistical) standard errors is for the volatility of volatility and leverage effect parameters, σ and ρ. This finding agrees with results reported by Chernov and Ghysels (2000), Eraker (2004), Polson and Stroud (2003) and Cheng et al. (2008). Finally, we note that the Monte Carlo (numerical) standard errors of the estimates of model parameters are quite small, implying that the E.I.S.-M.L. estimates are numerically extremely accurate.

The estimated parameters allow us to estimate the volatility, V_t, via the particle filter algorithm. The number of particles used in the empirical studies is 1000. Figure 2 plots the estimated volatilities based upon the joint data (solid line) and single returns data (dotted line). It can be seen from the figure that although there is a consistent trend, there are large discrepancies in the estimates with the single data and joint data. In fact, the volatilities estimated using the joint data are less volatile and more persistent than their counterparts based upon the single returns data, which is consistent with the estimate of volatility of volatility parameter σ in Table 2. In addition, the estimates of volatilities with the joint data are higher than using the single data in most cases.

Figure 2. Estimated volatilities: Single data vs. joint data. Source: Author calculation.

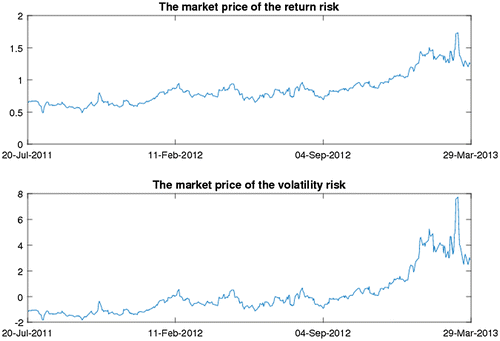
As noted in Section 2.2, the estimation of the complete objective and risk-neutral parameters and spot volatility based upon the joint data allow us to compute the market prices of risks. Therefore, we can compute the sample paths for the market prices of risks appearing in Equations (8(8) $${\lambda }_{1t}=\frac{\mu -r}{\sqrt{V_t}}$$(8) ) and (9(9) $${\lambda }_{2t}=\frac{c_1}{V_t}-\frac{c_2}{\sqrt{V_t}}-c_3$$(9) ). These parameters are reported in Figure 3. It can be seen from the figure that both the asset and volatility risks are priced by the market.

Figure 3. Time series of the market prices of the return and volatility risks. Source: Author calculation.

4.3. Option price fit

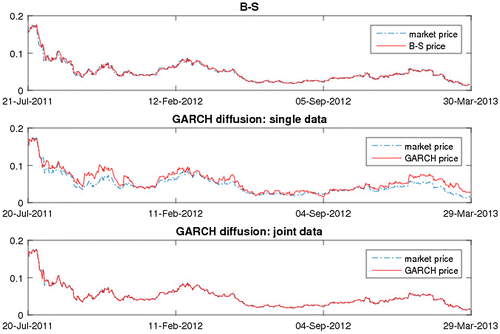
In this section, we discuss the empirical performance of the G.A.R.C.H. diffusion model based upon the single data and joint data in fitting the historical option prices. For the purpose of comparison, we also report the pricing results of the classical Black–Scholes (B.-S.) model with the volatility estimate based on the implied volatility.

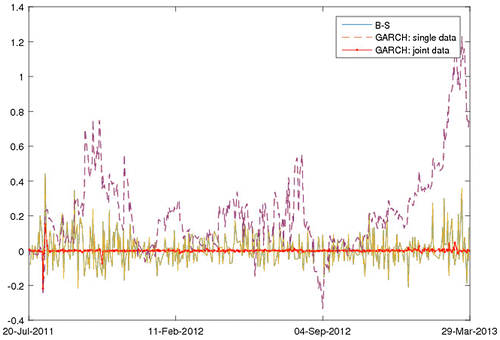
Figure 4 plots the pricing results for the different models. As can be seen from the figure, the B.-S. model with implied volatility and G.A.R.C.H. diffusion model base upon the joint data fit the option data reasonably well. The G.A.R.C.H. diffusion model seems to perform relatively poorly whenever the calculations are based on parameter estimates obtained using single returns data, i.e., under a zero market price of the volatility risk assumption. Figure 5 presents further evidence on the fit of the various models. The figure plots the percentage pricing errors for the different models. Notice that the percentage pricing errors for the G.A.R.C.H. diffusion model based upon the joint data are smallest and close to zero in most cases.⁶ In fact, we compute the mean percentage pricing error for the G.A.R.C.H. diffusion model based upon the joint data is 0.43%, while it is 6.11% for the B.-S. model with implied volatility and 23.86% for the G.A.R.C.H. diffusion model based upon the single data. Thus, the use of parameter estimates based upon joint data on the underlying asset and option prices provide economically significant performance enhancements. In other words, the market price of the volatility risk plays an important role in fitting option prices.

Figure 4. The pricing results. Source: Author calculation.

Figure 5. The percentage pricing errors. Source: Author calculation.

5. Conclusion

In this paper we proposed an estimation procedure for extracting the market prices of risks in the context of a G.A.R.C.H. diffusion model of non-affine specification using joint data on the underlying asset and option prices. This approach is flexible and can be applied in other S.V. option pricing models. Moreover, it is simple to implement. The proposed estimation procedure is based on the M.L. method, where the likelihood function of the model is evaluated using the E.I.S. technique. A quasi-closed form pricing formula for European options in the G.A.R.C.H. diffusion model is derived. It is efficient enough to apply the E.I.S.-M.L. method to the estimation of model (objective and risk-neutral) parameters from the joint data. To estimate the latent state variable, we developed a particle filter algorithm based upon the joint data. The empirical results from data on the H.S.I. and index warrant prices show that both the return and volatility risks are priced by the market. Moreover, an option pricing study demonstrates that the market price of the volatility risk plays an important role in fitting option prices.

Funding

This work was supported by the National Natural Science Foundation of China under Grant Nos. 71501001 and 71101001; M.O.E. (Ministry of Education in China) Project of Humanities and Social Sciences under Grant No. 14YJC790133; China Postdoctoral Science Foundation under Grant No. 2015M580416; Natural Science Foundation of Anhui Province of China under Grant No. 1408085QG139; Anhui Province College Excellent Young Talents Fund of China under Grant No. 2013SQRW025ZD.

Disclosure statement

No potential conflict of interest was reported by the authors.

Acknowledgements

We would like to thank the editor and two anonymous referees for their insightful and helpful comments and suggestions that greatly improved the paper.

Notes

1. While we focus on the G.A.R.C.H. diffusion model, it should be noted that our analysis is not limited to any particular model. The choice of the G.A.R.C.H. diffusion model is motivated by our previous discussion. It should be mentioned that any model that admits a formulation of the option pricing formula could be considered with the same methodology.

2. Joint estimation of the objective and risk-neutral parameters using both the underlying asset and option prices is necessary to maintain the internal consistency of the objective and risk-neutral measures. More precisely, the volatility of volatility and the correlation between the return and volatility shocks should be equal under the objective and risk-neutral measures. Broadie et al. (2007) find the evidence that it is easy to obtain misleading results if one ignores the theoretical restrictions that certain parameters must be consistent across measures. Hence, an efficient estimation procedure would use both the underlying asset and option prices and estimate the objective and risk-neutral parameters jointly.

3. Assuming that there are 250 trading days per year, then the time interval Δ for one trading day is 1/250 year, and in this case the discretisation bias of Euler scheme is expected to be negligible (see Duan & Yeh, 2010; Eraker et al., 2003; Johannes et al., 2009; Jones, 2003).

4. Warrants are contracts that give the holder the right, but not the obligation, to buy (call warrant) or to sell (put warrant) an underlying asset at a pre-determined price (the exercise price) on a specified date (the maturity date). As the definition of warrants is similar to that of options, it is natural to value warrants using the standard option pricing models.

5. There are also other ways to exploit the information available in option prices. For example, Pan (2002) selected each day the option closest to the money. The choices should not substantially affect the estimation results when the option pricing model adopted is accurate.

6. Notice in particular that the effects of the Standard & Poor on 5 August 2011 cut the long-term U.S. credit rating to AA-plus on concerns about the government’s budget deficits and rising debt burden, the H.S.I. index on 9 August 2011 fell 1159.87 points. However, the HS-HSI@EC1309 price on that day does not fall but rises. The event seems to have been captured by the option pricing error which reached –34.17% on that day.

Appendix A. Explicit expressions for the characteristic functions

Following Heston (1993), the characteristic functions, f_j, j = 1, 2, satisfy the following partial differential equations (P.D.E.s):(A.1) $$\begin{array}{c}\frac{1}{2}{V}_t\frac{{\partial }^2{f}_1}{\partial ln{S}_t^2}+\rho \sigma V_t^{3/2}\frac{{\partial }^2{f}_1}{\partial ln{S}_t\partial V_t}+\frac{1}{2}{\sigma }^2{V}_t^2\frac{{\partial }^2{f}_1}{\partial V_t^2}+(r+\frac{1}{2}{V}_t)\frac{\partial f_1}{\partial ln{S}_t}\\ +({\alpha }^{\ast }-{\beta }^{\ast }{V}_t+\rho \sigma V_t^{3/2})\frac{\partial f_1}{\partial V_t}-\frac{\partial f_1}{\partial \tau }=0\\ \end{array}$$(A.1)

and(A.2) $$\begin{array}{c}\frac{1}{2}{V}_t\frac{{\partial }^2{f}_2}{\partial ln{S}_t^2}+\rho \sigma V_t^{3/2}\frac{{\partial }^2{f}_2}{\partial ln{S}_t\partial V_t}+\frac{1}{2}{\sigma }^2{V}_t^2\frac{{\partial }^2{f}_2}{\partial V_t^2}+(r-\frac{1}{2}{V}_t)\frac{\partial f_2}{\partial ln{S}_t}\\ +({\alpha }^{\ast }-{\beta }^{\ast }{V}_t)\frac{\partial f_2}{\partial V_t}-\frac{\partial f_2}{\partial \tau }=0\\ \end{array}$$(A.2)

with the boundary conditions:

(A.3) $$f_j(t+\tau ,0,ln{S}_{t+\tau },V_{t+\tau };\varphi )=e^{i\varphi ln{S}_{t+\tau }},j=1,2$$(A.3)

It is apparent that Equations (A.1(A.1) $$\begin{array}{c}\frac{1}{2}{V}_t\frac{{\partial }^2{f}_1}{\partial ln{S}_t^2}+\rho \sigma V_t^{3/2}\frac{{\partial }^2{f}_1}{\partial ln{S}_t\partial V_t}+\frac{1}{2}{\sigma }^2{V}_t^2\frac{{\partial }^2{f}_1}{\partial V_t^2}+(r+\frac{1}{2}{V}_t)\frac{\partial f_1}{\partial ln{S}_t}\\ +({\alpha }^{\ast }-{\beta }^{\ast }{V}_t+\rho \sigma V_t^{3/2})\frac{\partial f_1}{\partial V_t}-\frac{\partial f_1}{\partial \tau }=0\\ \end{array}$$(A.1) ) and (A.2(A.2) $$\begin{array}{c}\frac{1}{2}{V}_t\frac{{\partial }^2{f}_2}{\partial ln{S}_t^2}+\rho \sigma V_t^{3/2}\frac{{\partial }^2{f}_2}{\partial ln{S}_t\partial V_t}+\frac{1}{2}{\sigma }^2{V}_t^2\frac{{\partial }^2{f}_2}{\partial V_t^2}+(r-\frac{1}{2}{V}_t)\frac{\partial f_2}{\partial ln{S}_t}\\ +({\alpha }^{\ast }-{\beta }^{\ast }{V}_t)\frac{\partial f_2}{\partial V_t}-\frac{\partial f_2}{\partial \tau }=0\\ \end{array}$$(A.2) ) are non-linear P.D.E.s, and there is no known exact analytical solutions to these equations. To overcome this problem, we utilise a perturbation method to derive an approximate solution (Chacko & Viceira, 2003; Wu et al., 2012). The idea is to approximate $V_t^{3/2}$ and $V_t^2$ in the P.D.E.s using Taylor expansions around the long-run mean of volatility V_t = α^*/β^* as follows:

(A.4) $$V_t^{3/2}\approx -\frac{1}{2}{\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^{3/2}+\frac{3}{2}\sqrt{\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}}{V}_t$$(A.4)

(A.5) $$V_t^2\approx -{\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^2+\frac{2{\alpha }^{\ast }}{{\beta }^{\ast }}{V}_t$$(A.5)

Plugging Equations (A.4(A.4) $$V_t^{3/2}\approx -\frac{1}{2}{\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^{3/2}+\frac{3}{2}\sqrt{\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}}{V}_t$$(A.4) ) and (A.5) into Equation (A.1(A.1) $$\begin{array}{c}\frac{1}{2}{V}_t\frac{{\partial }^2{f}_1}{\partial ln{S}_t^2}+\rho \sigma V_t^{3/2}\frac{{\partial }^2{f}_1}{\partial ln{S}_t\partial V_t}+\frac{1}{2}{\sigma }^2{V}_t^2\frac{{\partial }^2{f}_1}{\partial V_t^2}+(r+\frac{1}{2}{V}_t)\frac{\partial f_1}{\partial ln{S}_t}\\ +({\alpha }^{\ast }-{\beta }^{\ast }{V}_t+\rho \sigma V_t^{3/2})\frac{\partial f_1}{\partial V_t}-\frac{\partial f_1}{\partial \tau }=0\\ \end{array}$$(A.1) ) and Equation (A.2(A.2) $$\begin{array}{c}\frac{1}{2}{V}_t\frac{{\partial }^2{f}_2}{\partial ln{S}_t^2}+\rho \sigma V_t^{3/2}\frac{{\partial }^2{f}_2}{\partial ln{S}_t\partial V_t}+\frac{1}{2}{\sigma }^2{V}_t^2\frac{{\partial }^2{f}_2}{\partial V_t^2}+(r-\frac{1}{2}{V}_t)\frac{\partial f_2}{\partial ln{S}_t}\\ +({\alpha }^{\ast }-{\beta }^{\ast }{V}_t)\frac{\partial f_2}{\partial V_t}-\frac{\partial f_2}{\partial \tau }=0\\ \end{array}$$(A.2) ), we have(A.6) $$\begin{array}{c}\frac{1}{2}{V}_t\frac{{\partial }^2{f}_1}{\partial ln{S}_t^2}+\rho \sigma \left[-\frac{1}{2}{\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^{3/2}+\frac{3}{2}\sqrt{\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}}{V}_t\right]\frac{{\partial }^2{f}_1}{\partial ln{S}_t\partial V_t}\\ +{\sigma }^2\left[-\frac{1}{2}{\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^2+\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}{V}_t\right]\frac{{\partial }^2{f}_1}{\partial V_t^2}+(r+\frac{1}{2}{V}_t)\frac{\partial f_1}{\partial ln{S}_t}\\ +\left\{{\alpha }^{\ast }-{\beta }^{\ast }{V}_t+\rho \sigma \left[-\frac{1}{2}{\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^{3/2}+\frac{3}{2}\sqrt{\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}}{V}_t\right]\right\}\frac{\partial f_1}{\partial V_t}-\frac{\partial f_1}{\partial \tau }=0\\ \end{array}$$(A.6)

and(A.7) $$\begin{array}{c}\frac{1}{2}{V}_t\frac{{\partial }^2{f}_2}{\partial ln{S}_t^2}+\rho \sigma \left[-\frac{1}{2}{\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^{3/2}+\frac{3}{2}\sqrt{\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}}{V}_t\right]\frac{{\partial }^2{f}_2}{\partial ln{S}_t\partial V_t}\\ +{\sigma }^2\left[-\frac{1}{2}{\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^2+\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}{V}_t\right]\frac{{\partial }^2{f}_2}{\partial V_t^2}+(r-\frac{1}{2}{V}_t)\frac{\partial f_2}{\partial ln{S}_t}\\ +({\alpha }^{\ast }-{\beta }^{\ast }{V}_t)\frac{\partial f_2}{\partial V_t}-\frac{\partial f_2}{\partial \tau }=0\\ \end{array}$$(A.7)

The linear P.D.E.s (A.6(A.6) $$\begin{array}{c}\frac{1}{2}{V}_t\frac{{\partial }^2{f}_1}{\partial ln{S}_t^2}+\rho \sigma \left[-\frac{1}{2}{\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^{3/2}+\frac{3}{2}\sqrt{\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}}{V}_t\right]\frac{{\partial }^2{f}_1}{\partial ln{S}_t\partial V_t}\\ +{\sigma }^2\left[-\frac{1}{2}{\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^2+\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}{V}_t\right]\frac{{\partial }^2{f}_1}{\partial V_t^2}+(r+\frac{1}{2}{V}_t)\frac{\partial f_1}{\partial ln{S}_t}\\ +\left\{{\alpha }^{\ast }-{\beta }^{\ast }{V}_t+\rho \sigma \left[-\frac{1}{2}{\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^{3/2}+\frac{3}{2}\sqrt{\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}}{V}_t\right]\right\}\frac{\partial f_1}{\partial V_t}-\frac{\partial f_1}{\partial \tau }=0\\ \end{array}$$(A.6) ) and (A.7(A.7) $$\begin{array}{c}\frac{1}{2}{V}_t\frac{{\partial }^2{f}_2}{\partial ln{S}_t^2}+\rho \sigma \left[-\frac{1}{2}{\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^{3/2}+\frac{3}{2}\sqrt{\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}}{V}_t\right]\frac{{\partial }^2{f}_2}{\partial ln{S}_t\partial V_t}\\ +{\sigma }^2\left[-\frac{1}{2}{\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^2+\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}{V}_t\right]\frac{{\partial }^2{f}_2}{\partial V_t^2}+(r-\frac{1}{2}{V}_t)\frac{\partial f_2}{\partial ln{S}_t}\\ +({\alpha }^{\ast }-{\beta }^{\ast }{V}_t)\frac{\partial f_2}{\partial V_t}-\frac{\partial f_2}{\partial \tau }=0\\ \end{array}$$(A.7) ) have exponential-affine solutions of the form

(A.8) $$f_j(t,\tau ,ln{S}_t,V_t;\varphi )=e^{C_j(\tau )+D_j(\tau )V_t+i\varphi ln{S}_t},j=1,2$$(A.8)

with the boundary conditions

(A.9) $$C_j(0)=D_j(0)=0,j=1,2$$(A.9)

Plugging Equation (A.8(A.8) $$f_j(t,\tau ,ln{S}_t,V_t;\varphi )=e^{C_j(\tau )+D_j(\tau )V_t+i\varphi ln{S}_t},j=1,2$$(A.8) ) into Equations (A.6(A.6) $$\begin{array}{c}\frac{1}{2}{V}_t\frac{{\partial }^2{f}_1}{\partial ln{S}_t^2}+\rho \sigma \left[-\frac{1}{2}{\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^{3/2}+\frac{3}{2}\sqrt{\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}}{V}_t\right]\frac{{\partial }^2{f}_1}{\partial ln{S}_t\partial V_t}\\ +{\sigma }^2\left[-\frac{1}{2}{\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^2+\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}{V}_t\right]\frac{{\partial }^2{f}_1}{\partial V_t^2}+(r+\frac{1}{2}{V}_t)\frac{\partial f_1}{\partial ln{S}_t}\\ +\left\{{\alpha }^{\ast }-{\beta }^{\ast }{V}_t+\rho \sigma \left[-\frac{1}{2}{\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^{3/2}+\frac{3}{2}\sqrt{\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}}{V}_t\right]\right\}\frac{\partial f_1}{\partial V_t}-\frac{\partial f_1}{\partial \tau }=0\\ \end{array}$$(A.6) ) and (A.7(A.7) $$\begin{array}{c}\frac{1}{2}{V}_t\frac{{\partial }^2{f}_2}{\partial ln{S}_t^2}+\rho \sigma \left[-\frac{1}{2}{\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^{3/2}+\frac{3}{2}\sqrt{\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}}{V}_t\right]\frac{{\partial }^2{f}_2}{\partial ln{S}_t\partial V_t}\\ +{\sigma }^2\left[-\frac{1}{2}{\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^2+\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}{V}_t\right]\frac{{\partial }^2{f}_2}{\partial V_t^2}+(r-\frac{1}{2}{V}_t)\frac{\partial f_2}{\partial ln{S}_t}\\ +({\alpha }^{\ast }-{\beta }^{\ast }{V}_t)\frac{\partial f_2}{\partial V_t}-\frac{\partial f_2}{\partial \tau }=0\\ \end{array}$$(A.7) ), we have(A.10) $$\begin{array}{c}\frac{\partial C_1}{\partial \tau }+\frac{\partial D_1}{\partial \tau }{V}_t=-\frac{1}{2}{\sigma }^2{\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^2{D}_1^2+\left[{\alpha }^{\ast }-\frac{1}{2}\rho \sigma {\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^{3/2}(i\varphi +1)\right]D_1+ri\varphi \\ +\left\{{\sigma }^2\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}{D}_1^2+\left[\frac{3}{2}\rho \sigma \sqrt{\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}}(i\varphi +1)-{\beta }^{\ast }\right]D_1+\frac{1}{2}i\varphi (i\varphi +1)\right\}{V}_t\\ \end{array}$$(A.10)

and(A.11) $$\begin{array}{c}\frac{\partial C_2}{\partial \tau }+\frac{\partial D_2}{\partial \tau }{V}_t=-\frac{1}{2}{\sigma }^2{\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^2{D}_2^2+\left[{\alpha }^{\ast }-\frac{1}{2}\rho \sigma {\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^{3/2}i\varphi \right]D_2+ri\varphi \\ +\left\{{\sigma }^2\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}{D}_2^2+\left[\frac{3}{2}\rho \sigma \sqrt{\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}}i\varphi -{\beta }^{\ast }\right]D_2+\frac{1}{2}i\varphi (i\varphi -1)\right\}{V}_t\\ \end{array}$$(A.11)

These lead to the following ordinary differential equations (O.D.E.s)

(A.12) $$\frac{\partial C_1}{\partial \tau }=-\frac{1}{2}{\sigma }^2{\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^2{D}_1^2+\left[{\alpha }^{\ast }-\frac{1}{2}\rho \sigma {\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^{3/2}(i\varphi +1)\right]D_1+ri\varphi$$(A.12)

(A.13) $$\frac{\partial D_1}{\partial \tau }={\sigma }^2\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}{D}_1^2+\left[\frac{3}{2}\rho \sigma \sqrt{\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}}(i\varphi +1)-{\beta }^{\ast }\right]D_1+\frac{1}{2}i\varphi (i\varphi +1)$$(A.13)

and

(A.14) $$\frac{\partial C_2}{\partial \tau }=-\frac{1}{2}{\sigma }^2{\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^2{D}_2^2+\left[{\alpha }^{\ast }-\frac{1}{2}\rho \sigma {\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^{3/2}i\varphi \right]D_2+ri\varphi$$(A.14)

(A.15) $$\frac{\partial D_2}{\partial \tau }={\sigma }^2\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}{D}_2^2+\left[\frac{3}{2}\rho \sigma \sqrt{\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}}i\varphi -{\beta }^{\ast }\right]D_2+\frac{1}{2}i\varphi (i\varphi -1)$$(A.15)

Solving these linear O.D.E.s, we can obtain(A.16) $$\begin{array}{c}{C}_1(\tau )=i\varphi r\tau -\frac{{\beta }^{\ast }}{2{\sigma }^2{\alpha }^{\ast }}\left[{\alpha }^{\ast }-\frac{1}{2}\rho \sigma (i\varphi +1){\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^{3/2}\right]\\ \times \left[2ln\left(\frac{2d_1-(d_1-g_1)(1-e^{-d_1\tau })}{2d_1}\right)+(d_1-g_1)\tau \right]\\ -\frac{1}{2}{\sigma }^2{\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^2\left[-\frac{16g_1{\zeta }_1^2}{{(d_1^2-g_1^2)}^2}ln\left(\frac{2d_1-(d_1-g_1)(1-e^{-d_1\tau })}{2d_1}\right)\right.\\ \left.+\frac{4\tau {\zeta }_1^2(d_1^2-g_1^2)+4\tau {\zeta }_1^2{(d_1-g_1)}^2{e}^{-d_1\tau }-8{\zeta }_1^2(d_1+g_1)(1-e^{-d_1\tau })}{{(d_1+g_1)}^2(d_1-g_1)[2d_1-(d_1-g_1)(1-e^{-d_1\tau })]}\right]\\ \end{array}$$(A.16)

(A.17) $$D_1(\tau )=\frac{2{\zeta }_1(1-e^{-d_1\tau })}{2d_1-(d_1-g_1)(1-e^{-d_1\tau })}$$(A.17)

where ${\zeta }_1=\frac{1}{2}i\varphi (i\varphi +1),d_1=\sqrt{g_1^2-4{\sigma }^2{\zeta }_1\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}},g_1={\beta }^{\ast }-\frac{3}{2}\rho \sigma \sqrt{\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}}(i\varphi +1)$,

and(A.18) $$\begin{array}{c}{C}_2(\tau )=i\varphi r\tau -\frac{{\beta }^{\ast }}{2{\sigma }^2{\alpha }^{\ast }}\left[{\alpha }^{\ast }-\frac{1}{2}\rho \sigma i\varphi {\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^{3/2}\right]\\ \times \left[2ln\left(\frac{2d_2-(d_2-g_2)(1-e^{-d_2\tau })}{2d_2}\right)+(d_2-g_2)\tau \right]\\ -\frac{1}{2}{\sigma }^2{\left(\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}\right)}^2\left[-\frac{16g_2{\zeta }_2^2}{{(d_2^2-g_2^2)}^2}ln\left(\frac{2d_2-(d_2-g_2)(1-e^{-d_2\tau })}{2d_2}\right)\right.\\ \left.+\frac{4\tau {\zeta }_2^2(d_2^2-g_2^2)+4\tau {\zeta }_2^2{(d_2-g_2)}^2{e}^{-d_2\tau }-8{\zeta }_2^2(d_2+g_2)(1-e^{-d_2\tau })}{{(d_2+g_2)}^2(d_2-g_2)[2d_2-(d_2-g_2)(1-e^{-d_2\tau })]}\right]\\ \end{array}$$(A.18)

(A.19) $$D_2(\tau )=\frac{2{\zeta }_2(1-e^{-d_2\tau })}{2d_2-(d_2-g_2)(1-e^{-d_2\tau })}$$(A.19)

where ${\zeta }_2=\frac{1}{2}i\varphi (i\varphi -1)$, $d_2=\sqrt{g_2^2-4{\sigma }^2{\zeta }_2\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}}$, $g_2={\beta }^{\ast }-\frac{3}{2}\rho \sigma \sqrt{\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}}i\varphi$.

Appendix B. E.I.S. distribution and explicit expression for ln χ_t

Assuming that E.I.S. density m_t(h_t|x_t, h_t-1, a_t) is normally distributed with mean ${\mu }_{a_t}$ and variance ${\sigma }_{a_t}^2$, its log density is given by

(B.1) $$\begin{array}{c}ln{m}_t(h_t|x_t,h_{t-1},a_t)=-\frac{1}{2}ln2\pi {\sigma }_{a_t}^2-\frac{1}{2}{\left(\frac{h_t-{\mu }_{a_t}}{{\sigma }_{a_t}}\right)}^2\\ =-\frac{1}{2}ln2\pi {\sigma }_{a_t}^2-\frac{h_t^2}{2{\sigma }_{a_t}^2}+\frac{{\mu }_{a_t}}{{\sigma }_{a_t}^2}{h}_t-\frac{{\mu }_{a_t}^2}{2{\sigma }_{a_t}^2}\\ \end{array}$$(B.1)

Also, from Equations (28(28) $$m_t(h_t|x_t,h_{t-1},a_t)=\frac{k_t(h_t|x_t,h_{t-1},a_t)}{{\chi }_t(x_t,h_{t-1},a_t)}$$(28) ) and (30(30) $$k_t(h_t|x_t,h_{t-1},a_t)=p(h_t|x_t,h_{t-1},\mathrm{\Theta })exp\{a_{1,t}{h}_t+a_{2,t}{h}_t^2\}$$(30) ), we have(B.2) $$\begin{array}{c}ln{m}_t(h_t|x_t,h_{t-1},a_t)=ln{k}_t(h_t|x_t,h_{t-1},a_t)-ln{\chi }_t(x_t,h_{t-1},a_t)\\ =-\frac{1}{2}ln2\pi {\sigma }_t^2+\left(a_{2,t}-\frac{1}{2{\sigma }_t^2}\right)h_t^2+\left(a_{1,t}+\frac{{\mu }_t}{{\sigma }_t^2}\right)h_t-\frac{{\mu }_t^2}{2{\sigma }_t^2}-ln{\chi }_t(x_t,h_{t-1},a_t)\\ \end{array}$$(B.2)

where μ_t and ${\sigma }_t^2$ are the mean and variance of the N.I.S. density p(h_t|x_t, h_t-1, Θ), respectively, which are defined in Equations (22(22) $${\mu }_t=h_{t-1}+(\alpha e^{-h_{t-1}}-\beta -\frac{1}{2}{\sigma }^2)\mathrm{\Delta }+\sigma \rho \frac{x_t-(\mu -\frac{1}{2}{e}^{h_{t-1}})\mathrm{\Delta }}{e^{h_{t-1}/2}}$$(22) ) and (23(23) $${\sigma }_t^2={\sigma }^2(1-{\rho }^2)\mathrm{\Delta }$$(23) ).

Compare (B.1) and (B.2), we have$${\mu }_{a_t}={\sigma }_{a_t}^2\left(a_{1,t}+\frac{{\mu }_t}{{\sigma }_t^2}\right),{\sigma }_{a_t}^2=\frac{{\sigma }_t^2}{1-2a_{2,t}{\sigma }_t^2}$$ $$ln{\chi }_t(x_t,h_{t-1},a_t)=\frac{1}{2}ln\frac{{\sigma }_{a_t}^2}{{\sigma }_t^2}+\frac{{\mu }_{a_t}^2}{2{\sigma }_{a_t}^2}-\frac{{\mu }_t^2}{2{\sigma }_t^2}$$