Difference or not to difference an integrated time series? An empirical investigation

Abstract

This paper uses the gross domestic product growth rates of Malaysia, Thailand, Indonesia and China in an empirical examination to determine whether an integrated time series should be differenced before it is used for forecasting. The results reveal that Mallows model combination (M.M.A.) of original and differenced series is a better choice than just differencing the series only if the perturbation instability measure is more than 1.25 for autoregressive (A.R.) model, and 1.105 for moving average (M.A.) model and autoregressive fractional integrated moving average (A.R.F.I.M.A.) model. Furthermore, it is found that M.M.A. performs better in forecasting with better model stability for the case of M.A. and A.R.F.I.M.A. than A.R. However, M.M.A. is very sensitive in financial crisis.

Keywords:

• Mallows model combination (MMA)
• predictive ability
• model selection
• perturbation instability measure
• forecast strain

JEL classifications:

• C530
• C180
• O470

1. Introduction

It is normal practice to difference an integrated time series to remove the unit root before conducting any empirical analysis, especially for forecasting. This step is taken to ensure that the forecasting series is stationary, as stationarity is the basic criterion for forecasting. However, this practice gives rise to four issues. First, differencing may remove some important information from the data series; second, testing the existence of unit root at 5% significance level or less is not suitable because the unit root test is a pretest for the existence of cointegration and therefore a 25% significance level is more appropriate (Maddala & Kim, 1998); third, near unit root cases are difficult to assess as they result in substantial size distortions for tests on the coefficients of cointegrating vector (Elliott, 1995a); and fourth, even if the test is significant, it still has a trivial probability of 5% or less that the test is negative. All these four issues involve hypothesis testing. And since hypothesis testing in this case encounters so many problems, the question is: can we circumvent it by using other measures of the optimality of the model, especially in the aspect of forecasting? This paper attempts to shed some light on this issue and thereafter attempts to answer this research question explicitly. From this perspective, we propose an indirect method to circumvent this problem of whether to difference or not by selecting the best forecasting model based on the criterion of minimum risk which is measured by in-sample mean squared error (M.S.E.) and out-of-sample expected squared forecast error (M.S.F.E.). In addition, using the perturbation instability measure (P.I.M.), we ensure that the parameters and weights of the models are relatively more stable for the best forecasting model. Put differently, the best forecasting model (be it single or combination) should have the minimum M.S.F.E. and M.S.E. values and also an appropriate P.I.M. value (see Section 4.1).

This indirect method is more plausible since it involves comparison of autoregressive (A.R.), moving average (M.A.) and autoregressive fractional integrated moving average (A.R.F.I.M.A.) models with Mallows model combination (M.M.A.), which are usually used for forecasting. In general, a forecasting model can be a single parsimonious model or it can be a combination of two or more single models. Which one is the best and under what conditions is the major issue that confronts us. A model combination of two or more single models may have a better set of M.S.F.E. and M.S.E. values than a single parsimonious model if certain specific conditions are met. A qualitative explanation is: any model may possess good and bad characteristics. If, in the process of combining, the good characteristic of one model is combined with the good characteristic of another model, then the combined model should have better M.S.F.E. and M.S.E. values than either one of the single models. However, if the bad characteristics of both models are combined, then the forecasting accuracy of the combined model would lose out to each of the single models. Thus two questions arise: (1) how do we determine when model combination is better than a single parsimonious model? (2) How do we ensure that we have combined the best characteristics from all the single models? A smaller M.S.F.E. and M.S.E. than either one of the single models may be the answer. However, M.S.F.E. and M.S.E. alone are not good enough because they may be sample specific only. We need a quantitative measure and a relative measure to confirm the role of M.S.F.E. and M.S.E. in determining when to combine the models.

For quantitative measure, Yuan and Yang (2005) investigated this aspect and they proposed a rule of thumb in their use of the P.I.M. to determine when to combine models. P.I.M. is described in Section 4.1. However, their rule of thumb is for simple regression models only.

Explicitly, this paper uses a model selection technique to identify the best parsimonious model (series) and then combines the two estimators of both the differenced (constrained) and original (unconstrained) series of the best model by using a model combination technique, specifically M.M.A.

Then, we compare the performance of the combined estimators and the constrained estimators on their ability to deliver both in-sample and out-of-sample forecasting. By using model combination method in this way, the loss of information due to differencing is minimised. Specifically, we have provided a solution to our research question.

Next, we analyse our empirical results to see if they fit into the model combination criterion as specified by Yuan and Yang (2005). The M.M.A. technique is used because theoretically, the M.M.A. estimate has been proven to be an unbiased estimate of M.S.F.E. plus a constant (Hansen, 2010), and moreover, this technique is the most recently developed model combination technique in the literature. In addition, Hansen (2007, 2008, 2009, 2010) has also verified that M.M.A. achieves optimal asymptotic M.S.E. by using asymptotic theory and simulation study. For model selection, as Bayesian information criterion (B.I.C.) is the most consistent information criterion (Hayashi,2000), we use it to select the best model from each of the A.R., M.A. and A.R.F.I.M.A. Three different types of models are used, namely A.R., M.A. and A.R.F.I.M.A., for the purpose of checking the robustness of our results.

The rest of the paper is organised as follows. Section 2 presents the literature review while Section 3 introduces the M.M.A., A.R., M.A. and A.R.F.I.M.A. models. Section 4 introduces P.I.M.s. Section 5 describes the framework for the empirical study, while Section 6 presents the empirical results. Section 7 concludes the paper and suggests areas for further research.

2. Literature review

We present a brief literature review on model selection, model combination techniques, perturbation theory of instability and forecast strains in this section. Standard forecasting is usually based on a well-specified model which is chosen from a set of candidate models by using distinctive estimation criteria.

There are many well-known criteria of this category which include Akaike information criterion (A.I.C.) (Akaike, 1973), Mallows criterion (Mallows, 1973), B.I.C. (Schwarz, 1978), the focused information criterion (Hjort & Claeskens, 2003) and many others. This method of selecting the best forecasting model is known as the model selection procedure. However, the model selection procedure suffers a number of concerns; notably, the accuracy of the inference depends heavily on the so-called best selected model. Parameter uncertainty is not incorporated into the inference of model selection, and there is underestimation of uncertainty about the quantities of interests. All these will result in overoptimistic views and biased inferences. These undesirable effects of model selection on inference have been extensively examined and discussed by many researchers. Draper (1995) discusses the cost of ignoring model uncertainty. Chatfield (1995) studies model uncertainty, data mining and statistical inference. McQuarrie and Tsai (1998) review the frequentist model selection approach using information and related criteria. In addition, Potscher (1991) shows that the A.I.C. model selection method results in distorted inference while Buhlmann (1999) examines and reveals conditions under which post-model-selection (P.M.S.) estimators are mostly adaptive. Furthermore, Leeb and Potscher (2003, 2005, 2006) investigate the unconditional and conditional distribution of P.M.S. estimators and find that they cannot be uniformly estimated. This brief literature review on model selection methods suggests that model selection may not be an optimal method to construct the best model for forecasting, because of the existence of model selection uncertainty. Many other procedures of forecasting have been proposed to overcome this shortcoming. Among these procedures, model combination is considered as a likely alternative to model selection in the sense that it can reduce estimation variance and at the same time control omitted variable bias (Hansen, 2007).

There is a large amount of literature on model combination, notably Bayesian literature and an ever-growing frequentist literature. Raftery, Madigan, and Hoeting (1997) made seminal contributions to Bayesian model combination. In the frequentist literature, contributors include Buckland, Burnham, and Augustin (1997) and Burnham and Anderson (2002), where both studies have suggested exponential A.I.C. weights for model combination. Among all these model combination procedures, there is one proposed by Hansen (2007) which uses weights that minimise the Mallows criterion. Hansen (2007) applies asymptotic theory and simulation study to show that M.M.A. produces excellent theoretical results in pseudo out-of-sample forecasting that surpasses many other methods such as those using the Dickey–Fuller t-test as pretest. At this point it is pertinent to note that models can be nested or non-nested, as there is some difference between model combination for non-nested and nested models. The asymptotic optimality of M.M.A. has been proven by Hansen (2007) for the case of nested models and by Wan, Zhangx, and Zau (2010) for the case of non-nested models. However, to date, literature on M.M.A. forecasting in an empirical environment is scarce. One rare example is the paper by Diks and Vrugt (2010). This scarcity constitutes an additional motivation for us to conduct this empirical analysis whereby we intend to find a solution to the problem of differencing as well as to address the issue of how the existence of outliers, such as financial crisis, can affect the forecasting ability of model combination method.

The question of whether model combination is always better than model selection has been investigated by only a few researchers, notably Breiman (1996) and Yuan and Yang (2005). Breiman uses perturbations to compare instabilities of regression procedures. He obtains different versions of the estimators and then combines them into a final estimator for better performance in forecasting. Yuan and Yang (2005), on the other hand, use perturbation to measure the instability of a regression procedure quantitatively. The study comes out with a P.I.M. and the rule of thumb for when to combine models.

3. The models

This section describes the models used in this empirical study. We use only univariate time series of gross domestic product (G.D.P.) growth for comparing forecasting ability. In addition, M.M.A., A.R., M.A. and A.R.F.I.M.A. models are used for the empirical analysis. The reasons are: (i) A.R., M.A. and A.R.F.I.M.A. are closely related to one another with A.R. as the core model, and so they are nested models, and (ii) to check the robustness of our results. The use of the A.R. model as the core model is based on the research findings of three papers which supported the relatively better forecasting power of the simple models. Banerjee, Marcellino, and Masten (2003) compare the forecasting accuracy of models using leading indicators and simple A.R. model for forecasting G.D.P. growth. Their results indicate that the pure A.R. model, which works on univariate time series, has a better forecasting ability. Ang, Bekaert, and Wei (2007) investigate whether macroeconomic variables, asset markets or surveys best forecast U.S. inflation. Their results show that surveys best forecast inflation. Granger and Newbold (1986) find that forecasting with simple models is only marginally less accurate than with models built using complex techniques. They suggest that only when the benefits of complex techniques outweigh the additional costs of using them should they be the preferred choice.

3.1. Mallows model combination

This subsection explains briefly the concept of M.M.A. and shows how it is applied to combine constrained¹ and unconstrained estimators in order to obtain a combined estimator which is more accurate than either. Hansen (2007) has used the Mallows criterion for selecting the weight vector W in a model combination (averaging) procedure.

The model combination estimator for N number of models using Mallows criterion is given as follows:

(1) $$\begin{array}{c}{C}_n(W)={\mathrm{E}}^{\prime }\mathrm{E}+2{\sigma }^{2}k(W)\\ \mathrm{E}=(Y-X_N\widehat{\mathrm{\Theta }})\\ \end{array}$$(1)

where n, C_n(W) k(W) are the sample size, Mallows criterion and the effective number of parameters, respectively. σ²is the unknown variance and needs to be replaced by an estimate. In addition, X_N is the matrix of regressors for N number of models and $\widehat{\Theta }$is the estimated parameter vector as shown in Equation (2).

(2) $$\widehat{\mathrm{\Theta }}=\sum _{m=1}^N{w}_m\left(\begin{array}{c}{\widehat{\mathrm{\Theta }}}_m\\ 0\end{array}\right)$$(2)

where w_m are elements of the weight vector W.

To combine estimators from different candidate models, suitable weights need to be assigned to each estimator. Suitable weights are chosen which are contained in a weight vector W by minimising the Mallows criterion C_n(W) using an optimisation procedure. This weight vector W is defined in Equation (3).

(3) $$\widehat{W}=\underset{W\in {\mathrm{H}}_n}{arg\text{min}}{C}_n(W)$$(3)

where H_n is given by Equation (4).

(4) $$H_n=\left\{W\in {[0,1]}^N:\sum _{m=1}^N{w}_m=1\right\}$$(4)

where W denotes the weight vector which is made up of weights with values between 0 and 1.

Since we have N models for averaging, we would have N × 1 vector of the number of parameters in the N models. Our final Mallows criterion will become as follows:

(5) $$C_n(W)=W^{\prime }{e}^{\prime }eW+2{\sigma }^2{K}^{\prime }W$$(5)

where $e=({\widehat{e}}_1,....,{\widehat{e}}_N)$is a n × N matrix which collects all the residuals, and K = (k₁, ...., k_N)are the N × 1 vector of the number of parameters in the N models.

However, in our empirical analysis, we deal only with univariate time series which can be stationary, or nonstationary. In normal practice, the estimator of an original integrated time series before undergoing differencing is termed as unconstrained estimator. However, most time series are integrated of order one, I(1), because each contains stochastic trend. We difference the I(1) series so as to transform the original series into a stationary one. The estimator involved in this case is termed as a constrained estimator. A constrained estimator is widely recognised as having lost certain useful information due to the process of differencing. The M.M.A. estimator is a combination of the constrained and unconstrained estimators.

Hereafter, we follow the approach by Hansen (2010) with regard to assigning Mallows weights to the unconstrained and constrained estimator. First, the optimal Mallows criterion M_w is defined, for the clear-cut case of unit root, that is the local to unity parameter. c is set to be zero. By theorem 6 of Hansen (2010), M_w is defined as:$$M_w=n{\widehat{\sigma }}^2(w)+2{\widehat{\sigma }}^2(2w+p+k)$$

where p and k, respectively, denote time trend and second lag onwards for the A.R. model. Since we use mainly AR(1) model without time trend and second lag onwards (p = 0 and k = 0), the above definition is then simplified to become Equation (6):

(6) $$M_w=n{\widehat{\sigma }}^2(w)+4w{\widehat{\sigma }}^2$$(6)

We minimise M_w over w ∊ [0, 1] to obtain the Mallows selected weight $\widehat{w}$. Then by Theorem 7 of Hansen (2010), we obtain the following:

(7) $$\widehat{w}=\left\{\begin{array}{c}\begin{array}{cc}1-\frac{2}{G_n}& \text{if}{G}_n>2\end{array}\\ \begin{array}{cc}\text{0}& \text{otherwise}\end{array}\end{array}\right.$$(7)

where $G_n=n\left(\frac{{\tilde{\sigma }}^2-{\widehat{\sigma }}^2}{{\widehat{\sigma }}^2}\right)$. With that, the Mallows averaging estimator given by

(8) $$\begin{array}{c}{\widehat{\theta }}_t^m=w{\widehat{\theta }}_t+(1-w){\tilde{\theta }}_t\\ =\left\{\begin{array}{c}{\tilde{\theta }}_{\text{t}}\text{if}{G}_n\le 2\\ (1-\frac{2}{G_n}){\widehat{\theta }}_t+(\frac{2}{G_n}){\tilde{\theta }}_t\text{otherwise}\end{array}\right.\\ \end{array}$$(8)

where ${\tilde{\theta }}_{\text{t}}$is the constrained estimator and ${\widehat{\theta }}_t$ is the unconstrained estimator. The Mallows averaging estimator in Equation (8) has been shown to have smaller risk and that it has low asymptotic mean squared error (A.M.S.E.) and asymptotic forecast risk when the local to unity c is small by Hansen (2010). However, for our case we have set c = 0, which satisfies Hansen’s criterion for the value of c to be small. Thus, our M.M.A. model has a very low A.M.S.E. and also asymptotic forecast risk. The values of these two measures are low, which essentially means that our combined estimator is optimal under theoretical consideration.

3.2. Autoregressive model, AR(p)

A.R. models are commonly applied models with the predictable component of y_t which assumes the linear combination of p of its lagged values. Its basic function is to use past data to predict present and future data. Its general equation is written as in Equation (9).

(9) $$y_t={\beta }_1{y}_{t-1}+{\beta }_2{y}_{t-2}+\cdots +{\beta }_p{y}_{t-p}+{\epsilon }_t\text{t}=\text{1,}\cdots \text{,n}$$(9)

Equation (9) can be written in a more concise form by using the lag operator L as shown in Equation (10).

(10) $${\beta }_p(L)y_t={\epsilon }_t$$(10)

where L is defined by L^ky_t = y_t-k.and β_p(L) = 1 - β₁L - ... - β_pL^p.

The A.R. model turns out to be very useful for descriptive and forecasting purposes. However, y_t can be stationary, nonstationary or explosive depending on the values of β_p. In fact the AR(1) model has been proven to be extremely good in forecasting and this good property is also manifested in our empirical analysis. However, throughout the analysis, it is assumed that the error term in the A.R. model is white noise, which is a rather practical assumption. In our analysis, we use only AR(1) or AR(2) model after using B.I.C. for determining the lag length in the autoregression. AR(1) model is shown in Equation (11).

(11) $$y_t=\alpha +{\beta }_1{y}_{t-1}+{\epsilon }_t\text{t}=\text{1,}\cdots \text{,n}$$(11)

where α is the intercept term or simply the unconditional mean of y_t.

3.3. Moving average model, MA(q)

The M.A. model assumes that the predictable part of y_t is a linear combination of the q most recent shocksɛ_t-1, ɛ_t-2, ...., ɛ_t-q

(12) $$y_t={\epsilon }_t+{\alpha }_1{\epsilon }_{t-1}+\cdots +{\alpha }_q{\epsilon }_{t-q}+{\epsilon }_t\text{t}=\text{1,}\cdots \text{,n}$$(12)

where α is the coefficients of shocks.

An M.A. model is able to capture the autocorrelation that is normally present in any time series. Because of this property, M.A. is expected to do well for modelling the autocorrelation of the time series. However, the assumption that all autocorrelations are set to be zero if its position number j > q, implies that q has to be large if an MA(q) is to display large autocorrelation coefficients. A formula for its autocorrelation function ρ(j)will make this point clear.

(13) $$\rho (j)=\frac{{\alpha }_j+{\sum }_{i=1}^{q-j}{\alpha }_{j+i}{\alpha }_i}{1+{\sum }_{i=1}^q{\alpha }_i^2}\text{for j}\le \text{q,}\rho \text{(j)}=\text{0, otherwise}$$(13)

For an MA(1) model, the largest possible absolute value of ρ(1) is about 0.5. This suggests that if M.A. modelling is to be effective, we have to examine its autocorrelation graph for an estimate of its absolute value of autocorrelation. We use MA(1) or MA(2) for forecasting and then compare its effectiveness when both models are combined by M.M.A.

3.4. Autoregressive fractional integrated moving average model, A.R.F.I.M.A.

The A.R.F.I.M.A. model is the general model which encompasses A.R., M.A., A.R.M.A. and A.R.I.M.A. The parameter which describes A.R. is p, M.A. is q, and A.R.I.M.A. is p, q and I where I is an integrated number starting from 0, 1, 2 or higher. However, the usual cases for I is 0, 1 or 2. For A.R.F.I.M.A., the parameters are p, q and d where d is the memory parameter. When d takes the value of 0, it is a stationary process. If d takes the value of 1, it is an integrated process with a single unit root. However, when d lies in the range of 0 to 0.5, it indicates a long memory process, while if the value of d is between 0.5 and 0, the process is called intermediate memory. The problematic part is when d is near to 1. This situation will cause confusion in the unit root test. The formula for A.R.F.I.M.A. is as follows:

(14) $$\beta (L){(1-L)}^d{y}_t=A(L)u_t,u_{\text{t}}\sim iid(0,{\sigma }_u^2)$$(14)

where $\beta (L)\text{and}A(L)$are the respective lag polynomials.

The general specification of A.R.F.I.M.A. is ARFIMA(p,d,q). Thus AR(1) model is equivalent to ARFIMA(1,0,0) because its p = 1 (1 lag), d = 0 (stationary process) and q = 0 (no M.A. component). For an autoregressive M.A. model such as ARMA(1,1) its specification is ARFIMA(1,0,1) if A.R.M.A. is a stationary process. In our empirical analysis, we use only ARMA(1,1). ARMA(1,2) and ARMA(1,3) for forecasting and then compare the combined model by M.M.A. with each of the models.

4. Model instability measures

A well-specified forecasting model may be sample specific only, as the economy and the forecasting ability of models may not be stable over time. The most probable cause is the instability in the model’s parameters as well as other instabilities in the data-generating process, such as the variance of the disturbances change for a quadratic loss. In addition, the trend and seasonal properties may change over time. All these issues need to be addressed so that any forecasting results remain plausible and acceptable. This issue is addressed here by using P.I.M., which will be introduced briefly in the next section (4.1), as a quantitative measure to overcome the model instability problem.

4.1. Perturbation instability measures (P.I.M.)

Consider a model selection for homoskedastic linear autoregression model. The original autoregressive model is represented by (y,h,σ) where h denotes the number of lag terms. We inject an additional noise into this original model, and this additional noise is represented by ρσ where ρ is known as the perturbation size taking values between 0 and 1. Thus the perturbed model should be:(15) $$(\tilde{y},h,\sigma \sqrt{!+{\rho }^2})$$(15)

The regression is run again using this perturbed model. We estimate the P.I.M. for the coefficient of y_t-1. For simple linear regression model, Yuan and Yang (2005) have shown by simulation and empirical study that if P.I.M. > 0.5, model combination procedure is preferable. However, when P.I.M. < 0.5, a good model selection method is likely to work better.

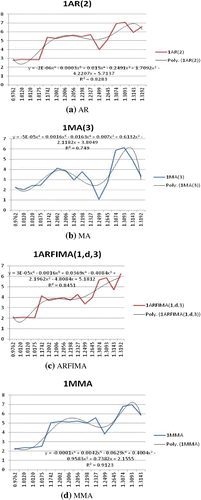
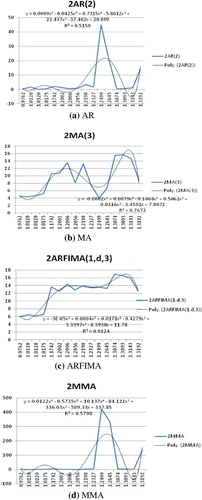
However, for this study G.D.P. growth rate data are used, and these data are subject to changes according to the economic environment. Thus, the cut-off point for model combination to be implemented may not be the same. Appendix 2 describes how the P.I.M. for each model is estimated, while Figures 1 and 2 display graphs of A.R., M.A., A.R.F.I.M.A. and M.M.A. against the respective P.I.M. values for the case of M.S.E. and M.S.F.E. errors used, respectively. Our main interest is in Figure 2, where out-of-sample forecast is used. Figure 2(a) shows that at P.I.M. = 1.25, the values of AR(2) starts to spike up sharply, indicating that the model starts to be unstable at a P.I.M. value more than 1.25 and then after a certain period, it achieves stability again. This suggests that in this approach, for the sake of caution, for values of P.I.M. > 1.25 we should use model combination like M.M.A. for forecasting, and when P.I.M. < 1.25, we should use model selection, in this case the A.R. model. The same goes for Figure 2(b) and Figure 2(c), where in both cases the first spike up occurs at P.I.M. = 1.015 for MA(3) and ARFIMA(1,0,3), respectively.

Figure 1. Nonlinear relationship between P.I.M. and forecasting errors (M.S.E.). Source: Authors’ calculation.

Figure 2. Nonlinear relationship between P.I.M. and forecasting errors (M.S.F.E.). Source: Authors’ calculation.

5. The empirical study framework

This section describes how and why we formulate our empirical study framework. We start with the data, and the source, with a description of how and why we select the specific samples. This is followed by the selection of A.R. specification, M.A. and A.R.F.I.M.A. Finally, we introduce briefly the M.M.A. technique.

5.1. The data

The data set consists of the G.D.P. growth rate of Malaysia, Thailand, Indonesia, and China. All the four² data series are quarterly and seasonal adjusted by X12arima which is produced by U.S. Department of Commerce, Bureau of the Census X-12 seasonal adjustment with regARIMA. By doing this, we have de-seasonalised the quarterly series.

For Malaysian, Thai, and Indonesian G.D.P. growth rate, each data series commences from 1976q1 to 2006q4, totalling 124 data points in each series. However, for China the data series starts from 1979q1 to 2006q4 and are real data. We generate the data from 1976q1 to 1978q4 by using cubical spline basing on the real data. Since the sets of data are not large, we use a rolling sample technique to construct four rolling samples for forecasting. Rolling sample is preferred for two reasons: one, it can minimise the effect of parameter uncertainty and two, it enables us to construct four rolling samples of a reasonably large sample size of 95 each. These four data sets are selected on the basis that strong dynamic Association of Southeast Asian Nations (A.S.E.A.N.)–China relations will create significant economic opportunities which will benefit A.S.E.A.N. member states. Malaysia, Thailand and Indonesia, being among the more advanced as well as the three largest A.S.E.A.N. economies, are expected to maintain data which are relatively more comprehensive and faithful, characteristics of which could be of advantage to our empirical study. At the same time, higher forecasting accuracy will help A.S.E.A.N. economies to better position themselves to take advantage of the benefits from the various strategic pan-regional economic plans of China such as the One Belt One Road economic development strategy.

5.2. Selection of maximum lag lengths for A.R. and M.A. models

For A.R. and M.A. models, we select the maximum lag length by using Schwedt’s formula:

(16) $$P_{max}(T)=\left[12·{\left(\frac{T}{100}\right)}^{0.25}\right]$$(16)

where T is the sample size and P_max(T) is an integrated part of the answer in the formula. After obtaining the maximum lag length, we use the general to specific rule to obtain the final lag. We start with maximum lags (Schwarz, 1978), then progressively eliminate the insignificant lag based on t statistic. By using this method, we ascertain the lag length of A.R., M.A. and A.R.F.I.M.A. models.

However, a general to specific rule may not produce accurate lag length for all the three models, A.R., M.A. and A.R.F.I.M.A. To be doubly sure of the determined lag lengths, we conduct a corrective measure for the number of lags determined by drawing the autocorrelation graph for the series to analyse the size of its values. If the values of autocorrelation are large, then we would contemplate increasing the lags appropriately if M.A. modelling is involved. This is because small lags for M.A. are not effective in M.A. modelling.

5.3. Unit root test

Since G.D.P. growth rates are time series, we have to test each of the series for unit root. The presence of unit root in the series will cause the series to be nonstationary, making it unsuitable for forecasting purposes. We subject each series through a battery of unit root tests. We start with the Augmented Dicky–Fuller (A.D.F.) test, which uses the null hypothesis that there is a unit root. Next we conduct the Kwiatkowski–Phillips–Schmidt–Shin (K.P.S.S.) unit root test, which uses the null hypothesis that there is no unit root. Thus if A.D.F. returns a significant test result and K.P.S.S. returns an insignificant result, we can safely conclude that no unit root is present in the series. In addition, we also conduct the Dicky–Fuller Generalised Least Squares (D.F.-G.L.S.) unit root test which uses the null hypothesis that there is a unit root. This last test is a very powerful test. If all the three tests give consistent positive results, then unit root is confirmed to exist. Otherwise, the existence of unit root will depend on the result of the last test. Once a unit root is confirmed to exist, we difference the respective series once to obtain a stationary series, which we term as the constrained data series. The unconstrained data series is the one before any differencing is done. Even though we use a battery of unit root tests, there is still about 5% trivial probability that the test is not accurate. On top of this, quite a number of series, especially the money supply, may have the parameter value close to 1 but not 1. This type of series is characterised by the fact that differencing cannot turn the series into stationary. However, we do not include this type of series into our empirical analysis.

5.4. M.M.A.

We run the M.M.A. Gauss³ procedure to estimate the parameters and their respective weights. We have only two weights: one for the constrained estimator, which is equivalent to the estimator after differencing the series, and the other for the unconstrained estimator, which is the intrinsic estimator (without doing any transformation or calculation). By using these estimated weights, we obtain in-sample and out-of-sample forecasts together with the expected M.S.F.E. and M.S.E. With these computed forecast values, we compute the forecasts from the M.M.A. estimator.

6. Empirical results

For ease of comparing the relative values of M.S.F.E. to determine which model has the best forecasting ability, we define and use two measures to compare the predictive performance of A.R., M.A. and A.R.M.A. with that of M.M.A. The two measures are out-of-sample predictive performance index (O.S.-P.P.I.), and forecast strain (F.S.⁴) which are defined in Equations (17) and (18), respectively. O.S.-P.P.I. is used to compare the predictive ability of other models with respect to M.M.A., with O.S.-P.P.I. > 1 implying that M.M.A. is superior over the single model. And when O.S.-P.P.I. < 1, this implies that the M.M.A. approach is comparatively inferior. F.S., on the other hand, is used to estimate the stability of model selection or model combination. F.S. > 1 implies that the model (selection or combination) is stable while F.S. < 1 implies instability of the model.

(17) $$OS-PPI=\frac{\text{MSFE from model selection}}{\text{MSFE from model averaging MMA}}$$(17) (18) $$FS=\frac{\mathit{MSFE}}{\mathit{MSE}}$$(18)

We compare out-of-sample forecasting accuracy of A.R., M.A. and A.R.F.I.M.A. separately with that of M.M.A. using P.I.M., O.S.-P.P.I. and F.S. The forecasting results are shown in Table 1 (A.R. versus M.M.A.), Table 2 (M.A. versus M.M.A.) and Table 3 (A.R.F.I.M.A. versus M.M.A.). Before we proceed with the discussion of the empirical results, we need to test for the existence of structural breaks in all the series, the presence of which indicates the non-constancy in parameter, meaning the series is not perfectly stationary. For this purpose the parameter constancy forecast tests for the period 1976q1–1998q4 are conducted. It is found that both the chi-square test and Chow’s structural break test are significant, thereby confirming the existence of structural break. Furthermore, we find that this structural break coincides with the Asian financial crisis (1997). For the rest of the periods, we do not reject the parameter constancy hypothesis. As a result, we divide our period of comparison into two: 1976q1–1998q4 and 1999q1–2005q3, and based on these two main periods, we construct four different rolling samples. They are: rolling sample (A): 1976q3–1998q4 (with pseudo out of sample from 1999q1 to 2000q1), rolling sample (B): 1979q1–2001q2 (with pseudo out of sample from 2001q3 to 2002q3), rolling sample (C): 1980q1–2002q2 (with pseudo out of sample from 2002q3 to 2003q3), and rolling sample (D): 1982q1–2004q2 (with pseudo out of sample from 2004q3 to 2005q3). These four rolling samples are constructed by using a rolling sample procedure which can minimise model uncertainty and compensate for insufficient data.

Table 1. Empirical results for comparing performance of A.R. and M.M.A. models.

Sample	Range (Sample size)	Pseudo out of sample	Models	MSE	MSFE	OS-PPI	FS
		MALAYSIA
(A)	1976q3 - 1998q4 (90)	1999q1 - 2000q1 (5)	AR(2)	5.1308	20.4692	0.0616	3.99
	(PIM=1.1742)		MMA	5.0796	332.138	1	65.39
(B)	1979q1 - 2001q2 (90)	2001q3 - 2002q3 (5)	AR(2)	5.6787	1.7807	0.483	3.19
	(PIM=1.2006)		MMA	5.5751	3.6866	1	1,51
(C)	1980q1 - 2002q2 (90)	2002q3 - 2003q3 (5)	AR(2)	5.6287	0.8201	0.9628	6.86
	(PIM=1.2056)		MMA	5.2228	0.8518	1	6.13
(d)	1982q1 - 2004q2 (90)	2004q3 - 2005q3 (5)	AR(2)	5.2477	1.192	0.436	4.4
	(PIM=1.2002)		MMA	5.1722	2.7342	1	1.89
		THAILAND
(A)	1976q3 - 1998q4 (90)	1999q1 - 2000q1 (5)	AR(1)	6.5876	14.008	0.1053	2.13
	(PIM=1.3192)		MMA	6.4389	133.0787	1	20.67
(B)	1979q1 - 2001q2 (90)	2001q3 - 2002q3 (5)	AR(1)	7.0729	0.7324	0.1847	9.66
	(PIM=1.3093)		MMA	6.9848	3.9649	1	1.76
(C)	1980q1 - 2002q2 (90)	2002q3 - 2003q3 (5)	AR(1)	6.9434	0.2883	0.0767	24.8
	(PIM=1.3074)		MMA	6.7766	3.7573	1	1.8
(d)	1982q1 - 2004q2 (90)	2004q3 - 2005q3 (5)	AR(1)	5.9442	1.0246	0.7804	5.8
	(PIM=1.3143)		MMA	5.8819	1.313	1	4.48
		INDONESIA
(A)	1976q3 - 1998q4 (90)	1999q1 - 2000q1 (5)	AR(2)	3.9977	45.0706	0.1069	11.27
	(PIM=1.2645)		MMA	3.8434	421.6933	1	109.72
(B)	1979q1 - 2001q2 (90)	2001q3 - 2002q3 (5)	AR(2)	5.4777	3.3995	0.9782	1.61
	(PIM=1.2499)		MMA	4.9889	3.4753	1	1.44
(C)	1980q1 - 2002q2 (90)	2002q3 - 2003q3 (5)	AR(2)	5.4801	0.401	0.2726	13.67
	(PIM=1.2327)		MMA	5.1272	1.4712	1	3.49
(d)	1982q1 - 2004q2 (90)	2004q3 - 2005q3 (5)	AR(2)	5.3868	2.1826	0.2996	2.47
	(PIM=1.2198)		MMA	5.0124	7.2846	1	1.45
		CHINA
(A)	1976q3 - 1998q4 (90)	1999q1 - 2000q1 (5)	AR(1)	2.8521	0.3615	0.2256	1.1336
	(PIM=1.0175)		MMA	2.5159	1.6022	1	1
(B)	1979q1 - 2001q2 (90)	2001q3 - 2002q3 (5)	AR(1)	2.8603	1.6276	2.1321	1.2136
	(PIM=1.012)		MMA	2.3569	0.7634	1	1
(C)	1980q1 - 2002q2 (90)	2002q3 - 2003q3 (5)	AR(1)	2.8331	0.0326	0.0108	1.2026
	(PIM=1.012)		MMA	2.3559	3.0281	1	1
(d)	1982q1 - 2004q2 (90)	2004q3 - 2005q3 (5)	AR(1)	2.778	0.2253	0.1039	1.257
	(PIM=0.9762)		MMA	2.21	2.1697	1	1

Note: MSE = mean square error; MSFE = mean square forecast error; OS-PPI = Out-of-sample predictive performance index; FS = Forecast Strains PIM = Perturbation Instability Measure.

Source: Authors’ calculation.

Table 2. Empirical results for comparing the performance of M.A. and M.M.A.

Sample	Range (Sample size)	Pseudo out of sample	Models	MSE	MSFE	OS-PPI	FS
		MALAYSIA
(A)	1976q3 - 1998q4 (90)	1999q1 - 2000q1 (5)	MA(3)	2.6864	6.6705	0.0201	2.48
	(PIM=1.1742)		MMA	5.0796	332.138	1	65.39
(B)	1979q1 - 2001q2 (90)	2001q3 - 2002q3 (5)	MA(3)	2.844	7.5288	2.0422	2.65
	(PIM=1.2006)		MMA	5.5751	3.6866	1	1.51
(C)	1980q1 - 2002q2 (90)	2002q3 - 2003q3 (5)	MA(3)	2.9719	8.1764	9.599	2.75
	(PIM=1.2056)		MMA	5.2228	0.8518	1	6.13
(d)	1982q1 - 2004q2 (90)	2004q3 - 2005q3 (5)	MA(3)	4.1305	10.6729	3.9035	2.58
	(PIM=1.2002)		MMA	5.1722	2.7342	1	1.89
		THAILAND
(A)	1976q3 - 1998q4 (90)	1999q1 - 2000q1 (5)	MA(3)	3.3353	8.8059	0.0662	2.64
	(PIM=1.3192)		MMA	6.4389	133.0787	1	20.67
(B)	1979q1 - 2001q2 (90)	2001q3 - 2002q3 (5)	MA(3)	6.1602	15.6559	3.9486	2.54
	(PIM=1.3093)		MMA	6.9848	3.9649	1	1.76
(C)	1980q1 - 2002q2 (90)	2002q3 - 2003q3 (5)	MA(3)	5.8679	15.494	4.1237	2.64
	(PIM=1.3074)		MMA	6.7766	3.7573	1	1.8
(d)	1982q1 - 2004q2 (90)	2004q3 - 2005q3 (5)	MA(3)	4.9409	14.6997	11.1955	2.98
	(PIM=1.3143)		MMA	5.8819	1.313	1	4.48
		INDONESIA
(A)	1976q3 - 1998q4 (90)	1999q1 - 2000q1 (5)	MA(4)	1.0768	4.0088	0.0095	3.72
	(PIM=1.2645)		MMA	3.8434	421.6933	1	109.72
(B)	1979q1 - 2001q2 (90)	2001q3 - 2002q3 (5)	MA(4)	3.7778	13.2772	3.8205	3.51
	(PIM=1.2499)		MMA	4.9889	3.4753	1	1.44
(C)	1980q1 - 2002q2 (90)	2002q3 - 2003q3 (5)	MA(4)	3.8865	13.5922	9.2388	3.5
	(PIM=1.2327)		MMA	5.1272	1.4712	1	3.48
(d)	1982q1 - 2004q2 (90)	2004q3 - 2005q3 (5)	MA(4)	3.3604	10.6052	1.4558	3.16
	(PIM=1.2198)		MMA	5.0124	7.2846	1	1.45
		CHINA
(A)	1976q3 - 1998q4 (90)	1999q1 - 2000q1 (5)	MA(3)	2.4609	5.1892	3.2388	0.9781
	(PIM=1.0175)		MMA	2.5159	1.6022	1	1
(B)	1979q1 - 2001q2 (90)	2001q3 - 2002q3 (5)	MA(3)	2.009	4.4249	5.7963	0.8524
	(PIM=1.012)		MMA	2.3569	0.7634	1	1
(C)	1980q1 - 2002q2 (90)	2002q3 - 2003q3 (5)	MA(3)	2.4309	4.6465	1.5345	1.0318
	(PIM=1.012)		MMA	2.3559	3.0281	1	1
(d)	1982q1 - 2004q2 (90)	2004q3 - 2005q3 (5)	MA(3)	2.2027	4.452	2.0519	0.9967
	(PIM=0.9762)		MMA	2.21	2.1697	1	1

MSE = mean square error; MSFE = mean square forecast error; OS-PPI = Out-of-sample predictive performance index; FS = Forecast Strains PIM = Perturbation Instability Measure.

Source: Authors’ calculation.

Table 3. Empirical results for comparing the performance of A.R.F.I.M.A. and M.M.A.

Sample	Range (Sample size)	Pseudo out of sample	Models	MSE	MSFE	OS-PPI	FS
		MALAYSIA
(A)	1976q3 - 1998q4 (90)	1999q1 - 2000q1 (5)	ARFIMA(1,d,3)	3.969	13.2472	0.0399	3.34
	(PIM=1.1742)		MMA	5.0796	332.138	1	65.39
(B)	1979q1 - 2001q2 (90)	2001q3 - 2002q3 (5)	ARFIMA(1,d,3)	4.2678	13.5836	3.6846	3.18
	(PIM=1.2006)		MMA	5.5751	3.6866	1	1.51
(C)	1980q1 - 2002q2 (90)	2002q3 - 2003q3 (5)	ARFIMA(1,d,3)	3.9678	12.8551	15.0916	3.24
	(PIM=1.2056)		MMA	5.2228	0.8518	1	6.13
(d)	1982q1 - 2004q2 (90)	2004q3 - 2005q3 (5)	ARFIMA(1,d,3)	3.7133	12.5083	4.5748	3.37
	(PIM=1.2002)		MMA	5.1722	2.7342	1	1.89
		THAILAND
(A)	1976q3 - 1998q4 (90)	1999q1 - 2000q1 (5)	ARFIMA(1,d,3)	6.2325	12.661	0.0951	2.03
	(PIM=1.3192)		MMA	6.4389	133.0787	1	20.67
(B)	1979q1 - 2001q2 (90)	2001q3 - 2002q3 (5)	ARFIMA(1,d,3)	5.8625	16.5867	4.1834	2.83
	(PIM=1.3093)		MMA	6.9848	3.9649	1	1.76
(C)	1980q1 - 2002q2 (90)	2002q3 - 2003q3 (5)	ARFIMA(1,d,3)	5.6555	16.9505	4.5114	3
	(PIM=1.3074)		MMA	6.7766	3.7573	1	1.8
(d)	1982q1 - 2004q2 (90)	2004q3 - 2005q3 (5)	ARFIMA(1,d,3)	4.7054	16.0159	12.1979	3.4
	(PIM=1.3143)		MMA	5.8819	1.313	1	4.48
		INDONESIA
(A)	1976q3 - 1998q4 (90)	1999q1 - 2000q1 (5)	ARFIMA(1,0,3)	3.3583	13.6155	0.0323	4.05
	(PIM=1.2645)		MMA	3.8434	421.6933	1	109.72
(B)	1979q1 - 2001q2 (90)	2001q3 - 2002q3 (5)	ARFIMA(1,0,3)	3.7408	14.0654	4.0472	3.76
	(PIM=1.2499)		MMA	4.9889	3.4753	1	1.44
(C)	1980q1 - 2002q2 (90)	2002q3 - 2003q3 (5)	ARFIMA(1,0,3)	3.8533	14.3746	9.7706	4.07
	(PIM=1.2327)		MMA	5.1272	1.4712	1	3.49
(d)	1982q1 - 2004q2 (90)	2004q3 - 2005q3 (5)	ARFIMA(1,0,3)	4.1269	13.6544	1.8744	3.31
	(PIM=1.2198)		MMA	5.0124	7.2846	1	1.45
		CHINA
(A)	1976q3 - 1998q4 (90)	1999q1 - 2000q1 (5)	ARFIMA(1,0,3)	2.0246	6.5392	4.0814	0.8047
	(PIM=1.0175)		MMA	2.5159	1.6022	1	1
(B)	1979q1 - 2001q2 (90)	2001q3 - 2002q3 (5)	ARFIMA(1,0,3)	2.0892	6.4999	8.5145	0.8864
	(PIM=1.012)		MMA	2.3569	0.7634	1	1
(C)	1980q1 - 2002q2 (90)	2002q3 - 2003q3 (5)	ARFIMA(1,0,3)	2.0877	6.1537	2.0322	0.8862
	(PIM=1.012)		MMA	2.3559	3.0281	1	1
(d)	1982q1 - 2004q2 (90)	2004q3 - 2005q3 (5)	ARFIMA(1,0,3)	2.0249	5.9031	2.7207	0.9163
	(PIM=0.9762)		MMA	2.21	2.1697	1	1

Note: MSE = mean square error; MSFE = mean square forecast error; OS-PPI = Out-of-sample predictive performance index; FS = Forecast Strains PIM = Perturbation Instability Measure

Source: Authors’ calculation.

Rolling sample (A)’s pseudo out-of-sample range for all four countries is of particular interest. It contains forecast information immediately after a period of financial crisis which coincided with the structural break in the series. On the other hand, rolling samples (B), (C) and (D) each contains forecasts of about 5 years and more after a financial crisis. This implies the gradually reduced effects of the financial crisis over time on forecasting errors for each of these rolling samples. In the case of China, the Asian financial crisis has exerted relatively less impact on its G.D.P. growth rate, as basically it has weathered the crisis very well. In addition, the results from sample (A) exhibit an interesting general behaviour. Therefore, we commence our empirical analysis with a separate focus on the results of sample (A) with each of the chosen statistical models for all the countries.

6.1. Comparing the predictive ability of A.R., M.A. and A.R.F.I.M.A. with M.M.A. for the case of sample (A) – Tables 1–3

In Tables 1–3, with regard to the three A.S.E.A.N. countries, all values of the O.S.-P.P.I. obtained from the M.M.A. approach are 1 or less, implying that model combination performance is inferior to that of the single parsimonious models of A.R., M.A. or A.R.F.I.M.A. The results of sample (A) for China, in contrast, do not follow the consistent trend of the O.S.-P.P.I. ratio exhibited by those of the three A.S.E.A.N. member states. This consistent trend could be a result of the high volatility of the asset markets in A.S.E.A.N. during the financial crisis period, while the deviation displayed by the sample (A) results of China could be a direct result of the fact that the Chinese G.D.P. was relatively much less affected. In addition, for all four countries, the F.S. values (>1) suggest that the models are of stable forecasting ability. Hence the conclusion derived from the results at this point is that in an environment of financial crisis, the single model of A.R. is a better choice for forecasting for all four countries. M.A. and A.R.F.I.M.A. single model selection offers better results in the three A.S.E.A.N. countries only, while for China, the results support the M.M.A. approach.

6.2. Comparing the predictive ability of A.R., M.A. and A.R.F.I.M.A. models with the respective M.M.A. model for all the sample cases – sample (A), (B), (C) and (D)

We analyse in general the predictive power of each type of single model, comparing with the predictive ability of the combination model. From the behaviour exhibited by the ratios of O.S.-P.P.I. and F.S. as well as the P.I.M. values, we attempt to draw the general conclusions on the relative predictive power between model selection and model combination.

6.2.1. Comparing the predictive ability of A.R. with M.M.A. (Table 1) for the case of sample (A), (B), (C) and (D)

In general, for samples (A), (B), (C) and (D) in Table 1, the O.S.-P.P.I. ratios suggest that the A.R. model has better forecasting ability than the M.M.A. model, especially for the sample (A) case of Malaysia, sample (A) case of Indonesia, sample (C) case of Thailand and sample (C) case of China. These O.S.-P.P.I. ratios are below 1, and each represents the lowest value in its respective group. Moreover, the forecasting ability of the A.R. model in each case is more stable as indicated by the respective F.S. ratio (> 1).

In addition, P.I.M. is less than 1.25 for Malaysia, Indonesia and China, verifying that A.R. is preferable. Nevertheless, P.I.M. for Thailand returns a value of > 1.25, suggesting that M.M.A. may be suitable based on Yuan’s criterion for model combination. However, this contradicts the finding using O.S.-P.P.I. This discrepancy could be due to the fact that the economic growth of Thailand during the research period is relatively less stable, and the resulting combination dynamics not suitable for M.M.A. (Compare with the conclusion in the preceding part where the empirical readings suggest that M.M.A. is not a suitable forecasting choice in a volatile economic environment.) However, this trend of superiority of the A.R. model is reversed for the case of China, where in sample (B) the forecasting ability of M.M.A. is revealed to be more superior. In addition, it is found that AR(1) and AR(2) seem to have equal forecasting ability. The reason could be that the volatility of G.D.P. growth is rather large.

In perspective, for samples (B), (C) and (D) in Table 1, it is clear that A.R. (that is, model selection) performs better than M.M.A. (model combination) in terms of M.S.F.E. for Malaysia, Thailand, Indonesia and China. This result is manifested in the O.S.-P.P.I. index where a ratio value of less than 1 implies that A.R. is better than M.M.A. The stable forecasting ability of the A.R. is also confirmed by the F.S. ratios which are all greater than the value 1.

6.2.2. Comparing the predictive ability of M.A. with M.M.A. (Table 2) for the case of sample (A), (B), (C) and (D)

In Table 2 as noted earlier, the results for sample (A) of the three A.S.E.A.N. countries show that M.A.⁵ performs better than M.M.A. with their respective O.S.-P.P.I. ratios above the value of 1, while the F.S. values confirm the stable forecasting ability of the M.A. models. On the other hand, for sample (B), (C) and (D), M.M.A. performs better consistently based on the O.S.-P.P.I. results, where all the values of this ratio exceed the value 1. We observe that generally all the M.M.A. forecast strain ratios are above 1, while the P.I.M. values also exceed the cut-off point of 1.015⁶, confirming the stability of forecasting ability of the M.M.A. models (combining differenced and original series), thereby suggesting that the combination of models is a better choice for forecasting. When the values of the O.S.-P.P.I. measure are examined, it is found that M.M.A. would have optimum performance relative to M.A. about 5 years after the Asian financial crisis. This suggests that M.M.A. has a better ability to moderate financial market volatility. Furthermore, it is found that M.M.A. outperforms all other specifications of MA(3) not only in terms of the O.S.-P.P.I., but also in the relatively smaller M.S.F.E. figures. The values of P.I.M. indicate that MA(3) is not that stable even though it outperforms other M.M.A. specifications. It is found that the smallest values of P.I.M. occurred for sample (A) for Malaysia and sample (D) for China. In addition, it is found that the MA(3) is more stable in terms of the F.S. measure in China only. This could be due to the fact that China has weathered the financial crisis better than the other three countries. In this context, we can again conclude that model combination should provide better forecasting results.

6.2.3. Comparing the predictive ability of A.R.F.I.M.A. with M.M.A. for the case of sample (A), (B), (C) and (D)

Table 3 reveals that with sample (A) for all the four countries, A.R.F.I.M.A. performs better than M.M.A., as indicated by the O.S.-P.P.I. values, while the F.S. values indicate that the A.R.F.I.M.A. models have stable forecasting ability except for the case of China. For samples (B), (C) and (D) the empirical results show better performance of the M.M.A. model combination over the single A.R.F.I.M.A. model for all the four candidate countries. Based on the F.S. ratios, all the models have stable forecasting ability. Nevertheless, the P.I.M. values are all larger than the critical value of 1.015, meaning that using M.M.A. is preferable.

For the case of China, ARFIMA(1,0,3) performs better than M.M.A. in all four samples based on the P.I.M. results (below the threshold value of 1.015). However, its F.S. < 1 values suggest that the model is not stable. For Malaysia, Thailand and Indonesia, M.M.A. performs much better than ARFIMA(1,0,3) commencing about 5 years after the Asia financial crisis (1997), which indicates that forecasting performance of ARFIMA(1,0,3) is substantially influenced by the effect of financial crisis.

Table 4 shows the P.I.M. values for all the samples and the four countries. Mean P.I.M. values for China, Indonesia, Malaysia and Thailand are about 1.01, 1.25, 1.20 and 1.31, respectively. These P.I.M. values indicate that the G.D.P. of China is more resilient, while the resilience level of the three A.S.E.A.N. countries is about the same. Table 5 shows excellent correlation between P.I.M. and forecasting errors. The correlation coefficients are all positive; for M.S.E., it is about 0.84 which is very good correlation because the maximum value is 1. However, for M.S.F.E., the correlation coefficient for the A.R. model is about 0.24 and for M.A. and A.R.F.I.M.A. it is 0.74 and 0.95, respectively. As for M.M.A., its value is about 0.2. This gives further support for using P.I.M. to measure the stability of the models. Figure 1 and 2 depict this relationship. Furthermore, Figure 1 shows the nonlinear relationship between M.S.E. and P,I,M. ⁷ This nonlinear relationship can be verified by using the last equation in Appendix 2, where the left-hand side of the equation is the empirical $\sqrt{\mathit{MSE}}$ and the right-hand side is $PIM\times 0.1\times \widehat{\sigma }$. After manipulation, we obtain MSE ∝ PIM² which implies that P.I.M. and M.S.E. are nonlinearly related.

Table 4. P.I.M. for Economic Growth Series.

	1976q1 to 2000q1	1979q1 to 2002q3	1980q1 to 2003q3	1982q1 to 2005q3
China	1.0175	1.0120	1.0120	0.9762
Indonesia	1.2645	1.2499	1.2327	1.2198
Malaysia	1.1742	1.2006	1.2056	1.2002
Thailand	1.3192	1.3093	1.3074	1.3143

Source: Authors’ calculation.

Table 5. Correlation coefficients between P.I.M. and forecasting errors.

	PIM
MSE:
AR	0.9155
MA	0.6162
ARFIMA	0.9044
MMA	0.9225
MSFE:
AR	0.2434
MA	0.7420
ARFIMA	0.9521
MMA	0.1947

Source: Authors’ calculation.

7. Conclusion

From the analysis of the results of our empirical experiment, we can summarise as follows: we observe a more consistent behaviour of the results from M.A., A.R.F.I.M.A. and their corresponding M.M.A. models for all four countries, i.e., Malaysia, Thailand, Indonesia (A.S.E.A.N. member states) and China. In the environment of samples (B), (C) and (D), the model combination of constrained and unconstrained estimators by M.M.A. performs better in forecasting as revealed by the O.S.-P.P.I. values (>1). The respective M.M.A. models have more stable forecasting ability than the individual M.A. or A.R.F.I.M.A. model in all four countries as suggested by the P.I.M. values, which are all above the threshold value of 1.015, while the F.S. values (> 1) confirm the stability of the forecasting ability of all the M.M.A. models with the exception of the models of China in sample (B) and (D). However under sample (A), we observe a general reverse in trend, that is both M.A. and A.R.F.I.M.A. exhibit better forecasting performance than M.M.A. in all the countries with the exception of China. The P.I.M. values of the three A.S.E.A.N. countries are all less than their respective critical value of 1.015, while that of China hovers on the threshold value. In addition, the F.S. ratios for China are below unity which supports the preference for M.M.A. for better forecasting results.

With regard to the A.R. and the corresponding M.M.A. models comparison, we note that throughout the four rolling samples all the O.S.-P.P.I. ratios are less than 1 except for a case in China in sample (B). This means that the A.R. model has better predictive ability than the M.M.A. model under the environment of all four samples for all the candidate countries. Nevertheless, the respective P.I.M. values are not so consistent. While all the P.I.M. values (< 1.25) for Malaysia support the better forecasting power of the A.R., P.I.M. values for both Thailand and Indonesia reveal contrary results (P.I.M. > 1.015). Nonetheless, the relatively smaller M.S.F.E. values as well as the higher F.S. ratio do generally reflect the better performance and stability of the A.R. forecasting ability for these two countries. In the case of China too, the P.I.M. values hover around the threshold value of 1.015 for all four rolling samples, while the F.S. ratios of the A.R. are greater than unity. These results are therefore more in agreement with the superior predictive ability of the A.R. over M.M.A.

Hence, from the sample-specific results we can conclude that: (1) when the sample includes a financial crisis, A.R., M.A. and A.R.F.I.M.A. (model selection procedure) offer better forecasting ability than M.M.A. (model combination); (2) in the absence of financial crisis, the simple A.R. model can perform better than M.M.A.; (3) in the environment of little or absence of the effect of significant financial volatilities, M.M.A. model combination involving M.A. or A.R.F.I.M.A. performs better than the respective single model. This means that under a normal economic environment that calls for forecasting with M.A. or A.R.F.I.M.A., applying the combination of the respective differenced with the undifferenced model will offer a better forecast outcome.

Nevertheless, the sample-specific empirical results obtained in this study may not hold in advanced economies where financial crises are well moderated by policy makers, unlike in emerging economies. Nonetheless, the methodology used in this study can still be applied effectively for the case of advanced economies as we have used three effective measures for relative forecasting ability and model stability assessment. To confirm the robustness of our results, we suggest further research using state space model extension of the specifications tested in the current study. A comparison of the two sets of results will establish the validity of the present results.

Funding

This work was supported by Universiti Utara Malaysia [grant number PBIT (CodeS/O: 12617)]

Notes

1. see Appendix 1 for detail explanation of constrained and unconstrained estimators).

2. These five data series are obtained from website: courses.nus.edu.sg/course/ecstabey/Tilak.html.

3. M.M.A. Gauss procedure is written by B Hansen and downloaded from his website: http://www.ssc.wisc.edu/~bhansen/.

4. See Appendix 3 for explaining the intuitive validity of F.S.

5. In this M.A. section, M.A. refers to unconstrained series which is stationary in nature.

6. This threshold value of 1.015 is obtained from Figure 1 and 2 (the values where the P.I.M. is positively associated with the forecasting errors). This is the first positive range (1.015 to 1.20), and for out-of-sample forecasting errors of M.M.A. and A.R., it is 1.015 to 1.02, see Figure 1 and 2.

7. Nonlinear model estimates can also be obtained by applying S.T.A.R. and L.S.T.A.R. Specifications. However, as pointed out by the anonymous referee, this is not recommended. For details, see Bec, Salem and Carrasco (2004).

Appendix 1. Constrained and unconstrained estimator

We let y_t be the G.D.P. growth rate and ${\widehat{y}}_t$be its estimator. We use this estimator to generate out-of-sample forecast and thereby estimate the respective M.S.F.E. and also M.S.E. In general, any time series can produce two types of estimators: one before differencing and the other after differencing. For before differencing, the series is known as I(1), and after differencing it is I(0). I(1) series is known to exhibit nonstationarity behaviour which is characterised by the existence of a unit root.

Thus, we can convert nonstationarity into stationarity by differencing. However, we do not need to perform the differencing if the original series is I(0). If no differencing has been done to the series, it would produce what is known as unconstrained estimator.

A.R., M.A. and A.R.F.I.M.A. models work only on constrained estimator which is obtained after pretesting and is shown as follows:$$D{F}_n=\frac{\widehat{\beta }-1}{s(\widehat{\beta })}$$

where DF_n is the Dickey–Fuller t statistic $\widehat{\beta }$ is the slope coefficient in the AR(1) model and $s(\widehat{\beta })$ is the O.L.S. standard error for $\widehat{\beta }$ At asymptotic 5% the critical value is t_c = -3.41. Thus we have the pretest estimator be given by:$${\widehat{\theta }}_t^{\mathit{df}}={\widehat{\theta }}_{t}I(D{F}_n\le t_c)+{\tilde{\theta }}_{t}I(D{F}_n>t_c)$$

where ${\widehat{\theta }}_t$ and ${\tilde{\theta }}_t$ are the unconstrained and constrained estimator, respectively. However, we have a different scenario for M.M.A. and it is described in the Section 3.1.

Appendix 2. Perturbation instability measures

Procedure to calculate P.I.M.

(1)	Input yt = gdp with size 120. Run an A.R.(1) regression with error term as white noise N(0,σ2).

Save the estimated value for σ and name it as $\widehat{\sigma }$. The equation is given as:

$$\begin{array}{c}{y}_t=\alpha +{\beta }_1{y}_{t-1}+u_t\\ u_t\sim N(0,{\sigma }^2)\\ \end{array}$$

(2)	Generate a new set of perturbed errors by assuming that it is normally distributed with

$$w_t=N\left(0,{\rho }^2{\sigma }^2\right)\text{and}\rho =0.1,0.2.....,0.9,1.0$$

(3)	For ρ = 0.1, generate 120 data of wt where t runs from 1 to 120.

Compute ${\tilde{y}}_t=y_t+w_t$Run the AR(1) again for this new set of data with y_t-1 as the only regressor as before.$$\begin{array}{c}{\tilde{y}}_t=\alpha +{\beta }_1{y}_{t-1}+u_t\\ u_t\sim N(0,0.1{\widehat{\sigma }}^2)\\ \end{array}$$

(4)	Compute the fitted y, and name as ${\tilde{f}}_{j=1}$. Subsequently compute ${\tilde{f}}_{j=1}-\widehat{f}$where f is the fitted y for the original data.
(5)	Repeat step 4 with j runs from 2 to 100. Thus we have replication M = 100.
(6)	Then we compute average deviation as follows

$$S(\rho =0.1)=\frac{1}{100}\left(\sum _{j=1}^{100}[\sum _{t=1}^{120}{({({\tilde{f}}_j-\widehat{f})}^2/120)}^{1/2}\right)$$

We have the relationship:$$S(\rho =0.1)=\frac{1}{100}\left(\sum _{j=1}^{100}[\sum _{t=1}^{120}{({({\tilde{f}}_j-\widehat{f})}^2/120)}^{1/2}\right)=PIM\times 0.1\times \widehat{\sigma }$$

With that we can compute P.I.M.

We repeat step 6 for ρ runs from 0.1 to 0.9 in step of 0.1

Appendix 3. Forecast strain (F.S.)

Forecast Strain (F.S.) is defined as follows: $FS=\frac{\mathit{MSFE}}{\mathit{MSE}}$ where F.S. is designed to estimate whether model selection or combination is stable. For a single model, M.S.E. is always less than M.S.F.E. in a regression model estimation. The reason is shown below:$$\begin{array}{c}MSFE(m)\approx {\sigma }^2+E{\left((\widehat{\beta }(m)-\beta \right)}^{\prime }Q(m)\left((\widehat{\beta }(m)-\beta \right)\\ ={\sigma }^2+MSE(\widehat{\beta }(m))\\ \text{where}\\ MSE(\widehat{\beta }(m))=trE\left(Q(m)\left((\widehat{\beta }(m)-\beta \right){\left((\widehat{\beta }(m)-\beta \right)}^{\prime }\right)\\ \end{array}$$

The two equations shown above demonstrate that M.S.E. is always smaller than M.S.F.E. by the term σ²which is positive due to the square term. Thus we have the criterion that$$FS=\frac{\mathit{MSFE}}{\mathit{MSE}}>1$$

denotes model stability of a single or combination model. Thus, if F.S. < 1 then the single model is not stable. Since combination of models is a linear combination of single models, this criterion is also true for model combination. As model combination is influenced by combination dynamics, it is expected that deviations from the stability criterion are more likely.