Real time vibration measurement and inverse analysis for dynamic properties of an axisymmetric masonry structure

ABSTRACT

Historic buildings are public symbols, standing as sacred reminders. Many of them have been recognized as World Heritage Sites. In this study, real time vibration measurement of an important axisymmetric masonry pagoda was performed. With the measured vibration data, inverse analysis was proposed to backward determine its damping and natural period. The proposed algorithm utilizes Duhamel’s time integration method for solving the equation of motion and the Gauss-Newton algorithm to minimize the sum-of-squares error between the calculated and real-time measured accelerations of the structure. Four distant earthquake-induced vibrations were recorded and used for the analysis. The results show that the dynamic parameters determined by the proposed method agree with those obtained from the previous study adopting finite element analysis. The obtained dynamic properties of the two perpendicular directions are slightly different, indicating the non-homogenous body of the axisymmetric structure or there would be a particular damage zone. From the results, an onsite damage investigation can be specifically identified. In summary, continuous structural health monitoring and time-dependent deterioration of historic buildings are possible with real time measurement and the proposed analytical algorithm.

Graphical Abstract

KEYWORDS:

• Inverse analysis
• dynamic properties
• axisymmetric structure
• real-time vibration measurement
• structural health monitoring

1. Introduction

Earthquakes have the power to cause massive destruction to cities. As an earthquake cannot be avoided, many efforts have been made to establish an effective preparedness plan (Ketsap et al. 2019; Saicheur and Hansapinyo 2017). With limited earthquake mitigation resources, critical buildings have been identified and prioritized based on the impact of consequential loss. Among the different building types, historic buildings have been built for many years, and the construction techniques used at that time were substandard in terms of seismic consideration. In addition, the buildings are categorized as valuable symbols of people’s beliefs. Seismic damaged buildings or other infrastructure can be demolished and re-built. However, this is not possible for historic buildings. Hence, the buildings are classified and ranked as the most critical, requiring urgent seismic strengthening (Saicheur and Hansapinyo 2016). Many active faults have been found in the north of Thailand and there was a magnitude 6.3 earthquake in Chiang Rai Province on 5 May 2014. The strike caused damage to buildings across a large area (Hansapinyo, Latcharote, and Limkatanyu 2020). There are many historic unreinforced masonry buildings in the region that require seismic strengthening. To achieve the task, information about the dynamic properties of the structures, e.g., the damping ratio and fundamental period of vibration, is indispensable for seismic vulnerability analysis.

Modal analysis of a fully three-dimensional finite element model has been successfully adopted to estimate the dynamic properties for a numerical approach to vibration analysis. Ferraioli et al. (2017) adopted the finite element method for dynamic characterization and seismic assessment of medieval masonry towers. Adam et al. (2020) assessed minaret structural efficiency, safety margin, and serviceability limits using a 3D finite element model coded in ANSYS v.15 program. However, the method is limited to buildings with an available as-built drawing. Due to a lack of data on long-term-built historical buildings and time-related deterioration, using the modal analysis necessitates making unknown assumptions, resulting in an unrealistic result.

On the other approach, on-site dynamic-based monitoring has been widely adopted in recent years (Aloisio et al. 2021; Tantisukhuman et al. 2023; Azzara et al. 2018; Gentile, Ruccolo, and Saisi 2019). For a historic building, structural deterioration has been progressively developed over time due to repetitive loads, environmental effects, and vibration-induced loads. Hence, structural health monitoring (SHM) has been a popular research topic (Mishra, Lourenço, and Ramana 2022). Early detection of damage can avoid drastic failure and accomplish cost-effective maintenance. Although the damage is physically local behavior, there have been guidelines and many successful applications of the vibration test to determine the global response (AASHTO 1990; BS 7385–1 1990; ISO 4866 2010). Although, the on-site vibration measurement is costly and time-consuming, the high reliability of the measured data makes the instrument popular. Danish et al. (Danish, Tayyab, and Salim 2020) applied accelerometers to indicate the reduction in natural frequencies of damage detection of three reinforced concrete beams. Monti et al. (2018) introduced wireless accelerometers for the continuous “trigger-free” dynamic monitoring system for the Colosseum in Rome under vibrations induced by natural and man-made excitations. The ambient vibration test is a widely used technique to identify the dynamic properties of historical buildings, and it was conducted on the masonry roof of the Basilica of the Fourteen Holy Helpers in Bavaria, southern Germany (Compan, Pachón, and Cámara 2017). These dynamic structural parameters, identified using the operational modal analysis method (OMA), allow the adjustment of numerical models to obtain a more accurate estimation of the actual behavior of the structure. The ambient vibration test was also used in Lebanon and Turkey (Salameh et al. 2017; Altunişik et al. 2020). The method provides the vibration properties from a global point of view. As the ambient vibration intensity is a very low-intensity signal, it requires a meticulous procedure to identify the dynamic properties of specific elements with a local character. Civera, Mugnaini, and Fragonara (2022) proposed the novel-multistage clustering algorithm for automatic operational analysis (AOMA) and the vibration modes of a laboratory scaled-down replica of a masonry arch bridge were correctly identified up to the fifth mode. Another popular method to estimate the dynamic properties of buildings is inverse analysis. This method is driven by the precise measurement of the deformation of the structure during vibration, and the subsequent inverse mathematical analysis is then performed. The inverse analysis was applied to the diagnostics of a historic bridge in the Czech Republic (Klusáček, Nečas, and Bureš 2015). The key component of the inverse analysis method is the estimation of structural vibration via numerical time integration with initial values of dynamic parameters, i.e., damping ratio or stiffness. Then the dynamic parameters are adjusted to minimize the error between the measured vibration responses to the calculated response obtained from numerical time integration. The process is iterated until an error meets some specified tolerance value.

In the present work, the inverse analysis method was used to backward identify the dynamic properties of a masonry pagoda from the measured vibration responses. The ultimate goal is to develop an algorithm to early detect the change of dynamic properties, implying the occurrence of structural damage, and an on-site detail investigation can be performed without delay. Two vibrational sensors were installed on the pagoda at the top and base levels to monitor the vibration responses when an earthquake occurred. The responses had been real-time continuous triggered at a sampling rate of 100 times/sec. and stored on a cloud-based storage system. With the measured ground as the input excitation and initially assumed dynamic properties, the numerical solution of the equation of motion using Duhamel’s time integration for the top acceleration was determined. However, the difference between the measured and calculated top-level accelerations was certainly observed due to previously assumed wrong dynamic properties. Then, the Gauss-Newton algorithm was applied to obtain the dynamic parameters, which iteratively minimized the sum-of-squares error (SSE) between the calculated and real-time measured accelerations. The dynamic properties were iteratively converged when the SSE was smaller than a certain defined tolerance. In this study, the results of the estimated parameters from four distant earthquake waves were compared to identify the accuracy of the present method.

2. Pagoda and vibration measurement

2.1. Pagoda

The studied historic building is a pagoda in Umong temple (Figure 1), located west of Chiang Mai city. The pagoda was built in 1297 by King Mengrai. It’s height is 25.72 m from the base, and its diameter at the base is 16.48 m. The pagoda was constructed using medieval masonry without reinforcement, formed in an inverted-bell shape with circular cross-sections. Hence, the structure is axisymmetric about the vertical axis. The approximate volume of the pagoda is 1,655 m³. (Hansapinyo 2014).

Figure 1. Umong pagoda.

2.2. Acceleration measurements

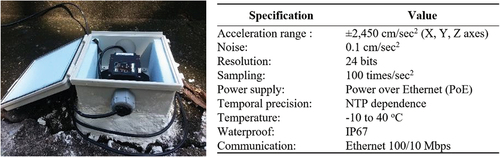
Two tri-axial accelerometer sensors from aLab Inc. were installed on the pagoda at the top, approximately 18.70 m from the ground, and base using waterproof glue cement. Figure 2 shows the specification and the installation. The sensors were securely kept in a box that protects them from severe environmental conditions such as temperature, humidity, and rain. The sensors measure acceleration in three components: two perpendicular horizontal and vertical directions. As the pagoda is axisymmetric, the sensors were placed to allow the two horizontal directions to coincide with the tangential and radial directions of the pagoda’s section. The acceleration of the pagoda was measured in real-time with a sampling rate of 100 times/sec. The measured acceleration data was sent to a cloud-based storage system through a local PC station. When the sensors detected a certain level of vibration larger than the normal ambient vibration, a notification message was sent out to the system administrator.

Figure 2. Specification and installation of accelerometer.

2.3. Earthquake data

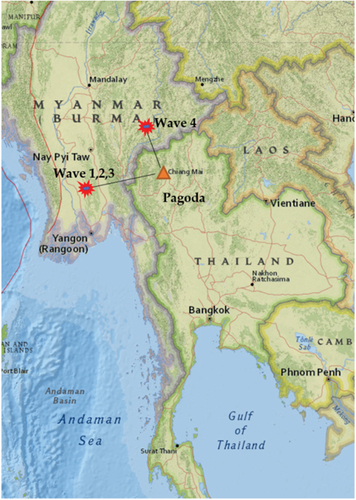
As shown in Table 1, four distant earthquake data sets were used to estimate the dynamic parameters. The epicenters of all earthquake events were in Myanmar (Figure 3). The first three earthquakes, which were located in the same area, are on the west side of the pagoda. The last earthquake was on the north side. The earthquake magnitude was mb 4.6–5.1, with a distance between the epicenters and the pagoda of 200–306 km. All the earthquakes occurred in the same time period, from 17 March 2018 to 1 July 2018. Hence, the influence of time-dependent deterioration is negligible. Figure 4 shows the real-time measurement of NS and EW ground accelerations in the time domain and frequency domain at the pagoda’s base of the earthquake wave no. 4. The real-time measured ground acceleration increased when the earthquake struck.

Figure 3. Locations of earthquake sources and pagoda.

Figure 4. Ground acceleration in time and frequency domains of the earthquake wave no. 4 in (a) North-South direction, and (b) East-West direction.

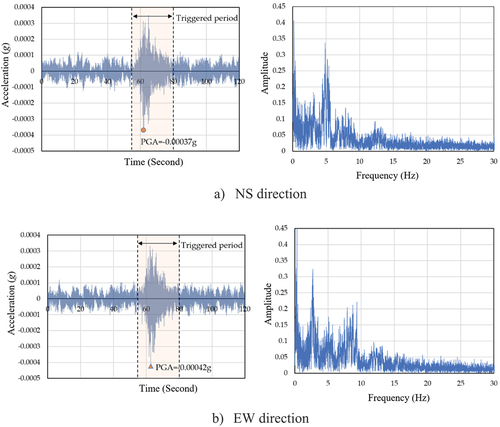
Table 1. Epicenters of seismic waves.

Wave	Date	Country	Location	Magnitude (mb)	Depth (km)	Distance (km)
Wave 1	17 March 2018	Pyu, Myanmar	18.385°N 96.151°E	5.1	19.1	300
Wave 2	20 April 2018	Pyu, Myanmar	18.322°N 96.160°E	5.0	17.1	300
Wave 3	17 June 2018	Pyu, Myanmar	18.275°N 96.070°E	5.0	10.0	306
Wave 4	1 July 2018	Loikaw, Myanmar	20.259°N 97.911°E	4.6	10.0	200

3. Estimation of dynamic parameters

In this section, theoretical issues employed in the inverse analysis for dynamic parameter estimation are addressed. First, the equation of motion to compute the response of a simplified equivalent single-degree of freedom system is described. Then, solving the equation of motion for the system’s acceleration numerically using Duhamel’s integral is explained. Finally, the Gauss-Newton iteration scheme to evaluate the dynamic parameters is illustrated.

3.1. Analytical model and equation of motion

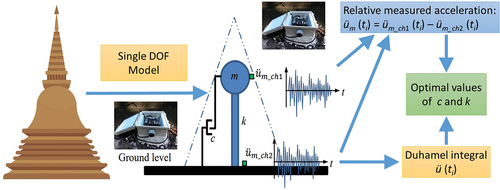
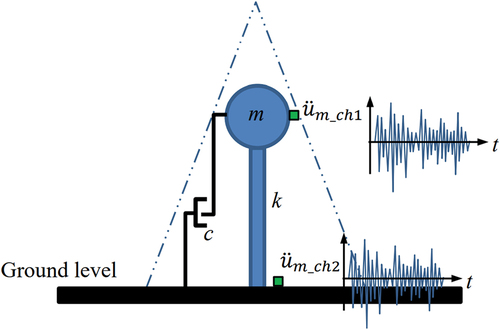
The pagoda’s inverted bell shape is considered a triangular-like shape, as indicated by the dotted line in Figure 5. The structure is axisymmetric in that every horizontal cross-section is circular, tapering toward the top without mass separation along the elevation. The structural vibration is naturally dominated by lateral movement. Hence, the vibration of the pagoda is simplified as a single degree of freedom system, and the equation of motion is expressed as

Figure 5. Simplified single degree of freedom (SDOF) system of the pagoda and position of accelerometers (green boxes).

(1) $m\stackrel{..}{u}+c\stackrel{\mathbf{.}}{u}+ku=-m\stackrel{..}{u_g}$(1)

where $u$, $\dot{u}$, and $\stackrel{..}{u}$ are relative lateral displacement, velocity, and acceleration of the pagoda, respectively. Structural mass is denoted by m. The damping coefficient and stiffness are represented by c and k respectively. Ground acceleration is denoted by ü_g.

To eliminate the mass parameter, dividing equation (1)(1) $m\stackrel{..}{u}+c\stackrel{\mathbf{.}}{u}+ku=-m\stackrel{..}{u_g}$(1) by the structural mass (m) results to

(2) $\stackrel{..}{u}+2\omega \zeta \stackrel{\mathbf{.}}{u}+{\omega }^{2}u=-\stackrel{..}{u_g}$(2)

where ω is the natural frequency of the structure $\omega =\sqrt{k/m}$ and ζ is the damping ratio $\zeta =\frac{c}{(2\omega )}$. Next, applying the theory of dynamic analysis (Clough and Penzien 1993), the numerical solution of relative acceleration in equation (2)(2) $\stackrel{..}{u}+2\omega \zeta \stackrel{\mathbf{.}}{u}+{\omega }^{2}u=-\stackrel{..}{u_g}$(2) due to input ground accelerations is obtained. In this work, Duhamel’s integral based on Simpson’s rule are performed.

3.2. Determination of acceleration response using duhamel’s integral

Solving equation (2)(2) $\stackrel{..}{u}+2\omega \zeta \stackrel{\mathbf{.}}{u}+{\omega }^{2}u=-\stackrel{..}{u_g}$(2) numerically using Duhamel’s integral, the equation is assumed to be a linear equation with constant dynamic parameters (ζ and ω). Hence, the solution at time t can be obtained from the superposition of structural responses due to unit-impulse ground acceleration. The equations for solving equation (2)(2) $\stackrel{..}{u}+2\omega \zeta \stackrel{\mathbf{.}}{u}+{\omega }^{2}u=-\stackrel{..}{u_g}$(2) are briefly described here, and more details can be found in structural dynamic textbooks (Clough and Penzien 1993). For a single-degree of freedom damped system with a unit mass and initially at rest, solutions for displacement u(t) and velocity $\dot{u}\left(t\right)$ in equation (2)(2) $\stackrel{..}{u}+2\omega \zeta \stackrel{\mathbf{.}}{u}+{\omega }^{2}u=-\stackrel{..}{u_g}$(2) become:

(3) $u\left(t\right)=A\left(t\right)sin{\omega }_{D}t-B\left(t\right)cos{\omega }_{D}t$(3)

(4) $\dot{u}\left(t\right)=-\zeta \omega u\left(t\right)+{\omega }_D\left[A\left(t\right)cos{\omega }_{D}t+B\left(t\right)sin{\omega }_{D}t\right]$(4)

where $\omega D=\omega \sqrt{1-{\zeta }^2}$ is the damped free-vibration frequency. To solve equations (3)(3) $u\left(t\right)=A\left(t\right)sin{\omega }_{D}t-B\left(t\right)cos{\omega }_{D}t$(3) and (4(4) $\dot{u}\left(t\right)=-\zeta \omega u\left(t\right)+{\omega }_D\left[A\left(t\right)cos{\omega }_{D}t+B\left(t\right)sin{\omega }_{D}t\right]$(4) ), time variant is discretized into a finite equal time interval ∆τ. The coefficients A(t) and B(t) can be expressed as follows:

(5) $A\left(t\right)=\frac{e^{-\zeta \omega t}}{{\omega }_D}{\int }_0^t{e}^{\zeta \omega \tau }x\left(\tau \right)d\tau$(5)

(6) $B\left(t\right)=\frac{e^{-\zeta \omega t}}{{\omega }_D}{\int }_0^t{e}^{\zeta \omega \tau }y\left(\tau \right)d\tau$(6)

where the function $x\left(\tau \right)=-\stackrel{..}{u_g}cos{\omega }_D\tau$ and $y\left(\tau \right)=-\stackrel{..}{u_g}sin{\omega }_D\tau$. Simpson’s rule is adopted for the numerical integration. Finally, the relative acceleration of the system is computed from the equation of motion, equation (2)(2) $\stackrel{..}{u}+2\omega \zeta \stackrel{\mathbf{.}}{u}+{\omega }^{2}u=-\stackrel{..}{u_g}$(2) , i.e.:

(7) $\stackrel{..}{u}=-\left({\stackrel{..}{u}}_g+2\omega \zeta \stackrel{\mathbf{.}}{u}+{\omega }^{2}u\right)$(7)

The calculated acceleration ($\stackrel{..}{u}$) of the system in equation (7)(7) $\stackrel{..}{u}=-\left({\stackrel{..}{u}}_g+2\omega \zeta \stackrel{\mathbf{.}}{u}+{\omega }^{2}u\right)$(7) is compared with the measured acceleration, the relative acceleration between $\stackrel{\mathrm{..}}{u}\text{}m\_ch1$, and $\stackrel{\mathrm{..}}{u}\text{}m\_ch2$ (Figure 5), and the convergence of the optimized dynamic parameters ζ and ω of the system is checked. The procedure to iteratively compute the dynamic parameters is explained in the next section.

3.3. Gauss-Newton algorithm for inverse analysis of dynamic parameters

The Gauss-Newton algorithm is a method to minimize the sum of squared function values. First, the dynamic parameters in equation (2)(2) $\stackrel{..}{u}+2\omega \zeta \stackrel{\mathbf{.}}{u}+{\omega }^{2}u=-\stackrel{..}{u_g}$(2) are redefined as b₁ ≡ 2ωζ and b₂ ≡ ω². Hence, equation (2)(2) $\stackrel{..}{u}+2\omega \zeta \stackrel{\mathbf{.}}{u}+{\omega }^{2}u=-\stackrel{..}{u_g}$(2) is re-expressed in terms of b₁ and b₂ as follows:

(8) $\stackrel{..}{u}+b_1\stackrel{\mathbf{.}}{u}+b_{2}u=-\stackrel{..}{u}{ }_g$(8)

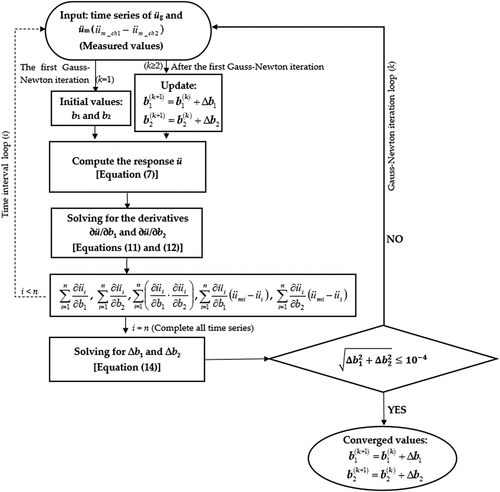
The calculation steps for determining the dynamic parameters b₁ and b₂ through the Gauss-Newton method is shown in Figure 6 (Miyamoto and Hanazato 2015). The measured ground excitation $\stackrel{\mathrm{..}}{u}g=\stackrel{\mathrm{..}}{u}\text{}m\_ch2$ is given first. Next, the initial values of ζ and ω are approximated to obtain the initial values of b₁ and b₂. Then, the relative acceleration of the Pagoda, ü according to equation (7)(7) $\stackrel{..}{u}=-\left({\stackrel{..}{u}}_g+2\omega \zeta \stackrel{\mathbf{.}}{u}+{\omega }^{2}u\right)$(7) , is numerically computed using Duhamel’s integral described in the previous section. Next, the Sum-Square-Error (SSE) between the calculated acceleration ü and the measured acceleration $\stackrel{\mathrm{..}}{u}\text{}m$ is determined, as seen in equation (9)(9) $SS{E}^{\left(k+1\right)}={\sum }_{i=0}^n\left[\stackrel{..}{u}\left(b_1^{\left(k+1\right)},b_2^{\left(k+1\right)},t_i\right)-{\stackrel{..}{u}}_m\left(t_i\right)\right]$(9) . It is noted from the equation that the SSE is numerically evaluated from i = 0 through all n time intervals, indicated by time t_i. The values of b₁ and b₂ are iteratively updated from the k to k + 1 Gauss-Newton iteration to minimize the Sum-Square-Error (SSE^(k+1)) between the acceleration obtained from Duhamel’s integral at time t_i, $\stackrel{..}{u}\left(b_1^{\left(k+1\right)},b_2^{\left(k+1\right)},t_i\right)$, versus the measured relative acceleration, ü_m(t_i) ($\stackrel{\mathrm{..}}{u}\text{}m\_ch1-\stackrel{\mathrm{..}}{u}\text{}m\_ch2$ at the time t_i).

Figure 6. Gauss-Newton procedure to determine the dynamic parameters b₁ and b_2.

(9) $SS{E}^{\left(k+1\right)}={\sum }_{i=0}^n\left[\stackrel{..}{u}\left(b_1^{\left(k+1\right)},b_2^{\left(k+1\right)},t_i\right)-{\stackrel{..}{u}}_m\left(t_i\right)\right]$(9)

The Gauss-Newton iteration is derived by introducing the linear approximation of the computed acceleration from Duhamel’s integral due to change of the dynamic parameters, ∆b₁ and ∆b₂, in each Gauss-Newton iteration, i.e.

(10) $\stackrel{..}{u}\left(b_1^{\left(k+1\right)},b_2^{\left(k+1\right)},t_i\right)\approx \stackrel{..}{u}\left(b_1^{\left(k\right)},b_2^{\left(k\right)},t_i\right)+\mathrm{\Delta }{b}_1\frac{\mathrm{\partial }{\stackrel{..}{u}}_i}{\mathrm{\partial }{b}_1}+\mathrm{\Delta }{b}_2\frac{\mathrm{\partial }{\stackrel{..}{u}}_i}{\mathrm{\partial }{b}_2}$(10)

where $\stackrel{\mathrm{..}}{u}\text{}i$ denotes an acceleration computed from Duhamel’s integral at time t_i from current values of dynamic parameters, $b_1^{\left(k\right)}$ and $b_2^{\left(k\right)}$.

Taking the partial derivative of equation (8)(8) $\stackrel{..}{u}+b_1\stackrel{\mathbf{.}}{u}+b_{2}u=-\stackrel{..}{u}{ }_g$(8) with respect to b₁ and b₂ results in two second-order linear ordinary differential equations as follows:

(11) $\frac{\mathrm{\partial }\stackrel{..}{u}}{\mathrm{\partial }{b}_1}+b_1\frac{\mathrm{\partial }\stackrel{\mathbf{.}}{u}}{\mathrm{\partial }{b}_1}+b_2\frac{\mathrm{\partial }\stackrel{\hspace{0.17em}}{u}}{\mathrm{\partial }{b}_1}=-\stackrel{\mathbf{.}}{u}$(11)

(12) $\frac{\mathrm{\partial }\stackrel{..}{u}}{\mathrm{\partial }{b}_2}+b_1\frac{\mathrm{\partial }{\stackrel{\mathbf{.}}{u}}_{\hspace{0.17em}}}{\mathrm{\partial }{b}_2}+b_2\frac{\mathrm{\partial }\stackrel{\hspace{0.17em}}{u}}{\mathrm{\partial }{b}_2}=-\stackrel{\hspace{0.17em}}{u}$(12)

With the obtained relative velocity and displacement from equation (8)(8) $\stackrel{..}{u}+b_1\stackrel{\mathbf{.}}{u}+b_{2}u=-\stackrel{..}{u}{ }_g$(8) , the partial derivative of the relative acceleration in equations (11)(11) $\frac{\mathrm{\partial }\stackrel{..}{u}}{\mathrm{\partial }{b}_1}+b_1\frac{\mathrm{\partial }\stackrel{\mathbf{.}}{u}}{\mathrm{\partial }{b}_1}+b_2\frac{\mathrm{\partial }\stackrel{\hspace{0.17em}}{u}}{\mathrm{\partial }{b}_1}=-\stackrel{\mathbf{.}}{u}$(11) and (12(12) $\frac{\mathrm{\partial }\stackrel{..}{u}}{\mathrm{\partial }{b}_2}+b_1\frac{\mathrm{\partial }{\stackrel{\mathbf{.}}{u}}_{\hspace{0.17em}}}{\mathrm{\partial }{b}_2}+b_2\frac{\mathrm{\partial }\stackrel{\hspace{0.17em}}{u}}{\mathrm{\partial }{b}_2}=-\stackrel{\hspace{0.17em}}{u}$(12) ), ∂ü/∂b₁ and ∂ü/∂b_2, are solved numerically using the Duhamel’s integral and then substituted into equation (10)(10) $\stackrel{..}{u}\left(b_1^{\left(k+1\right)},b_2^{\left(k+1\right)},t_i\right)\approx \stackrel{..}{u}\left(b_1^{\left(k\right)},b_2^{\left(k\right)},t_i\right)+\mathrm{\Delta }{b}_1\frac{\mathrm{\partial }{\stackrel{..}{u}}_i}{\mathrm{\partial }{b}_1}+\mathrm{\Delta }{b}_2\frac{\mathrm{\partial }{\stackrel{..}{u}}_i}{\mathrm{\partial }{b}_2}$(10) . With the previous iteration acceleration, $\stackrel{..}{u}\left(b_1^{\left(k\right)},b_2^{\left(k\right)},t_i\right)$, the left-hand term in equation (10)(10) $\stackrel{..}{u}\left(b_1^{\left(k+1\right)},b_2^{\left(k+1\right)},t_i\right)\approx \stackrel{..}{u}\left(b_1^{\left(k\right)},b_2^{\left(k\right)},t_i\right)+\mathrm{\Delta }{b}_1\frac{\mathrm{\partial }{\stackrel{..}{u}}_i}{\mathrm{\partial }{b}_1}+\mathrm{\Delta }{b}_2\frac{\mathrm{\partial }{\stackrel{..}{u}}_i}{\mathrm{\partial }{b}_2}$(10) can be solved. Finally, the SSE in equation (9)(9) $SS{E}^{\left(k+1\right)}={\sum }_{i=0}^n\left[\stackrel{..}{u}\left(b_1^{\left(k+1\right)},b_2^{\left(k+1\right)},t_i\right)-{\stackrel{..}{u}}_m\left(t_i\right)\right]$(9) can be obtained. Next, minimizing the total SSE^{(k + 1)} with respect to ∆b₁ and ∆b₂., as shown in equation (13)(13) $\frac{\mathrm{\partial }\left(SS{E}^{\left(k+1\right)}\right)}{\mathrm{\partial }\mathrm{\Delta }{b}_1}=0\begin{array}{cc}\hspace{0.17em}& and\begin{array}{cc}\hspace{0.17em}& \frac{\mathrm{\partial }\left(SS{E}^{\left(k+1\right)}\right)}{\mathrm{\partial }\mathrm{\Delta }{b}_2}=0\end{array}\end{array}$(13) , gets the algebraic equations (14)(14) $\left[\begin{array}{c}\begin{array}{cc}{{\sum }_{i=1}^n\left(\frac{\mathrm{\partial }\stackrel{..}{u_i}}{\mathrm{\partial }{b}_1}\right)}^2& {{\sum }_{i=1}^n\left(\frac{\mathrm{\partial }\stackrel{..}{u_i}}{\mathrm{\partial }{b}_1}.\frac{\mathrm{\partial }\stackrel{..}{u_i}}{\mathrm{\partial }{b}_2}\right)}^{\hspace{0.17em}}\end{array}\\ \begin{array}{cc}{\sum }_{i=1}^n\left(\frac{\mathrm{\partial }\stackrel{..}{u_i}}{\mathrm{\partial }{b}_1}.\frac{\mathrm{\partial }\stackrel{..}{u_i}}{\mathrm{\partial }{b}_2}\right)& {{\sum }_{i=1}^n\left(\frac{\mathrm{\partial }\stackrel{..}{u_i}}{\mathrm{\partial }{b}_2}\right)}^2\end{array}\end{array}\right]\left\{\begin{array}{c}\mathrm{\Delta }{b}_1\\ \mathrm{\Delta }{b}_2\end{array}\right\}=\left\{\begin{array}{c}{\sum }_{i=1}^n\frac{\mathrm{\partial }\stackrel{..}{u_i}}{\mathrm{\partial }{b}_1}.\left(\stackrel{..}{u_{mi}}-\stackrel{..}{u_i}\right)\\ {\sum }_{i=1}^n\frac{\mathrm{\partial }\stackrel{..}{u_i}}{\mathrm{\partial }{b}_2}.\left(\stackrel{..}{u_{mi}}-\stackrel{..}{u_i}\right)\end{array}\right\}$(14) for computing the incremental values of dynamic parameters, ∆b₁ and ∆b₂, as follows:

(13) $\frac{\mathrm{\partial }\left(SS{E}^{\left(k+1\right)}\right)}{\mathrm{\partial }\mathrm{\Delta }{b}_1}=0\begin{array}{cc}\hspace{0.17em}& and\begin{array}{cc}\hspace{0.17em}& \frac{\mathrm{\partial }\left(SS{E}^{\left(k+1\right)}\right)}{\mathrm{\partial }\mathrm{\Delta }{b}_2}=0\end{array}\end{array}$(13)

(14) $\left[\begin{array}{c}\begin{array}{cc}{{\sum }_{i=1}^n\left(\frac{\mathrm{\partial }\stackrel{..}{u_i}}{\mathrm{\partial }{b}_1}\right)}^2& {{\sum }_{i=1}^n\left(\frac{\mathrm{\partial }\stackrel{..}{u_i}}{\mathrm{\partial }{b}_1}.\frac{\mathrm{\partial }\stackrel{..}{u_i}}{\mathrm{\partial }{b}_2}\right)}^{\hspace{0.17em}}\end{array}\\ \begin{array}{cc}{\sum }_{i=1}^n\left(\frac{\mathrm{\partial }\stackrel{..}{u_i}}{\mathrm{\partial }{b}_1}.\frac{\mathrm{\partial }\stackrel{..}{u_i}}{\mathrm{\partial }{b}_2}\right)& {{\sum }_{i=1}^n\left(\frac{\mathrm{\partial }\stackrel{..}{u_i}}{\mathrm{\partial }{b}_2}\right)}^2\end{array}\end{array}\right]\left\{\begin{array}{c}\mathrm{\Delta }{b}_1\\ \mathrm{\Delta }{b}_2\end{array}\right\}=\left\{\begin{array}{c}{\sum }_{i=1}^n\frac{\mathrm{\partial }\stackrel{..}{u_i}}{\mathrm{\partial }{b}_1}.\left(\stackrel{..}{u_{mi}}-\stackrel{..}{u_i}\right)\\ {\sum }_{i=1}^n\frac{\mathrm{\partial }\stackrel{..}{u_i}}{\mathrm{\partial }{b}_2}.\left(\stackrel{..}{u_{mi}}-\stackrel{..}{u_i}\right)\end{array}\right\}$(14)

where $\stackrel{..}{u}{ }_{mi}$ denotes measured values of relative acceleration between the top (Ch1) and base (Ch2) of the pagoda at time t_i, shown in Figure 5. Then, the values of parameters b₁ and b₂ are updated using incremental values ∆b₁ and ∆b₂ obtained from equation (14)(14) $\left[\begin{array}{c}\begin{array}{cc}{{\sum }_{i=1}^n\left(\frac{\mathrm{\partial }\stackrel{..}{u_i}}{\mathrm{\partial }{b}_1}\right)}^2& {{\sum }_{i=1}^n\left(\frac{\mathrm{\partial }\stackrel{..}{u_i}}{\mathrm{\partial }{b}_1}.\frac{\mathrm{\partial }\stackrel{..}{u_i}}{\mathrm{\partial }{b}_2}\right)}^{\hspace{0.17em}}\end{array}\\ \begin{array}{cc}{\sum }_{i=1}^n\left(\frac{\mathrm{\partial }\stackrel{..}{u_i}}{\mathrm{\partial }{b}_1}.\frac{\mathrm{\partial }\stackrel{..}{u_i}}{\mathrm{\partial }{b}_2}\right)& {{\sum }_{i=1}^n\left(\frac{\mathrm{\partial }\stackrel{..}{u_i}}{\mathrm{\partial }{b}_2}\right)}^2\end{array}\end{array}\right]\left\{\begin{array}{c}\mathrm{\Delta }{b}_1\\ \mathrm{\Delta }{b}_2\end{array}\right\}=\left\{\begin{array}{c}{\sum }_{i=1}^n\frac{\mathrm{\partial }\stackrel{..}{u_i}}{\mathrm{\partial }{b}_1}.\left(\stackrel{..}{u_{mi}}-\stackrel{..}{u_i}\right)\\ {\sum }_{i=1}^n\frac{\mathrm{\partial }\stackrel{..}{u_i}}{\mathrm{\partial }{b}_2}.\left(\stackrel{..}{u_{mi}}-\stackrel{..}{u_i}\right)\end{array}\right\}$(14) , i.e.:

(15) ${b_1}^{\left(k+1\right)}={b_1}^{\left(k\right)}+\mathrm{\Delta }{b}_1$(15)

(16) ${b_2}^{\left(k+1\right)}={b_2}^{\left(k\right)}+\mathrm{\Delta }{b}_2$(16)

The dynamic parameters b₁ and b₂ are updated according to equations (15)(15) ${b_1}^{\left(k+1\right)}={b_1}^{\left(k\right)}+\mathrm{\Delta }{b}_1$(15) and (16(16) ${b_2}^{\left(k+1\right)}={b_2}^{\left(k\right)}+\mathrm{\Delta }{b}_2$(16) ). Solving the structural responses and updating the dynamic parameters have been repeated until the incremental values ∆b₁ and ∆b₂ are less than a certain tolerance level, i.e.:

(17) $\sqrt{{\left(\mathrm{\Delta }{b}_1\right)}^2+{\left(\mathrm{\Delta }{b}_2\right)}^2}\le {10}^{-4}$(17)

After the values of dynamic parameters (b₁ and b₂) are converged, the natural frequency and the damping ratio are then evaluated using the relations:

(18) $\omega =\sqrt{b_2}and\zeta =\frac{b_1}{2\sqrt{b_2}}$(18)

The natural frequency of structure in radian per second (ω) is then divided by factor 2π to obtain the natural frequency in Hz (f) as follows:

(19) $f=\frac{\omega }{2\pi }$(19)

In the next section, the dynamic parameters of Umong pagoda will be evaluated via Gauss-Newton process. Four earthquake waves are used to represent the ground acceleration in equation (8)(8) $\stackrel{..}{u}+b_1\stackrel{\mathbf{.}}{u}+b_{2}u=-\stackrel{..}{u}{ }_g$(8) . The converged values of the natural frequency and the damping ratio computed from four earthquake waves will be discussed.

4. Results and discussions

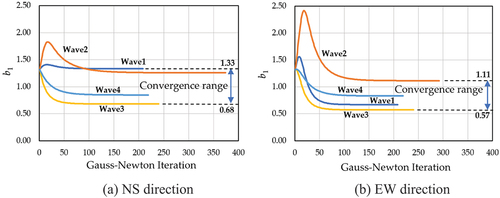
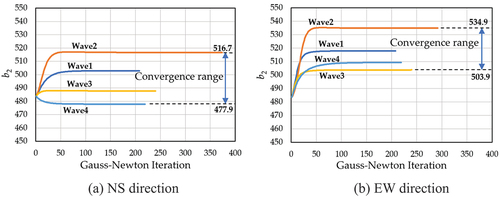
The dynamic parameters, b₁ and b₂, obtained by the inverse analysis using the four recorded earthquake waves, are demonstrated here. Figure 7 shows the convergence of the damping parameter b₁ in the NS and EW directions. The convergence range of b₁ is between 0.68 and 1.33 in the NS direction and 0.57–1.11 in the EW direction. For the parameter b₂, as shown in Figure 8, the convergence ranges between 477.9–516.7 and 503.9–534.9 in the NS and EW directions, respectively.

Figure 7. Convergence of damping parameter (b₁).

Figure 8. Convergence of stiffness coefficient (b₂).

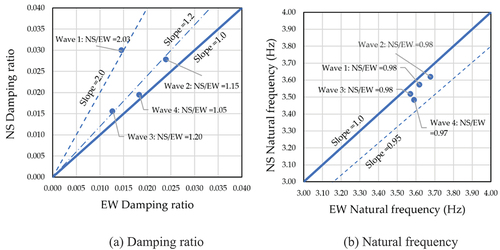
With the converged dynamic parameters b₁ and b₂, the values of natural frequency (f) and the damping ratio (ζ) can be computed using equations (18)(18) $\omega =\sqrt{b_2}and\zeta =\frac{b_1}{2\sqrt{b_2}}$(18) and (19(19) $f=\frac{\omega }{2\pi }$(19) ), as shown in Table 2. The average values (Avg.) and standard deviation (SD) of the damping ratio are 0.0231 and 0.0068 in the NS direction and 0.0175 and 0.0050 in the EW direction. The average values (Avg.) and standard deviation (SD) of the natural frequency are approximately 3.55 Hz and 0.06 Hz in the NS direction and 3.62 Hz and 0.05 Hz in the EW direction. The average natural frequency in this study is slightly lower than the 4.45 Hz of the modal analysis of the three-dimensional finite element model obtained from the previous research (Yanathanom 2010; Hansapinyo and Poovarodom 2014). This is because the finite element analysis rigidly assumed a full-solid body of the pagoda. Furthermore, the fully fixed base was used in the finite element model.

Table 2. The computed dynamic properties using the proposed algorithm.

Seismic Wave	NS direction					EW direction
	b1	ζ	b2	f (Hz)	Iteration	b1	ζ	b2	f (Hz)	Iteration
1	1.33	0.0298	502.9	3.57	208	0.67	0.0147	517.9	3.62	234
2	1.26	0.0277	516.7	3.62	374	1.11	0.0241	534.9	3.68	292
3	0.68	0.0154	487.8	3.52	240	0.57	0.0128	503.9	3.57	240
4	0.85	0.0194	477.9	3.48	219	0.83	0.0184	509.4	3.59	322
Avg.	-	0.0231	-	3.55	-	-	0.0175	-	3.62	-
SD	-	0.0068	-	0.06	-	-	0.0050	-	0.05	-

As the pagoda is ideally axisymmetric, the dynamic properties in any direction should be equally observed. Figure 9 shows the comparisons between the dynamic properties obtained in the NS direction (Y-axis) and the EW direction (X-axis). The equality line with a slope of 1.0 indicates identical properties in both directions. Figure 9(a) shows that the damping ratios obtained from the four waves are greater than the equality line. In other words, the damping ratios in the NS direction are greater than those in the EW direction. The ratio between the NS/EW damping ratios is less than 1.20 for Waves 2, 3, and 4. The ratio is about 2.03 for Wave 1. For the natural frequency, from Figure 9(b), the EW frequencies are higher than those values in the NS direction. Hence, the structural stiffness in the EW direction is greater than in the NS direction.

Figure 9. Comparisons of the obtained dynamic properties in the two orthogonal directions.

5. Conclusions

In this study, an algorithm of inverse analysis to evaluate the dynamic properties of a historic building is proposed. The proposed algorithm adopts the Duhamel’s integral to numerically solve the equation of motion and the Gauss-Newton algorithm to minimize the sum-of-squares error (SSE) between the calculated and real-time measured accelerations of the structure. Based on the real-time measured relative acceleration of the pagoda and the calculation using the proposed algorithm, the dynamic parameters are backward estimated. Four distant earthquake waves are used for the numerical experiments. Based on the study results, the following conclusions can be drawn.

From the real-time measured vibrations, the average damping ratios are 0.0231 in the NS direction and 0.0175 in the EW direction. The average natural frequencies are 3.55 Hz in the NS direction and 3.62 Hz in the EW direction. The average natural frequency in this study is slightly lower than the 4.45 Hz of the modal analysis of the three-dimensional finite element model obtained from the previous study (Yanathanom 2010); (Hansapinyo and Poovarodom 2014). This is because the analysis rigidly assumed a full-solid body of the pagoda. Furthermore, the fully fixed base was used in the analytical model.

As the pagoda is ideally axisymmetric, the dynamic properties in any direction should be equally observed. However, there are some discrepancies in the dynamic properties between the two orthogonal directions. The damping ratio in the NS direction is greater than in the EW direction. It may indicate more damage to the structure resisting lateral load in the NS direction. For the natural frequency, the EW frequencies are higher than those values in the NS direction. Hence, the structural stiffness resisting lateral load in the EW direction is probably greater than that in the NS direction. From the results, an onsite damage investigation can be specifically identified.

Although conducting finite element analysis to determine the dynamic properties is a convenient method, it is a time-consuming practice if high accuracy is required. In addition, the main drawback of using finite element analysis is that it involves various assumptions and modeling parameters that may not reflect the real-existing physical behavior. Hence, using the proposed technique is a powerful approach. With the attached sensor cooperating with the data processing, real-time monitoring can be done.Funding This research was funded by Chiang Mai University, NRCT (FF2022-CMU); TRF Research Scholar (RSA6280039); TRF Senior Research Scholar (RTA6280012); and Electricity Generating Authority of Thailand.

Acknowledgments

The second author would like to acknowledge supports from Fundamental Fund 2022, Chiang Mai University. The first author would like to acknowledge supports provided by Center of Excellence, Chiang Mai University.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data availability statement

Data available on request from the authors