An iterative output feedback controller-design strategy for energy-to-peak structural vibration control

ABSTRACT

To address the issue of inadequate control effect resulting from the challenge of measuring state feedback information comprehensively, this paper proposes an iterative output feedback energy-to-peak control method that solely depends on partial external observation data. This paper presents the computational steps for achieving a suboptimal solution to the output feedback bilinear matrix inequality constrained problem using an iterative linear matrix inequality approach. The proposed method overcomes the challenge of numerically solving the optimization problem. The unknown variables in the output feedback linear matrix inequality optimization problem are transformed equivalently to obtain a new linear matrix inequality optimization problem. The numerical results of the two optimization problems are then used to iterate with each other and obtain a suboptimal solution. A comprehensive analysis was conducted on an 8-story building structure, utilizing state feedback, output feedback, and iterative output feedback energy-to-peak control techniques. The results of the study indicate that the proposed iterative output feedback energy-to-peak control approach efficiently reduces the displacement and acceleration response of the structure, exhibiting superior control effectiveness than both the state feedback and output feedback energy-to-peak control methods. The findings demonstrate the practicality and versatility of the suggested method.

KEYWORDS:

• Energy-to-peak
• vibration control
• linear matrix inequality
• output feedback
• iteration

1. Introduction

In the field of civil engineering, the development and application of high-rise building structures (Wang et al. 2019; Wang, Shi, and Zhou 2019; Wang, Zhou, and Shi 2023b) are becoming increasingly common in cities. Therefore, continuous research is needed for the vibration control technology of these structures. There are now many technical devices available for vibration control, and research related to tuned mass dampers (Wang et al. 2020, 2020; Wang, Shi, and Zhou 2022) is particularly popular. These studies primarily focus on combining active control techniques with the passive control technique of tuned mass dampers for various applications (Wang et al. 2022, 2023; Wang, Zhou, and Shi 2023a).

Active control strategies (Li, Chen, and Teng 2019; Li et al. 2019; Xu et al. 2022) for building structures have been the focus of significant attention due to their ability to achieve effective control. State feedback methods (Al-Fahdawi and Barroso 2021; Chen et al. 2021; Saeed, Sun, and Elias 2022) are preferred by most researchers in designing active controllers, as they have demonstrated to be more efficient in improving system performance. However, the comprehensive measurement of state feedback information in practical applications can often prove challenging, rendering state feedback control systems technically difficult and expensive to implement. As a result, output feedback control strategies (Yang, Li, and Qiu 2019) that rely solely on externally measurable signals have emerged as a notable research pursuit.

In the field of automatic control, researchers have conducted extensive and profound research on output feedback strategy (Chandiramani 2016; Hao and Duan 2017; Kazemy, Zhang, and Han 2017; Lan et al. 2020; Rahmani, Ziaiefar, and Hashemi 2022), with particular emphasis on the challenging task of solving control problems. In the early stages, the main method utilized was the Riccati equation. However, this approach had some limitations as it required predetermined parameter settings which tended to lead to conservative analytical outcomes. As the interior point method emerged for solving convex optimization difficulties, and many control problems could be transformed into linear matrix inequality optimization or feasibility problems, it became convenient and efficient to solve output feedback control problems. Subsequently, researchers began applying the linear matrix inequality method extensively to address output feedback problems (Kazemy, Gyurkovics, and Takács 2020; Palacios-Quiñonero et al. 2017). The primary focus of the literature discussed above is to determine the solution of the output feedback gain matrix. Specifically, researchers aim to identify the feasible solution for the existence of the linear matrix inequality. Various methods have been proposed, including linearized convex-concave decomposition, alternating projection method, and resilient approach (Sadabadi and Peaucelle 2016). Among these methods, the variable transformation approach is the most straightforward to apply (Rubió-Massegú et al. 2013; Zecevic and Siljak 2004).

Different control algorithms produce varying control effects when solving control problems. The commonly used active control algorithms include classical $H_{\mathrm{\infty }}$ control (Palacios Quiñonero et al. 2019), PID control (Ahmed et al. 2020), and neural network control (Runge and Zmeureanu 2019). The $H_{\mathrm{\infty }}$ method is primarily designed to optimize the average response during vibration. However, structural vibration damage is often caused by the peak of the dynamic response. Therefore, the energy-to-peak control method, which can significantly suppress the peak response of the system, is a better choice.

This paper proposes a new iterative output feedback energy-to-peak control method by combining the iterative output feedback approach and the energy-to-peak control algorithm, based on the literature (Palacios-Quiñonero et al. 2019). The paper includes the method’s design process and utilizes an 8-story building structure for verifying the method’s feasibility.

2. Energy-to-peak control strategy

2.1. State feedback control

The state-space model of a dynamic system can be described by

(1) $\left\{\begin{array}{c}\dot{x}\left(\mathit{t}\right)=\mathit{Ax}\left(\mathit{t}\right)+\mathit{Bu}\left(\mathit{t}\right)+\mathit{Ew}\left(\mathit{t}\right)\\ \mathit{z}\left(\mathit{t}\right)=C_z\mathit{x}\left(\mathit{t}\right)+D_z\mathit{u}\left(\mathit{t}\right)\end{array}\right.$(1)

where, $\mathit{x}\left(\mathit{t}\right)\in {\mathbb{R}}^{n_x}$ is the state vector, $\mathit{u}\left(\mathit{t}\right)\in {\mathbb{R}}^{n_u}$ indicates the control input vector, $\mathit{w}\left(\mathit{t}\right)\in {\mathbb{R}}^{n_w}$ is the vector of external excitation, $\mathit{z}\left(\mathit{t}\right)\in {\mathbb{R}}^{n_z}$ indicates the controlled output vector; $\mathit{A}\in {\mathbb{R}}^{n_x\times n_x}$, $\mathit{B}\in {\mathbb{R}}^{n_x\times n_u}$, $\mathit{E}\in {\mathbb{R}}^{n_x\times n_w}$，$C_z\in {\mathbb{R}}^{n_z\times n_x}$, $D_z\in {\mathbb{R}}^{n_z\times n_u}$ represent the corresponding constant matrices.

To acquire a state gain matrix $\mathit{G}\in {\mathbb{R}}^{n_u\times n_x}$ for a state feedback controller $\mathit{u}\left(\mathit{t}\right)=\mathit{Gx}\left(\mathit{t}\right)$ and minimize the energy-to-peak norm, i.e.

(2) ${\gamma }_G=\underset{0<||w||{ }_2<\mathrm{\infty }}{sup}\frac{||z||{ }_{\mathrm{\infty }}}{||\mathit{w}||{ }_2}$(2)

$\mathrm{where}||\mathit{w}||{ }_2={\left(\underset{0}{\overset{\mathrm{\infty }}{\int }}{w}^T\left(\mathit{t}\right)\mathit{w}\left(\mathit{t}\right)\mathit{dt}\right)}^{\frac{1}{2}}$, $||\mathit{z}||{ }_{\mathrm{\infty }}=\underset{0\le \mathit{t}<\mathrm{\infty }}{sup}{\left(z^T\left(\mathit{t}\right)\mathit{z}\left(\mathit{t}\right)\right)}^{\frac{1}{2}}$.

The transfer function from the external excitation $\mathit{w}\left(\mathit{t}\right)$ to the controlled output $\mathit{z}\left(\mathit{t}\right)$ can be expressed as

(3) $T_s=C_G{\left(sI-A_G\right)}^{-1}\mathit{E}$(3)

where $A_G=\mathit{A}+\mathit{BG}$, $C_G=C_z+D_z\mathit{G}$.

The task of determining the state gain matrix $\mathit{G}$ can be converted into an optimization problem of linear matrix inequality as follows:

(4) ${\mathcal{F}}_s:\left\{\begin{array}{c}\mathit{minimize}\mathit{\eta }\\ \mathit{subject}\mathit{to}\mathit{X}>0,\mathit{\eta }>0,\\ \mathit{and}\mathit{the}\mathit{LMIs}\mathit{in}\left(5\right),\end{array}\right.$(4)

$\mathit{AX}+\mathit{X}{A}^T+\mathit{BGX}+\mathit{X}{G}^T{B}^T+\mathit{E}{E}^T<0,$

(5) $\left[\begin{array}{cc}\mathit{X}& \ast \\ C_z\mathit{X}+D_z\mathit{GX}& \mathit{\eta I}\end{array}\right]>0$(5)

in the expression, $\mathit{G}$ represents the gain matrix, $\mathit{X}$ denotes the symmetric variable matrix, and * denotes the transpose of the element in the symmetric position. By substituting $\mathit{GX}=\mathit{Y}$, it is possible to transform ${\mathcal{F}}_s$ into an optimization problem of linear matrix inequality, as shown below,

(6) ${\mathcal{F}}_s^{\prime }:\left\{\begin{array}{c}\mathit{minimize}\mathit{\eta }\\ \mathit{subject}\mathit{to}\mathit{X}>0,\mathit{\eta }>0,\\ \mathit{and}\mathit{the}\mathit{LMIs}\mathit{in}\left(7\right),\end{array}\right.$(6)

$\mathit{AX}+\mathit{X}{A}^T+\mathit{BY}+Y^T{B}^T+\mathit{E}{E}^T<0,$

(7) $\left[\begin{array}{cc}\mathit{X}& \ast \\ C_z\mathit{X}+D_z\mathit{Y}& \mathit{\eta I}\end{array}\right]>0$(7)

where $\mathit{Y}$ refers to the variable matrix. Once this optimization problem is successfully addressed, an optimal ${\eta }_s$ can be achieved simultaneously from a set of matrices $\left({\tilde{X}}_{\mathit{s}},{\tilde{Y}}_{\mathit{s}}\right)$, which eventually allows writing the state feedback gain matrix ${\tilde{G}}_{\mathit{s}}$ in the following format:

(8) ${\tilde{G}}_{\mathit{s}}={\tilde{Y}}_{\mathit{s}}{\tilde{X}}_{\mathit{s}}^{-1}$(8)

at the same time, the optimal value $\mathit{\gamma }$ can be computed by utilizing the following equation,

(9) ${\gamma }_{{\tilde{G}}_{\mathit{s}}}={\tilde{\eta }}_{\mathit{s}}^{1/2}$(9)

2.2. Output feedback control

Typically, it is challenging to measure the complete state vector information $\mathit{x}\left(\mathit{t}\right)$, and therefore, in the output feedback control method, the measured output $\mathit{y}\left(\mathit{t}\right)=C_y\mathit{x}\left(\mathit{t}\right)$, where $C_y\in {\mathbb{R}}^{n_y\times n_x}$ signifies the associated measured output matrix. Consequently, the static output feedback controller can be represented as

(10) $\mathit{u}\left(\mathit{t}\right)=\mathit{Ky}\left(\mathit{t}\right)$(10)

where $\mathit{K}\in {\mathbb{R}}^{n_u\times n_y}$ is a constant output feedback gain matrix and the transfer function of the system can be expressed as

(11) $T_k=C_K{\left(sI-A_K\right)}^{-1}\mathit{E}$(11)

where $A_K=\mathit{A}+\mathit{BK}{C}_y$, $C_K=C_z+D_z\mathit{K}{C}_y$.

The optimization problem of energy-to-peak output feedback control is converted into a linear matrix inequality problem, i.e.

(12) ${\mathcal{F}}_o:\left\{\begin{array}{c}\mathit{minimize}{\eta }_o\\ \mathit{subject}\mathit{to}\mathit{X}>0,{\eta }_o>0,\\ \mathit{and}\mathit{the}\mathit{LMIs}\mathit{in}\left(13\right),\end{array}\right.$(12)

$\mathit{AX}+\mathit{X}{A}^T+\mathit{BK}{C}_y\mathit{X}+\mathit{X}{C}_y^T{K}^T{B}^T+\mathit{E}{E}^T<0,$

(13) $\left[\begin{array}{cc}\mathit{X}& \ast \\ C_z\mathit{X}+D_z\mathit{K}{C}_y\mathit{X}& {\eta }_o\mathit{I}\end{array}\right]>0$(13)

here, $\mathit{X}=X^T$ and $\mathit{K}$ are the variable matrices. If the measurement output matrix $C_y$ is not a square matrix, i.e., $n_y<n_x$, variable substitution $\mathit{K}{C}_y\mathit{X}=\mathit{Y}$ cannot directly yield the output feedback gain matrix $\mathit{K}$ from the linear matrix inequality optimization problem ${\mathcal{F}}_o$. Hence, the variable substitution method (Kazemy, Gyurkovics, and Takács 2020) is implemented to address this issue.

In case the measured output matrix $C_y$ is a row full rank matrix, the following conversion is applied,

(14) $\mathit{X}=\mathit{Q}{X}_Q{Q}^T+\mathit{R}{X}_R{R}^T,\mathit{Y}=Y_R{R}^T$(14)

the variable transformation involves $X_Q\in {\mathbb{R}}^{\left(n_x-n_y\right)\times \left(n_x-n_y\right)}$ and $X_R\in {\mathbb{R}}^{n_y\times n_y}$, both of which are symmetric positive definite matrices, and $Y_R\in {\mathbb{R}}^{n_u\times n_y}$, an ordinary square matrix. Additionally, $\mathit{Q}\in {\mathbb{R}}^{n_x\times \left(n_x-n_y\right)}$ is a matrix with $\mathit{rank}\left(\mathit{Q}\right)=n_x-n_y$ and satisfies $C_y\mathit{Q}=\left[0\right]$. This means $\mathit{Q}$ is a basis of the kernel subspace $\ker \left(C_y\right)$ of the matrix $C_y$. Finally, $\mathit{R}\in {\mathbb{R}}^{n_x\times n_y}$ has the following form:

(15) $\mathit{R}=C_y^{\iota }+\mathit{QL}$(15)

Here, $C_y^{\iota }=C_y^T{\left(C_y{C}_y^T\right)}^{-1}$ denotes the Moore-Penrose pseudoinverse of $C_y$, and $\mathit{L}\in {\mathbb{R}}^{\left(n_x-n_y\right)\times n_y}$ is an arbitrary and constant matrix. Once the new matrix of variables (14) is substituted into (12), the initial energy-to-peak output feedback linear matrix inequality optimization problem ${\mathcal{F}}_o$ can be converted into a new linear matrix inequality optimization problem as shown below,

(16) ${\mathcal{F}}_o^{{ }^{\prime }}:\{\begin{array}{c}\mathit{minimize}{\eta }_o^{{ }^{\prime }}\\ \mathit{subjectto}{X}_Q>0,X_R>0,{\eta }_o^{{ }^{\prime }}>0,\\ \mathit{andtheLMIsin}\left(17\right),\end{array}$(16)

$\mathit{AQ}{X}_Q{Q}^T+\mathit{Q}{X}_Q{Q}^T{A}^T+\mathit{AR}{X}_R{R}^T+\mathit{R}{X}_R{R}^T{A}^T+\mathit{B}{Y}_R{R}^T+\mathit{R}{Y}_R^T{B}^T+\mathit{E}{E}^T<0,$

(17) $\left[\begin{array}{cc}\mathit{Q}{X}_Q{Q}^T+\mathit{R}{X}_R{R}^T& \ast \\ C_z\mathit{Q}{X}_Q{Q}^T+C_z\mathit{R}{X}_R{R}^T+D_z{Y}_R{R}^T& {\eta }_o^{{ }^{\prime }}\mathit{I}\end{array}\right]>0$(17)

Assuming the existence of a feasible solution to this linear matrix inequality optimization problem ${\mathcal{F}}_o^{{ }^{\prime }}$, an optimal value for ${\eta }_o^{{ }^{\prime }}$, along with the matrices ${\tilde{X}}_{\mathit{Q}}$, ${\tilde{X}}_{\mathit{R}}$, and ${\tilde{Y}}_{\mathit{R}}$, can be obtained. This can be achieved when the output feedback gain matrix is obtained from the following equation,

(18) $\tilde{K}={\tilde{Y}}_{\mathit{R}}{\left({\tilde{X}}_{\mathit{R}}\right)}^{-1}$(18)

the formula for the optimal value is

(19) ${\gamma }_{{\tilde{G}}_{\mathit{k}}}=\sqrt{{\tilde{\eta }}_{\mathit{o}}^{{ }^{\prime }}}$(19)

The above process highlights the importance of selecting matrix $\mathit{L}$ for solving the linear matrix inequality. Improper selection can lead to an infeasible solution. Per literature (Palacios-Quiñonero et al. 2014), the matrix L is chosen as

(20) $\mathit{L}=Q^{\iota }{\tilde{X}}_{\mathit{s}}{C}_y^T{\left(C_y{\tilde{X}}_{\mathit{s}}{C}_y^T\right)}^{-1}$(20)

here,

(21) $Q^{\iota }={\left(Q^T\mathit{Q}\right)}^{-1}{Q}^T$(21)

the matrix $Q^{\iota }$ represents the Moore-Penrose pseudoinverse of the matrix $\mathit{Q}$, and ${\tilde{X}}_{\mathit{s}}$ represents the optimal $\mathit{X}$ obtained from solving the state feedback optimization problem ${\mathcal{F}}_s^{{ }^{\prime }}$. With the specific $\mathit{L}$ selection, a feasible solution can be found for the linear matrix inequality optimization problem ${\mathcal{F}}_o^{{ }^{\prime }}$. Using this approach, an optimal output feedback controller can also be obtained.

3. Iterative output feedback control

In the preceding section, the design of the static output feedback controller involved selecting the matrix $\mathit{L}$ based on the optimal $\mathit{X}$ obtained from solving the state feedback optimization problem ${\mathcal{F}}_s^{{ }^{\prime }}$. This approach resulted in a more complex solution for the optimization problem. To simplify the process, this section presents an iterative output feedback energy-to-peak strategy that does not rely on the results of the state feedback solution. The iterative solution procedure requires an initialization setup as follows.

To begin with, in Equation (12)(12) ${\mathcal{F}}_o:\left\{\begin{array}{c}\mathit{minimize}{\eta }_o\\ \mathit{subject}\mathit{to}\mathit{X}>0,{\eta }_o>0,\\ \mathit{and}\mathit{the}\mathit{LMIs}\mathit{in}\left(13\right),\end{array}\right.$(12) , set $\mathit{K}$ as $\mathit{K}=K^{\left(0\right)}=\left[0\right]$. Solve the optimization problem ${\mathcal{F}}_o$ to obtain the optimal matrix ${\tilde{X}}^{\left(0\right)}$ and the optimal ${\gamma }_{{\mathit{k}}^{\left(0\right)}}={\tilde{\eta }}_{\mathit{o}}^{1/2}$. The matrix $\mathit{L}$ can then be represented as

(22) $L^{\left(0\right)}=Q^{\iota }{\tilde{X}}^{\left(0\right)}{C}_y^T{\left(C_y{\tilde{X}}^{\left(0\right)}{C}_y^T\right)}^{-1}$(22)

by substituting $L^{\left(0\right)}$ into Equation (15)(15) $\mathit{R}=C_y^{\iota }+\mathit{QL}$(15) , the resulting matrix is

(23) $R^{\left(0\right)}=C_y^{\iota }+\mathit{Q}{L}^{\left(0\right)}$(23)

To obtain the output feedback gain matrix $K^{\left(1\right)}$, the linear inequality optimization problem ${\mathcal{F}}_o^{{ }^{\prime }}$ needs to be solved. Once $K^{\left(1\right)}$ is obtained, substitute it into the linear matrix inequality optimization problem ${\mathcal{F}}_o$ from Equation (12)(12) ${\mathcal{F}}_o:\left\{\begin{array}{c}\mathit{minimize}{\eta }_o\\ \mathit{subject}\mathit{to}\mathit{X}>0,{\eta }_o>0,\\ \mathit{and}\mathit{the}\mathit{LMIs}\mathit{in}\left(13\right),\end{array}\right.$(12) . The iterative output feedback design procedure follows these steps:

Step i.a : the optimization problem ${\mathcal{F}}_o$ needs to be solved by replacing the matrix $K^{\left(\mathit{i}\right)}$ in Equation (12)(12) ${\mathcal{F}}_o:\left\{\begin{array}{c}\mathit{minimize}{\eta }_o\\ \mathit{subject}\mathit{to}\mathit{X}>0,{\eta }_o>0,\\ \mathit{and}\mathit{the}\mathit{LMIs}\mathit{in}\left(13\right),\end{array}\right.$(12) to obtain the optimal matrix ${\tilde{X}}^{\left(\mathit{i}\right)}$ and the optimal ${\gamma }_k^{(i)}$.

Step i.b : by defining $L^{\left(\mathit{i}\right)}=Q^{\iota }{\tilde{X}}^{\left(\mathit{i}\right)}{C}_y^T{\left(C_y{\tilde{X}}^{\left(\mathit{i}\right)}{C}_y^T\right)}^{-1}$, the corresponding $R^{\left(\mathit{i}\right)}=C_y^{\iota }+\mathit{Q}{L}^{\left(\mathit{i}\right)}$. To obtain a new output feedback gain matrix $K^{\left(\mathit{i}+1\right)}$, the linear matrix inequality optimization problem ${\mathcal{F}}_o^{{ }^{\prime }}$ from Eq (16(16) ${\mathcal{F}}_o^{{ }^{\prime }}:\{\begin{array}{c}\mathit{minimize}{\eta }_o^{{ }^{\prime }}\\ \mathit{subjectto}{X}_Q>0,X_R>0,{\eta }_o^{{ }^{\prime }}>0,\\ \mathit{andtheLMIsin}\left(17\right),\end{array}$(16) ) is required to be solved.

Upon iterating, an optimized value of ${\gamma }_{{\mathit{k}}^{\left(\mathit{i}\right)}}$ and the corresponding output feedback gain matrix $K^{\left(\mathit{i}\right)}$ are continuously obtained. Next, it will be explained that as the program runs, the value of ${\gamma }_{{\mathit{k}}^{\left(\mathit{i}\right)}}$ converges towards a lower bound. This provides a theoretical justification for the conditions under which this iteration can be terminated.

Theorem 1

If there’s a solution to the linear matrix inequality optimization problem ${\mathcal{F}}_o^{{ }^{\prime }}\left(,{\tilde{X}}_{\mathit{R}}^{\left(0\right)},{\tilde{Y}}_{\mathit{R}}^{\left(0\right)}\right)$, then the subsequent series of optimization problems ${\mathcal{F}}_o^{{ }^{\prime }}\left(,{\tilde{X}}_{\mathit{R}}^{\left(\mathit{i}\right)},{\tilde{Y}}_{\mathit{R}}^{\left(\mathit{i}\right)}\right)$, $\mathit{i}\ge 1$, would also have a solution. Moreover, the optimal $\mathit{\gamma }$ corresponding to each iteration would satisfy ${\gamma }_{{\mathit{k}}^{\left(\mathit{i}\right)}}\ge {\gamma }_{{\mathit{k}}^{\left(\mathit{i}+1\right)}}$ (Rubió-Massegú et al. 2020).

Proof. If an initial K is given, and solutions ${\tilde{X}}^{\left(0\right)}$ and ${\gamma }_{{\mathit{k}}^{\left(0\right)}}$ to the linear matrix inequality in Eq (13(13) $\left[\begin{array}{cc}\mathit{X}& \ast \\ C_z\mathit{X}+D_z\mathit{K}{C}_y\mathit{X}& {\eta }_o\mathit{I}\end{array}\right]>0$(13) ) are provided along with $\mathit{L}$ and $\mathit{R}$ in Eqs (22(22) $L^{\left(0\right)}=Q^{\iota }{\tilde{X}}^{\left(0\right)}{C}_y^T{\left(C_y{\tilde{X}}^{\left(0\right)}{C}_y^T\right)}^{-1}$(22) ) and (23(23) $R^{\left(0\right)}=C_y^{\iota }+\mathit{Q}{L}^{\left(0\right)}$(23) ), then optimization problem ${\mathcal{F}}_o^{{ }^{\prime }}$ would have solutions $\left({\tilde{X}}_{\mathit{Q}}^{\left(0\right)},{\tilde{X}}_{\mathit{R}}^{\left(0\right)},{\tilde{Y}}_{\mathit{R}}^{\left(0\right)},{\gamma }_{{\tilde{G}}_{\mathit{k}}}^{\left(0\right)}\right)$. Subsequently, $K^{\left(1\right)}$ can be obtained from Eq (18(18) $\tilde{K}={\tilde{Y}}_{\mathit{R}}{\left({\tilde{X}}_{\mathit{R}}\right)}^{-1}$(18) ), the optimization problem ${\mathcal{F}}_o$ would also have a solution ${\tilde{X}}^{\left(1\right)}$.

In Step i.a, if the optimization problem ${\mathcal{F}}_o$ can have solutions $\left({\tilde{X}}^{\left(\mathit{i}\right)},{\gamma }_{{\mathit{k}}^{\left(\mathit{i}\right)}}\right)$, we have ${\gamma }_{{\mathit{k}}^{\left(\mathit{i}\right)}}\le {\gamma }_{{\tilde{G}}_{\mathit{k}}}^{\left(\mathit{i}-1\right)}$. In Step i.b, if the optimization problem ${\mathcal{F}}_o^{{ }^{\prime }}$ has solutions $\left({\tilde{X}}_{\mathit{Q}}^{\left(\mathit{i}\right)},{\tilde{X}}_{\mathit{R}}^{\left(\mathit{i}\right)},{\tilde{Y}}_{\mathit{R}}^{\left(\mathit{i}\right)},{\gamma }_{{\tilde{G}}_{\mathit{k}}}^{\left(\mathit{i}\right)}\right)$, then also ${\gamma }_{{\mathit{k}}^{\left(\mathit{i}\right)}}\ge {\gamma }_{{\tilde{G}}_{\mathit{k}}}^{\left(\mathit{i}\right)}$. In Step i.a of the next iteration, we have ${\gamma }_{{\mathit{k}}^{\left(\mathit{i}+1\right)}}\le {\tilde{\eta }}_{o^{\left(\mathit{i}+1\right)}}$, resulting in ${\gamma }_{{\mathit{k}}^{\left(\mathit{i}+1\right)}}\le {\gamma }_{{\mathit{k}}^{\left(\mathit{i}\right)}}$, and the proof is complete.

Based on the findings of literature (Palacios-Quiñonero et al. 2017), the state feedback optimization problem ${\mathcal{F}}_s$ in Eq (4(4) ${\mathcal{F}}_s:\left\{\begin{array}{c}\mathit{minimize}\mathit{\eta }\\ \mathit{subject}\mathit{to}\mathit{X}>0,\mathit{\eta }>0,\\ \mathit{and}\mathit{the}\mathit{LMIs}\mathit{in}\left(5\right),\end{array}\right.$(4) ) can produce the value ${\gamma }_{{\tilde{G}}_{\mathit{s}}}$. If a feasible solution exists for ${\gamma }_{\tilde{K}}$ in the output feedback optimization problem ${\mathcal{F}}_o$ in Eq (12(12) ${\mathcal{F}}_o:\left\{\begin{array}{c}\mathit{minimize}{\eta }_o\\ \mathit{subject}\mathit{to}\mathit{X}>0,{\eta }_o>0,\\ \mathit{and}\mathit{the}\mathit{LMIs}\mathit{in}\left(13\right),\end{array}\right.$(12) ), and satisfies the condition ${\gamma }_{{\tilde{G}}_{\mathit{s}}}\le {\gamma }_{\tilde{K}}$, then combining it with Theorem 1, we find that the iterative output feedback ${\gamma }_{{\mathit{k}}^{\left(\mathit{i}\right)}}$ ensures that ${\gamma }_{{\tilde{G}}_{\mathit{s}}}\le {\gamma }_{{\mathit{k}}^{\left(\mathit{i}\right)}}$, implying that there is a lower bound on the value of ${\gamma }_{{\mathit{k}}^{\left(\mathit{i}\right)}}$.

In summary, the iterative output feedback strategy achieves an improved control effect by continuously optimizing the value of ${\gamma }_{{\mathit{k}}^{\left(\mathit{i}\right)}}$ through iterative computation towards its lower bound.

4. Numerical simulation and analysis

4.1. Building model

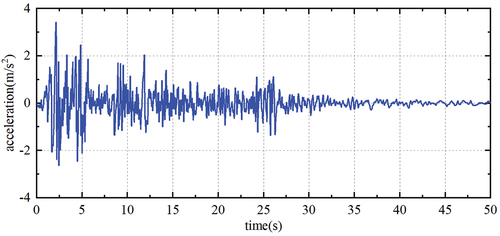
The 8-story building with $m_i=3.456\times {10}^5\mathit{kg}$，$k_i=3.404\times {10}^8\mathit{N}/\mathit{m}$，$c_i=1\times {10}^5\mathit{N}\cdot \mathit{s}/\mathit{m}$，$\left(\mathit{i}=1,2,\cdots ,8\right)$ in reference (Johansen 2008) is taken as an example. $m_i$, $k_i$, $c_i$ are the parameters of mass, stiffness, and damping for each story, respectively; The El Centro 1940 far-filed record is selected, the peak is 3.417$\mathit{m}/s^2$, the duration is 50 s, and the sampling step is 0.02 s. As shown in Figure 1.

Figure 1. El Centro 1940 ground-acceleration seismic record.

The building motion under seismic excitation can be formulated as

(24) $\mathit{M}\stackrel{\left(t\right)}{\mathit{q}}+C_d\dot{q}\left(\mathit{t}\right)+K_s\mathit{q}\left(\mathit{t}\right)=B_u\mathit{u}\left(\mathit{t}\right)+D_s\mathit{\omega }\left(\mathit{t}\right)$(24)

where, $\mathit{M}$, $C_d$, $K_s$ are the matrices of mass, stiffness, and damping, respectively; $\mathit{q}\left(\mathit{t}\right)$，$\dot{q}\left(\mathit{t}\right)$，$\ddot{q}\left(\mathit{t}\right)$ represent the vectors of displacement, velocity, and acceleration for each story, respectively, $B_u$ indicates the vector of control location, $\mathit{u}\left(\mathit{t}\right)$ denotes the control force matrix, $D_s$ is the matrix of external disturbance input, $\mathit{\omega }\left(\mathit{t}\right)$ is the vector of external excitation.

The matrices of mass, stiffness, and damping have the following forms:

(25) $\mathit{M}=\mathit{diag}\left\{m_1,m_2,\cdots \cdots ,m_8\right\}$(25)

(26) $K_s=\left[\begin{array}{ccccccc}{k}_1+k_2& -k_2& 0& \dots & 0& 0& 0\\ -k_2& k_2+k_3& -k_3& \dots & 0& 0& 0\\ 0& -k_3& k_3+k_4& \dots & 0& 0& 0\\ 0& 0& -k_4& \ddots & 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& \dots & -k_7& k_7+k_8& -k_8\\ 0& 0& 0& \dots & 0& -k_8& k_8\end{array}\right]$(26)

the damping matrix $C_d$ is obtained by substituting the stiffness parameters in $K_s$ with their corresponding damping parameters.

Using the inter-story actuation scheme, the form of $B_u$ (Palacios-Quiñonero et al. 2019) is

(27) $B_u=\left[\begin{array}{cccccccc}1& -1& 0& 0& 0& 0& 0& 0\\ 0& 1& -1& 0& 0& 0& 0& 0\\ 0& 0& 1& -1& 0& 0& 0& 0\\ 0& 0& 0& 1& -1& 0& 0& 0\\ 0& 0& 0& 0& 1& -1& 0& 0\\ 0& 0& 0& 0& 0& 1& -1& 0\\ 0& 0& 0& 0& 0& 0& 1& -1\\ 0& 0& 0& 0& 0& 0& 0& 1\end{array}\right]$(27)

the matrix of external disturbance input has the following form:

(28) $D_s=-\mathit{M}{\left[11111111\right]}^T$(28)

Considering the state vector,

(29) $x_1\left(\mathit{t}\right)={\left[q\left(t\right)\dot{q}\left(\mathit{t}\right)\right]}^{\mathit{T}}$(29)

by substituting it into Eq (24(24) $\mathit{M}\stackrel{\left(t\right)}{\mathit{q}}+C_d\dot{q}\left(\mathit{t}\right)+K_s\mathit{q}\left(\mathit{t}\right)=B_u\mathit{u}\left(\mathit{t}\right)+D_s\mathit{\omega }\left(\mathit{t}\right)$(24) ), the equation of motion for the structure can be transformed into the state-space model, which is given by:

(30) ${\dot{x}}_1\left(\mathit{t}\right)=A_1{x}_1\left(\mathit{t}\right)+B_1\mathit{u}\left(\mathit{t}\right)+E_1\mathit{\omega }\left(\mathit{t}\right)$(30)

where $A_1$, $B_1$, $E_1$ represent the matrices of state, control, and disturbance input, respectively, the specific forms are

$A_1=\left[\begin{array}{cc}{\left[0\right]}_{\left(8\times 8\right)}& I_8\\ -M^{-1}{K}_s& -M^{-1}{C}_d\end{array}\right],$

(31) $B_1=\left[\begin{array}{c}{\left[0\right]}_{\left(8\times 8\right)}\\ M^{-1}{B}_u\end{array}\right],E_1=\left[\begin{array}{c}{\left[0\right]}_{\left(8\times 1\right)}\\ -{\left[1\right]}_{\left(8\times 1\right)}\end{array}\right]$(31)

A new state vector $\mathit{x}\left(\mathit{t}\right)=\mathit{\phi }{x}_1\left(\mathit{t}\right)$ can be defined at this stage, which converts the displacements and velocities of $x_1\left(\mathit{t}\right)$ into the corresponding inter-story drifts and inter-story velocities. Here,

(32) $\mathit{\phi }=\left\{\begin{array}{c}{\phi }_{\mathit{i},\mathit{i}}=1\left(\mathit{i}=1,\cdots ,16\right)\\ {\phi }_{\mathit{i},\mathit{i}-1}=-1\left(\mathit{i}=2,\cdots ,8,10,\cdots ,16\right)\\ {\phi }_{\mathit{i},\mathit{j}}=0\mathit{else}\end{array}\right.$(32)

then the new state-space model is

(33) $\dot{x}\left(\mathit{t}\right)=\mathit{Ax}\left(\mathit{t}\right)+\mathit{Bu}\left(\mathit{t}\right)+\mathit{E\omega }\left(\mathit{t}\right)$(33)

where $\mathit{A}=\mathit{\phi }{A}_1{\phi }^{-1}$, $\mathit{B}=\mathit{\phi }{B}_1$, $\mathit{E}=\mathit{\phi }{E}_1$.

4.2. Design of the controllers

To solve the problem using a state feedback control strategy, the corresponding parameters of the controlled output $\mathit{z}\left(\mathit{t}\right)$ are chosen as follows:

(34) $C_z=\left[\begin{array}{cc}{I}_8& {\left[0\right]}_{8\times 8}\\ {\left[0\right]}_{8\times 8}& {\left[0\right]}_{8\times 8}\end{array}\right],D_z=\mathit{\alpha }\left[\begin{array}{c}{\left[0\right]}_{8\times 8}\\ I_8\end{array}\right]$(34)

The parameter $\mathit{\alpha }$ is adjustable and set to $\mathit{\alpha }={10}^{-7.55}$, it generally needs reasonable setting to obtain appropriate control effect. Solving the optimization problem ${\mathcal{F}}_s^{{ }^{\prime }}$ in Eq (6(6) ${\mathcal{F}}_s^{\prime }:\left\{\begin{array}{c}\mathit{minimize}\mathit{\eta }\\ \mathit{subject}\mathit{to}\mathit{X}>0,\mathit{\eta }>0,\\ \mathit{and}\mathit{the}\mathit{LMIs}\mathit{in}\left(7\right),\end{array}\right.$(6) ) results in the optimal value of $\mathit{\gamma }$, denoted as ${\gamma }_{\tilde{G}}=0.0753$, and the accompanying state feedback gain matrix is $\tilde{G}$.

When employing the static output feedback control strategy for solving, the feedback information corresponds to the velocity information, and the matrix $C_y$ becomes:

(35) $C_y=\left[{\left[0\right]}_{8\times 8}{I}_8\right]$(35)

In this case, the measured output $\mathit{y}\left(\mathit{t}\right)$ only contains the inter-story velocity of the structure. In the output feedback linear matrix inequality optimization problem ${\mathcal{F}}_o^{{ }^{\prime }}$ based on the state feedback results, the parameters of the controlled output $\mathit{z}\left(\mathit{t}\right)$ are chosen using the same state feedback control strategy. By solving Eq (16(16) ${\mathcal{F}}_o^{{ }^{\prime }}:\{\begin{array}{c}\mathit{minimize}{\eta }_o^{{ }^{\prime }}\\ \mathit{subjectto}{X}_Q>0,X_R>0,{\eta }_o^{{ }^{\prime }}>0,\\ \mathit{andtheLMIsin}\left(17\right),\end{array}$(16) ), the optimal value of $\mathit{\gamma }$, denoted as ${\gamma }_{\tilde{k}}=0.0754$, is obtained, and the corresponding output feedback gain matrix $\tilde{K}$ is also obtained.

The iterative output feedback control strategy is utilized to tackle the problem. The selection of $C_y$ is identical to the static output feedback strategy, while the selection of the controlled output parameters is the same as the state feedback control strategy. Once iteration is completed, the optimal values of $\mathit{\gamma }$ are displayed in Table 1,

Table 1. $\mathit{\gamma }$for each iteration step.

step i	0	1	2	3	4	5
${\gamma }_{{\mathit{k}}^{\left(\mathit{i}\right)}}$	0.5949	0.0759	0.0757	0.0756	0.0755	0.0755

According to the table content, the calculation is terminated when the iteration reaches the lower bound, and the corresponding iterative output feedback gain matrix ${\tilde{K}}_{\mathit{o}}$ is obtained.

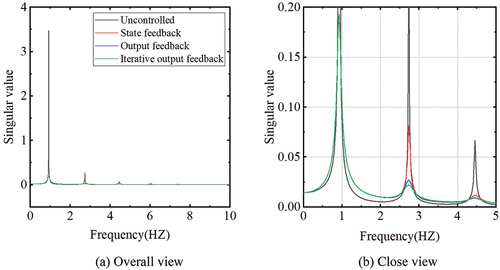
The frequency response plots for the aforementioned three methods are computed and displayed in Figure 2.

Figure 2. Maximum singular values of the FRFs. (a) overall view. (b) close view.

When compared to the uncontrolled building, all three control methods significantly produce a remarkable reduction of the main resonant peak, and exhibit superior attenuation effects on the first-order intrinsic frequency. The local plot of the frequency response shows that for the second-order intrinsic frequency position, the iterative output feedback control strategy manifests the best attenuation effect, followed by the output feedback control strategy, with the state feedback control strategy exhibiting slightly inferior performance.

4.3. Seismic response analysis

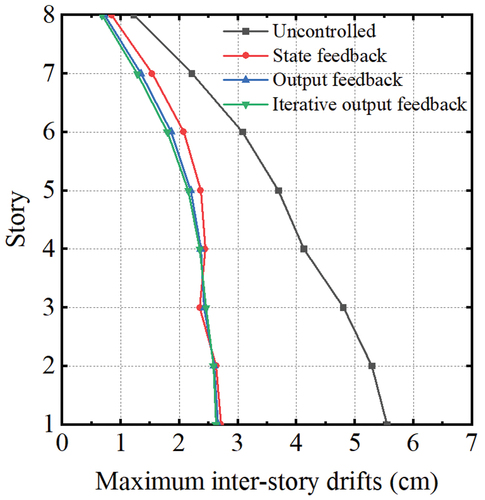
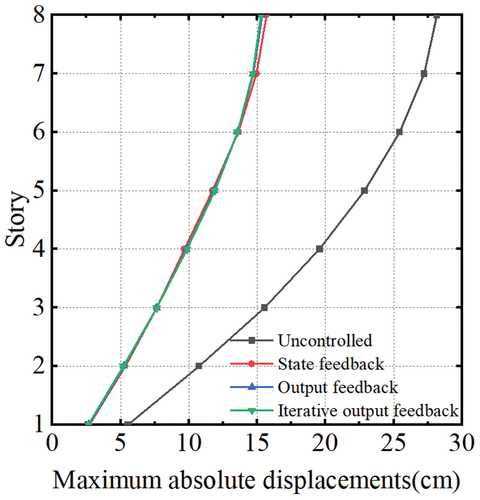
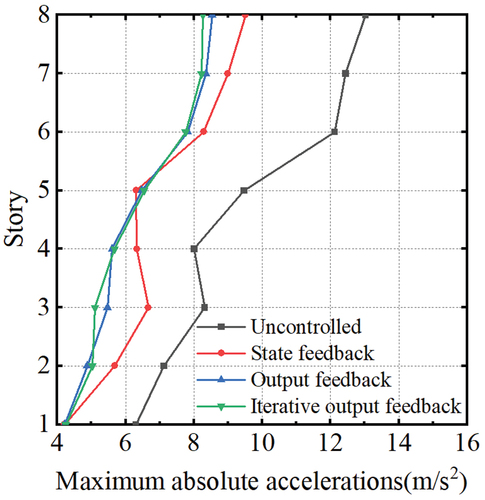
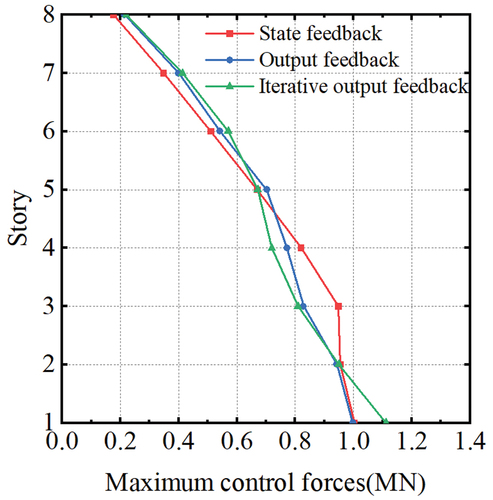
To substantiate the proposed iterative output feedback control strategy’s efficacy, the dynamic responses of the three control approaches are evaluated, and their results are compared. The maximum inter-story drifts, maximum absolute displacements, maximum absolute accelerations, and maximum control forces of the building are presented in Figures 3–6, respectively.

Figure 3. Maximum inter-story drifts.

Figure 4. Maximum absolute displacements.

Figure 5. Maximum absolute accelerations.

Figure 6. Maximum control forces.

The average control rate is calculated by

(36) $\frac{{\sum }_1^n{X_u}_{\mathit{i}}-{\sum }_1^n{X_c}_{\mathit{i}}}{{\sum }_1^n{X_u}_{\mathit{i}}}\times 100\mathrm{\%}$(36)

where ${X_u}_{\mathit{i}}$ and ${X_c}_{\mathit{i}}$ are the maximum response of each layer with and without control devices, respectively. Table 2 records some of the seismic dynamic response results, with cases 1, 2, 3, and 4 representing the four strategies: no control, state feedback, output feedback, and iterative output feedback, respectively.

Table 2. Partial record of seismic dynamic response results.

Stories	Inter-story drifts(cm)				Absolute accelerations(m/s^2)
	Case1	Case2	Case3	Case4	Case1	Case2	Case3	Case4
1	5.55	2.71	2.66	2.63	6.30	4.21	4.22	4.25
2	5.29	2.63	2.59	2.58	7.12	5.68	4.88	5.03
3	4.80	2.35	2.43	2.46	8.32	6.67	5.47	5.11
4	4.13	2.44	2.36	2.35	8.01	6.33	5.61	5.68
5	3.70	2.37	2.20	2.16	9.47	6.31	6.48	6.54
6	3.08	2.08	1.86	1.79	12.12	8.29	7.83	7.76
7	2.22	1.53	1.35	1.28	12.45	9.00	8.35	8.22
8	1.22	0.84	0.72	0.68	13.02	9.51	8.54	8.26

Figures 3 and 4 indicate that all three control methods produced favorable control outcomes. The inter-story drift’s average control rates for state feedback, output feedback, and iterative output feedback are 43.5%, 46.1%, and 46.9%, respectively, while the average control rates of absolute displacement are 47.5%, 47.8%, and 47.9%, respectively.

Figure 5 illustrates that all three control strategies showcase impressive control effects. The average acceleration control rates for state feedback, output feedback, and iterative output feedback are 27.1%, 33.1%, and 33.8%, respectively.

Figure 6 demonstrates that the control forces of all three control methods are virtually equivalent, implying that the proposed iterative output feedback control strategy exhibits superior performance to that of the state feedback and output feedback control approaches when matched by comparable control forces.

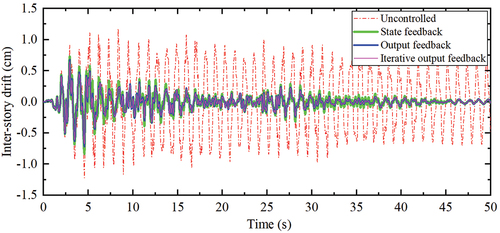
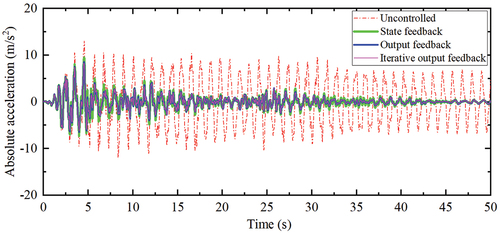
The time-history curves of the inter-story drift and absolute acceleration of the top layer of the building are presented in Figures 7 and 8, respectively.

Figure 7. The time-history curves of the inter-story drift in the top layer.

Figure 8. The time-history curves of the absolute acceleration in the top layer.

The effectiveness of all control strategies in mitigating inter-story drifts and accelerations at the top of the structure during the seismic excitation’s continuous action time is evident in Figures 7 and 8. As time progresses, the response diminishes and eventually stabilizes. Both the output feedback and iterative output feedback energy-to-peak control strategies are significantly superior to state feedback control. Furthermore, the control effect of the iterative output feedback energy-to-peak control strategy can surpass that of the energy-to-peak output feedback strategy.

Based on reference (Ohtori et al. 2004), the subsequent two evaluation indicators are presented in the following manner.

(37) $J_1=\mathit{max}\left\{\frac{\underset{\mathit{t},\mathit{i}}{max}\frac{\left|d_i\left(\mathit{t}\right)\right|}{h_i}}{{\delta }^{\mathit{max}}}\right\}$(37)

(38) $J_2=\mathit{max}\underset{\mathit{t},\mathit{i}}{\mathit{max}}\mathit{xai}\left(\mathit{t}\right)\mathit{xamax}$(38)

Where $d_i\left(\mathit{t}\right)$ is the inter-story drift of the above ground level over the time history of each earthquake, $h_i$ is the height of each story, ${\delta }^{\mathit{max}}$ is the maximum inter-story drift ratio of the uncontrolled structure, i.e.， ${\delta }^{\mathit{max}}=\underset{\mathit{t},\mathit{i}}{max}\left|d_i\left(\mathit{t}\right)/h_i\right|$; $\mathit{x}\mathit{ai}\left(\mathit{t}\right)$ is the absolute acceleration of each story with control devices, $\mathit{x}{a}^{\mathit{max}}$ is the maximum absolute acceleration of the uncontrolled structure. Table 3 contains the recorded results of the evaluation indicators for the three strategies.

Table 3. Results of evaluation indicators for different control strategies.

	State feedback	Output feedback	Iterative output feedback
$J_1$	0.488	0.479	0.473
$J_2$	0.731	0.655	0.635

As demonstrated by the data in Table 3, the iterative output feedback strategy exhibits smaller evaluation indicators compared to the other two strategies, with clear superiority of control.

5. Conclusion

An iterative output feedback energy-to-peak control method is introduced in this paper by merging the iterative output feedback strategy and energy-to-peak control algorithm. A numerical simulation study on the response of an 8-story building structure to earthquake excitation is executed, and the resulting conclusions are as follows:

1. The iterative output feedback energy-to-peak control method is simple and effective. By iterating the linear matrix inequality procedure to obtain a suboptimal solution for the control problem, the iterative output feedback energy-to-peak control method overcomes the numerical solution difficulty in the bilinear matrix inequality constraint problem. After an uncomplicated initialization and numerical iteration process, the method achieves an improved static output feedback gain matrix.

2. The iterative output feedback energy-to-peak control method significantly produce a remarkable reduction of the main resonant peak. The frequency response function results reveal that the state feedback, output feedback, and iterative output feedback energy-to-peak control strategies demonstrate superior effectiveness in reducing the first-order intrinsic frequency peak of the structure. Additionally, the iterative output feedback energy-to-peak control approach is more effective than the other two methods in suppressing the second-order intrinsic frequency peak of the structural response.

3. When the control forces are in proximity, the iterative output feedback energy-to-peak control method surpasses the state feedback and output feedback energy peak control methods in terms of vibration mitigation.

4. The iterative output feedback energy-to-peak control method manages to steer clear of the controller’s over-reliance on external feedback information, thereby enabling the effective control of the system with only partial access to external observations. It is evidently envisaged that this method has the potential for bridges and floors applications, an in-depth study can be conducted in response to the relevant literature (Wang et al. 2020, 2021, 2023).

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This study was financially supported by BIM Engineering Center of Anhui Province (No. AHBIM2021ZR02) and Natural Science Research Project of Higher Education Institutions in Anhui Province (NO. KJ2019A0748).

Notes on contributors

Qinghu Xu

Qinghu Xu, Ph.D., School of Civil Engineering, Anhui Jianzhu University, Hefei, China

Xiang Ruan

Xiang Ruan, Master Candidate, School of Civil Engineering, Anhui Jianzhu University, Hefei, China

Jianhao Wei

Jianhao Wei, Master Candidate, School of Civil Engineering, Anhui Jianzhu University, Hefei, China