Adjoint-based sensitivity analysis of quantities of interest of complex combustion models

Abstract

An adjoint-based approach for the sensitivity analysis of complex reaction mechanisms is presented. It builds purely on the evaluation of the governing equations. No adjoint equations have to be derived explicitly. Instead, the required adjoint operator is constructed numerically. The approach can be utilised for various kinetic models and in existing codes with minimal implementation effort. All dependencies on the state and on model parameters are fully evaluated without simplifications. Sensitivities are calculated more efficiently and more robustly compared with the often-used brute-force method. The approach is demonstrated for a homogeneous (zero-dimensional) reactor with different complex reaction mechanisms including several reaction types.

Keywords:

• complex reaction kinetics
• sensitivity analysis
• adjoint approach

1. Introduction

The methodology of sensitivity analysis [1,2] is intended to enhance the understanding of scientific and industrial systems of interest by emphasising the impact of inputs on outputs. In general, the system sensitivities on design parameters are determined by quantifying the changes of system outcomes for certain perturbation of input parameters experimentally or numerically. The obtained sensitivity coefficients, which represent the relationship between input and output variables of a system, provide on one hand essential information for model construction, modification, and simplification and, on the other hand, are of major relevance for uncertainty analyses of numerical simulations.

In the field of combustion chemistry, the sensitivity analysis is a standard approach to investigate the influence of chemical species and elementary reactions in kinetic models on the combustion quantities of interest (QoIs), such as ignition delay times and exhaust gas compositions. Detailed reviews can be found in [2–6]. The information gained from the sensitivity analyses is very useful for studies and purposes across all research areas of reaction kinetics [7–11]. First and most importantly, the sensitivity analysis identifies the important reaction pathways during the fuel combustion process, as it is designed. This provides researchers deep insights into the complex fuel combustion chemistry [7,8,12], leading to improved control of combustion processes. Second, in the case of mechanism modification and optimisation with large numbers of elementary reactions, preliminary sensitivity analyses can ease the calibration stage by only focusing on the most sensitive reactions [8]. While detailed mechanisms consist often of more than a thousand reactions, only a few reactions may need precise theoretical calculations or experimental measurements of their rate coefficients due to their dominance. Third, concerning the computational cost, reduced chemical mechanisms are always required for computational fluid dynamic simulations coupled with detailed combustion chemistry. Based on the results from sensitivity analyses, reduced mechanisms can be derived by removing insensitive species and reactions directly [9,13]. For all of these purposes, very accurate sensitivity coefficients are desirable. One possible approach to compute sensitivities is the very time-consuming brute-force method. Within the method, the rate coefficients of elementary reactions are perturbed successively and QoIs are determined as the forward solution using the perturbed model. The calculated finite differences of QoIs are then referred to as the sensitivity. Obviously, the computational effort of this brute-force approach is proportional to the number of reactions in the chemical mechanisms and can become very large for detailed chemical mechanisms.

A common alternative to the brute-force method for obtaining first-order local sensitivity coefficients is the decoupled-direct method [14,15]. Therein, differential equations for the sensitivities are derived from the model equations and solved decoupled from the governing system. The method is time-efficient and accurate. Several combustion codes make use of it. However, the method is not directly applicable for the calculation of sensitivities of derived quantities, such as ignition delay times.

Another alternative is Green's function method proposed by Rabitz and co-authors [4,16–18]. It allows to calculate efficiently the sensitivities of the governing system variables with respect to multiple parameters by solving a set of $n^2$ ordinary differential equations (ODEs), where n is the dimension of the system state. The set can be solved efficiently using the corresponding dual (adjoint) equations [19].

In contrast to Green's function method, here the proposed adjoint-based approach is restricted to calculating the sensitivity of one selected QoI, thereby reducing the number of ODEs to be solved to n.

The adjoint approach is an established tool also in other areas of engineering. For example, in fluid mechanics, the influence of the geometry on lift and drag of an aerofoil, as a QoI, is commonly analysed by the adjoint approach [20]. The adjoint method was applied to several reactive systems for different applications such as optimisation [21], uncertainty quantification [22,23], data assimilation [24], and sensitivity analysis [25].

Adjoint-based sensitivity analysis is also used by the package KPP [26,27], which is freely available and can be employed to automatically generate adjoint operators based on pre-defined reaction laws. In general it is found that the adjoint approach provides a substantial speed-up in comparison to the brute-force method, while the calculated sensitivities closely match those of the other methods. However, the describing system is usually simplified in order to derive the adjoint, as this can be cumbersome for complex rate laws. For example, the properties, whose sensitivities are of marginal interest, such as specific heats and the transport properties of chemical species, are often assumed to be constant for simplicity. This limits the broad application of the adjoint-based method and motivates further investigations. An adjoint method which can be applied easily and universally for all governing equations is of high interest.

In the present study, the goal is to develop an appropriate adjoint-based framework for sensitivity analyses of complex QoIs like ignition delay time in spatially homogeneous, unsteady systems considering dependencies on the system state and on model parameters without simplifications. In contrast to the work of Braman et al. [25] and the KPP-package, an adjoint method is applied, which makes use of a numerical operator reconstruction. This strongly simplifies the methodological application efforts by avoiding the analytical formulation of adjoint equations and allows the treatment of user-defined reaction laws. The method is demonstrated by calculating the sensitivities of ignition delay times for the homogeneous auto-ignition of hydrogen/air and methane/air mixtures. For the accuracy assessment, the sensitivities obtained using the adjoint-based method are compared to those from the brute-force method. In addition, the reduction of computational costs achieved by using the adjoint-based approach is quantified.

The presentation of this paper is organised as follows: first, the governing equations are described, followed by details of the employed reaction mechanisms. Then, the adjoint method is introduced for the considered system. Subsequently, the results of the adjoint-based sensitivity analysis are presented and discussed in detail.

2. Theory

In the following, the governing equations as well as the chemical kinetics used in the sensitivity analysis are briefly presented.

2.1. Governing equations

The model of a zero-dimensional (0D), homogeneous, constant volume reactor is used. It is described by the set of equations (1a) $\frac{\mathrm{\partial }{Y}_k}{\mathrm{\partial }t}=\frac{1}{\varrho }{\dot{\omega }}_k,$(1a) (1b) $\frac{\mathrm{\partial }T}{\mathrm{\partial }t}=\frac{1}{\varrho c_v}{\dot{\omega }}_T^{″}.$(1b) Therein, ϱ denotes the density, $Y_k$ the mass fraction of species $k=[1,\dots ,K]$, T the temperature, and $c_v$ the specific heat at constant volume. The heat release ${\dot{\omega }}_T^{″}$ is defined as (2) ${\dot{\omega }}_T^{″}=-\sum _{k=1}^K{e}_k{\dot{\omega }}_k$(2) with $e_k$ as specific energy (internal + chemical). The chemical production rate ${\dot{\omega }}_k$ of species k is defined as sum over all M reactions (3) ${\dot{\omega }}_k=\sum _{j=1}^M{\dot{\omega }}_{kj}.$(3) The reaction-based chemical production rates are ${\dot{\omega }}_{kj}={\mathcal{Q}}_j{W}_k{\nu }_{kj}$ with $W_k$ as molecular weight and ${\nu }_{kj}={\nu }_{kj}^{″}-{\nu }_{kj}^{\prime }$ as difference between molar stoichiometric coefficients of products and reactants of species k in reaction j. The reaction rates ${\mathcal{Q}}_j$ are defined by (4) ${\mathcal{Q}}_j=k_{\mathrm{forward},j}\prod _{k=1}^K{\left[X_k\right]}^{{\nu }_{kj}^{\prime }}-k_{\mathrm{reverse},j}\prod _{k=1}^K{\left[X_k\right]}^{{\nu }_{kj}^{″}},$(4) with $k_{\mathrm{forward},j}$ and $k_{\mathrm{reverse},j}$ as forward and reverse rate coefficients of reaction j, and $\left[X_k\right]$ being the molar concentration of species k. The set of equations is closed with the ideal gas law $p=\varrho \left(R/W\right)T$ with R as universal gas constant and W as mixture averaged molecular weight. The temperature dependence of the species-specific heats is expressed by means of NASA polynomials [28].

2.2. Rate coefficients

The rate coefficients $k_{\mathrm{forward},j}$ are modelled following Arrhenius temperature dependence. For reactions which are defined as reversible, the reverse rates $k_{\mathrm{reverse},j}$ are calculated from the forward rates and the equilibrium constants. Otherwise, $k_{\mathrm{reverse},j}$ is chosen to be zero. Also additional reaction types, such as three-body and unimolecular/recombination fall-off reactions, are considered. Lindemann and Troe forms are used to express the rate constants of pressure-dependent fall-off reactions.

2.3. Reaction mechanisms

All required coefficients are provided by reaction schemes taken from the literature. In this study, two different schemes are considered in detail.

2.3.1. h2_v1b mechanism

The first scheme under consideration is the hydrogen oxidation mechanism described by Ó Conaire et al. [29]. It includes 40 reactions among 10 species consisting of 5 elements, i.e. O, H, C, N, and Ar.

2.3.2. GRI mechanism

The second examined scheme is the well-known gri3.0 [30] reaction scheme. The model includes 325 reactions and 53 species consisting of the same elements as the h2_v1b mechanism.

This mechanism serves just as an example here and the following adjoint-based sensitivity method is independent of this specific choice.

2.4. Numerical implementation – governing equations

The above equations are implemented in a MatLab framework. For the temporal discretisation, the solver ode15s is employed, providing the solution in time by means of discrete time steps. However, also other time integration schemes are applicable. A relative error tolerance of ${10}^{-13}$, which applies to all components of the solution vector, is used. It is enforced that all components of the solution vector of governing system (1) are non-negative.

The implementation is verified by means of a comparison with Cantera [31] and FlameMaster [32]. For the verification, also constant pressure reactors were examined, see [33] for more details.

Details on the sensitivity calculation procedure are given in Section 3.4.

3. Adjoint approach

The adjoint plays a fundamental role in numerous areas of mathematics, such as optimisation, data assimilation, active and passive control, model reduction, and sensitivity analysis. It can be found under different names, e.g. dual variable or Green's function. For an extensive review, the reader is referred to [20,34].

In general, adjoint equations can be derived in different ways, namely by the continuous or the discrete approach. Also, automatic differentiation techniques are used to derive adjoint codes from existing numerical implementations. Despite having different discretisations, the approaches are consistent and applicable. Each approach has its own advantages, see [20] for a discussion.

In the following, the discrete and the continuous derivation are discussed. First, the adjoint approach is introduced in a discrete manner for the sake of simplicity, analogous to [24]. Subsequently, the adjoint equations used for the sensitivity analysis of complex reaction kinetics in the context of system (1) are derived in a continuous manner. The required operator is determined by means of an operator reconstruction.

3.1. Adjoint-based sensitivity

For the introduction of the adjoint approach, a matrix-vector notation is used. The vector space q is the full solution of the governing system (5) $\mathcal{B}(q,\alpha )=0$(5) in time. The dependency on the set of parameters α implies an implicit dependence of the system state $q=q\left(\alpha \right)$.

The corresponding adjoint equation originates from the so-called scalar-valued objective function J (6) $J=J\left(q\right(\alpha \left)\right),$(6) which can encode a design goal in terms of optimisation [21], a target state for data assimilation [24,35], or a QoI for sensitivity analysis.

For the latter, it is defined as the squared norm of the difference between the system state q and a modified state $q^{\left(\mathrm{mod}\right)}$ (see Section 4 for a detailed discussion): (7) $J=\frac{1}{2}{\left(q-q^{\left(\mathrm{mod}\right)}\right)}^{\mathrm{T}}\left(q-q^{\left(\mathrm{mod}\right)}\right)=\frac{1}{2}{\left|q-q^{\left(\mathrm{mod}\right)}\right|}^2.$(7)

If the objective function is non-linear, either due to a non-linear governing system operator or a direct non-linear dependence of J on q, a linearised formulation is needed. The linearisation of J around the base state $q=q_0+\delta q$ leads to (8) $\delta J=\underset{=g^{\mathrm{T}}}{\underbrace{{\left(q-q^{\left(\mathrm{mod}\right)}\right)}^{\mathrm{T}}}}\delta q.$(8) Therein, the change of state $\delta q$ is the solution of (5(5) $\mathcal{B}(q,\alpha )=0$(5) ) linearised with respect to q and α: (9) $\underset{=B}{\underbrace{\frac{\mathrm{\partial }\mathcal{B}}{\mathrm{\partial }q}}}\delta q+\underset{=f}{\underbrace{\frac{\mathrm{\partial }\mathcal{B}}{\mathrm{\partial }\alpha }}}\delta \alpha =0.$(9)

To derive the adjoint, under the constraint that (5(5) $\mathcal{B}(q,\alpha )=0$(5) ) needs to be satisfied, (9(9) $\underset{=B}{\underbrace{\frac{\mathrm{\partial }\mathcal{B}}{\mathrm{\partial }q}}}\delta q+\underset{=f}{\underbrace{\frac{\mathrm{\partial }\mathcal{B}}{\mathrm{\partial }\alpha }}}\delta \alpha =0.$(9) ) is added to (8(8) $\delta J=\underset{=g^{\mathrm{T}}}{\underbrace{{\left(q-q^{\left(\mathrm{mod}\right)}\right)}^{\mathrm{T}}}}\delta q.$(8) ) in a Lagrangian manner using a multiplier $q^{\ast }$, which will become the adjoint variable. This leads to (10) $\delta J=g^{\mathrm{T}}\delta q-{q^{\ast }}^{\mathrm{T}}\underset{=0}{\underbrace{\left(B\delta q+f\delta \alpha \right)}}$(10) (11) $=\delta q^{\mathrm{T}}\left(g-B^{\mathrm{T}}{q}^{\ast }\right)-{q^{\ast }}^{\mathrm{T}}f\delta \alpha .$(11) Since, according to (10(10) $\delta J=g^{\mathrm{T}}\delta q-{q^{\ast }}^{\mathrm{T}}\underset{=0}{\underbrace{\left(B\delta q+f\delta \alpha \right)}}$(10) ), where the term in parentheses is equal to zero, the value of $q^{\ast \mathrm{T}}$ is arbitrary, one can determine its value such that the change in the objective function becomes independent of $\delta q$ and only depends on the change of the parameters $\delta \alpha$. This allows to compute the sensitivity $\delta J/\delta \alpha$.

Hence, by demanding that the adjoint state $q^{\ast }$ is the solution of the so-called adjoint equation (12) $g-B^{\mathrm{T}}{q}^{\ast }=0,$(12) we obtain (13) $\delta J=-{q^{\ast }}^{\mathrm{T}}f\delta \alpha ,$(13) which is independent of $\delta q$.

The expression ${q^{\ast }}^{\mathrm{T}}f$ can be interpreted as the sensitivity of the objective function with respect to parameters α, since (14) $\frac{\delta J}{\delta \alpha }=-{q^{\ast }}^{\mathrm{T}}f.$(14)

3.2. Adjoint equations of the governing system

Following the previous considerations, the set of equations (1), rewritten as (15) $\mathcal{B}={\mathrm{\partial }}_{t}q-\mathrm{rhs}(q,\alpha )=0,$(15) with the right-hand side (rhs) containing the governing rate laws, has to be linearised with respect to the actual state $q=[Y_1,\dots ,Y_K,T]$, which is defined as a function of time here, and the considered parameters α: (16) $\frac{\mathrm{\partial }\mathcal{B}}{\mathrm{\partial }q}\delta q+\frac{\mathrm{\partial }\mathcal{B}}{\mathrm{\partial }\alpha }\delta \alpha ={\mathrm{\partial }}_t\delta q-\underset{=A^{\mathrm{lin}}}{\underbrace{\frac{\mathrm{\partial }\mathrm{rhs}(q,\alpha )}{\mathrm{\partial }q}}}\delta q-\underset{=f}{\underbrace{\frac{\mathrm{\partial }\mathrm{rhs}(q,\alpha )}{\mathrm{\partial }\alpha }}}\delta \alpha =0.$(16)

To derive the adjoint equations, the linearised equations are added to the linearisation of the objective function (17) $J=\frac{1}{2\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{\left|q-q^{\left(\mathrm{mod}\right)}\right|}^2\mathrm{d}t,$(17) which is defined as the integral difference between the actual state q and $q^{\left(\mathrm{mod}\right)}$ over the computational time span $\tau =t_{\mathrm{end}}-t_0$. A suitable definition of $q^{\left(\mathrm{mod}\right)}$ for the intended sensitivity analysis is discussed in Section 4. Using a Lagrange multiplier $q^{\ast }=[Y_1^{\ast },\dots ,Y_K^{\ast },T^{\ast }{]}^{\mathrm{T}}$ (18) $\delta J=\frac{1}{\tau }{\int }_{t_0}^{t_{\mathrm{end}}}\underset{=g^{\mathrm{T}}}{\underbrace{{\left(q-q^{\left(\mathrm{mod}\right)}\right)}^{\mathrm{T}}}}\delta q\mathrm{d}t-\frac{1}{\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{q^{\ast }}^{\mathrm{T}}\underset{=0}{\underbrace{\left({\mathrm{\partial }}_t\delta q-A^{\mathrm{lin}}\delta q-f\delta \alpha \right)}}\mathrm{d}t$(18) is obtained. The resulting equations (18(18) $\delta J=\frac{1}{\tau }{\int }_{t_0}^{t_{\mathrm{end}}}\underset{=g^{\mathrm{T}}}{\underbrace{{\left(q-q^{\left(\mathrm{mod}\right)}\right)}^{\mathrm{T}}}}\delta q\mathrm{d}t-\frac{1}{\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{q^{\ast }}^{\mathrm{T}}\underset{=0}{\underbrace{\left({\mathrm{\partial }}_t\delta q-A^{\mathrm{lin}}\delta q-f\delta \alpha \right)}}\mathrm{d}t$(18) ) are rearranged by means of integration by parts of the term (19) ${\int }_{t_0}^{t_{\mathrm{end}}}{q^{\ast }}^{\mathrm{T}}{\mathrm{\partial }}_t\delta q\mathrm{d}t={\left[{\delta q}^{\mathrm{T}}{q}^{\ast }\right]}_{t=t_0}^{t=t_{\mathrm{end}}}-{\int }_{t_0}^{t_{\mathrm{end}}}\delta q^{\mathrm{T}}{\mathrm{\partial }}_t{q}^{\ast }\mathrm{d}t$(19) and transpose, in particular of the operator $A^{\mathrm{lin}}$: (20) $\tau \delta J={\int }_{t_0}^{t_{\mathrm{end}}}\delta q^{\mathrm{T}}\left(g+{\mathrm{\partial }}_t{q}^{\ast }+A^{{\mathrm{lin}}^{\mathrm{T}}}{q}^{\ast }\right)\mathrm{d}t-{\left[{\delta q}^{\mathrm{T}}{q}^{\ast }\right]}_{t=t_0}^{t=t_{\mathrm{end}}}+{\int }_{t_0}^{t_{\mathrm{end}}}{q^{\ast }}^{\mathrm{T}}f\delta \alpha \mathrm{d}t.$(20) The dependency of $\delta q$ is removed by demanding (21) $g+{\mathrm{\partial }}_t{q}^{\ast }+A^{{\mathrm{lin}}^{\mathrm{T}}}{q}^{\ast }=0,$(21) resulting in the adjoint equation (22) ${\mathrm{\partial }}_t{q}^{\ast }=-A^{{\mathrm{lin}}^{\mathrm{T}}}{q}^{\ast }-g.$(22) As the temporal boundary term also depends on $\delta q$, it needs to vanish as well: (23) $-{\left[{\delta q}^{\mathrm{T}}{q}^{\ast }\right]}_{t=t_0}^{t=t_{\mathrm{end}}}=-{\left[{\delta q}^{\mathrm{T}}{q}^{\ast }\right]}_{t=t_{\mathrm{end}}}+{\left[{\delta q}^{\mathrm{T}}{q}^{\ast }\right]}_{t=t_0}=0.$(23) The right term vanishes as the initial condition for q is fixed and $\delta q\left(t_0\right)=0$ holds. To cancel the remaining term, the adjoint state is chosen as $q^{\ast }\left(t_{\mathrm{end}}\right)=0$, as the change of state $\delta q\left(t_{\mathrm{end}}\right)$ is arbitrary. Thus, the temporal (initial) condition of the adjoint system is given at final time. In general, the adjoint system is well-posed only if the adjoint initial state is defined at the end of the computational time and the system is integrated backwards (see~[20]).

The adjoint-based sensitivity results in (24) $\frac{\delta J}{\delta \alpha }=\frac{1}{\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{q^{\ast }}^{\mathrm{T}}f\mathrm{d}t,$(24) which is to be evaluated by integrating over the time-dependent expression ${q^{\ast }}^{\mathrm{T}}f$.

3.3. Adjoint operator

In particular for complex reaction kinetics, the analytic derivation as well as the numerical implementation of the operator ${A^{\mathrm{lin}}}^{\mathrm{T}}$ can be challenging. For example, the temperature dependence of the material parameters was excluded in the adjoint analysis of [21,25].

To circumvent the problem, we propose an easy on-the-fly construction of $A^{\mathrm{lin}}$ by means of a Fréchet derivative (25) $A^{\mathrm{lin}}\cdot e_i\approx \frac{\mathrm{rhs}\left(q_0+ϵe_i,{\alpha }_0\right)-\mathrm{rhs}\left(q_0,{\alpha }_0\right)}{ϵ}.$(25) Therein, $e_i$ is the unit vector with the same dimension as q with one entry in i. For the considered framework, the number of variables K+1 is sufficiently small, so that the full matrix $A^{\mathrm{lin}}$ can be easily constructed. After the construction of $A^{\mathrm{lin}}$, the desired adjoint operator is derived by a simple transpose. It is computed for each time step and kept constant during the time-wise integration of (22(22) ${\mathrm{\partial }}_t{q}^{\ast }=-A^{{\mathrm{lin}}^{\mathrm{T}}}{q}^{\ast }-g.$(22) ). The construction demands K+2 (all degrees of freedom plus one for the linearisation) calls of the rhs.

The expression f, needed for the calculation of the sensitivities from $q^{\ast }$, can be derived in the same manner: (26) $f\cdot e_i\approx \frac{\mathrm{rhs}\left(q_0,{\alpha }_0+ϵe_i\right)-\mathrm{rhs}\left(q_0,{\alpha }_0\right)}{ϵ}.$(26) Therein, the unit vector has the same dimension as the parameter vector α.

The choice of ε influences the approximation quality of $A^{\mathrm{lin}}$ and f. Here, we chose the parameter ε according to (27) $ϵ=c\sqrt{{ϵ}_{\mathrm{machine}}}$(27) with c=T for the temperature and c=1 for the species components, as it provides a good trade-off between truncation and round-off errors. For f, the considered parameter values are used for the scaling c.

The proposed operator construction is exempt from analytical derivation of $A^{\mathrm{lin}}$ and f. Furthermore, it keeps the adjoint equations consistent with the direct equations. All dependencies of the reaction dynamics on the state variables and model parameters are by design fully evaluated without simplifications. In addition, the approach is easily transferable to existing implementations.

3.4. Numerical implementation – adjoint-based sensitivity analysis

The calculation of the sensitivities for selected parameters proceeds as follows: at first, governing equations (1) are solved forward in time using an appropriate integrator. Here, the MatLab solver ode15s is used (see Section 2.4). All computed intermediate states and the corresponding time steps of the 0D system are stored, which should not lead to difficulties on modern workstations, even for large systems.

Subsequently, adjoint equations (22(22) ${\mathrm{\partial }}_t{q}^{\ast }=-A^{{\mathrm{lin}}^{\mathrm{T}}}{q}^{\ast }-g.$(22) ) are solved backwards in time with $q^{\ast }\left(t_{\mathrm{end}}\right)=0$ as initial condition. The same time stepper, which is used for the direct problem, can be employed with a negative time step. The required operator $A^{\mathrm{lin}}$ is constructed by means of Fréchet derivative (25(25) $A^{\mathrm{lin}}\cdot e_i\approx \frac{\mathrm{rhs}\left(q_0+ϵe_i,{\alpha }_0\right)-\mathrm{rhs}\left(q_0,{\alpha }_0\right)}{ϵ}.$(25) ) for each time step using the stored values of the direct calculation.

Based on the adjoint solution, also stored in time, the integrand in (24(24) $\frac{\delta J}{\delta \alpha }=\frac{1}{\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{q^{\ast }}^{\mathrm{T}}f\mathrm{d}t,$(24) ) is evaluated for all time steps and parameters, whose sensitivities are of interest. Finally, the sensitivities are obtained by integration over time. Details are discussed in Section 4.4.

4. Calculation of sensitivities

In this section, the presented adjoint-based approach is applied for sensitivity analyses of both considered reaction schemes, h2_v1b and gri3.0. The sensitivity of the ignition delay time with respect to the parameters A, β, and $E_a$ is determined.

To set up the adjoint formalism correspondingly, the change of the ignition delay is represented by the change of an integral objective. Such representation is advantageous for the presented adjoint approach, albeit any function measuring the ignition delay can in principle be used.

Two different objectives are considered in detail. For Section 4.1, the integral objective~J is defined in terms of temperature. 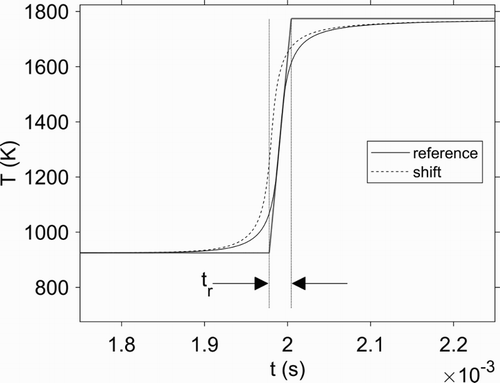Only the corresponding component of q and $q^{\left(\mathrm{mod}\right)}$ in (17(17) $J=\frac{1}{2\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{\left|q-q^{\left(\mathrm{mod}\right)}\right|}^2\mathrm{d}t,$(17) ) is evaluated: (28) $J=\frac{1}{2\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{\left(T-T^{\mathrm{shift}}\right)}^2\mathrm{d}t.$(28) Therein, the modified temperature profile $T^{\mathrm{shift}}$ refers to the reference profile, resulting from solving (1) with given parameters, shifted in time by $-{10}^{-2}\cdot t_r$. The $t_r$ is a characteristic time of the reaction defined by $t_r=\mathrm{\Delta }T/\left(\mathrm{\partial }T/\mathrm{\partial }t{|}_{\max }\right)$, with $\mathrm{\Delta }T$ as the difference between the initial and the equilibrium temperature after the reaction (see Figure 1). The weight g results to $g=(T-T^{\mathrm{shift}})$ and is a source term for the adjoint equation related to the component $T^{\ast }$.

Figure 1. Characteristic time $t_r$ used for the definition of the ignition delay. The shift of the profile $T^{\mathrm{shift}}$ is increased for better visibility.

For Section 4.2, the objective is defined in terms of the OH-species evolution as (29) $J=\frac{1}{2\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{\left(Y_{\mathrm{OH}}-Y_{\mathrm{OH}}^{\mathrm{shift}}\right)}^2\mathrm{d}t,$(29) with $Y_{\mathrm{OH}}^{\mathrm{shift}}$ as the shifted reference $\mathrm{OH}$ profile using the same time shift as before. The weight g results to $g=(Y_{\mathrm{OH}}-Y_{\mathrm{OH}}^{\mathrm{shift}})$ and is evaluated only in the adjoint component $Y_{\mathrm{OH}}^{\ast }$.

Each parameter change which affects the ignition delay will affect the defined objectives. In particular, for small parameter variations, the resulting small change of the objectives is a suitable measure of the change of the ignition delay. Since the adjoint approach determines the change of an objective with respect to a change of considered parameters, the defined objectives induce the desired sensitivity.

Note that by (28(28) $J=\frac{1}{2\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{\left(T-T^{\mathrm{shift}}\right)}^2\mathrm{d}t.$(28) ) and (29(29) $J=\frac{1}{2\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{\left(Y_{\mathrm{OH}}-Y_{\mathrm{OH}}^{\mathrm{shift}}\right)}^2\mathrm{d}t,$(29) ), no definition of the ignition delay time is given. However, it is suitable to deliver the desired sensitivities, since it corresponds to a shift of ignition in the 2-norm. A comparison of sensitivities based on common ignition delay time definitions is given in Section 4.3.

The adjoint-based sensitivities are validated by means of a comparison with the brute-force method of first order (30) ${\left.\frac{\delta J}{\delta \alpha }\right|}_{\mathrm{BF}}=\frac{J(q,{\alpha }_0+{ϵ}_{\mathrm{BF}})-J(q,{\alpha }_0)}{{ϵ}_{\mathrm{BF}}},$(30) where for the determination of each sensitivity, one forward solution is performed. The approach will be abbreviated as (BF) in the following. The parameter ${ϵ}_{\mathrm{BF}}$ is chosen as ${ϵ}_{\mathrm{BF}}={\alpha }_0\sqrt{{ϵ}_{\mathrm{machine}}}$. Zero-valent parameters are skipped in the validation.

Resulting sensitivities are presented by means of the sensitivity coefficient (31) $s_{\alpha }=\frac{\delta J}{\delta \alpha }\frac{{\alpha }_0}{J_0}.$(31) For better readability, all coefficients (adjoint and BF-based) are shown normalised with respect to each corresponding absolute maximum of $s_{\alpha }$ in the figures. The normalisation of each set of sensitivity coefficients removes a global factor. For the analysed schemes, the BF analysis under-estimates the adjoint sensitivities by a small factor, which has little impact since the ratios are unaffected. The deviation is assumed to originate from the one-sided finite difference of the brute-force method, but this is not examined in detail here.

The before-mentioned combustion schemes are considered. In the context of the h2_v1b scheme, hydrogen combustion with initial mole fractions of $X_{{\mathrm{H}}_2}=0.09$ and $X_{{\mathrm{O}}_2}=0.18$ in N${}_2$ is considered. For the gri3.0 scheme, methane combustion with initial mass fractions of $Y_{\mathrm{C}{\mathrm{H}}_4}=0.05$ and $Y_{{\mathrm{O}}_2}=0.2$ in N${}_2$ is examined. As initial temperatures 925 and 1000 K, respectively, at atmospheric pressure conditions are used.

4.1. Temperature evolution

4.1.1. h2v1b – validation in time

The present adjoint approach provides time-dependent sensitivity information, which describes also when a parameter change has an impact during the reaction progress. This can be helpful in analysing the dynamics of mechanisms. 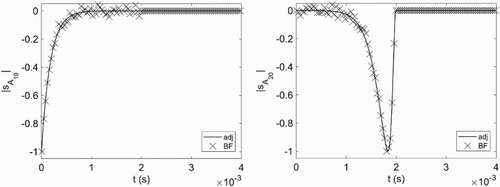The time-independent sensitivity of the reaction parameters is obtained by simply integrating (24(24) $\frac{\delta J}{\delta \alpha }=\frac{1}{\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{q^{\ast }}^{\mathrm{T}}f\mathrm{d}t,$(24) ). However, before transferring the temporal sensitivities to time-independent information, the approach is validated in time by introducing an artificial time dependence of the tested parameters, i.e. modifying the value of a parameter for one time step only.

As example, the parameters $A_{19}$ (reaction ${\mathrm{H}}_2+{\mathrm{O}}_2\to \mathrm{H}{\mathrm{O}}_2+\mathrm{H}$) and $A_{20}$ (reaction $\mathrm{H}{\mathrm{O}}_2+\mathrm{H}\to \mathrm{OH}+\mathrm{OH}$) of scheme h2_v1b are considered. In Figure 2, comparisons between the adjoint-based sensitivities and those based on a finite difference analysis are shown. Only at every fifth time step, a finite difference value is calculated. The results match in terms of the accuracy of the finite difference scheme. In contrast to the finite difference results, the adjoint provides smoother curves for the considered parameters. 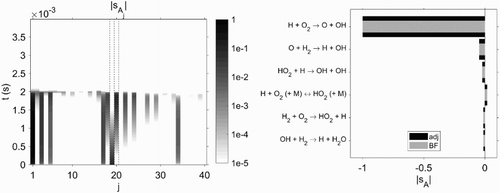The time-dependent sensitivities for all parameters $A_j$ are shown in Figure 3 (left). After ignition the sensitivities tend to zero.

Figure 2. Comparison between adjoint and finite difference-based sensitivities for parameters A, treated time-dependent, of reaction #19 ${\mathrm{H}}_2+{\mathrm{O}}_2\to \mathrm{H}{\mathrm{O}}_2+\mathrm{H}$ (left) and #20 $\mathrm{H}{\mathrm{O}}_2+\mathrm{H}\to \mathrm{OH}+\mathrm{OH}$ (right) in scheme h2_v1b.

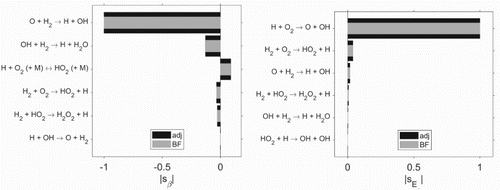
4.1.2. h2v1b – validation

The time-independent sensitivities of the parameters are computed by integrating the time-dependent sensitivity information (see Figure 3 (left)) corresponding to (24(24) $\frac{\delta J}{\delta \alpha }=\frac{1}{\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{q^{\ast }}^{\mathrm{T}}f\mathrm{d}t,$(24) ). In Figure 3 (right), the resulting sensitivities of parameters $A_j$ are compared to finite difference approach (30(30) ${\left.\frac{\delta J}{\delta \alpha }\right|}_{\mathrm{BF}}=\frac{J(q,{\alpha }_0+{ϵ}_{\mathrm{BF}})-J(q,{\alpha }_0)}{{ϵ}_{\mathrm{BF}}},$(30) ), also using the aforementioned integral objective J (28(28) $J=\frac{1}{2\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{\left(T-T^{\mathrm{shift}}\right)}^2\mathrm{d}t.$(28) ). Very good agreement is found. In Figure 4, a comparison of the parameters ${\beta }_j$ and $E_{a,j}$ is presented. Again, the adjoint-based sensitivity analysis provides reliable results.

Figure 3. Adjoint-based, time-dependent sensitivities for parameters $A_j$ of all reactions in scheme h2_v1b in logarithmic scale (left). The reactions marked by the dashed lines correspond to Figure 2. Comparison between adjoint and finite difference-based sensitivity for the top six most sensitive reactions with respect to the time-independent factor $A_j$ (right).

Figure 4. Comparison between adjoint and finite difference-based sensitivity for the top six most sensitive reactions with respect to the time-independent factors ${\beta }_j$ (left) and $E_{a,j}$ (right) in scheme h2_v1b.

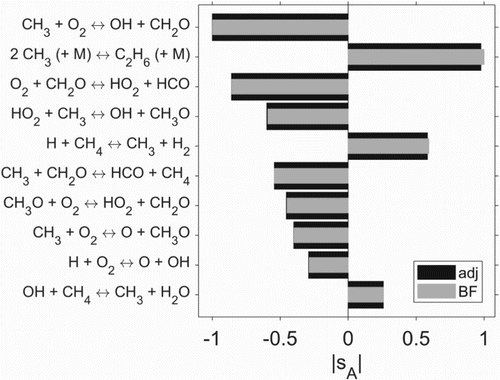
4.1.3. gri3.0 – validation

Also for methane oxidation simulation using the gri3.0 model, very good agreement between adjoint and finite difference-based sensitivities is found. In Figure 5, a comparison for the parameters $A_j$ is shown for the top 10 most sensitive reactions. The results are characterised by small differences in amplitude and order of the most sensitive reactions.

Figure 5. Comparison between adjoint and finite difference-based sensitivity for the top 10 most sensitive reactions with respect to the time-independent factor $A_j$ in scheme gri3.0.

4.2. Species evolution

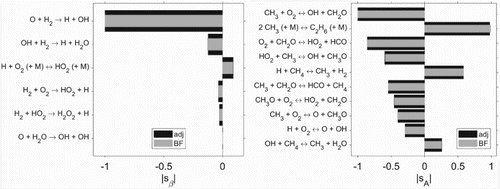
The comparison between adjoint-based and finite difference-based sensitivities of $\mathrm{OH}$-species-based integral objective (29(29) $J=\frac{1}{2\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{\left(Y_{\mathrm{OH}}-Y_{\mathrm{OH}}^{\mathrm{shift}}\right)}^2\mathrm{d}t,$(29) ) with respect to the parameters A, β, and $E_a$ in scheme h2_v1b shows very good agreement (see Figures 6 and 7 (left)). For the case using the gri3.0 mechanism, similar results are found. They are characterised by small differences in amplitude and order of the most sensitive reactions (see Figure 7 (right)).

Figure 6. Comparison between adjoint and finite difference-based sensitivity for the top six most sensitive reactions with respect to the time-independent factors $A_j$ (left) and $E_{a,j}$ (right) in scheme h2_v1b.

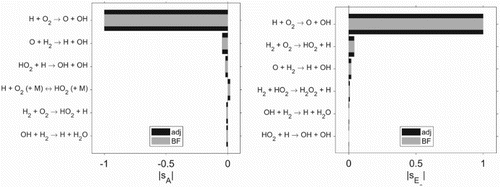
Figure 7. Comparison between adjoint and finite difference-based sensitivity for the top six most sensitive reactions with respect to the time-independent factor ${\beta }_j$ in scheme h2_v1b (left). Comparison between adjoint and finite difference-based sensitivity for the top 10 most sensitive reactions with respect to the time-independent factor $A_j$ in scheme gri3.0 (right).

4.3. Ignition delay time

In order to show that the employed objectives (28(28) $J=\frac{1}{2\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{\left(T-T^{\mathrm{shift}}\right)}^2\mathrm{d}t.$(28) ) and (29(29) $J=\frac{1}{2\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{\left(Y_{\mathrm{OH}}-Y_{\mathrm{OH}}^{\mathrm{shift}}\right)}^2\mathrm{d}t,$(29) ) are suitable measures for the sensitivity analysis of the ignition delay time, resulting sensitivities for (28(28) $J=\frac{1}{2\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{\left(T-T^{\mathrm{shift}}\right)}^2\mathrm{d}t.$(28) ) are compared with sensitivities produced by different measures for the ignition delay time. For the analyses, the above-described h2_v1b scheme setup is used.

4.3.1. Direct difference

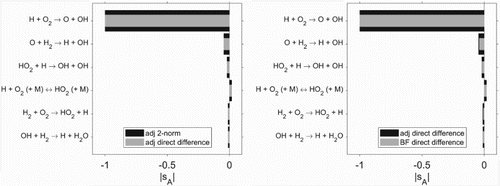
The first comparison is based on the following objective, where in comparison to (28(28) $J=\frac{1}{2\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{\left(T-T^{\mathrm{shift}}\right)}^2\mathrm{d}t.$(28) ) the square is dropped (32) $J=\frac{1}{2\tau }{\int }_{t_0}^{t_{\mathrm{end}}}\left(T-T^{\mathrm{shift}}\right)\mathrm{d}t.$(32) This allows a more intuitive interpretation of the objective, since it is, for an unchanged temperature profile, the ignition delay change times the total temperature rise.

In Figure 8, a comparison of the resulting sensitivities between 2-norm objective (28(28) $J=\frac{1}{2\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{\left(T-T^{\mathrm{shift}}\right)}^2\mathrm{d}t.$(28) ) and direct difference objective (32(32) $J=\frac{1}{2\tau }{\int }_{t_0}^{t_{\mathrm{end}}}\left(T-T^{\mathrm{shift}}\right)\mathrm{d}t.$(32) ) is shown as well as a comparison between adjoint-based sensitivities using (32(32) $J=\frac{1}{2\tau }{\int }_{t_0}^{t_{\mathrm{end}}}\left(T-T^{\mathrm{shift}}\right)\mathrm{d}t.$(32) ) and a corresponding brute-force calculation (30(30) ${\left.\frac{\delta J}{\delta \alpha }\right|}_{\mathrm{BF}}=\frac{J(q,{\alpha }_0+{ϵ}_{\mathrm{BF}})-J(q,{\alpha }_0)}{{ϵ}_{\mathrm{BF}}},$(30) ).

Figure 8. Comparison of sensitivities based on linear objective function (32(32) $J=\frac{1}{2\tau }{\int }_{t_0}^{t_{\mathrm{end}}}\left(T-T^{\mathrm{shift}}\right)\mathrm{d}t.$(32) ) with respect to quadratic objective (28(28) $J=\frac{1}{2\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{\left(T-T^{\mathrm{shift}}\right)}^2\mathrm{d}t.$(28) ), using the adjoint approach (left) and finite differences (right).

4.3.2. Maximum temperature rise

The ignition delay is often defined based on the time with the maximum slope of T. This definition is difficult to utilise within the adjoint approach, since the maximum is difficult to linearise: (33) $t_{\mathrm{ign}}=J={\left.{\mathrm{\partial }}_{t}T\left(t\right)\right|}_{\max }.$(33)

However, a comparison with respect to a brute-force calculation (30(30) ${\left.\frac{\delta J}{\delta \alpha }\right|}_{\mathrm{BF}}=\frac{J(q,{\alpha }_0+{ϵ}_{\mathrm{BF}})-J(q,{\alpha }_0)}{{ϵ}_{\mathrm{BF}}},$(30) ) using (33(33) $t_{\mathrm{ign}}=J={\left.{\mathrm{\partial }}_{t}T\left(t\right)\right|}_{\max }.$(33) ) shows that for the case investigated here, the results are consistent with the sensitivities based on quadratic objective (28(28) $J=\frac{1}{2\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{\left(T-T^{\mathrm{shift}}\right)}^2\mathrm{d}t.$(28) ) (see Figure 9 (left)). Differences are expected for a strongly changing temperature profiles.

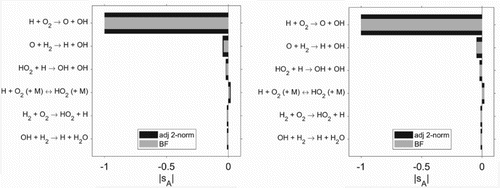
Figure 9. Comparison of sensitivities based on quadratic objective function (28(28) $J=\frac{1}{2\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{\left(T-T^{\mathrm{shift}}\right)}^2\mathrm{d}t.$(28) ) with respect to the definition by the maximum temperature gradient (left) and with the maximum OH mass fraction (right).

4.3.3. Maximum OH mass fraction

Also the formation of radicals can be exploited, e.g. (34) $t_{\mathrm{ign}}=J={\left.Y_{\mathrm{OH}}\left(t\right)\right|}_{\max }.$(34)

Using the maximum of the OH mass fraction in (30(30) ${\left.\frac{\delta J}{\delta \alpha }\right|}_{\mathrm{BF}}=\frac{J(q,{\alpha }_0+{ϵ}_{\mathrm{BF}})-J(q,{\alpha }_0)}{{ϵ}_{\mathrm{BF}}},$(30) ) produces practically the same sensitivities as objective function (28(28) $J=\frac{1}{2\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{\left(T-T^{\mathrm{shift}}\right)}^2\mathrm{d}t.$(28) ) used in the main part of this work (see Figure 9 (right)).

In summary, it can be stated that quadratic objective function (28(28) $J=\frac{1}{2\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{\left(T-T^{\mathrm{shift}}\right)}^2\mathrm{d}t.$(28) ) is a suitable measure for the sensitivity analysis of the ignition delay time. Only small deviations occur, visible by means of thin lines due to low-lying, respectively, protruding, bars in Figures 8 and 9.

4.4. Performance

The adjoint-based approach allows an efficient sensitivity analysis. While for a finite difference-based analysis, one full forward solution of governing (primal) equations (1) in time is needed for each parameter, the adjoint approach requires only one solution of the primal problem and one solution of adjoint (dual) problem (22(22) ${\mathrm{\partial }}_t{q}^{\ast }=-A^{{\mathrm{lin}}^{\mathrm{T}}}{q}^{\ast }-g.$(22) ).

However, the evaluation of (24(24) $\frac{\delta J}{\delta \alpha }=\frac{1}{\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{q^{\ast }}^{\mathrm{T}}f\mathrm{d}t,$(24) ), in particular f, requires one call of the governing rhs for each computed time step and parameter under consideration. Thus, the reduction of computational costs is limited to the reduced number of required rhs-calls – in comparison to the number of calls usually necessary for the brute-force method.

For the performed validation computations, a reduction of the computational costs by a factor of 2–3 is found. Note, that the adjoint-based sensitivity analysis, in particular the evaluation of (24(24) $\frac{\delta J}{\delta \alpha }=\frac{1}{\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{q^{\ast }}^{\mathrm{T}}f\mathrm{d}t,$(24) ), remains fully parallelisable.

A further reduction of the computational cost can be achieved considering Figure 2. The time-dependent sensitivity information, which is integrated to derive the time-independent sensitivity, can be interpolated by a certain number of sampling points. Then, only for these points in time, an evaluation of f is required.

In Figure 10, the deviation between an evaluation at each time step and interpolation-based results are presented. For the interpolation, every second, fifth, tenth and twenty-fifth time step is employed, which is directly related to the attainable speed-up factor.

Figure 10. Relative errors of the adjoint-based sensitivities with respect to the time-independent factor $A_j$ and different numbers of data points used for the interpolation and evaluation: in descending order with respect to $|s_A|$ in scheme h2_v1b (left) and for the top 10 most sensitive reactions in scheme gri3.0 (right).

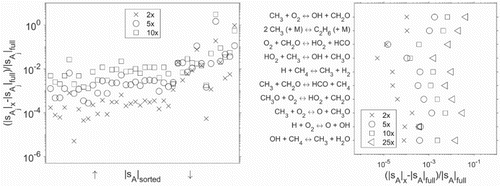
In general, sparser interpolations lead to stronger deviations. In particular, for weakly sensitive parameters, larger deviations are found (see Figure 10 (left)). However, this is acceptable, as the reactions with low sensitivities are usually of minor interest. For the most sensitive parameters in scheme gri3.0, relative errors in the range of ${10}^{-2}$ to ${10}^{-6}$ are found (see Figure 10 (right)). Alternatively, more sophisticated adaptive integration methods, reducing the number of required sampling points, could be used, but this is out of the scope of the present work. For the performance analysis, temperature-based objective (28(28) $J=\frac{1}{2\tau }{\int }_{t_0}^{t_{\mathrm{end}}}{\left(T-T^{\mathrm{shift}}\right)}^2\mathrm{d}t.$(28) ) is considered.

Depending on the required accuracy, the adjoint-based sensitivity analysis provides a speed-up of more than one order of magnitude with respect to the required computational time, if only the most sensitive parameters are of interest.

5. Conclusion

An adjoint-based approach for the sensitivity analysis of reaction parameters with respect to complex quantities of interest in a 0D environment is presented. In comparison to the standard brute-force finite difference technique, the advantages of the approach are two-fold: first, the approach derives exact gradients for the parameters and is exempt from the finite difference uncertainties. Second, the procedure allows a speed-up of sensitivity analyses by one order of magnitude terms of computation time, while remaining fully parallelisable.

The adjoint approach presented makes use of the implemented direct (primal) governing equations only. From this, all needed expressions are created numerically and no adjoint equations have to be derived analytically or implemented. The kinetic model is used as a black box. Thus, also non-standard rate laws can be considered with minimal effort. The proposed method is also independent of the kinetic model. This allows to use the approach within already existing codes like FlameMaster and Cantera.

Acknowledgements

The authors gratefully acknowledge the support of the Deutsche Forschungsgemeinschaft (DFG) as part of Collaborative Research Center CRC 1029 ‘Substantial efficiency increase in gas turbines through direct use of coupled unsteady combustion and flow dynamics’.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

The authors acknowledge funding by Deutsche Forschungsgemeinschaft (DFG) within the DFG project PE 241/46-1, SFB 1029.