Multiple steady state profiles in interconnected biological systems

Abstract

This paper deals with a generic approach for the analysis of interconnected biological systems. The equilibrium points as well as the asymptotic behaviour of these systems are investigated from a qualitative point of view. In particular, a new generic approach is used to show that a series of Continuously Stirred Tank Reactors (CSTRs) can exhibit multiple steady state profiles, for any non-monotonic kinetics. This multiplicity property disappears when the number of reactors becomes sufficiently large (for a given total volume). These results are to be taken in account when CSTRs in series are used to approximate a Piston Flow Reactor (PFR).

Keywords:

• Biological systems
• Multiple steady states
• Interconnected systems
• Convergence
• Substrate inhibited kinetics

1. Introduction

As for many chemical systems, biosystems with substrate inhibited kinetics exhibit multiple steady states. Existence of such a multiplicity for a single CSTR was first theoretically discussed in 1 while experimental evidence was first reported in 2. The existence of this multiplicity was studied and pointed out in 3 for complex biosystems such as biosystems in series in which a single bioreaction following a Haldane model occurs. Such complex systems are of prime importance since a series of CSTRs (Continuous Stirred Tank Reactors) is commonly used to approximate the behaviour of a single PFR (Piston Flow Reactor) (see for example 4). This practical advantage has motivated a large number of studies over the last thirty years on cascades of CSTRs. In particular, the optimal design (where ‘optimal’ has to be understood as the minimum total required volume to obtain a given conversion rate) of CSTRs in series has been investigated. Following this idea and using the mathematical optimization procedure proposed in 5, it has been shown in 6 that a cascade of only three perfectly mixed reactors with decreasing volumes could be used to approximate well the input – output performances than a PFR for a comparable total volume (see 7 for an overview of the available design procedures and applications of CSTRs in series).

However, all the available studies dealing either with the existence of multiple steady state solutions or with bioreactors in series have in common a very low degree of generality. In particular, all of these studies use a specific growth process, that is, the well-known Haldane model. Recently, the optimal design of two interconnected bioreactors has been revisited for a large class of kinetic models (see 8). Apart from some specific results proposed in this paper, the most important point of this last reference lies in its generic nature. In other words, the results are demonstrated in a qualitative manner in such a way that they are not only valid for systems with a specific kinetic model but for any kinetic function which verifies a specific condition (i.e. μ′(S)/μ²(S) decreasing where μ′(S) = ∂μ(S)/∂S). With respect to this, notice, for instance, that both Monod and Haldane kinetics verify this hypothesis.

In this paper, following this philosophy, the multiple steady state property of bioreactors in series is revisited. The existence of such a multiplicity of stable steady state profiles is pointed out for any biological reaction following a non-monotonic kinetic function. This way, the results proposed in 3 for systems following a Haldane model are extended to a more general class of growth rates. Conditions under which a multiplicity of the steady state profiles exists (based in particular on the kinetic function and the number N of reactors in series) are explicitly derived for a class of non-monotonic kinetic models. The stability of these equilibria is also investigated using Poincaré – Bendixon type results. Finally, it is shown that for sufficiently small volumes of CSTRs in series, there exists only one stable equilibrium.

The paper is organized as follows. In section 2, the dynamical model of N bioreactors in series is derived. In 3, the multiplicity of steady state profiles is pointed out. 4 is devoted to the stability analysis of the equilibria. In 5, the properties of the continuous model are established and analysed before some conclusions and future prospects are drawn in the last section.

2 Dynamical model

Consider N(N ∈ ℕ) interconnected bioreactors with the same and simple growth reaction (one biomass/one substrate) in each reactor. Assume that there is only transport flow between the reactors in series. The flow rate between reactors is assumed to be constant and equal to the influent one, with concentrations S _in and X _in of substrate and biomass, respectively. Denote by V_i the volume of the ith reactor, and by S_i and X_i the substrate and biomass concentrations in that reactor, respectively. For i = 1, …, N, the dynamics of the ith bioreactor is given by the following differential equations system:

and for i = 0 we set X ₀ = X _in and S ₀ = S _in. Q denotes the flow rate and μ denotes the specific growth rate. Basically the second equation of (1) contains a yield coefficient Y, but it is convenient to rescale X_i to X_i /Y in order to reduce the number of parameters and in consequence, the complexity of the mathematical study of the model.

2.1 Existence of equilibrium point

Let U_i  = X_i  + S_i for i = 0, …, N and M = X _in + S _in (which implies U ₀ = M). By replacing X_i by U_i  − S_i in the S_i equation of system (1), for all i = 1, …, N, we have

The steady states (([Sbar] ₁, [Ubar] ₁), …, ([Sbar]_i , [Ubar]_i ), …, …, ([Sbar]_N , [Ubar]_N )) of (2) are such that [Ubar]_N  = [Ubar] _N−1 = …[Ubar] ₁ = [Ubar] ₀ = M and:

This equation can be solved recursively since [Sbar] _i depends on [Sbar] _i−1. In order to simplify, for a given i, we set α _i  = V_i /Q and [Sbar] = [Sbar]_i . Then, for a given i, we have to solve the following equation:

where [Sbar] _i−1 is either equal to S _in or determined by the previous iteration.

The specific growth rate function is assumed to have the following properties:

• H1 μ(0) = 0 and μ(S) > 0 ∀S > 0;

• H2 The function S → μ(S) is smooth, to say μ ∈ C ³([0, ∞)).

Proposition 2.1

Under assumptions H1 and H2, equation (4) has at least one solution in[0, [Sbar] _i−1]. The solution is unique for any monotonic function S → μ(S). Moreover, the sequence ([Sbar] _i )_{1 ≤ i ≤ N} , where (([Sbar] ₁, M), …, ([Sbar] _N , M)) is an equilibrium point of (2), is decreasing.

Proof

Let us consider the continuous function φ : S ∈ [0, M[ → α _i μ(S) − (([Sbar] _i−1 − S)/(M − S)). Notice that the solutions of (4) coincide with the zeros of the function φ. So, since φ(0)φ([Sbar] _i−1) < 0, we deduce from the Intermediate Value Theorem that (4) has at least one solution on [0, [Sbar] _i−1]. If S → μ(S) is monotonic, then φ is strictly increasing and, therefore, (4) has a unique solution. Since M − [Sbar] _i  > 0 and α _i μ([Sbar] _i ) = ([Sbar] _i−1 − [Sbar] _i )/(M − [Sbar] _i ), one has [Sbar] _i−1 ≥ [Sbar] _i .

Remark 1

The decrease of ([Sbar] _i )_{1 ≤ i ≤ N} is physically meaningful since from a wastewater treatment point of view, the substrate concentration should decrease from a reactor to the following.

3 Multiplicity of equilibrium points

Denote by the hyperbola in the (S, Y)-plane defined by

and ( in case of a single reactor) the graph of the function S → α _i μ(S). By Proposition 2.1, the system (2) has one equilibrium for monotonic kinetic functions. Therefore, we make the following assumptions for the multiplicity:

• H3 The function S → μ(S) is non-monotonic.

• H4 There exists 1 ≤ i ≤ N and S* ∈ [0, M[ such that ([Sbar] _i−1−S*)/(M − S*) = α _i μ(S*) and Y′(S*) > α _i μ′(S*).

• H5 There exist Ŝ and S_c such that the function S → μ(S) is increasing on [0, Ŝ] and decreasing on [Ŝ, M]; μ is concave on [0, S_c ] and convex on [S_c , M[ and finally μ′′′(S) ≥ 0 on [Ŝ, M].

Proposition 3.1

(i) Under H1 – H4, system (2) has multiple (at least three) equilibrium points. (ii) Under H5, equation (4) has at most three solutions in[0,[Sbar] _i−1].

Proof

To prove (i), assume that there exist S* satisfying H4. The function ψ(S) = (([Sbar] _i−1−S)/(M−S))−α _i μ(S), 0 ≤ S ≤ M is then increasing in a neighbourhood of S*. Since ψ(0) > 0 and ψ ([Sbar] _i−1) < 0, it follows from the Intermediate Value Theorem that ψ has at least three zeros S  < S* < [Stilde] in [0, [Sbar] _i−1]. Then, system (2) has at least three equilibrium points.

(ii) Assumption H5 allows one to avoid the existence of continuum solutions of (4). So, only the following situations hold.

If ψ′′(Ŝ) ≤ 0 then, ψ is strictly monotone decreasing in [0, M] and has at most one zero.

If ψ′′(Ŝ) > 0, then there exists [Stilde] ∈ ]Ŝ, S c ] such that ψ′′([Stilde]) = 0. We have two possible cases. If ψ′([Stilde]) ≥ 0, then there exists [Stilde] 1 ∈ ]Ŝ, [Stilde]] and [Stilde] 2 ∈ ][Stilde], M[ such that ψ is strictly monotone decreasing in [0, [Stilde] 1] ∪ [[Stilde] 2, M[ and strictly monotone increasing in [[Stilde] 1, [Stilde] 2]. In this case, ψ has at most three zeros. If ψ′([Stilde]) < 0, then ψ is strictly monotone decreasing in [0, M[ and has at most one zero.

3.1 Application: the Haldane kinetic model

To illustrate the multiplicity of equilibrium points, we consider the well known Haldane kinetic function:

where K_S and K_I are the saturation constant and the inhibition constant, respectively. Let us introduce μ₁ = K_IK_S . By simple computations of the successive derivatives of μ, one can observe that there exists such that μ″(S_c ) = 0, μ″(S) < 0 for all S ∈ [0, S_c [ and μ″ (S) > 0 for all S ∈ ]S_c , +∞[. There exists S _μ ∈ ]S_c , + ∞[ such that μ″′(S _μ) = 0 and μ″′(S) > 0 for all It follows that if M ∈]S_c , S _μ[ then assumption H5 is satisfied.

Example 1

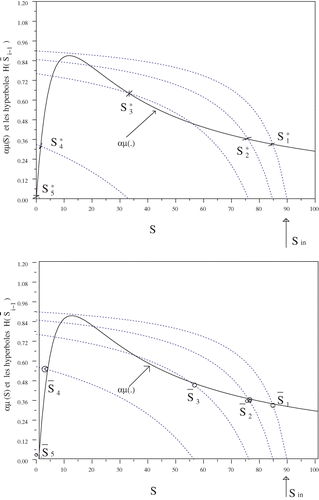
For numerical illustrations, we consider that: K_S  = 9.28 (mg l ⁻¹), K_I  = 15 (mg l ⁻¹), μ₀ = 0.64 (1/day), S _in = 90 (mg l ⁻¹), M = 100 (mg l ⁻¹), α = V_i /Q = 3.5, N = 5.

The multiplicity of the equilibrium points is illustrated in figure 1 and we represent two among the possible steady states. Note that [Sbar] _i is the intersection of the graph with the hyperbola In this example, five equi-volume bioreactors in series are considered. In figure 1, ([Sbar] ₁, [Sbar] ₂, [Sbar] ₃, [Sbar] ₄, [Sbar] ₅) is obtained by choosing the largest solution of (4) at each iteration (i = 1, …, 5). For , we choose the second solution of (4) at the third iteration (i = 3). Then, and . Following this reasoning, one can easily check that, in this example, system (2), with N = 5, has five possible steady states.

Figure 1. Multiple equilibria.

4 Stability analysis

4.1 The particular case: N = 1

First of all, we consider the case of a single CSTR with multiple equilibrium points and denote , 1 ≤ p ≤ m. Note that, when system (2) has a unique equilibrium point, for any N ∈ ℕ, this one is globally asymptotically stable according to the stability results of cascade systems (see for instance 9).

Assume N = 1 and consider the following set given by biological constraints. is invariant under (2) (N = 1). We have:

Proposition 4.1

(i) The equilibrium point is locally asymptotically stable for p odd and unstable otherwise.

(ii) For every , there exist p ∈ {1, …, m}such that

where (S(t), U(t)) is the solution of (2) through (S ⁰, U ⁰).

Proof

We assume that the case when and are tangent at is a limiting case, which is not considered by the first assertion (i). However, in this case, the equilibrium is unstable.

Let N = 1, the Jacobian matrix of (2) at is then given by

It is immediately clear that has two real eigenvalues, which are and λ₂ = −α⁻¹ < 0. Consider the function γ(S) = −μ(S)(M − S) + α⁻¹(S _in − S), we have . Since γ(0) = α⁻¹ S _in ≥ 0, then λ₁ < 0 when p is odd and λ₁ > 0 otherwise. This proves the first assertion.

The convergence of trajectories (S(t), U(t)) to equilibrium points, provided that , can be derived from the Poincaré – Bendixon trichotomy Theorem which we recall here.

Theorem (Poincaré – Bendixon)

Let

be a dynamical system inℝ².

Let ω(x ₀) be the ω-limit set of a forward bounded solution of (5) which remains in a compact subset K of ℝ², and suppose that K contains only a finite number of equilibrium points of (5). Then the following trichotomy holds:

1. ω(x ₀) is an equilibrium point,

2. ω(x ₀) is a periodical solution,

3. ω(x ₀) contains many equilibrium points that are cyclically chained to each other in ω(x ₀) by solutions of (5).

Situations (ii) and (iii) in the Theorem above cannot hold for our system (2) (for N = 1) since [Udot](t) = α⁻¹(M − U(t)) is independent and U(t) converges exponentially to M as t tends toward infinity for any initial condition U(0) = U ⁰. The system behaves like a one-dimensional system.

4.2 The general case

Let us consider now the general system of N reactors in series written in the following form:

which has as an equilibrium point. Since H1 holds, let us define the functions f ∈ C ¹(ℝ ^N ×ℝ ^N , ℝ ^N ) and g ∈ C ¹(ℝ ^N , ℝ ^N ) as follows:

for all S, U ∈ ℝ ^N . The jacobian matrix of the right-hand side term of (6) at (U*, S*) is given by: where B is a N×N matrix. Then, we have the following result

Proposition 4.2

(i) The equilibrium point (U*, S*) is locally asymptotically stable if and only if

for every 1 ≤ i ≤ N.

(ii) In the case of equi-volume reactors in series (α _i  = α₀) and under assumptions (H1 – H5), (U*, S*) is an unstable equilibrium of (6) if and only if there exists a unique i ∈ {1, …, N}such that

Proof

(i) Observe that the first block on the left-hand side in the matrix above (corresponding to the linear subsystem of (6)) is an Hurwitz matrix. So, the stability of (U*, S*) depends on the terms

Obviously, (U*, S*) is locally asymptotically stable if (∂f_i /∂S_i )(U*, S*) < 0, for all i = 1, …, N and (U*, S*) is unstable if there exists i ₀ ∈ {1, …, N} such that (∂f _{i 0} /∂S _{i 0} ) (U*, S*) > 0. If (∂f _{i 0} /∂S _{i 0} )(U*, S*) = 0, then we consider the function defined by

which satisfies ϕ([Sbar] _{i 0} ) = ϕ′([Sbar] _{i 0} ) = 0 and ϕ″([Sbar] _{i 0} ) ≠ 0 and there exists ϵ₀ > 0 such that one of the following situations holds:

or

So, it is not difficult to see that the equilibrium [Sbar] _{i 0} of the scalar equation

is unstable. Then, the instability of (U*, S*) follows.

(ii) It is easy to see, from above, that if such an i exists then (U*, S*) is unstable. Now let (U*, S*) be unstable, then there exists i ∈ {1, …, N} such that (∂f_i /∂S_i )(U*, S*) ≥ 0. Let j = min{i/(∂f_i /∂S_i )(U*, S*) ≥ 0, 1 ≤ i ≤ N} and let us consider the continuous functions

Φ _j−1 has three zeros (possibly two zeros or if (∂f_j /∂S_j ) (U*, S*) = 0) in . Then h _j−1(S) < α₀μ(S) for all . Since , we have h_j (S) ≤ h _j−1(S) for all . Therefore, h_j (S) < α₀μ(S) for all and Φ _j is then strictly increasing in the interval . Hence, Φ _j (S) has a unique zero in and (∂f _j+1/∂S _j+1)(U*, S*) < 0. Using similar arguments, we have the same result for k = j + 1, …, N.

The uniqueness in (ii) is very important for the proof of the result on asymptotic behaviour of the system which is treated in the remainder of this section.

Consider system (6) in the physically feasible set of state variables D = {(U, S) ∈ ℝ ^N ×ℝ ^N /0 ≤ S_i  ≤ S _in and 0 ≤ S_i  ≤ U_i  ≤ M, ∀i = 1, …, N} and the following (limiting) system:

in Ω = {S ∈ ℝ ^N /0 ≤ S_i  ≤ S _in∀i = 1, …, N}, since lim _t→∞ U_i (t) = M, for all i ∈{1, …, N} and for any initial condition U ⁰. We recall the following definition and give the following notation.

Definition and notation

	System (7) is said to have a cyclic chain if there exists a finite number of equilibrium points S *1, S *2, …, S *n 0 of (7) such that for any i ∈ {1, …, n 0}, there is a trajectory of (7) whose α-limit set consists of S *i and whose ω-limit set consists of S *i+1 (where S *n 0+1 = S *1 conventionally). We shall denote it by
	According to Proposition 4.2, we call the instability index ji of an unstable equilibrium point as being determined by the following number: ji  = min{1 ≤ j ≤ N/(∂fj /∂Sj )(U*, S*) ≥ 0}.

Now, let us introduce the following lemma.

Lemma 4.3

(i) System (7) has no periodical solution. In the case of equi-volume reactors (α _i  = α) we have: (ii) it has no cyclic chain and (iii) , where M ⁺(S ^*i ) is the stable manifold of S ^*i and m is the number of equilibrium points of (7).

Proof

(i) Consider the sub-system

of (7). If S(t) = (S ₁(t), S ₂(t), …, S_N (t)) is a periodical solution of (7) then S ₁(t) is a periodical solution of (8) too. However, it is easy to see from the proof of Proposition 4.1 that every solution of (8) converges to an equilibrium point and that equation (8) has no periodical solution. This ends the proof of (i).

(ii) Let α _i  = α and let us suppose that system (7) has a cyclic chain

Note that these equilibrium points are necessarily unstable, otherwise (9) is not possible. For convenience, let us denote by E(k), the sub-system of (7) which consists of the first k equations of (7). Assume that n ₀ > 1 and let S ^*i  → S ^*k with S ^*i  ≠ S ^*k , then there is a trajectory γ(t) of (7) such that α(γ) = S ^*i and ω(γ) = S ^*k . Note that where ( is a locally asymptotically stable equilibrium point of the independent sub-system E(j _i  − 1) according to the definition of the instability index. Then, there exists a neighbourhood V ₀ of such that for any S ⁰ ∈ V ₀,

where S(t, S ⁰) is the solution of E(j_i  − 1) through S ⁰. Let V be a neighbourhood of S ^*i such that for any S ∈ V, (S ₁, S ₂, …, S _{j i −1}) ∈ V ₀. Since α(γ) = S ^*i , there exists t ₀ ∈ ℝ such that γ(t ₀) ∈ V. Then (γ₁(t ₀), …, γ _{j i −1}(t ₀)) ∈ V ₀ and

Since ω(γ) = S ^*k , necessarily . Then j_i  ≤ j_k . Since S ^*i  ≠ S ^*k , by Proposition 4.2, we have j_i  < j_k , which contradicts (9). If n ₀ = 1, by similar arguments as in the proof of (i), we find that (9) is impossible.

(iii) It is enough to show that Ω is invariant under (7) and that every solution of (7) that starts in Ω converges to an equilibrium point. We begin by proving that Ω is invariant under system (7). This will be done recursively.

Throughout the paper, the expressions denote the powers of Ω₀ and for other variables it is a simple notation (for example S ⁰ is used to denote the initial condition of a system in S-variable).

	First, it is easy to see that Ω1 = Ω0 is invariant under (8).
	Suppose that is invariant under the subsystem E(n) of (7), 1 ≤ n ≤ N − 1 and let . Since E(n) is independent of the last equation in E(n + 1), its solution remains in Ω n and then Sn (t) ∈ [0, S in] ∀t ∈ ℝ. Thus

Hence S _n+1 ≤ y(t) for all t ≥ 0, where y(t) is the solution of under which Ω₀ is invariant. Then S _n+1(t) ∈[0, M] ∀t ∈ ℝ. It follows that Ω is invariant under (7). Now, let S(t, S ⁰) be a solution of (7) through S ⁰ ∈ Ω and ω its Ω-limit set. We have ω ≠ ø and let S* ∈ ω. From (i), (ii) above and Poincaré – Bendixon theorem, is an equilibrium point of the subsystem E(2) of (7). Now, if we assume that g ₃(S*) ≠ 0, then we consider the solution S(t, S*) of (7) through S*. Since , there is a point Ŝ in the ω-limit set of S(t, S*) such that (Ŝ ₁, Ŝ ₂, Ŝ ₃) is an equilibrium point of E(3). With ω being invariant under (7), we have Ŝ ∈ ω. Continuing this reasoning, we show that ω contains an equilibrium point. The equilibrium points of (7) are hyperbolic since the hyperbola and the graphs are assumed to be not tangent. Since (7) has no cyclic chain then, by Theorem 4.2 in 10, S(t, S ⁰) converges to an equilibrium point. Then, every solution of (7) which starts in Ω remains in it and converges to an equilibrium point. Hence, .

Following Lemma 4.3, we can state the convergence result for solutions of the general system (6). This shows the global asymptotic behaviour of the series of continuously stirred tank reactors under study. More precisely, we prove that the attracting sets of the solutions of the system are its steady states and almost all of the trajectories converge to stable equilibrium.

Proposition 4.4

Let H1 – H5 hold, then for every solution (U(t), S(t)) of (6) there exists some i such that,

Moreover, has Lebesgue measure zero, whereΛ⁺(U*, S ^*i_k ) is the stable manifold of the unstable equilibrium (U*, S ^*i_k ).

Proof

The system (6) is dissipative in the sense that there is a compact subset K of D into which every solution eventually enters and remains. Moreover, K can be chosen such that for any (U, S) ∈ K, we have S ∈ Ω. So considering the Lemma above, the proposition is proved in the same manner as Theorem F.1 in 11.

4.3 Numerical illustrations

Example 2

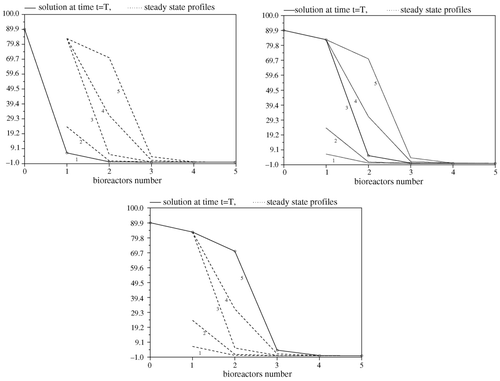
Due to the convergence of the solution U(t) of the linear subsystem of (6), the solutions of (6) eventually lie on the manifold {U_i  = M, for i = 1, …, N} where it is reduced to (7). In this example, we illustrate the convergence of solutions of (7) to its steady state profiles. So, we consider the Haldane kinetic model:

and K_S  = 9.28 (mmol l ⁻¹), K_I  = 15 (mmol l ⁻¹), μ₀ = 0.74 (1/day), S _in = 90 (mmol l ⁻¹), M = 100 (mmol l ⁻¹), α = V_i /Q = 3.5, N = 5, where K_S and μ₀ were experimentally identified in 12.

In figure 2, the five steady state profiles for five equivolume bioreactors in series are shown together with the solution of the system at final time. The equilibrium points, no. 2 and no. 4, are unstable since the corresponding Jacobian matrix does not fulfill condition (i) in Proposition 4.2. These numerical results illustrate the convergence of solutions of (6) to stable steady state profiles only. Note that this is in accordance with Proposition 4.4 since the stable manifolds of unstable steady states have Lebesgue measure zero. Here we show that, depending on the initial condition, the solution of the system (6) (for N = 5) converges to one of the stable equilibrium points (nos. 1, 3, 5). Moreover, we have noticed that the basin of attraction of the stable equilibrium points, nos. 1 and 3, are smaller compared with that of the last stable equilibrium point (no. 5).

Figure 2. Convergence of trajectories.

In the next section, we analyse the continuous model corresponding to the Plug Flow Reactor and we show that the steady state profiles of the discretized system converge to the unique steady state solution of the continuous model when N is sufficiently large.

5 The continuous model

Consider the continuous model given by the following system of partial differential equations:

with the initial and boundary conditions:

and A denoting the section of the reactor. The corresponding steady state problem is:

where c = A/Q and l is the total length of the reactor.

Under assumptions H1 – H2, we have that ψ is Lipschitz continuous on [0, M]. Moreover, ψ(0) = 0 and ψ(M) = 0. It follows that equation (11) has a unique solution for any S _in ∈ [0, M] and that [0, M] is invariant under (11).

5.1 Stability of the continuous model

Fix (t, z) and set

where (S(s), U(s)) is the solution of (10). Then

Let ([Sbar] _(t,0)(s), [Ubar] _(t,0)(s)) be the solution of (12) with [Sbar] _(t,0)(0) = S(t, 0) = S _in and [Ubar]_(t,0)(0) = U(t,0) = M. With U(t,0) = M for all t ≥ 0, we have for all s ∈ [0, cl] and for all t ≥ 0. Then U(t, z) = M for all z ∈ [0, l] and t ≥ cl.

[Sbar] _(t,0)(s) satisfies

Then for all s ∈ [0, cl], where [Sbar] ₀(s) is the solution of (11). We have for all s ∈ [0, cl]. It follows that S(t, z) = [Sbar] ₀(z), for all z ∈ [0, l] and t > cl.

5.2 Convergence of steady state profiles

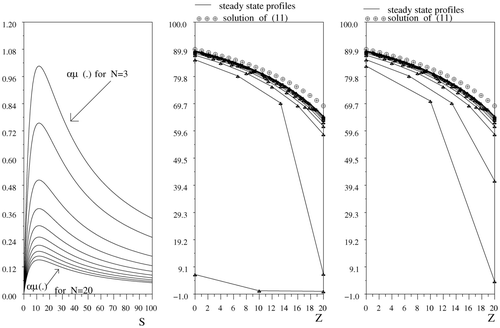
It is easy to see that (3) can be deduced from the Euler approximation of the stationary equation (11). This coincides with the numerical result given in the following simulations. Figure 3 shows steady state profiles of N interconnected bioreactors, N varying between 3 and 20. On the second graphic window from the left, the solutions [Sbar]_i of equation (4) are computed by choosing the minimum value [Sbar] _i−1 of the solution of (4) at the iteration i − 1. On the third graphic window from the left, the maximum value [Sbar] _i−1 is chosen to compute [Sbar]_i , for 1 ≤ i ≤ N. In both cases, the steady state profiles of system (6) converge, as N becomes sufficiently large, to the unique steady state solution of (10). On the first graphic window, are represented the graphs of the function S → αμ(S) depending on N, where α = α _i , for all i ∈ {1, …, N}.

Figure 3. Successive profiles depending on the number of reactors in series.

6 Conclusion

This paper is dedicated to the analysis of interconnected bioreactors. We have pointed out that a series of continuously stirred tank reactors can exhibit under some conditions multiple stable steady state profiles for a class of non-monotonic kinetic functions.

This result is interesting in the sense that interconnected bioreactors are often used to approximate a single Plug Flow Reactor which has one stable steady state profile independent of the kinetic model, as shown in the last part of the paper.

On the other hand it is shown that, when the number of bioreactors in series increases, the multiplicity property disappears and all the steady state profiles of the cascade of CSTRs converge to the unique profile of the PFR. Following this last result, the use of a cascade of CSTRs to approximate a single PFR can be justified provided one chooses judiciously this approximation in order to conserve the qualitative properties of the PFR, namely at steady states.

This study can also be considered in the sense of modelling and analysis of interconnected bioreactors. From this point of view, it is completed by the analysis of the asymptotic behaviour of the system of differential equations that describes the dynamics of the cascade of CSTRs. It is shown that the system has no strange behaviour like periodical solutions or heteroclinic cycles (cyclic chains).

If the existence of multiple steady states in substrate-inhibited bioreactions is not new in itself, the generic way to treat it here is the most interesting contribution of the present paper. From this point of view, it can be seen as a generalization of the existing literature. This work is the starting point of a more general study on interconnected biological systems. This study will also be concerned with the case of diffusion and make comparison with the present results and also the case studied in 11 for monotonic kinetic functions.

Acknowledgements

The first author thanks AUF (Agence Universitaire de la Francophonie), INRA (Institut National de la Recherche Agronomique, France) and CIMPA (Centre International de Mathématiques Pures et Appliquées) for their financial support.