A short note on SPSA techniques and their use in nonlinear bioprocess identification

Abstract

Simultaneous perturbation stochastic approximation (SPSA) is a gradient-based optimization method which has become popular since the 1990s. In contrast with standard numerical procedures, this method requires only a few cost function evaluations to obtain gradient information, and can therefore be advantageously applied when identifying a large number of unknown model parameters, as for instance in neural network models or first-principles models. In this paper, a first-order SPSA algorithm is introduced, which makes use of adaptive gain sequences, gradient smoothing and a step rejection procedure to enhance convergence and stability. The algorithm performance is illustrated with the estimation of the most-likely kinetic parameters and initial conditions of a bioprocess model describing the evolution of batch animal cell cultures.

Keywords:

• Mathematical modelling
• Identification
• Optimization
• Stochastic approximation
• Biotechnology

1. Introduction

Process modelling requires the estimation of several unknown parameters from noisy measurement data. In this connection, gradient-based optimization methods are popular tools for minimizing least-squares or maximum-likelihood cost functions – depending on the assumptions on the measurement noise – measuring the deviation between the model and real system outputs.

Several techniques for computing the gradient of the cost function are available, including finite difference approximations or direct differentiation, which involves the numerical solution of sensitivity equations.

In the above-mentioned techniques, the computational expense required to estimate the current gradient direction is directly proportional to the number of unknown model parameters, which becomes an issue for models involving a large number of parameters. This is typically the case in neural network (NN) modelling, but can also occur in other circumstances, such as the estimation of parameters and initial conditions in first-principles models. Moreover, the derivation of sensitivity equations requires analytic manipulation of the model equation, which is time consuming and prone to errors (note that an important stream of current research and development is dedicated to the automatic generation of such equations using symbolic manipulation).

In contrast to standard finite differences which approximate the gradient by varying all the parameters one at a time, the simultaneous perturbation (SP) approximation of the gradient proposed by Spall 1 makes use of a very efficient technique based on a simultaneous (random) perturbation in all the parameters. Hence, one gradient evaluation requires only two evaluations of the cost function. This approach has first been applied to gradient estimation in a first-order stochastic approximation (SA) algorithm 1, and more recently to Hessian estimation in an accelerated second-order SPSA algorithm 2.

Efficiency, simplicity of implementation and very modest computational costs make first-order SPSA (1SPSA) particularly attractive, even though it suffers from the classical drawback of first-order algorithms, i.e. a slowing down in the convergence as an optimum is approached. Unfortunately, this phenomenon is even more pronounced in the case of SP techniques since the gradient information is more delicate to ‘extract’ from the – usually rather ‘flat’ – neighbourhood of the optimum.

In this study, a variant of the original first-order algorithm is considered which makes use of adaptive gain sequences, gradient smoothing and a step rejection procedure, to enhance convergence and stability. To demonstrate the algorithm efficiency and versatility, attention is focused on the estimation of kinetic parameters (and initial conditions) in a macroscopic model of animal cell cultures. To this end, a maximum-likelihood cost function based on the experimental measurements of biomass, glucose, glutamine and lactate concentrations is minimized.

This paper is organized as follows. Section 2 introduces the basic principle of the first-order SPSA algorithm used throughout this study. In section 3, the algorithm is applied to the maximum-likelihood estimation of kinetic parameters and initial conditions of a bioprocess model from experimental measurements of several macroscopic component concentrations. Direct and cross-validation results demonstrate the good model agreement. Finally, section 4 is devoted to some concluding remarks.

2 A brief overview of SPSA

Consider the problem of minimizing a, possibly noisy, objective function J(θ) with respect to a vector θ of unknown parameters.

1SPSA is given by the following core recursion for the parameter vector θ1

in which a_k is a non-negative scalar gain coefficient, and is an approximation of the criterion gradient obtained by varying all the elements of simultaneously, i.e.

where c_k is a positive scalar and Δ _k  = (Δ _k1, Δ _k2, …, Δ _kp ) ^T with symmetrically Bernouilli distributed random variables {Δ _ki }.

In its original formulation 1, 1SPSA makes use of decaying gain sequences {a_k } and {c_k } in the form

in order to ensure formal convergence. In these expressions, a, A and c denote constant parameters. Finite sample experiments show, however, that the algorithm may get stuck somewhere in the parameter space if the criterion value becomes significantly worse (due to a poor current gradient approximation, a non-convex optimization problem, etc.) and the gain sequences are too small to recover from this situation.

In order to enhance convergence and stability, the use of an adaptive gain sequence for parameter updating is considered, i.e.

In addition to gain attenuation when the value of the criterion becomes worse, ‘blocking’ mechanisms 2 are also applied, i.e. the current step is rejected and, starting from the previous parameter estimate, a new step is accomplished (with a new gradient evaluation and a reduced updating gain). The parameter β in (4) represents the permissible increase in the criterion, before step rejection and gain attenuation occur.

A constant gain sequence c_k  = c could be used for gradient approximation, the value of c being selected so as to overcome the influence of (numerical or experimental) noise. In the optimum neighbourhood, a decaying sequence in the form (3) is required to evaluate the gradient with enough accuracy and avoid an amplification of the ‘slowing down’ effect mentioned in the introduction.

Finally, a gradient smoothing (GS) procedure is implemented, i.e. gradient approximations are averaged across iterations in the following way

where, starting with an initial value of ρ = ρ₀, ρ _k is decreased in a way similar to (4) when step rejection occurs (i.e. ρ _k  = μρ_k−1 with μ ≤ 1) and is reset to its initial value after a successful step.

The use of these numerical artifices, i.e. adaptive gain sequences, step rejection procedure and gradient smoothing, significantly improves the effective practical performance of the algorithm, which, in the following, is denoted ‘adaptive 1SP-GS’.

Inequality constraints can also be taken into account by a projection algorithm introduced in Sadegh 3: the current parameter estimate is projected onto a closed set included in the admissible region in such a way that no function evaluation is required outside this latter region. In this study, bound constraints (e.g. positivity constraints) are handled in this way.

3 Modelling batch CHO cell cultures

In this experimental study, rare and asynchronous measurements of biomass (X), glucose (G), glutamine (Gln) and lactate (L) concentrations are available. The measurement equation is given by

where ξ(t_i ) = [X(t_i ) G(t_i ) Gln(t_i ) L(t_i )] ^T , y(t_i ) and ϵ(t_i ) are the state, measurement and noise vectors at time t_i , respectively. The measurement errors are assumed to be normally distributed, white noises with zero mean and variance matrix Q(t_i ).

Data are collected from seven batch experiments corresponding to different initial glucose and glutamine concentrations. Five of these experiments are used for parameter estimation, the two remaining ones being used for cross-validation tests.

The parameter estimation procedure involves the minimization of a Gauss-Markov criterion

where y_i , Q_i and are the measurement vector, the measurement error covariance matrix and the state estimate obtained by integration of the model equations with the parameter vector θ.

The model equations are derived from mass balances and are given by

where the reaction term K φ(ξ) includes the reaction pseudo-stoichiometry matrix K defining the corresponding macroscopic reaction scheme and the kinetics φ(ξ).

The pseudo-stoichiometry can be estimated independently of the reaction kinetics by using a state transformation originally introduced in Bastin and Dochain 4, which is based on the following ideas.

If rank K = M, where M is the number of independent reactions, then there always exists a partition

where K _a ∈ℜ ^M×M is full rank, i.e. rank K_a = M.

Accordingly, the partition of ξ is given by

Given such a partition of K, the following matrix equation

(where O ∈ ℜ^{(N − M)×M} is a null matrix) has always a unique solution C ∈ℜ^{(N − M)×M} .

Using this solution, an auxiliary vector z∈ℜ ^N − M can be defined as

whose dynamics is independent of the kinetics

Based on equations (12) and (13), a maximum-likelihood estimation Ĉ of the matrix C can be computed 5, and estimations [Kcirc]_a and [Kcirc]_b of the matrices K_a and K_b can be deduced from equation (11). A systematic procedure for selecting the most-likely C-identifiable reaction scheme has been proposed in Bogaerts and Vande Wouwer 6.

This procedure can be applied to our case study with ξ _a  = [X G] ^T , ξ _b  = [G ln L] ^T , and dz(t)/dt = 0 (from equation (13) with D = 0). Then, the following macroscopic reaction scheme is derived.

Growth:

Maintenance:

where ν _Gln, ν _X and ν _L are pseudo-stoechiometry coefficients. The symbol →^ means that the growth reaction is auto-catalysed by X. The presence of ν _X X in both sides of the maintenance reaction means that X catalyses this latter reaction.

The estimated pseudo-stoichiometry matrix is then given by

The growth rate ϕ_g and the maintenance rate ϕ_m appearing in equations (14) and (15) are described by a general kinetic model structure proposed in Bogaerts and Hanus 5.

The mass equations (8) can therefore be written in a more explicit form

The eight kinetic coefficients in equations (17) and (18) and 20 initial concentrations appearing in equations (19) –  (22) for the five batch experiments under consideration (initial concentrations are corrupted by measurement noise and their most-likely values have to be identified) are estimated by minimizing the cost function (7) with the adaptive 1SP-GS algorithm.

The tuning parameters in equations (1) –  (5) are selected as follows: c = 10⁻⁶, γ = 1.5 (a decaying sequence c_k is used for gradient evaluation), a ₀ = 10⁻⁸, η = 1.01, μ = 0.9, β = 0 (no relative increase in the criterion is allowed), ρ₀ = 0.99. Starting with the measured initial concentrations (which are affected by measurement errors) and an initial guess for the kinetic parameters corresponding to a cost function J_ml  = 65760, the minimization (7) leads to a cost function J_ml  = 308 in 50 000 iterations. This number of iterations might appear quite large at first sight, but the computational cost is very modest as each iteration only requires two cost function evaluations (each of these evaluations involves five model simulations corresponding to the five experimental batches used in this identification phase). On the other hand, standard centred finite difference approximations would require 56 cost function evaluations per iteration!

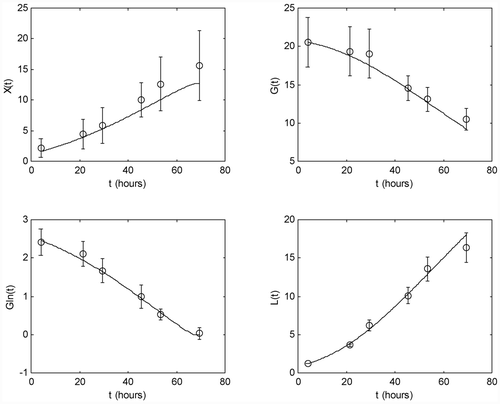
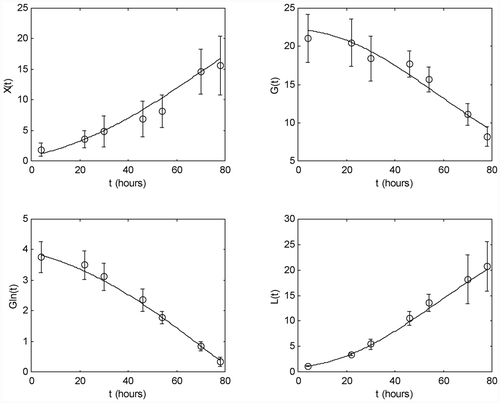
The parameter estimates are listed in table 1. Figure 1 compares the measurement data of one of the five experiments used in the parameter identification procedure with the model prediction (direct validation), whereas figure 2 shows the same kind of comparison with the measurement data of one of the remaining two experiments (cross-validation). In these graphs, the circled points are the measured data and the bars represent the 99% confidence intervals. The solid lines are the concentration trajectories predicted by the identified model.

Figure 1. Direct validation.

Figure 2. Cross-validation.

Table 1. Parameter estimates.

α g  = 0.0892	α m  = 0.0341
γ g,X  = 0.4609	γ m,X  = 1.1395
γ g,Gln = 0.1728	γ m,G  = 0.0822
β g,G  = 0.0089	β m,X  = 0.0980

These figures demonstrate the excellent model agreement.

4 Conclusion

The simultaneous perturbation approach developed by Spall 1,2 is a very powerful technique, which allows an approximation of the gradient of the objective function to be computed by effecting simultaneous random perturbations in all the parameters. Therefore, this approach is particularly well-suited to problems involving a relatively large number of design parameters. In this study, a first-order SP algorithm is described and applied to the maximum-likelihood estimation of the kinetic parameters and initial conditions of a bioprocess model from experimental measurements of a few macroscopic components. These applications, as well as previous studies by the authors 7, demonstrate the usefulness of the proposed SP-algorithm.

Acknowledgements

The authors are very grateful to Professor J. Wérenne (Université Libre de Bruxelles, Departement of Animal Cell Biotechnology) and Mr M. Cherlet for providing them with the measurement data relating to the CHO-animal cell cultures.