Linear differential-algebraic equations with properly stated leading term: A-critical points

Abstract

Time-domain models of dynamical systems are formulated in many applications in terms of differential-algebraic equations (DAEs). In the linear time-varying context, certain limitations of models of the form E(t)x′(t) + B(t)x(t) = q(t) have recently led to the properly stated formulation A(t)(D(t)x(t))′ + B(t)x(t) = q(t), which allows for explicit descriptions of problem solutions in regular DAEs with arbitrary index, and provides precise functional input-output characterizations of the system. In this context, the present paper addresses critical points of linear DAEs with properly stated leading term; such critical points describe different types of singularities in the system. Critical points are classified according to a taxonomy which reflects the phenomenon from which the singularity stems; this taxonomy is proved independent of projectors and also invariant under linear time-varying coordinate changes and refactorizations. Under certain working assumptions, the analysis of such critical problems can be carried out through a scalarly implicit decoupling, yielding a singular inherent ODE. Certain harmless problems for which this decoupling can be rewritten in explicit form are characterized. Some electrical circuit applications, including a linear time-varying analogue of Chua's circuit, are discussed for illustrative purposes.

Keywords:

• Chua's circuit
• Critical point
• Differential-algebraic equation
• Index
• Semi-state model
• Singular ODE

AMS Subject Classifications:

• 34A09
• 34A30
• 94C05

1. Introduction

In different engineering and applied science contexts, dynamical system models often take the form of a differential-algebraic equation (DAE) 1-4. As discussed below, the dynamical behaviour of regular DAEs (see section 2.2) can be eventually described in terms of an ordinary differential equation (ODE): from this point of view, the main differences between ODEs and DAEs arise therefore from the modelling and computational perspectives. In non-regular contexts, new dynamical phenomena can be displayed and DAE models are essential to capture this singular behaviour; these singularities typically preclude the existence of a global state space (ODE) model of the system. In particular, in circuit applications DAEs are nowadays pervasive, and modern simulation programs such as SPICE or TITAN set up circuit equations in differential-algebraic form 5-15. DAEs are encountered very often also in mechanics, controls, power system theory, chemical processes, etc., sometimes under other names such as descriptor, generalized, constrained or semi-state systems 1,3,16.

In a linear time-varying setting, DAE models are often set up in the form

with continuous (in t) matrix coefficients E(t), F(t) ∈ L(ℝ ^m ), E(t) being typically a singular matrix for all t. This formulation, however, presents several known drawbacks, specially when input-output functional characterizations and inverse models of the system are sought, in adjoint formulations, and also from a numerical point of view 17-19.

Therefore, recent attention has been driven to models taking the form

where the matrix coefficients A(t) ∈ L(ℝ ⁿ , ℝ ^m ), D(t) ∈ L(ℝ ^m , ℝ ⁿ ), B(t) ∈ L(ℝ ^m ) depend continuously on t. The leading term in (2) is intended to capture the components of x which actually need to be differentiated, arises in this form in different circuit and control applications, including adjoint formulations, and yields several interesting analytical and numerical properties. Background in this regard is given in section 2.1; more details can be found in 17,18,20-24.

Note that the form (2) comprises standard-form linear DAEs (1) if there exists a C ¹ basis for ker E(t) since, letting P(t) be a C ¹ projector along ker E(t), we may rewrite (1) as E(t)(P(t)x(t))′ + [F(t) − E(t)P′(t)]x(t) = q(t). Note that such a basis exists in particular if E(t) is C ¹ with constant rank. Therefore, all the results apply to linear DAEs in the classical formulation (1).

In this context, the present paper addresses singular or critical points of linear DAEs of the form (2), the results being applicable to (1) via the above-mentioned reformulation. Critical points may reflect different singular phenomena arising in the system, including impasse behaviour, bifurcations, voltage collapse in power system models, unboundedness of solutions, etc. (see 4 and the bibliography therein). But, beyond some particular structures, a complete analysis characterizing critical points in time-varying DAE models has not been developed so far; such a general analysis is allowed by the proper formulation (2).

Roughly speaking, critical points of linear DAEs are sometimes defined in terms of the non-existence or non-uniqueness of solutions at those points. This is the case for instance in 25, where a definition of a critical point is provided for analytic problems relying upon the impossibility to continue a given solution. In the present paper we face critical points from a different point of view, described below.

Most approaches to the analysis of DAEs 1,2,4,22,26-29 are based on an iterative or recursive definition of an index, and end up with some kind of related (underlying/inherent/reduced, etc.) ODE. The index definition usually implies that this ODE is regular, and all initial value problems are uniquely solvable. But, sometimes, although the analysis procedure can be completed, it ends up with a non-solvable (or a non-uniquely solvable) ODE. In linear cases, non-solvable continuous problems are related to singularities and, in the analytic setting, can be tackled via Fuchs – Frobenius theory. These singularities arise typically in the last step of the analysis procedure, and drive the problem to the setting of singular ODEs.

But we look at the somewhat pathological behaviour not from the ODE perspective but from the DAE viewpoint. Hence, broadly speaking, critical points will be those where the DAE analysis procedure cannot be pursued beyond a certain step; formally, a point will be called critical if no neighbourhood of t _* admits an index or, equivalently, there is no regularity interval including t _*. Instances of these phenomena, beyond the above-mentioned last-step singularities, are rank-changing points of identically singular, non-analytic matrix functions A(t) in (2) or E(t) in (1). Note that previous approaches 4,25,29 do not detail to what extent these critical points can be handled. If the analysis procedure can be adapted in order to accommodate these critical points, then it would typically end up with a singular ODE, although some (informally called harmless) cases may result in a non-singular (hence solvable) linear ODE. In contrast, in the most involved cases there is simply no way to obtain such an ODE.

From this point of view, we show in this paper how to adapt the projector-based analysis of linear DAEs introduced in 22-24 in order to accommodate critical points. We work with mild smoothness assumptions, driving the results beyond the analytic setting of 25,29. Our approach extends the results of 30 for index-1 DAEs in standard form, and is directly based on the work on regular points 19. Background in this direction is compiled in section 2.2.

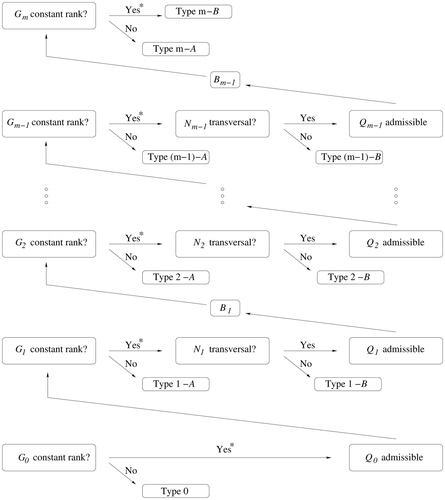
Critical points will be classified in section 3 according to a taxonomy which reflects the phenomenon from which the singularity stems. To emphasize that critical points arise at a well-defined step we use the notions of a nice at level k DAE, and admissible up to level k projector sequences. As shown in Theorem 3.3 in section 3.1, the different types of critical points are independent of projectors and invariant with respect to rescaling and linear, time-dependent coordinate changes. In addition, Theorem 3.5 shows that for sufficiently smooth (C ^m−1) problems, all critical points fall in the types A and B defined in the above-mentioned taxonomy. Several examples in section 3.2 illustrate these notions.

Section 4 focuses on A-critical points; in section 4.1, we discuss working assumptions which, allowing to relax constant rank conditions, still make it possible to construct a chain of continuous matrix functions which particularizes to a tractability chain at regular points. The main result in this section is Theorem 4.3 in section 4.2, which proves that, under these working assumptions, the dynamical behaviour of the DAE can be unveiled through a decoupling based on a scalarly implicit inherent ODE. Again, this is made possible by the proper formulation (2). Our working scenario allows for a uniform over singularities treatment, in problems which include non-isolated critical cases beyond the analytic setting of 25,29. The above-mentioned harmless phenomenon is then discussed in section 4.3. Type-B critical points are in the scope of future work.

Finally, this framework is applied in section 5 to the analysis of critical points of the linear, time-varying analogue of Chua's circuit with current-controlled resistors introduced in 19.

2 Background

2.1 Modelling semi-state systems via DAEs with properly stated leading term

DAEs have been the focus of increasing interest in the last decades as models for dynamical systems. The differential-algebraic nature stems from the wish to capture explicitly algebraic (non-differential) constraints, or may arise in more subtle ways, as discussed below 1,3,4. A classical, rather general model in this context is the quasilinear one

where A ∈ C^k (ℝ ⁿ⁺¹, ℝ ^n×n ), b ∈ C^k (ℝ ⁿ⁺¹, ℝ ⁿ ), A(x, t) being typically singular with constant rank. If in particular A has the block-diagonal structure diag(I, 0), we are led to the semi-explicit form

where an explicit algebraic constraint is given in (4b). On the other hand, in a linear time-varying (LTV) setting, (3) amounts to (1).

In the last few years, the more general model

has been introduced in order to overcome some difficulties met in the setting of (3). In (5), the leading term A(x, t)(d(x, t))′ is properly stated in a sense detailed in 17,18,31; the special form of this leading term was introduced following symmetry demands in adjoint problems, and attempts to capture the components of the semi-state vector x which need to be differentiated. It arises in this form in different fields (including circuit theory and control), as detailed below; additionally it provides several numerical advantages, and the formulation may be extended to abstract DAEs and linear partial differential-algebraic equations (PDAEs): see 14,17,18,20-24,31 and references therein. In the LTV context, this model amounts to (2), and the meaning of a properly stated leading term is detailed for this setting in section 2.2 below.

Note that linear time-varying systems of the form (1) and (2) arise often as linearizations of (3) and (5), respectively, along trajectories. In particular, the stability properties of periodic trajectories of non-linear DAEs of the form (3) are examined in 32,33 via an extension of Floquet theory to periodic linear DAEs in the context defined by (1). In the same direction, an application to the study of non-linear oscillations in electrical circuits using models of the form (2) and (5) can be found in 34.

In the following paragraphs, the advantages of (5) and (2) over (3) and (1), respectively, are discussed via applications in circuit theory, adjoint formulations relevant in control engineering, and also in terms of input-output system characterizations; the latter, together with the discussion carried out in section 2.2, clarifies in particular the relation between the modelling approach underlying the proper formulation and the functional characterization of problem solutions.

Circuit theory

Semi-state or differential-algebraic models are nowadays pervasive in circuit simulation programs. On the one hand, a global state-space (ODE) description of a non-linear circuit may not exist in the presence of singularities. On the other hand, allowing certain redundancy between model variables is crucial in order to set up automatically circuit equations: even if a global state equation exists for a non-linear circuit, its formulation can be simply impossible to obtain via a computer program, in contrast to what happens with semi-state models such as those arising in Modified Nodal Analysis (MNA) used in SPICE or TITAN 5-8,13-15,31. In the DAE context, the formulation of a state equation can be seen as a reduction problem for semi-state systems 12; it is also important to distinguish between hypotheses allowing for the derivation of such a state-space equation and conditions arising in qualitative analyses of circuit dynamics 11.

MNA models take the form

Here, A_R (resp. A_L , A_C , A_V , A_I ) describes the incidence between resistive (resp. inductive, capacitive, voltage source, current source) branches and nodes in the circuit. The vector e stands for node voltages; i _l , i_v represent currents in inductors and voltage sources, respectively, and i_s (t), v_s (t) denote currents and voltages in the (independent) sources. Capacitors, resistors, and inductors characteristics are , , and φ = ϕ(i _l , t), respectively.

Note that system (6) has the properly stated form (5). Only if the characteristics ψ, γ, and φ are smooth (what is not realistic in many real problems) it is possible to rewrite the system in the form (3) via incremental capacitance, conductance, and inductance matrices. Such a rewriting presents additional drawbacks from both numerical and analytical points of view: see 20,21 and the input-output discussion below, respectively.

The circuit models (17) and (30) below are LTV instances of (6). As detailed later, critical points in these models will reflect certain pathological circuit configurations depicted at given time instants. Note finally that also distributed systems have been recently framed in the context of PDAEs: see 6,13,14 and the bibliography therein.

Adjoint formulations

Adjoint systems 35 play an important role both in ODE theory and also in optimal control and engineering applications (see 36 as a sample). The extension of adjoint formulations to the DAE context in the setting of (1) finds, however, a fundamental drawback, given by the fact that the adjoint form −(E ^T(t)y)′ + F ^T(t)y = p(t) does not fall in the framework of (1). In contrast, the adjoint of (2) is −D ^T(t)(A ^T(t)y)′ + B ^T(t)y = p(t) and has the same structure as (2). This symmetry provides additional advantages regarding fundamental matrix solutions, Lagrange identities, indices and solvability. Details and also optimal control applications can be found in 17,37,38 and references therein.

Input-output semi-state system formulations and inverse models

As discussed in this paragraph, the properly stated leading term in (2) is also relevant in providing precise input-output functional descriptions of semi-state systems, and also in the formulation of inverse models: the latter in turn has applications within control theory 39.

In the form (1), if E is the identity and F is continuous, a linear explicit ODE results, and C ⁰ excitations q are well-known to be mapped bijectively onto C ¹ solutions x: the system behaves as an input-output smoothing operator. An initial condition x(t ₀) = x ₀ yields a bijection between the C ⁰ space of excitations q and the space {x ∈ C ¹: x(t ₀) = x ₀}. An inverse ODE model results, mapping x onto q via x → q = x′ + Fx

Now, addressing DAEs in the classical form (1) under an index-1 assumption, solutions x cannot be guaranteed to be C ¹ if the excitation q is just C ⁰ (see e.g. 19,30). Forcing q, E, F to be C ¹ is not of great help, since the solution will not be C ², and in a hypothetical inverse model mapping x ∈ C ¹ to q = Ex′ + Fx, q will not be in general C ¹. This shows that Cⁱ spaces and the formulation (1) are not the right ones to frame DAEs from an input-output functional perspective. In contrast, a continuous excitation q can be proved (see section 2.2) to yield a solution for the formulation (2) under an index-1 assumption within the space As detailed in 19, a bijection and an inverse model x → q = A(Dx)′ + Bx can be then precisely defined. The extension to higher index cases follows from the explicit problem solution depicted in (12), allowed by the specific form of (2).

2.2 Regular points

We compile below a summary of the results of 19 needed for our present discussion. The analysis will be focused on DAEs of the form (2); the DAE is said to be properly stated on a given interval if the coefficients A and D satisfy the transversality condition

for and both subspaces are C ¹, i.e. they have constant dimension and are spanned by C ¹ basis functions. Let R(t) denote the C ¹ projector function defined by im R(t) = im D(t), ker R(t) = ker A(t), .

Define

If the leading term is properly stated, then G ₀ has constant rank r ₀ on , and the DAE is said to be nice at level zero. Writing N ₀ := ker G ₀, let P ₀ be any continuous projector along N ₀, and take Q ₀ := I − P ₀. Such a projector is said to be admissible. Denote as D ⁻(t) the continuous in t generalized inverse of D(t) uniquely defined on by the four conditions

Now, for i ≥ 1 let

Denoting N_i  = ker G_i , we then check whether:

1. G_i has constant rank r_i on ;

2. (N ₀⊕ · · · ⊕N _i−1) ∩ N_i  = {0} on .

If condition (a) is met, we may choose a continuous projector P_i along N_i  = ker G_i , and write Q_i  = I − P_i . Since Q_i is a projector onto N_i , in virtue of (b) P_i (resp. Q_i ) can be chosen in a way such that N ₀⊕ · · · ⊕N _i−1 ⫅ ker Q_i , what is equivalent to the condition

• (b′)Q_iQ_j  = 0, for all 0 ≤ j < i and all .

A sequence Q ₀, Q ₁, …, Q_i (or, respectively, P ₀, P₁ , …, P_i ) satisfying requirements (a) and (b′) is called preadmissible up to level i; if such a sequence exists then the DAE is said to be algebraically nice up to level i. Adding the smoothness requirement

• (c) ,

define

A preadmissible sequence Q ₀, Q ₁, …, Q_i (or, respectively, P ₀, P ₁, …, P_i ) satisfying additionally condition (c) is called admissible up to level i; if such a sequence exists then the DAE is said to be nice up to level i, and this notion can be proved independent of the actual choice of admissible sequences [19, Corollary 1].

The procedure is then pursued by defining G _i+1, etc., If both A and D are invertible on , then system (2) is said to be regular with tractability index zero (on ); otherwise, the DAE (2) is said to be regular with tractability index μ ∈ ℕ on if there exists an admissible projector sequence Q ₀, …, Q _μ−1, and r _μ−1 < r _μ  = m. The latter identity can be rephrased as the non-singularity of G _μ on .

In virtue of the proper statement of the DAE, solutions of a regular system with arbitrarily high index can be computed explicitly in the original setting of the problem, in contrast to other approaches 27,29. Indeed, regular index μ DAE decouples into a system of the form 19,23:

where u = DP ₀ ⋯ P _μ−1 x, v ₀ = Q ₀ x, v_i  = P ₀ ⋯ P _i−1 Q_ix, i = 1, …, μ − 1, and solutions have the form

the component u coming from the inherent ODE (12a) in the invariant space im DP ₀ · · · P _μ−1. The coefficients , , , can be explicitly computed in terms of the admissible sequence Q ₀, · · · , Q _μ−1 19,23.

Now, a point is called regular if there exists an open interval , with , such that the DAE is regular on . It is shown in 19 that this notion yields a well-defined, maximal, projector-independent family of pairwise-disjoint regularity intervals, each one with a well-defined index μ _i . We denote as the open set of regular points.

The analysis of critical points, where the above regularity notion fails and the solution description (12) is not feasible, is the goal of the present work. We will restrict the analysis of critical points to sufficiently smooth problems, for which the conditions that may fail at every step are just (a) or (b): see Definition 3.2 and Theorem 3.5. The attention will be later focused on situations in which it is the constant rank condition (a) the one that fails, leading to the analysis of A-critical points carried out in section 4.

3 Critical points

Critical points have not been fully analysed in the context of standard-form linear DAEs (1): previous works 4,25,29 do not detail how the techniques presented there can accommodate critical points in non-analytic settings. Within the tractability index framework, some results for index-1 systems of the form (1) can be found in 30; however, the ability to handle problems with arbitrary index provided by the proper formulation (2) opens a way for the general discussion of critical points presented below.

3.1 Classification

Definition 3.1

Assume that the DAE (2) has continuous coefficients A(t), D(t), B(t). A point t _*is said to be critical if there is no regularity interval comprising it.

We will suppose the DAE coefficients to be smooth enough to avoid critical points arising from the failing of condition (c) on page 297; sufficient conditions for this will be given in Theorem 3.5. Our interest is directed to critical points corresponding to failures of the used algebraic constant-rank and transversality conditions, as acknowledged in Definition 3.2. Theorem 3.3 will prove that these notions are actually independent of the (admissible up to level k − 1) choice of projectors.

A continuous matrix function , an interval, has a rank drop at , if each neighbourhood of t _* contains points where the rank is different from rk G(t _*). Then, t _* is called a rank-change or rank-drop point of G.

Definition 3.2

Given the DAE (2) with continuous coefficients, will be said to be a critical point of

1. type 0 if G ₀ has a rank drop at t _*;

2. type k‐A, k ≥ 1, if there exists a neighbourhood of t _* where the DAE is nice up to level k − 1, but G_k has a rank drop at t _* for some (hence any) admissible sequence Q ₀, …, Q _k−1;

3. type k‐B, k ≥ 1, if there exists a neighbourhood of t _* where the DAE is nice up to level k − 1 and G_k has constant rank for some (hence any) admissible sequence Q ₀, …, Q _k−1, but the intersection N_k (t _*) ∩ {N ₀(t _*) ⊕ ⋯ ⊕N _k−1(t _*)} is non-trivial, for these (hence any other) projectors and G_k .

We will often speak of level-k critical points to refer either to type k‐A or type k‐B. A critical point is of type A or B if it has type k‐A or k‐B with arbitrary k; the terms A-critical and B-critical will also be used for critical points of types A and B, respectively.

A critical point of the DAE (2) is isolated if there is a neighbourhood of t _* such that all points different from t _* are regular. By definition, an isolated critical point t _* of type (k + 1) is the border of two regularity intervals, say and , , . The characteristic values r ₀, …, r_k apply to both intervals since there is a sequence Q ₀, …, Q_k that is admissible on . In case of a type (k + 1)-B critical point, G _k+1 has uniform rank r _k+1 on and . However, there may be different further characteristics μ⁻, , and μ⁺, on resp. . In case of a type (k + 1)-A critical point, there are possibly different characteristic values , , too.

Critical points of type 0, that is, rank drops in G ₀, may be caused by rank drops in A or D, or in both, but also by failures of the transversality condition (7) for ker A and im D. At those points, D ⁻, R and P ₀ are no longer continuous; however, they may have continuous extensions through the critical point. We will focus our interest on cases in which P ₀ has a continuous extension.

The taxonomy of critical points presented in Definition 3.3 should be required to be independent of projectors and invariant under linear time-varying coordinate changes x(t) = K(t)y(t) and premultiplication by a continuous matrix function L(t). This is indeed the case, as proved below.

Theorem 3.3

The definitions of critical points of types k-A and k-B are independent of the (admissible) choice of projectors.

Additionally, if t_* be a critical point of type k-A or k-B, 1 ≤ k ≤ m, or of type 0, for the DAE (2), then t_* is a critical point of the same type for the rescaled, transformed DAE

with non-singular L(t), , Ã(t) = L(t)A(t), [Dtilde](t) = D(t)K(t), [Btilde](t) = L(t)B(t)K(t).

Proof

Concerning the first assertion, let Q ₀, …, Q _k−1, and , k ≥ 1, be admissible (up to level k − 1) projector sequences on a given subinterval , and denote as G_i , the corresponding matrices constructed from these sequences. The fact that the notion of a critical point of type k‐A is independent of the choice of the admissible sequence follows from the identity . The latter in turn is due to the identity , with a non-singular factor defined recursively for i ≤ k as , for certain Z_ij [25, Th. 2.3]. Therefore, rank changes occur exactly at the same points for both matrices G_k and and the result for A-critical points is proved.

Regarding type k‐B critical points, we use the identity to check that . This leads to the identity for all i ≤ k−1, owing to the form of Z_i , since and, conversely, The direct sum is supported here on the admissibility (up to level k − 1) of the projector sequences.

Additionally, from the identity and the expression defining Z_k , we derive analogously and, conversely, We then get and, therefore, Type-B critical points are defined by the case in which this dimension is no longer zero and this occurs simultaneously for both projector sequences Q ₀, …, Q _k-1, and

The second assertion follows from the construction of the projectors [Qtilde]_i  = K ⁻¹ Q_iK 23 for (14), which results in the identities [Gtilde]_i  = LG_iK. The rank of G_i is therefore transferred to [Gtilde]_i and type 0 and type-A singularities are hence invariant. Additionally, Ñ_i  = ker [Gtilde]_i  = K ⁻¹ N_i , so that the loss of transversality in the N_i spaces defining type-B singularities is also transferred to Ñ_i .

From the proof of Theorem 3.3 above we immediately get the following result.

Corollary 3.4

With every critical point of type k we may associate a characteristic critical value in an invariant manner, namely:

1. rk G_k (t _*) for those of type A;

2. dim (N ₀ ⊕ ⋯ ⊕ N _k−1) ∩ N_k (t _*) for those of type B.

Furthermore, if t _* is an isolated k‐A critical point, and r_k  = rk G_k (t) is constant in some punctured neighbourhood , then we may speak properly of the rank deficiency at t _*, which is also independent of projectors.

In sufficiently smooth cases, the only critical points are those of types A and B, as proved below. This means that the types introduced in Definition 3.2 capture the different critical behaviour that can be displayed in linear DAEs with sufficiently smooth coefficients.

Theorem 3.5

Assume that the coefficients A(t), D(t), B(t) in the DAE (2) are C ^m−1. Then every critical point is of type k-A or k-B, with 1 ≤ k ≤ m, or of type 0.

Proof

Note that, if the DAE is algebraically nice at a given level k ≤ m − 1, then the smoothness requirement (iv) in [19 Definition 5] can be satisfied. This is due to the fact that, in the matrix chain construction, supposed the DAE to be algebraically nice at level 0, we can take Q ₀ in the class C ^m−1, so that G ₁ = G ₀ + BQ ₀ is also C ^m−1. If neither type 1-A nor type 1-B singularities are met, then we may choose a preadmissible Q ₁ in C ^m−1, so that Q ₁ will actually be admissible. Then B ₁ and so G ₂ will be in the class C ^m−2.

If no critical points are displayed in subsequent levels, we can continue the sequence in an admissible manner up to G _m−1, Q _m−1 in C ¹, so that continuous B _m−1 and G_m can be constructed. Now, if G_m is singular and has constant rank (so that regular points with index m and critical points of type m‐A are also ruled out), then (N ₀ ⊕ · · · ⊕ N _m−1) ∩ N_m  = ℝ ^m  ∩ N_m  = N_m  ≠ {0} and a critical point of type m‐B is met.

This means that, for sufficiently smooth (meaning in this context C ^m−1) DAEs, there will be no difficulties in the particular smoothness requirement (c) on page 297. In this situation, a DAE will be nice at a given level if and only if it is algebraically nice at the same level, and if a preadmissible sequence up to a given level exists, then an admissible one exists at the same level. This is implicit in the classification of critical points depicted in figure 1.

Figure 1 The smooth G-building and critical points in ℝ ^m . Note: Yes* means constant rank < m. Meeting the maximal rank m at some level k yields a regular index-k point.

3.2 Examples

Example 1

As indicated in the Introduction, critical points may well arise in the last step of the chain construction, leading to a singular inherent ODE. This is the case in the present example, where a type 1-A critical point is displayed in an index-1 context. Consider the DAE

which has a properly stated leading term with m = 2, n = 1, ker A = {0}, im D = ℝ, R = 1. The chain construction can be performed up to level k = 1:

with det G ₁ = 1−t, . While all points being not equal to 1 are regular (with index one), t _* = 1 is a critical point of type 1-A, since G ₁ undergoes a rank deficiency there. For t < 1 and t > 1 the solutions of the DAE (15) are given by the expression

where u solves the singular ODE coming from (12a)

Observe that here, for t > 1 and t < 1, the set S ₀(t): = {z ∈ ℝ² : B(t)z ∈ im G ₀(t)} (which comprises the solutions of homogeneous index-1 DAEs) reads

and

as long as t ≠ t _* = 1. Geometrically, the critical phenomenon occurring at t _* = 1 is the loss of transversality of these subspaces, since N ₀(t _*) ∩ S ₀(t _*) has dimension one. The canonical projector onto S ₀ along N ₀

is not well-defined for t = t _* = 1.

The homogeneous inherent ODE (16) with q ₁ = 0, q ₂ = 0 has the solutions u(t) = (t − 1)² u(0). The solutions of the homogeneous DAE (15) with q = 0 are then

which shows that the space of the solution values at t _* = 1 consists of the origin only while, for t ≠ t _*, the space S ₀(t) is filled by solution values. Uniqueness of solutions is lost at t _*.

Example 2

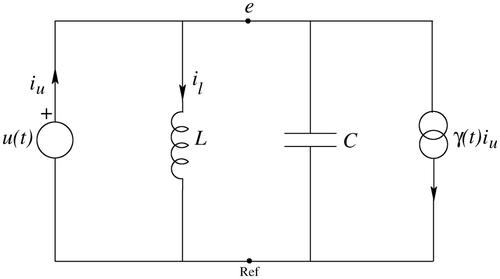
Consider the circuit displayed in figure 2, defined by a parallel connection of an independent voltage source, a capacitor and an inductor which are linear time-invariant, and a time-varying current-controlled current source (CCCS).

Figure 2 A linear time-varying circuit with a current attenuator/amplifier.

Modified Node Analysis (MNA) equations read for this circuit

and this system can be written as a DAE with properly stated leading term letting

The function γ(t) is continuous, and satisfies γ(t) < 1 if t < 0 and γ(t) > 1 if t > 0. At the point t = 0 it is γ(0) = 1 and the behaviour of the CCCS switches from that of an attenuator to one of an amplifier. From an electrical point of view, it is worth emphasizing that the network includes a C‐V loop, and that the controlling current of the CCCS is the one of a voltage source within a C‐V loop, hence falling out of the scope of 5 (see specifically item 4 of table V there).

Write in the sequel α(t) = γ(t) − 1, so that α(t) = 0 iff t = 0. Choose , and , so that results. The matrix G ₁(t) has constant rank r ₁ = 2, and the null space N ₁ = ker G ₁ is continuous. Compute N ₀(t) ∩ N ₁(t) = {z ∈ ℝ³ : z ₁ = 0, z ₂ = 0, α(t)z ₃ = 0}, hence N ₀(t) ∩ N ₁(t) = {0}, for t ≠ 0, N ₀(0) ∩ N ₁(0) = N ₀(0). Therefore, t _* = 0 is a critical point of type 1-B.

On ℝ⁻ and ℝ⁺ we may choose , yielding Q ₁ = Q ₁ P ₀, , , , . It results that G ₂(t) is non-singular except at the critical point t _* = 0, the problem hence being regular with index 2 in ℝ⁻ and ℝ⁺.

The systematic analysis of these B-critical points is the focus of future work.

Example 3

The last example in this section attempts to illustrate that critical points of type A do not necessarily yield a singular inherent ODE. This harmless phenomenon will be discussed in more detail in section 4.3. Consider the DAE

where α is a continuous scalar function, , n = 1, m = 2, D = [0 α], , B = I, . G ₀has constant rank r ₀ = 1 in a neighbourhood of t _*. There we may choose , , has constant rank r ₁ = 1, it holds that N ₀ ∩ N ₁ = {0}, Q ₀ and form an admissible projector sequence, DP ₀ P ₁ D ⁻ = 0, , hence r ₂ = 2, μ = 2. Therefore, all points t _* with α(t _*) ≠ 0 are regular ones.

On regularity intervals the solution of the DAE is given by the expression

where the coefficients are

On intervals where α(t) vanishes identically, we simply have , D = [0 0], , G ₀ = 0, Q ₀ = I, r ₀ = 0, G ₁ = I, r ₁ = 2, μ = 1, that is, the DAE (18) is there regular with index one. Letting Q ₁ = 0, P ₁ = I, G ₂ = G ₁, we find DP ₀ P ₁D ⁻  = 0 and (19), (20) are valid also in this case.

If t _*∈ (−∞, ∞) is such that α(t _*) = 0 but in any neighbourhood of t _* there are points t with α(t) ≠ 0, then t _* is no longer regular but a type 0 critical point. In the particular case

the DAE (18) is regular with index two on (0, ∞) but regular with index one on (−∞, 0). The point t _* = 0 is no longer regular. Here, at t _*, the characteristic numbers r ₀, r ₁ and μ change their value. Nevertheless, DP ₀ P ₁ D ⁻ = 0 and (20) hold true on both intervals (−∞, 0) and (0, ∞) so that all these terms have continuous extensions on (−∞, ∞), and the solution expression (19) holds true on (−∞, ∞).

If we consider (18) with α (t) = t ^k or with α(t) = t ^1/3 instead of (21), formulas (19), (20) result again, and, furthermore, now the characteristics r ₀ = 1, r ₁ = 1, r ₂ = 2, μ = 2 are equal for both (−∞, 0) and (0, ∞). Observe that, in all cases, it holds on regularity intervals that DP ₀ P ₁ D ⁻ = 0, so that there is a trivial smooth extension on the whole interval . Moreover, the function G ₂ can be continuously extended on and the extension remains non-singular.

4 A-critical points

4.1 Working assumptions

Generally speaking, the existence of critical points in precludes the construction of a tractability chain defined on the whole . We figure out in this section working assumptions which make possible a ‘uniform over singularities’ treatment, that is, the construction of a globally defined matrix chain which yields a tractability chain at regular points. These assumptions will allow us to unravel the behaviour through a scalarly implicit inherent ODE, as shown in Theorem 4.3 in section 4.2.

The first assumption defines a setting which includes, in particular, problems with isolated critical points. The latter (and therefore Assumption 1) is satisfied by linear DAEs with analytic coefficients and a non-trivial regular set.

Assumption 1

The set of regular points is dense in .

We restrict further the attention to problems with almost uniform characteristic values, defined by the following working hypothesis. Note that it captures situations in which there are rank changes in some of the G _i -matrices, as long as there exists a smooth extension of the kernels N _i through the critical points (what is again the case for analytic problems 29) and these extensions satisfy a transversality property analogous to (b) – (b′). The latter excludes type-B critical points, as proved in Proposition 4.2.

Assumption 2

There exist continuous projector functions Q ₀, …, Q _m−1 on such that, for 0 ≤ i ≤ m − 1:

1. Q _i is onto ker G _i for all ;

2. Q _i Q _j  = 0 for all , 0 ≤ j < i;

3. DP ₀ ⋯ P _i D ⁻ is continuously differentiable in , and (DP ₀ ⋯ P _i D ⁻)′,

   D ⁻(DP ₀ ⋯ P _i D ⁻)′D have continuous extensions on .

These working assumptions make it possible to define a matrix chain as in the regular setting. But now it accommodates rank deficiencies in some of the G _i matrices at critical points. This critical chain has two important properties, described in Propositions 4.1 and 4.2 below. In particular, Proposition 4.1 follows immediately from the constant rank condition on G_i in implied by the continuity of Q _i and condition (i) in Assumption 2.

Proposition 4.1

Under Assumptions 1 and 2, the DAE has the same characteristic values and, in particular, the same index μ in the whole .

Note that Q _μ  = … = Q _m−1 = 0 and then G _μ  = … = G _m in the whole . Since the projectors Q _i realize the ‘regular’ matrix chain on and are well-defined and continuous on the whole interval, we will say that the DAE is almost uniformly regular with index μ on .

Proposition 4.2

Assumptions 1 and 2 rule out type B critical points on .

Proof

Fix . Assume that the DAE is nice up to level k − 1, for some k ≥ 1, and that rk G _k is constant in some neighbourhood of t _*, so that t _* is not a type k-A critical point, and N_k  = ker G_k has constant dimension around t _*. We need to show that t _* cannot be a type k-B critical point, namely, that N_k (t _*) and N ₀(t _*) ⊕ · · · ⊕ N _k−1(t _*) intersect trivially. From item (ii) in Assumption 2, it follows that im Q _k (t) is transversal to N ₀ (t) ⊕ · · · ⊕ N _k−1(t) for all t in some neighbourhood of t _*; it then suffices to show that im Q _k (t _*) = N _k (t _*). On the one hand, both spaces have the same dimension due to the continuity of Q _k and the constant dimension of N _k ; on the other hand, from the vanishing of the continuous product G _k Q _k in the dense set , it follows that G _k (t _*) Q _k (t _*) = 0, so that im Q _k (t _*) ⫅ ker G _k (t _*) = N _k (t _*). This proves that type k-B critical points are precluded by Assumptions 1 and 2, for 1 ≤ k ≤ m.

We will hence call the matrix chain G _i constructed under Assumptions 1 and 2 an A-critical chain. This provides a setting beyond just μ-A critical points; note that these last step critical points do not put in question the matrix chain construction (and the regular framework could be essentially used), in contrast to the ones in previous levels.

4.2 Decoupling

The importance of Assumptions 1 and 2 above rely on the fact that they allow one to extend a tractability chain through critical points, making it possible to describe the behaviour of the properly stated DAE through a scalarly implicit decoupling which generalizes (12). This extends Theorem 3 of 30, which holds for index-1 problems in the classical form (1).

Theorem 4.3

Let Assumptions 1 and 2 hold. Then,, , is a solution of the DAE (2) if and only if it can be written as

where is a solution of the scalarly implicit ODE

on the locally invariant space im DP ₀ ⋯ P _μ−1, and , i = 1, …, μ − 1, satisfy

Here, ω _μ stands for det G _μ , and is the transposed matrix of cofactors of G _μ . The coefficients , , , are given in the appendix.

Proof

Let be a solution of (2) on some subinterval . Since the identity of the continuous matrix maps AR = A holds in the dense subset , it remains true in the whole . We may then write A = ADD ⁻ in (2). Premultiplying by and using

in the particular case k = 0, we transform (2) into

Now, writing

taking into account the definition of B _i as well as the relations

and premultiplying by DP ₀ ⋯ P _μ−1, we arrive at

which is the scalarly implicit inherent ODE (23) with u = DP ₀ ⋯ P _μ−1 x.

If we multiply (26) by Q _μ−1, then by P ₀ ⋯ P _μ−2 if μ ≥ 2, and in turn by Q ₀ P ₁ ⋯ P _μ−1 and P ₀ ⋯ P _k−1 Q _k P _k+1 ⋯ P _μ−1, we get the relations depicted in (24) for v ₀ = Q ₀ x, v _i = P ₀ ⋯ P _i−1 Q _i x, i = 1, …, μ−1.

The local invariance of the space im DP ₀ ⋯ P _μ−1 owes to the fact that α = (I−DP ₀ ⋯ P _μ−1 D ⁻)u satisfies the homogeneous equation ω _μ [α′ + (DP ₀ ⋯ P _μ−1 D ⁻)′α] = 0 on . Since ω _μ  ≠ 0 on a dense set, it follows that α′ + (DP ₀ ⋯ P _μ−1 D ⁻)′α = 0 on , and therefore a vanishing initial condition for α (in virtue of u = DP ₀ ⋯ P _μ−1 D ⁻ u) yields a trivial solution in the whole .

Conversely, we need to show that, provided that u, v ₀, …, v _μ−1 satisfy (23) – (24) in some subinterval , then x = D ⁻ u + v ₀ + ⋯ + v _μ−1 solves the DAE (2) on . From the smoothness properties of u, v ₀, …, v _μ−1 it follows that , and additionally we know the relation A(Dx)′ + Bx−q = 0 to be satisfied on . Now, A(Dx)′ + Bx − q is continuous and, again by density of , the identity A(Dx)′ + Bx − q = 0 must hold in the whole , showing that x actually solves (2).

Under Assumptions 1 and 2, the behaviour of a DAE with critical points is therefore addressed in terms of the scalarly implicit decoupling (23) – (24). This way, the analysis of a critical DAE is driven to the singular ODE setting; this is analogous to the approach carried out in the reduction approach of Rabier and Rheinboldt 29 and also in the framework of the strangeness index by Ilchmann and Mehrmann 25. Note that in those works the results hold only for analytic problems.

Note, however, that not necessarily ω _μ vanishes at all critical points. This reflects that critical points, defined in terms of the failing of the regularity assumptions in the chain construction, do not exclude cases with unique solvability properties. A well-known example is (29) below. The same phenomenon is acknowledged in the above-mentioned approaches 25,29. A complete formal characterization of these ‘harmless’ critical points is currently an open problem. Proposition 4.4 below provides a result in this direction. An important consequence of this proposition is that this type of harmless critical points cannot follow from rank deficiencies in the leading matrix in almost uniformly index-1 problems such as those of 30. Obviously, a type μ-A critical point will always yield a zero in ω _μ and therefore can never be harmless.

4.3 Harmless A-critical chains

As shown in section 4.2, the behaviour of critical DAEs, under Assumptions 1 and 2, can be unveiled through a scalarly implicit decoupling. The leading coefficient ω _μ will actually vanish iff G _μ is singular. Therefore we might speak of ‘harmless’ critical points t _* in A-critical chains if G _μ (t _*) is non-singular. Obviously, μ-A critical points are never harmless. But this is not always the case for lower level A critical points. Consider the DAE

with the type-0 critical point t _* = 0, and which is regular for t ≠ 0:

The DAE behaves as a regular one, x ₁ = q ₁(t), x ₂ = q ₂(t) − tq′₁(t) being a well-defined (actually unique) solution.

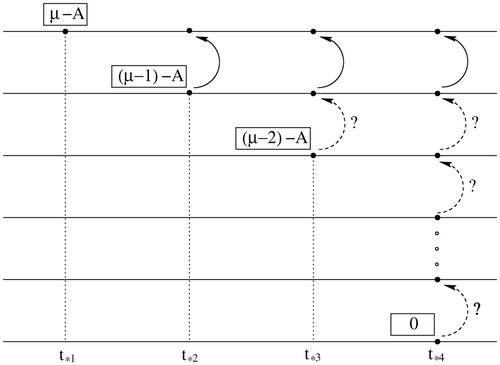
It therefore seems to be an interesting problem to check when type k-A critical points are lifted to the (k + 1)-level or, more generally, how rank deficiencies overlap or accumulate at different levels, for every critical point t _* (see figure 3). A result in this direction follows.

Figure 3 Accumulation or overlapping of rank deficiencies in an A-chain.

Proposition 4.4

Under Assumptions 1 and 2, a type (μ − 1)-A critical point t_* leads to a singular G _μ (t_*).

Proof

Note that the identity G _μ−1 Q _μ−1 = 0 holds in the whole by continuity and due to the fact that it holds in the dense subset . Since G _μ−1 undergoes a rank drop at t _*, and Q _μ−1 has constant rank by assumption, it follows that im Q _μ−1(t _*) is strictly contained in ker G _μ−1(t _*). Equivalently, there exists a non-trivial vector z ∈ ker G _μ−1(t _*) − im Q _μ−1(t _*). Because of this, it is

and

since G _μ (t _*)P _μ−1(t _*)z = G _μ (t _*)z = 0 and Q _μ−1(t _*)P _μ−1(t _*) = 0. This proves that ker G _μ (t _*) includes a non-vanishing vector.

Corollary 4.5

A necessary condition for t_* to be harmless is that G _μ−1 has constant rank in some neighbourhood of t_* .

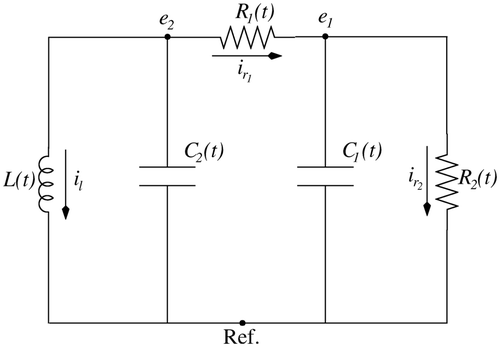
5 Critical points of a linear time-varying Chua circuit

Following 19, we consider the linear time varying analogue of Chua's circuit 40 with current-controlled resistors depicted in figure 4. The framework presented in previous sections will make it possible to classify the critical points arising in the DAE model of this circuit; in particular, the harmless nature of certain type-0 critical points owing to the vanishing of the values of reactances will be discussed in an index-2 context.

Figure 4 Linear time-varying Chua circuit with current-controlled resistors.

Due to the current-control assumption and the eventual vanishing of R ₁(t) and R ₂(t), resistors' currents appear as variables in the Modified Nodal Analysis (MNA) model

This setting precludes the standard state reduction to Chua's equation 40 and drives the problem to the DAE context.

We assume in the sequel that the resistor R ₁ verifies R ₁(t) > 0 for t < 0, and R ₁(t) = 0 for t ≥ 0. This models a persistent short-circuit in the interval [0, ∞); note that the model (30) is valid in the whole real line. Below we consider critical points due to the vanishing of R ₂, C ₁, C ₂ or L in both subintervals.

R ₁(t) > 0. In 19, it is shown that the simultaneous non-vanishing at a given t of R ₁, R ₂, C ₁, C ₂ and L defines t as a regular index-1 point. Assume that the non-vanishing of these values holds true in some open dense subset of ℝ⁻ (where R ₁ > 0), and let us analyse the effect of the vanishing of R ₂, C ₁, C ₂ or L. To this end, write

and

The vanishing of C ₁, C ₂ or L yields a rank-deficiency in D and G ₀, and therefore a critical point of type 0. Nevertheless, under the assumed density of the regular set , we may define there

P ₀, Q ₀ being continuous in the whole ℝ⁻. From the latter, we get

At points where C ₁, C ₂ and L do not vanish, but R ₂ = 0, we have a critical point of type 1‐A, due to the rank deficiency on G ₁. In contrast, at points where all C ₁, C ₂, L and R ₂ are non-zero, the problem is indeed regular with index-1, so that the problem is almost uniformly regular with index-1 in ℝ⁻.

Due to the asserted exclusion of harmless critical points in these almost uniform index-1 problems, the vanishing at a given t of any of the values C ₁, C ₂, L or R ₂ is expected to yield a singularity in the scalarly implicit decoupling of the DAE. This is indeed the case, since the scalarly implicit inherent ODE (23) can be checked to read

R ₁(t) > 0. Let us now consider the behaviour in ℝ⁺ ∪ {0}, where R ₁ does vanish. Assume that the conditions R ₂ ≠ 0, 0 ≠ C ₁ ≠ −C ₂ ≠ 0, L ≠ 0 hold in some dense subset of ℝ⁺, so that the DAE has index-2 there, according to 19. Let us again consider the effect of the vanishing of some of these values at certain points. We assume that no more than one of the values of R ₂, C ₁, C ₂ or L vanishes at a given t.

Looking at (31), the vanishing of C ₁, C ₂ or L yields again a critical point of type 0. Take P ₀ and Q ₀ as in (33), so that

The vanishing of R ₂ yields a rank drop in G ₁ and therefore the zeros of R ₂ define critical points of type 1‐A. But in the light of G ₁ we may get additional conclusions regarding critical points of type 0. When L does vanish, G ₁ undergoes a rank deficiency and, according to Corollary 4.5, critical points owing to the vanishing of L cannot be harmless. In contrast, the vanishing of C ₁ or C ₂ alone does not change rank in G ₁, so that these cases might well yield harmless critical points.

Assuming C ₁ + C ₂ ≠ 0, we may take

It can be checked that neither type-B nor type 2-A critical points are displayed under the condition C ₁ + C ₂ ≠ 0. In this setting, the matrix G ₂ is singular if and only if L = 0 or R ₂ = 0, so that the vanishing of C ₁ or C ₂ alone indeed defines a harmless critical point. The latter cases define non-singular points of the scalarly implicit inherent ODE

Acknowledgements

Research supported by the DFG Forschungszentrum Mathematics for Key Technologies (MATHEON) in Berlin. The second author (corresponding author) acknowledges additional support from Vicerrectorado de Investigación, Universidad Politécnica de Madrid; his work is framed in Projects MTM2004-5316 and MTM2005-3894 of Ministerio de Educación y Ciencia, Spain.

Appendix: The coefficients of (24)

For k = 1, …, μ − 1, j = k + 2, …, μ − 1:

For k = 0, in the top of these expressions, P ₀ ⋯ P _k−1 Q _k has to be replaced by Q ₀.